On the Convergence Rate of Clenshaw–Curtis Quadrature for Jacobi Weight Applied to Functions with Algebraic Endpoint Singularities
Abstract
1. Introduction
2. Numerical Analysis
2.1. The Convergence Rate of Clenshaw–Curtis Quadrature for Jacobi Weights Applied to Functions with Algebraic Endpoint Singularities
2.2. The Convergence Rate of Clenshaw–Curtis Quadrature for Jacobi Weights Applied to Analytic Functions
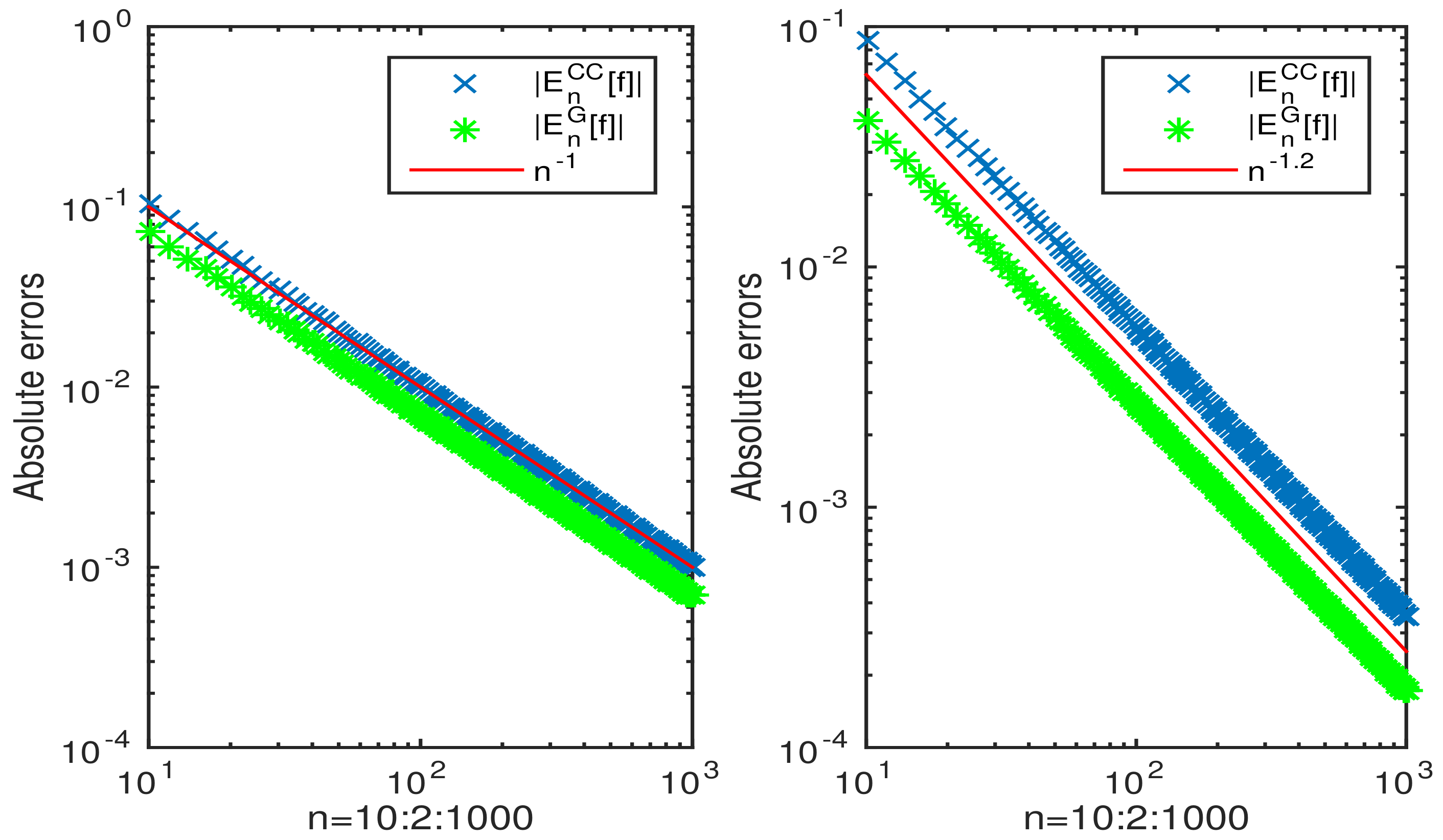
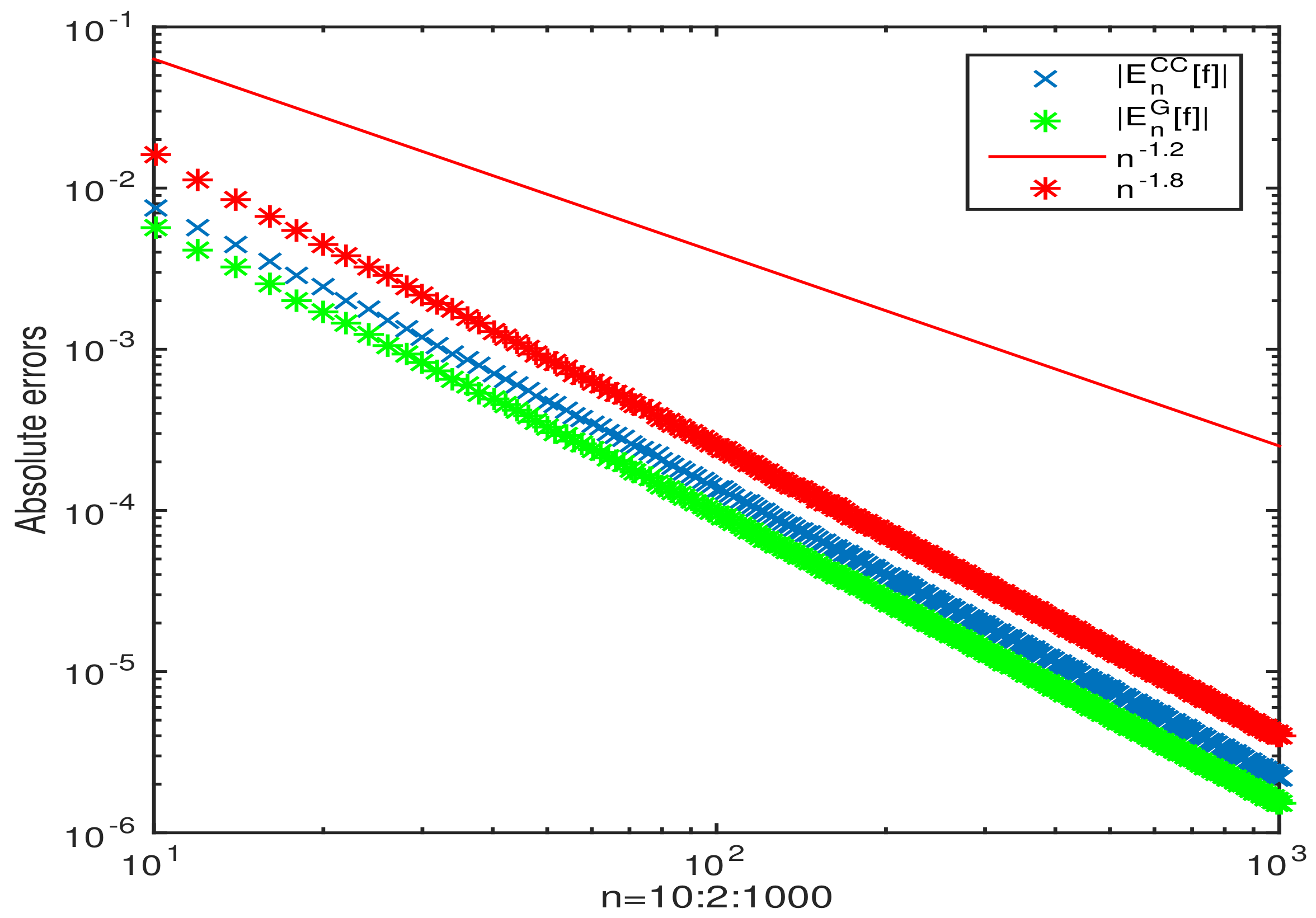
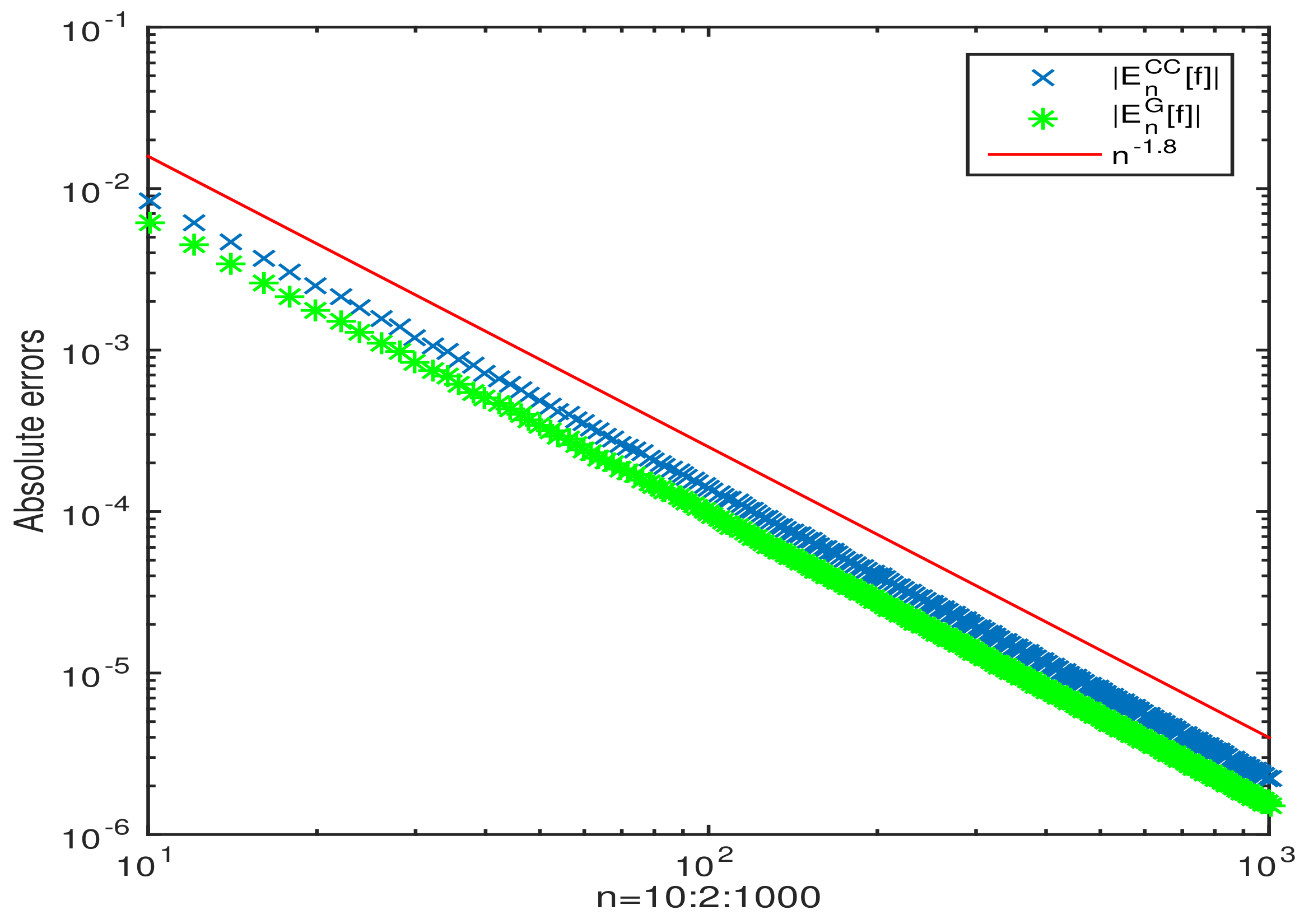
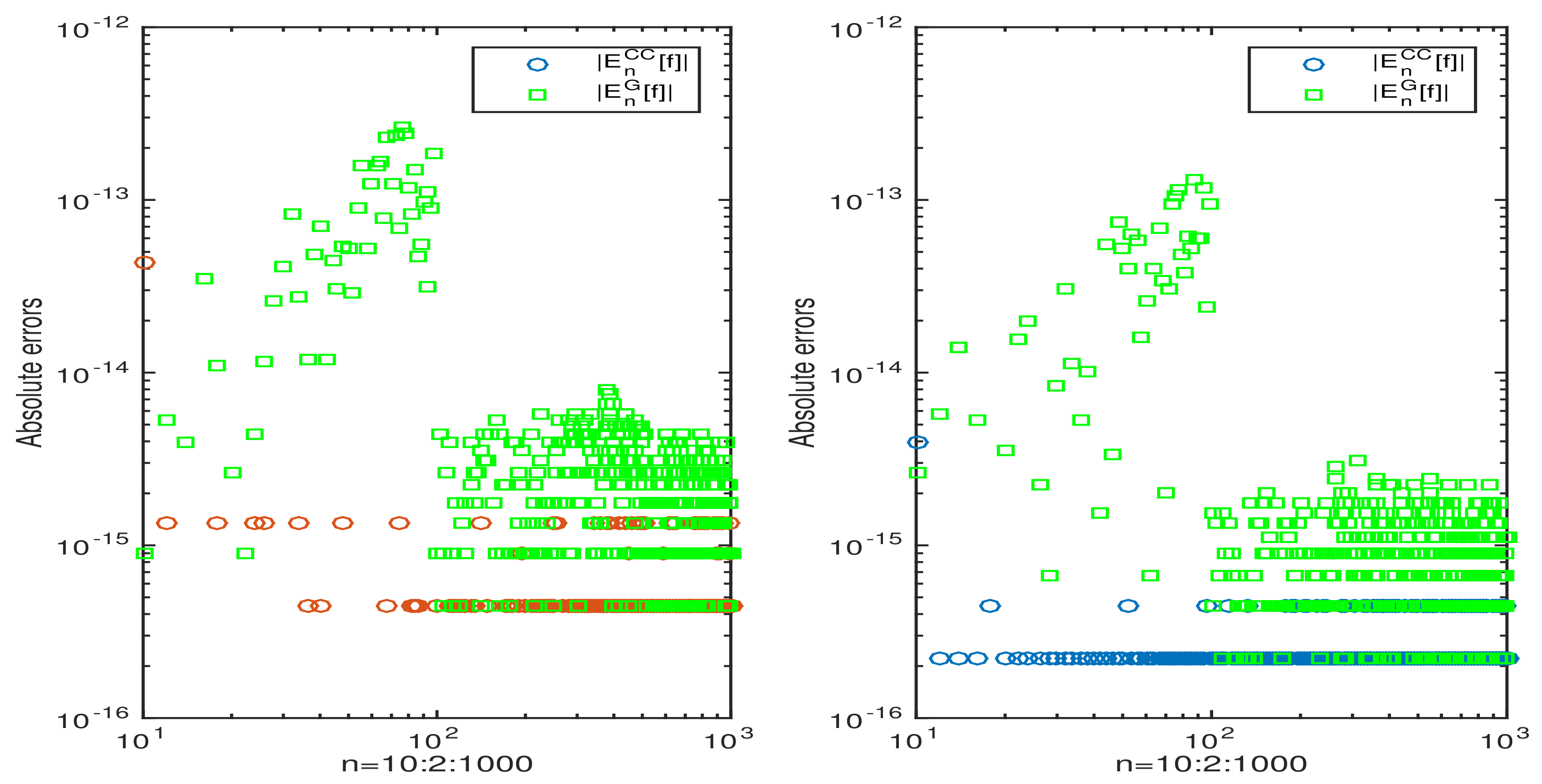
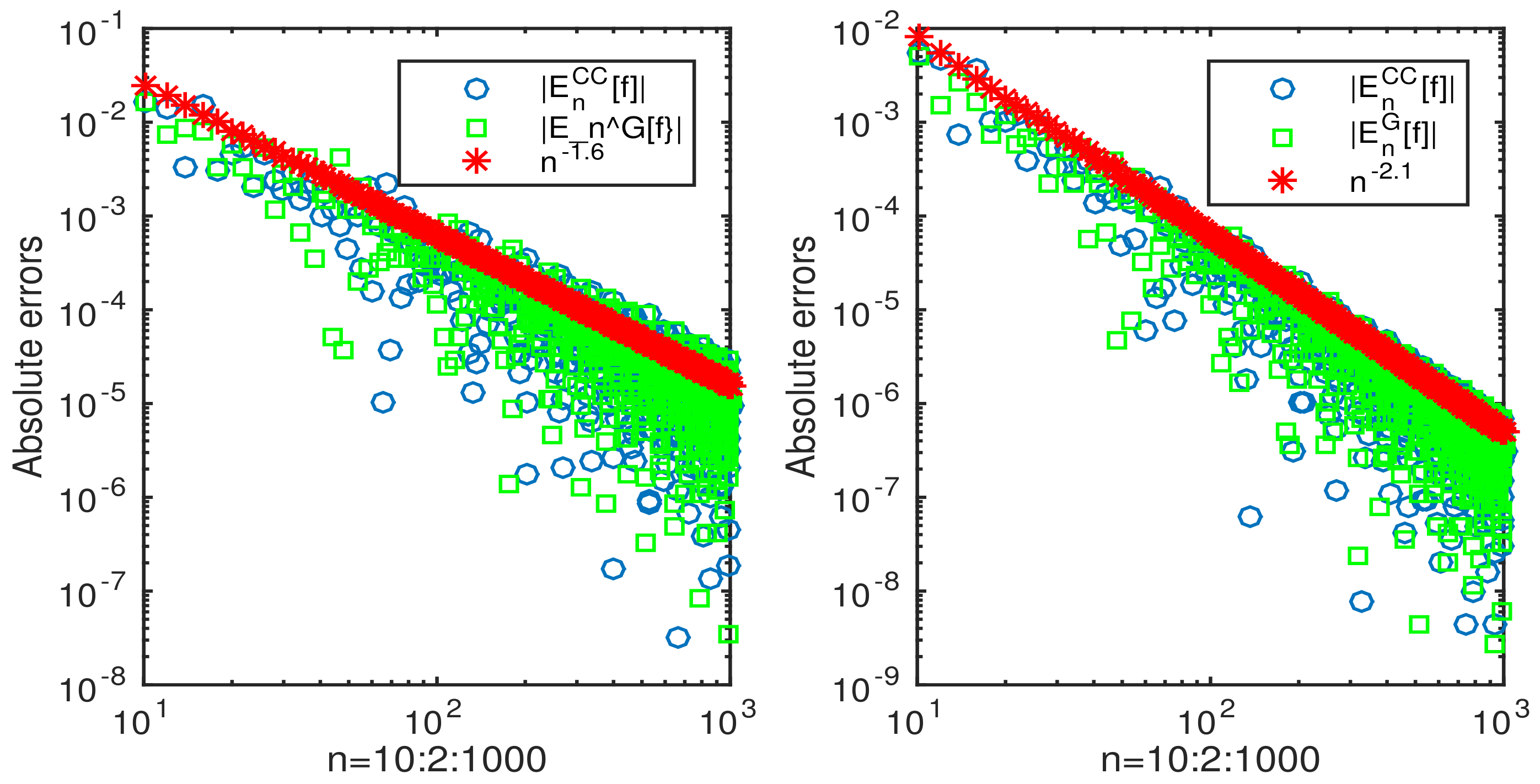
3. Numerical Examples
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Brass, H.; Petras, K. Quadrature Theory: The Theory of Numerical Integration on a Compact Interval; American Mathematical Society: Providence, RI, USA, 2011. [Google Scholar]
- Aimi, A.; Diligenti, M.; Monegato, G. New numerical integration schemes for applications of Galerkin BEM to 2D problems. Int. J. Numer. Methods Eng. 1997, 40, 1977–1999. [Google Scholar] [CrossRef]
- Diligenti, M.; Monegato, G. Integral evaluation in the BEM solution of (hyper)singular integral equations. 2D problems on polygonal domains. J. Comput. Appl. Math. 1997, 81, 29–57. [Google Scholar] [CrossRef]
- Fearwheather, G.; Rizzo, F.J.; Shippy, D.J. Computation of double integrals in the boundary integral equation method. In Advances in Computer Methods for Partial Differential Equations III; Vichnevetsky, R., Stepleman, R.S., Eds.; IMACS: New Brunswick, NJ, USA, 1979; pp. 331–334. [Google Scholar]
- Clenshaw, C.W.; Curtis, A.R. A method for numerical integration on an automatic computer. Numer. Math. 1960, 2, 197–205. [Google Scholar] [CrossRef]
- Gentleman, W.M. Implementing Clenshaw-Curtis quadrature. Commun. ACM 1972, 15, 337–346. [Google Scholar] [CrossRef]
- Waldvogel, J. Fast construction of the Fejér and Clenshaw-Curtis quadrature rules. BIT Numer. Math. 2006, 46, 195–202. [Google Scholar] [CrossRef]
- Driscoll, T.A.; Hale, N.; Trefethen, L.N. Chebfun Guide; Pafnuty Publications: Oxford, UK, 2014. [Google Scholar]
- Trefethen, L.N. Approximation Theory and Approximation Practice; SIAM: Philadelphia, PA, USA, 2013. [Google Scholar]
- Piessens, R. Modified Clenshaw-Curtis integration and applications to numerical computation of integral transforms. In Numerical Integration; Keast, P., Fairweather, G., Eds.; Springer: Dordrecht, The Netherlands, 1987; pp. 35–51. [Google Scholar]
- Piessens, R. Computing integral transforms and solving integral equations using Chebyshev polynomial approximations. J. Comput. Appl. Math. 2000, 121, 113–124. [Google Scholar] [CrossRef]
- Piessens, R.; Branders, M. The evaluation and application of some modified moments. BIT Numer. Math. 1973, 13, 443–450. [Google Scholar] [CrossRef]
- Piessens, R.; Branders, M. On the computation of fourier transforms of singular functions. J. Comput. Appl. Math. 1992, 43, 159–169. [Google Scholar] [CrossRef]
- Chawla, M.M.; Jain, M.K. Asymptotic error estimates for the Gauss quadrature formula. Math. Comp. 1968, 22, 91–97. [Google Scholar] [CrossRef]
- Kzaz, M. Convergence acceleration of some Gaussian quadrature formula for analytic functions. Appl. Numer. Math. 1992, 10, 481–496. [Google Scholar] [CrossRef]
- Lubinsky, D.S.; Rabinowitz, P. Rates of convergence of Gaussian quadrature for singular integrands. Math. Comp. 1984, 43, 219–242. [Google Scholar] [CrossRef]
- Rabinowitz, P. Gaussian integration of functions with branch poitns singularities. Int. J. Comput. Math. 1968, 2, 625–638. [Google Scholar] [CrossRef]
- Rabinowitz, P. Rates of convergence of Gauss, Lobatto and Radau intgeration rules for singular integrands. Math. Comp. 1986, 47, 625–638. [Google Scholar] [CrossRef]
- Sidi, A. Asymptotic expansion of Gausss-Legendre quadrature rules for intgrals with an endpoint singularities. Math. Comp. 2009, 78, 1593–1612. [Google Scholar] [CrossRef][Green Version]
- Sloan, I.H.; Smith, W.E. Product-integration with the Clenshaw-Curtis and related points. Num. Math. 1978, 30, 415–428. [Google Scholar] [CrossRef]
- Verlinden, P. Acceleration of Gauss-Legendre quadrature for an integrand with an endpoint singularity. J. Comput. Appl. Math. 1997, 77, 277–287. [Google Scholar] [CrossRef][Green Version]
- Wang, H. On the convergence rate of Clenshaw-Curtis quadrature for integrals with algebraic endpoint singularities. J. Comput. Appl. Math. 2018, 333, 87–98. [Google Scholar] [CrossRef]
- Xiang, S.; Bornemann, F. On the convergence rates of Gauss and Clenshaw-Curtis quadrature for functions of limited regularity. SIAM J. Numer. Anal. 2012, 50, 2581–2587. [Google Scholar] [CrossRef]
- Trefethen, L.N. Is Gauss quadrature better than Clenshaw-Curtis? SIAM Rev. 2008, 50, 67–87. [Google Scholar] [CrossRef]
- Xiang, S.; He, G.; Wang, H. On fast implementation of Clenshaw-Curtis and Féjer-type quadrature rules. Abstr. Appl. Anal. 2014, 2014, 436164. [Google Scholar] [CrossRef]
- Davis, P.J.; Rabinowitz, P. Methods of Numerical Integration, 2nd ed.; Academic Press: New York, NY, USA, 1984. [Google Scholar]
- Xiang, S.; He, G.; Cho, Y.J. On error bounds of Filon-Clenshaw-Curtis quadrature for highly oscillatory integrals. Adv. Comput. Math. 2015, 41, 573–597. [Google Scholar] [CrossRef]
- Liu, G.; Xiang, S. Clenshaw-Curtis-type quadrature rule for hypersingular integrals with highly oscilltory kernels. Appl. Math. Comput. 2019, 340, 251–267. [Google Scholar]
- Bernstein, S.N. Sur l’ordre de la meilleure approximation des fonctions continues par les polynomes de degré donné. Mem. Cl. Sci. Acad. Roy. Belg. 1912, 4, 1–103. [Google Scholar]
- Trefethen, L.N. Chebfun. Available online: https://www.chebfun.org (accessed on 13 February 2020).
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arama, A.; Xiang, S.; Khan, S. On the Convergence Rate of Clenshaw–Curtis Quadrature for Jacobi Weight Applied to Functions with Algebraic Endpoint Singularities. Symmetry 2020, 12, 716. https://doi.org/10.3390/sym12050716
Arama A, Xiang S, Khan S. On the Convergence Rate of Clenshaw–Curtis Quadrature for Jacobi Weight Applied to Functions with Algebraic Endpoint Singularities. Symmetry. 2020; 12(5):716. https://doi.org/10.3390/sym12050716
Chicago/Turabian StyleArama, Ahlam, Shuhuang Xiang, and Suliman Khan. 2020. "On the Convergence Rate of Clenshaw–Curtis Quadrature for Jacobi Weight Applied to Functions with Algebraic Endpoint Singularities" Symmetry 12, no. 5: 716. https://doi.org/10.3390/sym12050716
APA StyleArama, A., Xiang, S., & Khan, S. (2020). On the Convergence Rate of Clenshaw–Curtis Quadrature for Jacobi Weight Applied to Functions with Algebraic Endpoint Singularities. Symmetry, 12(5), 716. https://doi.org/10.3390/sym12050716




