On the Convergence Rate of Clenshaw–Curtis Quadrature for Jacobi Weight Applied to Functions with Algebraic Endpoint Singularities

Abstract

Applying the aliasing asymptotics on the coefficients of the Chebyshev expansions, the convergence rate of Clenshaw–Curtis quadrature for Jacobi weights is presented for functions with algebraic endpoint singularities. Based upon a new constructed symmetric Jacobi weight, the optimal error bound is derived for this kind of function. In particular, in this case, the Clenshaw–Curtis quadrature for a new constructed Jacobi weight is exponentially convergent. Numerical examples illustrate the theoretical results.

1. Introduction

The computation of the integral of the form

$$I\left[f\right]={\int }_{-1}^{1}w\left(x\right)f\left(x\right)dx,$$

(1)

is one of the oldest and most important topics in numerical analysis [1], where $w\left(x\right)={(1-x)}^{\alpha }{(1+x)}^{\beta }(\alpha >-1,\beta >-1)$ is the Jacobi weight function, $f\left(x\right)={(1-x)}^{\gamma }{(1+x)}^{\delta }\phi \left(x\right)$ ($\gamma >0,\delta >0$) is a function which has singularities at the endpoints, and $\phi \left(x\right)$ is a suitably smooth function in $[-1,1]$. This kind of integrals arise widely in several applications, in particular in the numerical solution of singular and weakly singular integral equations by boundary element methods [2,3,4].

Clenshaw–Curtis quadrature for $I\left[f\right]$ has been extensively studied since Clenshaw and Curtis [5] in 1960, whose formulae is usually derived from polynomial interpolation by a finite sum

$$I_n\left[f\right]=\sum _{k=0}^n{w}_{k}f\left(x_k\right),$$

(2)

based on the Chebyshev points $x_k=cos(k\pi /n)$ $(k=0,1,\dots ,n)$ and the weights $w_k$ which can be computed by sums of trigonometric functions. This rule is exact for the set of polynomials of degree up to n. A fast evaluation of its weights was given by Gentleman [6] and Woldvogel [7]. Its quadrature nodes with the Chebyshev density $\mu \left(x\right)={(1-x^2)}^{-\frac{1}{2}}$ are nested, which makes it a suitable method to achieve fast convergence. Then Clenshaw–Curtis quadrature is widely used for numerical integration [8,9]. For Jacobi weight function, Clenshaw-Curtis quadrature has been extensively studied in a series of papers of Piessens [10,11] and Piessens and Branders [12,13].

During the past few decades, the convergence rates of Gauss–Legendre quadrature for integrals with singularities at one or both endpoints have received considerable attention [14,15,16,17,18,19,20]. It was shown by Verlinden [21] that for the integrand $f\left(x\right)={(1-x)}^{\alpha }g\left(x\right)$ with $Re\left(\alpha \right)>-1$ being not an integer and $g\left(x\right)$ analytic inside a neighborhood of the interval $[-1,1]$, the asymptotic error expansion of the n-point Gauss–Legendre quadrature is $E_n^{GL}\left[f\right]\sim {\displaystyle \sum _{k=1}^{\infty }{a}_k{h}^{\alpha +k}},h={(n+\frac{1}{2})}^{-2}$ and the convergence rate is $O\left(n^{-2\alpha -2}\right)$. Recently, Wang [22] showed that for the integrand $f\left(x\right)={(1-x)}^{\gamma }{(1+x)}^{\delta }g\left(x\right)$ where $\gamma ,\delta >-\frac{1}{2}$ and $g\left(x\right)\in C^{\infty }\left([-1,1]\right)$, the error of an ($n+1$)-point Clenshaw–Curtis quadrature with $w\left(x\right)\equiv 1$ can be expanded as $E_n^{C-C}\left[f\right]\sim {\displaystyle \sum _{k=0}^{\infty }\frac{{\vartheta }_k}{n^{{\lambda }_k}}}$ where ${\vartheta }_k$ are some constants independent of n and ${\left\{{\lambda }_k\right\}}_{k\ge 0}={\displaystyle \bigcup _{k\ge 0,j\ge 0}\{d_k+2j+1\}}$, and the convergence rate is $O\left(n^{-s-2}\right)$, up to one power of n better than that given in Xiang and Bornemann [23] for this special case, where s is defined by

$$s=\left\{\begin{array}{cc}2min\left\{\gamma ,\delta \right\},\hfill & if\gamma ,\delta arenotintegers,\hfill \\ 2\gamma ,\hfill & if\delta isaninteger,\hfill \\ 2\delta ,\hfill & if\gamma isaninteger.\hfill \end{array}\right.$$

Here we study the convergence rate of the Clenshaw-Curtis quadrature rule for $I\left[f\right]$ for functions with algebraic endpoint singularities. We firstly show the convergence rate. From the proof of Theorem 1, it directly follows for general functions of limited regularities. In addition, using the symmetry of a new Jacobi weight with $\widehat{\alpha }=\widehat{\beta }$, it yields the optimal convergence rate. In particular, in the case the function with algebraic endpoint singularities is known $f\left(x\right)={(1-x)}^{\gamma }{(1+x)}^{\delta }g\left(x\right)$ where $\gamma ,\delta >0$, and $g\left(x\right)$ is analytic in Bernstein ellipse including $[-1,1]$, then we will see that the Clenshaw-Curtis quadrature is exponentially convergent from a new constructed Jacobi weight function.

2. Numerical Analysis

The Clenshaw–Curtis quadrature rule for Jacobi weights has been extensively studied in [7,8,9,10]. If a function $f\left(x\right)$ satisfies a Dini-Lipschitz condition on the interval $[-1,1]$, then its Chebyshev series expansion is

$$f\left(x\right)={\displaystyle \sum _{j=0}^{\infty }}{}^{\prime }{a}_j{T}_j\left(x\right),$$

(3)

where $T_j\left(x\right)=cos\left(j{cos}^{-1}x\right)$ is the first kind of Chebyshev polynomial of degree j, and the prime denotes the summation whose first term is halved. The Chebyshev coefficient $a_j$ is defined by

$$a_j=\frac{2}{\pi }{\int }_{-1}^1\frac{f\left(x\right)T_j\left(x\right)}{\sqrt{1-x^2}}dx,j=0,1,\dots$$

(4)

which can be efficiently computed by FFT [24].

The interpolant $P_n\left(x\right)$ of $f\left(x\right)$ at the Clenshaw-Curtis points $x_k=cos(k\pi /n)(k=0,1,\dots ,n)$, is of the form

$$P_n\left(x\right)={\displaystyle \sum _{k=0}^n}{}^{″}{b}_k{T}_k\left(x\right),$$

(5)

Then the Clenshaw–Curtis quadrature is defined by

$$I_n\left[f\right]={\int }_{-1}^{1}w\left(x\right)P_n\left(x\right)dx={\displaystyle \sum _{k=0}^n}{}^{″}{b}_k{M}_j,w\left(x\right)={(1-x)}^{\alpha }{(1+x)}^{\beta },$$

(6)

where

$$M_k(\alpha ,\beta )={\int }_{-1}^{1}w\left(x\right)T_k\left(x\right)dx$$

(7)

are the modified moments. The recurrence formulae for the evaluation of the modified moments are

$$(\beta +\alpha +k+2)M_{k+1}(\alpha ,\beta )+2(\alpha -\beta )M_k(\alpha ,\beta )+(\beta +\alpha -k+2)M_{k-1}(\alpha ,\beta )=0$$

(8)

with

$$M_0(\alpha ,\beta )=2^{\beta +\alpha +1}\frac{\Gamma (\alpha +1)\Gamma (\beta +1)}{\Gamma (\beta +\alpha +2)},M_1(\alpha ,\beta )=2^{\beta +\alpha +1}\frac{\Gamma (\alpha +1)\Gamma (\beta +1)}{\Gamma (\beta +\alpha +2)}\frac{\beta -\alpha }{\beta +\alpha +2}$$

(9)

(see [12]). Furthermore, the asymptotic expression is given by using the asymptotic theory of Fourier coefficients [12] as

$$\begin{array}{ll}& M_k(\alpha ,\beta )\\ \sim & -2^{\beta -\alpha }cos\left(\pi \alpha \right)\Gamma (2\alpha +2)[k^{-2-2\alpha }+O\left(k^{-2\alpha -4}\right)]\\ & +{(-1)}^{k+1}{2}^{\alpha -\beta }cos\left(\pi \beta \right)\Gamma (2\alpha +2)[k^{-2-2\beta }+O\left(k^{-2\beta -4}\right)],k\to \infty .\end{array}$$

(10)

The forward recursion is perfectly numerically stable [12], except in two cases:

$$\begin{array}{ccc}\hfill \alpha >\beta \mathrm{and}\beta & =& -\frac{1}{2},\frac{1}{2},\frac{3}{2},\dots ,\hfill \end{array}$$

(11)

$$\begin{array}{ccc}\hfill \beta >\alpha \mathrm{and}\alpha & =& -\frac{1}{2},\frac{1}{2},\frac{3}{2},\dots .\hfill \end{array}$$

(12)

For these two cases, the modified moments are stably computed by Oliver algorithm in [25] with one starting values and one end value to compute the modified moments. In this paper we consider $\alpha ,\beta >-1$.

Recalling (2.13.1.11) in [26] we know that

$$\left\{\begin{array}{cc}\hfill \frac{b_0-a_0}{2}& =a_{2n}+a_{4n}+a_{6n}+a_{8n}\cdots ,\hfill \\ \hfill b_1-a_1& =a_{2n-1}+a_{2n+1}+a_{4n-1}+a_{4n+1}+\cdots ,\hfill \\ \hfill \cdots \cdots \\ \hfill b_{n-2}-a_{n-2}& =a_{n+2}+a_{3n-2}+a_{3n+2}+a_{5n-2}+\cdots ,\hfill \\ \hfill b_{n-1}-a_{n-1}& =a_{n+1}+a_{3n-1}+a_{3n+1}+a_{5n-1}+\cdots ,\hfill \\ \hfill \frac{b_n}{2}-a_n& =a_{3n}+a_{5n}+a_{7n}+a_{9n}\cdots \hfill \end{array}\right.$$

(13)

which gives

$${\displaystyle \sum _{j=0}^{n-1}{}^{\prime }|b_j-a_j|+|\frac{b_n}{2}-a_n|\le \sum _{j=n+1}^{\infty }|a_j|}.$$

(14)

Lemma 1.

[27,28] Suppose that $\alpha ,\beta >-1$, and $\varphi \in C^{L+1}[a,b]$, then it holds that

$${\int }_a^b{(x-a)}^{\alpha }{(b-x)}^{\beta }{e}^{ikx}\varphi \left(x\right)dx=O\left(k^{-1-min(\alpha ,\beta )}\right),$$

(15)

where $L=\lceil min\{\alpha ,\beta \}\rceil$ and $\lceil z\rceil$ denotes the smallest integer not less than z.

Lemma 2.

[22] For $f\left(x\right)={(1-x)}^{\gamma }{(1+x)}^{\delta }g\left(x\right)$ where $\gamma ,\delta >-\frac{1}{2}$ and $g\left(x\right)\in C^{\infty }\left([-1,1]\right)$, the Chebyshev coefficients of $f\left(x\right)$ is given by

$$a_n=\left\{\begin{array}{cc}{(-1)}^{n+1}\frac{2^{\gamma -\delta +1}g(-1)sin\left(\delta \pi \right)}{\pi n^{2\delta +1}}\Gamma (2\delta +1)+O\left(n^{-min\{2\gamma +1,2\delta +3\}}\right),\hfill & \gamma >\delta \hfill \\ -\frac{2sin\left(\delta \pi \right)sin\left(\delta \pi \right)\Gamma (2\delta +1)}{\pi n^{2\gamma +1}}\left(g\left(1\right)+{(-1)}^{n}g(-1)\right)+O\left(n^{-2\gamma -3}\right),\hfill & \gamma =\delta \hfill \\ -\frac{2^{\delta -\gamma +1}g\left(1\right)sin\left(\gamma \pi \right)}{\pi n^{2\gamma +1}}\Gamma (2\gamma +1)+O\left(n^{-min\{2\gamma +3,2\delta +1\}}\right),\hfill & \gamma <\delta .\hfill \end{array}\right.$$

(16)

Further, if one of γ and δ is an integer, then

$$a_n=\left\{\begin{array}{cc}{(-1)}^{n+1}\frac{2^{\gamma -\delta +1}g(-1)sin\left(\delta \pi \right)}{\pi n^{2\delta +1}}\Gamma (2\delta +1)+O\left(n^{-2\delta -3}\right),\hfill & if \gamma is an integer\hfill \\ -\frac{2^{\delta -\gamma +1}g\left(1\right)sin\left(\gamma \pi \right)}{\pi n^{2\gamma +1}}\Gamma (2\gamma +1)+O\left(n^{-2\gamma -3}\right),\hfill & if \delta is an integer.\hfill \end{array}\right.$$

(17)

2.1. The Convergence Rate of Clenshaw–Curtis Quadrature for Jacobi Weights Applied to Functions with Algebraic Endpoint Singularities

In this Section, based on the decay rate of Chebyshev coefficients and the aliasing errors of integration of Chebyshev polynomials (13), we derive the convergence rate of Clenhshaw–Curtis quadrature for Jacobi weights applied to functions with algebraic endpoint singularities.

Theorem 1.

Let $f\left(x\right)={(1-x)}^{\gamma }{(1+x)}^{\delta }\phi \left(x\right)$ where $\gamma ,\delta >0$, $\phi \left(x\right)\in C^{L+1}[-1,1]$ with $L=\lceil min\{2\gamma ,2\delta \}\rceil$. Then, the convergence rate of n-point Clenshaw-Curtis quadrature rule for the Jacobi weights $w\left(x\right)={(1-x)}^{\alpha }{(1+x)}^{\beta }(\alpha ,\beta >-1)$ is

$$E_n^{CC}\left[f\right]=\left\{\begin{array}{cc}O\left(n^{-2min\{\gamma ,\delta \}-2-2min(\alpha ,\beta \}}\right),\hfill & max\{\alpha ,\beta \}<-\frac{1}{2}\hfill \\ O\left(n^{-2min\{\gamma ,\delta \}-2-2\beta }\right),\hfill & \alpha =-\frac{1}{2},\beta <-\frac{1}{2}\hfill \\ O\left(n^{-2min\{\gamma ,\delta \}-2-2\alpha }\right),\hfill & \alpha <-\frac{1}{2},\beta =-\frac{1}{2}\hfill \\ O\left(n^{-2min\{\gamma ,\delta \}-1}\right),\hfill & min\{\alpha ,\beta \}\ge -\frac{1}{2}.\hfill \end{array}\right.$$

(18)

Proof. 

From

$$f\left(x\right)={(1-x)}^{\gamma }{(1+x)}^{\delta }\phi \left(x\right),$$

it follows

$$\begin{array}{ll}{a}_k& =\frac{2}{\pi }{\int }_{-1}^1\frac{f\left(x\right)T_k\left(x\right)}{\sqrt{1-x^2}}dx\\ & =\frac{2}{\pi }{\int }_0^{\pi }f(cos\left(t\right))cos\left(kt\right)dt\\ & =\frac{2}{\pi }{\int }_0^{\pi }{(1-cost)}^{\gamma }{(1+cost)}^{\delta }\phi (cos\left(t\right))cos\left(kt\right)dt\\ & =\frac{2}{\pi }{\int }_0^{\pi }{2}^{\gamma +\delta }{(sin\frac{t}{2})}^{2\gamma }{(cos\frac{t}{2})}^{2\delta }\phi (cos\left(t\right))cos\left(kt\right)dt\\ & =\frac{2}{\pi }{\int }_0^{\pi }{t}^{2\gamma }{(\pi -t)}^{2\delta }\widehat{\phi }\left(t\right)cos\left(kt\right)dt,\end{array}$$

where

$$\widehat{\phi }(t)=2^{\gamma +\delta }{(t^{-1}sin\frac{t}{2})}^{2\gamma }{({(\pi -t)}^{-1}cos\frac{t}{2})}^{2\delta }\phi (cost).$$

From Lemma 1, we obtain for large k

$$a_k=O(k^{-2min(\gamma ,\delta )-1}).$$

(19)

From (13), we see that

$$\begin{array}{ll}{E}_n^{CC}\left[f\right]& =I\left[f\right]-I_n\left[f\right]={\int }_{-1}^{1}w\left(x\right)(f\left(x\right)-P_n\left(x\right))dx\\ & ={\displaystyle \sum _{j=0}^{n-1}{}^{\prime }(a_j-b_j)M_j+(a_n-\frac{b_n}{2})M_n+\sum _{j=n+1}^{\infty }{a}_j{M}_j}\\ & ={\displaystyle \sum _{j=0}^n{}^{\prime }\sum _{\ell =1}^{\infty }(a_{2\ell n-j}+a_{2\ell n+j})M_j+(a_n-\frac{b_n}{2})M_n+\sum _{j=n+1}^{\infty }{a}_j{M}_j}\end{array}$$

and

$$\begin{array}{ll}{\displaystyle \sum _{\ell =1}^{\infty }(a_{2\ell n-j}+a_{2\ell n+j})}& ={\displaystyle \sum _{\ell =1}^{\infty }\left(O({(2\ell n-j)}^{-2min\{\gamma ,\delta \}-1})+O({(2\ell n+j)}^{-2min\{\gamma ,\delta \}-1})\right)}\\ & =O[{\left(2n\right)}^{-2min\{\gamma ,\delta \}-1}]{\displaystyle \sum _{\ell =1}^{\infty }}\left\{\frac{1}{{(\ell -\frac{j}{2n})}^{2min\{\gamma ,\delta \}+1}}+\frac{1}{{(\ell +\frac{j}{2n})}^{2min\{\gamma ,\delta \}+1}}\right\}\\ & =O\left(n^{-2min\{\gamma ,\delta \}-1}\right),j=0,1,\dots ,n.\end{array}$$

since $2min\{\gamma ,\delta \}+1>1$, which, together with (10), yields

$${\displaystyle \sum _{j=0}^{n-1}}{}^{\prime }(a_j-b_j)M_j=O(n^{-2min\{\gamma ,\delta \}-1})\left\{\sum _{j=1}^n{j}^{-2-2\alpha }+\sum _{j=1}^n{j}^{-2-2\beta }\right\}$$

$$(a_n-\frac{b_n}{2})M_n=O(n^{-2min\{\gamma ,\delta \}-1})\left\{n^{-2-2\alpha }+n^{-2-2\beta }\right\}$$

and

$${\displaystyle \sum _{j=n+1}^{\infty }{a}_j{M}_j=O\left(1\right)\sum _{j=n+1}^{\infty }\left\{j^{-2min(\gamma ,\delta \}-3-2\alpha }+j^{-2min(\gamma ,\delta \}-3-2\beta }\right\}.}$$

Then we have

$$E_n^{CC}\left[f\right]=\left\{\begin{array}{cc}O\left(n^{-2min\{\gamma ,\delta \}-2-2min\{\alpha ,\beta \}}\right),\hfill & max\{\alpha ,\beta \}<-\frac{1}{2}\hfill \\ \left(n^{-2min\{\gamma ,\delta \}-2-2\beta }\right),\hfill & \alpha =-\frac{1}{2},\beta <-\frac{1}{2}\hfill \\ O\left(n^{-2min\{\gamma ,\delta \}-2-2\alpha }\right),\hfill & \alpha <-\frac{1}{2},\beta =-\frac{1}{2}\hfill \\ O\left(n^{-2min\{\gamma ,\delta \}-1}\right)+O\left(n^{-2min\{\gamma ,\delta \}-1}\right),\hfill & min\{\alpha ,\beta \}>-\frac{1}{2}.\hfill \end{array}\right.$$

In the case $\alpha =\beta =-\frac{1}{2}$, it follows $M_k(\alpha ,\beta )={\int }_{-1}^{1}w\left(x\right)T_k\left(x\right)dx=0$ for $k=1,2,\dots$, and $M_0(\alpha ,\beta )=\pi$, then

$$E_n^{CC}\left[f\right]={\displaystyle M_0\sum _{\ell =1}^{\infty }{a}_{2\ell n}=O\left(n^{-2min\{\gamma ,\delta \}-1}\right)}.$$

These together lead to (18). □

Remark 1.

We will see from the numerical examples in Section 3 that in the case $min\{\alpha ,\beta \}<-\frac{1}{2}$ and $min\{\alpha ,\beta \}+min\{\gamma ,\delta \}=min\{\alpha +\gamma ,\beta +\delta \}$, the bound (18) is attainable and then optimal. In other cases, we may define $\widehat{\alpha }=\widehat{\beta }=min\{\alpha ,\beta \}-c$ such that $-1<\widehat{\alpha }=\widehat{\beta }<-\frac{1}{2}$ and the integral can be rewritten as

$$I\left[f\right]={\int }_{-1}^1\widehat{w}\left(x\right){(1-x)}^{\gamma +\alpha -\widehat{\alpha }+c}{(1+x)}^{\delta +\beta -\widehat{\alpha }+c}\phi \left(x\right)dx=:{\int }_{-1}^1\widehat{w}\left(x\right)\widehat{f}\left(x\right)dx,\widehat{w}\left(x\right)={(1-x)}^{\widehat{\alpha }-c}{(1+x)}^{\widehat{\alpha }-c},$$

(20)

and then for the new Jacobi weight function $\widehat{w}\left(x\right)$, from Theorem 1, we get

$$E_n^{CC}\left[\widehat{f}\right]=O(n^{-2min\{\alpha +\gamma ,\beta +\delta \}-2}),$$

which is optimal.

Remark 2.

If $f\left(x\right)={(1-x)}^{\gamma }{(1+x)}^{\delta }\phi \left(x\right)$ where $\gamma ,\delta >-\frac{1}{2}$, and $\phi \left(x\right)\in C^{\infty }[-1,1]$, then the integral can be represented as

$$I\left[f\right]={\int }_{-1}^{1}w\left(x\right)f\left(x\right)dx={\int }_{-1}^1{(1-x)}^{\gamma +\alpha }{(1+x)}^{\delta +\beta }\phi \left(x\right)dx=:{\int }_{-1}^1\tilde{f}\left(x\right)dx$$

then, from Wang [22], if $min\{\gamma +\alpha ,\delta +\beta \}>-\frac{1}{2}$, we see that the Clenhsaw-Curtis quadrature with $\tilde{w}\left(x\right)\equiv 1$ for $\tilde{f}\left(x\right)$ has the convergence rate

$$E_n[\tilde{f}]=O(n^{-2min\{\gamma +\alpha ,\delta +\beta \}-2}).$$

For this case, in Section 2.2 we may construct a new Jacobi weight such that the Clenshaw-Curtis quadrature is exponentially convergent if $\phi \left(x\right)$ is analytic inside a neighborhood of the interval $[-1,1]$.

Let $X^r=\{f:[-1,1]\to \mathcal{R}:a_k\left[f\right]=O\left(k^{-r-1}\right)\}$ ($r>0$) [23]. From the proof of Theorem 1, it directly follows for general functions of limited regularities.

Corollary 1.

Suppose $f\in X^r$ ($r>0$), then the convergence rate of n-point Clenshaw-Curtis quadrature rule for the Jacobi weight $w\left(x\right)={(1-x)}^{\alpha }{(1+x)}^{\beta }(\alpha ,\beta >-1)$ satisfies

$$E_n^{CC}\left[f\right]=\left\{\begin{array}{cc}O\left(n^{-r-2-min\{\alpha ,\beta \}}\right),\hfill & max\{\alpha ,\beta \}<-\frac{1}{2}\hfill \\ O\left(n^{-r-2-2\beta }\right),\hfill & \alpha =-\frac{1}{2},\beta <-\frac{1}{2}\hfill \\ O\left(n^{-r-2-2\alpha }\right),\hfill & \alpha <-\frac{1}{2},\beta =-\frac{1}{2}\hfill \\ O\left(n^{-r-1}\right),\hfill & min\{\alpha ,\beta \}\ge -\frac{1}{2}.\hfill \end{array}\right.$$

(21)

2.2. The Convergence Rate of Clenshaw–Curtis Quadrature for Jacobi Weights Applied to Analytic Functions

Lemma 3.

(Bernstein [29]) If f is analytic with $|f(z)|\le M$ in the region bounded by the ellipse with foci $\pm 1$ and major and minor semiaxis lengths summing to $\rho >1$, then for each $j\ge 0$,

$$|a_j|\le {\displaystyle \frac{2M}{{\rho }^j}}.$$

In the case $f\left(x\right)={(1-x)}^{\gamma }{(1+x)}^{\delta }\phi \left(x\right)$ and $\phi \left(x\right)$ an analytic function, the Clenshaw–Curtis quadrature is exponentially convergent with $\tilde{w}\left(x\right)={(1-x)}^{\gamma +\alpha }{(1+x)}^{\delta +\beta }$.

$$I\left[f\right]={\int }_{-1}^1{(1-x)}^{\alpha }{(1+x)}^{\beta }{(1-x)}^{\gamma }{(1+x)}^{\delta }\phi \left(x\right)dx={\int }_{-1}^1\tilde{w}\left(x\right)\phi \left(x\right)dx.$$

Without loss of generality, for analyzing the convergence rate, assume $\gamma =\delta =0$ and $\alpha$ and $\beta$ instead of $\gamma +\alpha$ and $\delta +\beta$, respectively.

Theorem 2.

If f is analytic with $\left|f\right(z\left)\right|\le M$ in the region bounded by the ellipse with foci $\pm 1$ and major and minor semiaxis lengths summing to $\rho >1$, then

$$E_n^{CC}\left[f\right]=\left\{\begin{array}{cc}{n}^{-1-2min\{\alpha ,\beta \}}O\left({\rho }^{-n}\right),\hfill & max\{\alpha ,\beta \}<-\frac{1}{2}\hfill \\ n^{-1-2\beta }O\left({\rho }^{-n}\right),\hfill & \alpha =-\frac{1}{2},\beta <-\frac{1}{2}\hfill \\ n^{-1-2\alpha }O\left({\rho }^{-n}\right),\hfill & \alpha <-\frac{1}{2},\beta =-\frac{1}{2}\hfill \\ O\left({\rho }^{-n}\right),\hfill & min\{\alpha ,\beta \}\ge -\frac{1}{2}.\hfill \end{array}\right.$$

(22)

Proof. 

From (13) and Lemma 3, we see that

$${\displaystyle \sum _{\ell =1}^{\infty }(a_{2\ell n-j}+a_{2\ell n+j})=O\left({\rho }^{-n}\right),j=0,1,\dots ,n,(a_n-\frac{b_n}{2})=O\left({\rho }^{-n}\right),}$$

then it follows

$${\displaystyle \sum _{j=0}^{n-1}{}^{\prime }(a_j-b_j)M_j=O\left({\rho }^{-n}\right)\left\{\sum _{j=1}^n{j}^{-2-2\alpha }+\sum _{j=1}^n{j}^{-2-2\beta }\right\}}$$

$$(a_n-\frac{b_n}{2})M_n=O({\rho }^{-n})\left\{n^{-2-2\alpha }+n^{-2-2\beta }\right\}$$

and

$${\displaystyle \sum _{j=n+1}^{\infty }{a}_j{M}_j=O\left({\rho }^{-n}\right)\sum _{j=n+1}^{\infty }\left\{j^{-2-2\alpha }+j^{-2-2\beta }\right\},}$$

which leads to

$$E_n^{CC}\left[f\right]=\left\{\begin{array}{cc}{n}^{-1-2\alpha }O\left({\rho }^{-n}\right)+n^{-1-2\beta }O\left({\rho }^{-n}\right),\hfill & max\{\alpha ,\beta \}<-\frac{1}{2}\hfill \\ n^{-1-2\beta }O\left({\rho }^{-n}\right),\hfill & \alpha =-\frac{1}{2},\beta <-\frac{1}{2}\hfill \\ n^{-1-2\alpha }O\left({\rho }^{-n}\right),\hfill & \alpha <-\frac{1}{2},\beta =-\frac{1}{2}\hfill \\ O\left({\rho }^{-n}\right)+O\left({\rho }^{-n}\right),\hfill & min\{\alpha ,\beta \}>-\frac{1}{2}.\hfill \end{array}\right.$$

In the case $\alpha =\beta =-\frac{1}{2}$, it follows $M_k(\alpha ,\beta )={\int }_{-1}^{1}w\left(x\right)T_k\left(x\right)dx=0$ for $k=1,2,\dots$, and $M_0(\alpha ,\beta )=\pi$, then

$$E_n^{CC}\left[f\right]={\displaystyle M_0\sum _{\ell =1}^{\infty }{a}_{2\ell n}=O\left({\rho }^{-2n}\right)}.$$

These together lead to the desired result. □

3. Numerical Examples

In this section, we confirm the convergence rate of Clenshaw–Curtis quadrature for Jacobi weights and compare it with Gauss–Jacobi quadrature All the numerical results are computed in an Apple laptop with 1.6 GHz Intel Core i5 and 4 GB 1600 MHz DDR3.

For the n-point Clenshaw–Curtis quadrature rule (6), the coefficients $b_k$ of the interpolant $P_n\left(x\right)$ is evaluated by FFT, and the moments $M_k$, except in two cases (11) and (12), are computed by the forward recursion (9), which is perfectly numerically stable. For these two cases, the moments $M_k$ are calculated by the Oliver algorithm in [25]. While for the Gauss–Jacobi quadrature, we cite $[x,w]=\mathrm{jacpts}(n,\alpha ,\beta )$ in Chebfun [30], which costs $O\left(n\right)$ operations for n-point Gauss–Jacobi quadrature.

Example 1.

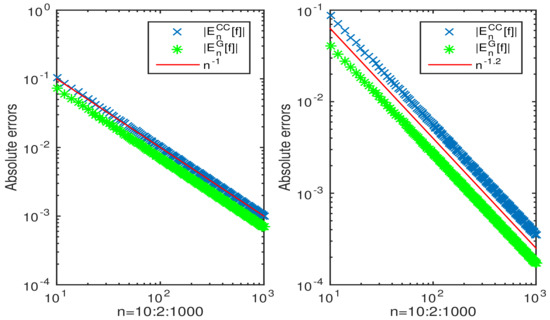
Let us consider

$${\int }_{-1}^1{(1-x)}^{\alpha }{(1+x)}^{\beta }{(1-x)}^{\gamma }{(1+x)}^{\delta }f\left(x\right)dx,$$

(23)

where $\alpha =-0.8$, $\beta =-0.7$, $\gamma =0.3$, $\delta =0.6$ and $f\left(x\right)=cos\left(x\right)$, and $\alpha =0.6$, $\beta =-0.7$, $\gamma =0.6$, $\delta =0.3$ and $f\left(x\right)=e^x$, respectively. Both the case satisfy $min\{\alpha ,\beta \}+min\{\gamma ,\delta \}=min\{\alpha +\gamma ,\beta +\delta \}$. The error bound (18) with $O(n^{-2min\{\alpha ,\beta \}-2min\{\gamma ,\delta \}-2})$ is attainable, which is displayed in Figure 1.

Figure 1. The absolute errors for the n-point Clenshaw–Curtis quadrature rule for integral (23) compared with the absolute errors of Gauss-Jacobi quadrature for $n=10:2:1000$: $\alpha =-0.8$, $\beta =-0.7$, $\gamma =0.3$, $\delta =0.6$ and $f\left(x\right)=cos\left(x\right)$ (left column), and $\alpha =0.6$, $\beta =-0.7$, $\gamma =0.6$, $\delta =0.3$ and $f\left(x\right)=e^x$ (right column), respectively.

Example 2.

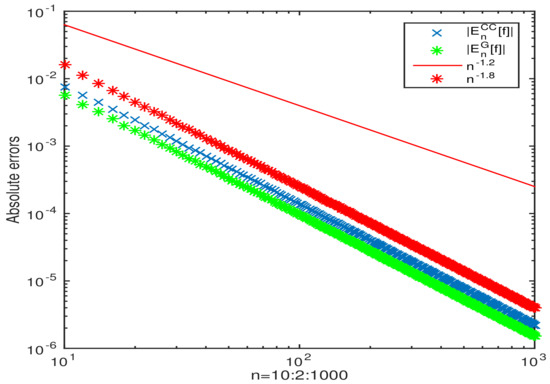
Let us consider

$${\int }_{-1}^1{(1-x)}^{\alpha }{(1+x)}^{\beta }{(1-x)}^{\gamma }{(1+x)}^{\delta }{e}^{x}dx,$$

(24)

where $\alpha =0.6$, $\beta =-0.7$, $\gamma =0.6$, and $\delta =0.3$, is not satisfied $min\{\alpha ,\beta \}+min\{\gamma ,\delta \}=min\{\alpha +\gamma ,\beta +\delta \}$. The numerical example shows the convergence rate is $O(n^{-1.8})$ better than the error bound (18) with $O(n^{-2min\{\alpha ,\beta \}-2min\{\gamma ,\delta \}-2})$ (see Figure 2).

Figure 2. The absolute errors for the n-point Clenshaw–Curtis quadrature rule for integral (24) compared with the absolute errors of Gauss-Jacobi quadrature for $n=10:1000$ $\alpha =0.6$, $\beta =-0.7$, $\gamma =0.3$, $\delta =0.6$ and $f\left(x\right)=e^x$ (right column), respectively.

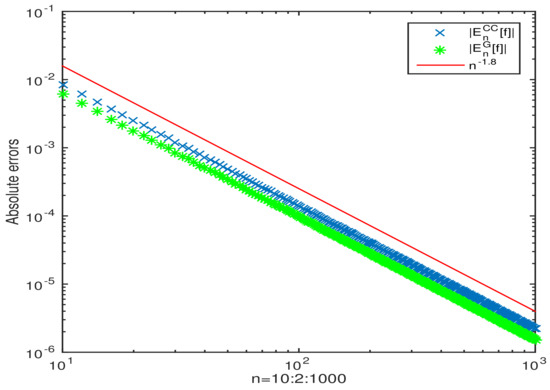
Setting $\widehat{\alpha }=\widehat{\beta }=-0.7$, then the n-point Clenshaw-Curtis quadrature rule with the new Jacobi weight function $\widehat{w}\left(x\right)$ for $\widehat{f}\left(x\right)={(1-x)}^{1.6}{(1+x)}^{0.3}{e}^x$ have the optimal convergence rate $O(n^{-2min\{\widehat{\alpha },\widehat{\beta }\}-2min\{\widehat{\gamma },\widehat{\delta }\}-2})$. The absolute errors are displayed in Figure 3.

Figure 3. The absolute errors for the n-point Clenshaw–Curtis quadrature rule for $I[\widehat{f}]={\int }_{-1}^1\widehat{w}\left(x\right)\widehat{f}\left(x\right)dx$ compared with the absolute errors of Gauss-Jacobi quadrature for $n=10:2:1000$.

Example 3.

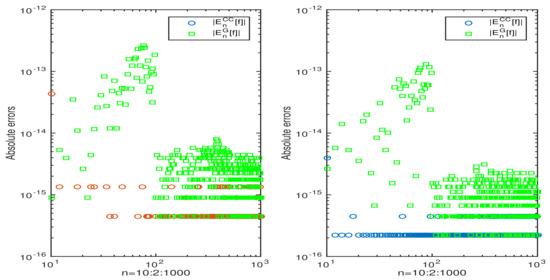
Let us consider

$${\int }_{-1}^1{(1-x)}^{\alpha }{(1+x)}^{\beta }f\left(x\right)dx,$$

(25)

where $\alpha =-0.3$, $\beta =-0.4$ and $f\left(x\right)=e^x$, and $\alpha =0.3$, $\beta =0.4$ and $f\left(x\right)=cos\left(x\right)$, respectively. Figure 4 illustrates the exponential convergence both for the n-point Clenshaw–Curtis quadrature rule and Gauss–Jacobi quadrature.

Figure 4. The absolute errors for the n-point Clenshaw–Curtis quadrature rule for integral (25) compared with the absolute errors of Gauss-Jacobi quadrature for $n=10:2:1000$: $\alpha =-0.3$, $\beta =-0.4$ and $f\left(x\right)=e^x$ (left column), and $\alpha =0.3$, $\beta =0.4$ and $f\left(x\right)=cos\left(x\right)$ (right column), respectively.

Example 4.

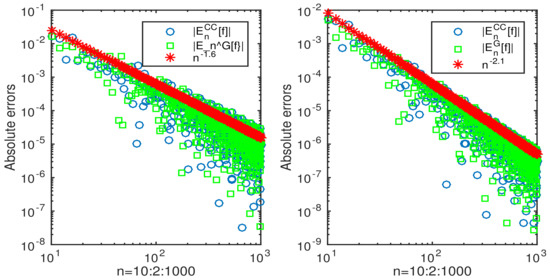
Let us consider

$${\int }_{-1}^1{(1-x)}^{\alpha }{(1+x)}^{\beta }f\left(x\right)dx,$$

(26)

where $\alpha =-0.3$, $\beta =-0.4$ and $f\left(x\right)={|x-0.3|}^{0.6}$, and $\alpha =0.3$, $\beta =0.4$ and $f\left(x\right)={|x-0.3|}^{1.1}$, respectively. For functions of interior singularities, the estimated convergence rate (20) is attainable too (see Figure 5).

Figure 5. The absolute errors for the n-point Clenshaw–Curtis quadrature rule for integral (26) compared with the absolute errors of Gauss–Jacobi quadrature for $n=10:2:1000$: $\alpha =-0.3$, $\beta =-0.4$ and $f\left(x\right)={|x-0.3|}^{0.6}$ (left column), and $\alpha =0.3$, $\beta =0.4$ and $f\left(x\right)={|x-0.3|}^{1.1}$ (right column), respectively.

Both the n-point Clenshaw–Curtis quadrature rule and Gauss–Jacobi quadrature are efficient. For the n-point Clenshaw-Curtis quadrature rule for computing each integral for n = 10:2:1000, the elapsed time totally is 0.333967 s, while the elapsed time totally is 11.982476 s for the Gauss–Jacobi quadrature.

4. Conclusions

In this paper, we have studied the convergence rate of Clenshaw–Curtis quadrature for integrals with Jacobi weights and functions with algebraic endpoint singularities. The decay rate of the Chebyshev coefficients for the integrand multiplied by Jacobi weights is combined with the aliasing errors of the integration of Chebyshev polynomials by Clenshaw–Curtis quadrature.