Frequency-Selective Wallpaper for Indoor Interference Reduction and MIMO Capacity Improvement

Abstract

This paper presents the design and features of frequency-selective wallpaper—based on periodic and symmetric metallic hexagons—intended to be attached to standard walls for filtering out 5 GHz signals (e.g., IEEE 802.11a systems) without blocking other selected radio communication services (e.g., cellular mobile communication signals). It analyzes the characteristics of the radio channel—as found within standard indoor environments—with both regular walls and walls with the proposed frequency-selective wallpaper, examined using a ray-launching program for single-input single-output (SISO) and multiple-input multiple-output (MIMO) systems. This allows the harvesting of parameters, including channel capacity, power delay profile, and signal-to-interference ratio, for proper comparison between the two environments under study: with and without the presented wallpaper. The achieved results clearly show that the use of the proposed frequency-selective wallpaper in an indoor scenario reduces interference levels by an additional attenuation of up to 20 dB in comparison to an unpapered wall. Additionally, with MIMO systems, radio channel characteristics, such as capacity, are improved due to the increase in the magnitude of all singular values of the channel transfer matrix compared to the unpapered wall case, thereby leading to the existence of more relevant subchannels.

1. Introduction

Over the last 10 years, the increase in wireless communication systems has made it necessary to minimize the interference between different systems in the same environment, and to resolve difficulties of capacity caused by strains imposed by user numbers and spectrum availability. Techniques proposed for mitigating these problems have included new antenna designs and advanced signal processing technology. Unfortunately, these measures are frequently complicated and/or costly. An alternative means of addressing this problem in indoor environments would be modification of the physical wave propagation environment by applying frequency-selective (F-S) wallpaper to the walls to block (reflect) unwanted interference while still allowing the desired radio communication services to pass through [1,2,3,4,5,6,7]. Such a strategy can improve the signal-to-interference ratio (SIR) [8,9].

Because F-S wallpapers restrict the frequency signal of the systems that are being blocked to the room where they are located, radio channel characteristics can experience improvement using high-performance systems, e.g., multiple-input multiple-output (MIMO) systems, that usually gain within rich scattering environments and where radio channel capacities are expanded by the quantity of uncorrelated channels and the strength of each [10]. Therefore, this paper, extending the analysis carried out in previous studies where the performance solely of single-input single-output (SISO) systems was examined in indoor environments with F-S surfaces [1,2,3,4,5,6,7,8,9,11], presents the design and features of new F-S wallpaper when both SISO and MIMO systems are considered. The wallpaper—based on periodic and symmetric metallic hexagons—is intended to be attached to standard walls for filtering out 5 GHz signals (e.g., IEEE 802.11a systems) without blocking other selected radio communication services (e.g., cellular mobile communication signals). This way, the presented work analyzes the characteristics of the radio channel—as found within standard indoor environments—with both regular walls and walls with the proposed F-S wallpaper, examined using a ray-launching program. Thus, the capacity for the proposed F-S wallpaper to effect improvements in SIR and to achieve improved radio channel characteristics for MIMO systems is evaluated, while at the same time analyzing the singular values for the channel transfer matrix.

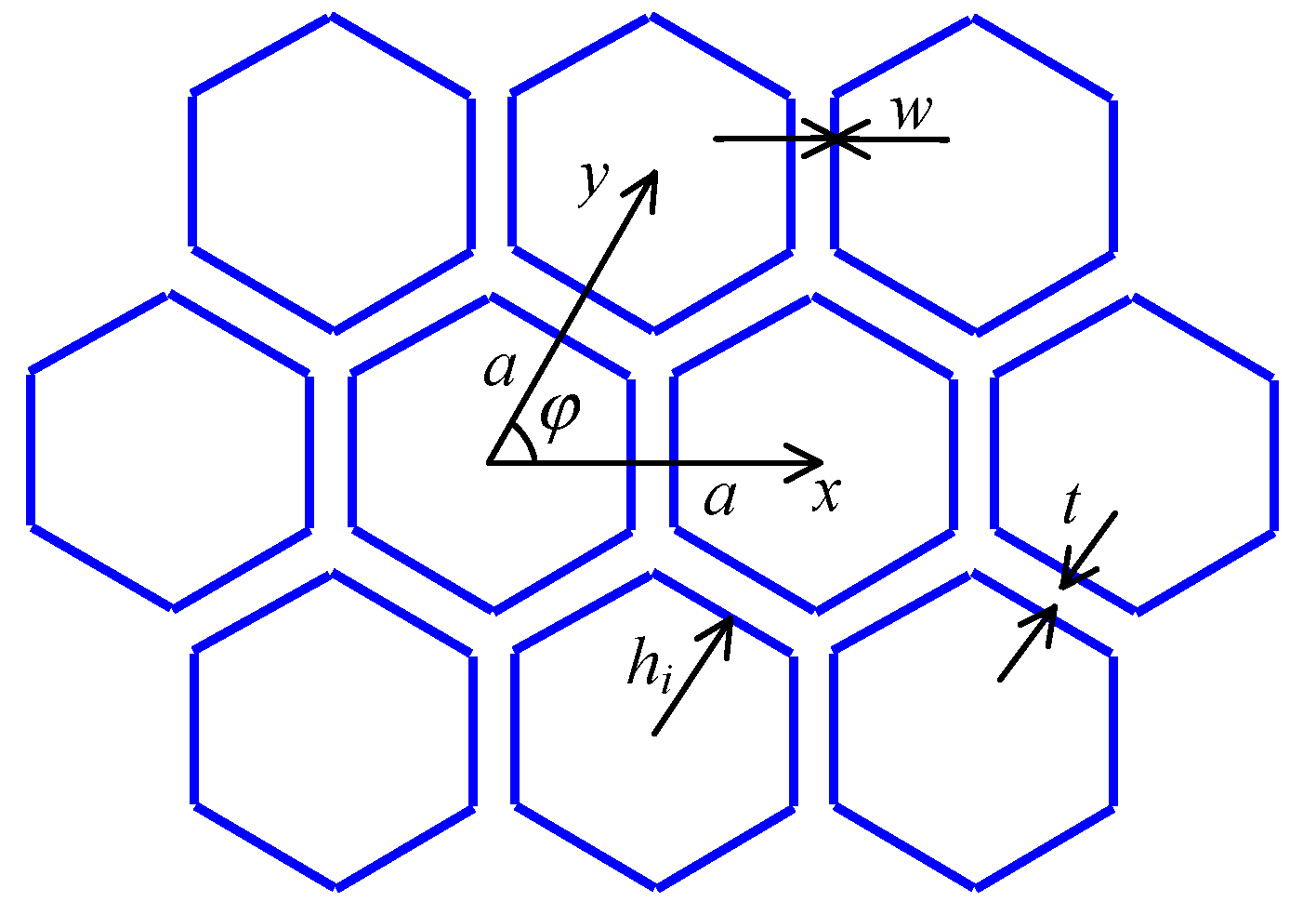
2. Wallpaper Design

2.1. Frequency-Selective Surfaces

Numerous antenna systems for modern fixed and mobile communications services rely on F-S surfaces (FSSs). FSSs effectively comprise array structures consisting of many thin conducting elements, frequently supported by being printed on dielectric substrate. They act as passive electromagnetic filters. Such arrays often act as periodic apertures within the conducting plane. If an FSS comprises a conductor array, reflection occurs at the surface of incident waves for particular frequencies (stop band or reflection band); at other frequencies the service allows these waves to pass through (pass-band or transmission band). With conducting arrays, these resonances occur because of high-induced element currents. This makes the surface act as a metallic sheet at certain resonances. If an aperture array is employed, the majority of the FSS is reflective, exhibiting a pass-band as a resonance resulting from strong fields within apertures [12,13].

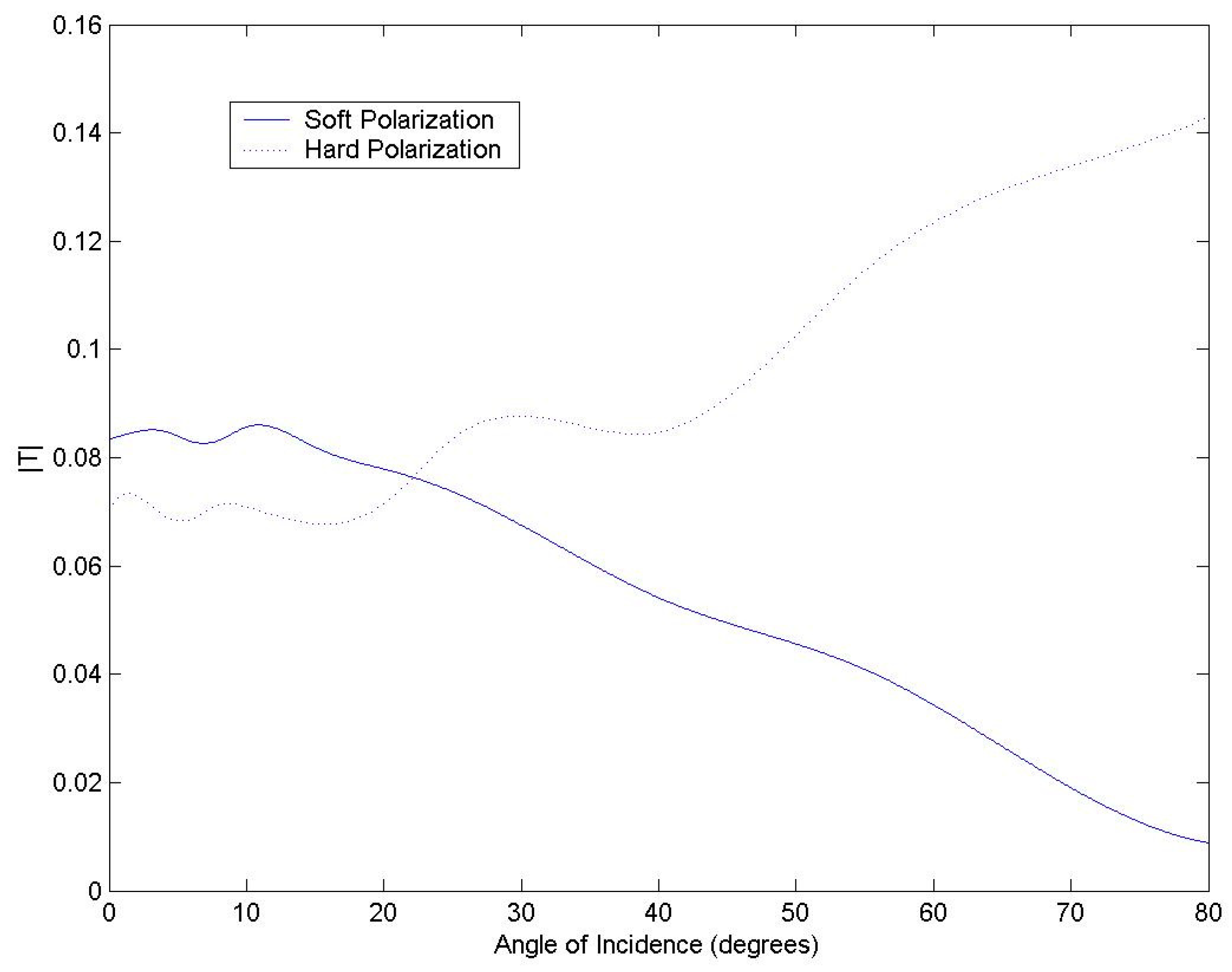
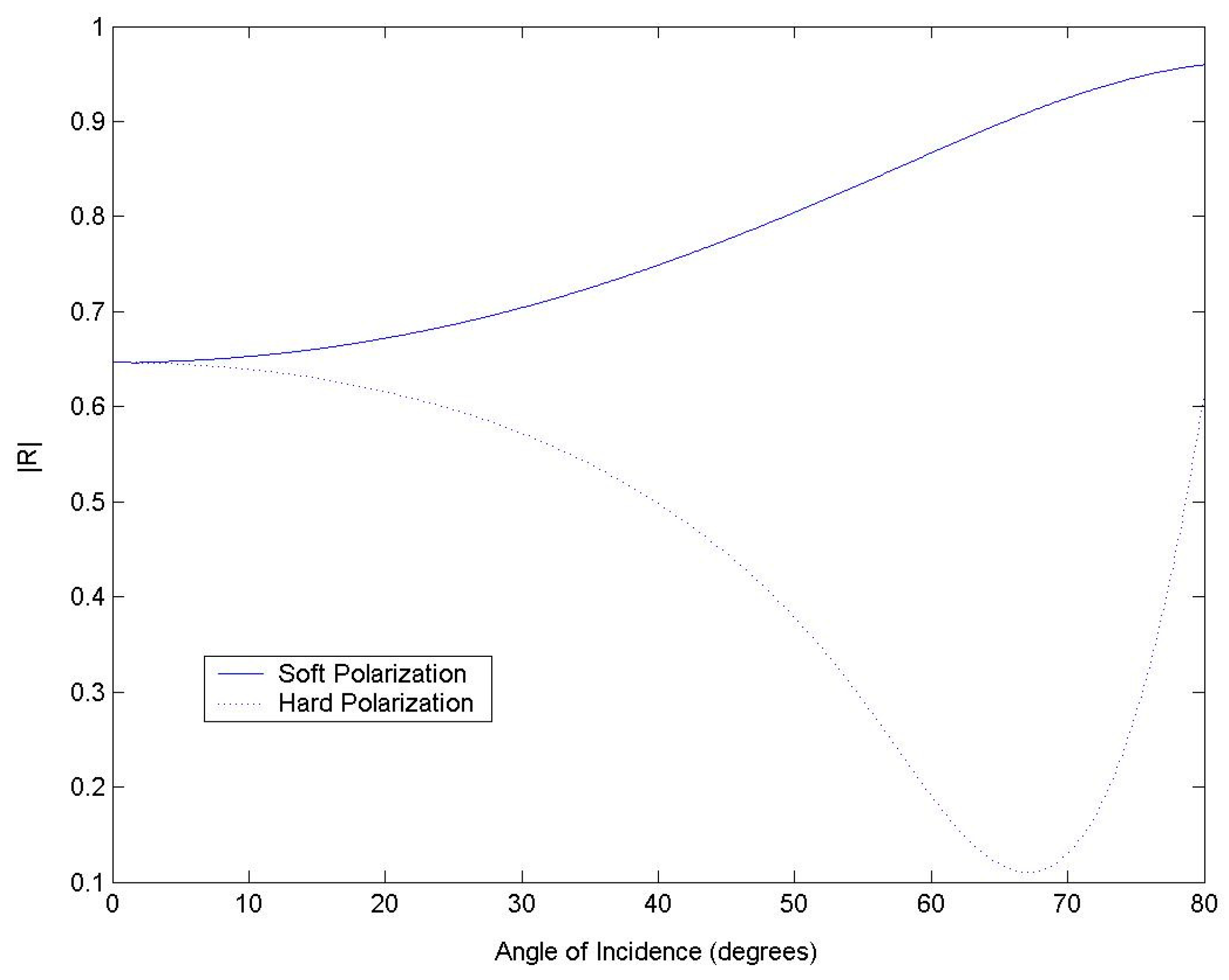
2.2. Wallpaper with Low Transmission at 5 GHz

The wallpaper was designed using the software Periodic Boundary Finite-difference Time-domain (PB-FDTD), centered on unit cell analysis techniques with a baseline numerical technique being the FDTD methodology. This program employs periodic boundary conditions for the reduction of computational volumes to single-unit cells. In the unit cell technique, the number of possible scan angles is a discrete number, which is determined by the number of FDTD cells in the unit cell (it should be noted that the FDTD mesh needs to be periodic). Such a number of possible scan angles increases with the number of FDTD cells. Then, the elements of the array are excited with broadband Gaussian pulses with appropriate time delays to scan the array in the desired direction. This way, the simulation continues until the field at a test point of the FDTD volume has decreased within a specific factor. The main goal of such wallpaper was to block or confine 5 GHz signals (for example IEEE 802.11a systems), while simultaneously permitting wireless services on different frequencies (for example, cellular mobile communication signals) access. For this purpose, we considered the FSS geometry illustrated in Figure 1.

It can be seen that there is a periodic and symmetric pattern of perfectly electric conducting (PEC) metallic hexagons with a representing periodicity on the x and y axes. Moreover, t is the distance between metallic hexagons, w is the width, and h_i is the height. The FSS dimensions were selected using a parameter study that led to these optimal values: w = 0.4 mm, t = 1.3 mm, and a = 11.1 mm.

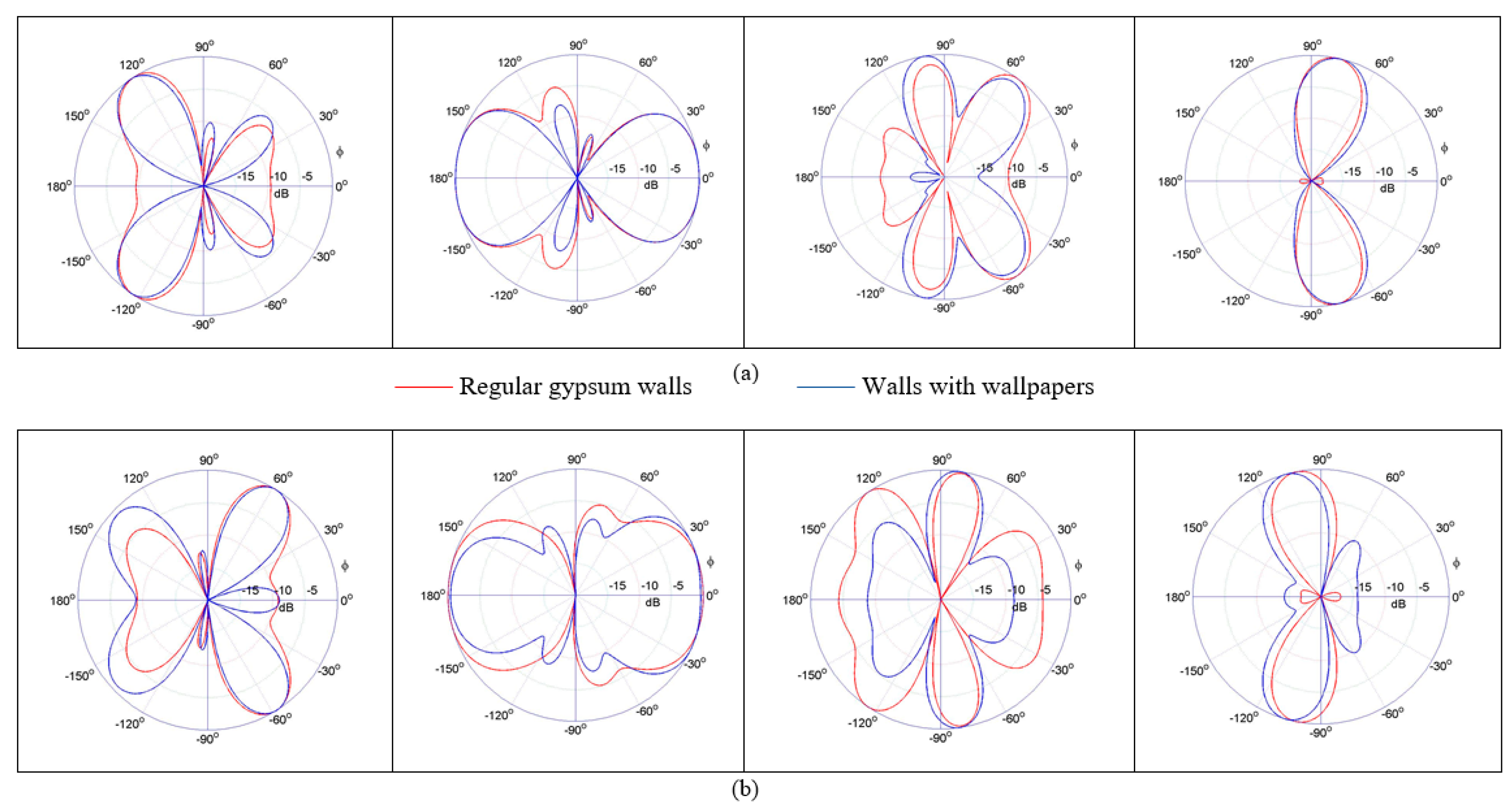
2.2.1. Wallpaper with Gypsum Wall

In this case, for evaluation of the wallpaper’s performance, the simulations employed a structure that consisted of FSS attached to a gypsum wall, as shown in Figure 2. The assumed thickness of the wall was T = 51.5 mm with a relative conductivity of σ = 0.0084 Am⁻² and a permittivity of ε_r = 5.

This F-S wall’s transmission and reflection coefficients, as expressed in [14], are presented in Figure 3 and Figure 4, respectively, in dB, being a function of frequency for a variety of incidence angles, as well as for both soft (horizontal) and hard (vertical) polarizations. It should be noted that, in this work, as indicated in [14], the so-called soft polarization is considered when the electric field is perpendicular to the plane of incidence (defined as the plane formed by a unit vector normal to the reflecting interface and the vector in the direction of incidence). This way, since the electric field is parallel to the interface, it is also known as horizontal. On the other hand, the so-called hard polarization is considered when the electric field is parallel to the plane of incidence. Since, in this case, a component of the electric field is perpendicular to the interface when the magnetic field is parallel to the interface, it is also known as vertical. The incidence angles shown in the plots (θ) correlate with the broadside (BS) direction shown in Figure 2. These plots also illustrate, for comparison purposes, an instance where BS incidence is assumed for the gypsum wall alone without wallpaper.

It may be seen that at 5 GHz an extra transmission attenuation of 20 dB appears for both polarizations in comparison to the wall without wallpaper, as intended. Moreover, with angles of incidence ranging from BS to 69.6°, resonant frequencies vary only by 0.4 GHz. On the other hand, an almost perfect reflection is observed at 5 GHz when considering the F-S wall.

The transmission and reflection coefficients of the gypsum wall with the wallpaper are given in Figure 5 and Figure 6, respectively, as a function of the angle of incidence θ specified in Figure 2, assuming a frequency of 5 GHz, for both soft and hard polarizations. The curves were obtained by interpolating 12 different values corresponding to 12 different angles of incidence—equally spaced along the range from 0° to 80°—through cubic spline data interpolation performed with MATLAB. It can be noted how the good transmission and reflection characteristics for the mentioned frequency remain valid for the entire range of angles considered.

2.2.2. Gypsum Wall Only

For comparison purposes, a similar analysis to that undertaken in the previous subsection for the F-S wall is next performed considering the gypsum wall only (again, T = 51.5 mm, εr = 5, and σ = 0.0084 Am⁻²), as indicated in Figure 7.

Therefore, the corresponding transmission and reflection coefficients are depicted in Figure 8 and Figure 9, respectively, as a function of frequency, for different angles of incidence, and both soft and hard polarizations.

In addition, the transmission and reflection coefficients are depicted as a function of the angle of incidence, considering a frequency of 5 GHz, in Figure 10 and Figure 11, respectively, for both soft and hard polarizations.

It can be noted from Figure 8, Figure 9, Figure 10 and Figure 11 that the transmission through a common gypsum wall is high at 5 GHz compared to the wallpaper case and, moreover, the attenuation in signal strength significantly varies when different angles of incidence are considered.

2.2.3. Wallpaper Attached onto Other Structures

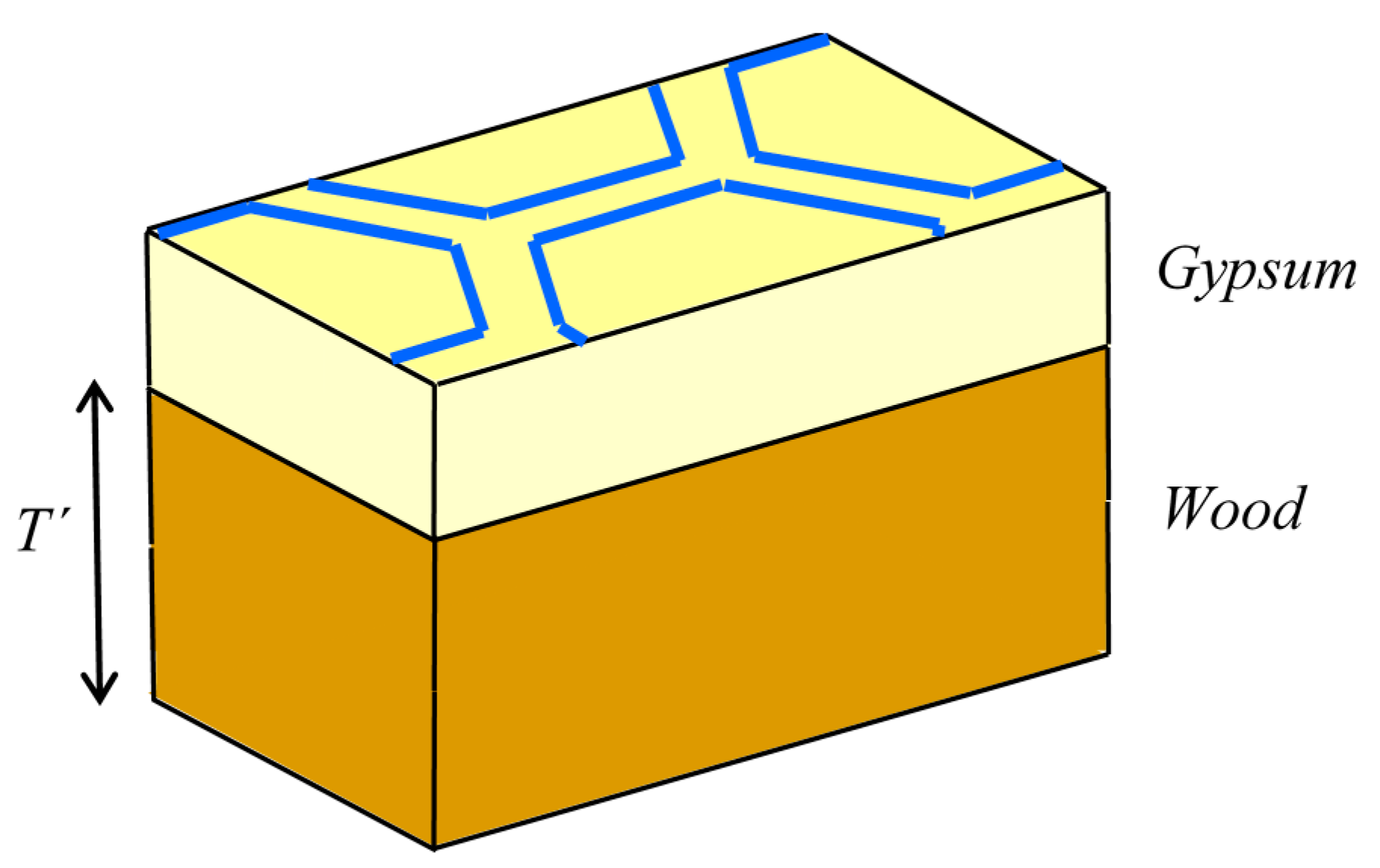
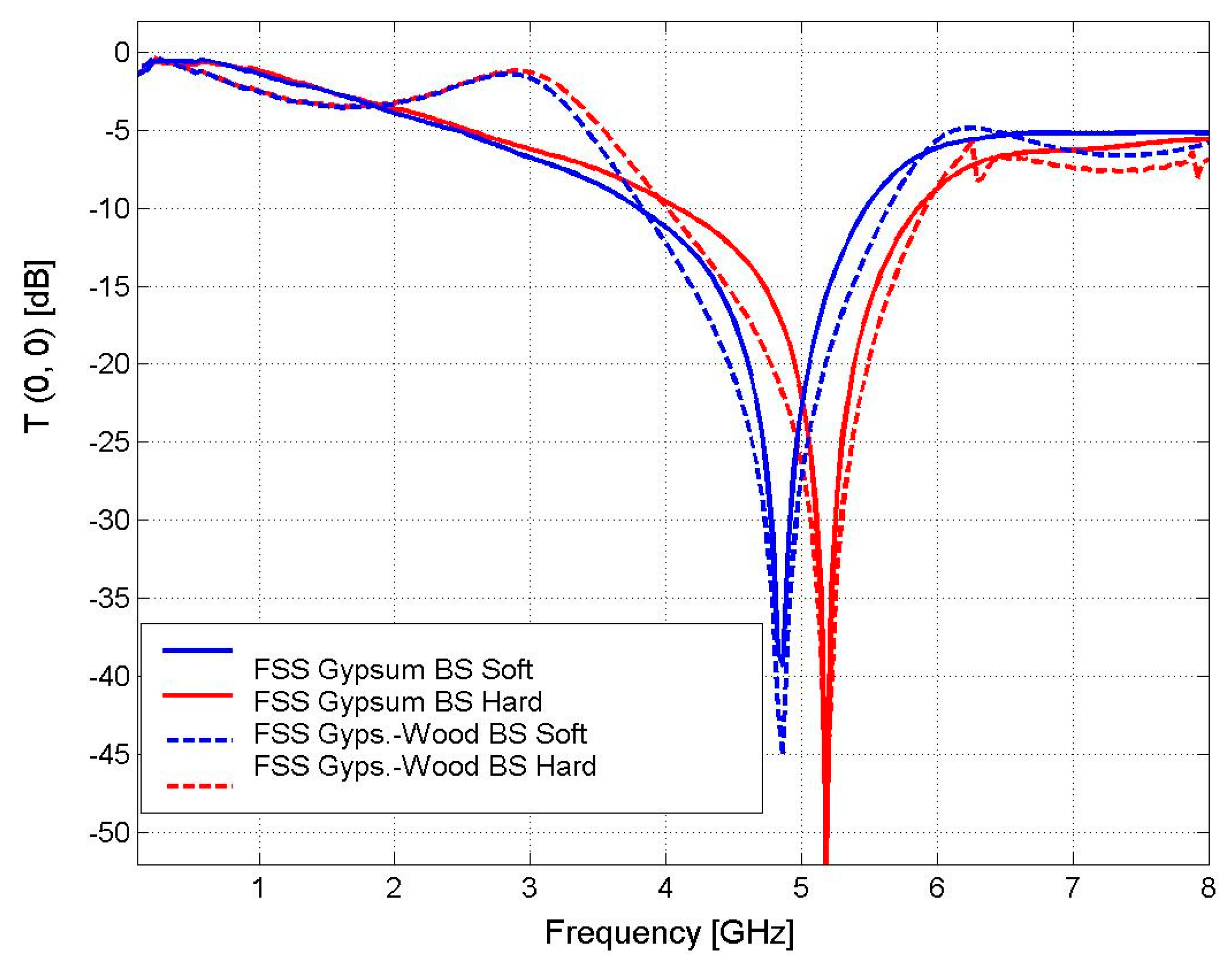
Wallpaper with Gypsum–Wood Wall

In order to check the versatility of the designed wallpaper, simulations were performed considering that the latter is covering a gypsum–wood wall, as can be seen in Figure 12. Parameters of ε_r = 5, σ = 0 Am⁻², and a thickness of T’ = 102.9 mm were assumed for the wood layer. Dimensions and material properties for the gypsum layer remained the same as those considered in previous sections.

The transmission and reflection coefficients for the described structure can be observed in Figure 13 and Figure 14, respectively, as a function of frequency, considering BS incidence.

It should be noted how the resonant frequencies are not shifted when considering the wallpaper with a gypsum–wood structure and, furthermore, their difference in attenuation as compared to the wallpaper–gypsum wall case is only 5 dB for soft polarization, therefore confirming that the performance of the designed wallpaper remains efficient with a gypsum–wood structure. Specifically, a transmission loss of around 45 dB can be found for both polarizations for the gypsum–wood structure around 5 GHz. Furthermore, the −18 dB bandwidth at resonant frequencies is approximately 350 MHz, which should be sufficient for band filtering purposes. On the other hand, the desired perfect reflection at 5 GHz, which was achieved with the gypsum wall, is maintained at 5 GHz when considering a gypsum–wood structure.

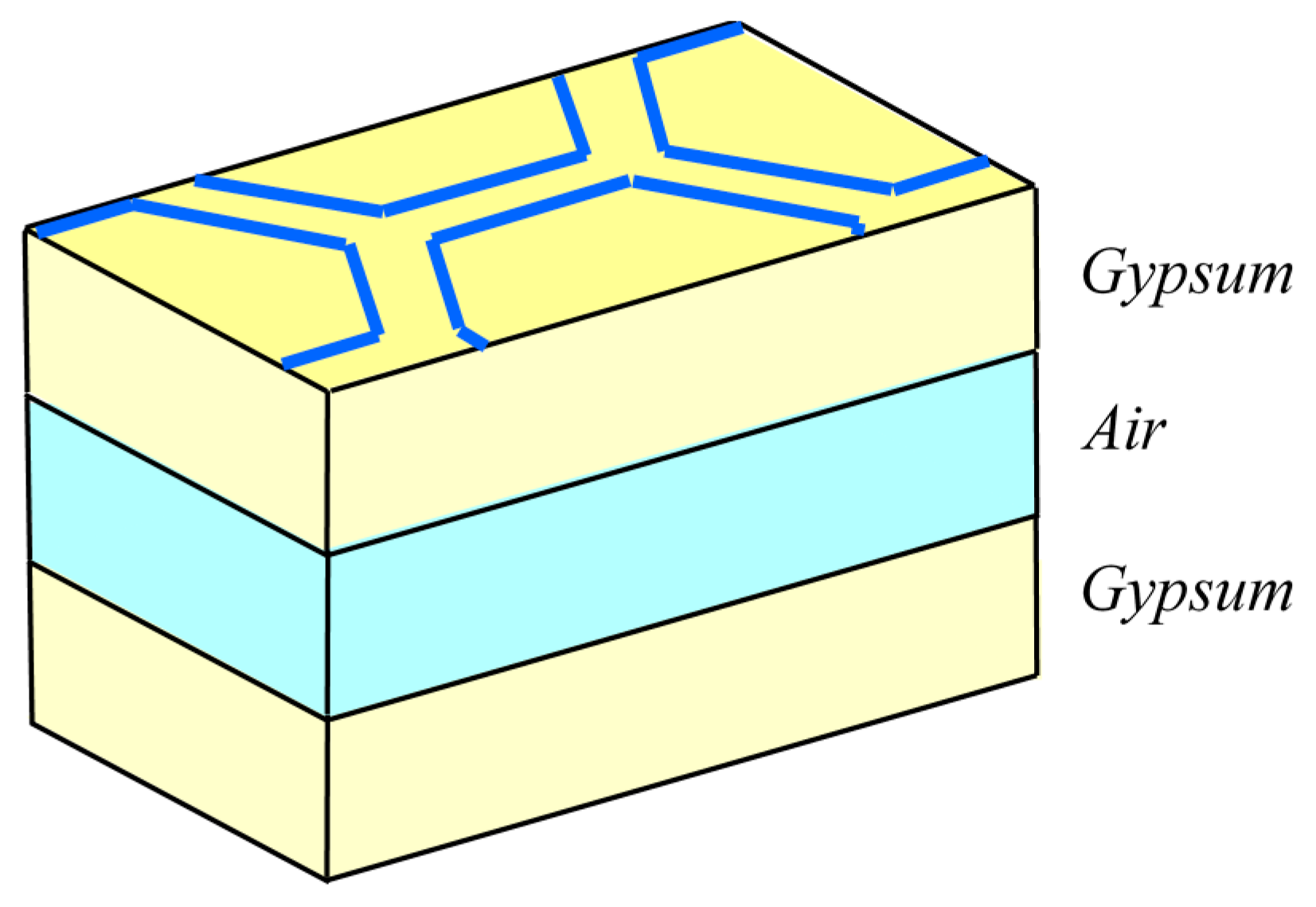
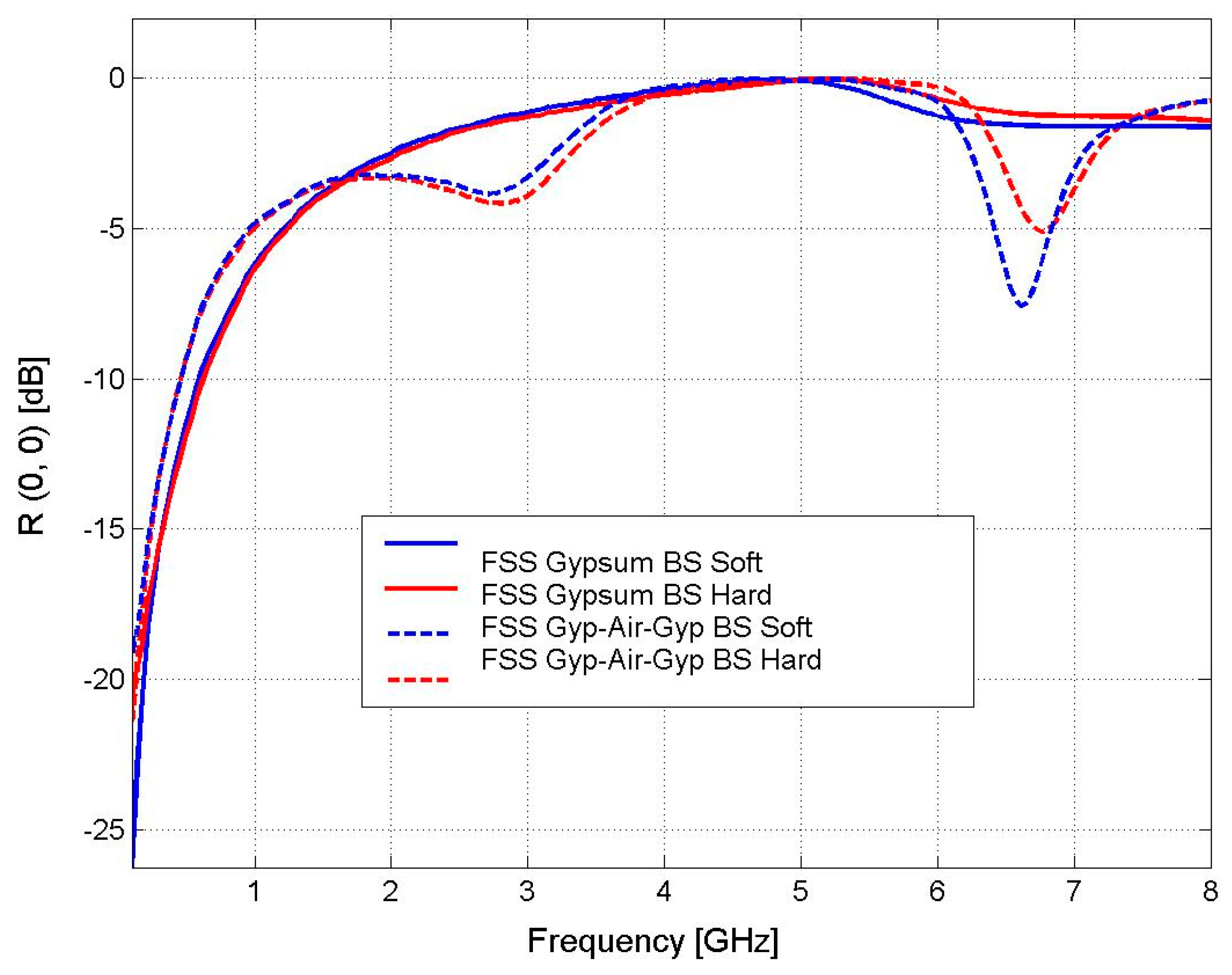
Wallpaper with Gypsum–Air–Gypsum Wall

The same analysis described in the previous subsection was carried out considering the wallpaper attached to a gypsum–air–gypsum wall, as shown in Figure 15.

Dimensions and material properties for the gypsum layers remained the same as those considered in previous sections and a separation of 51.5 mm (air) was assumed between both boards.

Again, it can be seen in Figure 16 and Figure 17 how the band-stop response of the newly considered structure is still exhibiting the good properties seen in the wallpaper–gypsum wall case regarding the blocking/confining of the signal. Specifically, a transmission loss of around 37 dB and 47 dB for soft and hard polarizations, respectively, can be observed for the gypsum–wood structure around 5 GHz. Moreover, the −18 dB bandwidth at resonant frequencies is approximately 400 MHz, which, again, should be sufficient for band filtering purposes. On the other hand, as observed in the gypsum–wood case, the desired perfect reflection at 5 GHz, which was achieved with the gypsum wall, is again kept at 5 GHz when considering a gypsum–air–gypsum structure.

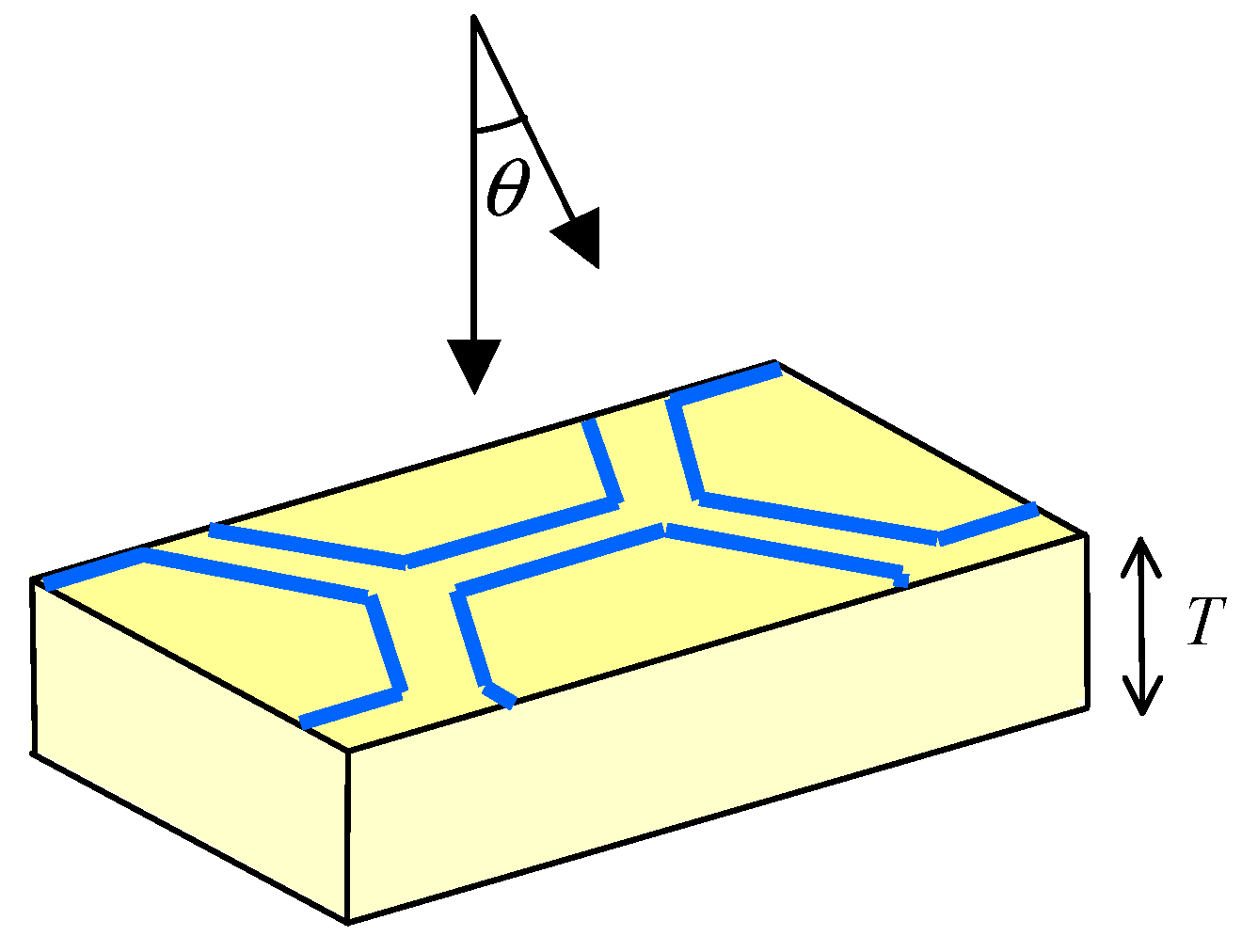
3. Ray-Launching Method

To achieve the results shown in this paper, the simulations were performed employing a ray-launching program centered on ray optics and the uniform theory of diffraction (UTD). With ray-launching techniques, rays are shot at various discrete angles that undergo interaction with any objects in situ during propagation. Thus, the rays that have been launched undergo reflection, transmission, diffraction, and scattering across their environment. Random rays passing near the location of the receiver are employed for predicting the true propagation pulse and thus we may evaluate the total field registered by the receiver as being a coherent summation of every contribution that impinges upon it.

The ray-launching tool employed in this research may be used for analyzing both MIMO and SISO systems. With the MIMO system results, the assumption is made that there is an equal number of receiving antennae (Nr) and transmitting antennae (Nt), meaning N = Nt = Nr. N×N simulations were performed for every receiver position for obtaining the channel transfer matrix (G_N×N). For each simulation, a calculation is made of the coefficient G(n,m), being the coherent sum of every ray received by the antenna m with transmissions only coming from the antenna n.

The received rays taken into consideration comprise: direct (E₁), multiple reflected (E₂), multiple transmitted (E₃), multiple diffracted (E₄), multiple reflected/diffracted (E₅), multiple transmitted/diffracted (E₆), and multiple transmitted/reflected (E₇) rays. Thus, the matrix G for any specific receiver position is found with [15]:

$$\begin{array}{c}G(n,m)={\displaystyle \sum _{c=1}^7{E}_c(n,m)}\end{array}$$

(1)

with direct, reflected, transmitted, diffracted, reflected/diffracted, transmitted/diffracted, and transmitted/reflected components being ascertained with [15]:

$$\begin{array}{cc}{E}_1(n,m)=\frac{E_o}{r}{e}^{-jkr}& \end{array}$$

(2)

$$\begin{array}{cc}{E}_2(n,m)={\displaystyle \sum _{i=1}^p{R}_i\frac{E_o}{r_i}{e}^{-jk{r}_i}}& \end{array}$$

(3)

$$\begin{array}{cc}{E}_3(n,m)={\displaystyle \sum _{i=1}^p{T}_i\frac{E_o}{r_i}{e}^{-jk{r}_i}}& \end{array}$$

(4)

$$\begin{array}{cc}{E}_4(n,m)={\displaystyle \sum _{i=1}^p\frac{E_o}{s_i^{\prime }}{e}^{-jk{s}_i^{\prime }}{D}_i\sqrt{\frac{s_i^{\prime }}{s_i(s_i+s_i^{\prime })}}{e}^{-jk{s}_i}}& \end{array}$$

(5)

$$\begin{array}{c}{E}_5(n,m)={\displaystyle \sum _{i=1}^p\frac{E_o}{s_i^{\prime }}{e}^{-jk{s}_i^{\prime }}{D}_i{R}_i\sqrt{\frac{s_i^{\prime }}{s_i(s_i+s_i^{\prime })}}{e}^{-jk{s}_i}}\end{array}$$

(6)

$$\begin{array}{cc}{E}_6(n,m)={\displaystyle \sum _{i=1}^p\frac{E_o}{s_i^{\prime }}{e}^{-jk{s}_i^{\prime }}{D}_i{T}_i\sqrt{\frac{s_i^{\prime }}{s_i(s_i+s_i^{\prime })}}{e}^{-jk{s}_i}}& \end{array}$$

(7)

$$\begin{array}{cc}{E}_7(n,m)={\displaystyle \sum _{i=1}^p{T}_i{R}_i\frac{E_o}{r_i}{e}^{-jk{r}_i}}& \end{array}$$

(8)

where E_o represents emitted field strength, k the wave number, p the total number of contributions considered, r and r_i the propagation path lengths from source n to receiver m, s’ the path length from source to the diffracting wedge, s the path length from diffracting wedge to receiver, D_i the diffraction coefficient for finitely conducting wedges shown in [16], T_i the transmission coefficient, and R_i the reflection coefficient. For this instance, T_i and R_i are dependent on the incident wave polarization, angle of incidence, conductivity, and permittivity.

For analytical purposes, the assumption is made that power is distributed equally for every transmitter and that the transmitter has no prior channel knowledge [17].

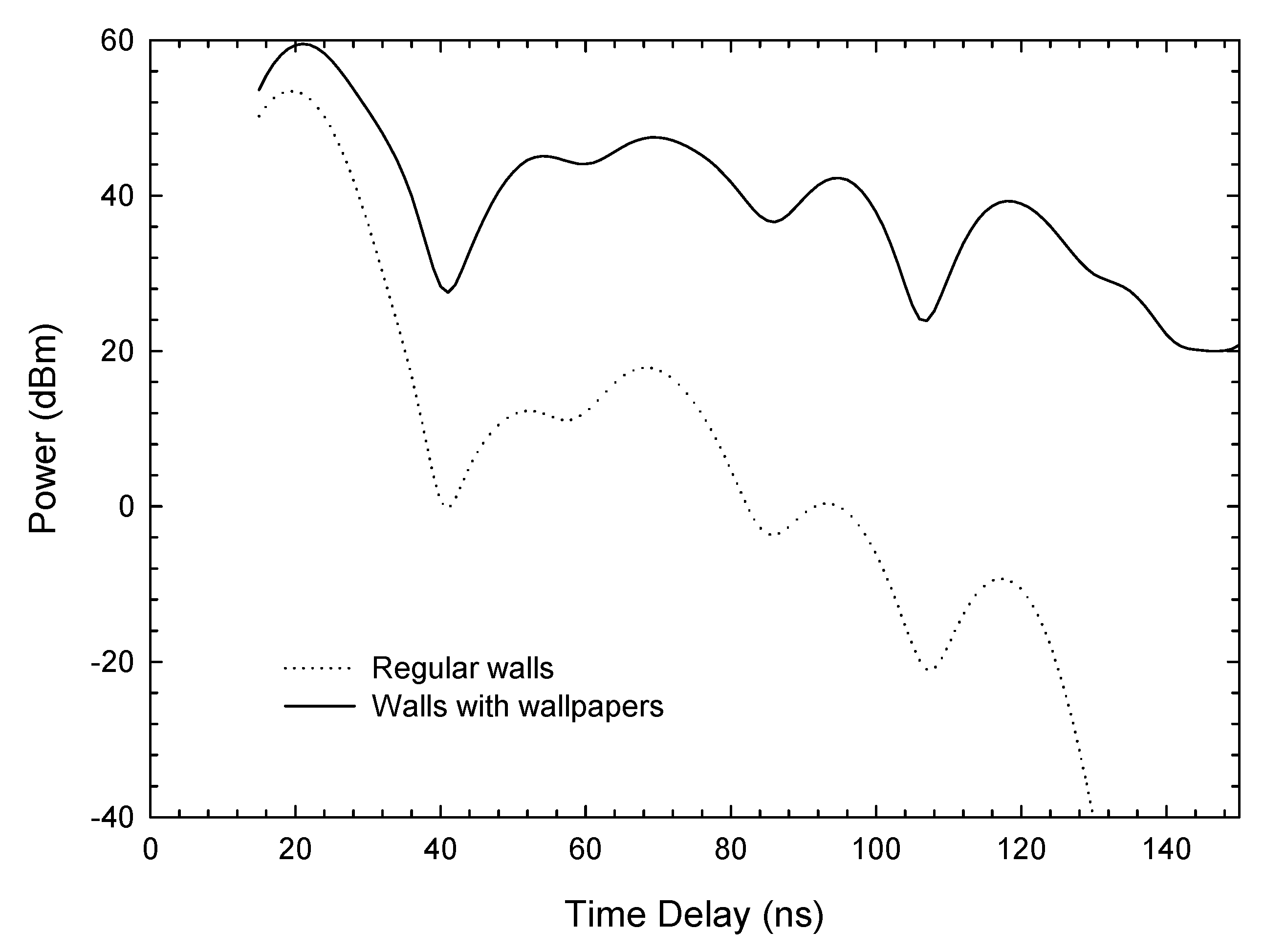
4. Results and Discussion

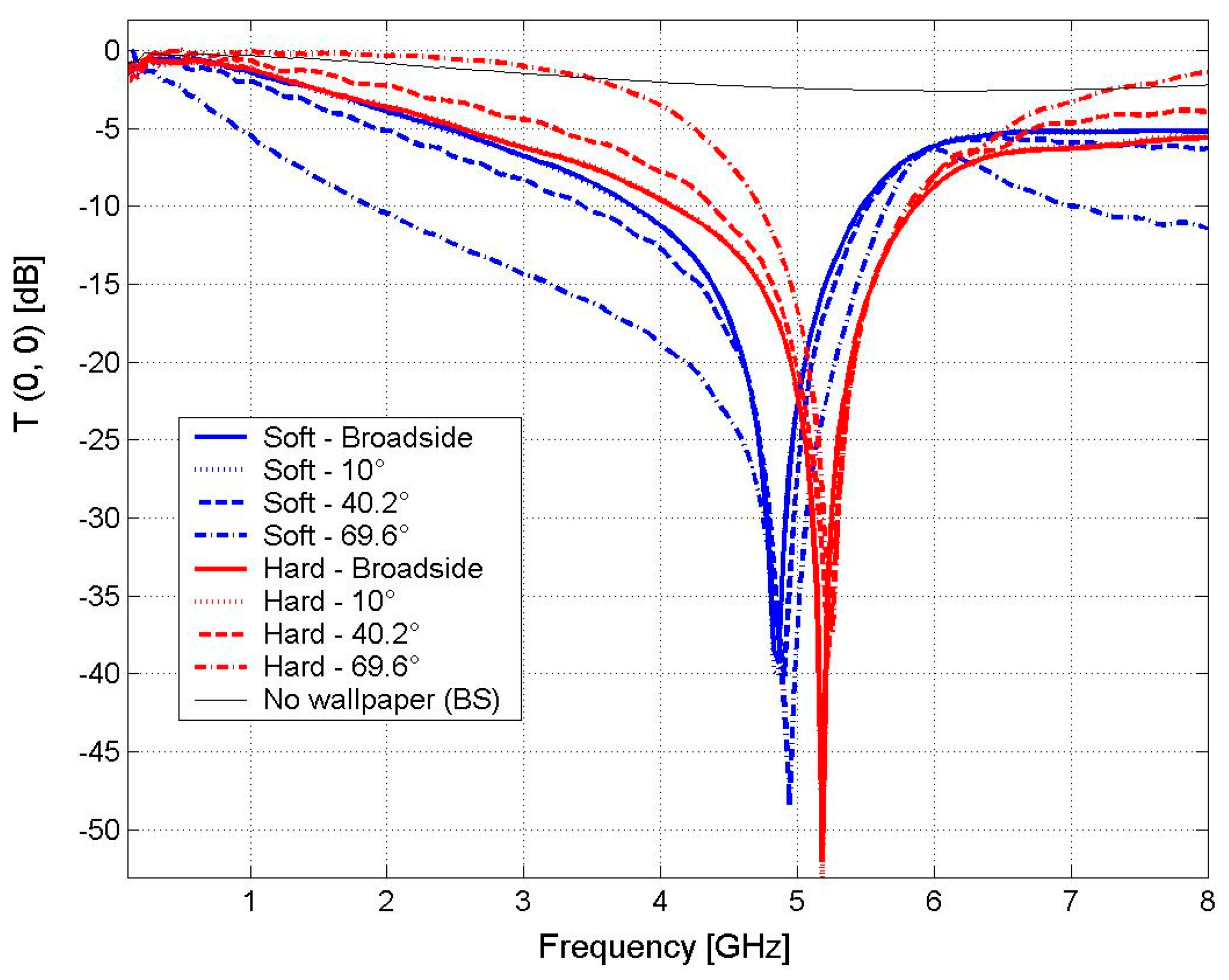
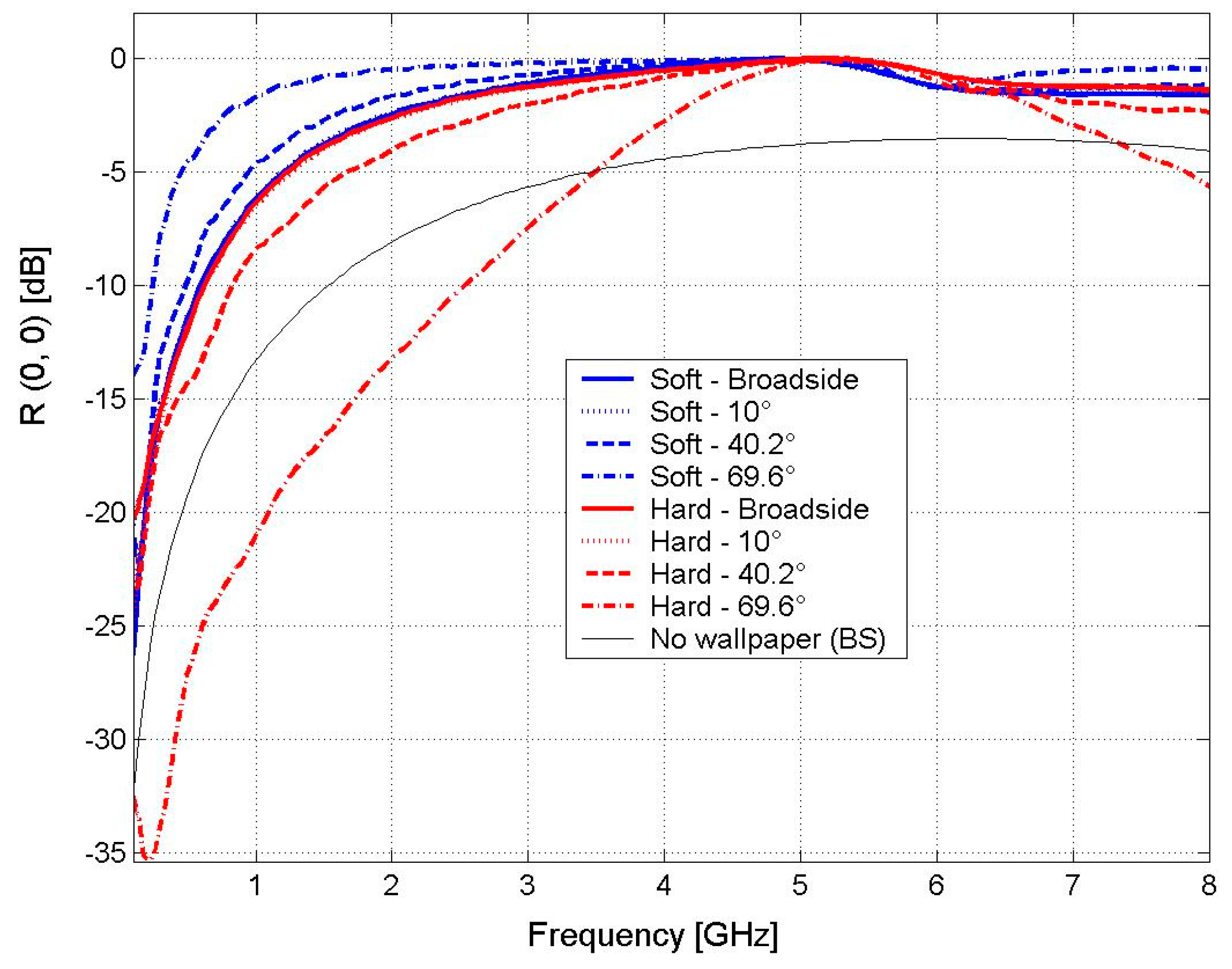
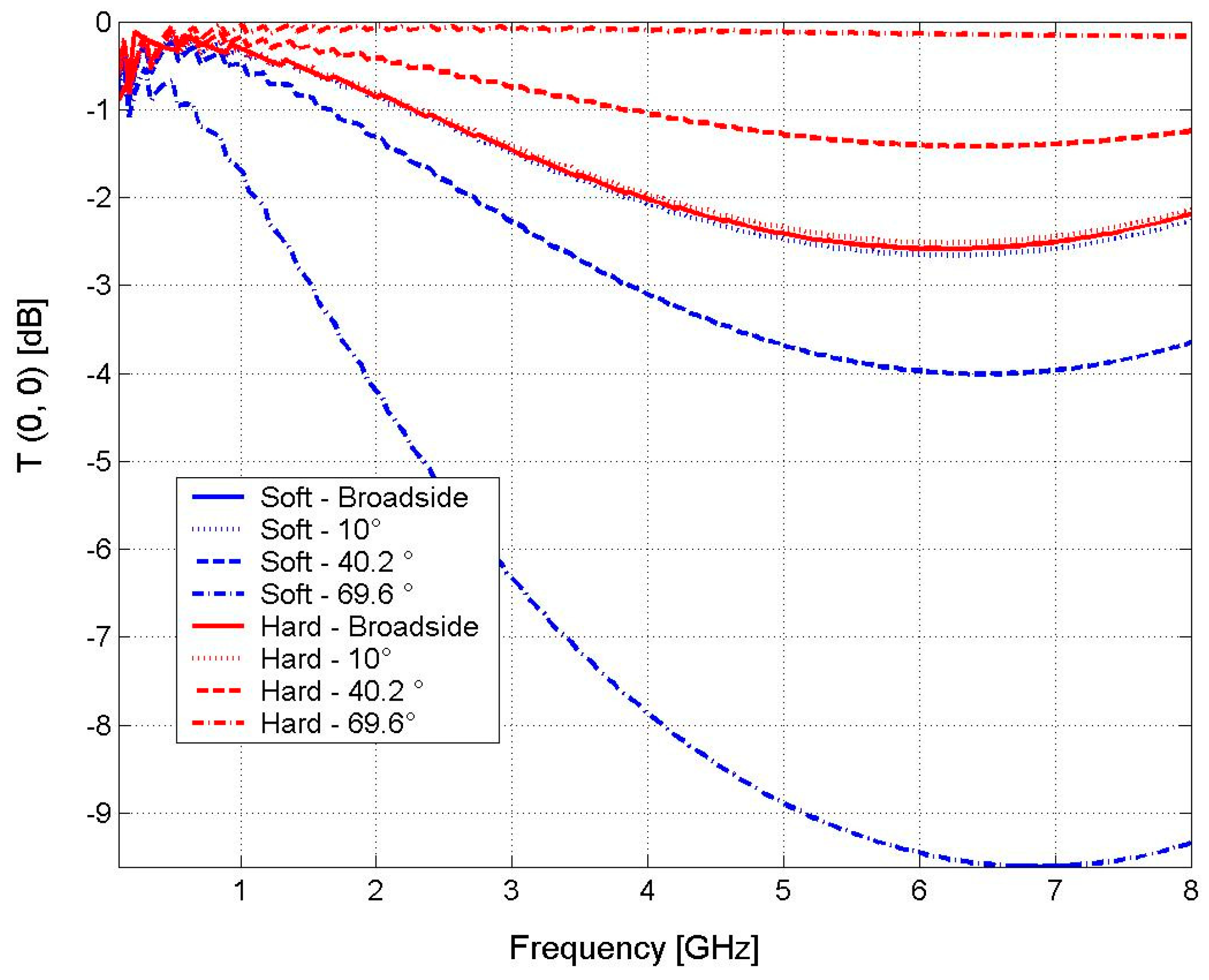
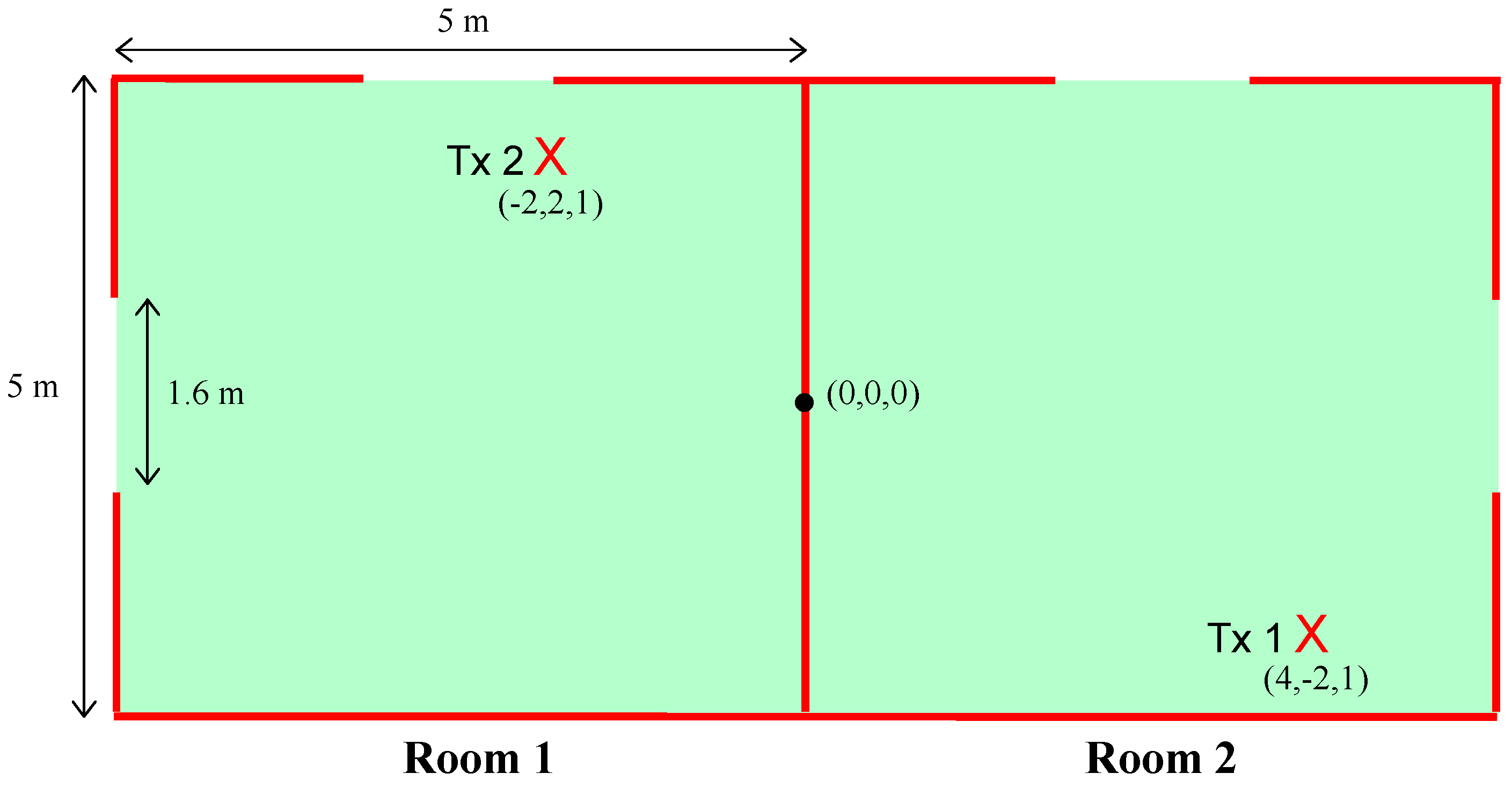
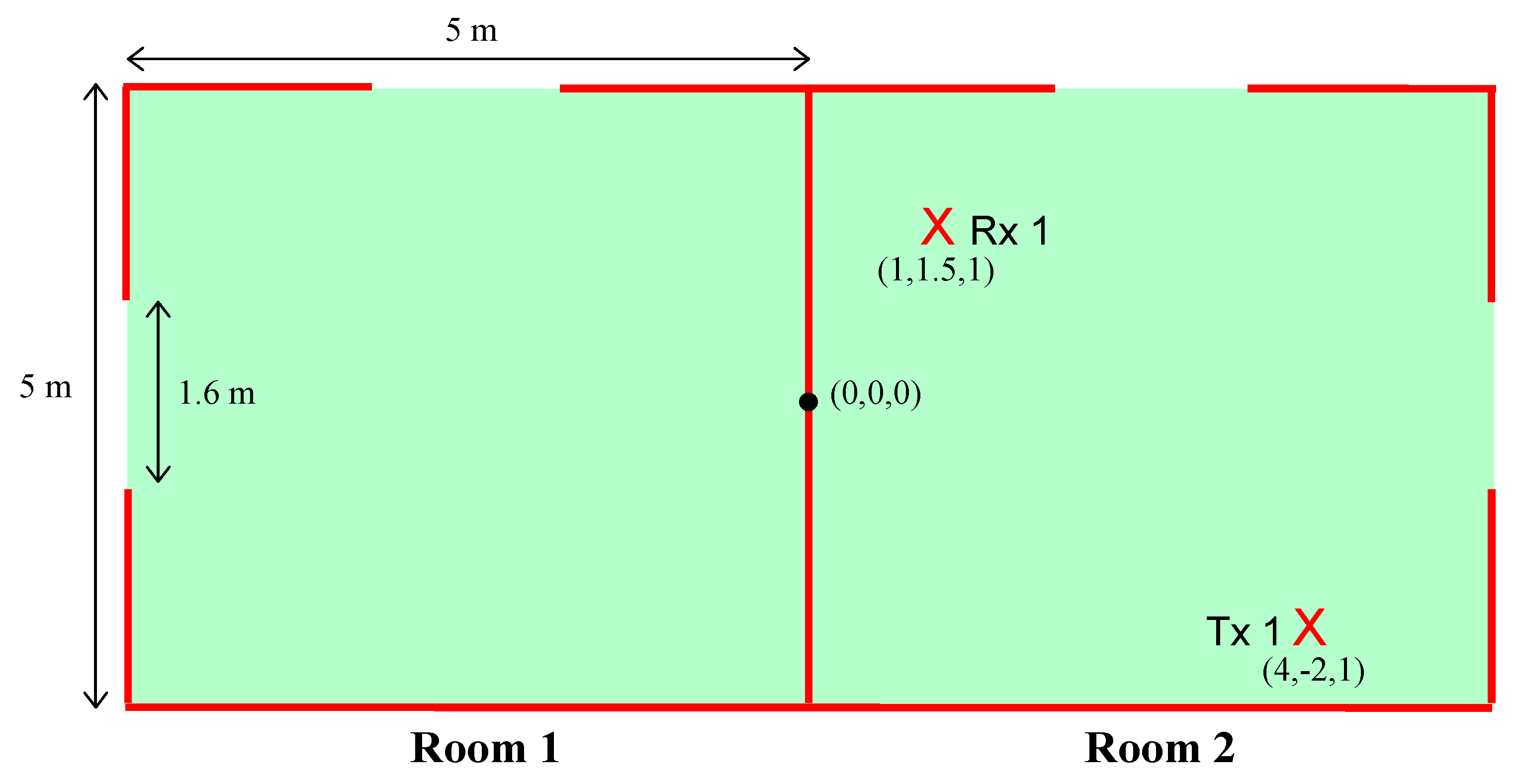
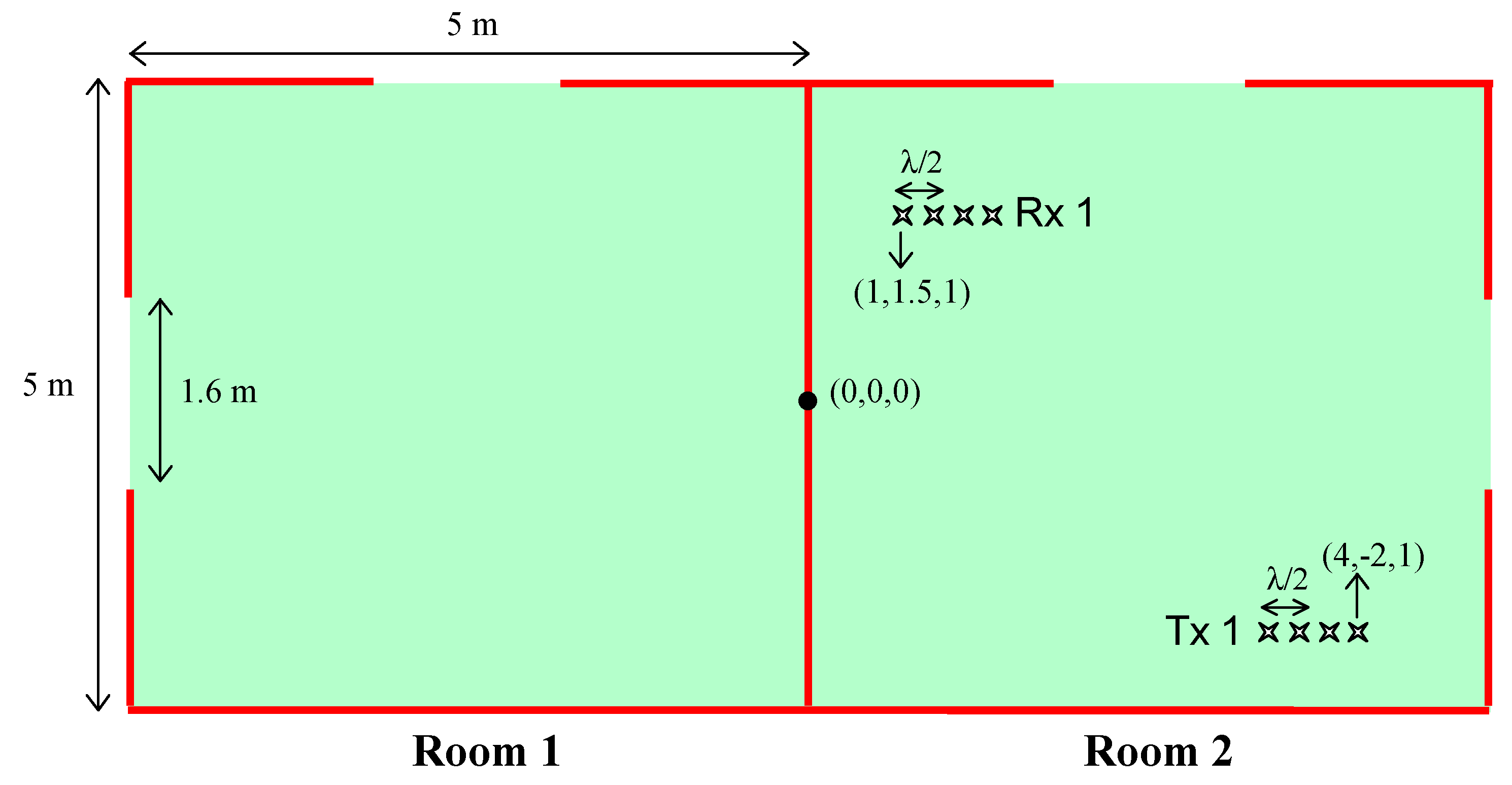
4.1. SISO Case

The deployment of the F-S wallpaper in an indoor scenario was undertaken employing the aforementioned ray-launching software; the first experiment was undertaken using an SISO system in a two-room environment, the top view of which is shown in Figure 18 (distances in meters).

As may be observed, the floor comprises two 25 m² rooms, each having two apertures corresponding to squared windows of 1.6 m width; the experiment assumes that the rooms have a height of 3 m. The T × 1 transmitter is located within Room 2, providing coverage in that location. T × 2 is located within Room 1 so that when its signal enters Room 2, it becomes an interference.

As an example, in Figure 19, the signal-to-interference ratio (SIR), in dB, over every point at a horizontal plane of 1 m height in Room 2 is depicted considering the two cases in which (a) regular gypsum walls are considered and (b) wallpaper–gypsum walls are assumed. The following simulation parameters were taken into account in the ray-launching code:

• Omnidirectional antennas
• Frequency: 5 GHz
• Soft Polarization
• T × 1 and T × 2 bearing a 1 m height
• Number of rays launched: 7200
• Number of considered reflections: 14
• Number of considered reflections of diffracted rays: 4
• Number of considered transmissions: 4
• Number of considered transmissions of diffracted rays: 2.

Figure 20 shows the cumulative distribution function (CDF) for the signal-to-interference ratio (SIR) for every point of Room 2 for both instances of uncovered walls and walls covered with the designed wallpaper. An assumption is made that the antennae are omnidirectional, the frequency is 5 GHz, both transmitters are 1 m in height (the third coordinator that may be observed in the positioning of the transmitters in Figure 18), and that the polarization is soft (horizontal).

We can see that the F-S walls create an improvement of approximately 20 dB in the SIR. This agrees with predicted values, as shown in Figure 3.

For evaluation of the power delay profile (PDP) from transmitter to receiver in Room 2 for both papered and unpapered walls, we considered the scheme illustrated in Figure 21, containing transmitter T × 1 and receiver R × 1.

For this instance, the aforementioned PDP may be seen in Figure 22 for both papered and unpapered walls. The simulation parameters considered in the ray-launching code were the following:

• Omnidirectional antennas
• Frequency: 5 GHz
• Hard Polarization
• T × 1 and T × 2 bearing a 1 m height
• Number of rays launched: 7200
• Number of considered reflections: 14
• Number of considered reflections of diffracted rays: 4
• Number of considered transmissions: 4
• Number of considered transmissions of diffracted rays: 2.

The curves show 20 realizations on average harvested at various frequencies between 4.9 and 5.1 GHz measured in 0.01 GHz increments. Additionally, low-pass filtering with 40 MHz was undertaken within the frequency domain with a Blackman window for all realizations. An assumption is made that the antennae are omnidirectional, the frequency is 5 GHz, and both transmitters are 1 m in height. It may be seen that the PDP curve generated in the instance of the wall being papered with F-S wallpaper has a slower decrease when the time delay increases. This means that a wide range of outstanding paths come to the receiver, which increases the root-mean-square (r.m.s) delay spread. An r.m.s. delay spread of 22 ns can be ascertained from the papered wall results (coherence bandwidth approximately 7 MHz), in comparison to the unpapered wall, which has a value of 4 ns (coherence bandwidth of approximately 42 MHz).

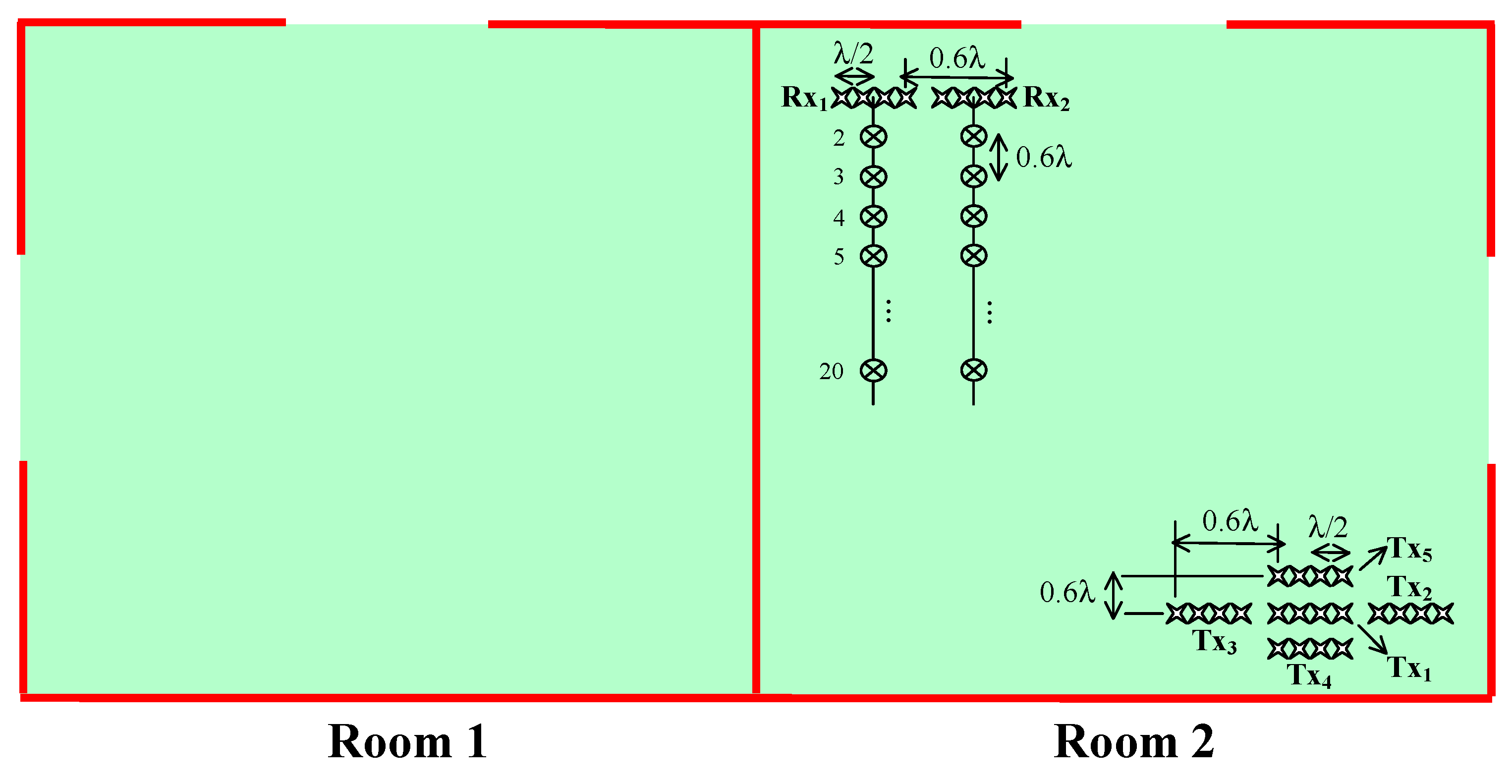
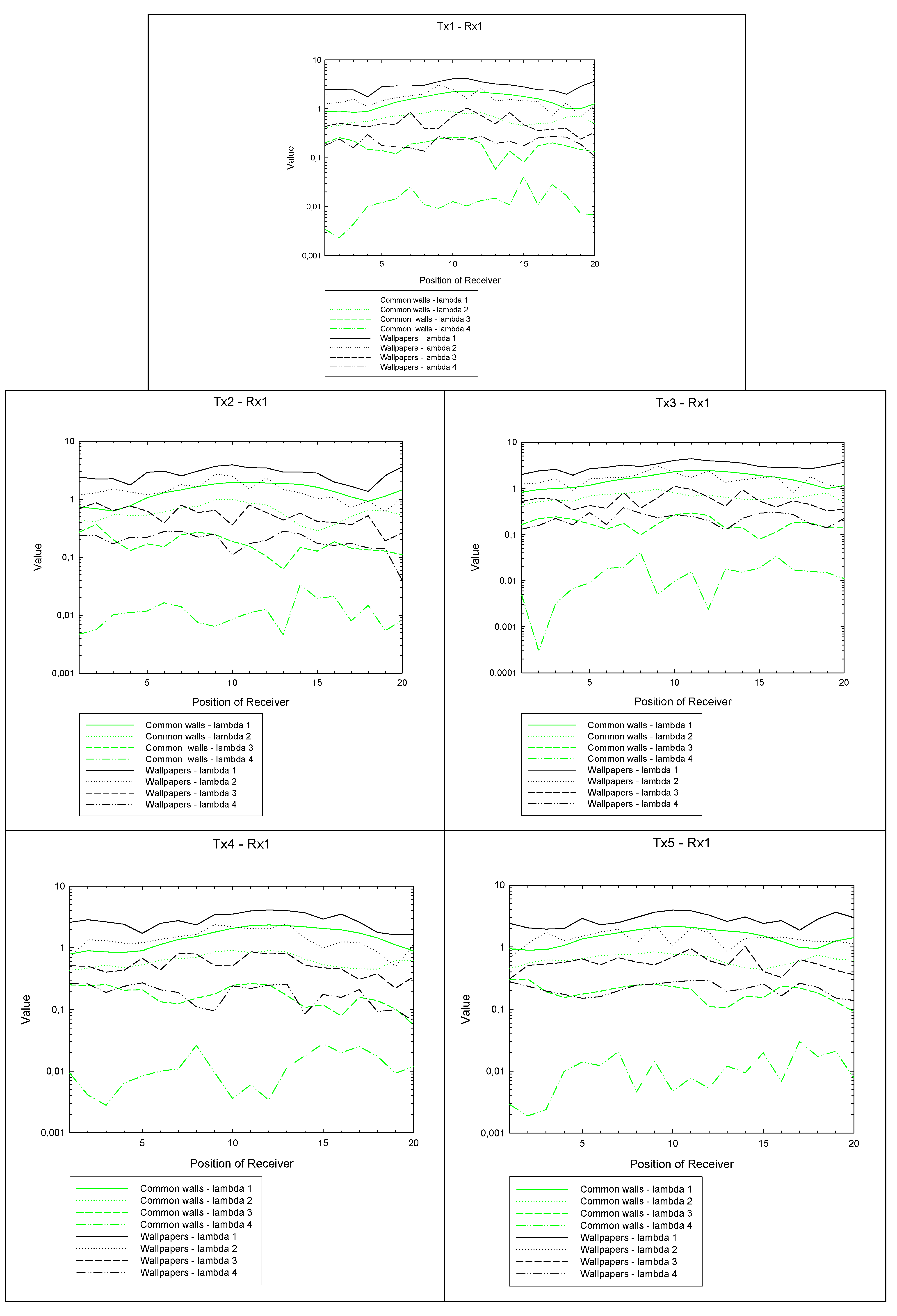
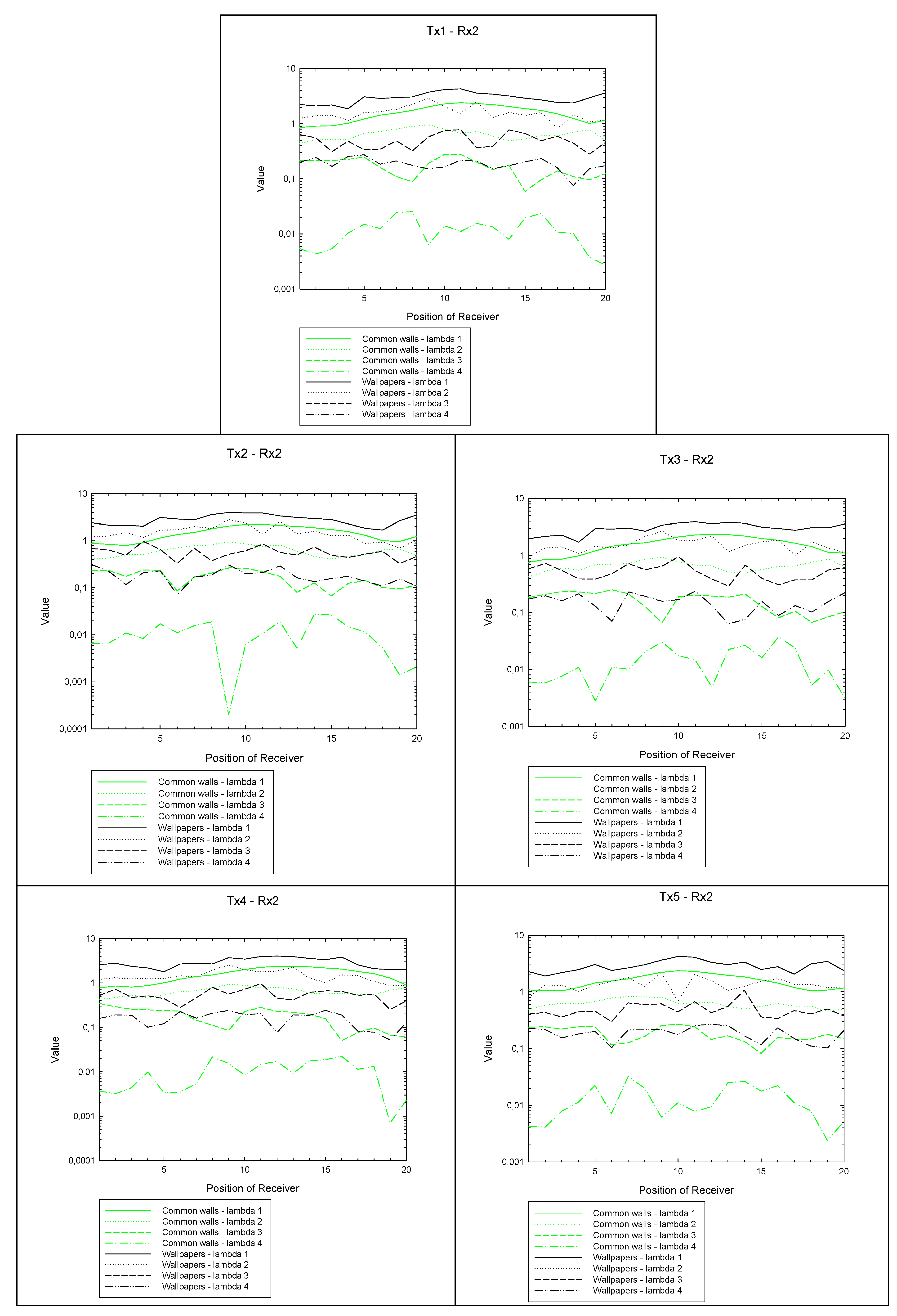
4.2. MIMO Case

A further analysis of the employment of F-S wallpaper in an indoor scenario, but this time using a MIMO system, was undertaken. Figure 23 shows the layout in this instance, with Room 2 holding the transmitter and receiver T × 1 and R × 1, respectively, comprising a quartet of omnidirectional antennae spaced at λ/2.

Using this setup, Figure 24 shows the singular values (lambda 1 to 4) for the channel transfer matrix G (square roots of the eigenvalues of G^TG and GG^T) as a function of frequency with both unpapered and papered walls. The simulation parameters considered in this case in the ray-launching code were the following:

• Omnidirectional antennas
• Hard Polarization
• 4 Tx and 4 Rx bearing a 1 m height
• Number of rays launched: 7200
• Number of considered reflections: 9
• Number of considered reflections of diffracted rays: 4
• Number of considered transmissions: 4
• Number of considered transmissions of diffracted rays: 3.

We can say that with unpapered walls there is a trio of main singular values (the fourth being negligible for practical purposes). When the F-S paper covers every wall, there is an increase in the magnitude of all four singular values, with the fourth value being emphasized, so that, in this instance, we have four relevant subchannels rather than three. In this instance, an extra degree of freedom is added in comparison to the unpapered walls, and thus the capacity of the radio channel is increased.

In order to further the previous study, the radiation diagrams calculated from the eigenvectors of GG^T and G^TG, concerning the antenna arrays T × 1 and R × 1, can be observed in Figure 25 for a frequency of 5 GHz and the two types of walls under study.

As expected, the radiation diagrams located on the very left column—for both T × 1 and R × 1—which were calculated from the first eigenvectors of GG^T and G^TG, present the lobes (at 120° in the transmitter and −60° in the receiver), making reference to the line of sight (LoS) path.

We can obtain the channel capacity, where the transmitters and receivers are Nt and Nr and the averaged signal-to-noise rate (SNR) is ρ at each receiving antenna, with the following Equation [18]:

$$\begin{array}{ccc}C={\log }_2\left(\det \left(I_{N_r}+\frac{\rho }{N_t}H{H}^H\right)\right)& \mathrm{bits}/\mathrm{s}/\mathrm{Hz}& \end{array}$$

(9)

where I_Nr is the Nr × Nr identity matrix, ( )H is the Hermitian transposition, and H is the normalized channel transfer matrix.

We normalize the channel transfer matrix, G, so that the path loss component is removed. Thus, solely the relative variations for responses across all elements are revealed. This gives us an average signal-to-noise ratio that remains constant and is not dependent on receiver position. The normalization mentioned above can be undertaken using the Frobenius norm, thus [19]:

$$\begin{array}{cc}H=\frac{G}{\sqrt{\frac{{\displaystyle \sum _{j=1}^{N_r}{\displaystyle \sum _{k=1}^{N_t}{\left|G_{j,k}\right|}^2}}}{N_t{N}_r}}}& \end{array}$$

(10)

With this method we calculated the CDF of capacity for Room 2, as shown in Figure 23, for both types of walls being examined, taking the frequency variation analysis illustrated in Figure 24 into account and using a variety of receiver/transmitter positions, as shown in Figure 26.

As shown, we assumed five unique transmitter positions, each 0.6λ apart (T × 1 to T × 5), and each comprising an array of four omnidirectional antennae with λ/2 spacing. For each position, we considered a pair of linear paths, evaluating 20 unique receiver positions with 0.6λ spacing (comprising arrays of four omnidirectional antennas with λ/2 spacing). We assumed that both the transmitter and receiver are at the same locations as shown in Figure 23. The simulation parameters considered in the ray-launching code were the following:

• Omnidirectional antennas
• Frequency: 5 GHz
• Hard Polarization
• Transmitting and receiving antennas bearing a 1 m height
• Number of rays launched: 7200
• Number of considered reflections: 9
• Number of considered reflections of diffracted rays: 4
• Number of considered transmissions: 4
• Number of considered transmissions of diffracted rays: 3.

Figure 27 shows the previously mentioned CDF of capacity for Room 2 with both papered and un-papered walls with an SNR of 10 dB. The plot also incorporates the CDF of the capacity for an independent and identically distributed (I.I.D) Rayleigh fading channel for comparison purposes.

We can see that employing the F-S wallpaper leads to improved MIMO capacity; in particular, the capacity’s mean value, for unpapered walls, is 8.6 bits/s/Hz; when the wall is papered, this rises to 9.4 bit/s/Hz.

In Figure 28 and Figure 29, the calculated singular values (lambda 1 to 4) for the different transmitter and receiver positions are shown for the two types of walls under study. As can be observed, the additional degree of freedom previously seen in Figure 24 in the wallpaper case with the study performed as a function of frequency is also obtained for all the transmitter and receiver locations, which means that the improvement in capacity due to the use of the designed wallpapers does not depend on the position of the transmitter and receiver.

The above-mentioned advantage can also be noted in

Table 1. Mean and standard deviation of the singular values (lambda 1 to 4) obtained for all transmitter and receiver positions of Figure 26.

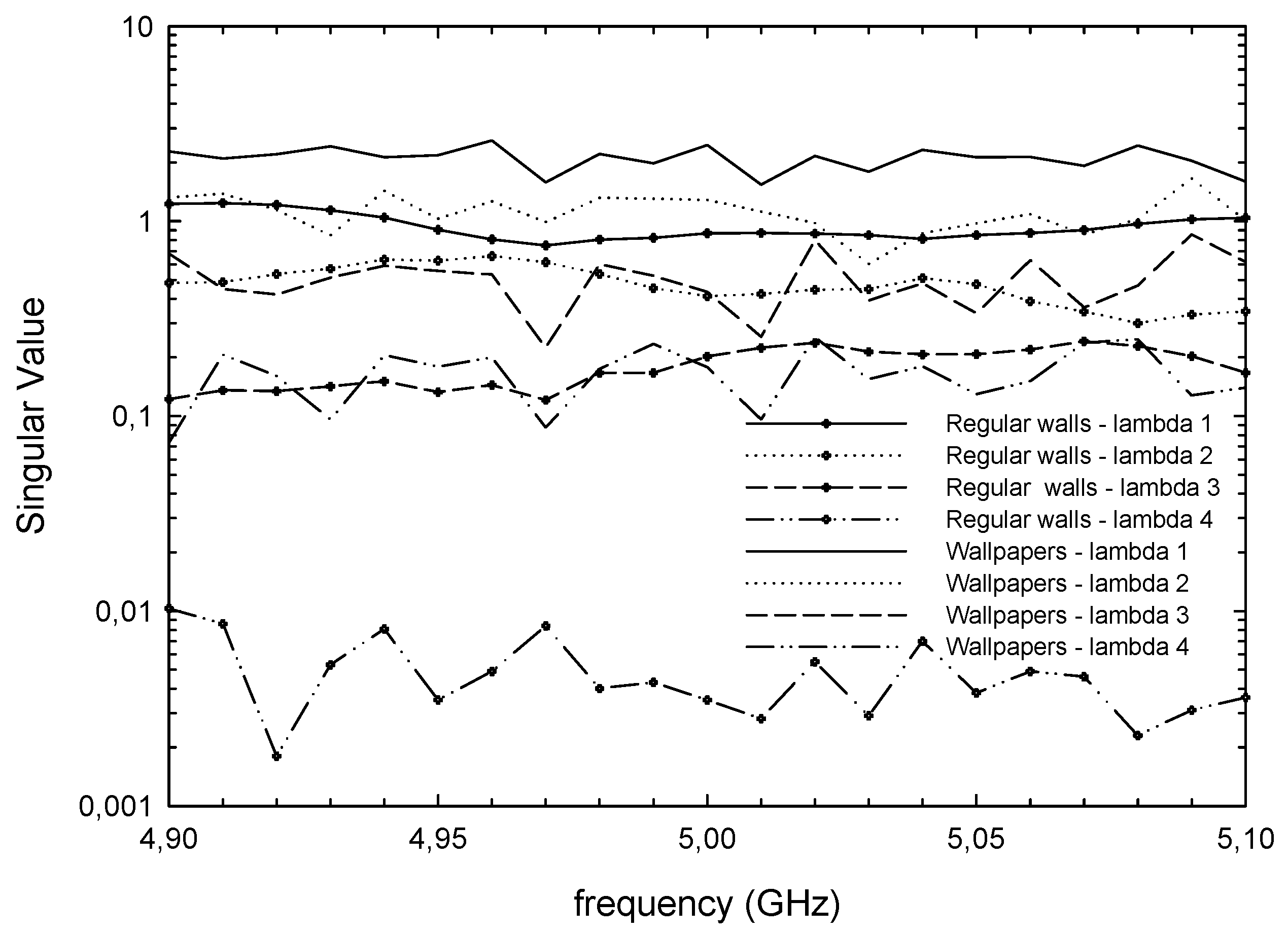
		Mean	Standard Deviation
	Lambda1	1.5254	0.50602
Regular	Lambda2	0.63897	0.14742
Walls	Lambda3	0.17615	0.064675
	Lambda4	0.012362	0.0081471
	Lambda1	2.9068	0.68067
Walls with	Lambda2	1.5055	0.49311
Wallpaper	Lambda3	0.53912	0.18192
	Lambda4	0.19102	0.061508

, where the mean and standard deviation of the four singular values calculated for all considered positions are shown, for both regular (common) gypsum and frequency selective wall cases.

5. Conclusions

F-S wallpaper has been designed with the intention of being mounted on standard walls to allow filtering of signals operating at 5 GHz while simultaneously permitting required radio communication services on other frequencies to be received. The outcomes of this experiment unequivocally demonstrated that using this wallpaper in an indoor scenario reduces interference levels by an additional attenuation of 20 dB in comparison to an unpapered wall. Additionally, with MIMO systems, radio channel characteristics, such as capacity, are improved due to the increase in the magnitude of all singular values of the channel transfer matrix compared to the unpapered wall case, thereby leading to the existence of more relevant subchannels.