New Exact Solutions of the Conformable Space-Time Sharma–Tasso–Olver Equation Using Two Reliable Methods
Abstract
1. Introduction
2. Mathematical Preliminaries
2.1. Conformable Derivative and Its Properties
- (1)
- , .
- (2)
- .
- (3)
- .
- (4)
- .
- (5)
- , provided that is differentiable.
2.2. Description of the Methods
2.2.1. Description of the Novel -Expansion Method
2.2.2. Description of the Generalized Kudryashov Method
3. Application of the Methods
3.1. Obtaining Exact Solutions of Equation (15) Using the Novel -Expansion Method
3.2. Obtaining Exact Solutions of Equation (15) Using the Generalized Kudryashov Method
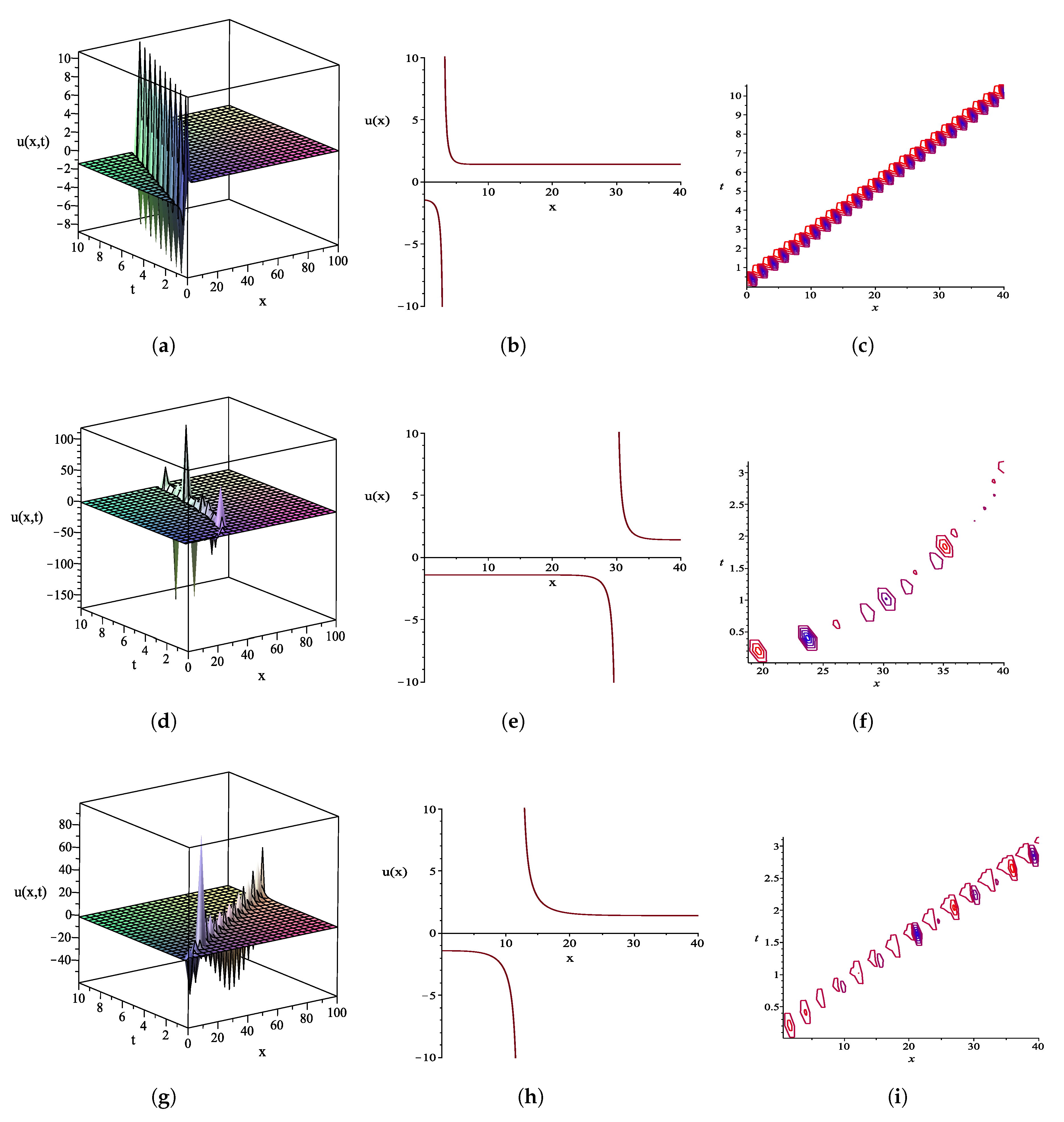
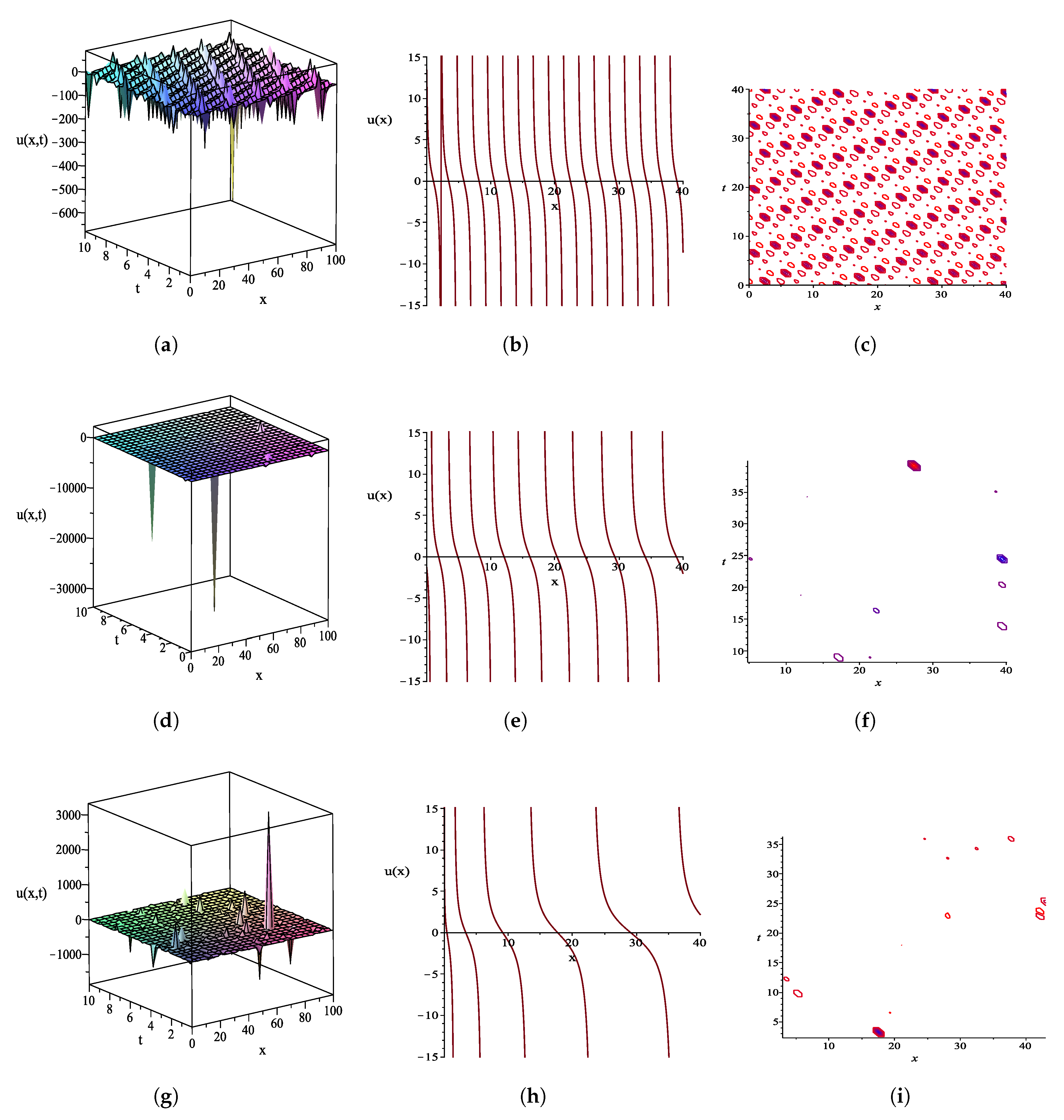
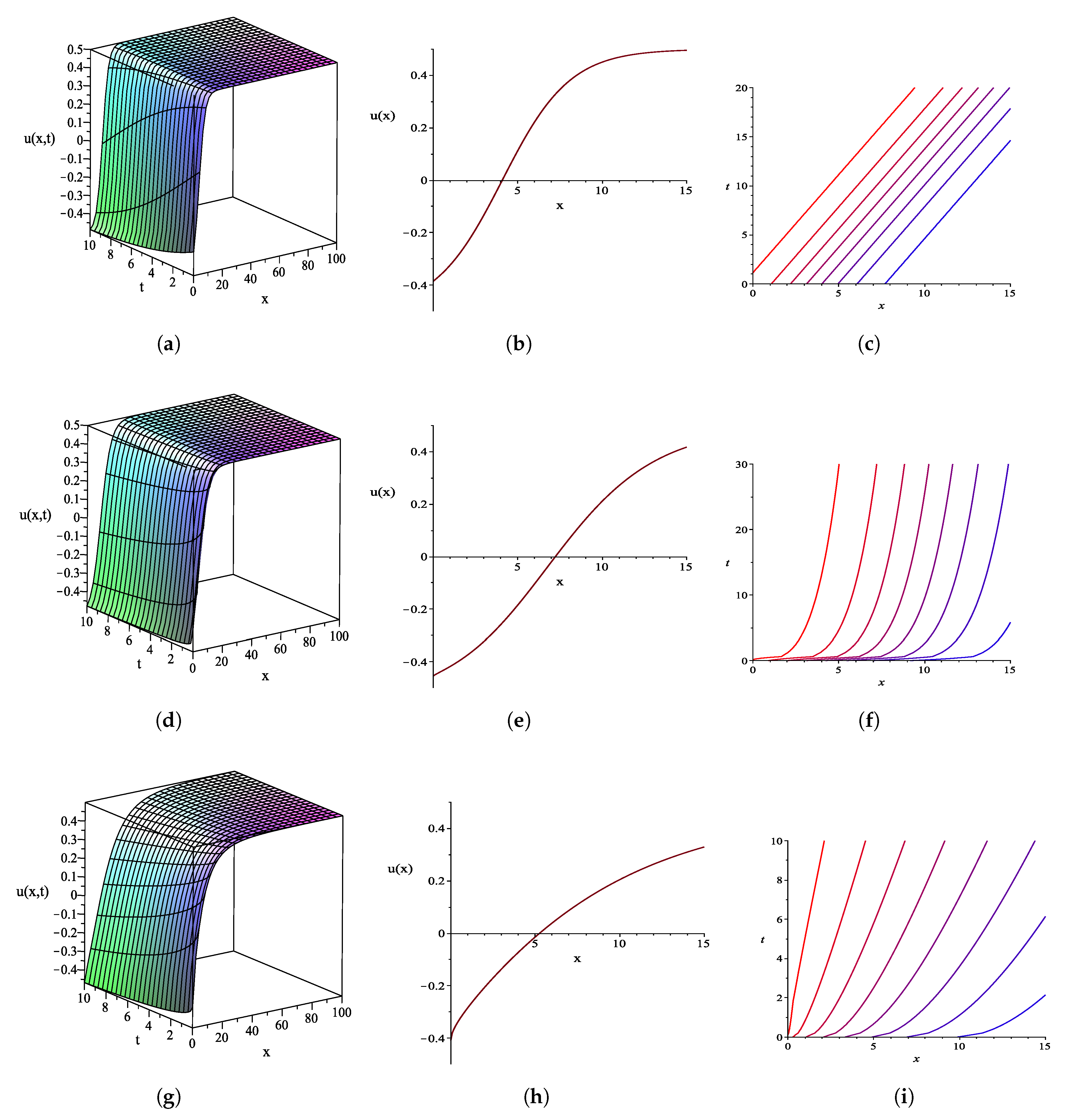
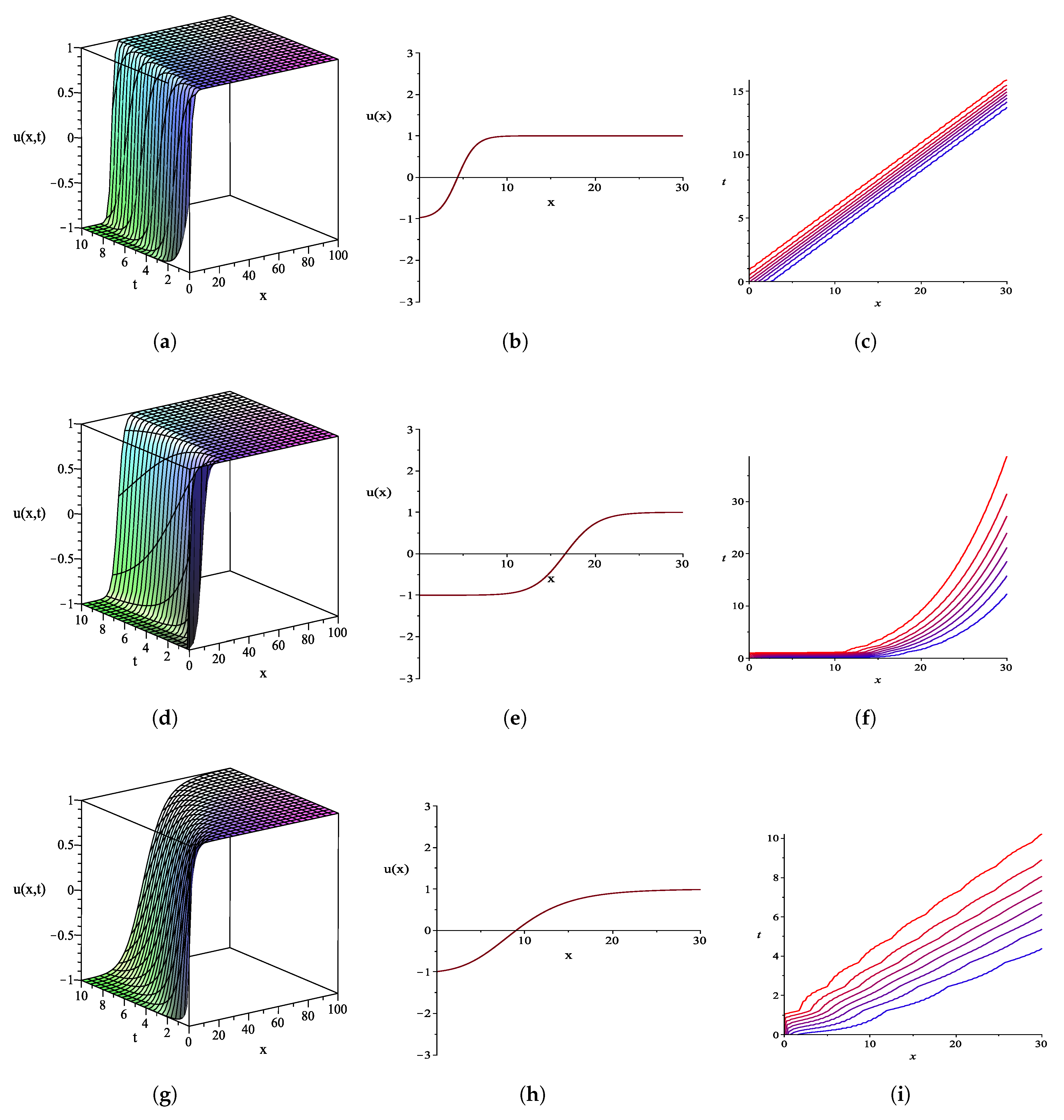
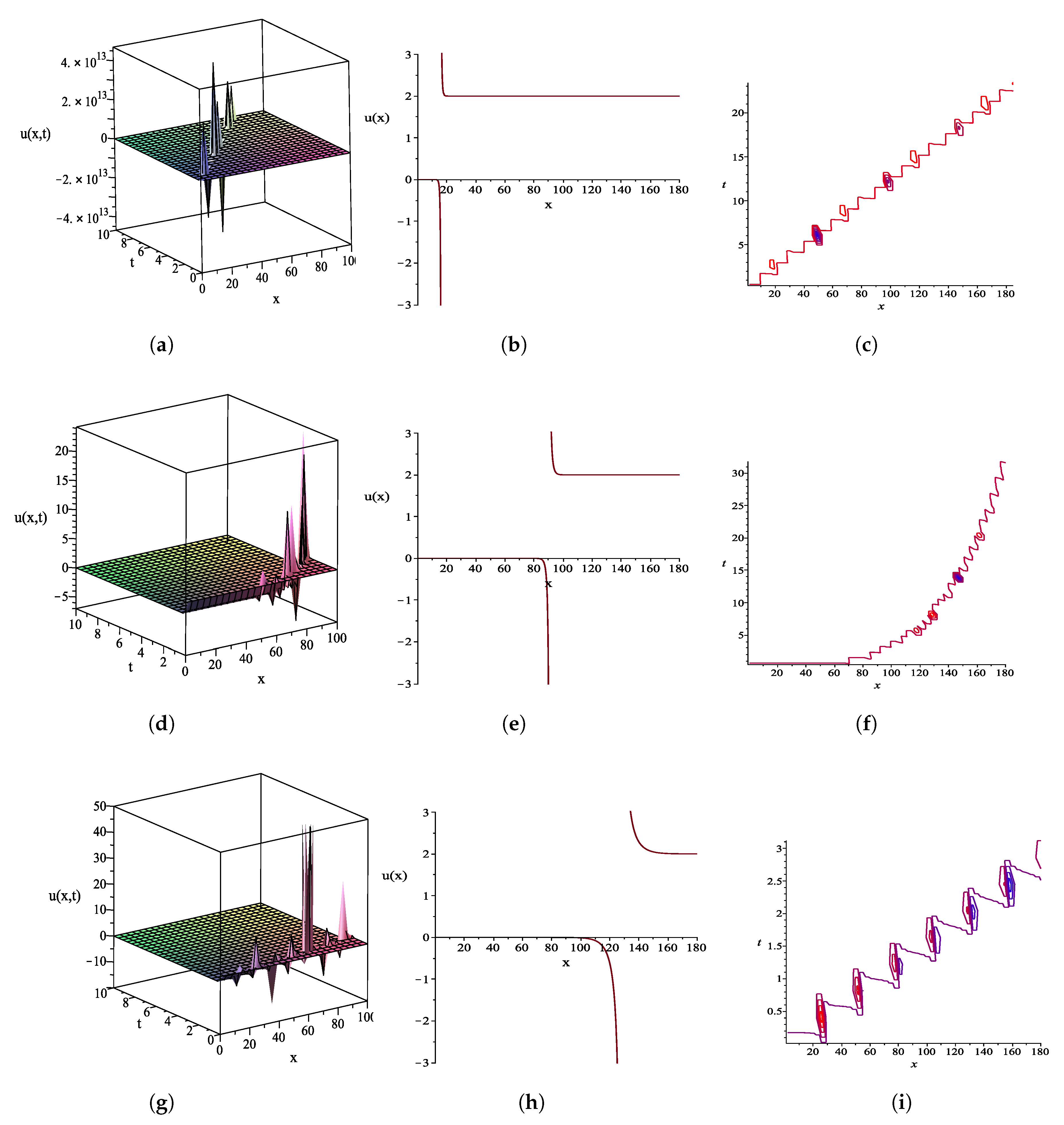
4. Graphical Representations of Some Exact Solutions and Their Physical Explanations
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hashim, I. Adomian decomposition method for solving BVPs for fourth-order integro-differential equations. J. Comput. Appl. Math. 2006, 193, 658–664. [Google Scholar] [CrossRef]
- Basak, K.C.; Ray, P.C.; Bera, R.K. Solution of non-linear Klein-Gordon equation with a quadratic non-linear term by Adomian decomposition method. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 718–723. [Google Scholar] [CrossRef]
- Gorder, R.A.V. The variational iteration method is a special case of the homotopy analysis method. Appl. Math. Lett. 2015, 45, 81–85. [Google Scholar] [CrossRef]
- Wazwaz, A. The variational iteration method: A reliable analytic tool for solving linear and nonlinear wave equations. Comput. Math. Appl. 2007, 54, 926–932. [Google Scholar] [CrossRef]
- Nazari, D.; Shahmorad, S. Application of the fractional differential transform method to fractional-order integro-differential equations with nonlocal boundary conditions. J. Comput. Appl. Math. 2010, 234, 883–891. [Google Scholar] [CrossRef]
- Bera, P.; Sil, T. Homotopy perturbation method in quantum mechanical problems. Appl. Math. Comput. 2012, 219, 3272–3278. [Google Scholar] [CrossRef]
- Nik, H.S.; Effati, S.; Shirazian, M. An approximate-analytical solution for the Hamilton-Jacobi-Bellman equation via homotopy perturbation method. Appl. Math. Model. 2012, 36, 5614–5623. [Google Scholar]
- Qin, Z.; Mu, G.; Ma, H. The ()-expansion method for the fifth-order forms of KdV-Sawada-Kotera equation. Appl. Math. Comput. 2013, 222, 29–33. [Google Scholar] [CrossRef]
- Aslan, İ. Exact solutions for fractional DDEs via auxiliary equation method coupled with the fractional complex transform. Math. Methods Appl. Sci. 2016, 39, 5619–5625. [Google Scholar] [CrossRef]
- Guner, O.; Bekir, A.; Ünsal, Ö. Two reliable methods for solving the time fractional Clannish Random Walkers Parabolic equation. Opt. Int. J. Light Electron Opt. 2016, 127, 9571–9577. [Google Scholar] [CrossRef]
- Abdel-Salam, E.A.B.; Gumma, E.A. Analytical solution of nonlinear space-time fractional differential equations using the improved fractional Riccati expansion method. Ain Shams Eng. J. 2015, 6, 613–620. [Google Scholar] [CrossRef]
- Abdel-Salam, E.A.B.; Yousif, E.A.; El-Aasser, M.A. Analytical solution of the space-time fractional nonlinear Schrödinger equation. Rep. Math. Phys. 2016, 77, 19–34. [Google Scholar] [CrossRef]
- Gómez, S.; Cesar, A. A nonlinear fractional Sharma–Tasso–Olver equation: New exact solutions. Appl. Math. Comput. 2015, 266, 385–389. [Google Scholar] [CrossRef]
- Hubert, M.B.; Betchewe, G.; Doka, S.Y.; Crepin, K.T. Soliton wave solutions for the nonlinear transmission line using the Kudryashov method and the ()-expansion method. Appl. Math. Comput. 2014, 239, 299–309. [Google Scholar] [CrossRef]
- Ryabov, P.N.; Sinelshchikov, D.I.; Kochanov, M.B. Application of the Kudryashov method for finding exact solutions of the high order nonlinear evolution equations. Appl. Math. Comput. 2011, 218, 3965–3972. [Google Scholar] [CrossRef]
- Mohyud-Din, S.T.; Nawaz, T.; Azhar, E.; Akbar, M.A. Fractional sub-equation method to space-time fractional Calogero-Degasperis and potential Kadomtsev-Petviashvili equations. J. Taibah Univ. Sci. 2017, 11, 258–263. [Google Scholar] [CrossRef]
- Abdel-Salam, E.A.; Hassan, G.F. Solutions to class of linear and nonlinear fractional differential equations. Commun. Theor. Phys. 2016, 65, 127. [Google Scholar] [CrossRef]
- Wang, M.; Li, X.; Zhang, J. The ()-expansion method and travelling wave solutions of nonlinear evolution equations in mathematical physics. Phys. Lett. A 2008, 372, 417–423. [Google Scholar] [CrossRef]
- Zhang, J.; Jiang, F.; Zhao, X. An improved ()-expansion method for solving nonlinear evolution equations. Int. J. Comput. Math. 2010, 87, 1716–1725. [Google Scholar] [CrossRef]
- Akbar, M.A.; Ali, N.H.M.; Zayed, E.M.E. A generalized and improved ()-expansion method for nonlinear evolution equations. Math. Probl. Eng. 2012, 2012, 459879. [Google Scholar] [CrossRef]
- Hafez, M.; Alam, M.N.; Akbar, M.A. Exact traveling wave solutions to the Klein-Gordon equation using the novel ()-expansion method. Results Phys. 2014, 4, 177–184. [Google Scholar] [CrossRef]
- Alam, M.N.; Akbar, M.A.; Mohyud-Din, S.T. A novel ()-expansion method and its application to the Boussinesq equation. Chin. Phys. B 2014, 23, 020203. [Google Scholar] [CrossRef]
- Alam, M.N.; Akbar, M.A. Traveling wave solutions of the nonlinear (1+1)-dimensional modified Benjamin-Bona-Mahony equation by using novel ()-expansion method. Phys. Rev. Res. Int. 2014, 4, 147–165. [Google Scholar]
- Hafez, M.G.; Zheng, B.; Akbar, M. Exact travelling wave solutions of the coupled nonlinear evolution equation via the Maccari system using novel ()-expansion method. Egypt. J. Basic Appl. Sci. 2015, 2, 206–220. [Google Scholar] [CrossRef][Green Version]
- Alam, M.N.; Belgacem, F.B.M.; Akbar, M.A. Analytical Treatment of the Evolutionary (1+ 1)-Dimensional Combined KdV-mKdV Equation via the Novel ()-Expansion Method. J. Appl. Math. Phys. 2015, 3, 1571. [Google Scholar] [CrossRef]
- Alam, M.N.; Hafez, M.; Belgacem, F.B.M.; Akbar, M.A. Applications of the novel ()-expansion method to find new exact traveling wave solutions of the nonlinear coupled Hsiggs field equation. Nonlinear Stud. 2015, 22, 613–633. [Google Scholar]
- Hafez, M. New travelling wave solutions of the (1+1)-dimensional cubic nonlinear Schrödinger equation using novel ()-expansion method. Beni-Suef Univ. J. Basic Appl. Sci. 2016, 5, 109–118. [Google Scholar] [CrossRef]
- Alam, M.N.; Belgacem, F.B.M. Exact Traveling Wave Solutions for the (1+ 1)-Dimensional Compound KdVB Equation via the Novel ()-Expansion Method. Int. J. Mod. Nonlinear Theory Appl. 2016, 5, 28. [Google Scholar] [CrossRef]
- Akbar, M.A.; Alam, M.N.; Hafez, M.G. Application of the novel ()-expansion method to construct traveling wave solutions to the positive Gardner–KP equation. Indian J. Pure Appl. Math. 2016, 47, 85–96. [Google Scholar] [CrossRef]
- Islam, M.S.; Khan, K.; Arnous, A.H. Generalized Kudryashov method for solving some (3+ 1)-dimensional nonlinear evolution equations. New Trends Math. Sci. 2015, 3, 46. [Google Scholar]
- Kaplan, M.; Bekir, A.; Akbulut, A. A generalized Kudryashov method to some nonlinear evolution equations in mathematical physics. Nonlinear Dyn. 2016, 85, 2843–2850. [Google Scholar] [CrossRef]
- Mahmud, F.; Samsuzzoha, M.; Akbar, M.A. The generalized Kudryashov method to obtain exact traveling wave solutions of the PHI-four equation and the Fisher equation. Results Phys. 2017, 7, 4296–4302. [Google Scholar] [CrossRef]
- Biswas, A.; Sonmezoglu, A.; Ekici, M.; Mirzazadeh, M.; Zhou, Q.; Moshokoa, S.P.; Belic, M. Optical soliton perturbation with fractional temporal evolution by generalized Kudryashov’s method. Optik 2018, 164, 303–310. [Google Scholar] [CrossRef]
- Nestor, S.; Justin, M.; Douvagai; Betchewe, G.; Doka, S.Y.; Kofane, T. New Jacobi elliptic solutions and other solutions with quadratic–Cubic nonlinearity using two mathematical methods. Asian-Eur. J. Math. 2018, 13, 2050043. [Google Scholar] [CrossRef]
- Houwe, A.; Justin, M.; Doka, S.Y.; Crepin, K.T. New traveling wave solutions of the perturbed nonlinear Schrödingers equation in the left–handed metamaterials. Asian-Eur. J. Math. 2018, 13, 2050022. [Google Scholar] [CrossRef]
- Lu, D.; Seadawy, A.R.; Khater, M.M. Structure of solitary wave solutions of the nonlinear complex fractional generalized Zakharov dynamical system. Adv. Differ. Equ. 2018, 2018, 266. [Google Scholar] [CrossRef]
- Demiray, S.T.; Bulut, H. Soliton solutions of some nonlinear evolution problems by GKM. Neural Comput. Appl. 2019, 31, 287–294. [Google Scholar] [CrossRef]
- Habib, M.; Ali, H.S.; Miah, M.M.; Akbar, M.A. The generalized Kudryashov method for new closed form traveling wave solutions to some NLEEs. AIMS Math. 2019, 4, 896. [Google Scholar] [CrossRef]
- Wazwaz, A.M. New solitons and kinks solutions to the Sharma-Tasso-Olver equation. Appl. Math. Comput. 2007, 188, 1205–1213. [Google Scholar] [CrossRef]
- Pan, J.T.; Chen, W.Z. A new auxiliary equation method and its application to the Sharma-Tasso-Olver model. Phys. Lett. A 2009, 373, 3118–3121. [Google Scholar]
- Bekir, A.; Boz, A. Exact solutions for nonlinear evolution equations using Exp-function method. Phys. Lett. A 2008, 372, 1619–1625. [Google Scholar] [CrossRef]
- He, Y.; Li, S.; Long, Y. Exact solutions to the Sharma-Tasso-Olver equation by using improved ()-expansion method. J. Appl. Math. 2013, 2013, 247234. [Google Scholar] [CrossRef]
- Uğurlu, Y.; Kaya, D. Analytic method for solitary solutions of some partial differential equations. Phys. Lett. A 2007, 370, 251–259. [Google Scholar] [CrossRef]
- Khalil, R.; Horani, M.A.; Yousef, A.; Sababheh, M. A new definition of fractional derivative. J. Comput. Appl. Math. 2014, 264, 65–70. [Google Scholar] [CrossRef]
- Kumar, D.; Seadawy, A.R.; Joardar, A.K. Modified Kudryashov method via new exact solutions for some conformable fractional differential equations arising in mathematical biology. Chin. J. Phys. 2018, 56, 75–85. [Google Scholar] [CrossRef]
- Rezazadeh, H.; Korkmaz, A.; Eslami, M.; Vahidi, J.; Asghari, R. Traveling wave solution of conformable fractional generalized reaction Duffing model by generalized projective Riccati equation method. Opt. Quantum Electron. 2018, 50, 150. [Google Scholar] [CrossRef]
- Korkmaz, A. Explicit exact solutions to some one-dimensional conformable time fractional equations. Waves Random Complex Media 2019, 29, 124–137. [Google Scholar] [CrossRef]
- Ekici, M.; Mirzazadeh, M.; Eslami, M.; Zhou, Q.; Moshokoa, S.P.; Biswas, A.; Belic, M. Optical soliton perturbation with fractional-temporal evolution by first integral method with conformable fractional derivatives. Optik 2016, 127, 10659–10669. [Google Scholar] [CrossRef]
- Tarasov, V.E. No nonlocality. No fractional derivative. Commun. Nonlinear Sci. Numer. Simul. 2018, 62, 157–163. [Google Scholar] [CrossRef]
- He, J.H.; Elagan, S.; Li, Z. Geometrical explanation of the fractional complex transform and derivative chain rule for fractional calculus. Phys. Lett. A 2012, 376, 257–259. [Google Scholar] [CrossRef]
- Su, W.H.; Yang, X.J.; Jafari, H.; Baleanu, D. Fractional complex transform method for wave equations on Cantor sets within local fractional differential operator. Adv. Differ. Equ. 2013, 2013, 97. [Google Scholar] [CrossRef]
- Güner, O.; Bekir, A.; Cevikel, A.C. A variety of exact solutions for the time fractional Cahn–Allen equation. Eur. Phys. J. Plus 2015, 130, 146. [Google Scholar] [CrossRef]
- Sirisubtawee, S.; Koonprasert, S.; Khaopant, C.; Porka, W. Two Reliable Methods for Solving the (3 + 1)-Dimensional Space-Time Fractional Jimbo-Miwa Equation. Math. Probl. Eng. 2017, 2017, 1–30. [Google Scholar] [CrossRef]
- Zhu, S.D. The generalizing Riccati equation mapping method in non-linear evolution equation: Application to (2+1)-dimensional Boiti-Leon-Pempinelle equation. Chaos Solitons Fractals 2008, 37, 1335–1342. [Google Scholar]
- Zheng, C.L. Comments on “The generalizing Riccati equation mapping method in nonlinear evolution equation: Application to (2 + 1)-dimensional Boiti-Leon-Pempinelle equation”. Chaos Solitons Fractals 2009, 39, 1493–1495. [Google Scholar] [CrossRef]
- Uddin, M.H.; Khan, M.A.; Akbar, M.A.; Haque, M.A. Multi-solitary wave solutions to the general time fractional Sharma–Tasso–Olver equation and the time fractional Cahn–Allen equation. Arab. J. Basic Appl. Sci. 2019, 26, 193–201. [Google Scholar] [CrossRef]
- Guner, O.; Korkmaz, A.; Bekir, A. Dark soliton solutions of space-time fractional Sharma–Tasso–Olver and potential Kadomtsev–Petviashvili equations. Commun. Theor. Phys. 2017, 67, 182. [Google Scholar] [CrossRef]
- Kaplan, M.; Bekir, A. A novel analytical method for time-fractional differential equations. Optik 2016, 127, 8209–8214. [Google Scholar] [CrossRef]
- Jafari, H.; Tajadodi, H.; Baleanu, D.; Al-Zahrani, A.; Alhamed, Y.; Zahid, A. Fractional sub-equation method for the fractional generalized reaction Duffing model and nonlinear fractional Sharma-Tasso-Olver equation. Open Phys. 2013, 11, 1482–1486. [Google Scholar] [CrossRef]
- Chen, C.; Jiang, Y.L. Simplest equation method for some time-fractional partial differential equations with conformable derivative. Comput. Math. Appl. 2018, 75, 2978–2988. [Google Scholar] [CrossRef]
- Rezazadeh, H.; Khodadad, F.S.; Manafian, J. New structure for exact solutions of nonlinear time fractional Sharma–Tasso–Olver equation via conformable fractional derivative. Appl. Appl. Math. Int. J. 2017, 12, 13–21. [Google Scholar]
- Yaslan, H.Ç.; Girgin, A. Exp-function method for the conformable space-time fractional STO, ZKBBM and coupled Boussinesq equations. Arab. J. Basic Appl. Sci. 2019, 26, 163–170. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sirisubtawee, S.; Koonprasert, S.; Sungnul, S. New Exact Solutions of the Conformable Space-Time Sharma–Tasso–Olver Equation Using Two Reliable Methods. Symmetry 2020, 12, 644. https://doi.org/10.3390/sym12040644
Sirisubtawee S, Koonprasert S, Sungnul S. New Exact Solutions of the Conformable Space-Time Sharma–Tasso–Olver Equation Using Two Reliable Methods. Symmetry. 2020; 12(4):644. https://doi.org/10.3390/sym12040644
Chicago/Turabian StyleSirisubtawee, Sekson, Sanoe Koonprasert, and Surattana Sungnul. 2020. "New Exact Solutions of the Conformable Space-Time Sharma–Tasso–Olver Equation Using Two Reliable Methods" Symmetry 12, no. 4: 644. https://doi.org/10.3390/sym12040644
APA StyleSirisubtawee, S., Koonprasert, S., & Sungnul, S. (2020). New Exact Solutions of the Conformable Space-Time Sharma–Tasso–Olver Equation Using Two Reliable Methods. Symmetry, 12(4), 644. https://doi.org/10.3390/sym12040644




