Mass, Spacetime Symmetry, de Sitter Vacuum, and the Higgs Mechanism

Abstract

We address the question of the intrinsic relation between mass, gravity, spacetime symmetry, and the Higgs mechanism implied by involvement of the de Sitter vacuum as its basic ingredient (a false vacuum). Incorporating the de Sitter vacuum, the Higgs mechanism implicitly incorporates the generic relation between mass, gravity, and spacetime symmetry revealed in the frame of General Relativity for all objects involving the de Sitter vacuum. We overview two observational cases which display and verify this relation, the case known as “negative mass square problem” for neutrino, and appearance of a minimal length scale in $e^{+}{e}^{-}$ annihilation.

1. Introduction

In the Higgs mechanism, fermions acquire masses via spontaneous symmetry breaking of incorporated scalar fields so that a symmetry of the Lagrangian is not respected by the vacuum states [1,2,3] (for overview [4,5]).

In the current literature, there exist proposals concerning the relation of mass with spacetime symmetry [6,7] and the relation of mass with gravity [8].

The first proposal is developed on the basis of the concept of spontaneous breaking of the Lorentz symmetry [6]. The related mechanism for mass generation [7] is called Higgs-like since it appeals to the basic idea of the Higgs mechanism, but presents an alternative mechanism for generation of fermion masses within the frame of the standard theory without introducing arbitrary parameters for charged leptons. This mechanism does not involve the Yukawa couplings depending on arbitrary parameters neither requires the preparation of right-handed singlets in advance to distinguish charged leptons from neutrinos and generates the mass of a charged lepton by the vacuum expectation values of gauge potentials. In this mechanism, a right-handed fermion is generated from a left-handed doublet by absorbing the Nambu-Goldstone mesons generated by spontaneous breaking of the Lorentz symmetry [7].

In the second proposal, a mass is related to gravity presented in the frame of ratio gravity (RG) which considers gravity as gravitational field in the flat (Minkowski) spacetime; the curvature originates from a deformation of a cross ratio, resulting in a mathematical structure similar to general relativity ([9,10] and references therein). Mass generation is considered in a simple RG model in the flat spacetime, in which equations admit two wave solutions coupled to a symmetry broken scalar field. Theory based on the Lagrangian with massless fermion doublets coupling a scalar field, gives in one-loop approximation the positive masses for the lepton and quark families originated by different SU2 algebras of gauge transformation [8].

In this paper, we point out the generic relation of the Higgs mechanism for mass generation with gravity and spacetime symmetry, implicitly encoded in it due to involvement of the de Sitter vacuum (as a false vacuum with $p=-\rho$), and overview two observational cases which display and verify this relation. The point is that by invoking the spontaneous symmetry breaking for scalar fields, the Higgs mechanism incorporates the de Sitter vacuum as its basic ingredient. The key point is that in the frame of General Relativity mass of an object involving de Sitter vacuum as its basic ingredient (instead of a central singularity), is generically related to gravity and breaking of spacetime symmetry [11]. Incorporating de Sitter vacuum, the Higgs mechanism actually implicitly incorporates the relation of a particle mass with gravity and spacetime symmetry.

In all cases of appearance of the de Sitter vacuum in a compact object its stress-energy tensor in the Einstein equations has the algebraic structure such that $T_t^t=T_r^r$, where $T_t^t$ and $T_r^r$ are the eigenvalues of a stress-energy tensor in the comoving reference frame (co-rotating in the case of a spinning object), identified as $T_t^t=\rho ;T_t^t=-p_r;T_{\theta }^{\theta }=T_{\varphi }^{\varphi }=-p_{\perp }$ in the spherical and axial coordinates $r,\theta ,\varphi$ centered in the origin of an object ($\rho$ is the density and $p_r,p_{\perp }$ are the principal pressures). In this case mass of an object is generically related to its interior de Sitter vacuum, $T_{\nu }^{\mu }=\Lambda {\delta }_{\nu }^{\mu },\Lambda =8\pi G\rho (r\to 0)$, and breaking of spacetime symmetry from the de Sitter group in its origin to the Poincaré group at infinity in the asymptotically flat spacetime, $\left(deSittergroup\right)0\leftarrow r\to \infty (Poincaregroup)$ [11], or to the de Sitter group with another value of vacuum density in the de Sitter background, $T_{\nu }^{\mu }=\lambda {\delta }_{\nu }^{\mu },\lambda =8\pi G\rho (r\to \infty )$, with $\lambda <\Lambda$ (for a review [12]). This is the basic property of all objects described by regular solutions of this class independently on a physical origin of a source term in the Einstein equations. It is well known that there exists infinitely many distributions of matter which contribute to a source term in the Einstein equation which behaves as a cosmological constant, $T_{\mu \nu }={\left(8\pi G\right)}^{-1})\Lambda g_{\mu \nu };\Lambda =8\pi G\rho =const$ (see, e.g., [13]), responsible for repulsive gravity due to basic properties of the de Sitter geometry, independently of an underlying particular model. In the case of the Higgs mechanism it is the scalar field in the state of the de Sitter vacuum that represents the matter distribution responsible for the de Sitter geometry.

The direct consequence of involvement of de Sitter geometry generated by the de Sitter vacuum with the non-zero energy density is the essential and intrinsic involvement of gravity in the interaction vertex. The symmetry group induced by the Higgs mechanism in the gravito-electroweak vertex is the de Sitter group, and particles in the vertex are presented by the eigenstates of the Casimir operators in the de Sitter spacetime. The further evolution of particle states in the Minkowski background results in the symmetry change. One can expect that the flavor could emerge due to breaking of spacetime symmetry from the de Sitter group around the vertex [14,15].

Applying this approach to the observational case of neutrino mass-square differences, we find that the de Sitter symmetry in the gravito-electroweak vertex leads to the exact bi-maximal mixing which allows explaining the anomalous results known as “negative mass squared problem” for neutrino and to estimate the gravito-electroweak scale from the data on the solar and atmospheric neutrino which yields the same scale, $M_{unif}\sim (6-15)$ TeV, as predicted by theories of gravito-electroweak unification [14,15,16].

Another observational case is the appearance of a minimal length scale in $e^{+}{e}^{-}$ annihilation. Experimental data collected during fourteen years and worked out by the standard QED methods with the $O\left({\alpha }^3\right)$ accuracy, reveal with a $5\sigma$ significance the existence of a characteristic minimal length $l_e=1.57\times {10}^{-17}$ cm at the scale $E=1.253$ TeV in the annihilation reaction $e^{+}{e}^{-}\to \gamma \gamma \left(\gamma \right)$ [17,18]. It is the purely electromagnetic reaction and we can base analysis on the results obtained in the nonlinear electrodynamics coupled to gravity (NED-GR) and satisfying the weak energy condition (WEC) which requires non-negative energy density as measured by any local observer and ensures positivity of density in the de Sitter interiors.

The NED-GR equations predict, for an arbitrary gauge invariant lagrangian without any additional requirements except WEC, the existence of spinning electrically charged electromagnetic solitons related by electromagnetic and gravitational interactions, with the gyromagnetic ratio $g=2$ for a distant observer. They are described in the self-consistent way by the source-free NED-GR dynamical equations; the source term in the Einstein equations is presented by the nonlinear electromagnetic field itself which always has the algebraic structure $T_t^t=T_r^r$. The basic generic model-independent feature of the electromagnetic soliton is the equatorial disk of the de Sitter vacuum with properties of a perfect conductor and ideal diamagnetic [19]. Along the ring confining the de Sitter disk flows a superconducting current which serves as a nondissipative source of the electromagnetic fields responsible for an unlimited life time of a spinning object [20], and as the source of its intrinsic magnetic momentum [21]. For electromagnetic spinning soliton with the parameters of the electron, $m_{e}a=\hslash /2,g=2$, a superconducting ring current is evaluated as $j_{\varphi }=79.277A$ [21]. Basic model-independent features of an electromagnetic soliton visualizing the electron as an extended particle, can shed some light on the physical mechanism underlying appearance of a minimal length scale in annihilation [18].

This case suggests and illustrates also another direct consequence of the intrinsic involvement of the de Sitter vacuum in mass generation by the Higgs mechanism - the implicit promotion of an extended (instead of a point-like) massive particle with the de Sitter vacuum trapped in its interior.

In what follows, we overview these two observational cases which show and verify the deep intrinsic relation between the Higgs mechanism, gravity and spacetime symmetry existing due to intrinsic involvement of the de Sitter vacuum.

In Section 2 we overview the case of negative mass-squared difference for neutrinos, and in Section 3 the case of the minimal length in annihilation and its possible explanation by the basic properties of spinning electrically charged electromagnetic soliton. Section 4 contains conclusions.

2. Spacetime Symmetry as Origin of Mass-Square Differences for Neutrino and Gravito-Electroweak Scale

In particle physics theory, masses of particles are exactly zero only if they are protected by the unbroken gauge symmetry, for example the photon is protected by U(1) gauge symmetry of electromagnetism, associated with the conservation of the electric charge. There is no corresponding exact gauge symmetry to protect the lepton number, so it is expected to be violated and neutrinos to acquire masses. This is the generally accepted interpretation of the observed neutrino oscillations, eventually due to mixing the non-degenerate mass eigenstates [22,23]. The origin of particle masses is expected to be found at energies ∼${10}^3$ GeV [22].

The appearance of the de Sitter vacuum in the interaction region, induced by the Higgs mechanism intrinsically involving false vacuum, requires the description of a particle state by the eigenstates of the Casimir operators in the de Sitter spacetime.

In the interaction vertex, a particle is described by an eigenstate of the de Sitter Casimir invariants, $|I_1^{\prime },I_2^{\prime }⟩$ which are the eigenvalues of the de Sitter Casimir operators $I_1$ and $I_2$ [24]. To study influence of de Sitter vacuum on a mass we need $I_1$ which reads

$$I_1=-{\Pi }_{\mu }{\Pi }^{\mu }-\frac{1}{2r_0^2}{J}_{\mu \nu }{J}^{\mu \nu }$$

(1)

where

$${\Pi }_{\mu }=\left(1+\frac{r^2-c^2{t}^2}{4r_0^2}\right)P_{\mu }+\frac{1}{2r_0^2}{x}^{\nu }{J}_{\mu \nu }.$$

(2)

The scale $r_0$ is the characteristic de Sitter radius related to the vacuum density ${\rho }_0$ as $r_0^2=3c^2/\left(8\pi G{\rho }_0\right)$. In the interaction region $r^2-c^2{t}^2\ll r_0^2$ [14], and the operator $I_1$ is approximated by

$$I_1\approx -P_{\mu }{P}^{\mu }-\frac{1}{r_0^2}\left({\mathbf{J}}^2-{\mathbf{K}}^2\right)$$

(3)

where $J_{ij}=-J_{ji}={ϵ}_{ijk}{J}_k$ and $J_{i0}=-J_{0i}=-K_i$, the indices $i,j,k$ take the values $1,2,3$. The operators $\mathbf{J}$ are generators of rotation and $\mathbf{K}$ are generators of Lorentz boosts:

$${\mathbf{J}}_R=\hslash \frac{\sigma }{2},{\mathbf{K}}_R=-i\hslash \frac{\sigma }{2};{\mathbf{J}}_L=\hslash \frac{\sigma }{2},{\mathbf{K}}_L=+i\hslash \frac{\sigma }{2}$$

(4)

for the right-handed and left-handed fields, respectively. Here $\sigma$ denotes the Pauli matrices.

This gives for the Casimir operator $I_1$ and its eigenvalues which are denoted by the prime

$$I_1\approx --P_{\mu }{P}^{\mu }-\frac{{\hslash }^2}{2r_0^2}{\sigma }^2;I_1^{\prime }={\mu }^2{c}^2\pm \frac{{\hslash }^2}{2r_0^2}.$$

(5)

where the additional term $\pm {\hslash }^2/2r_0^2$ is related to the eigenvalues of the unit matrix which is the product of the Pauli matrices $\sigma$. De Sitter spacetime has the same maximal symmetry as the Minkowski spacetime, since it is spacetime of the constant (positive) curvature which is its only but essential difference from the Minkowski spacetime. In the case when its curvature radius $r_0\to \infty$ (Minkowski spacetime) the additional term disappears.

When the state $|I_1^{\prime }⟩$ propagates in the Minkowski space, it appears as a linear superposition of two different mass eigenstates [14]

$$m_1^2={\mu }^2+\frac{{\hslash }^2}{2c^2{r}_0^2},m_2^2={\mu }^2-\frac{{\hslash }^2}{2c^2{r}_0^2}$$

(6)

with the equal weights. The de Sitter symmetry in the gravito-electroweak vertex produces an exact bi-maximal mixing for neutrinos. For ${\hslash }^2/\left(2r_0^2\right)>{\mu }^2{c}^2$, $m_2^2$ becomes negative.

De Sitter bi-maximal mixing offers the natural explanation [16] for the anomalous results referred to as the “negative mass square problem”. The average value given by the Particle Data Group in 1994 [25] $m_{\nu }^2=-54\pm 30{\mathrm{eV}}^2/c^4$ displays a shift to the unphysical region. Later measurements confirm this effect [26,27,28,29,30,31,32,33], e.g., $m_{{\overline{\nu }}_e}^2=-22\pm 4.8{\mathrm{eV}}^2/c^4$ [27].

The data on the solar and atmospheric neutrino yield, in two-flavor mixing approximation, the following values of mass-squared difference for the neutrino oscillation [23]

$$\Delta m_{atm}^2=2.5\times {10}^{-3}{\mathrm{eV}}^2;\Delta m_{sol}^2=6.9\times {10}^{-5}{\mathrm{eV}}^2$$

(7)

which allow relating the gravito-electroweak unification scale from the observational data. With taking into account $r_0^2=3c^2/\left(8\pi G{\rho }_0\right)$, the mass-squared difference reads

$$\Delta m^2=\frac{{\hslash }^2}{c^2{r}_0^2}=\frac{8\pi }{3}\frac{{\rho }_0}{{\rho }_{Pl}}{m}_{Pl}^2$$

(8)

for both the right and left handed fields [14].

Identifying ${\rho }_0$ as the gravito-electroweak scale $M_{unif}$, we obtain the relation which connects the mass-squared difference with the unification scale [14]

$$\Delta m^2=\frac{8\pi }{3}{\left(\frac{M_{unif}}{m_{Pl}}\right)}^4{m}_{Pl}^2,$$

(9)

and the unification scale is immediately read off from (9) as

$$M_{unif}={\left[\frac{3}{8\pi }\left(\frac{\Delta m^2}{m_{Pl}^2}\right)\right]}^{1/4}{m}_{Pl}.$$

(10)

For the mass-squared differences of neutrinos produced by the de Sitter mixing, the mass-squared difference for atmospheric and solar neutrino data in (7) yield the unification scale

$$M_{unif\left(atm\right)}\simeq 14.5\mathrm{TeV};M_{unif\left(sol\right)}\simeq 5.9\mathrm{TeV}$$

(11)

These values correspond to $r_{0\left(atm\right)}=0.4\times {10}^{-3}$ cm, and $r_{0\left(sol\right)}=2.3\times {10}^{-3}$ cm, which justifies accuracy of approximation (3): for a particle with mass $<m{>}_{{\nu }_e}=0.39$ eV, characteristic geometrical size $r_s\propto {\left(r_0^2{r}_g\right)}^{1/3}$ (where $r_g=2Gm{c}^{-2}$) is $r_s\sim {10}^{-23}$, and the Compton size ${\lambda }_c=\hslash /mc$ is ${\lambda }_c\sim {10}^{-5}$ cm.

Estimates for the gravito-electroweak scale (11) appear at the same scale as predicted by theories of the gravito-electroweak unification [34,35,36].

3. Minimal Length Scale in $e^{+}{e}^{-}$ Annihilation

3.1. Observational Case

Research on the annihilation reaction ${\mathit{e}}^{\mathbf{+}}{\mathit{e}}^{\mathbf{-}}\mathbf{\to }\mathit{\gamma }\mathit{\gamma }\mathbf{\left(}\mathit{\gamma }\mathbf{\right)}$ has been carried out since 1989 to 2003 with the data from VENUS, TOPAZ, ALEPH, DELPHI, L3 and OPAL at energies from $\sqrt{s}$ = 55 GeV to 207 GeV where $\sqrt{s}$ is the center-of-mass energy. It resulted in the limit on the maximal resolution at the energy $E=1.253$ TeV by the length scale $l_e\simeq 1.57\times {10}^{-17}$ cm with the 5$\sigma$ significance [17,18]. The 2.6$\sigma$ effect was reported for the $e^{+}{e}^{-}\to e^{+}{e}^{-}\left(\gamma \right)$ reaction [37]. In our case the higher significance resulted from the richer statistics with including in the ${\chi }^2$ test the most extensive available data set, which ultimately allowed to get the convincing minimum in the ${\chi }^2$ curve shown in Figure 1 [17,18].

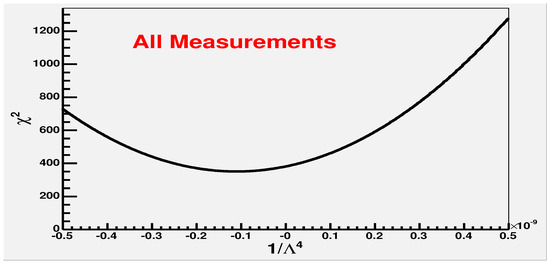
Figure 1. A minimum in the ${\chi }^2$ fit with $P=1/{\Lambda }^4$.

The reaction $e^{+}{e}^{-}\to \gamma \gamma \left(\gamma \right)$ is purely electromagnetic. It proceeds via the exchange of a virtual electron in the t- and u-channels with the forbidden s-channel, and is not interfered by the $Z^0$ decay. Differential cross sections have been measured at the energies ranging from $\sqrt{s}$ = 55 GeV to 207 GeV [38,39,40,41,42,43,44,45,46]. The calculations in the frame of QED-${\alpha }^3$ with the radiative corrections up to $O\left({\alpha }^3\right)$ and comparison of the QED predictions with the experimental data has been carried out [47] by constraining the models with an excited electron replacing the virtual electron [48,49,50] and with the deviation from QED due to an effective interaction with the non-standard $e^{+}{e}^{-}\gamma$ couplings and $e^{+}{e}^{-}\gamma \gamma$ contact terms [51,52,53]. Applying the standard QED methods assumes a scattering center as a point. For an extended particle, the QED cross section would be modified provided that the characteristic particle size exceeds the test distances (corresponding to the CM-scattering energies). For the electron, both its Compton size ${\lambda }_e=\hslash /\left(m_{e}c\right)=3.9\times {10}^{-11}$ cm and its classical electromagnetic radius $r_e=e^2/\left(m_e{c}^2\right)=2.8\times {10}^{-13}$ cm are much larger than the characteristic length $l_e=1.57\times {10}^{-17}$ cm appeared in the ${\chi }^2$ test. The applied QED hypotheses predict an increase in the total QED-${\alpha }^3$ cross-section. Contrary to the QED predictions, the ${\chi }^2$ fit displays with the $5\sigma$ significance, the minimum with the negative fit parameter $P={(1/{\Lambda }^4)}_{best}=-(4.05\pm 0.73)\times {10}^{-13}{\mathrm{GeV}}^{-4}$ [17,18], where $\Lambda$ is the QED cutoff parameter.

The minimum in the ${\chi }^2$ fit corresponds to the distance of the closest approach of annihilating particles, $l_e=1.57\times {10}^{-17}$ cm at the energy $E=1.253$ TeV. This case suggests a description of annihilating particles as extended objects and requires some idea about their internal structure. Story of an extended electron goes back to its discovery by Sir Joseph John Thomson in 1897. The early models of an extended electron involving a charge distribution, encountered the problem of preventing an electron from scattering apart by the Coulomb repulsion, which enforced to introduce cohesive forces of non-electromagnetic origin (the Poincaré stress) [54] (for a review [18]). At present time various comprehensive models have been developed without appealing to a charge distribution ([20,55,56,57,58] and references therein).

To look for a physical mechanism responsible for appearance of the minimal length in annihilation by involving gravity and the de Sitter vacuum which is able to prevent a formation of singularities (and related divergences of physical quantities) by its intrinsic negative pressure, we appeal to the relevant generic model-independent feature of a spinning electrically charged NED-GR soliton—its interior de Sitter vacuum [19] (for a review [59,60,61]).

3.2. Basic Features of Spinning Electromagnetic Soliton

In nonlinear electrodynamics developed by Born and Infeld with the aim (i) to describe particles and electromagnetic field in the frame of one physical entity and (ii) to avoid the divergences of physical quantities [62], electromagnetic energy was made finite by imposing an upper cut-off on the electric field related to the electron radius, but geometry remained singular [62]. Five decades later NED theories were identified as the effective low-energy limits of the string/M-theories [63,64,65].

Both basic points of the Born-Infeld program can be realized in the self-consistent way in nonlinear electrodynamics minimally coupled to gravity. Source-free NED-GR equations admit the class of regular solutions, which describe regular electrically charged objects [19,59,66] including electromagnetic spinning solitons defined, following Coleman [67], as non-singular non-dissipative particle-like structures keeping themselves together by their self-interaction (in this case electromagnetic and gravitational).

The NED-GR dynamical equations are obtained with the action

$$S=\frac{1}{16\pi G}\int d^{4}x\sqrt{-g}[R-\mathcal{L}\left(F\right)];F=F_{\mu \nu }{F}^{\mu \nu }$$

(12)

where R is the scalar curvature, and $F_{\mu \nu }={\partial }_{\mu }{A}_{\nu }-{\partial }_{\nu }{A}_{\mu }$ is the electromagnetic field. The gauge-invariant electromagnetic Lagrangian $\mathcal{L}\left(F\right)$ is an arbitrary function of the field invariant F. The Lagrangian $\mathcal{L}\left(F\right)$ and its derivative ${\mathcal{L}}_F=d\mathcal{L}\left(F\right)/dF$ must have the Maxwell limits in the weak field region (details and subtleties of the Lagrange dynamics for regular electrically charged structures have been analyzed in [68]).

The source-free dynamic field equations for electromagnetic field read

$${\nabla }_{\mu }\left({\mathcal{L}}_F{F}^{\mu \nu }\right)=0;{\nabla }_{\mu }{}^{*}{F}^{\mu \nu }=0;{}^{☆}{F}^{\mu \nu }=\frac{1}{2}{\eta }^{\mu \nu \alpha \beta }{F}_{\alpha \beta };{\eta }^{0123}=-\frac{1}{\sqrt{-g}}$$

(13)

where g is the determinant of the metric tensor $g_{\mu \nu }$.

The stress-energy tensor of a nonlinear electromagnetic field, calculated in the standard way with the electromagnetic lagrangian $\mathcal{L}\left(F\right)$

$$T_{\nu }^{\mu }=-2{\mathcal{L}}_F{F}_{\nu \alpha }{F}^{\mu \alpha }+\frac{1}{2}{\delta }_{\nu }^{\mu }\mathcal{L}$$

(14)

provides the source of the gravitational field for the Einstein equations $T_{\nu }^{\mu }=-8\pi G{T}_{\nu }^{\mu }$.

Stress-energy tensors of electromagnetic fields have the algebraic structure such as $T_t^t=T_r^r(p_r=-\rho )$. Spherically symmetric metrics typically applied for constructing axially symmetric solutions which describe spinning objects, belong to the Kerr-Schild class ([60] and references therein)

$$d{s}^2=g\left(r\right)d{t}^2-\frac{d{r}^2}{g\left(r\right)}-r^{2}d{\Omega }^2;g\left(r\right)=1-\frac{2\mathcal{M}\left(r\right)}{r};\mathcal{M}\left(r\right)=4\pi {\int }_0^r\rho \left(x\right)x^{2}dx$$

(15)

and can be transformed in general model-independent setting to the axially symmetric metrics by the Gürses-Gürsey formalism [69] (which includes the Newman-Janis algorithm [70] most frequently applied for obtaining the axial metrics). In the Boyer-Lindquist coordinates the metric has the form

$$d{s}^2=\frac{2f-\Sigma }{\Sigma }d{t}^2+\frac{\Sigma }{\Delta }d{r}^2+\Sigma d{\theta }^2-\frac{4af{sin}^2\theta }{\Sigma }dtd\varphi +\left(r^2+a^2+\frac{2f{a}^2{sin}^2\theta }{\Sigma }\right){sin}^2\theta d{\varphi }^2$$

(16)

where the Lorentz signature is $[-+++]$, and

$$\Sigma =r^2+a^2{cos}^2\theta ;\Delta =r^2+a^2-2f\left(r\right);f\left(r\right)=r\mathcal{M}\left(r\right).$$

(17)

In the case when spherical solutions satisfy WEC, $\mathcal{M}\left(r\right)$ monotonically grows from $\mathcal{M}\left(r\right)=4\pi \rho \left(0\right)r^3/3$ as $r\to 0$ and to $\mathcal{M}\left(r\right)=m-e^2/2r$ as $r\to \infty$ [66], where m is the total gravitational mass of an object, and the metric (16) asymptotically goes to the Kerr-Newman metric with the associated electromagnetic potential $A_i=-(er/\Sigma )[1;0,0,-a{sin}^2\theta ]$ [71]. The parameter e appears as a constant of integration identified as an electric charge by the asymptotic Coulomb behavior in the weak field regime.

The Kerr-Newman metric represents the exterior fields of a rotating charged object as seen by a distant observer. As was discovered by Carter [72], the basic parameter a couples with the mass m producing the angular momentum $J=ma$, and with the charge e producing an asymptotic magnetic momentum $\mu =ea$, which yields the same gyromagnetic ratio $g=2$ as predicted by the Dirac equation for a spinning particle [72].

In the axially symmetric geometry the surfaces $r=constant$ are the confocal ellipsoids

$$r^4-(x^2+y^2+z^2-a^2)r^2-a^2{z}^2=0$$

(18)

which for $r=0$ degenerate to the equatorial disk

$$x^2+y^2\le a^2,z=0$$

(19)

confined by the ring $x^2+y^2=a^2,z=0$ [73].

The eigenvalues of the stress-energy tensor (14) in the co-rotating references frame with the angular velocity $\omega \left(r\right)=u^{\varphi }/u^t=a/(r^2+a^2)$, are defined as ${\Sigma }^2\rho =2(f^{\prime }r-f)=r^4\tilde{\rho }\left(r\right);p_r=-\rho ;$ ${\Sigma }^2{p}_{\perp }=2(f^{\prime }r-f)-f^{″}\Sigma$ [69], where $p_{\perp }$ is the transversal pressure, and $\tilde{\rho }\left(r\right)$ is the density profile of a related spherical solution. The prime denotes the derivative with respect to r.

In the equatorial plane $(p_{\perp }+\rho )=-r^3{\tilde{\rho }}^{\prime }\left(r\right)/2\Sigma$ [19]. For the spherical solutions satisfying WEC regularity requires $r{\tilde{\rho }}^{\prime }\left(r\right)\to 0$ as $r\to 0$ [66]. As a result, on the disk (19) $p_{\perp }+\rho =0\to p_{\perp }=p_r=p$, and the equation of state

$$p=-\rho$$

(20)

represents the rotating de Sitter vacuum in the corotating frame [19].

Introducing the field vectors $\mathbf{E}=\left\{F_{\beta 0}\right\};\mathbf{D}=\left\{{\mathcal{L}}_F{F}^{0\beta }\right\};\mathbf{B}=\left\{{}^{*}{F}^{\beta 0}\right\};\mathbf{H}=\left\{{\mathcal{L}}_F{}^{*}{F}_{0\beta }\right\}$, we can write the field Equation (13) in the conventional form of the Maxwell equations $\nabla ·\mathbf{D}=0;\nabla \times \mathbf{H}=\partial \mathbf{D}/\partial t$; $\nabla ·\mathbf{B}=0;\nabla \times \mathbf{E}=-\partial \mathbf{B}/\partial t$.

The electric induction $\mathbf{D}$ and magnetic induction $\mathbf{B}$ are connected with the electric and magnetic field intensities $\mathbf{E}$ and $\mathbf{H}$ by $D^{\alpha }={ϵ}_{\beta }^{\alpha }{E}^{\beta };B^{\alpha }={\mu }_{\beta }^{\alpha }{H}^{\beta }$, where ${ϵ}_{\alpha }^{\beta }$ and ${\mu }_{\alpha }^{\beta }$ are the tensors of the electric and magnetic permeability [19]

$${ϵ}_r^r=\frac{(r^2+a^2)}{\Delta }{\mathcal{L}}_F;{ϵ}_{\theta }^{\theta }={\mathcal{L}}_F;{\mu }_r^r=\frac{(r^2+a^2)}{\Delta {\mathcal{L}}_F};{\mu }_{\theta }^{\theta }=\frac{1}{{\mathcal{L}}_F}.$$

(21)

The field Equations (13) form the system of four equations for two independent functions. The condition of compatibility for this system [59], and the dynamical Equations (13) are satisfied by the functions [19,59] $F_{01}=-e{\left({\Sigma }^2{\mathcal{L}}_F\right)}^{-1}(r^2-a^2{cos}^2\theta );F_{02}=e{\left({\Sigma }^2{\mathcal{L}}_F\right)}^{-1}{a}^{2}rsin2\theta ;F_{31}=a{sin}^2\theta F_{10};a{F}_{23}=(r^2+a^2)F_{02}$ in the strongly nonlinear regime, which is the case on the disk (19) where the density achieves the maximum. Applying these solutions we obtain [19,59]

$${\mathcal{L}}_F=\frac{2e^2}{{\Sigma }^2(p_{\perp }+\rho )};F=-\frac{{(p_{\perp }+\rho )}^2{\Sigma }^2}{2e^2}.$$

(22)

As a result on the disk ${\mathcal{L}}_F\to \infty$, the magnetic permeability ${\mu }_r^r={\mu }_{\theta }^{\theta }=1/{\mathcal{L}}_F$ vanishes, the electric permeability ${ϵ}_r^r={ϵ}_{\theta }^{\theta }={\mathcal{L}}_F$ tends to infinity, and the disk (19) displays the properties of a perfect conductor and ideal diamagnetic [19,59].

The surface current is defined by $4\pi j_k=\left[e_{\left(k\right)}^{\alpha }{F}_{\alpha \beta }{n}^{\beta }\right]$, where $e_{\left(k\right)}^{\alpha }$ are the base vectors related to the coordinates on the disk $t,\varphi$, $0\le \xi \le \pi /2$; the vector $n_{\alpha }={\delta }_{\alpha }^1{(1+q^2/a^2)}^{-1/2}cos\xi$ is the unit normal to the disk, and the symbol $[..]$ denotes a jump across the disk in the direction orthogonal to it [74]. On the de Sitter disk ${\mu }_r^r={\mu }_{\theta }^{\theta }=\mu$, this gives [20]

$$j_{\varphi }=-\frac{ec}{2\pi a}\sqrt{1+e^2/a^2}{sin}^2\xi \frac{\mu }{{cos}^3\xi }.$$

(23)

Due to the zero magnetic permeability $\mu$, the surface current $j_{\varphi }$ zeros out over the whole disk except the ring $\xi =\pi /2$, where both terms in the second fraction vanish independently, as a result the current can be any and amount to a non-zero total value, which is the general criterion for a superconducting current [75]. Such a current flows without resistance in the region with the perfect conductor behavior, and represents a non-dissipative source of the electromagnetic fields, which can in principle ensure a practically unlimited life time of an object [20].

For the electromagnetic soliton with the parameters of the electron $mac=\hslash /2$. In the region of the distant observers $r\gg {\lambda }_e$ we get [20]

$$E_r=-\frac{e}{r^2}\left(1-\frac{{\hslash }^2}{m_e^2{c}^2}\frac{3{cos}^2\theta }{4r^2}\right);E_{\theta }=\frac{e{\hslash }^2}{m_e^2{c}^2}\frac{sin2\theta }{4r^3};$$

(24)

$$B^r=-\frac{e\hslash }{m_{e}c}\frac{cos\theta }{r^3}=2{\mu }_e\frac{cos\theta }{r^3};B_{\theta }=-{\mu }_e\frac{sin\theta }{r^4}.$$

(25)

The Planck constant enters here in accordance with discovered by Carter ability of the Kerr-Newman asymptotics to represent the electron as seen by a distant observer [72]. In terms of the Coleman lump, the leading term in $E_r$ evidently presents the Coulomb law as the classical limit $\hslash =0$, while the higher terms give the quantum corrections [20].

A circular superconducting current (23) produces a magnetic momentum ${\mu }_{in}$ which is intrinsic since the dynamical Equations (13) are source-free [21]. This concerns all regular spinning electrically charged NED-GR objects.

At approaching the disk (19), $r\to 0$ and the function $f\left(r\right)$ in (16) achieves the de Sitter asymptotic $2f\left(r\right)\to r^4/r_0^2;r_0^2=3/8\pi G\rho \left(0\right)$, the disk is thus intrinsically flat [19] and the magnetic momentum is simply ${\mu }_{in}=c^{-1}{j}_{\varphi }S$ where S is the disk area. Expressing the current (23) in the form $j_{\varphi }=-(ec/2\pi a)\sqrt{1+e^2/a^2}U$ where U is an uncertain coefficient, we rewrite the magnetic momentum as ${\mu }_{in}=-(eS/2\pi a)\sqrt{1+q^2/a^2}U$. When the intrinsic magnetic moment of the spinning object is known, the uncertain coefficient U can be restored from ${\mu }_{in}$. For an electromagnetic soliton with the parameters of the electron this gives $j_{\varphi }=79.277$ A [21].

3.3. Origin of the Minimal Length in Annihilation

The outlined above results are obtained by analysis of regular solutions of source-free NED-GR equations for an arbitrary gauge-invariant Lagrangian. Asymptotic solutions for electromagnetic fields in the interior region determine the behavior of fields on the disk, while the stress-energy tensor calculated with these asymptotic solutions determines the equation of state and generic behavior of geometry on the de Sitter disk in the model-independent way.

The fundamental generic property of an electromagnetic spinning soliton with the positive energy density is the existence of the de Sitter vacuum disk in its deep interior.

This basic property of the electromagnetic soliton suggests some idea about the origin of the minimal length scale $l_e$. The evident feature of annihilation process is that at its certain stage a region of interaction is neutral and spinless. Keeping in mind de Sitter interiors of annihilating particles, we can roughly model it by a spherical lump with the de Sitter vacuum interior, asymptotically Schwarzschild as $r\to \infty$.

The basic inherent property of the de Sitter geometry is the repulsive gravity. The gravitational acceleration, $\ddot{a}\propto -a(\rho +3p)$ for a homogeneous and isotropic medium, in the de Sitter vacuum with $p=-\rho$ changes the sign and becomes repulsive. Due to this fundamental property, de Sitter vacuum is able to power the inflationary dynamics in the very early Universe and to support its observed accelerated expansion.1 For all structures with the de Sitter interior, there exists the characteristic zero gravity surface $r_{*}\sim {\left(r_0^2{r}_g\right)}^{1/3}$ at which the strong energy condition ($\rho +\sum p_k\ge 0$) is violated and beyond which the gravitational acceleration becomes repulsive [78,79].

Adopting for the interior de Sitter vacuum the electroweak scale $E_{EW}=246$ GeV related to the electron mass [4], we obtain the de Sitter radius $r_0=1.374$ cm. For a lump with the energy $E\simeq 1.253$ TeV, the characteristic radius of zero gravity surface is $r_{*}\sim 0.86\times {10}^{-16}$ cm, so that the scale $l_e=1.57\times {10}^{-17}$ cm fits inside a region where gravity is repulsive. The minimal length scale $l_e$ can be thus understood as a distance at which electromagnetic attraction is stopped by the gravitational repulsion of the interior de Sitter vacuum.

Regular NED-GR solutions provide a de Sitter cutoff on self-interaction whose numerical value depends on the choice of a density profile. Qualitatively it can be evaluated by [66]

$$\frac{e^2}{r_c^4}\simeq 8\pi G{\rho }_0=\frac{3}{r_0^2}.$$

(26)

This gives $r_c\simeq 1.05\times {10}^{-17}$ cm as a characteristic distance where electromagnetic attraction is balanced by de Sitter gravitational repulsion which is sufficiently close to the minimal length $l_e$ revealed in experiments [18].

4. Conclusions

The Higgs mechanism endows a particle with a mass via spontaneous symmetry breaking of intrinsically incorporated scalar fields in a false vacuum state which satisfies the equation of state for the de Sitter vacuum, $p=-\rho$.

The direct consequence of the involvement of the de Sitter vacuum with the non-zero energy density is the essential and generic involvement of gravity presented by the de Sitter geometry, and breaking of spacetime symmetry from the de Sitter group.

This picture is confirmed by two observational cases. The first concerns the negative mass square problem for neutrino. The symmetry group implicitly induced by the Higgs mechanism around the gravito-electroweak vertex is the de Sitter group, and particles in the vertex are described by the eigenstates of the Casimir operators in the de Sitter spacetime. Their further propagation in the Minkowski spacetime involves breaking the spacetime symmetry to the Poincaré group. This leads to an exact bi-maximal mixing for neutrino which provides an explanation for negative mass square problem and allows connecting the mass-squared differences for neutrino with the gravito-electroweak unification scale and to read off the energy values characterizing this scale from the solar and atmospheric neutrino data (in accordance with predictions of theories of gravito-electroweak unification).

The second observational case concerns the appearance of the minimal length scale in the $e^{+}{e}^{-}$ annihilation reaction which can be approached by applying nonlinear electrodynamics coupled to gravity. NED-GR dynamical equations admit the class of regular solutions describing in the self-consistent way the electrically charged spinning electromagnetic solitons whose basic generic property is the existence of the de Sitter vacuum disks in their deep interiors. The minimal length scale in $e^{+}{e}^{-}$ annihilation is related to the distance of the closest approach of annihilating particles at which their electromagnetic attraction is balanced by the gravitational repulsion of the intrinsically involved de Sitter vacuum.

All of this allows concluding that the deep generic relation of a particle mass with gravity and spacetime symmetry is implicitly encoded in the Higgs mechanism. Incorporating the de Sitter vacuum, the Higgs mechanism implicitly incorporates the generic relation between mass, gravity, and spacetime symmetry breaking revealed in the frame of General Relativity for all objects involving de Sitter vacuum.