Optimal System and Invariant Solutions of a New AKNS Equation with Time-Dependent Coefficients
Abstract
1. Introduction
2. Symmetry Analysis
3. Optimal System of Subalgebras
3.1.
3.2.
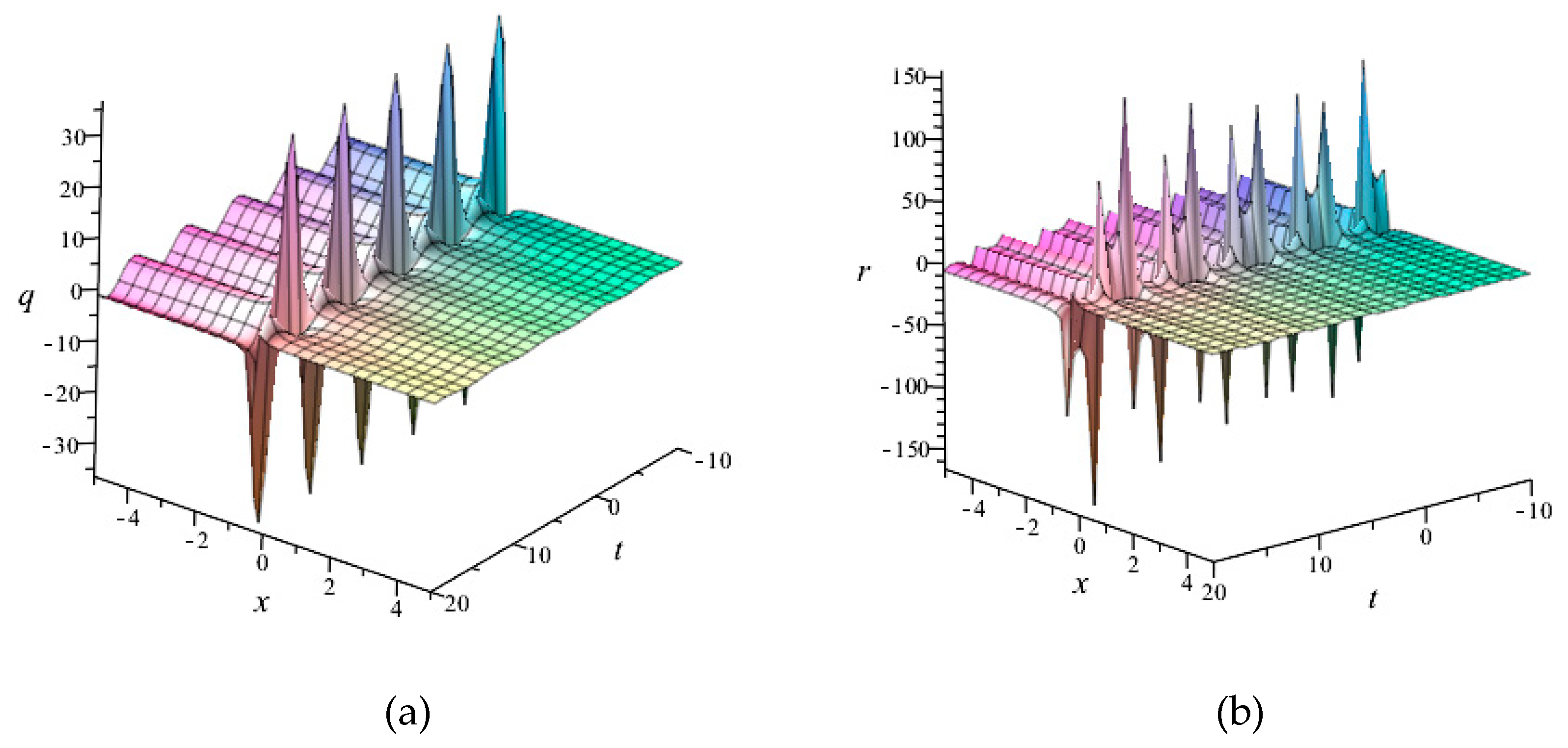
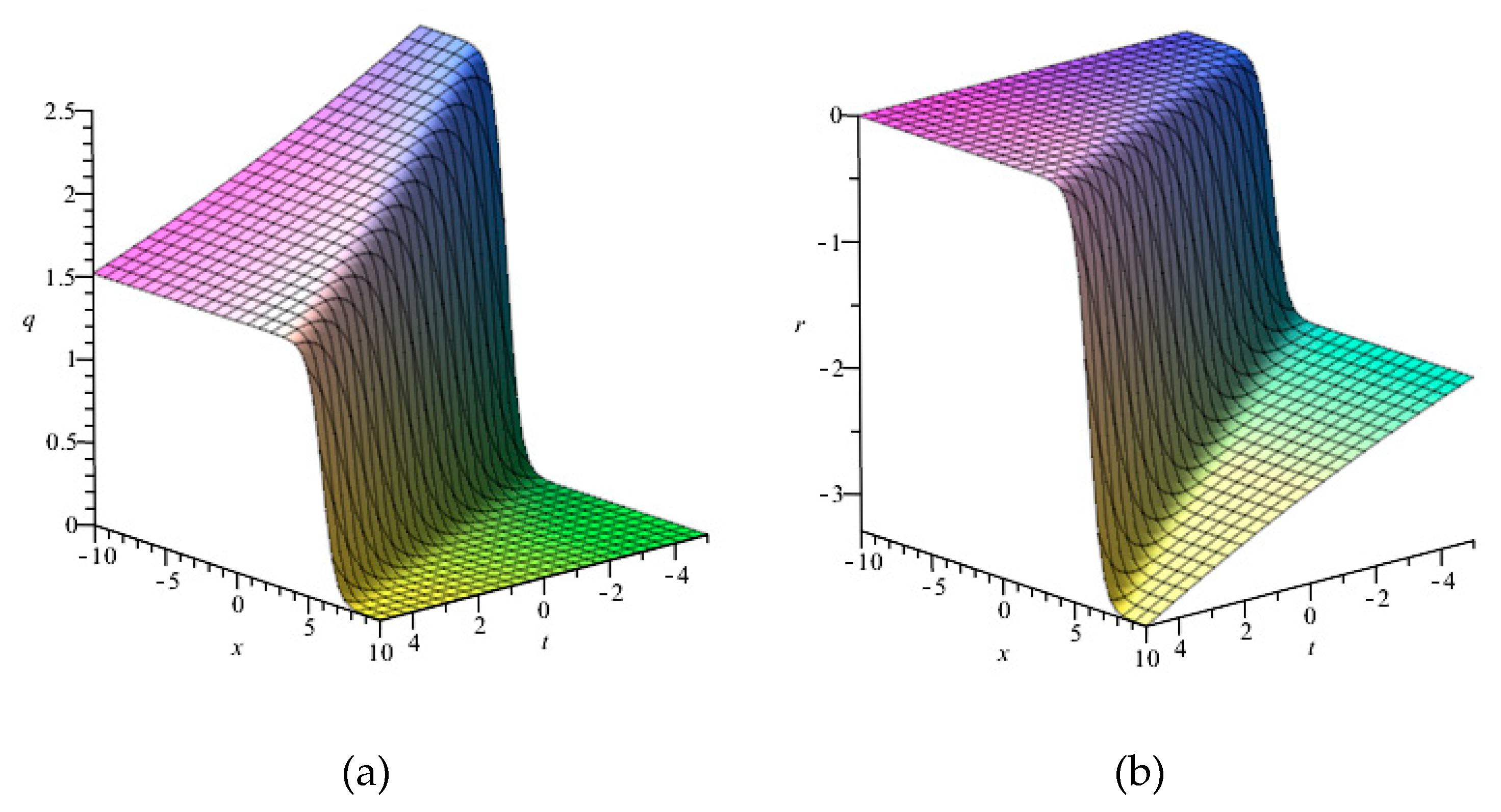
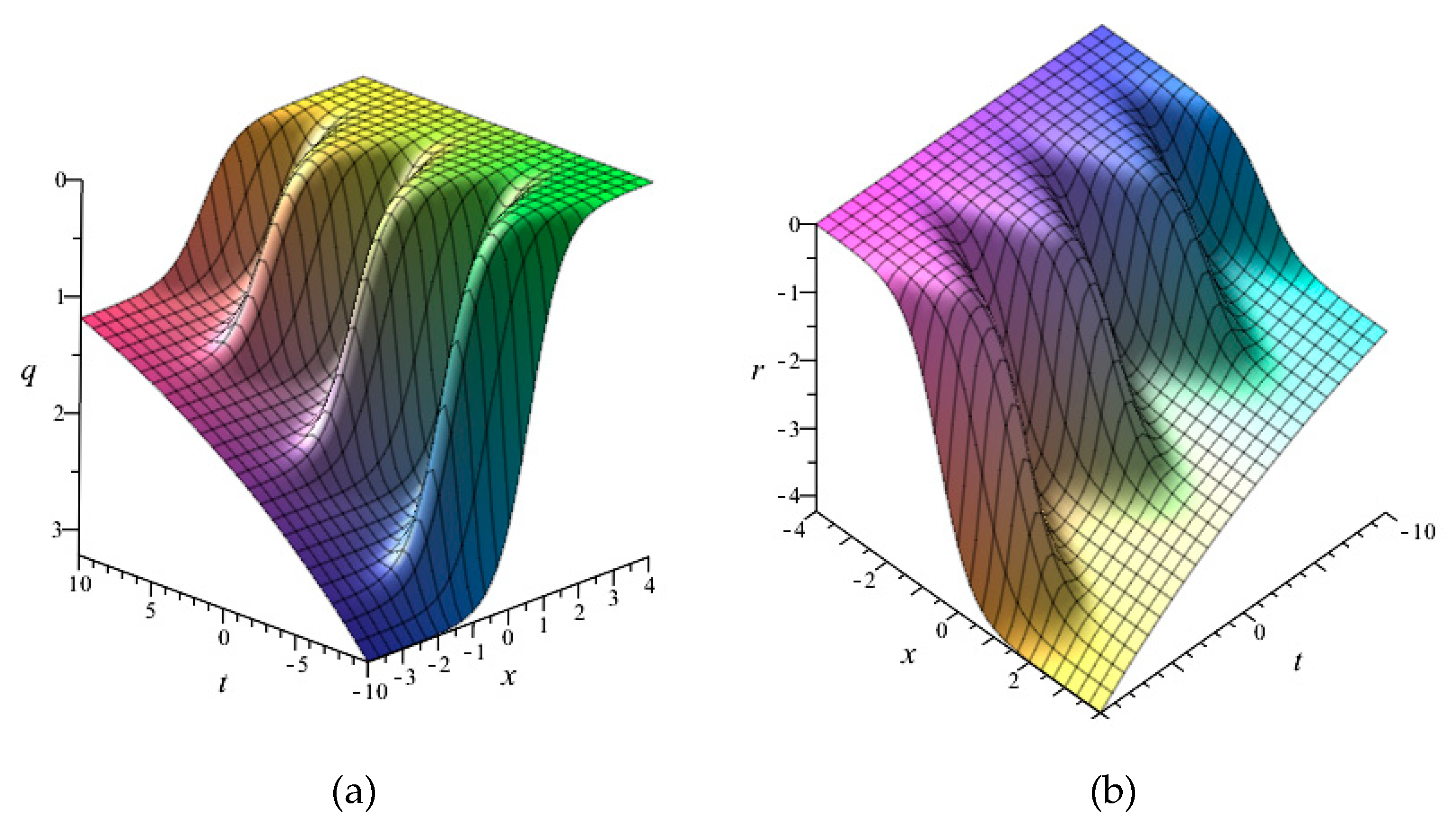
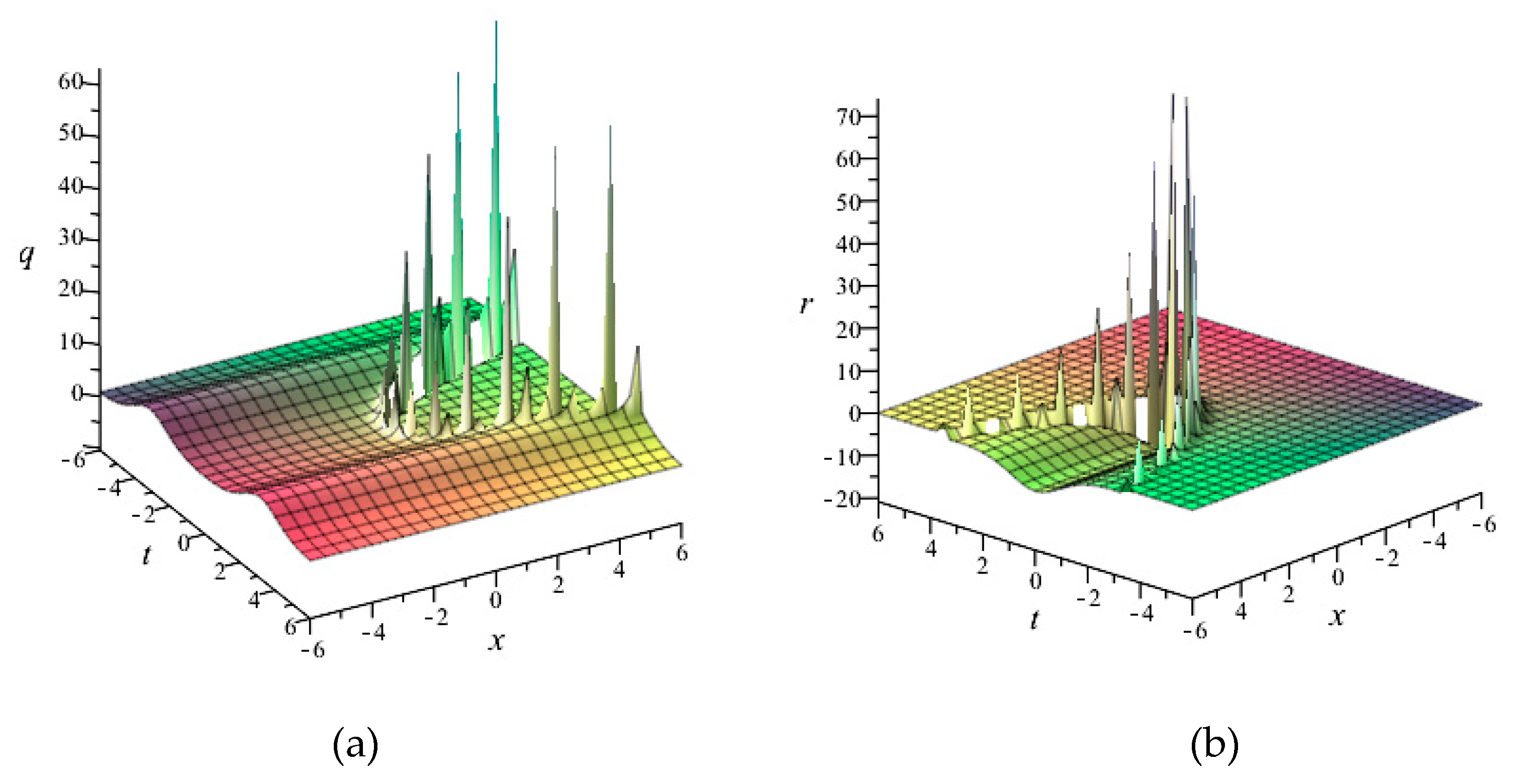
4. Symmetry Reductions and Exact Solutions
4.1. Solutions through
4.2. Solutions through
4.3. Solutions through
4.4. Solutions through
4.5. Solutions through
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Kudryashov, N.A. Solitary wave solutions of hierarchy with non-local nonlinearity. Appl. Math. Lett. 2020, 103, 106155. [Google Scholar] [CrossRef]
- Chen, K.; Zhang, D.Z. Solutions of the nonlocal nonlinear Schrödinger hierarchy via reduction. Appl. Math. Lett. 2018, 75, 82–88. [Google Scholar] [CrossRef]
- Cui, W.Y.; Zha, Q. Multiple rogue wave and breather solutions for the (3+1)-dimensional KPI equation. Appl. Math. Comput. 2018, 76, 1099–1107. [Google Scholar] [CrossRef]
- Xu, G.X. Painlevé analysis, lump-kink solutions and localized excitation solutions for the (3+1)-dimensional Boiti-Leon-Manna-Pempinelli equation. Appl. Math. Lett. 2019, 97, 81–87. [Google Scholar] [CrossRef]
- Xie, X.Y.; Tian, B.; Sun, W.R.; Sun, Y. Rogue-wave solutions for the Kundu-Eckhaus equation with variable coefficients in an optical fiber. Nonlinear Dyn. 2015, 81, 1349–1354. [Google Scholar] [CrossRef]
- Wu, X.F.; Hua, G.S.; Ma, Z.Y. Evolution of optical solitary waves in a generalized nonlinear Schrödinger equation with variable coefficients. Nonlinear Dyn. 2012, 70, 2259–2267. [Google Scholar] [CrossRef]
- Lü, X.; Zhu, H.W.; Meng, X.H.; Yang, Z.C.; Tian, B. Soliton solutions and a Bäcklund transformation for a generalized nonlinear Schrödinger equation with variable coefficients from optical fiber communications. J. Math. Anal. Appl. 2007, 336, 1305–1315. [Google Scholar] [CrossRef]
- Zhang, H.Q.; Yuan, S.S. Dark soliton solutions of the defocusing Hirota equation by the binary Darboux transformation. Nonlinear Dyn. 2017, 89, 531–538. [Google Scholar] [CrossRef]
- Kudryavtsev, A.G. Nonlocal Darboux transformation of the two-dimensional stationary Schrödinger equation and its relation to the Moutard transformation. Theor. Math. Phys. 2016, 187, 455–462. [Google Scholar] [CrossRef]
- Su, J.J.; Gao, Y.T.; Ding, C.C. Darboux transformations and rogue wave solutions of a generalized AB system for the geophysical flows. Appl. Math. Lett. 2019, 88, 201–208. [Google Scholar] [CrossRef]
- Yomba, E. Construction of new soliton-like solutions for the (2+1) dimensional KdV equation with variable coefficients. Chaos Solitons Fractals 2004, 21, 75–79. [Google Scholar] [CrossRef]
- Adem, A.R. Symbolic computation on exact solutions of a coupled Kadomtsev-Petviashvili equation: Lie symmetry analysis and extended tanh method. Appl. Math. Comput. 2017, 74, 1897–1902. [Google Scholar] [CrossRef]
- Hong, B.; Lu, D. New Jacobi elliptic function-like solutions for the general KdV equation with variable coefficients. Math. Comput. Model. 2012, 55, 1594–1600. [Google Scholar] [CrossRef]
- Kuzenov, V.V.; Ryzhkov, S.V. Numerical modeling of laser target compression in an external magnetic field. Math. Models Comput. Simul. 2018, 10, 255–264. [Google Scholar] [CrossRef]
- Bluman, G.W.; Anco, S.C. Symmetry and Integration Methods for Differential Equations; Springer: New York, NY, USA, 2002. [Google Scholar]
- Olver, P.J. Applications of Lie Groups to Differential Equations; Springer: Berlin/Heidelberg, Germany, 1993. [Google Scholar]
- Ovsiannikov, L.V. Group Analysis of Differential Equations; Academic Press: New York, NY, USA, 1982. [Google Scholar]
- Wang, G.W.; Liu, Y.X.; Han, S.X.; Wang, H.; Su, X. Generalized symmetries and mCK method analysis of the (2+1)-Dimensional coupled Burgers equations. Symmetry 2019, 11, 1473. [Google Scholar] [CrossRef]
- Abdulwahhab, M.A. Optimal system and exact solutions for the generalized system of 2-dimensional Burgers equations with infinite Reynolds number. Commun. Nonlinear Sci. Numer. Simul. 2015, 20, 98–112. [Google Scholar] [CrossRef]
- Kaur, L.; Wazwaz, A.M. Painlevé analysis and invariant solutions of generalized fifth-order nonlinear integrable equation. Nonlinear Dyn. 2018, 94, 2469–2477. [Google Scholar] [CrossRef]
- Shi, D.D.; Zhang, Y.F.; Liu, W.H.; Liu, J.G. Some exact solutions and conservation laws of the coupled Time-Fractional Boussinesq-Burgers system. Symmetry 2019, 11, 77. [Google Scholar] [CrossRef]
- Liu, H.; Li, J.; Liu, L. Painlevé analysis, Lie symmetries, and exact solutions for the time-dependent coefficients Gardner equations. Nonlinear Dyn. 2009, 59, 497–502. [Google Scholar] [CrossRef]
- Gupta, R.K.; Kumar, V.; Jiwari, R. Exact and numerical solutions of coupled short pulse equation with time-dependent coefficients. Nonlinear Dyn. 2014, 79, 455–464. [Google Scholar] [CrossRef]
- Liu, N. Similarity reduction and explicit solutions for the variable-coefficient coupled Burger’s equations. Appl. Math. Comput. 2010, 217, 4178–4185. [Google Scholar] [CrossRef]
- Kumar, R.; Gupta, R.K.; Bhatia, S.S. Invariant solutions of variable coefficients generalized Gardner equation. Nonlinear Dyn. 2016, 83, 2103–2111. [Google Scholar] [CrossRef]
- Singh, K.; Gupta, R.K.; Kumar, S. Benjamin-Bona-Mahony (BBM) equation with variable coefficients: Similarity reductions and Painlevé analysis. Appl. Math. Comput. 2011, 217, 7021–7027. [Google Scholar] [CrossRef]
- Zhang, S.; Gao, X. Exact N-soliton solutions and dynamics of a new AKNS equation with time-dependent coefficients. Nonlinear Dyn. 2016, 83, 1043–1052. [Google Scholar] [CrossRef]
- Chen, D.Y.; Zhang, D.J.; Bi, J.B. New double Wronskian solutions of the AKNS equation. Sci. China Ser. A Math. 2008, 51, 55–69. [Google Scholar] [CrossRef]
- Chen, K.; Deng, X.; Lou, S.Y.; Zhang, D.J. Solutions of local and nonlocal equations reduced from the AKNS hierarchy. arXiv 2018, arXiv:1710.10479v2. [Google Scholar]
- Grigoriev, Y.N.; Meleshko, S.V.; Ibragimov, N.K.; Kovalev, V.F. Symmetry of Integro-Differential Equations: With Applications in Mechanics and Plasma Physics; Springer: New York, NY, USA, 2010. [Google Scholar]
- Arrigo, D.J. Symmetry Analysis of Differential Equations; Wiley: New York, NY, USA, 2015. [Google Scholar]
- Zhao, Z.L.; Han, B. Lie symmetry analysis of the Heisenberg equation. Commun. Nonlinear Sci. Numer. Simul. 2017, 45, 220–234. [Google Scholar] [CrossRef]
- Wang, M.L.; Li, X.; Zhang, J. The -expansion method and travelling wave solutions of nonlinear evolution equations in mathematical physics. Phys. Lett. A 2008, 372, 417–423. [Google Scholar] [CrossRef]
- Kudryashov, N.A. Simplest equation method to look for exact solutions of nonlinear differential equations. Chaos Solitions Fractals 2005, 24, 1217–1231. [Google Scholar] [CrossRef]
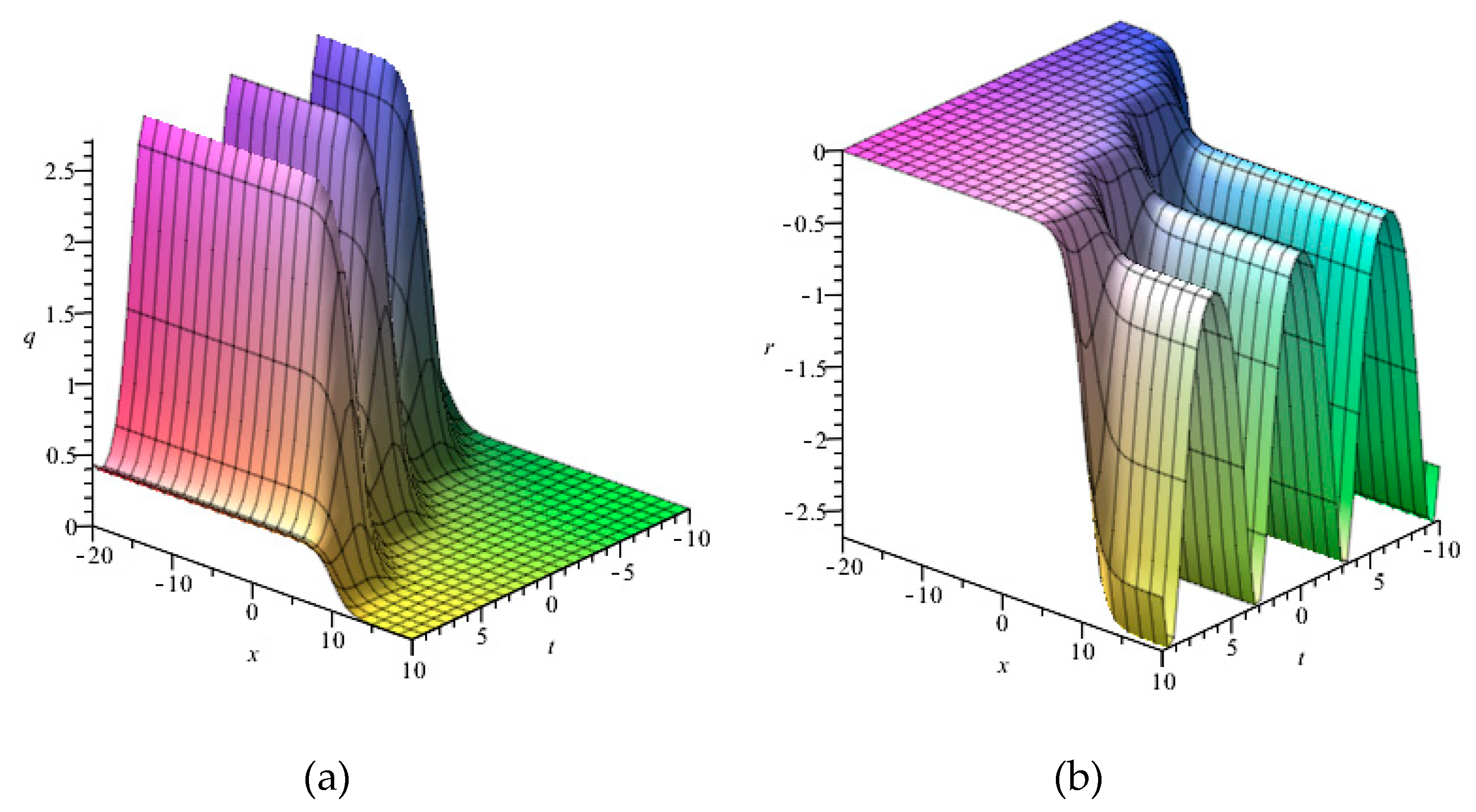
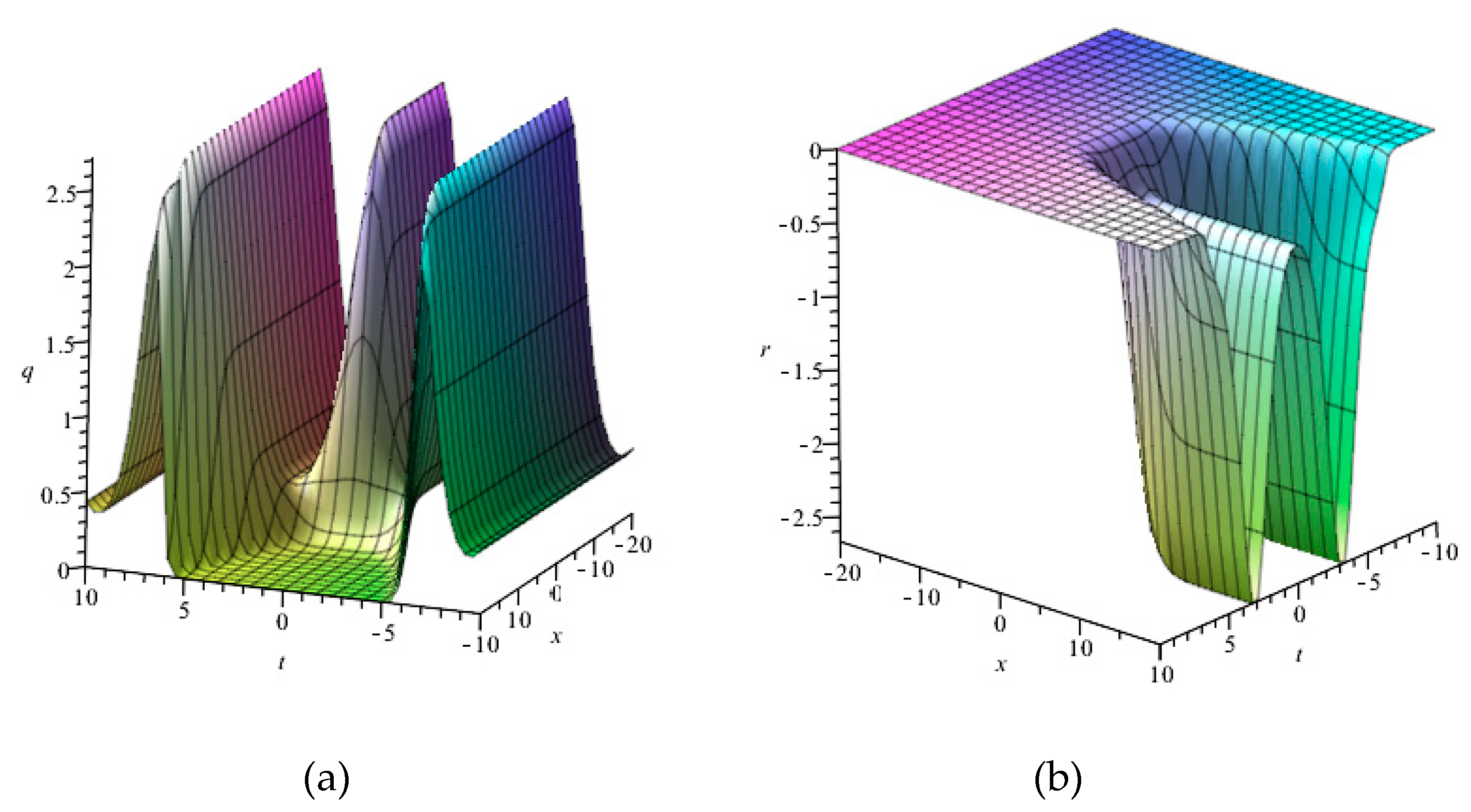
| 0 | |||
| 0 | 0 | ||
| 0 | 0 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, N. Optimal System and Invariant Solutions of a New AKNS Equation with Time-Dependent Coefficients. Symmetry 2020, 12, 522. https://doi.org/10.3390/sym12040522
Liu N. Optimal System and Invariant Solutions of a New AKNS Equation with Time-Dependent Coefficients. Symmetry. 2020; 12(4):522. https://doi.org/10.3390/sym12040522
Chicago/Turabian StyleLiu, Na. 2020. "Optimal System and Invariant Solutions of a New AKNS Equation with Time-Dependent Coefficients" Symmetry 12, no. 4: 522. https://doi.org/10.3390/sym12040522
APA StyleLiu, N. (2020). Optimal System and Invariant Solutions of a New AKNS Equation with Time-Dependent Coefficients. Symmetry, 12(4), 522. https://doi.org/10.3390/sym12040522




