Anticipating the Length of Employees’ Working Time
Abstract
1. Introduction
2. Materials and Methods
Methods
3. Results
3.1. Multiple Regresion Method
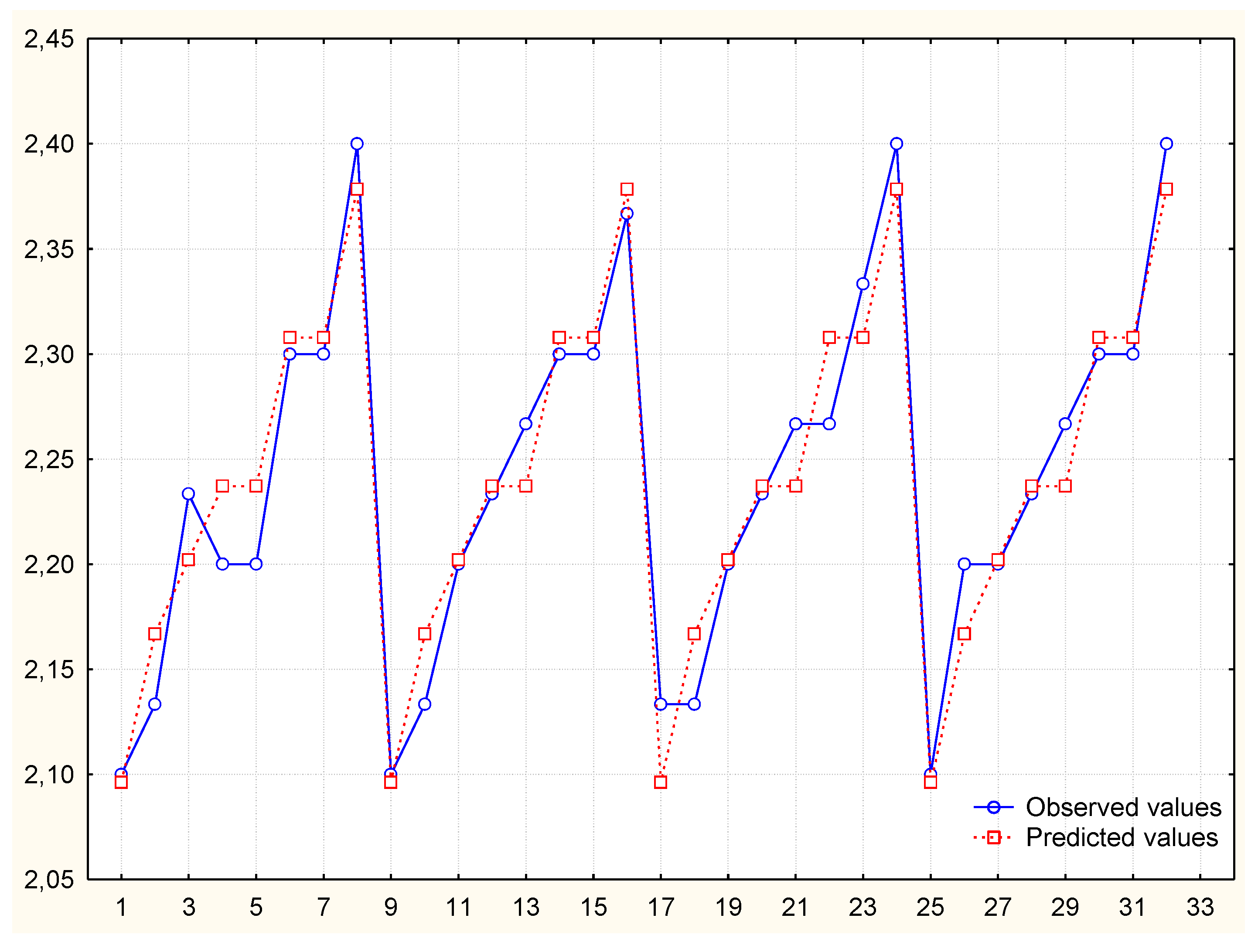
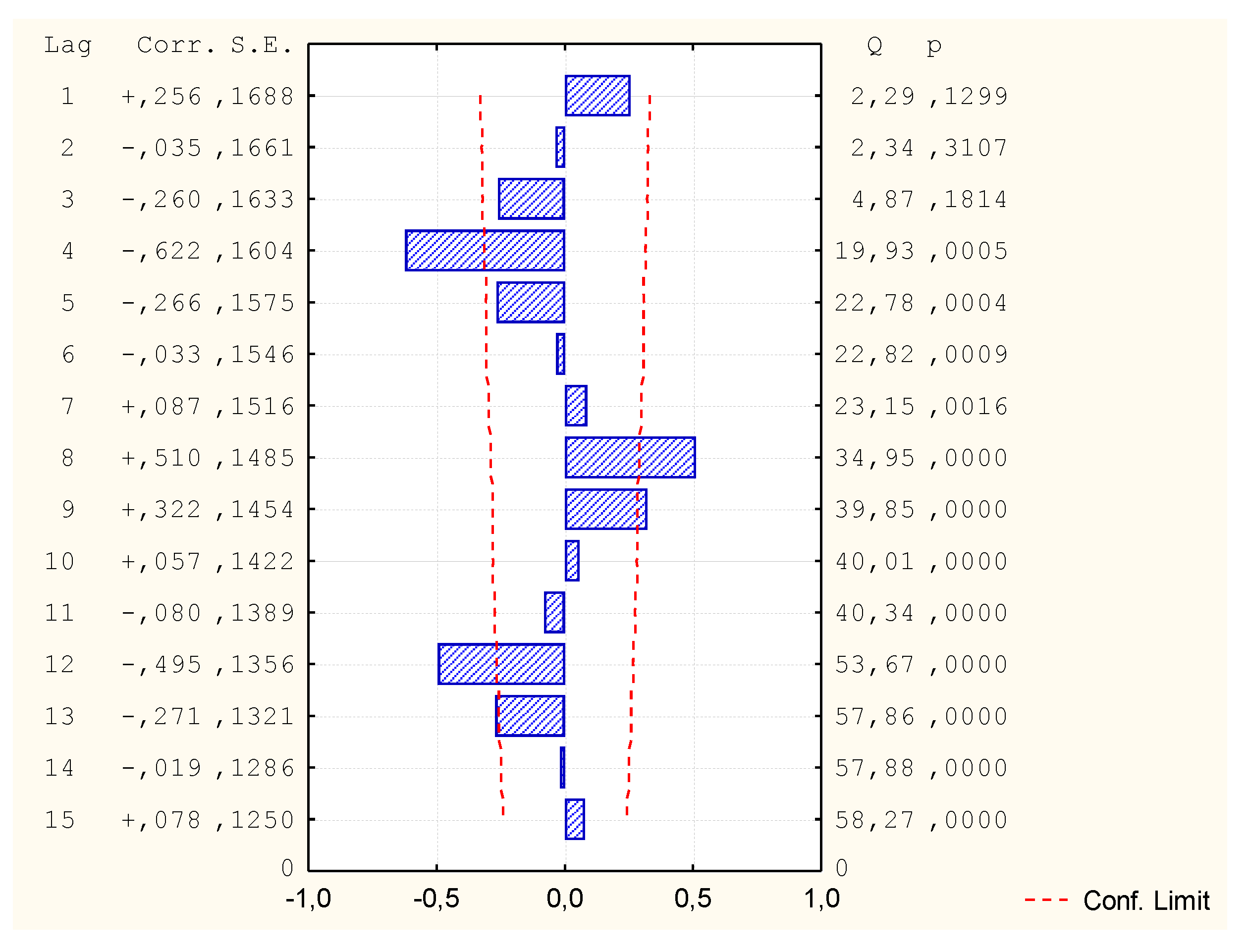
3.1.1. MR1
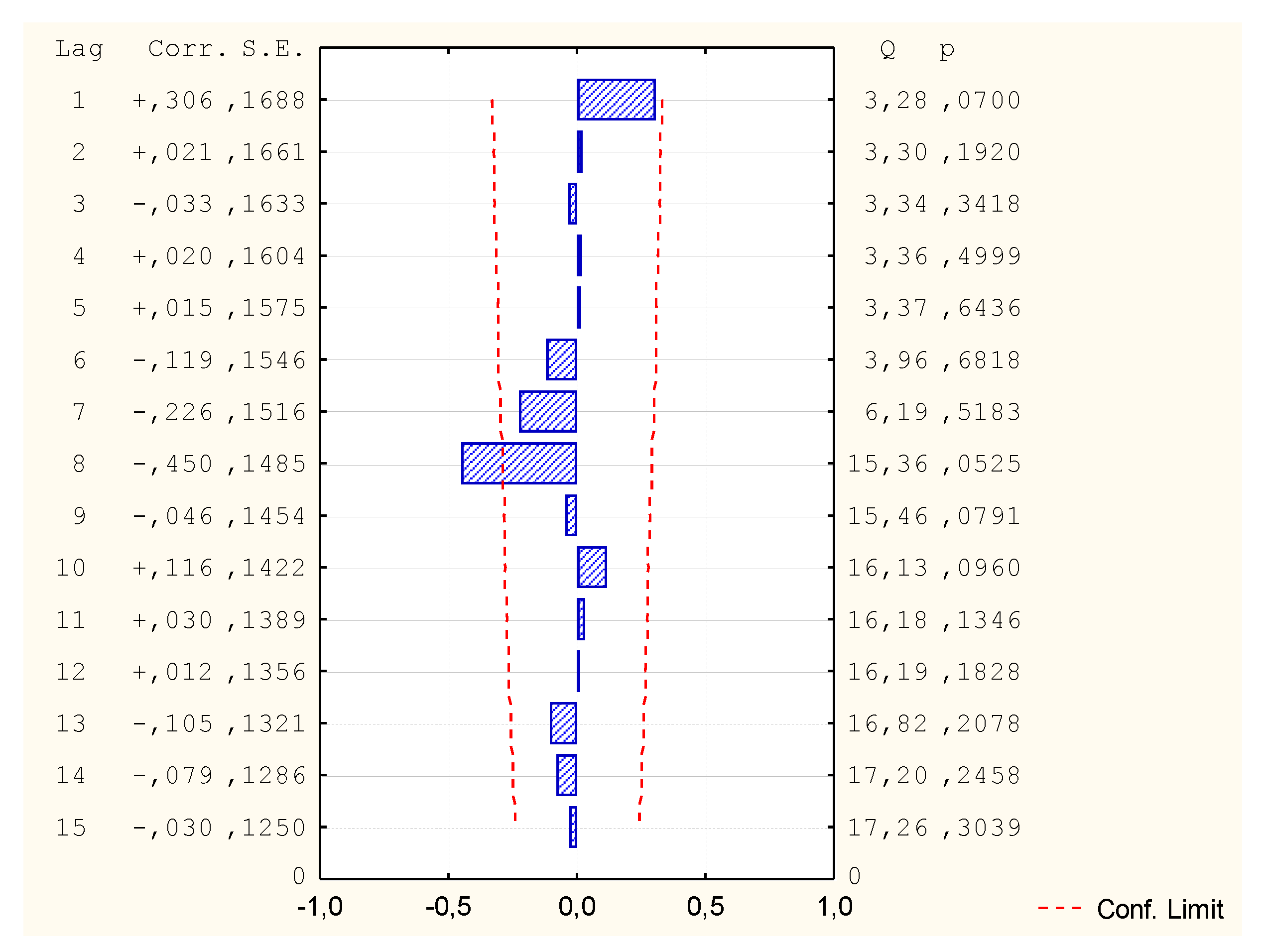
3.1.2. MR2
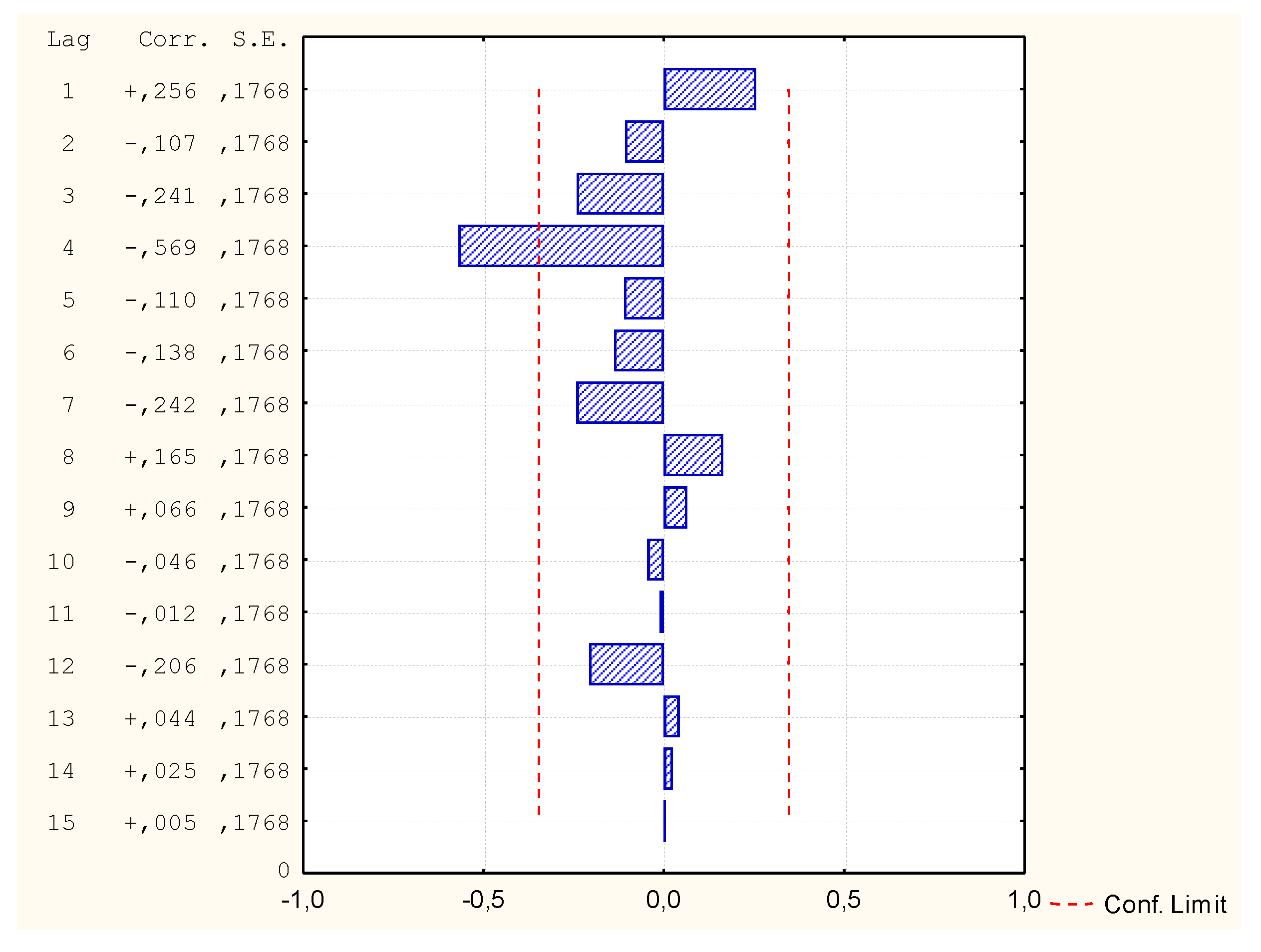
3.2. Multivariate Adaptive Regression Splines Method
3.3. Generalized Additive Models Method
3.3.1. GAM1
3.3.2. GAM2
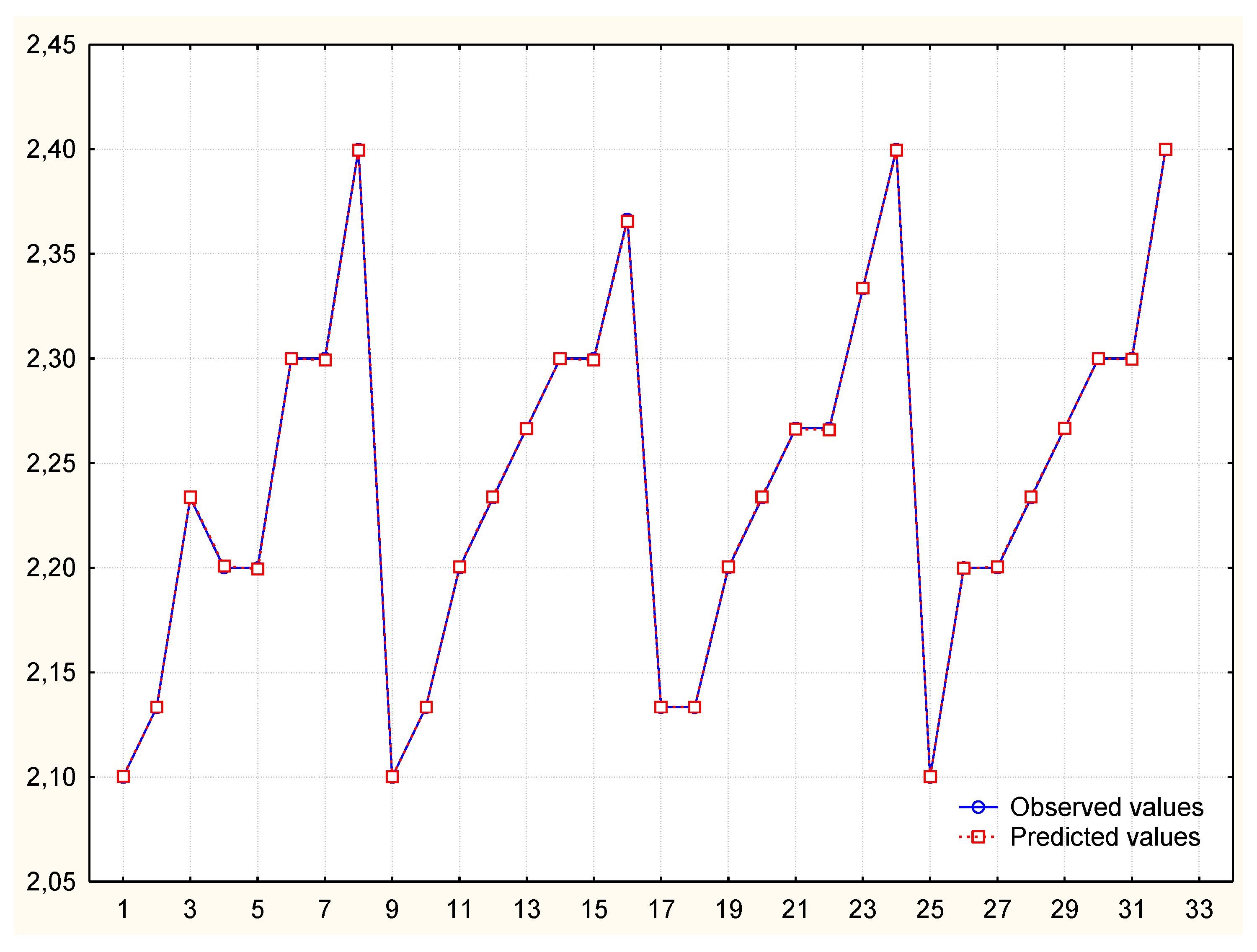
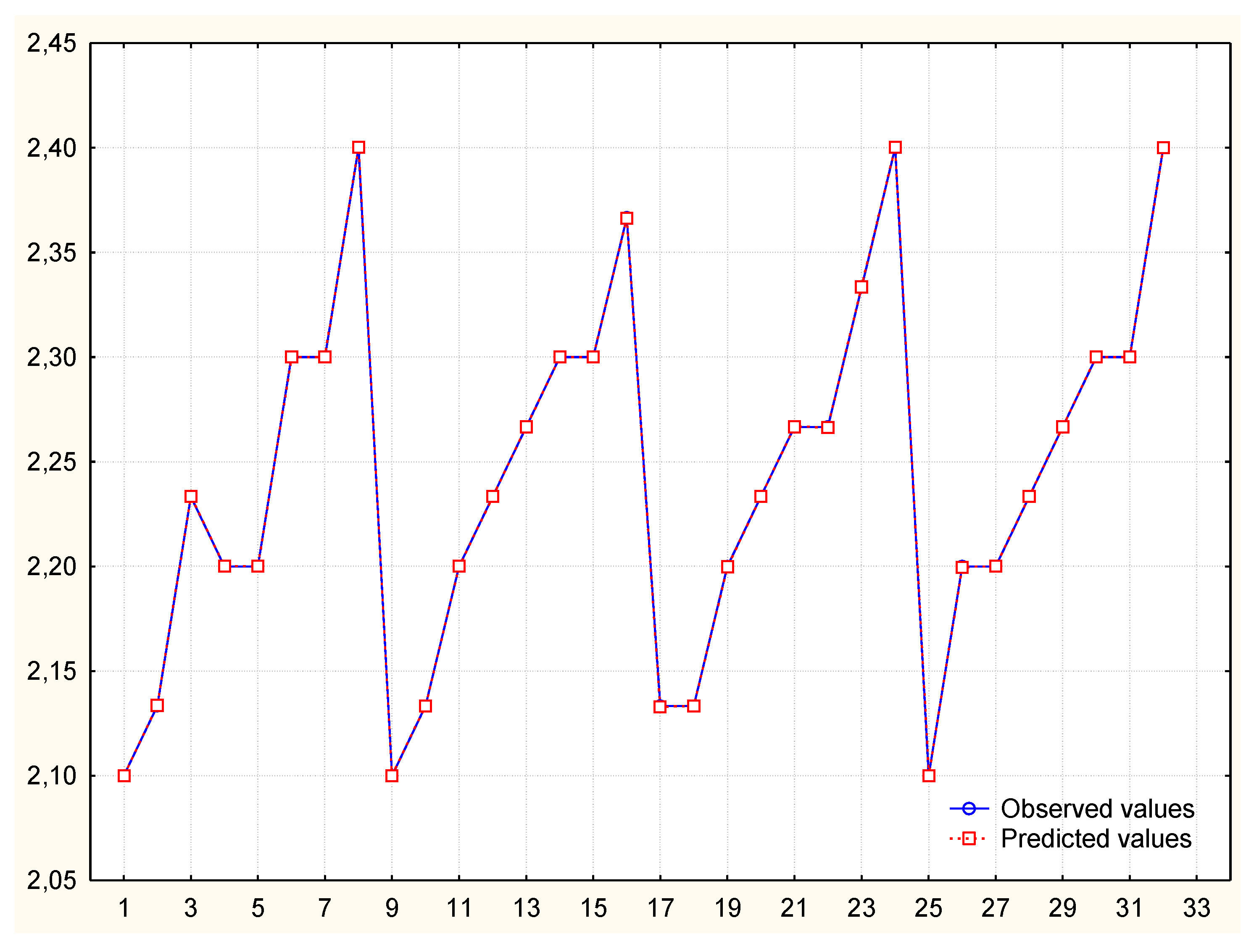
3.4. Neural Networks Method
4. Discussion
5. Conclusions
- (1)
- Forecasting and prediction is possible based on the regression formula of employee performance by the MMSM method. The method shows how certain characteristic variables for this process have an impact on the duration of works;
- (2)
- Half of the analyzed models is correct and reflects employee performance very accurately. It is possible to use selected models to assess employee performance and the duration of work for a specific order;
- (3)
- The best forecast was obtained using the automatic neural network method, MAPE = 0.02%. The disadvantage of this method is the lack of a regression pattern, which limits its universality. New calculations can be made by a person who has all previous data and a neural network.
Author Contributions
Funding
Conflicts of Interest
Signs
| MMSM | Multivariate Method of Statistical Models |
| MR | Multiple Regresion |
| MARS | Multivariate Adaptive Regression Splines |
| GAM | Generalized Additive Models |
| NN | Neural Networks |
| MAPE | Mean Absolute Percentage Error |
References
- Paprocka, I. The model of maintenance planning and production scheduling for maximising robustness. Int. J. Prod. Res. 2019, 57, 4480–4501. [Google Scholar] [CrossRef]
- Plebankiewicz, E.; Juszczyk, M.; Malara, J. Estimation of task completion times with the use of the pert method on the example of a real construction project. Arch. Civ. Eng. 2015, 61, 51–62. [Google Scholar] [CrossRef]
- Sawicki, M.; Szostak, M.; Beben, D.; Rak, A.; Perkowski, Z. Analysis of the Dependence between the Number of Accidents at Workplaces that Involve Scaffolding and Changes in Work Efficiency. In Proceedings of the 3rd Scientific Conference Environmental Challenges in Civil Engineering (ECCE 2018), Opole, Poland, 23–25 April 2018; Volume 174. [Google Scholar]
- Beck, J.; Shen, W. The Effects of US Presidential Elections on Work Engagement and Job Performance. Appl. Psychol. Int. Rev. Psychol. Appl. Rev. Int. 2019, 68, 547–576. [Google Scholar] [CrossRef]
- Kuprenas, J.; Ghafoori, N. Influence of Construction Costs on Schedule Performance. In Challenges, Opportunities and Solutions in Structural Engineering and Construction; CRC Press: Boca Raton, FL, USA, 2010; pp. 903–905. [Google Scholar]
- Hasan, M.; Qayyum, Z.; Hasan, S. Planning and Scheduling of Manpower in an Annualized Hours Environment Integrating Workers Willingness and Efficiency. Ind. Eng. Manag. Syst. 2019, 18, 1–24. [Google Scholar] [CrossRef]
- Li, K.; Xu, S.; Fu, H. Work-break scheduling with real-time fatigue effect and recovery. Int. J. Prod. Res. 2019, 58. [Google Scholar] [CrossRef]
- Tucker, P. The impact of rest breaks upon accident risk, fatigue and performance: A review. Work Stress 2003, 17, 123–137. [Google Scholar] [CrossRef]
- Pahos, N.; Galanaki, E. Staffing Practices and Employee Performance: The Role of Age. In Evidence-Based HRM: A Global Forum for Empirical Scholarship; Emerald Publishing Limited: Bingley, UK, 2019; Volume 7, pp. 93–112. [Google Scholar]
- Aliekperova, N. Motivating factors effecting work efficiency of empoyees in ukrainian pharmaceutical sector. Econ. Sociol. 2018, 11, 61–74. [Google Scholar] [CrossRef] [PubMed]
- Khalil, F. Sexual frustration, religiously forbidden actions and work efficiency-a case study from the Pakistan perspective. Contemp. Islam-Dyn. Muslim Life 2016, 10, 477–487. [Google Scholar] [CrossRef]
- Rogalska, M. Multifactorial Models in Forecasting the Time of Construction Processes; Lublin Technical University: Lublin, Poland, 2016. [Google Scholar]
- Krzysztofiak, M.; Luszniewicz, A. Statistics; PWE: Warszawa, Poland, 1976. [Google Scholar]
- Shapiro, S.S.; Wilk, M.B. An analysis of variance test for normality (complete samples). Biometrika 1965, 52, 591–611. [Google Scholar] [CrossRef]
- Navarra, A.; Simoncini, V.; Navarra, A.; Simoncini, V. Multiple Linear Regression Methods. In Guide to Empirical Orthogonal Functions for Climate Data Analysis; Springer: New York, NY, USA, 2010; pp. 123–146. [Google Scholar]
- Rogalska, M. Forecasting the Duration of Failure of Wheeled Excavators Using the Methods of Neural Networks, Multiple Regression and ARIMA; Lublin Technical University: Lublin, Poland, 2012. [Google Scholar]
- Giudici, P. Applied Data Mining. Statistical Methods for Business and Industry; John Wiley & Sons Ltd.: Chichester, UK, 2003. [Google Scholar]
- Friedman, J.; Hastie, T.; Tibshirami, R. The Elements of Statistical Learning. Data Mining, Inference, and Prediction, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Hastie, T.; Tibshirani, R. Generalized Additive-Models—Some Applications. J. Am. Stat. Assoc. 1987, 82, 371–386. [Google Scholar] [CrossRef]
- Hestie, T.J.; Tibshirani, R.J. Generalized Additive Models; Chapman Hall: London, UK, 1990. [Google Scholar]
- De Myttenaere, A.; Golden, B.; Le Grand, B.; Rossi, F. Mean Absolute Percentage Error for regression models. Neurocomputing 2016, 192, 38–48. [Google Scholar] [CrossRef]
- Chanas, S.; Zieliński, P. Critical Path Analysis in the Network with Fuzzy Activity Times. Fuzzy Sets Syst. 2001, 122, 195–204. [Google Scholar] [CrossRef]
- Chen, S.P. Analysis of Critical Paths in Project Network with Fuzzy Activity Times. Eur. J. Oper. Res. 2007, 183, 442–459. [Google Scholar] [CrossRef]
- Rogalska, M.; Hejducki, Z. Time buffers in construction process scheduling. J. Civ. Eng. Manag. 2007, 13, 143–148. [Google Scholar] [CrossRef]
- Steyn, H. Project management applications of the theory of constraints beyond critical chain scheduling. Int. J. Proj. Manag. 2002, 20, 75–80. [Google Scholar] [CrossRef]
- Li, C.; Wang, K. The risk element transmission theory research of multi-objective risk-time-cost trade-off. Comput. Math. Appl. 2009, 57, 1792–1799. [Google Scholar] [CrossRef]
- Prakash, A.; Felix, T.S.; Chan, F.T.S.; Deshmukh, S.G. FMS scheduling with knowledge based genetic algorithm approach. Expert Syst. Appl. 2011, 38, 3161–3171. [Google Scholar] [CrossRef]
- Nassar, K. Evolutionary optimization of resource allocation in repetitive construction schedules. J. Inf. Technol. Constr. 2005, 10, 265. [Google Scholar]
- Rogalska, M.; Hejducki, Z. Shortening the realisation time of building project with application of theory of constraints and critical chain scheduling. J. Civ. Eng. Manag. 2004, 10, 99–105. [Google Scholar]
- Kowalczyk, Z.; Zabielski, J. Cost Estimation and Standardization in Construction; WSiP: Warszawa, Poland, 2012. [Google Scholar]
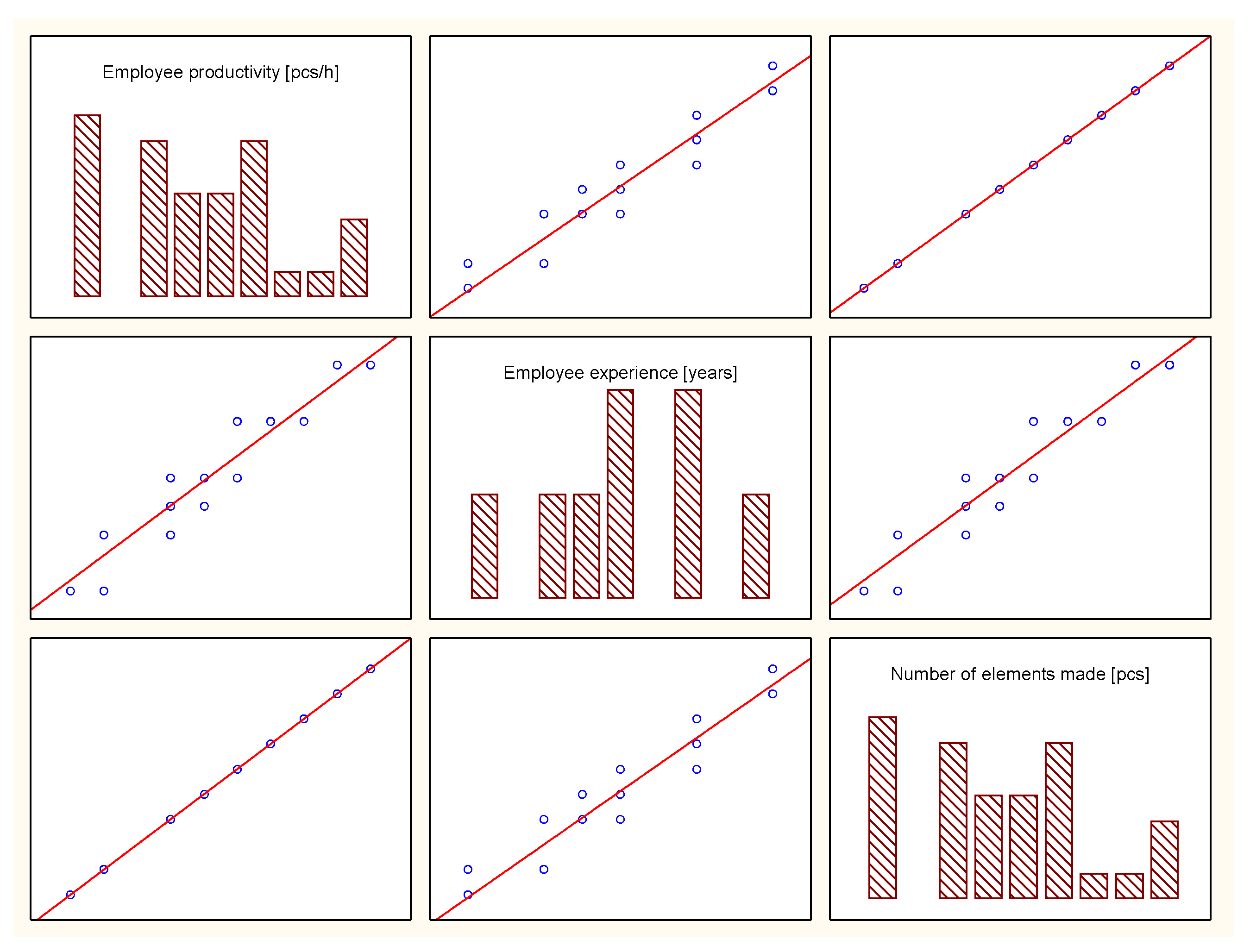




| Employee Productivity [pcs/h] | Employee Experience [years] | Number of Elements Made [pcs] | Failure/Equipment Repair [%] | Temp. [°C] | Grinding Time [h] | Well-Being Assessment [1–5] | |
|---|---|---|---|---|---|---|---|
| Day 1 | 2.10 | 1 | 15.75 | 3.5 | 21 | 4 | 3 |
| 2.13 | 3 | 16.00 | 3 | 21 | 3.25 | 3 | |
| 2.23 | 4 | 16.75 | 5 | 21 | 3 | 4 | |
| 2.20 | 5 | 16.50 | 4.5 | 21 | 3.25 | 4 | |
| 2.20 | 5 | 16.50 | 5.5 | 21 | 3 | 5 | |
| 2.30 | 7 | 17.25 | 4 | 21 | 3.25 | 3 | |
| 2.30 | 7 | 17.25 | 4.3 | 21 | 3.25 | 3 | |
| 2.40 | 9 | 18.00 | 4.3 | 21 | 3.25 | 5 | |
| Day 2 | 2.10 | 1 | 15.75 | 3.5 | 21.5 | 3.5 | 4 |
| 2.13 | 3 | 16.00 | 3 | 21.5 | 3.75 | 4 | |
| 2.20 | 4 | 16.50 | 5 | 21.5 | 3 | 4 | |
| 2.23 | 5 | 16.75 | 4.5 | 21.5 | 3.25 | 3 | |
| 2.27 | 5 | 17.00 | 5.5 | 21.5 | 3 | 4 | |
| 2.30 | 7 | 17.25 | 4 | 21.5 | 3.25 | 3 | |
| 2.30 | 7 | 17.25 | 4.3 | 21.5 | 3.25 | 4 | |
| 2.37 | 9 | 17.75 | 4.3 | 21.5 | 2.75 | 3 | |
| Day 3 | 2.13 | 1 | 16.00 | 3.5 | 20.5 | 3.25 | 4 |
| 2.13 | 3 | 16.00 | 3 | 20.5 | 3.75 | 3 | |
| 2.20 | 4 | 16.50 | 5 | 20.5 | 3.5 | 2 | |
| 2.23 | 5 | 16.75 | 4.5 | 20.5 | 3.25 | 3 | |
| 2.27 | 5 | 17.00 | 5.5 | 20,5 | 3.25 | 4 | |
| 2.27 | 7 | 17.00 | 4 | 20.5 | 3 | 2 | |
| 2.33 | 7 | 17.50 | 4.3 | 20.5 | 2.75 | 3 | |
| 2.40 | 9 | 18.00 | 4.3 | 20.5 | 3 | 4 | |
| Day 4 | 2.10 | 1 | 15.75 | 3.5 | 21 | 3.5 | 3 |
| 2.20 | 3 | 16.50 | 3 | 21 | 3.5 | 4 | |
| 2.20 | 4 | 16.50 | 5 | 21 | 3 | 3 | |
| 2.23 | 5 | 16.75 | 4.5 | 21 | 3.25 | 3 | |
| 2.27 | 5 | 17.00 | 5.5 | 21 | 2.75 | 4 | |
| 2.30 | 7 | 17.25 | 4 | 21 | 3.25 | 3 | |
| 2.30 | 7 | 17.25 | 4.3 | 21 | 2.75 | 4 | |
| 2.40 | 9 | 18.00 | 4.3 | 21 | 2.5 | 3 |
| No. | Variable Name | Chart | W |
|---|---|---|---|
| v1 | Employee productivity [pcs/h] | 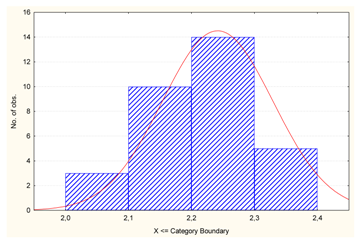 | 0.948 |
| v2 | Employee experience [years] | 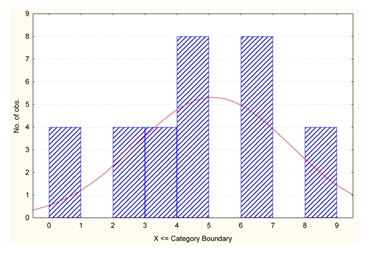 | 0.930 |
| v3 | Number of elements made [pcs] | 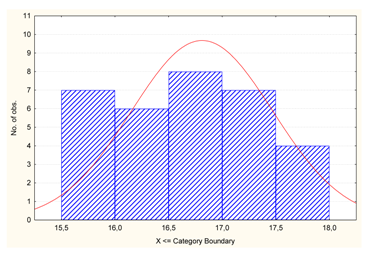 | 0.948 |
| v4 | Failure/equipment repair [%] | 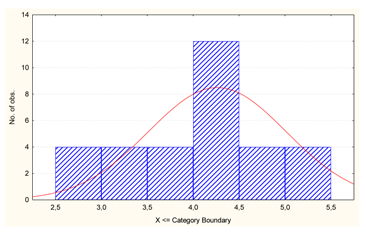 | 0.933 |
| v5 | Temp. [°C] |  | 0.810 |
| v6 | Grinding time [h] | 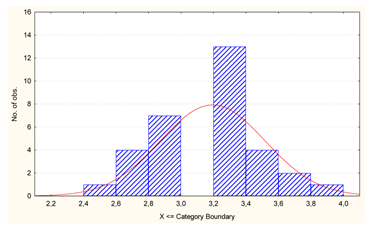 | 0.938 |
| v7 | Well-being assessment | 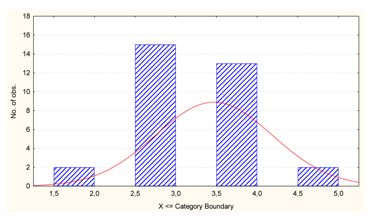 | 0.839 |
| Variable | Correlations Marked Correlations are Significant at p < 0.05000 N = 32 (Casewise Deletion of Missing Data) CumulativePe | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Means | Std.Dev. | Employee Productivity [pcs/h] | Employee Experience [years] | Number of Elements Made [pcs] | Failure/Equipment Repair [%] | Temp. [℃] | Grinding Time [h] | Well-Being Assessment [1–5] | |
| Employee productivity [pcs/h] | 2.242 | 0.088 | 1.000 | 0.965 | 1.000 | 0.379 | −0.034 | −0.676 | 0.055 |
| Employee experience [years] | 5.125 | 2.406 | 0.965 | 1.000 | 0.965 | 0.324 | 0.000 | −0.636 | −0.016 |
| Number of elements made [pcs] | 16.813 | 0.660 | 1.000 | 0.965 | 1.000 | 0.379 | −0.034 | −0.676 | 0.055 |
| Failure/equipment repair [%] | 4.263 | 0.752 | 0.379 | 0.324 | 0.379 | 1.000 | 0.000 | −0.555 | 0.213 |
| Temp. [°C] | 21.000 | 0.359 | −0.034 | 0.000 | −0.034 | 0.000 | 1.000 | 0.000 | 0.250 |
| Grinding time [h] | 3.195 | 0.322 | −0.676 | −0.636 | −0.676 | −0.555 | 0.000 | 1.000 | −0.095 |
| Well-being assessment [1–5] | 3.469 | 0.718 | 0.055 | −0.016 | 0.055 | 0.213 | 0.250 | −0.095 | 1.000 |
| MR1 (v1; v2, v5, v6, v7) Dependent Variable: v1; Independent Variable: v2, v5, v6, v7 | ||||||
|---|---|---|---|---|---|---|
| N = 32 | Regression Summary for Dependent Variable: Employee Productivity [pcs/h] R = 0.97151969 R2 = 0.94385051 Adjusted R2 = 0.93553207 F(4.27) = 113.46 p < 0.00000 Std.Error of estimate: 0.02234 | |||||
| Beta | Std. Err. of Beta | B | Std. Err. of B | t (27) | p-Level | |
| Intercept | 2.390392 | 0.244150 | 9.79067 | 0.000000 | ||
| v2 | 0.908220 | 0.059407 | 0.033210 | 0.002172 | 15.28803 | 0.000000 |
| v6 | −0.091091 | 0.059686 | −0.024881 | 0.016303 | −1.52617 | 0.138598 |
| v7 | 0.074736 | 0.047582 | 0.009162 | 0.005833 | 1.57067 | 0.127906 |
| v5 | −0.052723 | 0.047132 | −0.012914 | 0.011545 | −1.11863 | 0.273151 |
| MR2 (v1; Log(v3), v4, v7) Dependent Variable: v1; Independent Variable: Log(v3), v4, v7 | ||||||
|---|---|---|---|---|---|---|
| N = 32 | Regression Summary for Dependent Variable: Employee Productivity [pcs/h] R = 0.99984602 R2 = 0.99969206 Adjusted R2 = 0.99965907 F(3.28) = 30300, p < 0.0000 Std.Error of Estimate: 0.00162 | |||||
| Beta | Std. Err. of Beta | B | Std. Err. of B | t (27) | p-Level | |
| Intercept | −4.11047 | 0.022218 | −185.009 | 0.000000 | ||
| Log(v3) | 1.004722 | 0.003602 | 2.25307 | 0.008078 | 278.909 | 0.000000 |
| v4 | −0.013375 | 0.003682 | −0.00157 | 0.000431 | −3.633 | 0.001114 |
| v7 | 0.004819 | 0.003396 | 0.00059 | 0.000416 | 1.419 | 0.166949 |
| Model Specifications | Model Summary |
|---|---|
| Value | |
| Independents | 5 |
| Dependents | 1 |
| Number of terms | 2 |
| Number of basis functions | 1 |
| Order of interactions | 1 |
| Penalty | 2.000000 |
| Threshold | 0.000500 |
| GCV error | 0.000629 |
| Prune | Yes |
| Dependents | Number of References to Each Predictor Number of Times Each Predictor is Referenced (Used) |
|---|---|
| References | |
| Employee experience [years] | 1 |
| Failure/equipment repair [%] | 0 |
| Temperature [°C] | 0 |
| Grinding time [h] | 0 |
| Well-being assessment [1–5] | 0 |
| Coefficients, Knots and Basis Functions | Model Coefficients NOTE: Highlighted Cells Indicate Basis Functions of Type Max(0, Independent-Knot), otherwise Max(0, Knot-Independent) | ||||||
|---|---|---|---|---|---|---|---|
| Coefficients v1 | Knots v2 | Knots v3 | Knots v4 | Knots v5 | Knots v6 | Knots v7 | |
| Intercept | 2.096123 | - | - | - | - | - | - |
| Term.1 | 0.035283 | 1.00 | - | - | - | - | - |
| Variable Index | Degrees of Freedom | GAM Coefficient | Std. Err. | Result Std. | p-Level | |
|---|---|---|---|---|---|---|
| Intercept | 0 | 1.000000 | −0.020311 | 0.012648 | −1.6058 | |
| v2 | 1 | 3.999711 | −0.000897 | 0.000204 | −4.3932 | 0.000000 |
| v3 | 2 | 3.998411 | 0.134833 | 0.000779 | 173.1406 | 0.000000 |
| v4 | 3 | 4.001388 | 0.000079 | 0.000206 | 0.3823 | 0.000000 |
| v6 | 4 | 4.000114 | −0.000198 | 0.000595 | −0.3329 | 0.933869 |
| Variable Index | Degrees of Freedom | GAM Coefficient | Std. Err. | Result Std. | p-Level | |
|---|---|---|---|---|---|---|
| Intercept | 0 | 1.000000 | −0.193360 | 0.001631 | −118.549 | |
| v2 | 1 | 3.999711 | −0.000019 | 0.000026 | −0.703 | 0.000000 |
| v3 | 2 | 3.998411 | 0.059500 | 0.000100 | 592.487 | 0.000000 |
| v4 | 3 | 4.001388 | −0.000024 | 0.000027 | −0.919 | 0.948296 |
| v6 | 4 | 4.000114 | −0.000096 | 0.000077 | −1.255 | 0.580771 |
| Index | Net. Name | Training Perf. | Test Perf. | Training Error | Test Error |
|---|---|---|---|---|---|
| 1 | MLP 6-7-1 | 0.999985 | 0.999991 | 0.000002 | 0.000002 |
| Training Algorithm | Error Function | Hidden Activation | Output Activation |
|---|---|---|---|
| BFGS 17 | SOS | Tanh | Identity |
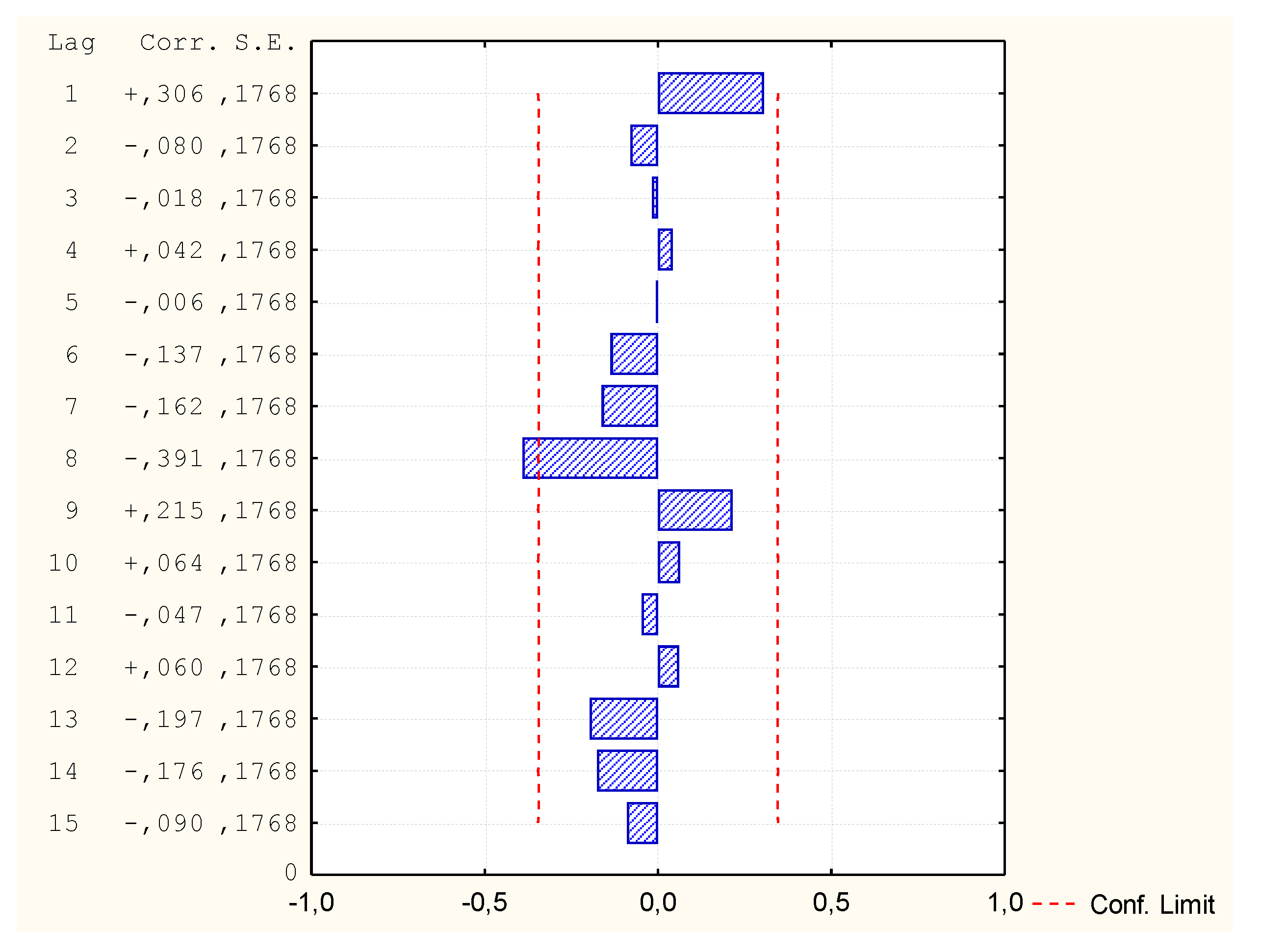
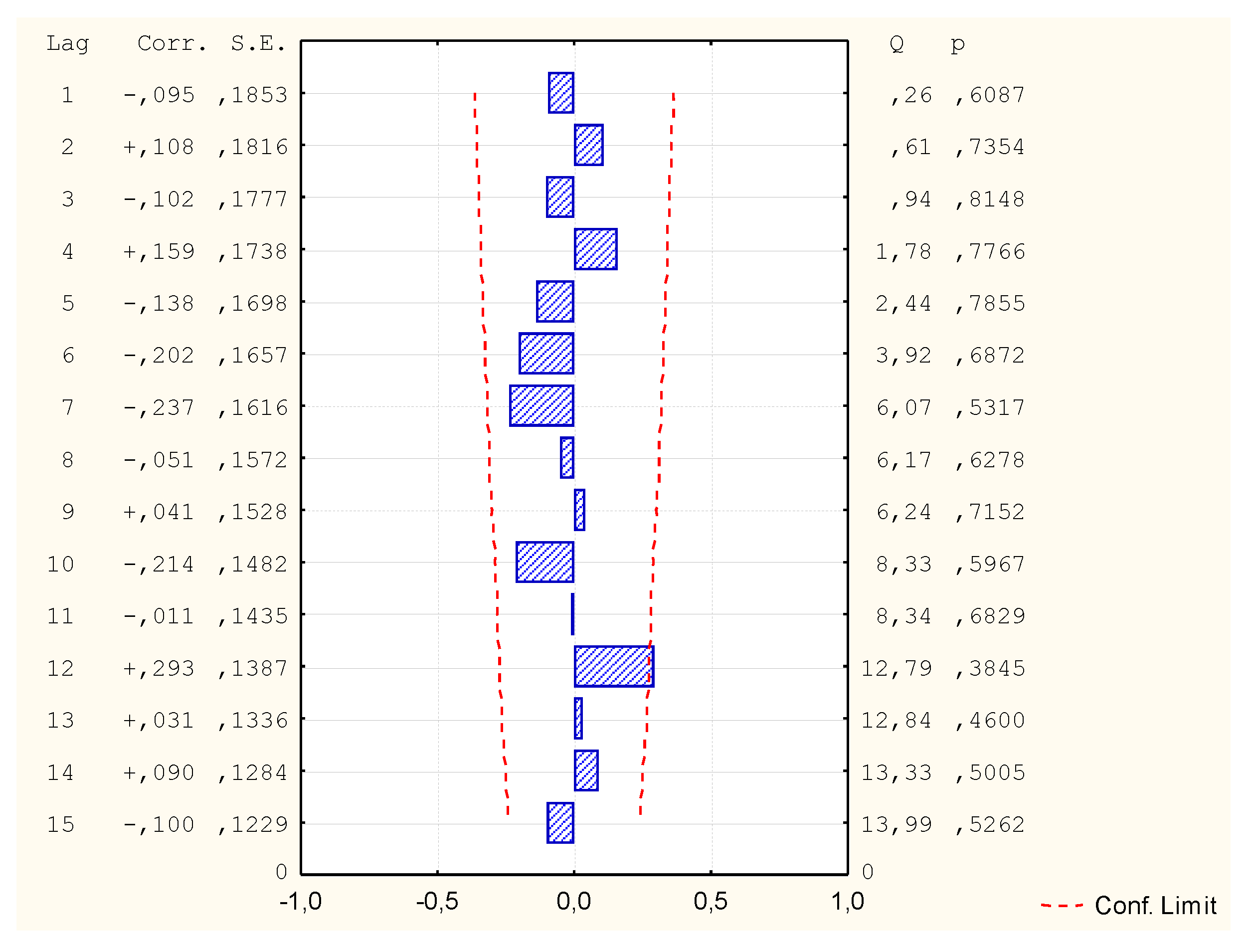
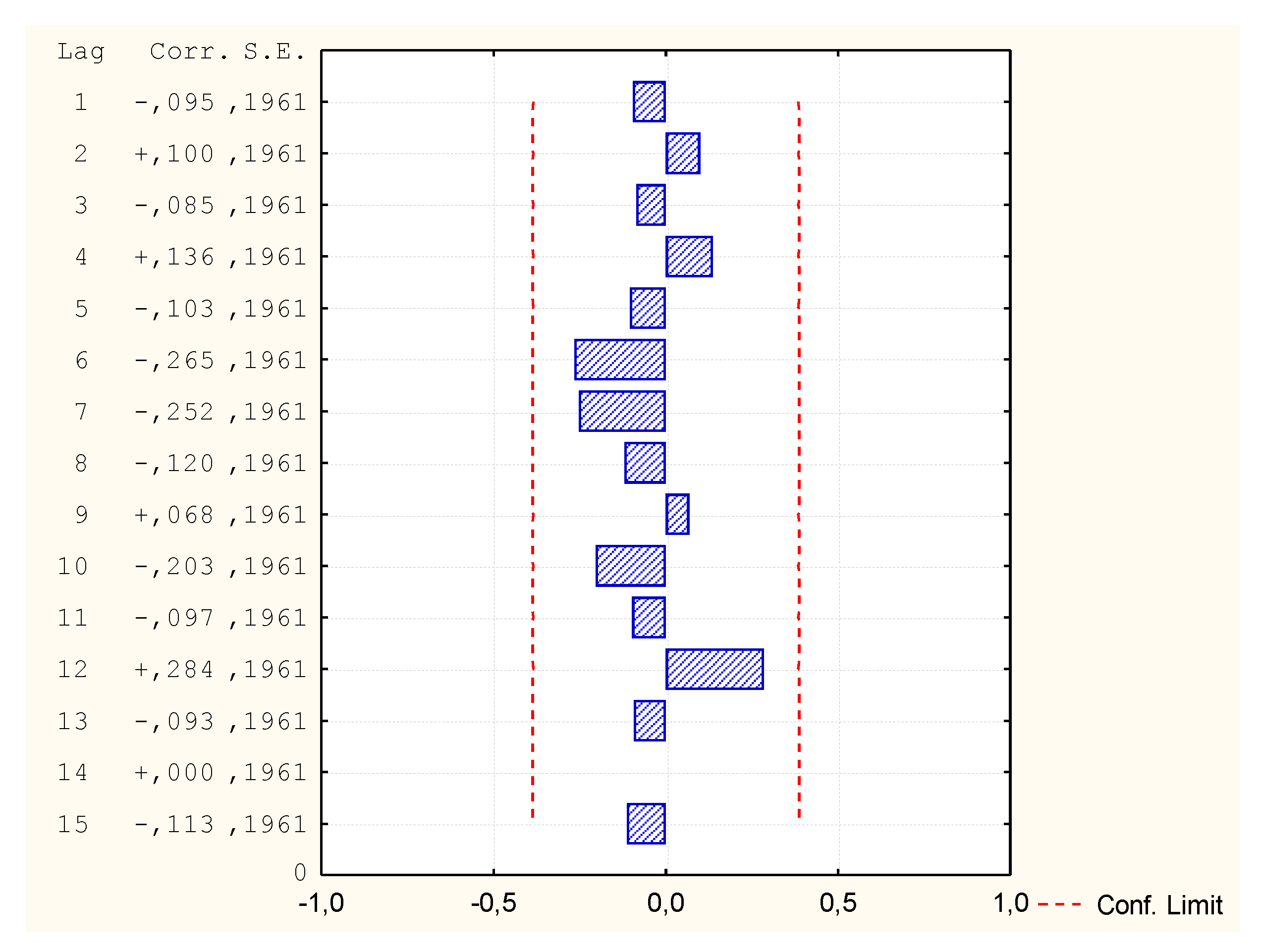
| Method Name | Autocorrelation of Residues or Partial Residues | Model Correctness | MAPE Error [%] |
|---|---|---|---|
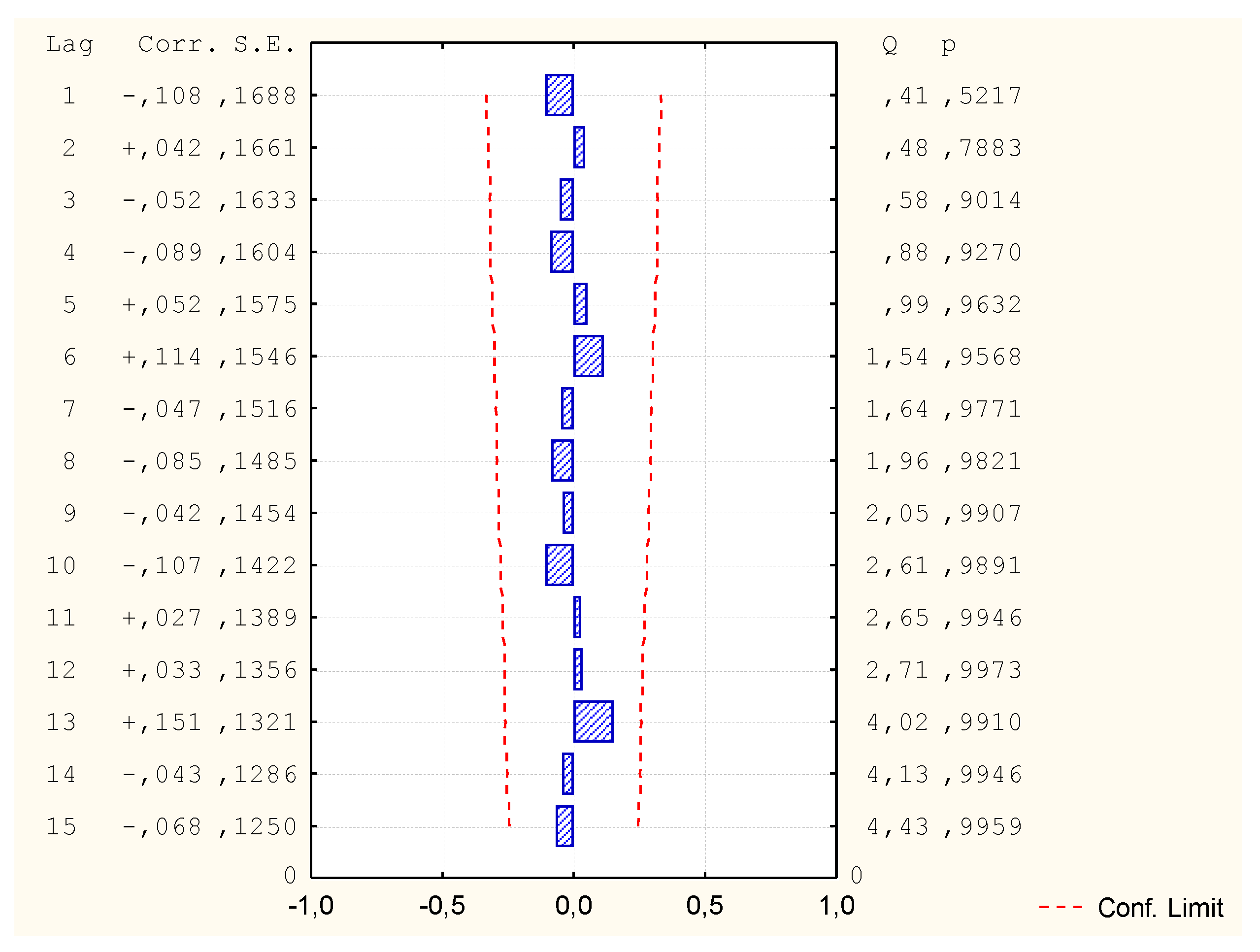
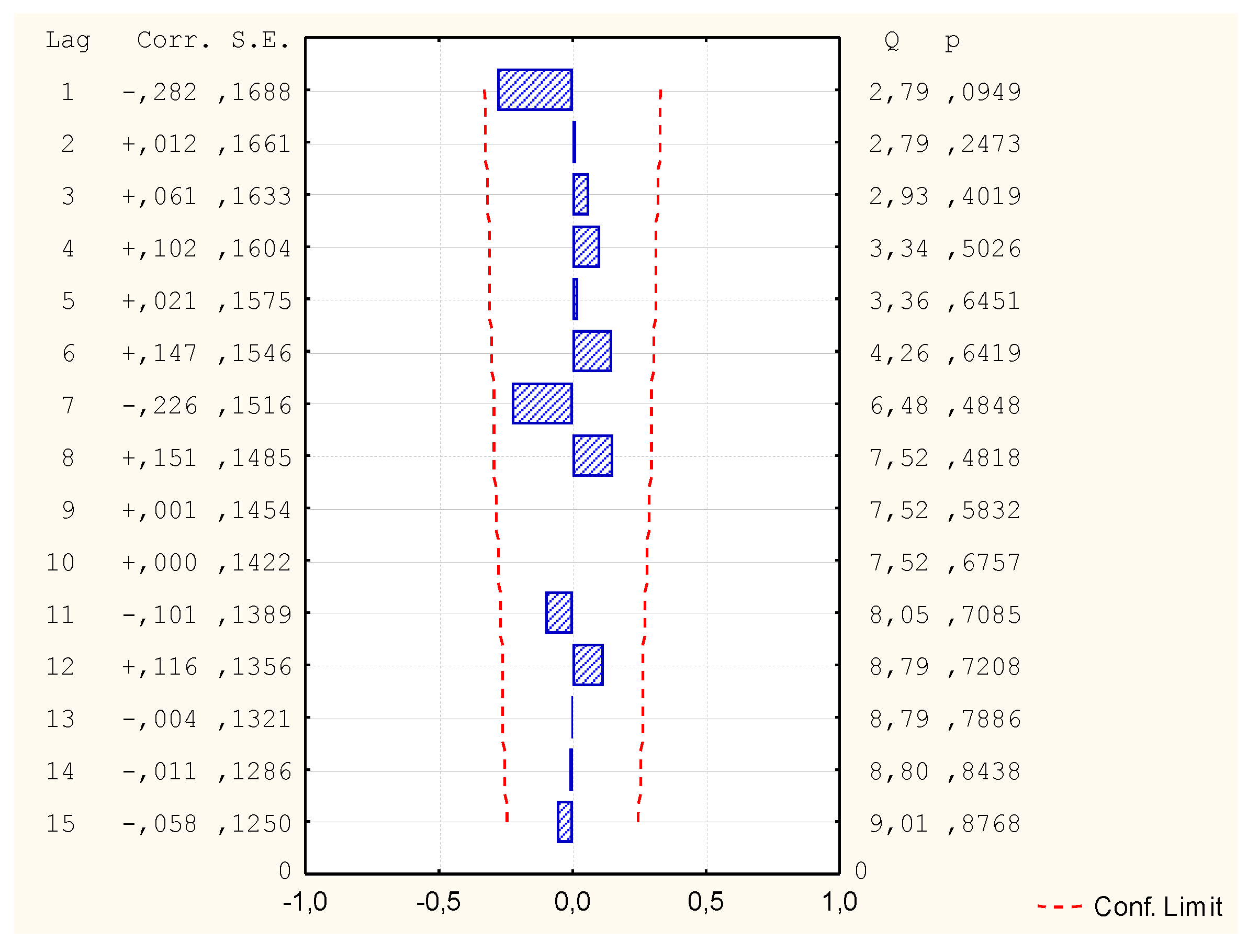
| MR1 (v1; v2, v5, v6, v7) | Does not occur | Correct | 0.72 |
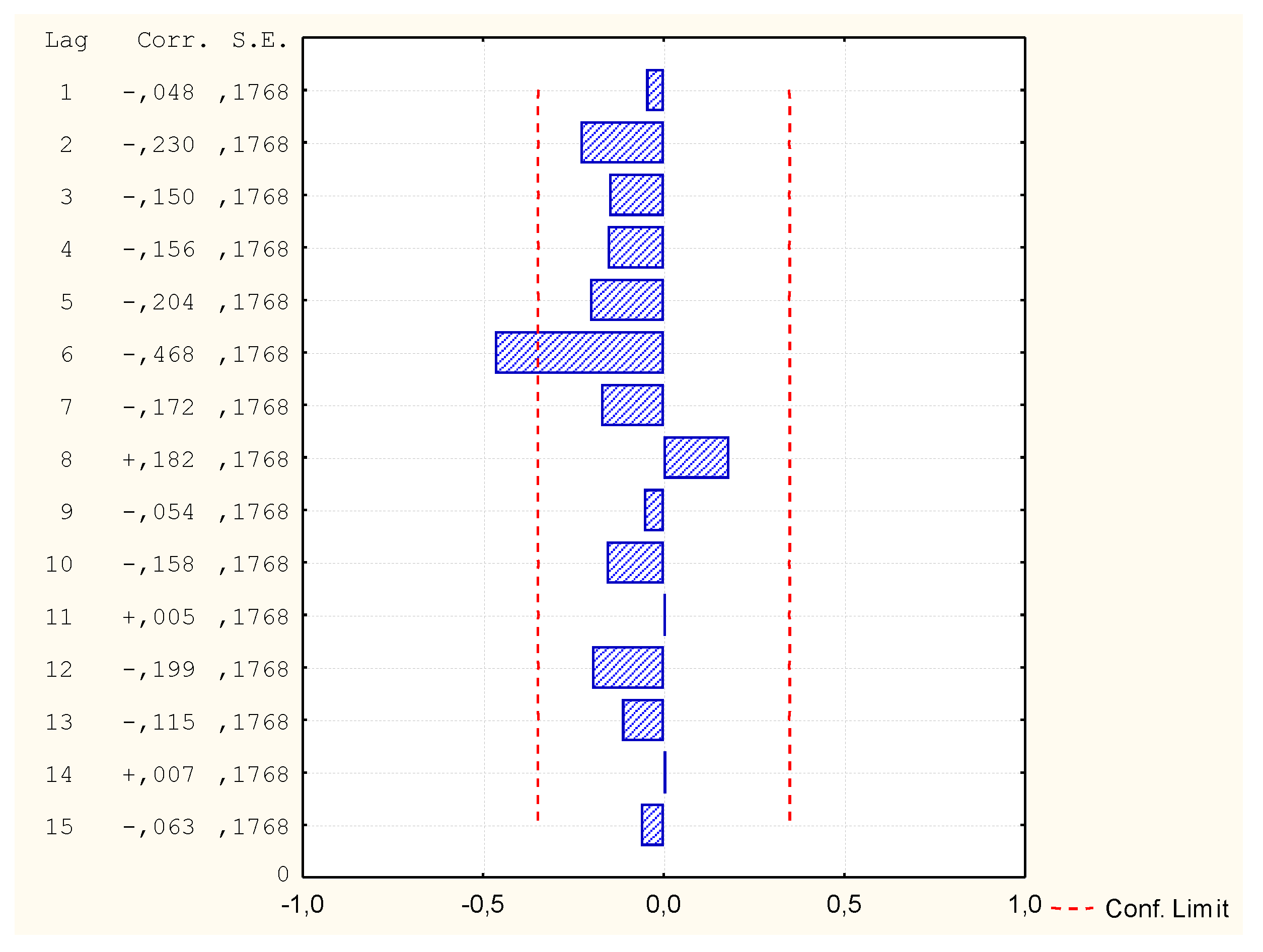
| MR2 (v1; Log(v3), v4, v7) | In 6th place | Incorrect | - |
| MARS1 (v1; v2, v4, v5, v6, v7) | Does not occur | Correct | 0.82 |
| GAM1 (v1; v2, v3, v4, v6 | In 4th place | Incorrect | - |
| GAM2 (v1; v2, v3, v4, v5, v6, v7) | In 8th place | Incorrect | - |
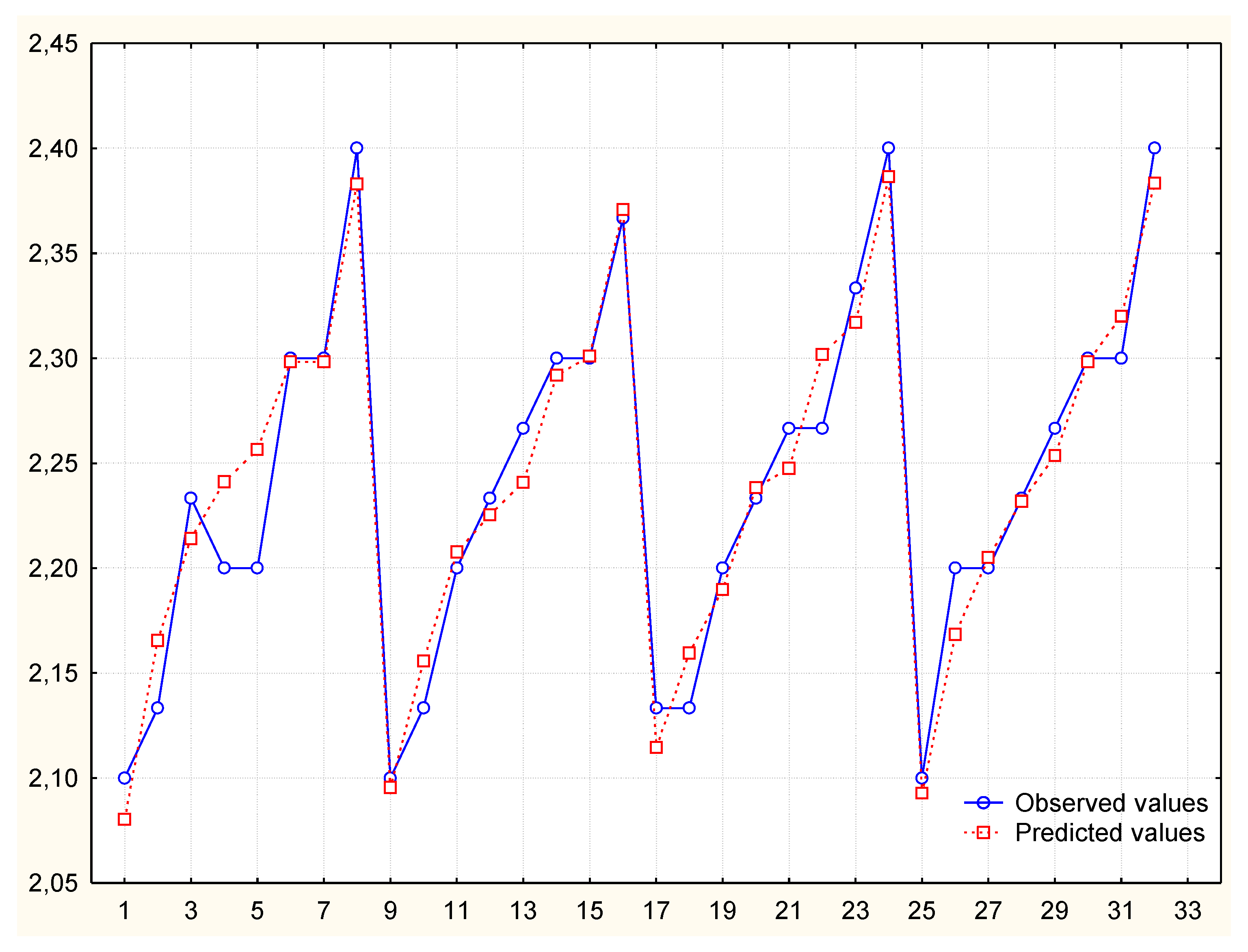
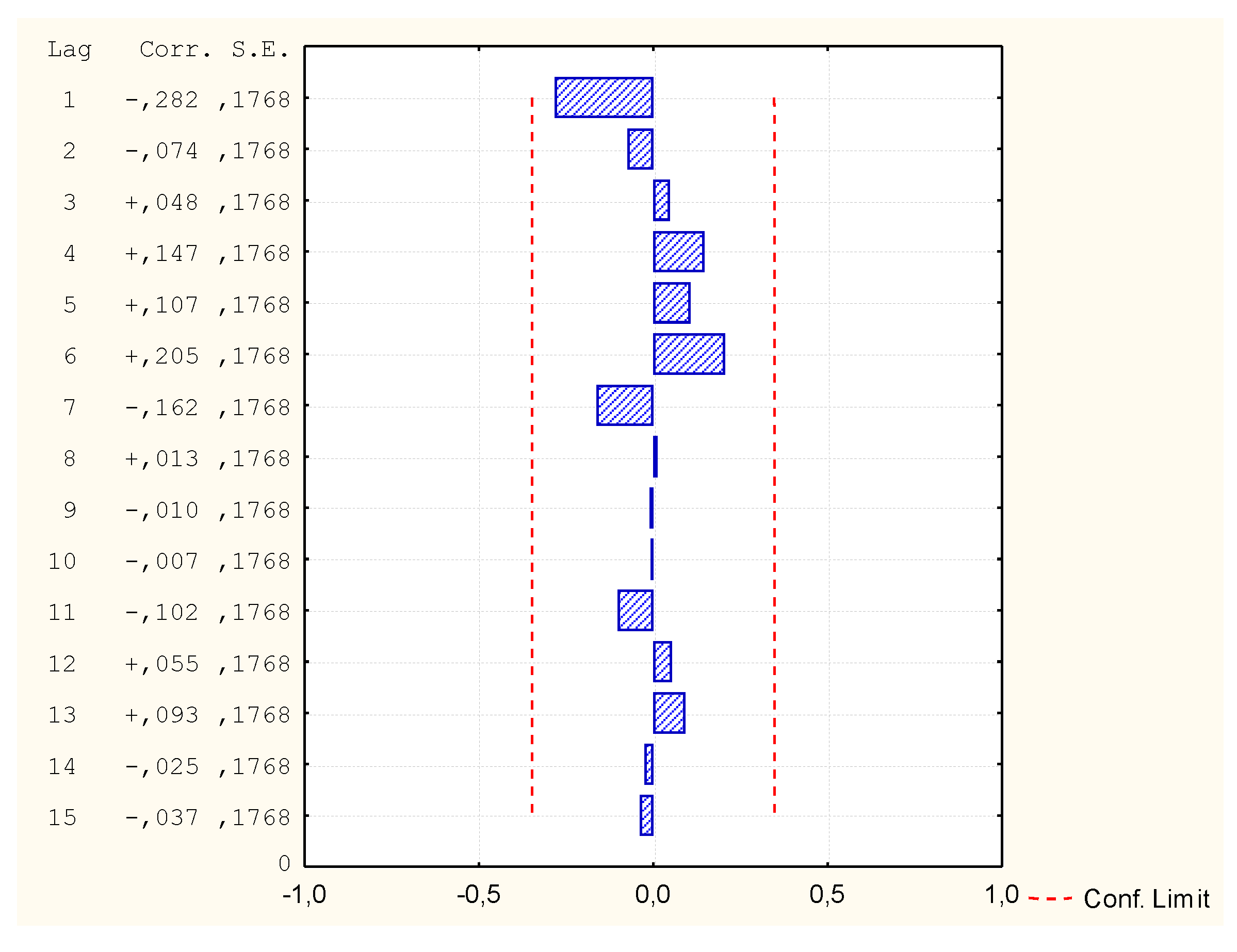
| NN1 (v1; v2, v3, v4, v5, v6, v7) | In 12th place | Correct | 0.02 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kostrzewa-Demczuk, P.; Rogalska, M. Anticipating the Length of Employees’ Working Time. Symmetry 2020, 12, 413. https://doi.org/10.3390/sym12030413
Kostrzewa-Demczuk P, Rogalska M. Anticipating the Length of Employees’ Working Time. Symmetry. 2020; 12(3):413. https://doi.org/10.3390/sym12030413
Chicago/Turabian StyleKostrzewa-Demczuk, Paulina, and Magdalena Rogalska. 2020. "Anticipating the Length of Employees’ Working Time" Symmetry 12, no. 3: 413. https://doi.org/10.3390/sym12030413
APA StyleKostrzewa-Demczuk, P., & Rogalska, M. (2020). Anticipating the Length of Employees’ Working Time. Symmetry, 12(3), 413. https://doi.org/10.3390/sym12030413






