Abstract
A novel scheme is presented for image compression using a compatible form called Chimera. This form represents a new transformation for the image pixels. The compression methods generally look for image division to obtain small parts of an image called blocks. These blocks contain limited predicted patterns such as flat area, simple slope, and single edge inside images. The block content of these images represent a special form of data which be reformed using simple masks to obtain a compressed representation. The compression representation is different according to the type of transform function which represents the preprocessing operation prior the coding step. The cost of any image transformation is represented by two main parameters which are the size of compressed block and the error in reconstructed block. Our proposed Chimera Transform (CT) shows a robustness against other transform such as Discrete Cosine Transform (DCT), Wavelet Transform (WT) and Karhunen-Loeve Transform (KLT). The suggested approach is designed to compress a specific data type which are the images, and this represents the first powerful characteristic of this transform. Additionally, the reconstructed image using Chimera transform has a small size with low error which could be considered as the second characteristic of the suggested approach. Our results show a Peak Signal to Noise Ratio (PSNR) enhancement of for DCT, for WT and for KLT. In addition, a Structural Similarity Index Measure (SSIM) enhancement of for DCT, for WT and for KLT.
1. Introduction
With the significant increase of multimedia technology in mobile devices and diverse applications, image compression is essential in reducing the amount of data. Nowadays, large amounts of images transfer between mobile devices through wireless communication requiring a fast and robust scheme for image compression. In this regard, a compact representation of a digital image is required to transfer important information using image compression. When the amount of digital information is reduced, it will speed-up the exchange of information and free-up more space for storage in mobile devices [1].
Moreover, the lossy image compression is a powerful technique in the computer image processing field. It is the standard tool to save an image because the technique gives good quality with small memory size for storage [2]. Also, the lossy image compression technique is dependent on two factors. The first factor is that the input data must be sorted in dependent or semi-dependent form and the second factor is that this processed data must use a procedure to rearrange this data into a useful form [3].
There are many applications which participate with the image compression in their schemes. Object detection is one of the applications which required a reduced representation of digital image. This reduction will limit the size of detector model, parameters, and the data storage for this purpose [4]. Biometric authentication in mobile devices represents another application which demands image compression. This application uses the image modality such as faces, iris, and eyebrows to identify people via matching process with the template stored in remote database. Such applications need a fast match and information transfer for the data by data reduction using image compression [5,6].
Multimedia mobile communication [7] uses wireless image transmission to exchange important information between portable devices. Such applications pose a substantial impact for users in recent times. These applications are required to reduce the data redundancy in digital image before transmission. There are different types of lossy image compression such as JPEG and JPEG2000 which use Discrete Cosine Transform (DCT) and Wavelet Transform (WT). These techniques are considered traditional transforms which use a general transform for any data. Thus the proposed approach of this paper uses a specific technique to deal with image data specifically. There are some metrics which are used to evaluate different types of lossy image compression schemes. Namely, Mean Squared Error (MSE), Peak Signal to Noise Ratio (PSNR), Structural Similarity Index Measure (SSIM), and Compression Ratio (CR). MSE calculates the cumulative squared error between the compressed image and original image. PSNR detects the logarithmic scale of the error of an image before and after compression. SSIM is considered as a subjective metric for image quality degradation which is used to measure the similarity between the original and reconstructed image. Finally, the CR is used to evaluate the compression scheme.
DCT and WT are used to compress data across different dimensions such as voice signal (1D), gray image (2D), and movies (3D). Artusi et al. [8] implemented a new scheme of compression for high dimensional images. The suggested scheme involved a new coding method called JPEG XT which is based on two layers which are basic and extension layer and contain low and full dynamic range of an image respectively. Kaur et al. [9], introduced a lossless image compression using Huffman based LZW. The proposed scheme used Retinex Algorithm which involved Huffman coding, word concatenation, and Contrast enhancement. Mathur et al. [10], proposed another image compression scheme which removed the redundant codes using Huffman coding. While Jagadeesh et al. suggested a compression method using an adaptive Huffman coding but this scheme is based on binary tree. This method shows an improved result comparing with LWZ method [11]. Karhunen-Loeve Transform (KLT) was used for transforming a block of signal in terms of energy and decorrelation compaction performances [12].
Image compression has been implemented using curve fitting models as in the work of Khalaf et al. [13], which was derived from a hyperbolic tangent function with only three coefficients. In this regard, the used function had the benefits of a symmetric property to minimize the construction error and to enhance some details with texture for the reconstructed image. Their results show an enhancement of up to of PSNR. In addition, Khalaf et al. shows the effects of preprocessing and postprocessing on the compressed images using DCT which address the issues of the monochrome images [14]. Lu et al. extended an optimal piecewise linear approximation for images from 1D curve fitting to 2D surface fitting by a dual-agent algorithm. Their algorithm achieved compact code length with guaranteed error bound, through providing a more dedicated representation of image features [15]. Some compression algorithms have used Singular Value Decomposition (SVD) [16]. This scheme involved a prediction error using Recursive Neural Network (RNN), and Vector Quantization techniques. Other compression methods suggested a 2D image modeling algorithm based on stochastic state-space system to fit quarter plane causal dynamic Roesser model to an image. The results were causal, recursive, and separable-in-denominator [17,18,19].
Embedded Zerotree Wavelet Transform has also been implemented in lossy image compression and perceived that the performance, for example; Set Partitioning in Hierarchical Trees (SPIHT) encoding technique produced good results in comparison with other encoding schemes [20]. A. Losada et al. modified Shapiro’s Embedded Zerotree Wavelet algorithm (EZW) for image codec which is based on the Wavelet Transform and on the self-similarity inherent in images through applying a multi-iteration EZW to optimise the combination of ZT and Huffman coding [21]. Oufai et al. proposed another modification of the EZW algorithm by using four symbols instead of using six as Shapiro’s distributed the entropy in EZW and also optimized the coding by a binary grouping of elements before coding [22].
Our study focuses on image compression. Two contributions in this study were done as follows:
- 1
- Suggest a novel scheme for image compression which will be compatible with different image conditions.
- 2
- Propose three hypotheses, the first and the second hypotheses summarize the important requirements of the lossy image compression, while the third hypothesis uses the first and the second hypotheses to implement a powerful transform.
2. Problem Statement of the Lossy Image Compression
The image compression is designed to work with a small part of image namely, block. This block has pixels each pixel has independent value. Note that, the image is a combination of pixels which is considered as a reflection for connected areas and deterministic objects.
In this trend, the block involves some special cases of data combination. Whereas the block could not be considered as a pure random data, therefore blocks will not be represented as a dependent form like a deterministic relation or function. In general, the pixels inside image block could be grouped into one, two or three connected groups, and these groups could be distributed randomly.
There are three suggested hypotheses which are proposed in this paper. The first two suggested hypotheses will impact on the lossy image compression and data redundancy. The first hypothesis is related to the limitation of useful pattern inside the block. However, the pattern of a block could be considered as an useful pattern, if the block has a random data. While, the second hypothesis is related to the redundancy of the data inside image due to similarity between the blocks of a certain image. Consequently, this process does not affect the entire image as a result of similarity between blocks. Thus, the proposed approach makes use of this property to substitute a current block with a similar one.
Moreover, the lossy image compression techniques could be implemented using data transformation such as DCT to obtain an image of type JPEG. This transformation can transfer the data from spacial domain to frequency domain. This process could be considered as a rearrangement tool for the information inside each block. In this regards, the possibility of data rearrangement could be considered as a changing rule for data distribution, then this data could be restored in a useful form for quantization and coding processes. Consequently, the amount of coded data can become smaller than before [23].
In addition, the lossy image compression used different techniques of transformation according to the form of data distribution inside the block. For instance, DCT is much more efficient than Walsh-Hadamard (WH) in which the blocks contain wavy or smooth changes. In contrast, WH is more functional than DCT in the case of edgy blocks [24]. Also, the Wavelet Transform works more efficiently when the blocks have a flat area or edgy [25].
The Concept of Chimera Transform
A cross correlation within image block using few coefficients represents a key point for any image transformation to be considered as an efficient scheme. With this regards, an image transformation gives one coefficient of high value while the residue coefficients are very small values (almost zeros) for an image block which affords a maximum cross correlation. In this case, the gain of quantization and coding is very high (small number of bits) which gives a good quality for the retrieved image.
Theoretically, a suggested transform could be designed using the proposed approach which is named Chimera. Chimera (Figure 1) is a fictional animal consisting of body parts which are taken from different animals. This mythical animal is used to describe anything composed of different disparate parts which are wildly imaginative, implausible, or dazzling.

Figure 1.
Chimera, a fictional animal.
The proposed transformation is based on the Chimera methodology in which has a multiple aspects to be compatible with most block patterns. However, this transformation has three challenges, namely, orthogonality, complexity and a large number of coefficients. The first challenge could be mitigated using a mask of ones for the selected coefficient with max correlation, and masks of zeros for the other coefficients. This solution could work if all possible cases of image blocks are estimated. On other hand, the complexity could be reduced by separating the DC value (minimum value of the block) from other components, then saving it as a separate coefficient. So that, the remaining components (without DC value) have to be normalized with respect to the maximum value in this block. The third challenge represents the main challenge of the proposed approach due to the large number of possible cases. For instance, a block gray image needs () which is greater than of possible cases. The first and second suggested hypotheses could be considered as the key point of the proposed approach which are used to solve this problem.
Moreover, the first and second suggested hypotheses offer a way to find an acceptable set of coefficients to implement Chimera transform. In this case, a 256 free coefficients were implemented according to the suggested hypotheses. In other words, a image block was converted into three coefficients which are (A) for DC component (minimum), (B) for normalization (maximum − minimum) and (C) for mask label.
3. The Proposed Approach
The overall stages of the proposed work is shown in Figure 2 which consists of Chimera mask calculation for image compression, and image restoration as will be explained in the next sections.
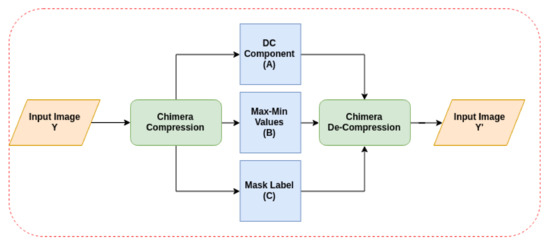
Figure 2.
The diagram of the overall Chimera approach.
3.1. Chimera Coefficients Calculation
The first stage in the proposed approach is coefficients calculation. This stage involved a cascaded steps to compress the image in this proposed work. The steps are image division, block isolation, block normalization, correlation calculation and best mask estimation. Figure 3 shows the steps of the coefficients calculation stage.
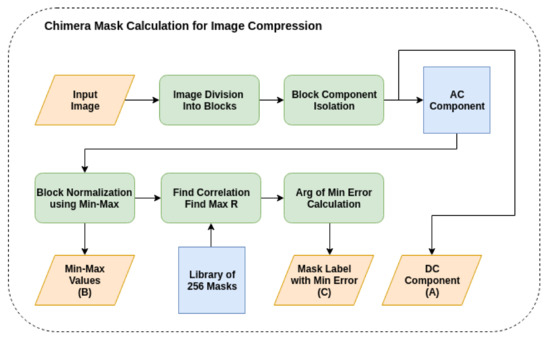
Figure 3.
The Chimera mask calculation for image compression.
First of all, the entire input image was divided into N blocks of size . Then, for each block the minimum value was isolated and was considered as coefficient (A). Consequently, the resulted component of the block was normalized using min-max normalization using Equation (1). The min-max value was considered as coefficient (B).
where is input value, is the output value (normalized) and x is the block.
The correlation coefficient (R) was calculated between the normalized block (z) and the library of 256 free masks and used to estimate the best mask for the specific block. The best mask was estimated using argument calculation for the min error (i.e., maximum value of R). Finally, the mask label (C) for the best estimated mask and the min-max value (B) of normalized block (z) was saved for the next stage of an image restoration. Figure 4 shows the calculated components for some test images (man and boat images).

Figure 4.
The calculated components for man and boat images: (A,E) are the original images, (B,F) are coefficient A, (C,G) are coefficient B, and (D,H) are coefficient C.
The small set of the 256 masks was acquired from the proposed transform. Consequently, these masks were added a minimum amount of errors to the reconstructed block. With this trend, the error minimization could be dependent on coefficients number and mask pattern.
The masks were proposed using the suggested hypotheses to obtain a set of arrays of size. This satisfied our aim by estimating a set of masks for all possible cases for the input block. While the number of the masks depends on two parameters, namely, the block size and the data complexity. A powerful analysis for a large number of masks leads to obtain a low output error, however; as a result the number of masks inside the mask library will be increased. As shown in the experimental section, the selection of 256 masks for block size is dependent on the suggested hypotheses to obtain a robust results.
Moreover, each 256 masks were designed as matrix size and the values of these matrix elements were in range of . The mask implementation was not a simple process, therefore this operation consists of three main steps. The first step of mask implementation was proposed to generate a 16 vectors of size as explained in Table 1. Subsequently, a vector transpose and multiplication was applied on the 16 vectors to obtain a 256 of possible cases (masks). In the third step, the resulted masks were enhanced to obtain the final matrices.

Table 1.
Code generation for Chimera mask implementation.
Moreover, Table 1 was based on our suggested hypotheses which states that each 4 one dimension neighbored points ( vector) in the image, there are a 16 useful cases were divided over 5 groups as follows: group 1 is the Base that has one flat case, group 2 is the Slope that has two slow growing cases, group 3 is the Simple edge that has six cases, group 4 is the One bit that has four cases and group 5 is the Step that has three cases. Finally, according to our suggested hypotheses, a (16) possible cases were generated and divided into the 5 groups as shown in Table 1. Consequently, the 16 useful possible cases (generations) were scaled to the value of 24 to avoid fraction numbers in the mask calculation (we used an integer number 24 which is the least common multiple of the values of 1, , , , ...). With this assumption, each generation should contain a maximum value of 24 and a minimum value of 0. However, the first group (Base) and last group (Step) were excluded from the previous assumption in which the maximum and minimum values were 24 and 12, respectively. The second step is demonstrated in Equation (2) which was used to generate 256 masks, each of size.
The third step was involved an enhancement process which applied on the mask was considered as unsystematic and statistical process. Also, the suggested hypotheses were used to detect useful patterns (generated cases) and conserve the desired masks. Table 2 shows the excluded patterns and the reasons for excluding. The first five cases are equal and the other cases have no zero value, therefore; these cases were excluded from the mask library.

Table 2.
The excluding cases and the reason for excluding.
Since, all the generated masks were symmetric, an anti-symmetry operation was required to mitigate this issue with other special masks. Thus, the suggested hypotheses were designed to overcome the symmetrical problem for masks by proposing suggested matrices as shown in Table 3. However, the Non-Changed (NC) cases are left for future work.

Table 3.
The proposed coefficients to overcome symmetrical masks.
In addition, the proposed algorithm for the suggested compression (Algorithm 1) and de-compression (Algorithm 2) approaches are explained below.
| Algorithm 1: The Proposed Algorithm for Image Compression |
 |
| Algorithm 2: The Proposed Algorithm for Image De-Compression |
 |
3.2. Chimera Image Restoration
Image restoration represents the second stage in the Chimera proposed approach. This stage consists of four steps which are de-normalization, DC component restoration, block aggregation, and image enhancement. Figure 5 shows the consequences of these four steps.
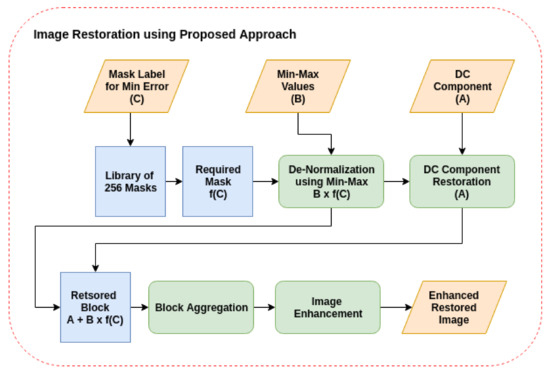
Figure 5.
The Chimera image restoration.
The mask label (C) from the previous stage (Chimera mask calculation) was used to locate the desired mask from the library of 256 masks. Then, this mask was de-normalized using coefficient (B) which was saved in the previous stage. Subsequently, the required block was restored using DC component (coefficient A). This operation was applied to all blocks of size for the entire image. Consequently, these blocks were aggregated to construct the required image. An additional step involved image enhancement to remove the undesired boundaries between the aggregated blocks a consequence of the previous step.
4. Experiments
This section describes our results and comparative evaluation. A comparative evaluation was applied between the proposed approach and the standard transforms which are used in the lossy image compression. Moreover, PSNR for the same compression ratio (image size) was used in this comparative study. Also, the reported results of the proposed approach show an outstanding over the tradition methods.
4.1. Results
Eight standard images were used in the evaluation to show the robustness of our proposed approach and to gain the subjective and objective metrics for these images. Subsequently, these results were compared with standard lossy transforms for image compression. As mentioned in the previous section, three image transformations were used, two of them are independent of the image content which are Discrete Cosine Transform (DCT) which produces JPEG and Wavelet Transform (WT) which produces JPEG2000, and a content-dependent transform which is Karhunen-Loeve Transform (KLT) [12].
An image block of size was used in this evaluation and each block was tested and evaluated using the suggested approach and the standard methods. The reported result was quantized into three coefficients of 8-bit size.
The Compression Ratio (CR) was set to 5.3:1, meaning that bpp (bits per pixel) was used for all tests. The results were evaluated without coding. The coding process was excluded since this process does not effect on the quality of the resulted image and CR could be considered as a random parameter for coding.
Figure 6 shows some of visual results for image de-compression using different image transforms. For instance, Lena image which represents de-compression using suggested Chimera Transform (CT) is shown in Figure 6B. Clearly, the proposed CT shows a better visualization than the others, namely, the DCT (Figure 6C), the WT (Figure 6D), and the KLT (Figure 6E).

Figure 6.
A visual result for image compression: (A) Lena original image, (B) Lena-CT, (C) Lena-DCT, (D) Lena-WT, (E) Lena-KLT, (F) Boat original image, (G) Boat-CT, (H) Boat-DCT, (I) Boat-WT, and (J) Boat-KLT.
4.2. Comparative Evaluation
In order to show the robustness of the proposed approach, a comparative evaluation was involved in this work. In this evaluation, four different approaches were compared to obtain four evaluation scores. Figure 7 shows the entire process for this evaluation.
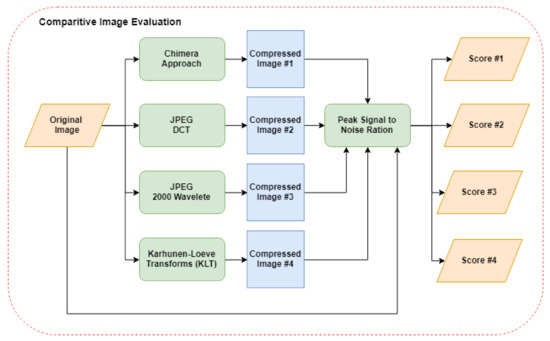
Figure 7.
The comparative evaluation of the proposed approach with existence approaches.
Peak Signal to Noise Ratio (PSNR) was used to evaluate the Chimera proposed approach with three other approaches which are JPEG (DCT), JPEG 2000 (WT), and KLT. Also, the evaluation scores were obtained using PSNR between the original image and compressed image for each of the compression approaches.
Table 4 shows the comparative results using image compression metrics namely, Peak Signal to Noise Ratio (PSNR) and Structural Similarity Index Measure (SSIM). These metrics were applied to the proposed Chimera Transform (CT), DCT, WT, and KLT.

Table 4.
Evaluation metric for four different approaches.
Figure 8 shows the comparative evaluation between the proposed Chimera Transform (CT) and the DCT, WT and KLT transforms. This figure shows that CT overcame other transforms in both PSNR and SSIM metrics.
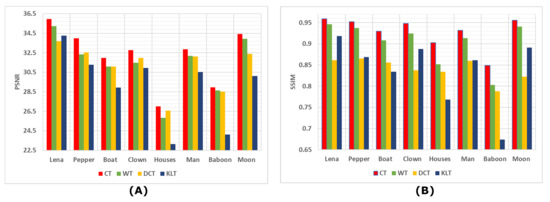
Figure 8.
Evaluation metrics: (A) PSNR, (B) SSIM between the suggested transform, WT, DCT and KLT transforms.
5. Conclusions and Future Work
We have introduced a new transform called Chimera which shows a robustness against other standard transforms such as Discrete Cosine Transform (DCT), Wavelet Transform (WT) and Karhunen-Loeve Transform (KLT). The suggested approach was designed to compress a specific data type of the images and this represents the first powerful characteristic of this transform. Also, the reconstructed image using Chimera transform has a small size with low error which could be considered as the second characteristic of the suggested approach.
The reported results show a PSNR of for CT while, for DCT, for WT and for KLT. In addition, the suggested approach shows a of SSIM for CT, for DCT, for WT and for KLT. The reported results were evaluated on the Moon image of size . Table 4 shows the other evaluations which applied on eight different standard images of same size for each reconstructed image.
Other aspects of the suggested approach are not mentioned in this paper. These aspects relate to preprocessing, post-processing and coding. For future work, coding operation could be considered after CT to improve the quality of the image compression. Image block of size could be considered and evaluated to increase the Compression Ratio (CR). Also, the number of masks and coefficients could be increased to gain a low level of error in the reconstructed image. In addition, the deep machine learning such as the convoluational Neural Network (CNN) could be introduced to generate the mask library instead of hand-craft mask generation as shown in the Table 1 and Table 2 in the compression.
Author Contributions
Conceptualization, D.Z. and W.K.; Methodology, D.Z.; Software, A.S.M.; Validation, W.K. and A.S.M.; Formal analysis, W.K.; Investigation, A.S.M.; Resources, D.Z.; Data curation, W.K. and A.S.M.; Writing–original draft preparation, W.K. and D.Z.; Writing–review and editing, A.S.M.; Visualization, W.K.; Supervision, D.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
We would like to present our thanks to Mustansiriyah university for supporting our experiments in providing us all the necessary data and software.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CR | Compression Ratio |
| PSNR | Peak Signal-to-Noise Ratio |
| MSE | Mean Squared Error |
| bpp | bits per pixel |
| DCT | Discrete Cosine Transform |
| WT | Wavelet Transform |
| SSIM | Structural Similarity Index |
| JPEG | Joint Photographic Experts Group |
References
- Khobragade, P.; Thakare, S. Image compression techniques-a review. Int. J. Comput. Sci. Inf. Technol. 2014, 5, 272–275. [Google Scholar]
- Taubman, D.S.; Marcellin, M.W. Image Compression Overview. In JPEG2000 Image Compression Fundamentals, Standards and Practice; Springer: New York, NY, USA, 2002; pp. 3–21. [Google Scholar]
- Cebrail, T.; Sarikoz, S. An overview of image compression approaches. In Proceedings of the 3rd International conference on Digital Telecommunications, Bucharest, Romania, 29 June–5 July 2008. [Google Scholar]
- Mohammad, A.S.; Rattani, A.; Derakhshani, R. Comparison of squeezed convolutional neural network models for eyeglasses detection in mobile environment. J. Comput. Sci. Coll. 2018, 33, 136–144. [Google Scholar]
- Xu, Y.; Lin, L.; Zheng, W.S.; Liu, X. Human re-identification by matching compositional template with cluster sampling. In Proceedings of the IEEE International Conference on Computer Vision, Sydney, Australia, 1–8 December 2013; pp. 3152–3159. [Google Scholar]
- Mohammad, A.S. Multi-Modal Ocular Recognition in Presence of Occlusion in Mobile Devices. Ph.D. Thesis, University of Missouri, Kansas City, MO, USA, 2018. [Google Scholar]
- Reaz, M.B.I.; Akter, M.; Mohd-Yasin, F. Image compression system for mobile communication: Advancement in the recent years. J. Circuits Syst. Comput. 2006, 15, 777–815. [Google Scholar] [CrossRef]
- Artusi, A.; Mantiuk, R.K.; Richter, T.; Hanhart, P.; Korshunov, P.; Agostinelli, M.; Ten, A.; Ebrahimi, T. Overview and evaluation of the JPEG XT HDR image compression standard. J. Real Time Image Process. 2019, 16, 413–428. [Google Scholar] [CrossRef]
- Kaur, D.; Kaur, K. Huffman based LZW lossless image compression using retinex algorithm. Int. J. Adv. Res. Comput. Commun. Eng. 2013, 2, 3145–3151. [Google Scholar]
- Mathur, M.K.; Loonker, S.; Saxena, D. Lossless Huffman coding technique for image compression and reconstruction using binary trees. Int. J. Comput. Technol. Appl. 2012, 3, 76–79. [Google Scholar]
- Jagadeesh, B.; Ankitha, R. An approach for Image Compression using Adaptive Huffman Coding. Int. J. Eng. Technol. II 2013, 12, 3216–3224. [Google Scholar]
- Soh, J.W.; Lee, H.S.; Cho, N.I. An image compression algorithm based on the Karhunen Loève transform. In Proceedings of the 2017 Asia-Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA ASC), Kuala Lumpur, Malaysia, 12–15 December 2017; pp. 1436–1439. [Google Scholar]
- Khalaf, W.; Zaghar, D.; Hashim, N. Enhancement of Curve-Fitting Image Compression Using Hyperbolic Function. Symmetry 2019, 11, 291. [Google Scholar] [CrossRef]
- Khalaf, W.; Al Gburi, A.; Zaghar, D. Pre and Postprocessing for JPEG to Handle Large Monochrome Images. Algorithms 2019, 12, 255. [Google Scholar] [CrossRef]
- Lu, T.; Le, Z.; Yun, D. Piecewise linear image coding using surface triangulation and geometric compression. In Proceedings of the Data Compression Conference, Snowbird, UT, USA, 28–30 March 2000; pp. 410–419. [Google Scholar]
- Mukherjee, R.; Chandran, S. Lossy image compression using SVD coding, compressive autoencoders, and prediction error-vector quantization. In Proceedings of the 4th International Conference on Opto-Electronics and Applied Optics (Optronix), Kolkata, India, 2–3 November 2017; pp. 1–5. [Google Scholar]
- Ramos, J.A.; Mercere, G. Image modeling based on a 2-D stochastic subspace system identification algorithm. Multidimens. Syst. Signal Process. 2017, 28, 1133–1165. [Google Scholar] [CrossRef]
- Tourapis, A.; Leontaris, A. Predictive Motion Vector Coding. U.S. Patent App. 16/298,051, 7 November 2019. [Google Scholar]
- Zhou, Q.; Yao, H.; Cao, F.; Hu, Y.C. Efficient image compression based on side match vector quantization and digital inpainting. J. Real Time Image Process. 2019, 16, 799–810. [Google Scholar] [CrossRef]
- Suruliandi, A.; Raja, S. Empirical evaluation of EZW and other encoding techniques in the wavelet-based image compression domain. Int. J. Wavelets Multiresolution Inf. Process. 2015, 13, 1550012. [Google Scholar] [CrossRef]
- Losada, M.A.; Tohumoglu, G.; Fraile, D.; Artés, A. Multi-iteration wavelet zero-tree coding for image compression. Signal Process. 2000, 80, 1281–1287. [Google Scholar] [CrossRef]
- Ouafi, A.; Ahmed, A.T.; Baarir, Z.; Zitouni, A. A modified embedded zerotree wavelet (MEZW) algorithm for image compression. J. Math. Imaging Vis. 2008, 30, 298–307. [Google Scholar] [CrossRef]
- Rao, K.R.; Yip, P. Discrete Cosine Transform: Algorithms, Advantages, Applications; Academic Press: San Diego, CA, USA, 2014. [Google Scholar]
- Venkataraman, S.; Kanchan, V.; Rao, K.; Mohanty, M. Discrete transforms via the Walsh-Hadamard transform. Signal Process. 1988, 14, 371–382. [Google Scholar] [CrossRef]
- Kondo, H.; Oishi, Y. Digital image compression using directional sub-block DCT. In Proceedings of the 2000 International Conference on Communication Technology, Beijing, China, 21–25 August 2000; pp. 985–992. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).