1. Introduction
In the literature, fluid dynamics have been modelled into mathematical equations in the forms of partial differential equations. For example, Lee [
1] used the forced KdV equation to model dynamics of trapped solitary waves. Shi et al. [
2] studied the coupled time-fractional Boussinesq–Burgers system and provided some exact solutions to the system. Caputo et al. [
3] reported some coupling conditions for water waves at forks. Paliathanasis [
4] researched the two-dimensional rotating ideal gas dynamics and found a one-dimensional optimal system approximation. Castaings and Navon [
5] proposed a numerical method for solving reaction–diffusion problems. These fluid dynamics often relate to the theory of conservation laws [
6,
7,
8,
9] with finite volume methods [
10,
11,
12,
13] as solving techniques. Overall, we can choose a fluid dynamics model in the literature that best suits the problem we want to solve.
This paper deals with fluid dynamics and focuses on solving the shallow water equations numerically using an adaptive mesh finite volume method with weak local residuals as the refinement indicators. Weak local residuals of the one-dimensional scalar conservation law were proved by Karni and Kurganov [
14] to have lower degrees of accuracy at discontinuities than at smooth regions. Therefore, a weak local residual can be used as a smoothness indicator of numerical solutions of the one-dimensional scalar conservation law. Furthermore, even though the theory developed by Karni and Kurganov [
14] is valid only for the one-dimensional scalar conservation law, the same behaviour of weak local residuals was seen to also be true for systems of conservation laws by numerical simulations [
14,
15,
16].
A weak local residual formulation depends on the choice of test functions having a compact support on the computational domain. Karni et al. [
15] chose to take quadratic B-splines as the test functions for both time and space variables. Constantin and Kurganov [
16] chose linear B-splines for both time and space variables leading to a less expensive computational formulation of the weak local residual. All weak local residuals of the aforementioned work of Kurganov et al. [
15,
16] assume uniform discretisation of spatial domain.
Our main contribution in this paper is the weak local residual formulation as refinement or coarsening indicators in adaptive mesh finite volume methods used to solve shallow-water-type equations in generic dimensions, including one, one and a half, and two dimensions. This generic formulation for different dimensions, and more importantly, for two dimensions in triangular grids, has never been published by the authors and any other researchers. By adaptive mesh we mean that the spatial domain discretisation can be non-uniform as the time evolves because of mesh refinement and mesh coarsening processes. We extend the work of Constantin and Kurganov [
16] and so we choose linear B-splines as the test functions for both time and space variables in the formulation of weak local residuals.
Three shallow-water-type equations are considered, namely, one-, one-and-a-half-, and two-dimensional shallow water equations. Weak local residuals that we formulate are implemented in adaptive mesh finite volume methods to solve shallow water problems. Our numerical solutions show that weak local residuals are successful in detecting non-smooth regions of the solutions and lead to adaptive mesh methods which result in accurate numerical solutions.
There are several adaptive methods in the literature using other than weak local residuals as their refinement or coarsening indicator. One of them is the adaptive method based on the numerical entropy production, as proposed by Puppo and Semplice [
17]. The theory of numerical entropy production was given by Puppo [
18,
19]. This method is tested for shallow water equations by Mungkasi [
20,
21]. The numerical entropy production is calculated using iterations of the discretised entropy inequality. Therefore, the computation of this refinement or coarsening indicator can be expensive. Another adaptive method is based on the gradient of the solution for the refinement and coarsening indicator, as used by Felcman and Kadrnka [
22]. However, the gradient of the solution is actually not an error indicator, so the error indication may not be accurate.
In contrast, the weak local residual is cheap to compute and it is an error indicator. In each iteration of the conserved quantities, the residual can be obtained using a very short algebraic formula. Due to this reason, we choose a weak local residual as the coarsening or refinement indicator in our adaptive method in the present paper.
This paper is organised as follows. We recall the formulations of the weak local residuals (WLR) of Kurganov et al. [
14,
15,
16] in
Section 2.
Section 3 presents weak local residuals for shallow-water-type equations. In
Section 4, we implement the weak local residuals as error indicator for adaptive mesh refinement or coarsening. Some concluding remarks are then drawn in
Section 5.
2. Balance Laws and Their Weak Local Residuals
In this section, we provide our numerical method of weak local residuals for detecting the smoothness of the solutions to balance laws. We follow the work described by Mungkasi [
20]. We note that Kurganov et al. [
14,
15,
16] have formulated weak local residuals of conservation laws. Mungkasi and Roberts [
23,
24] have extended those weak local residual formulations for balance laws. In this section, we recall the weak local residual formulations for balance laws. The formulations following Mungkasi et al. [
20,
23,
24,
25] are indeed important for the completeness of our work in the present paper.
We consider the scalar balance law
Here,
x represents the one-dimesional spatial variable,
t represents the temporal variable,
q denotes the conserved quantity,
s is the source function, and
f denotes the flux function. In addition,
is an arbitrary function which is defined as an initial condition. We construct the weak form of problem Equation (
1)
where
is an arbitrary test function. The derivation of this weak form can be found in the work of Knobel [
26] and Smoller [
27].
Let
be approximate values of
computed by a conservative numerical method and suppose that we have uniform grids (
,
). Using the notations of Karni and Kurganov [
14], the corresponding approximation
(which is piecewise constant) is defined as
where
and
. We choose localized linear B-splines as our test functions
, where
and
are centered at
and
with support of size
and
. These are
and
This leads to the weak local residual
which can be expressed straightforwardly as
Constantin and Kurganov [
16] proposed the use of linear B-splines in the construction of the test function for conservation laws. Therefore, the weak local residual Equation (
7) is denoted by CK (Constantin–Kurganov) indicator.
3. Shallow Water Equations and Their Weak Local Residuals
In this section, we focus on formulating weak local residuals for shallow water equations. We follow the methods of Mungkasi [
20]. The one-dimensional shallow water equations (1D SWE) are
which are the mass and the momentum equations, respectively. Here,
x is a free variable denoting the one-dimensional position,
t is a free variable denoting the time,
represents the fluid velocity dependent on
x and
t,
represents the fluid height (depth) dependent on
x and
t,
is the topography (bed elevation) dependent on
x measured from the horizontal reference, and
g is constant representing the acceleration due to gravity. We introduce an additional variable called the stage
representing the position of water surface from the horizontal reference.
In the computation of CK indicator in this case, we have three options. We can compute the CK indicator based on either the equation of mass conservation, that of momentum conservation, or a combination between equations of mass and momentum conservations. The simplest computation is the one based on the mass equation
defined at time
and position
, where the superscript
h in
represents the mass quantity (height). Here
is the width of the
ith cell, and
is the time step of the
nth iteration. Computing the residuals of the mass equation is simpler than computing those of the momentum equation, because we do not need to deal with any source term. This is a similar situation to that in the computation of numerical entropy production as a smoothness indicator as in the work of Mungkasi and Roberts [
28]. If we choose to compute the weak local residuals of the the momentum equation, then the source term must be accounted for, so that the computation of the weak local residuals is well-balanced. Mungkasi and Roberts [
24] have proposed a well-balanced computation of weak local residuals for the the momentum equation. As in the work of Mungkasi and Roberts [
24], we observed that weak local residuals with respect to the momentum and mass equations have similar behaviour [
24].
We define
, for one-dimensional problems, as the minimum cell width over the whole discretised spatial domain to be substituted in Equation (
10) and
is the time step, which varies from an iteration to another one. We conjecture that over the whole discretised spatial domain, both
and
in Equation (
10) can be taken as constants. The difference of the order between rough and smooth regions makes
able to detect the smoothness of the numerical solution. This is guaranteed as the order of
is
around discontinuities and
at smooth regions [
16] when the numerical method has the formal order
r.
Equation (
10) is defined at each vertex of computational cells. We take one having the largest magnitude of two available indicators at its cell vertices, and we take the absolute value of them in order to define the CK indicator at the centroids of each cell. Therefore, the CK indicator at the centroid of the
ith cell is given by
We note some remarks as follows. The assignment of the maximum indicator to the cell centroid is not the only choice. We can also use a linear interpolation to get the centroid value. However, we use the maximum, because it is better for the indicator to pick a cell to be refined, so that we maintain the solution to be more accurate. This is important when we are not sure that a cell is to be refined or coarsened, especially if the indicators have values close to the tolerance for refinement.
An extended application of the CK indicator for one-and-a-half-dimensional problems needs special treatment. An available model for one-dimensional shallow water flows involving a passive tracer is the one-and-a-half-dimensional shallow water equation. We can also consider it a model of one-dimensional shallow water flows involving a shear or transverse velocity. We recall the one-and-a-half-dimensional shallow water equations (1.5 D SWE)
Here, is the concentration of the passive tracer for the passive tracer model. Alternatively, we consider here as the horizontal velocity orthogonal to the x-axis, that is, the transverse velocity. Note that the variables, except the additional variable v, are the same as those in the one-dimensional model.
Variable
must be incorporated in the computation of WLR for the one-and-a-half dimensional shallow water model. This means that WLR is also able to detect the smoothness of the tracer solution. The concentration
of the passive tracer does not influence the fluid dynamics. If we exclude
from the WLR formulation, computing WLR based on momentum or mass equation or a combination of both equations only will not detect the smoothness of the tracer solution. We propose to use the combination of WLR with respect to passive transport and mass equations. We do not need to deal with a source term if we use these two equations. Alternatively, one may consider using the combination of either the equations of passive transport and momentum or the equations of passive transport, momentum and mass. This alternative needs a well-balanced WLR implementation, because we deal with source terms. A discussion on well-balanced WLR has been given in our previous work [
24].
Particularly, we calculate the WLR of the passive transport equation denoted by
and of the mass equation denoted by
at vertices. Here
is given by Equation (
10). In addition,
is given by
where the superscript
in
represents the passively transported quantity and these are defined at position
and time
.
We choose one of four available indicators with the largest magnitude at its cell vertices in order to define the CK indicator at the centroids of each cell. Let
Then CK indicator at the centroid of
ith cell is
As follows, we extend the discussion of the CK indicator for two-dimensional problems. The two-dimensional shallow water equations (2D SWE) have the forms of the following system of equations
Here,
t denotes the time variable,
represents the coordinate in two dimensions,
g is the acceleration due to gravity,
is the topography (bed elevation),
denotes the fluid height,
denotes the fluid velocity along the
x-axis, and
denotes the fluid velocity along the
y-axis. We discretise the spatial domain into triangular cells in order to solve the two-dimensional shallow water equations numerically. We can use the one-dimensional formulation Equation (
10) locally in the computation of the CK indicator in order to define the CK indicator at the middle point of an edge. For one-dimensional problems, our conjecture is that over the whole discretised spatial domain, both
and
in Equation (
10) can be taken as constants.
In the finite volume method evolution, we recall that
is the time step. We take
over the whole discretised spatial domain and substitute it into in Equation (
10) in order to define the CK indicator for two-dimensional problems. Dependent on fluid velocity, wave propagation velocity, and the CFL (Courant-Friedrichs-Lewy) number, the values of
may vary from an iteration to another one. Then one having the largest magnitude of the available indicator values at its edges defines the CK indicator at the centroid of a cell.
Before we continue to the next section, we provide some remarks here.
Remark 1. The assignment of the maximum indicator to the cell centroid is actually not the only choice. We can also use a linear interpolation to get the centroid value of the indicator. However, we use the maximum, because it is better for the indicator to pick a cell to be refined, so that we maintain the solution to be more accurate. This is important when we are not sure that a cell is to be refined or coarsened, especially if some indicators have values close to or the same as the tolerance for refinement.
Remark 2. In this paper, we use the triangle centered finite volume scheme. The mesh is constructed using the uniform bisection of triangles. In iFEM [29,30], the procedure is called UNIFORMBISECT.
4. Numerical Tests
In this section, we simulate implementations of the adaptive mesh finite volume method based on weak local residuals. Numerical flux due to Kurganov, Noelle, and Petrova (KNP) [
31] is used. Quantities are measured in SI units. We implement the well-balanced finite volume method [
32]. The numerical flux is described as follows.
We consider the problem stated in Equation (
1). The semi-discrete central-upwind scheme for this problem is
where the numerical flux
is given by [
31]
Here
and
are the right and the left approximate interpolant values of the conserved quantities at
, where the interpolant is reconstructed at each time step from the previously computed cell averages,
. In order to have a stable method, it is necessary that the time step
satisfies the Courant–Friedrichs–Lewy (CFL) condition [
31], that is,
where
is the CFL number and
. For SWE,
and the variables with star signs are obtained from the hydrostatic reconstruction [
32,
33,
34]
In one dimension (1D) and one-and-a-half dimensions (1.5D),
L is the minimum cell width among all cells in the whole spatial domain in the corresponding time step. In the two-dimensional (2D) case,
L is the minimum incircle radius of triangle among all the triangular cells in the corresponding time step. As follows, we provide four numerical tests.
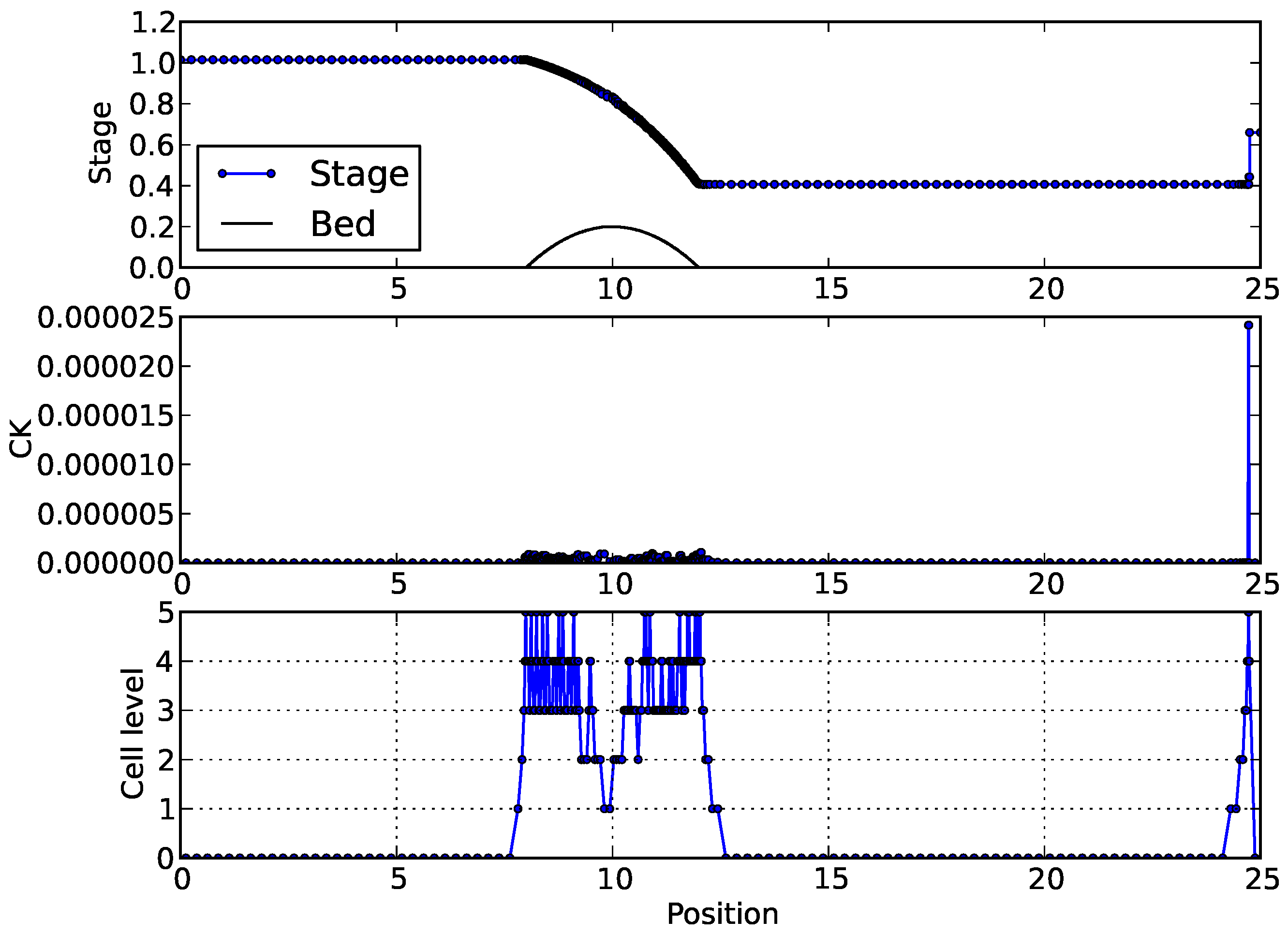
4.1. A One-Dimensional Problem with Topography
As the first numerical test, we consider a one-dimensional problem with topography as studied by Felcman and Kadrnka [
22].
Let us assume that we have a channel of length 25 with topography
together with the Dirichlet boundary conditions
and the initial condition
The width of the coarsest cell allowed is
. The maximum level of the binary refinement is 5. Cells with
are coarsened, whereas those with
are refined. Two neighbouring cells are coarsened as long as they are at the same level and have the same parent. The tolerance of the CK indicator is
where CK is defined as in Equation (
11). The spatial domain is discretised initially into 100 cells.
Figure 1 shows the simulation results when the flow is at the steady state (time
). We observe that refinement is done by the adaptive method above the parabolic bump, as this region is rougher than other regions. In addition, refinement is also done close to the right boundary, because there is a bore (a static shock) in this region. This means that the adaptive method is successful in simulating the problem.
4.2. A One-Dimensional Dam Break with Passive Tracer
In this simulation, a one-dimensional problem with horizontal topography is considered. We shall show that our proposed method produces an accurate solution around the rarefaction, the contact discontinuity, and the shock.
Suppose that we have a dam break problem involving a passive tracer (1.5D dam break problem) on horizontal topography
The initial condition is
The width of the coarsest cell allowed is set to be 250. The maximum level of the binary refinement is set to be 10. We take
where CK is defined as in Equation (
17). The spatial domain is discretised initially into 16 uniform cells.
We may use the same numerical flux formulation for all three (transport, momentum, and mass) equations in order to solve this problem numerically. However, we choose to use the standard flux formulation (Kurganov, Noelle, and Petrova (KNP) [
31]) only to mass and momentum equations so that we obtain a more accurate solution at the contact discontinuity of the passive tracer solution. The passive transport flux is
where
is the mass flux at
. This passive transport flux is the upwind flux based on
as proposed by Bouchut [
35]. Two neighbouring cells are coarsened as long as they are at the same level and have the same parent. Cells with
are coarsened, whereas those with
are refined.
A representative of our simulation is
Figure 2, where at this time, the number of cells is 2748. This figure shows the flow with passive tracer at time
. In these results, the contact discontinuity remains sharp. In addition, rarefaction and shock occuring in the water surface solution are well-resolved. This indicates that our adaptive method indeed leads to a very accurate solution over the whole region. Recall that contact discontinuities are much harder to resolve than shocks, and numerical solutions are diffusive around contact discontinuities generally [
17,
36].
4.3. A Planar Dam Break in Two Dimensions
Suppose that we have all
in
as the spatial domain. The initial condition is given by
The domain is discretised initially into 2048 triangular cells. We simulate this problem with the time step being taken in such a way that the CFL condition is satisfied and the method is stable. We stop the simulation at time
. We have five different areas of cells after coarsening or refinement, because the maximum level of refinement and coarsening is set to be 2. That is, an original initial triangular cell can be coarsened or refined up to two level coarser or two level finer. The CK tolerance is
(see
Section 3 about how to compute CK indicator for a two-dimensional problem). Cells having CK smaller than
are candidates for coarsening; otherwise for refinement. We use the iFEM algorithm to do the coarsening and refinement. The data structure and description of iFEM can be found in a technical report authored by Chen [
29] and a research paper written by Chen and Zhang [
30].
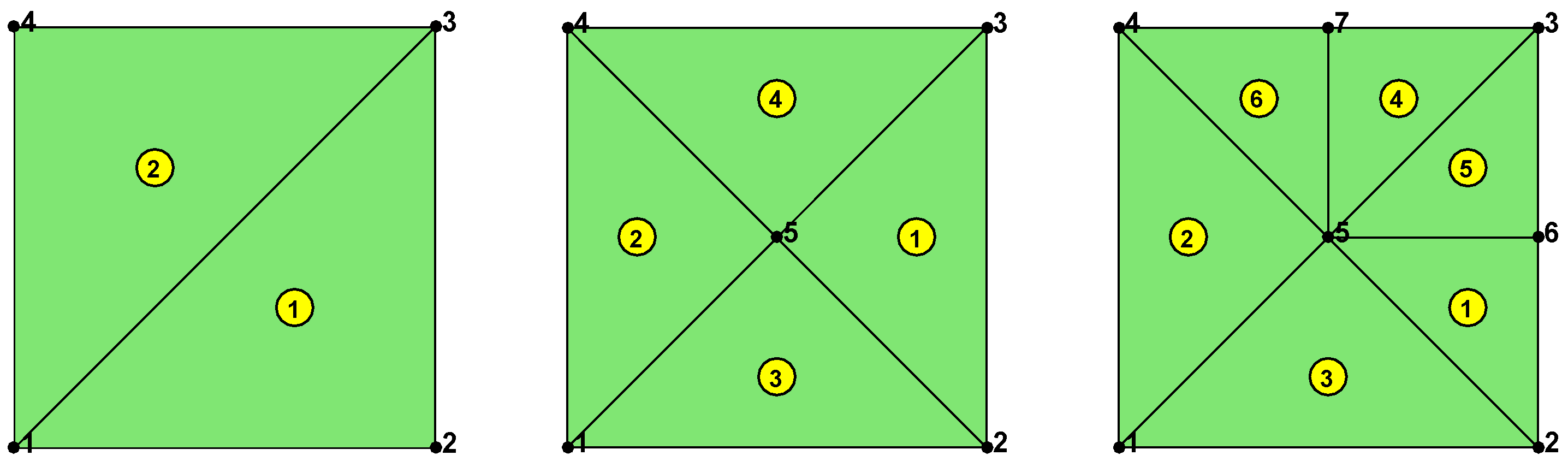
Before we proceed, let us recall the mesh adaptivity algorithm in iFEM, where an illustrative example is given in
Figure 3. Suppose that initially we have the nodes
which are the coordinates
,
,
,
, respectively. The elements are initially set to be two triangles with the nodes
as triangle
and the nodes
as triangle
, as shown in the left subfigure of
Figure 3. The order of the nodes in a triangle is started from the node in front of the longest edge followed by other nodes in the counter-clockwise direction. Suppose that we want to refine the area around the node
, that is, the area around the coordinates
. Triangle
is bisected, so the node
having coordinates
is created. The bisection of triangle
becomes the new
and
. To maintain the conformity, triangle
is also bisected into the new
and
. This lead to the subfigure shown in the middle of
Figure 3. For the next refinement, we use the same procedure. As we want to refine the area around the node
, triangle
is bisected into new triangles
and
; and triangle
is bisected into new triangles
and
. (Note that the coarsening algorithm is the reverse of this refinement algorithm.)
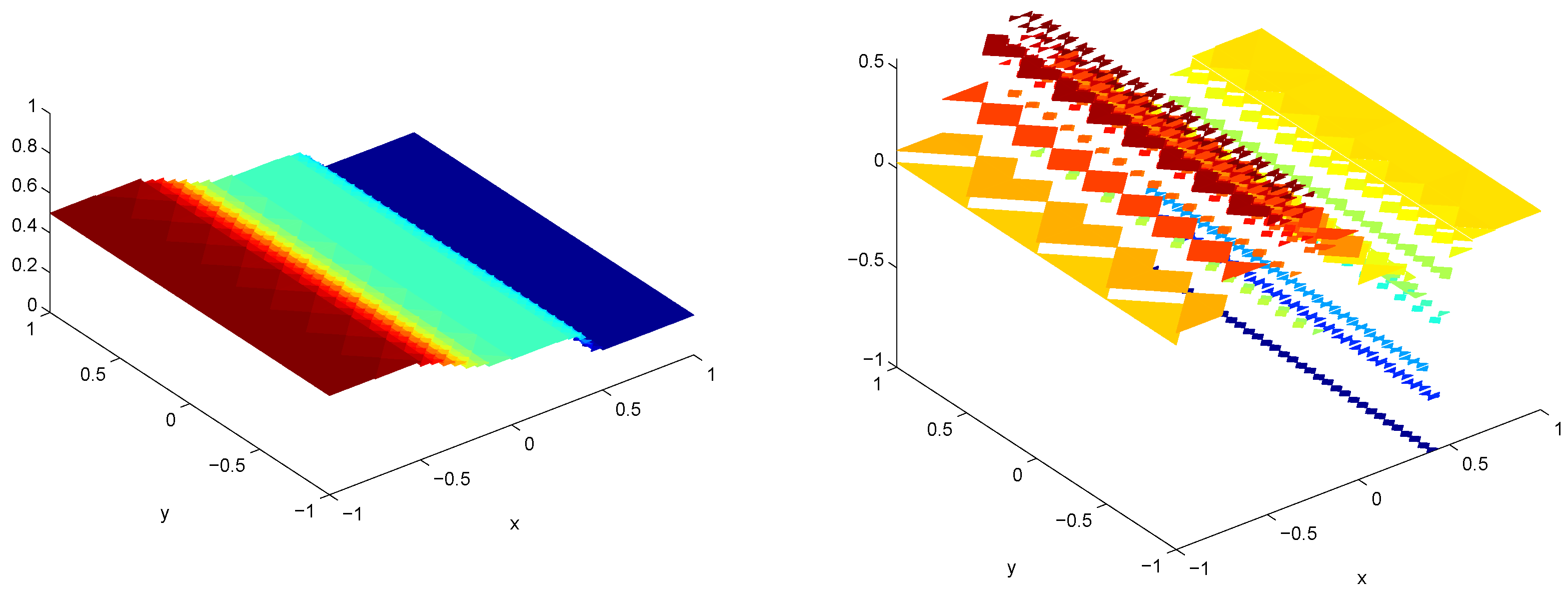
Representatives of the results of our simulation are illustrated in
Figure 4 and
Figure 5.
Figure 4 shows results at time
the scaled CK indicator
and the water surface. At this time (
), the number of triangles is 1656.
Figure 5 depicts the corresponding momentum and mesh. We see from these results that in order to get an accurate solution, the numerical method achieves refinements around the rarefaction and the shock.
4.4. A Radial Dam Break in Two Dimensions
Suppose that we have the spatial domain as all
in
. The initial condition is given by
The time step is taken in such a way that the CFL condition is satisfied and the method is stable. The domain is discretised initially into 2048 triangular cells. We stop the simulation at time
. The maximum level of coarsening and refinement is 2. That is the original initial triangular cells can be refined or coarsen twice at the maximum. As a result, we have five different areas of cells. The NEP tolerance is
. Cells having absolute CK smaller than
are candidates for coarsening, while otherwise are candidates for refinement.
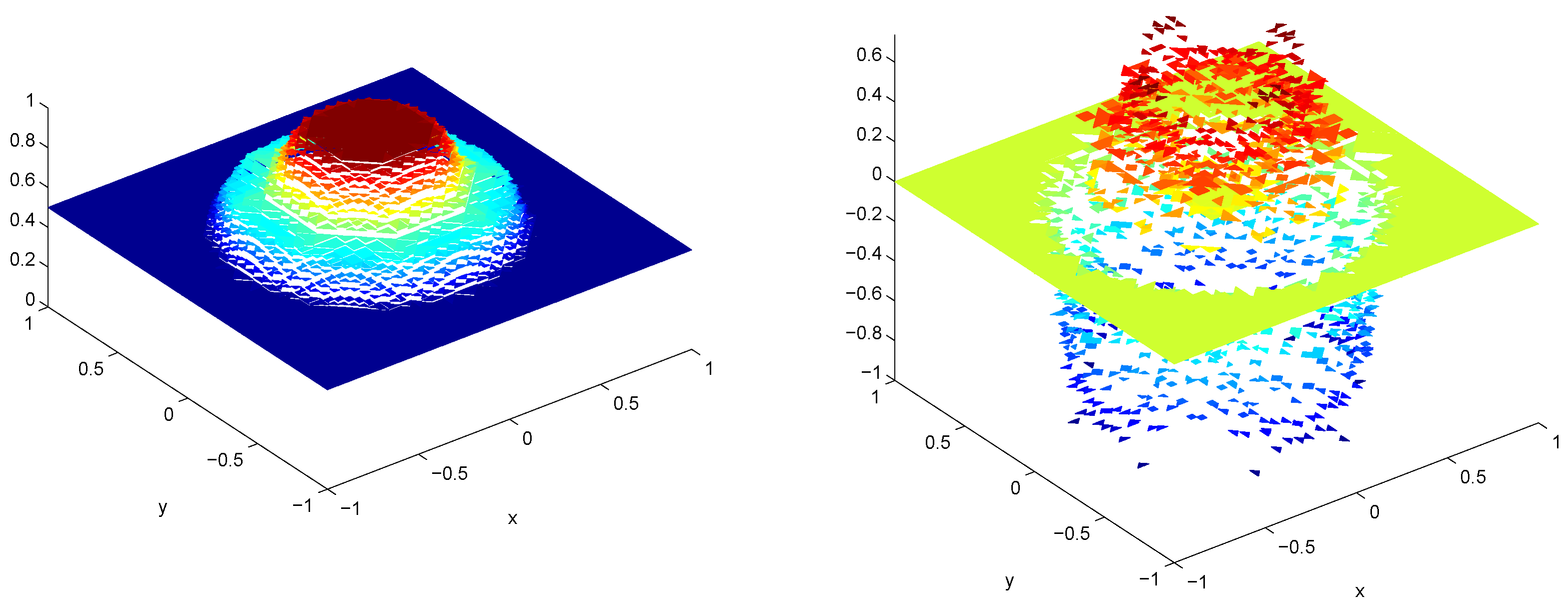
Figure 6 and
Figure 7 show representatives of our simulation results. At time
,
Figure 6 depicts the scaled CK indicator
and the water surface. At this time (
), the number of triangles is 2168.
Figure 7 shows the corresponding momentum and mesh. Like in the case of the planar dam simulation, we observe that refinements occur around the rarefaction and the shock leading to an accurate solution.
Before we conclude the paper, we provide some remarks as follows.
Remark 4. The tolerance for the weak local residuals is a matter of choice to the users of the proposed method. If the tolerance is too strict, then the refinement will be excessive, but if the tolerance is too loose then the mesh will be too coarse. We indicate that the tolerance is about 5% of the maximum weak local residual for the refinement and 0.5% of the maximum weak local residual for the refinement. That is, if a cell has the value of residual which is larger than 5% of the maximum weak local residual, then the cell must be refined as long as the cell area has not reached the minimum value of the allowed area. If a cell has the value of residual which is smaller than 0.5% of the maximum weak local residual, then the cell must be coarsened as long as the cell area has not reached the maximum value of the allowed area. However, once again, the tolerance is a matter of choice of the users.
Remark 5. For the first order method, if a cell is bisected, then each of the two new cells has the same quantity values as those of the original cell. That is, suppose that the triangle T is bisected into two trianglesand. The quantityof the triangleand the quantityof the triangleare the same as the quantityof the original triangle T. In mathematical formulas For the second order method, if a cell is bisected, then quantities of each of the two new cells should be computed using proportional values of the linear reconstruction of the quantities of the original cell after implementing a slope limiter.
If two cells are coarsened, then the new cell has quantity values that are computed from the quantity values of the two old cells with respect to area-based weights. That is, supposed that two trianglesandare coarsened to be the triangle T. The quantity of the triangle T is computed aswheremeans the area of the triangle T. In all of our 1D, 1.5D, and 2D cases in this paper,