1. Introduction
In recent years, many researchers have become interested in multi-sensor data convergence and data integration technologies based on sensors such as cameras, light detection and ranging (LiDAR), and radar as sensing technologies have developed for environment perception [
1]. In particular, in robots and autonomous systems, the complementary modality between sensors is an important issue. Especially in intelligent vehicles, object detection must be fast and accurate enough to enable the control system to react and perform the required corrections. However current state-of-the-art literature describes a highly accurate object detection system using vision and range sensing sensors, though there are still several issues to be solved in the context of autonomous driving. For example, detecting the object distance is one limitation of the current object detection approaches. Regarding object distance estimation, there are several approaches that have been proposed, depending on the modality of the sensors used, such as radar, LiDAR, or camera. Each sensor modality is capable of perceiving the environment with a specific perspective and is limited by detecting certain attribute information of objects. More specifically, vision-based approaches are more robust and accurate in object detection but fail in estimating the distance of the object accurately. In contrast, LiDAR-based methods are very robust and accurate in measuring the distance of the object but are limited by the object classification ability. As an alternative, there are a few approaches based on the stereo vision camera because of its ability to perceive the environment in 3D [
2]. However, the main constraint is the real-time processing of dense frames and measurement and estimation errors [
3]. Hence, considering the ability and limitation of the camera and LiDAR sensor, the sensor-fusion-based approach appears to be ideal for addressing object detection at a distance from the vehicle’s current position. In addition, sensor fusion approaches broadly are classified into three main categories based on the different levels of data used for fusion, namely low-level fusion, feature-level fusion, and high-level fusion [
4,
5]. In the low-level fusion, the raw measurement from the sensors is fused based on the sensor’s physical location, and feature-level fusion extracts the certain feature from the raw measurement through a series of preprocessing. In the high-level fusion, each sensor independently carries out object detection or a tracking algorithm and then performs fusion. Although each fusion approach demonstrates well-known advantages and disadvantages when compared to each other, low-level fusion appears to be more optimal for autonomous vehicles because of its real-time performance and the more precise fusion of data.
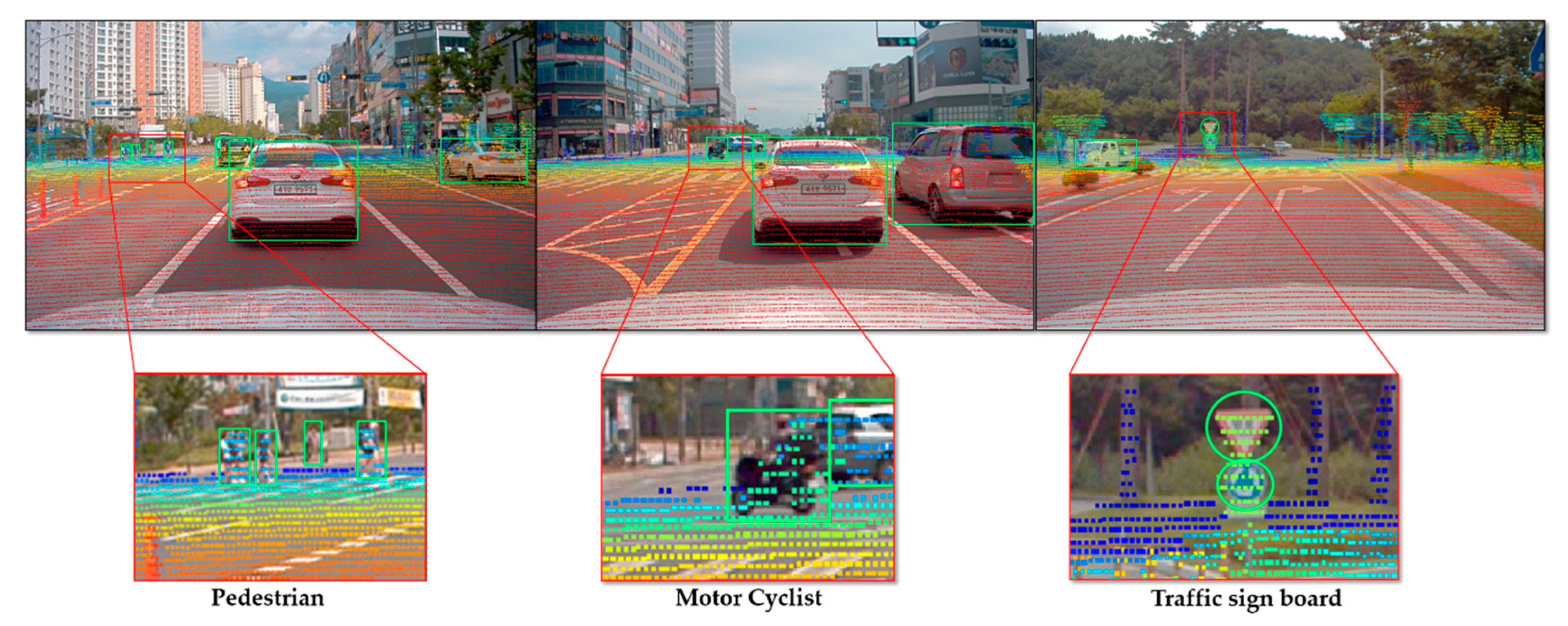
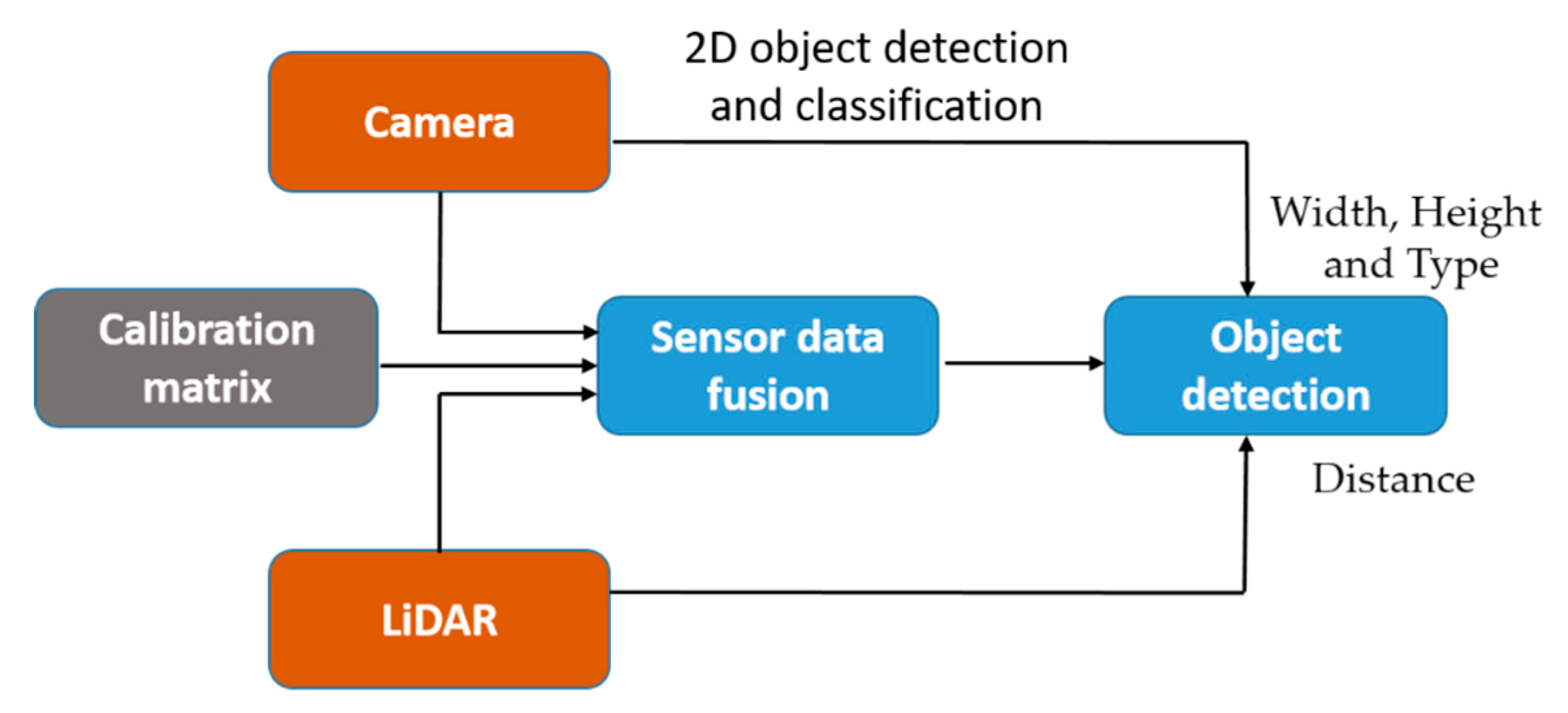
However, it is possible to solve the problem of complementary modality and overcome the limitation of each sensor by fusing the advantages of the respective sensors. It is also possible to provide a great deal of information such as type, height, width, and distance of an object in the surrounding environment from the current position by using the fusion data acquired from these sensors [
3]. For example, range sensors such as high-speed 3D LiDAR can be used with RGB cameras to enable a robot to perform various detection tasks. More specifically, a 3D LiDAR sensor can provide 3D position and depth information of classified objects, whereas RGB cameras provide 2D position and color information. Therefore, in the real world, the objects can be visualized by mapping information from the 3D position onto the 2D image. However, to fuse the information, it is necessary to find the relative positions and original directions of the sensors. As sensor fusion technology is applied to various fields, the calibration issue between sensors has become increasingly important. In particular, the development of fusion technology using cameras and LiDAR in autonomous vehicles requires an accurate relative position (including posture and direction information) of the camera and LiDAR sensor as an absolute necessity. This can be accomplished by finding the conversion matrix between heterogeneous sensors as extrinsic parameter problems. Therefore, to detect unique features in the point cloud data of LiDAR and the image data of the camera, it is necessary to determine an accurate corresponding relationship between the sensors. In this paper, we propose a precise data fusion method between a camera and a LiDAR sensor to estimate object distance, which is necessary to enable a self-driving vehicle driving along a real road by sensing its surrounding environment more precisely.
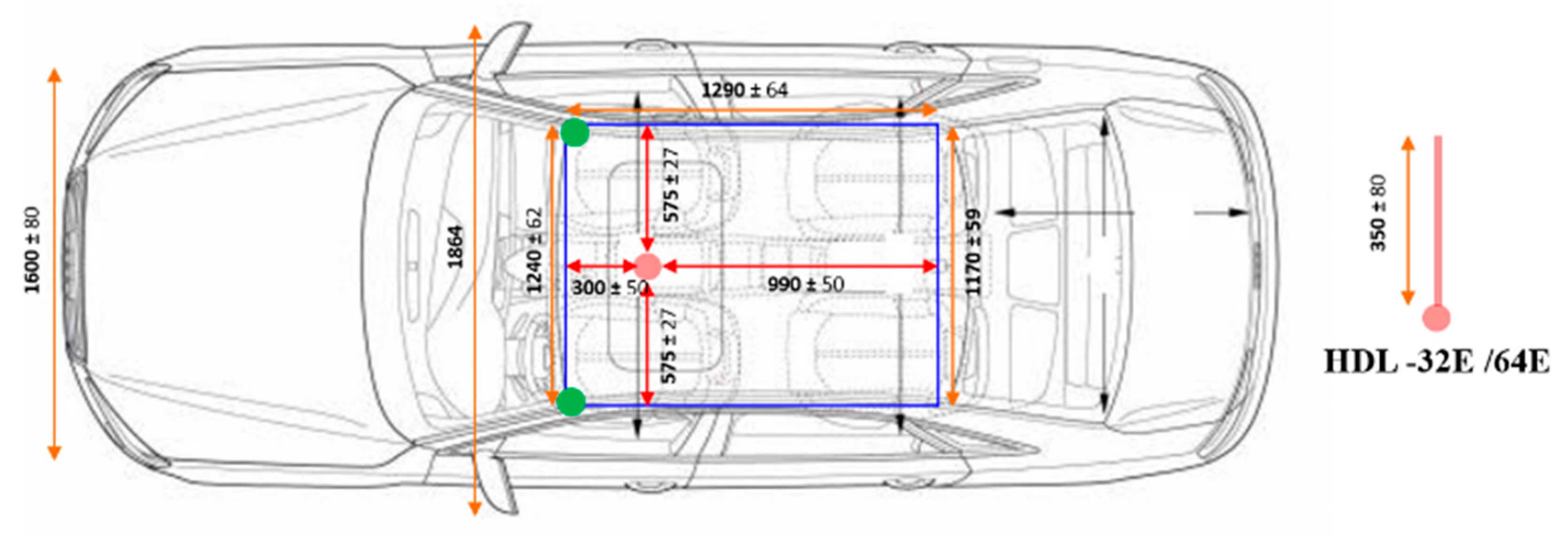
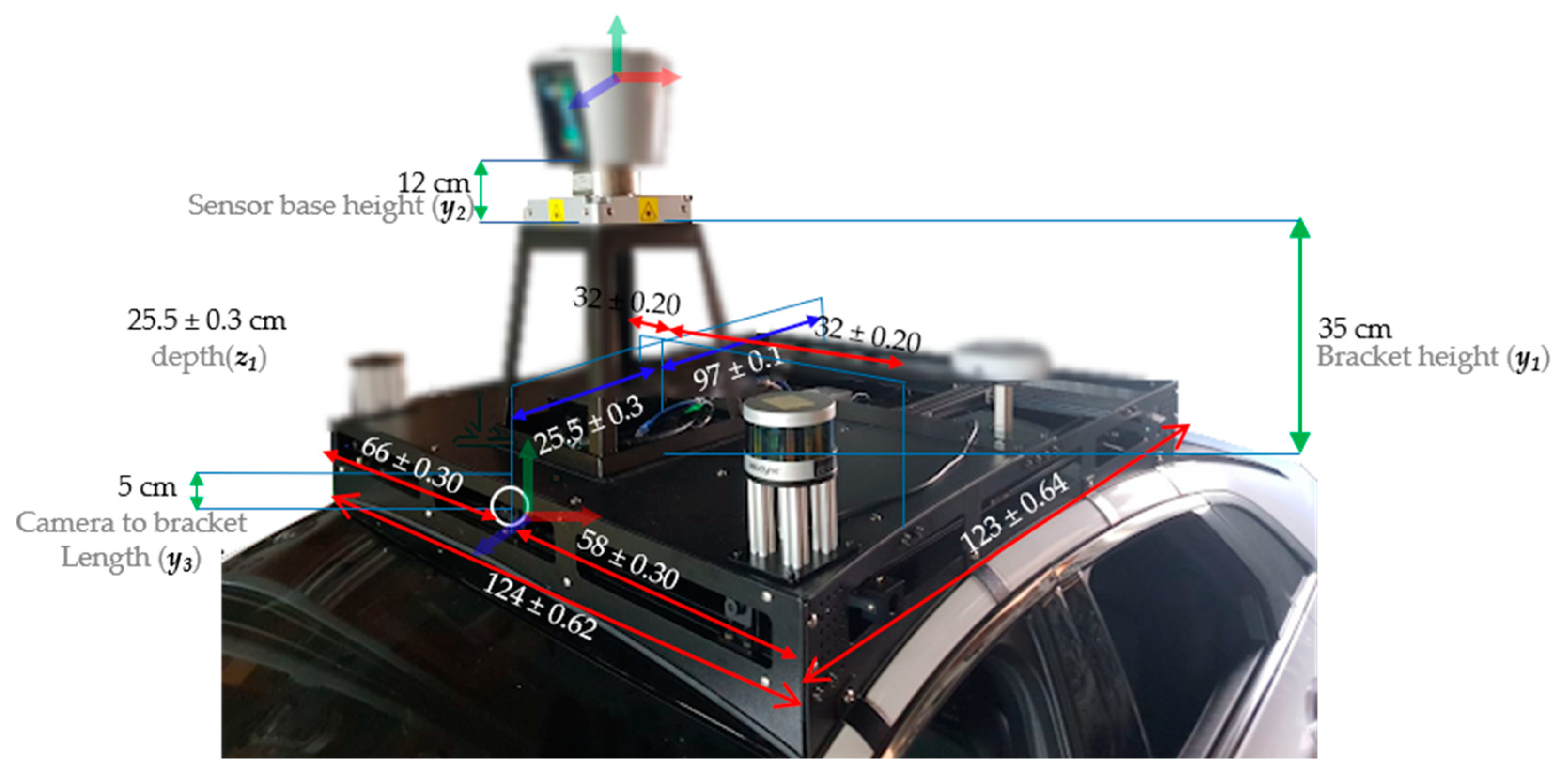
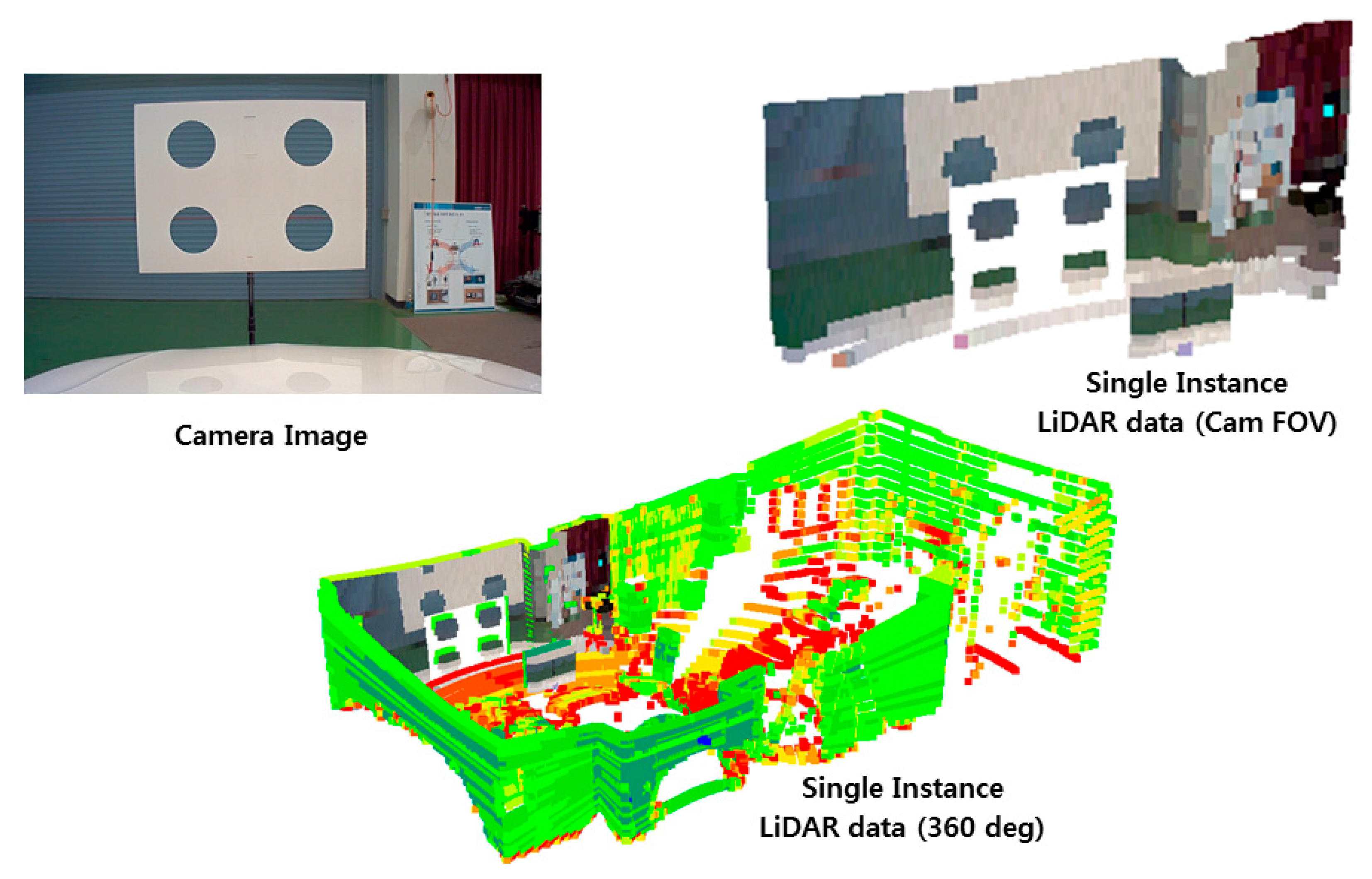
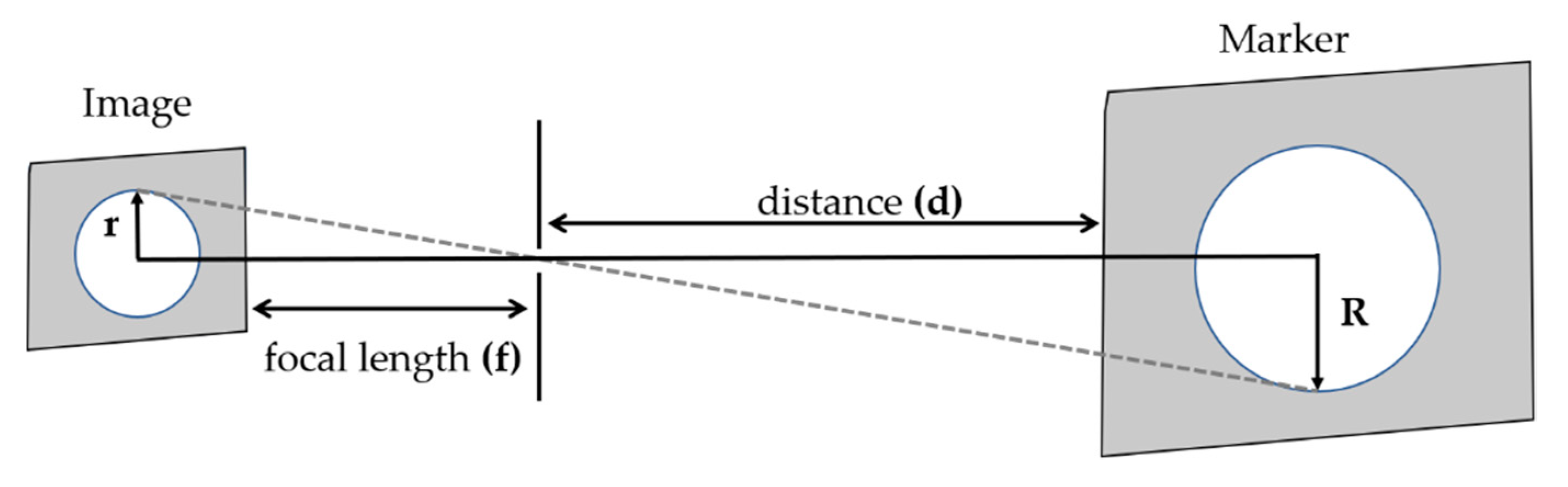
In order to estimate the object distance information, first, we consider fusing the data acquired from the camera and LiDAR sensor using the calibration matrix estimated by performing sensors calibration. In the sensor fusion approaches, it is very important to consider the relative position of sensors in order to fuse the data accurately. After sensor data fusion, the distance of an object in the vehicle’s path is detected utilizing the object detection output from the camera and distance data from the LiDAR. Hence, the object detection process requires an accurate sensor fusion approach to integrate camera and LiDAR data. For the fusion of camera and LiDAR data, studies have been shown that polygonal planes, such as a checkerboard or box, are necessary to perform the calibration between the camera and LiDAR. However, these methods either cause measurement errors or affect the calibration result whenever there are a few changes such as the plane position or the sensor’s relative position. In particular, if the positional change between the sensors is large, it is difficult to accurately detect the edge of the plane and to precisely calibrate the sensors. In addition, remote targets with different shapes and colors may generate different fusion results because of the various experimental environments and characteristics of the sensors. Therefore, in order to improve the accuracy of the calibration, the previously proposed methods are performed by mounting the sensors as close to each other as possible. In addition, it is difficult to apply the previous calibration methods to an autonomous driving system, which requires the recognition of distant objects, because the methods are performed after arranging the sensors closely and detecting the short-distance objects in the field of view. In this paper, correspondence between the sensors positioned in large displacement was established by performing the precise calibration using 3D marker.
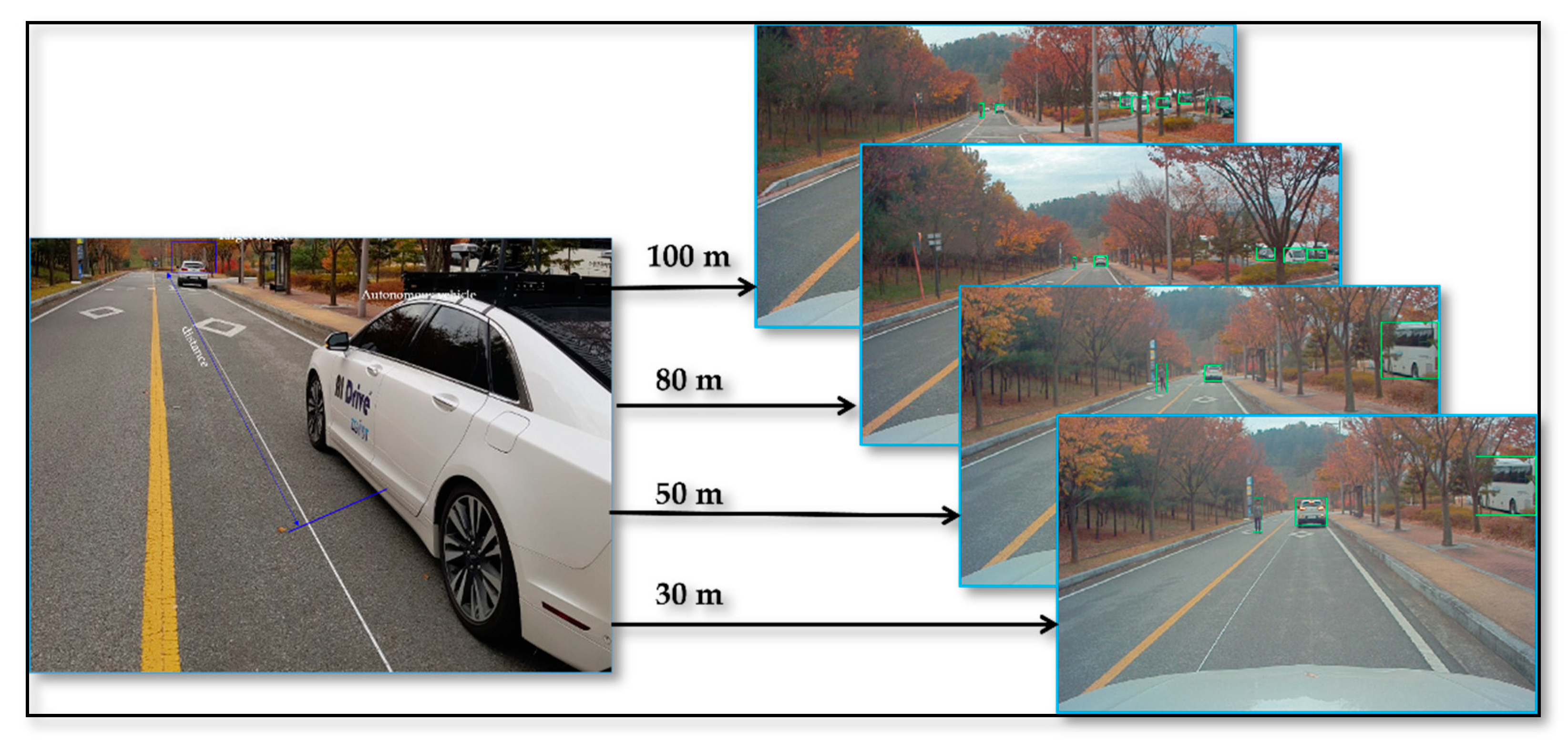
However, the calibration approach seems to be more common but there is few research found regarding sensor fusion for object distance estimation, as well as with a limited experimental evaluation. Hence, understanding the necessity of the sensor fusion approach in the context of object distance estimation for the autonomous vehicle, in this article, we present, in detail, a pipeline for object distance estimation in autonomous vehicles by using a sensor fusion approach. It is based on detailed experimental evaluation using a 3D marker-based calibration and sensor-fusion-based distance estimation to recognize short- and long-distance objects, as required by an autonomous driving system. Experimental results and analysis based on the real and simulated environment in the article help the readers to understand the ability of the sensor fusion approach in distance estimation and further direction for improvements.
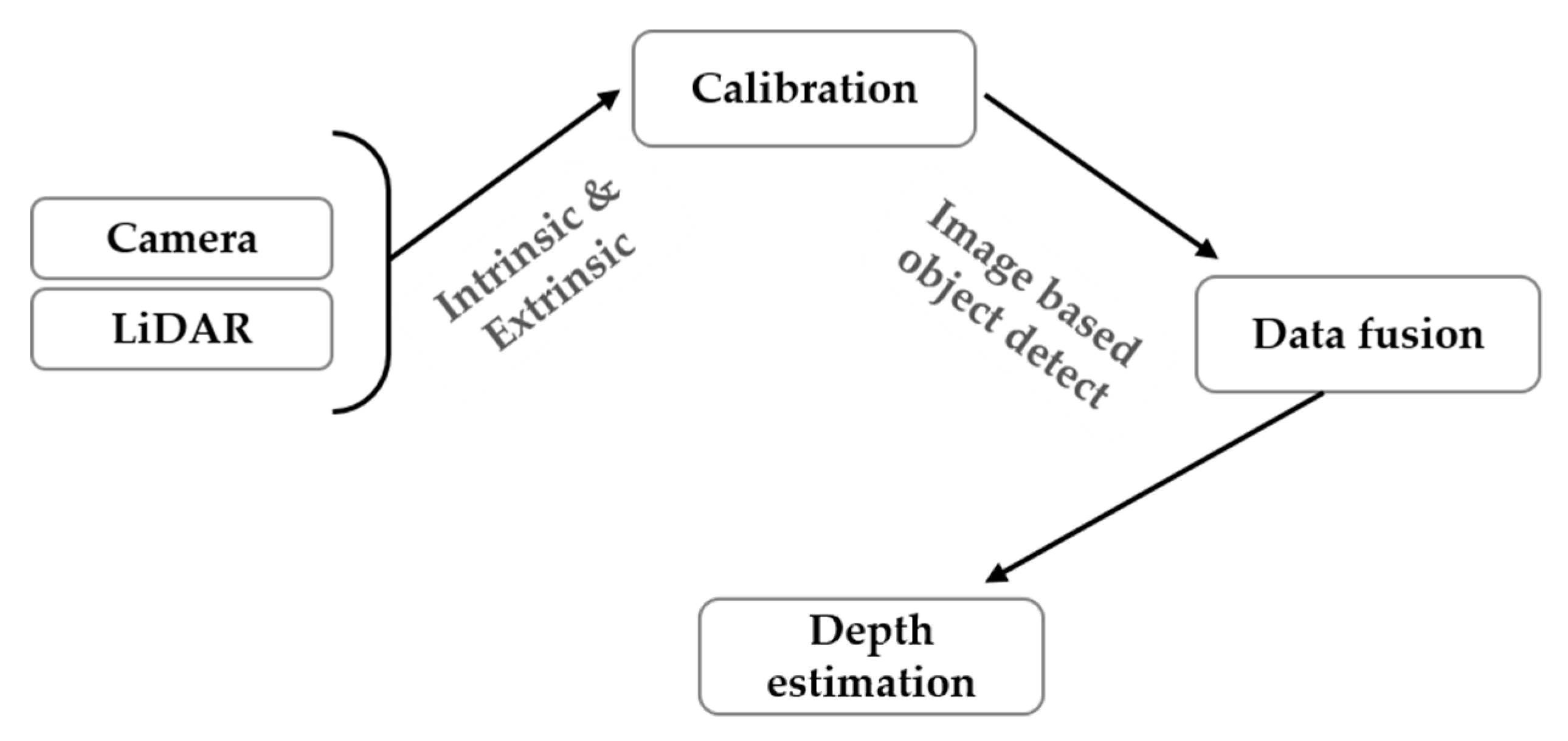
Figure 1 shows the overall process flow of the proposed technology including the data fusion-based depth estimation method and an alignment score-based accuracy evaluation method.
Section 2 describes previous sensor fusion methods and related techniques used for object distance estimation, and
Section 3 presents our proposed method to fuse the data acquired by the camera and LiDAR of a self-driving vehicle. A detailed description of the approach follows to evaluate the effectiveness of the data fusion is provided.
Section 4 discusses the evaluation of the distance estimation method in terms of quantity and qualitative analysis. Additionally, detailed experimental results are presented based on the real and simulated environment to provide insightful information to the readers.
Section 5 contains the conclusion and alludes to future work.
2. Related Work
Autonomous vehicles use various sensors, such as LiDAR, radar, cameras, and ultrasonic sensors, to map and recognize the environment surrounding the vehicle [
5]. In this field, sensor fusion techniques, in particular, have been proposed for object detection, and in other areas such as localization and path planning. For instance, conventional LiDAR and radar fusion focus on detecting moving objects such as vehicles and motorcycles. At that time, for the object detection, the velocity is fused using Doppler information extracted from radar and the width and length of vehicles obtained from LiDAR. In the article [
6], the authors introduced RoadPlot-DATMO for moving object detection using multiple LiDAR sensors. However, multiple LiDAR sensor-based object detection and tracking were limited by object classification ability. Among the more recent approaches, the stereo-vision based method seems to be more suitable for generic object detection because of its ability to represent a scene in 3D but real-time performance is a critical issue [
7]. In addition, the collaborative fusion between the laser scanner and camera approach presented in [
8] limited to vehicle detection, though it is difficult to detect static objects such as pedestrians, motorcyclists, and so on.
As an alternative, considering real-time performance, object detection, classification ability, and accurate distance estimation, LiDAR and camera fusion techniques have been introduced for object detection based on different levels of data fusion. The fusion technique establishes a correspondence between the 3D points from LiDAR to the object detected by a camera to reduce the entire processing time. This is possible because sensor fusion compensates for the disadvantages between the sensors and improves the robustness and detection accuracy. For example, the resolution of a typical camera is considerably higher than that of LiDAR, but the camera has a limited field of view and cannot precisely estimate the distance to objects in comparison with LiDAR. In addition, a camera is very sensitive to light changes and has complex image processing in the case of using only images, and LiDAR has difficulty recognizing color and classifying objects in comparison with a camera. However, by using sensor fusion, it is possible not only to acquire complementary information about the environment surrounding an autonomous vehicle by using sensor data with different characteristics, but also to overcome the limitations of each sensor and to reduce the uncertainty of individual sensors. Therefore, an autonomous vehicle inevitably requires sensor fusion technology for safety and reliability. In the paper [
3], the author proposed cooperative fusion for multi-objects detection by means of stereo vision and a laser scanner based on feature-level fusion. However, this approach requires sensors to extract the feature from the raw measurement. Another fusion method based on fuzzy logic was proposed in the article [
9], which parses the image and point cloud data independently for object detection and performs fusion to get the distance of the object. In this study, sensors data fusion at low-level presented for the robust object detection and the method is verified with the on-road experiment.
In order to fuse the camera and LiDAR data at the low-level, the first essential step of the fusion process is extrinsic calibration between sensors. This means that the geometrical parameters such as the position and orientation of each sensor must be determined by taking into account the relative position and orientation of the other sensors [
10,
11,
12]. Therefore, calibration for fusing sensor data is performed by finding the correspondence between the 3D points and 2D image pixels. The important point for fusing heterogeneous sensor data is to identify the features from each sensor and determine the geometric relation between the sensors [
13]. A normal solution is to recognize a target with heterogeneous sensors and then match the data collected from different angles and positions.
In this paper, we focus on precise distance estimation as well as object detection in the path of an autonomous vehicle. In particular, in sensor data fusion, to estimate the depth of moving objects, the accuracy of calibration between sensors is very important. Most calibration methods check the correspondence between the two sensors by using external objects such as a trihedral rig [
14,
15,
16], circles, board patterns [
17,
18], checkerboard, and others [
19,
20,
21]. Typical methods for fusing the data of a camera with data from other sensors have used a calibration technique using checkerboard patterns. The board is used to fuse data acquired by the optical camera with that from the 2D laser scanner, and the calibration method is based on nonlinear least-squares optimization [
22]. To avoid the many errors caused by the checkerboard pattern, a black circular plane board is used, which locates the object by estimating the 3D coordinates of the center of the circle and the vector normal to the plane [
23]. In addition, most researchers use the well-known Levenberg–Marquardt algorithm to improve calibration accuracy when transforming LiDAR and camera coordinates [
24,
25]. Recently, many researchers have also proposed automatic calibration methods [
26]. These methods find the target object because each sensor automatically detects the center of the object and circles on a plane. The random sample consensus (RANSAC) algorithm is used to extract the plane, and the iterative closest point (ICP) algorithm based on nonlinear optimization is employed to accurately refine the external parameters for data fusion [
16,
27]. Another approach to automatic calibration is to use a plane with four circular holes on a white background [
28]. This enables 3D LiDAR point cloud data and camera images to detect the four holes automatically but requires high-resolution LiDAR. Another calibration method uses single-scan data of LiDAR and data captured once by the camera [
29]. This requires multiple checkerboards and two cameras installed in different positions. An alternative calibration method uses a stereo camera and LiDAR. The method constructs a 3D scene from camera data by using the speeded-up robust features (SURF) algorithm, and this is matched with LiDAR and camera data by applying the ICP algorithm to fuse the data [
26,
30,
31]. These studies have only focused on improving the accuracy of data fusion between sensors for object detection. However, most of the previous methods performed calibration between sensors in a limited space [
32,
33,
34,
35] and these methods have not been shown to accurately perform with experiments in real-time dataset [
36] and have not been compared with other methods. In addition, in conventional fusion methods, because calibration and data fusion is performed by mounting the sensors as close to each other as possible to improve the detection accuracy of an object, only objects located within a short distance can be recognized [
37]. Therefore, the previous methods are not suitable for autonomous vehicle platforms that need to recognize distant objects and to detect them in real-time.
In this study, we determine 3D marker types by carrying out various experiments to find the types of markers that can fuse the data with high accuracy regardless of the relative positions of the sensors. This 3D marker for detecting remote objects with LiDAR and camera is utilized for precise data fusion in the autonomous vehicle system. Then, we propose a method of fusing the data of the camera and LiDAR for detecting the surrounding objects and a method estimating the distance to objects detected by fusing data on a real road. In addition, we evaluate the performance of the data fusion method in various experiments while driving along an actual road using an autonomous vehicle platform. The experimental results show that the proposed methods can estimate the precise depth of objects and recognize objects accurately. Therefore, we demonstrate that the proposed methods to fuse camera and LIDAR data and to estimate the depth of objects have the potential to be used in a self-driving vehicle.