Blind Image Watermarking in Canonical and Cepstrum Domains Based on 4-Connected t-o’clock Scrambling
Abstract
1. Introduction
2. Background Information
2.1. The Discrete Linear Canonical Transform (DLCT)
2.2. The Cepstrum Transform (CT)
3. Proposed Watermarking Framework
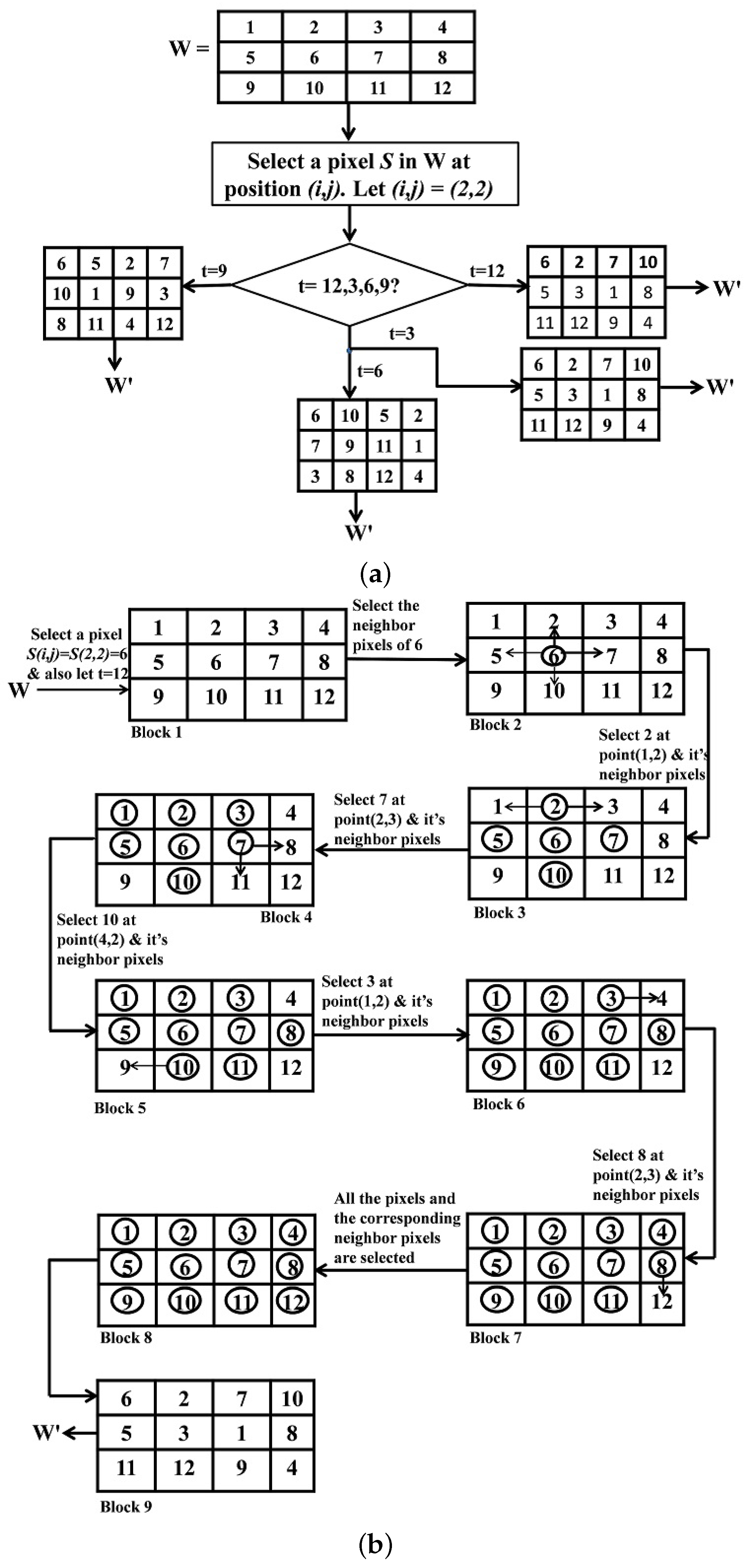
3.1. Watermark Preprocessing
3.2. Embedding Location
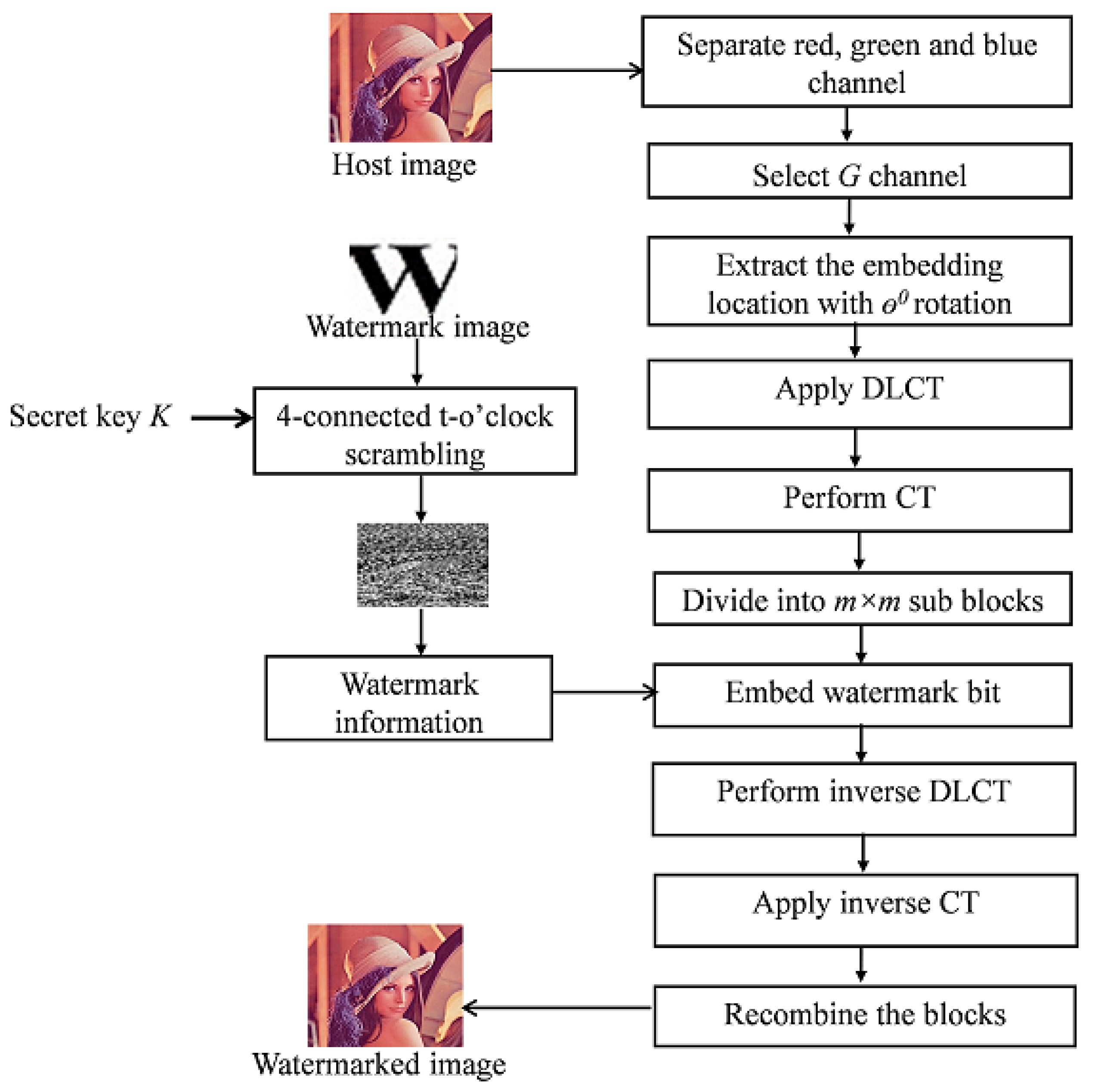
3.3. Watermark Embedding Framework
- The original host image H is separated into three channels R, G, and B.
- Select the channel G for embedding watermark information.
- Apply DLCT to R to obtain , using Equation (2).
- The cepstrum region C is segmented into L non-overlapping blocks B with size , where .
- Watermark image W is encrypted using four-connected t-o’clock scrambling to get W’ image.
- Watermark bit is embedded into each blocks B using max-heap tree and min-heap tree property to obtain B’, where . A max-heap is a complex binary tree in which the value of each internal node is greater than or equal to the value of the children of that node. For the min-heap tree, the value of each internal node is less than its child node. If , then apply max heap tree procedure to the block. If , then apply min-heap tree property. This process is described in Figure 3.
- After embedding all watermark bits, concatenate all sub-blocks B’ to obtain watermarked CT region C’.
- Then, apply inverse CT to C’ to obtain watermarked region T’.
- Apply inverse DLCT to T’ to obtain watermarked region R’.
- Reinsert the watermarked region R’ to obtain G’ channel and finally concatenate all three channels to get the watermarked image H’.
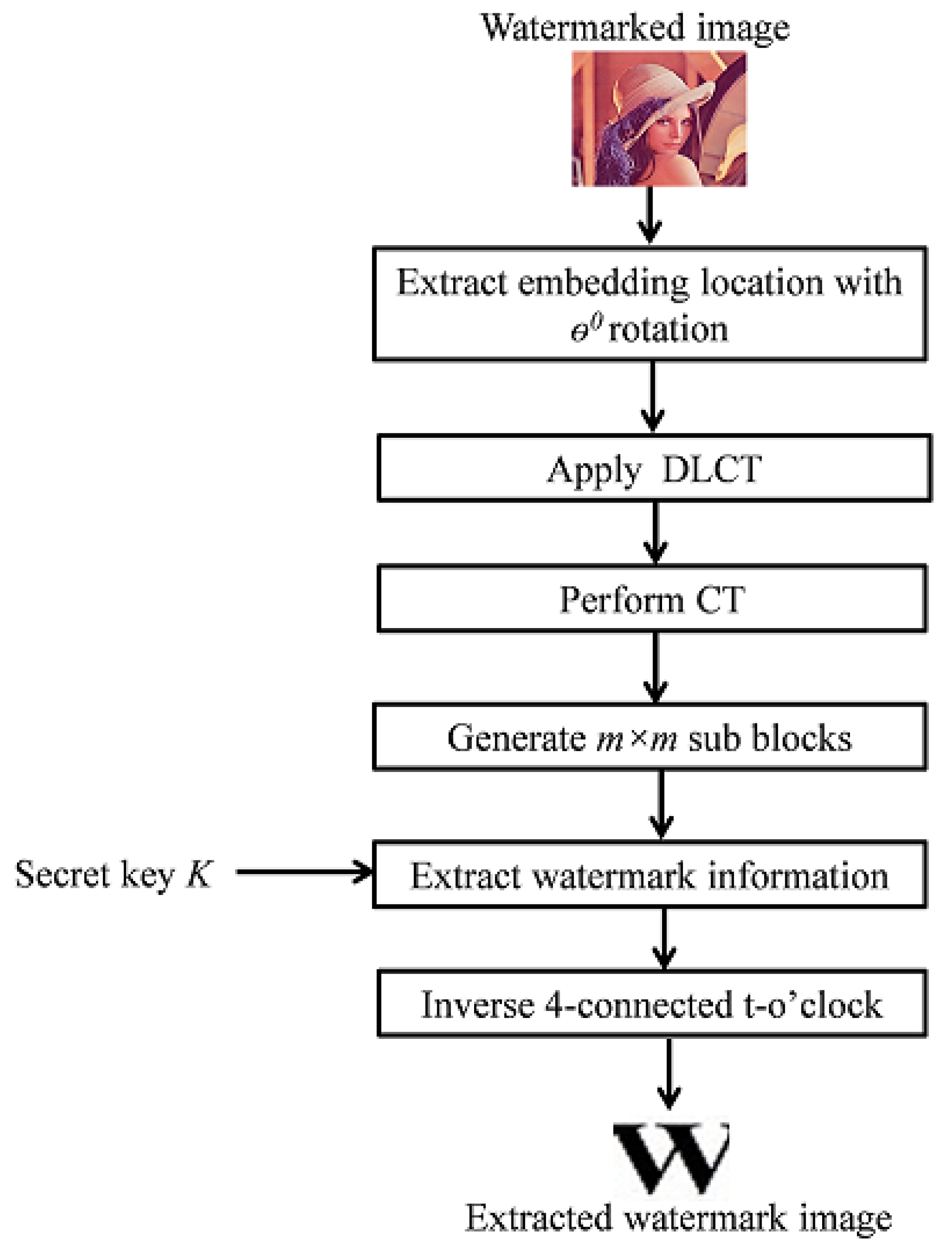
3.4. Watermark Extraction Framework
- Apply DLCT to the extracted region R* to get T* and then apply CT to that region T* to obtain region C*.
- Divide the C* region into non-overlapping block B* with size .
- Extract the watermark bit from each block. If a selected block satisfies the max-heap tree property, then the watermark bit will be 1. If the selected block satisfies the min-heap tree property, then the watermark bit will be 0.
- Finally, the inverse four-connected t-o’clock method is applied to reconstruct each component of watermark image W*.
4. Experimental Results
4.1. Imperceptibility Test
4.2. Robustness Test
- JPEG compression: JPEG compression is a standard lossy compression technique in which an image is compressed to reduce its memory space and bandwidth requirements for transmission over the Internet. In our simulation, JPEG compression with was applied to the watermarked images.
- Cropping: The watermarked images were cropped 50% from the top.
- Rotation attack: The watermarked images were rotated by and the rotated images were re-rotated in a counter-clockwise for extraction of watermark images.
- Gaussian noise: Gaussian noise with variance 0.1 was applied to the watermarked images.
- Speckle noise: Speckle noise with variance 0.01 was applied to the watermarked images.
- Salt and pepper noise: Salt and pepper noise with variance 0.01 was applied to the watermarked images.
- Poison noise: Poison noise was applied to the watermarked images.
- Contrast adjustment: Contrast adjustment with minimum 0.2 and maximum 0.6 was applied to the watermarked images.
- Sharpening: Sharpening with tolerance 0.1 was applied to the watermarked images.
- Median filtering: median filter was applied to the watermarked images.
- Wiener filtering: wiener filter was applied to the watermarked images.
4.3. The Computational Time Comparison Analysis
4.4. Security Analysis of Proposed Scrambling Method
4.4.1. Correlation Coefficient (CC)
4.4.2. Information Entropy (IE)
4.4.3. Relative Entropy (RE)
4.4.4. Differential Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Cox, I.J.; Miller, M.L. The first 50 years of electronic watermarking. EURASIP J. Adv. Signal Process. 2002, 2002, 820936. [Google Scholar] [CrossRef]
- Naderahmadian, Y.; Hosseini-Khayat, S. Fast and robust watermarking in still images based on QR decomposition. Multimed. Tools Appl. 2014, 72, 2597–2618. [Google Scholar] [CrossRef]
- Pizzolante, R.; Castiglione, A.; Carpentieri, B.; De Santis, A.; Castiglione, A. Protection of microscopy images through digital watermarking techniques. In Proceedings of the 2014 International Conference on Intelligent Networking and Collaborative Systems, Salerno, Italy, 10–12 September 2014; pp. 65–72. [Google Scholar]
- Liu, S.; Pan, Z.; Song, H. Digital image watermarking method based on DCT and fractal encoding. IET Image Process. 2017, 11, 815–821. [Google Scholar] [CrossRef]
- Li, J.; Zhang, C. Blind and robust watermarking scheme combining bimodal distribution structure with iterative selection method. Multimed. Tools Appl. 2019, 79, 1–35. [Google Scholar] [CrossRef]
- Parah, S.A.; Sheikh, J.A.; Loan, N.A.; Bhat, G.M. Robust and blind watermarking technique in DCT domain using inter-block coefficient differencing. Digit. Signal Process. 2016, 53, 11–24. [Google Scholar] [CrossRef]
- Roy, S.; Pal, A.K. A robust blind hybrid image watermarking scheme in RDWT-DCT domain using Arnold scrambling. Multimed. Tools Appl. 2017, 76, 3577–3616. [Google Scholar] [CrossRef]
- Roy, S.; Pal, A.K. A blind DCT based color watermarking algorithm for embedding multiple watermarks. AEU Int. J. Electron. Commun. 2017, 72, 149–161. [Google Scholar] [CrossRef]
- Abdulrahman, A.K.; Ozturk, S. A novel hybrid DCT and DWT based robust watermarking algorithm for color images. Multimed. Tools Appl. 2019, 78, 17027–17049. [Google Scholar] [CrossRef]
- Hamidi, M.; El Haziti, M.; Cherifi, H.; El Hassouni, M. Hybrid blind robust image watermarking technique based on DFT-DCT and Arnold transform. Multimed. Tools Appl. 2018, 77, 27181–27214. [Google Scholar] [CrossRef]
- Cedillo-Hernández, M.; García-Ugalde, F.; Nakano-Miyatake, M.; Pérez-Meana, H.M. Robust hybrid color image watermarking method based on DFT domain and 2D histogram modification. Signal Image Video Process. 2014, 8, 49–63. [Google Scholar] [CrossRef]
- Preda, R.O. Self-recovery of unauthentic images using a new digital watermarking approach in the wavelet domain. In Proceedings of the 2014 10th International Conference on Communications (COMM), Bucharest, Romania, 29–31 May 2014; pp. 1–4. [Google Scholar]
- Hu, J.; Shao, Y.; Ma, W.; Zhang, T. A robust watermarking scheme based on the human visual system in the wavelet domain. In Proceedings of the 2015 8th International Congress on Image and Signal Processing (CISP), Shenyang, China, 14–16 October 2015; pp. 799–803. [Google Scholar]
- Keshavarzian, R.; Aghagolzadeh, A. ROI based robust and secure image watermarking using DWT and Arnold map. AEU Int. J. Electron. Commun. 2016, 70, 278–288. [Google Scholar] [CrossRef]
- Ahmad, A.; Sinha, G.; Kashyap, N. 3-level DWT Image watermarking against frequency and geometrical attacks. Int. J. Comput. Netw. Inf. Secur. 2014, 6, 58. [Google Scholar] [CrossRef][Green Version]
- Sheth, R.K.; Nath, V. Secured digital image watermarking with discrete cosine transform and discrete wavelet transform method. In Proceedings of the 2016 International Conference on Advances in Computing, Communication, & Automation (ICACCA) (Spring), Dehradun, India, 8–9 April 2016; pp. 1–5. [Google Scholar]
- Su, Q.; Yuan, Z.; Liu, D. An Approximate Schur Decomposition-Based Spatial Domain Color Image Watermarking Method. IEEE Access 2018, 7, 4358–4370. [Google Scholar] [CrossRef]
- Rasti, P.; Anbarjafari, G.; Demirel, H. Colour image watermarking based on wavelet and QR decomposition. In Proceedings of the 2017 25th Signal Processing and Communications Applications Conference (SIU), Antalya, Turkey, 15–18 May 2017; pp. 1–4. [Google Scholar]
- Guo, J.M.; Prasetyo, H. False-positive-free SVD-based image watermarking. J. Vis. Commun. Image Represent. 2014, 25, 1149–1163. [Google Scholar] [CrossRef]
- Çerkezi, L.; Çetinel, G. RDWT and SVD based secure digital image watermarking using ACM. In Proceedings of the 2016 24th Signal Processing and Communication Application Conference (SIU), Zonguldak, Turkey, 16–19 May 2016; pp. 149–152. [Google Scholar]
- He, Y.; Hu, Y. A proposed digital image watermarking based on DWT-DCT-SVD. In Proceedings of the 2018 2nd IEEE Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC), Xi’an, China, 23–28 March 2018; pp. 1214–1218. [Google Scholar]
- Fazli, S.; Moeini, M. A robust image watermarking method based on DWT, DCT, and SVD using a new technique for correction of main geometric attacks. Optik Int. J. Light Electron Opt. 2016, 127, 964–972. [Google Scholar] [CrossRef]
- Singh, C.; Ranade, S.K. Geometrically invariant and high capacity image watermarking scheme using accurate radial transform. Opt. Laser Technol. 2013, 54, 176–184. [Google Scholar] [CrossRef]
- Su, Q.; Wang, G.; Zhang, X.; Lv, G.; Chen, B. A new algorithm of blind color image watermarking based on LU decomposition. Multidimens. Syst. Signal Process. 2018, 29, 1055–1074. [Google Scholar] [CrossRef]
- Pu, C. Image scrambling algorithm based on image block and zigzag transformation. Comput. Model. New Technol. 2014, 18, 489–493. [Google Scholar]
- Ding, M.; Jing, F. Digital image encryption algorithm based on improved Arnold transform. In Proceedings of the 2010 International Forum on Information Technology and Applications, Kunming, China, 16–18 July 2010; Volume 1, pp. 174–176. [Google Scholar]
- Tang, Z.; Zhang, X. Secure image encryption without size limitation using Arnold transform and random strategies. J. Multimed. 2011, 6, 202. [Google Scholar] [CrossRef]
- Li, B.Z.; Shi, Y.P. Image watermarking in the linear canonical transform domain. Math. Probl. Eng. 2014, 2014, 1–9. [Google Scholar] [CrossRef]
- Zhang, M.-R.; Lu, C.-H.; Yi, K. Cepstrum digital image watermarking algorithm. In Proceedings of the 2004 IEEE International Symposium on Industrial Electronics, Ajaccio, France, 4–7 May 2004; Volume 1, pp. 283–286. [Google Scholar]
- Lipschutz, S. Data Structures with C (Schaum’s Outline Series); Tata McGraw-Hill Education Pvt. Ltd.: New York, NY, USA, 2011; p. 7.55. [Google Scholar]
- The USC-SIPI Image Database. 2009. Available online: http://sipi.usc.edu/database/ (accessed on 7 January 2019).
- Ahmed, N.; Asif, H.M.S.; Saleem, G. A Benchmark for Performance Evaluation and Security Assessment of Image Encryption Schemes. Int. J. Comput. Netw. Inf. Secur. 2016, 8, 18–29. [Google Scholar] [CrossRef]
- Ye, Z.; Yin, H.; Ye, Y. Quantitative Comparison of Discrete Wavelet Chaotic Watermarking and Dual Chaotic Watermarking. In Proceedings of the 2018 4th International Conference on Computing Communication and Automation (ICCCA), Greater Noida, India, 14–15 December 2018; pp. 1–6. [Google Scholar]






| Images | PSNR | SSIM |
|---|---|---|
| Lena | 53.04 | 0.9980 |
| Pepper | 52.71 | 0.9985 |
| Mandrill | 51.02 | 0.9969 |
| Fruits | 53.39 | 0.9988 |
| Watermarking Methods | Cover Image | PSNR | SSIM |
|---|---|---|---|
| [17] | Lena | 41.5391 | 0.9975 |
| Mandrill | 40.8315 | 0.9918 | |
| Pepper | 39.8431 | 0.9821 | |
| Fruits | 41.4162 | 0.9972 | |
| [24] | Lena | 38.5471 | 0.9804 |
| Mandrill | 41.2176 | 0.9870 | |
| Pepper | 41.3236 | 0.9908 | |
| Fruits | 40.59041 | 0.9911 | |
| Proposed Method | Lena | 53.04 | 0.9980 |
| Mandrill | 51.02 | 0.9969 | |
| Pepper | 52.71 | 0.9985 | |
| Fruits | 53.39 | 0.9988 |
| Attack Type | [17] | [24] | Proposed Method |
|---|---|---|---|
| Gaussian | 0.9625 | 0.8823 | 0.9925 |
| Speckle noise | 0.9663 | 0.9647 | 0.9915 |
| Cropping | 0.6482 | 0.8619 | 0.9719 |
| Sharpening | 0.9935 | 0.9882 | 0.9567 |
| Rotation () | 0.9361 | 0.9225 | 0.9760 |
| Wiener filtering | 0.9578 | 0.9765 | 0.9934 |
| Salt and pepper noise | 0.9478 | 0.9733 | 0.9945 |
| Median filtering | 0.9419 | 0.8997 | 0.9902 |
| JPEG Compression | 0.9998 | 0.9791 | 0.9986 |
| Method | Embedding Time | Extraction Time | Total Time |
|---|---|---|---|
| [17] | 0.274117 | 0.238315 | 0.512432 |
| [24] | 0.810820 | 0.269506 | 1.080326 |
| Proposed Method | 0.5016456 | 0.2394905 | 0.7411361 |
| CC | [17] | [24] | Proposed Method |
|---|---|---|---|
| Horizontal | 0.0074 | 0.0082 | 0.00040 |
| Vertical | 0.0065 | 0.0070 | 0.0024 |
| Diagonal | 0.0098 | 0.0058 | 0.0039 |
| Scrambling Methods | Watermarked Image | ||
|---|---|---|---|
| Red | Green | Blue | |
| [17] | 2.2902 | 2.3444 | 2.4673 |
| [24] | 2.6372 | 2.4108 | 2.1091 |
| Proposed Method | 3.3553 | 3.4476 | 3.3274 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chowdhury, F.S.; Dhar, P.K.; Deb, K.; Koshiba, T. Blind Image Watermarking in Canonical and Cepstrum Domains Based on 4-Connected t-o’clock Scrambling. Symmetry 2020, 12, 266. https://doi.org/10.3390/sym12020266
Chowdhury FS, Dhar PK, Deb K, Koshiba T. Blind Image Watermarking in Canonical and Cepstrum Domains Based on 4-Connected t-o’clock Scrambling. Symmetry. 2020; 12(2):266. https://doi.org/10.3390/sym12020266
Chicago/Turabian StyleChowdhury, Farhana Shirin, Pranab Kumar Dhar, Kaushik Deb, and Takeshi Koshiba. 2020. "Blind Image Watermarking in Canonical and Cepstrum Domains Based on 4-Connected t-o’clock Scrambling" Symmetry 12, no. 2: 266. https://doi.org/10.3390/sym12020266
APA StyleChowdhury, F. S., Dhar, P. K., Deb, K., & Koshiba, T. (2020). Blind Image Watermarking in Canonical and Cepstrum Domains Based on 4-Connected t-o’clock Scrambling. Symmetry, 12(2), 266. https://doi.org/10.3390/sym12020266






