Abstract
In this paper, we propose an image encryption algorithm based on four-dimensional chaotic system to generate key and improve advanced encryption standard. The encryption algorithm is optimized by using the pipeline and parallel computing features of Field Programmable Gate Array (FPGA). First, the chaotic system is used as a key generator for the encryption algorithm. Next, in the improved advanced encryption standard, ShiftRows and SubByres are modified with Spin-Sort and Cubic S-Box, and the round of encryption is reduced. We implement the encryption algorithm and the wired image transmission system to the ARM-based SoC-FPGA. The HPS software runs on Linux and is used to control the FPGA encryption algorithm and image transmission. Finally, the results from the encryption security analysis show that the proposed image encryption algorithm is safe and effective.
1. Introduction
Recently, with the rapid development of network communication technology, the opportunities for global users to access the Internet have become more and more popular, and the dissemination of information and data has become more frequent. Multimedia and visual content already exist and are widely used in many domains, such as sharing military and medical personal information. Encryption methods are not only used in image multimedia, but also important for user security information (such as credit card numbers), cloud usage, etc. A good encryption scheme to protect information transmission security is of great significance. Therefore, encryption technology is receiving more and more attention. The image encryption scheme based on chaotic system has been widely studied, and its inherent characteristics such as initial sensitivity, unpredictability, and pseudo-randomness [1,2,3], thus observing the close relationship between chaotic systems and cryptography.
In 1989, Matthews first proposed an encryption scheme based on chaotic systems [4]. The first paper devoted to image encryption was published by Friedrich in 1998 [5]. A random number generator is used to generate a sequence of random numbers for encryption. When the generated number is more random, the encryption effect is better. Chaotic-based random number generator design is one of the common areas of chaotic systems used for encryption [6,7]. A permutation image encryption algorithm based on Logistic mapping and image segmentation is proposed in [8], in which the initial values and parameters of the Logistic map are used as secret keys. The diffusion and confusion methods is proposed by Shannon in [9]. Confusion causes the position of the pixel to be randomly disturbed, Cao et al. [10] using breadth-first search as the confusion algorithm. The confusion process has good encryption effect, but the pixel values do not change. It causes the histogram of the encrypted image to be similar to the original image. Therefore, its security is threatened by statistical analysis. All pixels have modified values during the diffusion process. The diffusion may result in higher security than confusion, but the encryption effect is not good. After these two operations, the normal image cannot be recognized correctly. S-Box performs replacement, which is one of the most important parts of the block encryption algorithm. Therefore, because they bring nonlinearity to the encryption process, using a powerful S-Box structure helps to achieve secure encryption.
The main reasons for the destruction of the image cryptosystem are: (1) the encryption key stream is only related to the secret key, but unrelated to the plain images; (2) the encryption method itself has a defect, so that partial information of cipher images is easily cracked and causes the entire encryption scheme to fail. In order to resist the choice of plaintext and known plaintext attacks, [11,12] adopts the method of generating key stream according to plaintext, that is, different original images will produce completely different key streams. High-dimensional chaotic maps have more variables and parameters. It usually exhibits good hyper-chaos properties and is more suitable for encryption. Therefore, we propose a chaotic encryption algorithm, combined with high-dimensional chaotic mapping and improved confusion and diffusion of AES, implemented on SoC FPGA. To avoid the defect of Shannon’s entropy. In [13,14], another scheme is proposed to verify the randomness of the image, called “Shannon’s local entropy.” We also use Shannon local entropy analysis to validate our purposed scheme [15,16,17,18,19,20,21,22,23,24,25,26,27].
The rest of the paper is organized as follows. Section 2 presents our designed four-dimensional chaotic system and proposed image encryption scheme. Section 3 explains how to implement the wire image transmission encryption system on the FPGA. The security analysis and evaluation are presented in Section 4. Finally, in Section 5 some conclusions are drawn.
2. Algorithm Design
In this section, we introduce a newly designed four-dimensional chaotic system. First, the characteristics of chaotic systems using various techniques including phase portrait and Lyapunov exponent are verified. Second, an improved chaotic encryption algorithm is proposed based on advanced encryption standard (AES) and key generator. Finally, the encryption scheme of this paper is represented by a flow chart.
2.1. Chaotic System
The three-dimensional chaotic Rössler system [18] is used for image encryption. It can be described as Equation (1).
Base on Rössler system, we design a 4D chaotic dynamic system as Equation (2).
where the x, y, z, and w are the states and a, b, c, and d are parameters of the system.
To use the fourth-order Runge–Kutta method in MATLAB, the parameters are chosen as a = 0.4, b = 0.6, c = 3, and d = 0.8 and designed the initial values x, y, z, w = [1, 1, 1, 1]. We obtained phase portraits of the new 4D chaotic system. Phase portrait is one of the direct observation methods to determine chaotic system. The trajectory of chaotic motion is a never-closing curve. The reciprocating movement in the orbit curve is confined to a bounded area and forms a strange attractor [20]. The Figure 1 shows the two-dimensional phase portraits of the new 4D chaotic system.
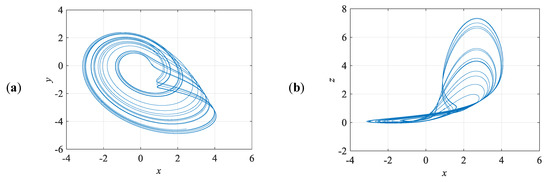
Figure 1.
Chaos system x-y (a) and x-z (b) dimension phase portrait.
Figure 2 shows the diagrams of Lyapunov exponents by changing the parameter d of the new chaotic system between 0 and 1. When λ < 0, the orbit is attracted to a stable periodic motion or fixed point, and the system is dissipative. If λ = 0 is called Lyapunov stability, its orbit is a neutral fixed point. It means that the system is conservative. If λ > 0, the system is sensitive to the initial value. It means that the system is chaotic and unstable. Figure 2 exhibits that the new chaotic system has chaotic characteristic values between 0 and 1.
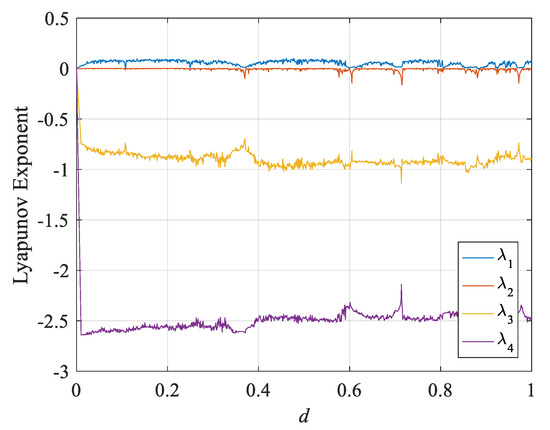
Figure 2.
D chaotic system with parameter d.
2.2. Purpose of New Chaotic Encryption Algorithm
AES is a well-known block cipher that has several advantages in data encryption. It is a fast encryption scheme and AES algorithm more robust against hacking. For 128-bit key, about 2128 attempts are needed to crack. However, it is not suitable in multimedia data because multimedia data has high redundancy. Only using AES encrypted images cannot achieve good encryption. In order to solve the shortcomings of AES encrypted images, we combine the features of chaotic systems, such as initial value sensitivity, ergodicity and generation of pseudo-random numbers, and modification of confusion and diffusion in the AES. It enhances the complexity of encryption and greatly increases security.
Each round of AES encryption (except for the last round) consists of four steps [16].
- i.
- AddRoundKey: Each byte in the matrix uses XOR to manipulate the round key; a subkey is derived from the main key using Rijndael’s key schedule.
- ii.
- SubBytes: Change each byte using an 8-bit substitution box. This step provides the nonlinear substitution of the replacement function.
- iii.
- ShiftRows: In the ShiftRows step, bytes in each row of the state are shifted cyclically to the left. The shifted number of places each byte is depended on the number of rows.
- iv.
- MixColumns: In order to properly mix linear operations in a matrix, this step uses a linear transformation to mix four bytes per line. The last encryption loop omits the MixColumns step and replaces it with another AddRoundKey.
In Ref. [11], it presents Cubic S-Box for diffusion. We use Cubic S-Box to replace AES SubBytes. The Figure 3 show the block of AES. Stack block I, II, III, and IV as z axis. It enhances the original S-box become a three-dimensional matrix named by Cubic S-box as shown in Figure 4.
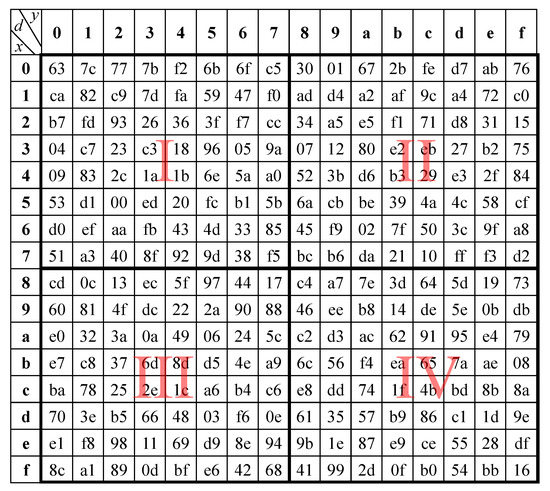
Figure 3.
Block of S-box.
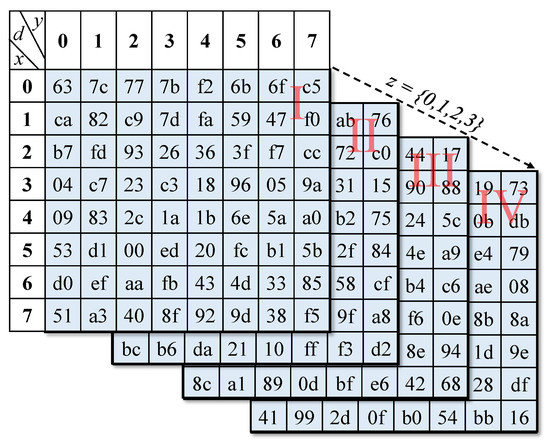
Figure 4.
Cubic S-box.
For a given 1-byte data d, transform d to binary form “d7d6d5d4d3d2d1d0” where di ∈ {0,1}, (i = 0, 1, …, 7). Any 1-byte value is represented by hexadecimal value “xyz,” where x = d7d6d5, y = d4d3d2, and z = d1d0. Substitute values by querying columns, rows, and depth in Cubic S-box. For example, input d = (58)16, transfer to binary d = (00111010)2. Then, x = (001)2, y = (110)2, and z = (10)2. Substituted values can be obtained by third block, second row and seventh column. The output d’ = (90)16. There are six different options for express 1-byte date d. The example d = “xyz” is one option. We also can express d = “xzy,” “yxz,” “yzx,” “zxy,” and “zyx.” Compared with S-box, Cubic S-box is more suitable to generate two different numbers from one 1-byte data. The security of the cryptosystem can be enhanced. We use two types of “yxz” and “zyx.” The input 128-bit chaotic sequence key is used as a parameter to select the type.
Since ShiftRows of AES has only one form of diffusion. A 16-form of diffusion is proposed. It used to replace the ShiftRows of AES. Name by Spin-Sort. Its steps are as follows:
- Step. i.
- In the Spin-Sort, we can express the plaintext as a 4 × 4 matrix in Figure 5a. Where x0, x1, x2, …, x15 are 8-bit values.
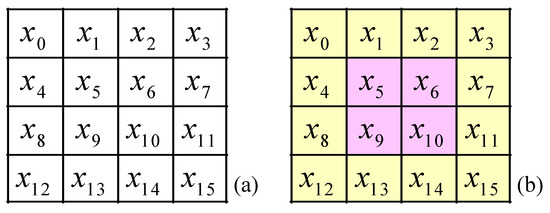 Figure 5. (a) Plaintext; (b) mark inner and outer blocks.
Figure 5. (a) Plaintext; (b) mark inner and outer blocks. - Step. ii.
- Mark the matrix as an outer and inner blocks as Figure 5b.
- Step. iii.
- Take a vertex of the outer(inner) block as the root.
- Step. iv.
- Sorted by the root, clockwise (counterclockwise) from the outer (inner) block to the inner (outer) block.
According to step i to step iv, obtain 16 sequences as Equation (3). Figure 6 shows a sorting process of Spin-Sort.
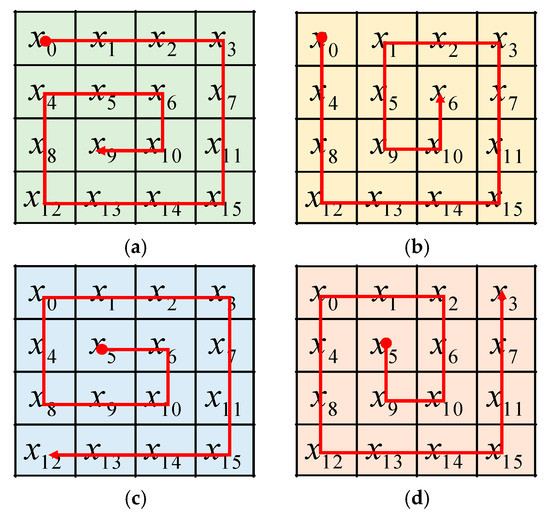
Figure 6.
Spin-Sort (a) start from outer-top-left vertex and clockwise; (b) start from outer-top-left vertex and counterclockwise; (c) start from inner-top-left vertex and clockwise; (d) start from inner-top-left vertex and counterclockwise.
Each 24-bit image file can be express as Figure 7a. A pixel includes 3 byte data, respectively R/G/B. To enhance the complexity of the encryption algorithm, before performing algorithm, add a diffusion method called diversion of pixel. All pixels of image into RGB channels. As shown in Figure 7b, reconstitute a new image.
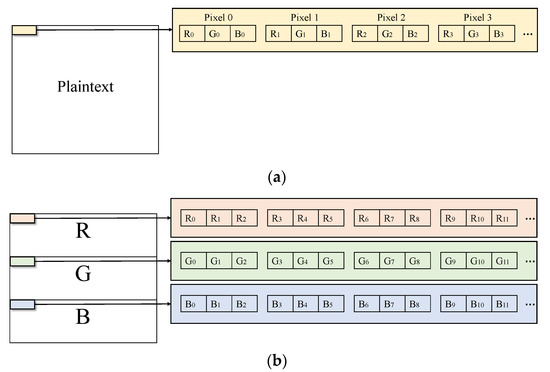
Figure 7.
(a) Pixel composition of the image. (b) Diversion of pixel.
2.3. Key Generator Design
The encryption key stream is only related to the secret key, but unrelated to the plain images. This is the main reason for destroying the image cryptosystem. To make the cryptosystem depend on the plain image, the encryption key uses the initial values x0, y0, z0, and w0 in the 4D chaotic system and features of image pixel. After a certain number of iterations, the initial 128-bit key is generated. Every block encryption finish will iterate again to generate a new encryption key. Therefore, the encryption key generated by the 4D chaotic system is not only related to the initial value, but also related to the plaintext. That means different plaintexts will produce completely different key streams. The following is the process of key generator:
- Step. i.
- Select the proper values to be the initial conditions for the 4D chaotic system.
- Step. ii.
- Execute pre-iteration nr rounds, where nr is 2000 rounds.
- Step. iii.
- Calculate summation of image pixel, according to Equation (6).where m and n are the image dimension, Pixel(i, j) is the i row and j column pixel unsigned values of plain image.
- Step. iv.
- Use Sumpixel as parameter to iterate np rounds as in Equation (7).
- Step. v.
- The initial 128-bit key generate after iterate np rounds in 4D chaotic system as Equation (8).
- Step. vi.
- Iterate once every 16-byte block encryption.
2.4. Flow Chart of Encryption
We describe the entire encryption process via a flow chart. Figure 8 shows the flow chart of encryption algorithm. It contains the steps of AES, Spin-Sort, Cubic S-Box, Diversion of pixel, and uses the chaotic key generator. Standard AES uses nine rounds with an initial round and a final round. In this paper, four rounds are used, an initial round and a final round. The decryption algorithm is the reverse process of encryption algorithm.
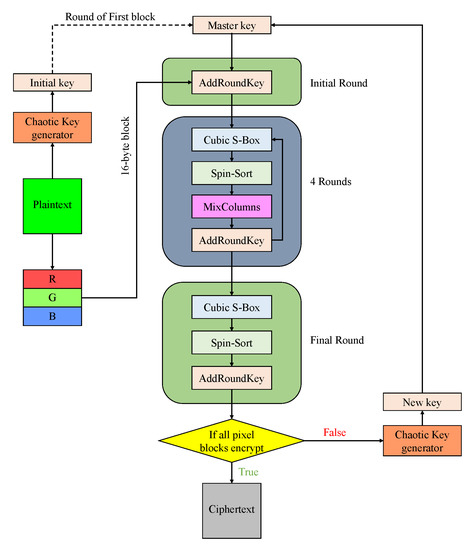
Figure 8.
Flow chart of encryption in this proposal method.
3. FPGA Implementation
In this section, the entire experiment is conducted in Altera DE10-standard. The DE10-Standard use CycloneV system-on-a-chip (SoC) is composed of two distinct portions a dual-core Arm Cortex-A9 hard processor system (HPS) and an FPGA. A LXDE Linux program in the SD card and running on the ARM processor. Next, describe how to implement Euler’s method chaotic system on the FPGA and hardware implementation of our encryption system. Wired image transmission system showed in Figure 9.

Figure 9.
Wired image transmission system.
3.1. Chaos System Discretization
In order to implement the chaotic system on FPGA, we use Euler’s method to implement the discretization. The chaotic system of Equation (2) can be rewritten according to our system as shown in Equation (9).
where a = 0.4, b = 0.6, c = 3, d = 0.8, the initial values x, y, z, w = [1, 1, 1, 1] and the step size Δt is 0.001.
According to Equation (9), our system contains addition, subtraction, and multiplication. We use the floating point IP-CORE ALTFP_ADD_SUB and ALTFP_MULT, provided by Altera, as shown in Table 1. The two IP-CORE follows the IEEE-754 Standard. The IP-CORE ALTFP_ADD_SUB can run add or subtract operation and ALTFP_MULT handles floating-point multiplication. There are different latency times in these two IP-CORE, ALTFP_ADD_SUB is 7 clocks and ALTFP_MULT is 5 clocks. We need to wait for these clocks to make sure the calculations are correct.

Table 1.
Time latency of floating point IP-CORE.
In hardware design, we split every step of the operation in Equation (9), first. Figure 10 shows the entire chaos system operations. Our chaotic system requires six steps to get the next iterations. Then we use the adder, subtractor, and multiplier in the IP-CORE of Altera’s floating-point arithmetic unit to implement Equation (9). The system’s clock for the entire architecture is 50 MHz. Actually, we need to wait one more clock in each operation, since the system’s clock is a positive edge trigger. The latency time of ALTFP_ADD_SUB is 8 clocks, ALTFP_MULT is 6 clocks. It can be calculated that the operation time of entire architecture is 44 clocks.
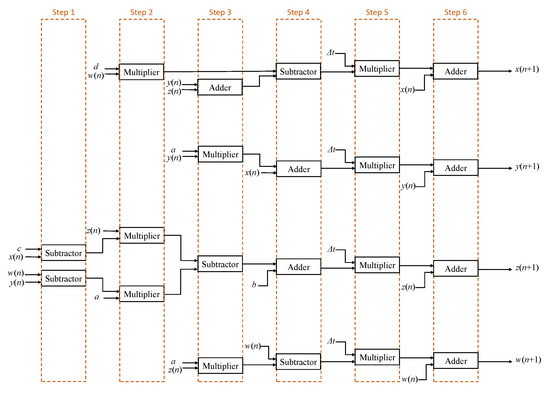
Figure 10.
Operation of chaotic system.
For the entire hardware, the chaotic system is just one of the modules. It uses the signals of CHAOS_STEP, CHAOS_RESET, and CHAOS_DONE to control this module. The signal CHAOS_STEP is the start signal. When 44 clocks are passed, an iteration is completed to generate new values x (n + 1), y (n + 1), z (n + 1) and w (n + 1). At this time, the signal CHAOS_DONE triggers. The signal CHAOS_RESET is used to reset the chaotic system, and the iteration value will be reset back to initial values x0, y0, z0, and w0.
3.2. Encryption System Hardware Implementation
The Figure 11 shows the entire system of image encryption. It contains FPGA encryption, HPS software, SDRAM, VGA display, and wired transmission. There are two boards that are connected to a router. The router is not connected to the Internet. Use the router’s dynamic host configuration protocol (DHCP) to dynamically assign different IP addresses to the two boards. A computer and two DE10 boards form an internal network.
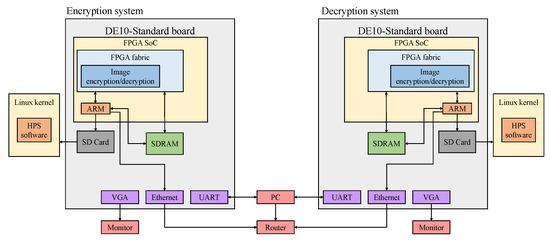
Figure 11.
Application block diagram of FPGA image encryption/decryption system.
3.2.1. SDRAM Access
In order to achieve our FPGA encryption system and VGA display, the image data need to be stored in a memory that HPS and FPGA can access. The FPGA 64MB SDRAM is a suitable memory. The image data is relatively large, so we use HPS-to-FPGA Bridge to connect SDRAM and HPS. The HPS software use mapped address of the SDRAM to transfer the image data into the SDRAM. Since the frame reader will read R/G/B/A 4 bytes at a time, it needs to fill in an empty byte for each pixel. The HPS use the control signal of the frame reader to display image through VGA.
The SDRAM is a 16-bit data bus, it means only read 2 bytes at a time. The FPGA uses a 50 MHz clock but the SDRAM uses a 100 MHz clock. To synchronize data originating from different clock domains, the SDRAM controller uses two FIFOs (first in, first out) to store read data and write data respectively. Since the encryption system represents 16 byte data as a 4 × 4 matrix, the encryption process requires 16 bytes of data. We use the pipeline feature to read 2 bytes from FIFO at a time, stored in a 128-bit register until it meets 128 bits. Then trigger a control signal to start the encryption module. When encryption is complete, store data in another 128-bit register. The encrypted 128-bit data will also be written to the write FIFO in sequence.
3.2.2. Encryption System
In the previous section, we mentioned Cubic S-Box, Spin-Sort, and MixColumn, AddRoundKey of AES. These encryption methods require four rounds of execution. Using FPGA parallel computing architecture, four rounds can be completed in four clocks. The step of encryption system on FPGA design as follows:
- Step. i.
- Posedge clock, count a register dcnt to confirm if the number of rounds is 4.
- Step. ii.
- Posedge clock, module aes_key_expand_128 generate new round key.
- Step. iii.
- Posedge clock, check whether is initial round. If is initial round, registers sam,n are divided 128-bits input data XOR first round key, Else, assign by sam,n_next which is sam,n_mc XOR round key,
- Step. iv.
- Wire connected module aes_Csbox, spin_sort and mix_col. The module aes_Csbox produced sam,n_cs, the module spin_sort produced sam,n_ss, the module mix_col produced sam,n_mc.
- Step. v.
- Posedge clock, the output data is assigned sam,n_ss XOR round key.
Where m is 0, 1, 2, 3 and n is 0, 1, 2, 3. It is worth noting that all steps are performed simultaneously, instead of step by step. The Figure 12 shows the flow chart of encryption system.
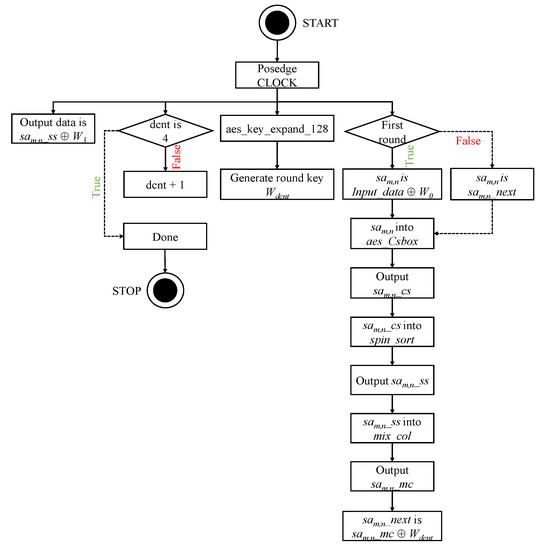
Figure 12.
Flow chart of encryption system on FPGA design.
4. Security Analyisis
In order to analyze our encryption performance, we use histogram analysis, correlation analysis, differential attack analysis, and information entropy analysis to verify the security of our proposed encryption algorithm. For test images, we chose 24-bits BMP that include Lena, Airplane, Pepper, and Mandrill.
4.1. Histogram Analysis
The histogram of the image reflects the distribution of pixel values of an image. A color image can be used to treat the three channels of red, green, and blue as a special gray image, and the one-dimensional histogram method of gray image is used to analyze the performance of the encryption algorithm. The ciphertext generated by a secure encryption algorithm should be nearly evenly distributed in the histogram, and has significant difference compared with the histogram of the original image. The Figure 13 is histogram test of Lena, and (a) and (b) are the RGB histograms of the plaintext and its chipertext encrypted by our proposed chaotic encryption. It can be seen that the histogram of the encrypted image is nearly completely consistent and has a significant difference from the original image. So our chaotic encryption algorithm are safe in histogram analysis. Figure 14 and Figure 15 shown the Correlation of each channel in plain image Lena and in cipher image Lena, respectively.
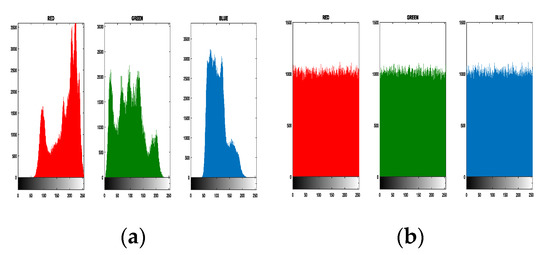
Figure 13.
Histogram analysis of Lena plaintext (a) and its chipertext encrypted (b) by our proposed chaotic encryption.
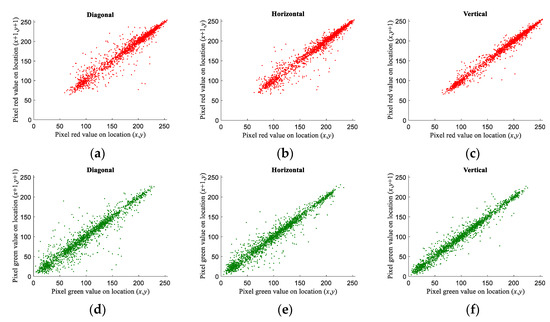
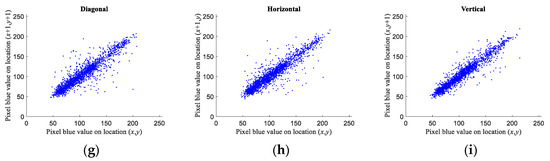
Figure 14.
Correlation of each channel in plain image Lena. (a) Diagonal correlation of red color; (b) horizontal correlation of red color; (c) vertical correlation of red color; (d) diagonal correlation of green color; (e) horizontal correlation of green color; (f) vertical correlation of green color; (g) diagonal correlation of blue color; (h) horizontal correlation of blue color; (i) vertical correlation of blue color.
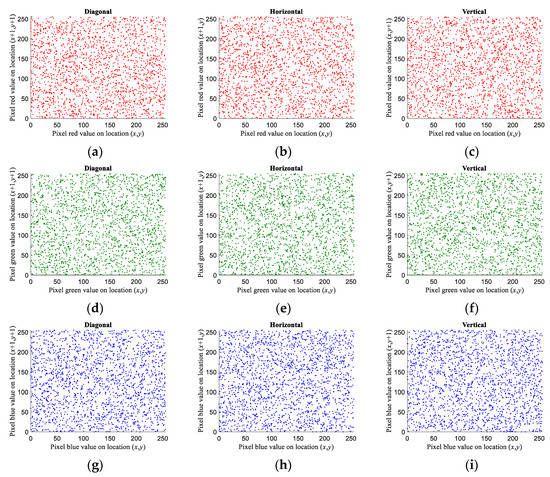
Figure 15.
Correlation of each channel in cipher image Lena. (a) Diagonal correlation of red color; (b) horizontal correlation of red color; (c) vertical correlation of red color; (d) diagonal correlation of green color; (e) horizontal correlation of green color; (f) vertical correlation of green color; (g) diagonal correlation of blue color; (h) horizontal correlation of blue color; (i) vertical correlation of blue color.
4.2. Correlation Analysis
Correlation analysis is used to measure the relationship between two adjacent pixels in an image. The adjacent pixels of the original image have high correlation in the horizontal, vertical, and diagonal directions. In order to improve the resistance of statistical attacks, an ideal image encryption scheme should reduce the correlation between the two adjacent pixels [22]. The correlation coefficient can be calculated by
where x and y are values of two adjacent pixel in the image, n is the number of pixel pairs, D(x) is the variance, E(x) is the mean and cov(x, y) is the covariance.
The correlation coefficient is shown in Table 2, Table 3, Table 4 and Table 5. We can find that proposed encryption algorithm has a sufficiently safe performance.

Table 2.
Correlation coefficients on test images.

Table 3.
Comparison of correlation coefficients on Lena (red).

Table 4.
Comparison of correlation coefficients on Lena (green).

Table 5.
Comparison of correlation coefficients on Lena (blue).
4.3. Differential Attack Analysis
A differential attack is usually a plaintext attack. The attacker encrypts with a small change in plaintext. Then the corresponding ciphertext is generated for statistical analysis to obtain the key. A secure encryption scheme should be very sensitive to plain images. To measure the impact of this type of attack, pixel rate of change (NPCR) and uniform mean change intensity (UACI) are calculated as follows:
where, C1 is an encrypted image from original plain image and C2 is an encrypted image from plain image with small change, i.e., one pixel difference. And i and j are the pixel positions, H and W are height and width of the ciphertext image.
where C1, C2, i, j, W, and H are the same as in Equations (14) and (15).
The test result of the differential attacks analysis NPCR and UACI is shown in Table 6 and Table 7. We can find that the NPCR score is close to 100%, and the UACI is close to the theoretical value of 33.33%. It means that the proposed encryption algorithm is sufficient to resist differential attacks.

Table 6.
Comparative of NPCR scores.

Table 7.
Comparative of UACI scores.
4.4. Information Entropy Analysis
Information entropy is a quantitative measure of randomness of a system, proposed by Shannon [9]. The global entropy H(m) of a message source m can be calculated as
where P(mi) means the probability of each symbol appearance. For color images, each color channel(red, green, or blue) is described as 8-bits that have pixel values ranging from 0 to 255. The maximum value of entropy is 8. A good image encryption scheme, the global entropy value of the encrypted image should be close to 8. There are two disadvantages to the global entropy measurement. First, the global Shannon entropy fails to measure the true randomness of the image if the image contains some image blocks with low Shannon entropy. Second, the global information entropy may be affected by different image size, because larger images contain more information. To complement these disadvantages, use local Shannon entropy measures image randomness. The local entropy can be calculated as
where k is non-overlapping image blocks and H(Si) is the information entropy of block i.
Referring to [15,16], we randomly select 30 non-overlapping 44 × 44 image blocks to calculate the average of information entropy. If the average information entropy (called local information entropy) is greater than 7.9, the image randomness is high. The encryption algorithm has sufficient security. Thus, Table 8 and Table 9 show the global and local Shannon entropy of the encrypted images. The results of global entropy are close to the theoretical value 8 and the results of local entropy is higher than 7.9. This means that the image encrypted by the proposed encryption scheme has good randomness.

Table 8.
Comparative of global entropy of propose scheme.

Table 9.
Comparative of local entropy of propose scheme.
5. Conclusions
In the paper, we design a new chaotic system based on the Rössler system and implemented on the Altera FPGA DE10-standard board. Using the Euler method with the given value as the initial condition and the sum of the image pixels as the iteration parameter, four pseudo-random numbers are generated as the encryption key. Each time a 16-bytes block is encrypted, the new encryption key is generated.
The encryption method uses AES as the basis, reducing the number of encryption rounds to 4 and changing the original shiftRows and SubBytes to be replaced by Spin-Sort and Cubic S-Box. In order to increase the complexity of encryption, 16-form sorting process of Spin-Sort and two types of Cubic S-Box are used. The entire encryption algorithm is implemented on the FPGA, using HPS software to control encryption and wired transmission and display images instantly on the VGA port.
Finally, we use histogram analysis, correlation analysis, differential attack analysis, and entropy analysis to verify the safety and performance of our proposed scheme. In Section 4, all the experimental results show that the algorithm can encrypt the color image effectively and resist various typical attacks. Our proposed scheme is secure and useful for image encryption.
Author Contributions
Conceptualization, C.-H.Y.; methodology, Y.-S.C.; software, C.-H.Y. and Y.-S.C.; validation, C.-H.Y. and Y.-S.C.; formal analysis, C.-H.Y. and Y.-S.C.; data curation, C.-H.Y. and Y.-S.C.; writing—original draft preparation, C.-H.Y. and Y.-S.C.; writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wu, J.; Liao, X.; Yang, B. Color image encryption based on chaotic systems and elliptic curve ElGamal scheme. Signal Process. 2017, 141, 109–124. [Google Scholar] [CrossRef]
- Amigo, J.M.; Kocarev, L.; Szczepanski, J. Theory and practice of chaotic cryptography. Phys. Lett. A 2007, 366, 211–216. [Google Scholar] [CrossRef]
- Jakimoski, G.; Kocarev, L. Chaos and cryptography: Block encryption ciphers based on chaotic maps. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2001, 48, 163–169. [Google Scholar] [CrossRef]
- Matthews, R. On the Derivation of a “Chaotic” Encryption Algorithm. Cryptologia 1989, 13, 29–42. [Google Scholar] [CrossRef]
- Fridrich, J. Symmetric ciphers based on two–dimensional chaotic maps. Int. J. Bifurc. Chaos 1998, 8, 1259–1284. [Google Scholar] [CrossRef]
- Pareschi, F.; Setti, G.; Rovatti, R. Implementation and testing of high-Speed CMOS true random number generators based on chaotic systems. IEEE Trans. Circuits Syst. I Regul. Pap. 2010, 57, 3124–3137. [Google Scholar] [CrossRef]
- Özkaynak, F. Cryptographically secure random number generator with chaotic additional input. Nonlinear Dyn. 2014, 78, 2015–2020. [Google Scholar] [CrossRef]
- Yen, J.-C.; Guo, J.-I. Efficient hierarchical chaotic image encryption algorithm and its VLSI realization. IEEE Proc. Vis. Image Signal Process. 2000, 147, 167–175. [Google Scholar] [CrossRef]
- Shannon, C.E. Communication theory of secrecy systems. Bell Labs Tech. J. 1949, 28, 656–715. [Google Scholar] [CrossRef]
- Cao, C.; Sun, K.; Liu, W. A Novel Bit-Level Image Encryption Algorithm Based on 2D-LICM Hyperchaotic Map. Signal Process. 2018, 143, 122–133. [Google Scholar] [CrossRef]
- Yin, Q.; Wang, C. A New Chaotic Image Encryption Scheme Using Breadth-First Search and Dynamic Diffusion. Int. J. Bifurc. Chaos 2018, 28, 1850047. [Google Scholar] [CrossRef]
- Zhang, Y. The unified image encryption algorithm based on chaos and cubic S-Box. Inf. Sci. 2018, 450, 361–377. [Google Scholar] [CrossRef]
- Wang, X.; Zhao, Y.; Zhang, H.; Guo, K. A novel color image encryption scheme using alternate chaotic mapping structure. Opt. Lasers Eng. 2016, 82, 79–86. [Google Scholar] [CrossRef]
- Norouzi, B.; Mirzakuchaki, S. A fast color image encryption algorithm based on hyper-chaotic systems. Nonlinear Dyn. 2014, 78, 995–1015. [Google Scholar] [CrossRef]
- Boriga, R.; Dăscălescu, A.C.; Priescu, I. A new hyperchaotic map and its application in an image encryption scheme. Signal Process. Image Commun. 2014, 29, 887–901. [Google Scholar] [CrossRef]
- Wu, Y.; Zhou, Y.; Saveriades, G.; Agaian, S.; Noonan, J.P.; Natarajan, P. Local Shannon entropy measure with statistical tests for image randomness. Inf. Sci. 2013, 222, 323–342. [Google Scholar] [CrossRef]
- Bhatnagar, G.; Wu, Q.M.J. Biometric Inspired Multimedia Encryption Based on Dual Parameter Fractional Fourier Transform. IEEE Trans. Syst. Man Cybern. Syst. 2014, 44, 1234–1247. [Google Scholar] [CrossRef]
- Mandal, M.K.; Kar, M.; Singh, S.K.; Barnwal, V.K. Symmetric key image encryption using chaotic Rossler system. Secur. Commun. Netw. 2013, 7, 2145–2152. [Google Scholar] [CrossRef]
- Chandrasekaran, J.; Subramanyan, B.; Selvanayagam, R. A Chaos Based Approach for Improving Non Linearity in S Box Design of Symmetric Key Cryptosystems. In Proceedings of the International Conference on Computer Science and Information Technology CCSIT 2011, Bangalore, India, 2–4 January 2011; pp. 516–522. [Google Scholar]
- SunSun, K. Chaotic Secure Communication: Principles and Technologies; De Gruyter Gruyter: Berlin, Germany, 2016. [Google Scholar]
- Pak, C.; Huang, L. A New Color Image Encryption Using Combination of the 1D Chaotic Map. Signal Process. 2017, 138, 129–137. [Google Scholar] [CrossRef]
- Wu, X.; Zhu, B.; Hu, Y.; Ran, Y. A novel colour image encryption scheme using rectangular transform-enhanced chaotic tent maps. IEEE Access 2017, 5, 6429–6436. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, H.-L. A color image encryption with heterogeneous bit-permutation and correlated chaos. Opt. Commun. 2015, 342, 51–60. [Google Scholar] [CrossRef]
- Niyat, A.Y.; Moattar, M.H.; Torshiz, M.N. Color image encryption based on hybrid hyper-chaotic system and cellular automata. Opt. Lasers Eng. 2017, 90, 225–237. [Google Scholar] [CrossRef]
- Wu, Y.; Noonan, J.P.; Agaian, S. NPCR and UACI randomness tests for image encryption. Cyber J. Multidiscip. J. Sci. Technol. J. Sel. Areas Telecommun. 2011, 1, 31–38. [Google Scholar]
- Yang, C.-H.; Wu, H.-C.; Su, S.-F. Implementation of Encryption Algorithm and Wireless Image Transmission System on FPGA. IEEE Access 2019, 7, 50513–50523. [Google Scholar] [CrossRef]
- Wang, X.-Y.; Zhang, Y.-Q.; Bao, X.-M. A Colour Image Encryption Scheme Using Permutation-Substitution Based on Chaos. Entropy 2015, 17, 3877–3897. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).