Abstract
Nontrivial topological gluon configuration is one of the remarkable features of the Quantum Chromodynamics (QCD). Due to chiral anomaly, the chiral imbalance between right- and left-hand quarks can be induced by the transition of the nontrivial gluon configurations between different vacuums. In this review, we will introduce the origin of the chiral chemical potential and its physical effects. These include: (1) the chiral imbalance in the presence of strong magnetic and related physical phenomena; (2) the influence of chiral chemical potential on the QCD phase structure; and (3) the effects of chiral chemical potential on quark stars. Moreover, we propose for the first time that quark stars are likely to be a natural laboratory for testing the destruction of strong interaction CP.
1. Introduction
1.1. The Problem, Chiral Anomaly, and Instantons
The QCD Lagrangian is given as
where M is the mass matrix of quarks, , and , respectively, denote the gluon fields and quark fields, is the covariant derivative. Since , for the two-flavor Lagrangian, it has an approximate symmetry . The symmetry and are so-called chiral or axial symmetry. As the appearance of nucleon and pion multiples in the hadrons spectrum, it has been manifested that, in fact, the isospin and baryonic symmetries are good approximate symmetry of nature. For the chiral symmetry, it is spontaneously broken due to the nonzero quark condensations. According to the Goldstone theorem, there should be four Nambu–Goldstone bosons associated with the broken chiral symmetry. It is believed that Nambu–Goldstone bosons associated with are the pions which are pseudoscalar light mesons with isospin . If is also a true symmetry of QCD, the corresponding Nambu–Goldstone boson is an pseudoscalar light meson. However, there is no such candidate because the meson is too heavy to be interpreted as a Goldstone Boson.
This problem was resolved by ‘t Hooft [1,2], who was aware of the complexity of the vacuum structure and took the contributions of topological instantons into account in the QCD Lagrangian. The existence of the nontrivial topological solutions such as instantons in QCD make not a true symmetry of QCD, although the QCD Lagrangian is invariant under the transformation in the massless limit. ‘t Hooft’s solution to the problem relies on two facts: one is the Adler–Bell–Jackiw anomaly [3,4], another is the existence of instantons in QCD. The Adler–Bell–Jackiw anomaly identity in massless limit is
where is flavor number, is a dual form of gauge field tensor , and are the generators of the gauge group which satisfy . This chiral anomaly can be obtained from axial Ward-identity or the path integral method introduced by Fujikawa [5]. The right-hand side of the Equation (2) can be expressed as a total divergence
where
and . As we can see, although we can define a current as
this current is not physical because is not gauge invariant. Due to the chiral anomaly, under the transformation , the action changes
We will see that the instantons with nontrivial topological configuration can make the integral nonzero, thus breaking the symmetry.
For a gauge field with the temporal gauge , at , the gauge field is expected to be vacuum configuration and can be represented as pure gauges:
where are elements of gauge group G. Assuming that the gauge field at vanishes, so the space point at infinity is mapped to a constant group element. Therefore, the gauge field can be regarded as a map : . Considering , these maps can be classified by third homotopy group . In the gauge theory, the generators are which satisfy , the third homotopy group and the topological invariant is given as [6]
If and only if two maps are homotopy equivalent, they have the same topological invariant. For the gauge theory, we have shown that the topological configuration of vacuum can be classified by an integer which is called winding number. The tunneling events between these vacuums are called instantons. After the instantons tunneling, the difference of winding number between two vacuums at can be expressed as
This identity shows that the chiral charge is not conserved and changes as
where is the winding number of the instanton and we assume at . This identity indicates that the instantons can flip the helicities of quarks from the right hand to the left hand or vice versa, and the symmetry is broken by instantons tunneling.
1.2. -Vacuum and Strong CP Problem
The tunneling probability between two different vacuums under semi-classical approximation is
where denotes the gauge field configurations with winding number . According to the Bogomol’nyi inequality [7], this tunneling probability is suppressed by a factor . Since the tunneling between two vacuums with different winding numbers is possible, we may ask what the true vacuum is. We want to construct a series of vacuums which are the superposition of those vacuums with certain winding numbers
and transitions between these vacuums are forbidden. Thus, we expect these bases to satisfy
which implies
where means that the integral domain of the functional integral is restricted to the gauge field configurations with winding number , i.e.,
It is obvious that we can choose , and the -vacuum is defined as [8]. The true vacuum may be the -vacuum which is invariant after the instantons tunneling. Since the different -vacuums do not communicate with each other, we cannot determine which vacuum our world is in a priori way [8]. In the Minkowski space, the transitions between -vacuums is represented as
where is the winding number of instantons which is denoted as Equation (9). This path integral takes into account the contribution of all the gauge configurations, and it is equivalent to add a -term to the QCD Lagrangian. If is nonzero, this term breaks the P and T symmetry, so it violates CP invariance. We can cancel the angle by redefining the fermion fields as , but at the price of introducing P and CP violating phases in a mass matrix of fermions [9,10]. Thus, the complex mass of fermions is unphysical and also leads to P and CP violation. Thus, the basis-independent observable angle of CP violation is defined as
where M is the mass matrix of fermions. Theoretically, the CP invariance is not a necessary requirement of QCD theory. Paradoxically, experimentally, there is no obvious signal of the global P and CP violation. The estimate of the strong CP phase from the neutron electric dipole moment (NEDM) is very small () [11,12,13]. This fine-tuning problem of Equation (17) is called a Strong CP Problem.
There are main three possible solutions to the strong CP problem: massless up quark solution, Peccei–Quinn (PQ) mechanism [14,15], and the Nelson–Barr mechanism [16,17]. For the first solution, if the up quark is massless, we can always redefine the fermions field to cancel the -term without any influence, thus there is no strong CP problem. Unfortunately, the ‘t Hooft determinantal interaction may generate a mass for up quark even if the bare mass of up quark is zero [18]. Thus, this solution is ruled out. For the Peccei–Quinn mechanism, a global chiral symmetry is introduced and is suggested to be a dynamical field called axion, which is the Nambu–Goldstone boson of the broken symmetry [19,20]. In addition, at the minimum of the effective potential for the axion, the -term is canceled out and is conserved [21]. The last scenario proposes that the CP symmetry is an exact symmetry at a very high scale, and -term is forbidden there. Then, CP symmetry is broken spontaneously, and it will generate a large CKM angle and a small strong CP violation angle [22,23].
Although several solutions have been proposed to explain the strong CP problem, there is no direct evidence for which one is right. So far, the strong CP problem remains a mystery in physics.
1.3. Event by Event P and CP Violation and Chiral Chemical Potential
In recent years, the topological fluctuation effects induced by nontrivial gauge configurations (instantons or sphalerons) have attracted much attention. Although the global strong CP violation has not been observed, the topological fluctuation in hot matter provides the possibility to observe the local P and CP violation.
As mentioned above, the QCD vacuums have a lot of topological structures which are classified by integers called winding numbers. In addition, each of them is separated from the others by a potential barrier of scale . At low temperatures, a transition between different vacuums depends on instantons tunneling. The instantons density with winding number at zero temperature was given in Refs. [24]
where is the size of instantons, and denotes the renormalized coupling constant. At the finite temperature because of the Debye screening and asymptotic freedom, contributions from large size instantons are ignored, and the coupling constant gradually goes to zero as temperature increases. Thus, raising the temperature will lead to the decrease of instantons density. Instantons density at a finite temperature is specifically calculated in Ref. [25]
where and . At high temperatures, although the instantons density is extremely low, the actual transition rate between different vacuums increases instead of decreasing due to the sphaleron configurations in hot QCD [26]. If the temperature is high enough, the sphalerons can have enough energy to leap over the potential barrier, and then dramatically increase the transition rate. In Ref. [27], the sphaleron rate is estimated to be
where .
In the quark–gluon plasma (QGP), these gluon configurations with nonzero winding numbers can be generated anywhere at anytime. Once this gluon configuration is excited at some space-time point, the topological charge of the vacuum around that point will be changed by these gluon configurations. Due to the chiral anomaly in Equations (9) and (10), this process will lead to chiral imbalance between left-hand and right-hand quarks. Local chiral imbalance means the is broken locally. Since there is no global P and violation, gluon configurations with negative and positive winding numbers have the same possibility to be excited, so the average chirality of many events vanishes. Therefore, we can say that the P and violation caused by nontrivial gluon configurations is local and event-by-event [28]. The spontaneous parity violation in hot QCD was proposed in Refs. [29,30,31,32], which argues that the P-odd metastable vacuum state can be produced in the vicinity of the deconfinement phase transition. It is also suggested in Refs. [33,34] that an arbitrary induced -vacuum state should be created in heavy-ion collisions through a non-equilibrium phase transition. We can imagine that, in heavy-ion collisions, some P-odd bubbles are produced, and is nonzero inside these bubbles but zero outside. Such bubbles may also be regarded as the space-time regions filled by gauge field configurations with a nontrivial winding number.
In order to mimic the local P and CP violation and the topological fluctuation, we assume that the angle in the Lagrangian depends on the space-time [28,35,36], i.e.,
The -term can be canceled out by performing an axial transformation on fermion fields
and, due to the chiral anomaly, the Lagrangian changes as follows:
Thus, the local -term is equivalent to a fermionic contribution. If we further assume that the angle is only or mainly dependent on time, i.e., , we can define a chiral chemical potential as [37]. In addition, then the Lagrangian can be written as
The chiral chemical potential is coupling to the chiral charge density operator . In addition, just like the chemical potential being able to reflect the quark number density, the chiral chemical potential can also mimic the chiral charge density. However, the chiral charge is not conserved because of the chiral anomaly, and we cannot treat as a true chemical potential. The chiral chemical potential is nothing but an indication of the magnitude of the chiral imbalance. Although chiral chemical potential is generated by the topological charge fluctuation, we are concerned with the effects of the chiral imbalance rather than these dynamical processes, so we treat it as a free, dynamically independent parameter. Moreover, it is very convenient for us to study the chiral imbalanced systems by adding the chiral chemical potential into the Lagrangian.
2. The Effects of Chiral Imbalance
2.1. The Charge Separation Effect (CSE) and Chiral Magnetic Effect (CME)
Relativistic heavy-ion collisions can produce a fireball with energy density of /fm [38,39], which is already above the predicted energy density 1 GeV/fm of the deconfinement phase transition. Some experimental evidence suggests that the quark–gluon plasma has been produced in relativistic heavy-ion collisions [39,40]. In the hot matter created in heavy-ion collisions, chiral imbalance is more obvious because of the sphaleron-like transition at high temperature [26,27]. In the non-central heavy-ion collisions, the fast-moving spectator protons can produce a strong magnetic field perpendicular to the reaction plane on the Tesla scale [41]. Due to the high energy density and strong magnetic field, heavy-ion collisions can provide an excellent environment for the observation of local P and CP violation.
The chiral imbalanced system has many interesting effects, especially when a magnetic field is applied. Considering a system in which both strong and electromagnetic interactions are involved, the Lagrangian of the gauge theory is
where and are, respectively, the gluon fields and photon field, are the generators of gauge group which satisfy , and we assume that the angle is local. Through the triangle diagram of the chiral anomaly, the electromagnetic field and the Chern–Simons current are coupled together. Therefore, we introduce an effective Lagrangian which is used in axion electrodynamics [42],
where
and represents the color number. As shown in Equation (3), can be represented as a total divergence of Chern–Simons current,
By subtracting a total divergence term , then the Lagrangian (26) can be written as
In addition, the following form of the Euler–Lagrange equation can be obtained by the variation of the effective Lagrangian (29):
Due to the Jacobi identity , the other pair of Maxwell equations does not change:
Then, the axion Maxwell Equations (30) and (31) can be written in terms of electromagnetic fields and :
One can see from the above equations that the local CP violation angle leads to significant alteration of Maxwell equations. The local angle will induce a four-dimension current density
It indicates that, in the case of a strong electromagnetic field, the local P and CP violation can have observable effects.
In the extremely strong magnetic field, all charged particles stay at the lowest Landau level. Let us assume that the magnetic is uniform and points in a certain direction. The spins of positively charged particles point in the direction of the magnetic field, while the spins of negatively charged particles point in the opposite direction. For massless fermions, the momentum and spin of the right-hand particle point in the same direction, and the momentum and spin of left-hand particle point in opposite directions. Therefore, for positively charged particles such as u quarks, right-hand u quarks will move in the direction of magnetic field, while left-hand u quarks move in the opposite direction. At the same time, for the negatively charged particles such as d quarks, left-hand d quarks will move in the direction of a magnetic field, while right-hand d quarks move in the opposite direction. Thus, the total net charge moving in the direction of magnetic field is
where f is the flavor index, and is the charge of quarks. Because of the chiral imbalance induced by the nontrivial gauge field configurations (see the Equation (10)), the total net charge is nonzero and can be represented as
where denotes the wind number of these nontrivial gauge field configurations. It indicates that, in the case of strong magnetic, the chiral imbalance can induce an electric current along the direction of magnetic field. This phenomenon is called a chiral magnetic effect [28,35,36,37]. In addition, at the boundary of the chiral imbalanced domain, a charge difference can be produced between the two boundaries perpendicular to the magnetic field. This is called charge separation effect [28,36,43]. This process is illustrated in Figure 1.
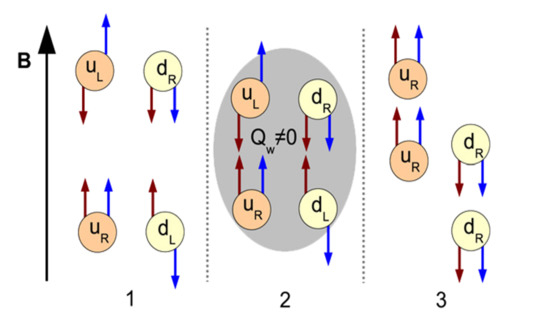
Figure 1.
The illustration of the charge separation effect and chiral magnetic effect. The blue arrows and the red arrows respectively denote the spin and the momentum of quarks. (1) At the beginning, the u and d quarks are all in the lowest Landau level and can only move along the direction of the magnetic field. (2) The quarks interact with a nontrivial gauge configuration with . Assuming , this gauge configuration can convert the chiralities of quarks from left-hand to right-hand. It will lead to the chiral imbalance between the left- and right-hand quarks. (3) In the presence of a strong magnetic, the u quarks (or d quark) with different chiralities move in different directions. Due to the chiral imbalance, the total net charge moving along the direction of the magnetic is . In addition, it will result in a charge difference between two domain walls perpendicular to the magnetic field. Reprinted from [28], with permission from Elsevier.
Let us revisit this process in terms of the axion Maxwell Equations (32). As mentioned above, the local chiral imbalanced domains can be regarded as the P-odd bubbles occupied by nontrivial gluon configurations. The angle inside these bubbles is nonzero, but zero outside. We assume that the external magnetic field is uniform and points in a certain direction, so , and there is no external electric field. If the angle is static, , from the second equation of Equation (32), we can immediately obtain that a non-vanishing charge appears on the -domain-walls (see Figure 2) [28,36,43]:
where ± correspond to the opposite two domain walls perpendicular to the magnetic field and S is their area. If the angle is mainly dependent on time, i.e., , from the first equation of Equations (32), we can see that there is an induced electric current (see Figure 3):
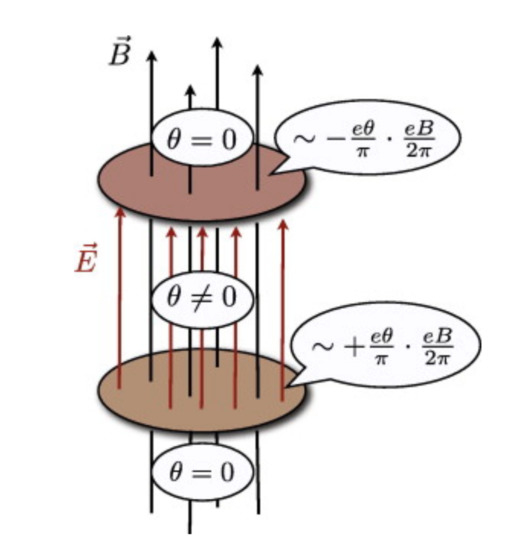
Figure 2.
Charge separation effect—the regions inside the domain walls with , outside with . The domain walls is charged in the case of a strong magnetic field, with the surface charge density ∼. Reprinted from [36], with permission from Elsevier.
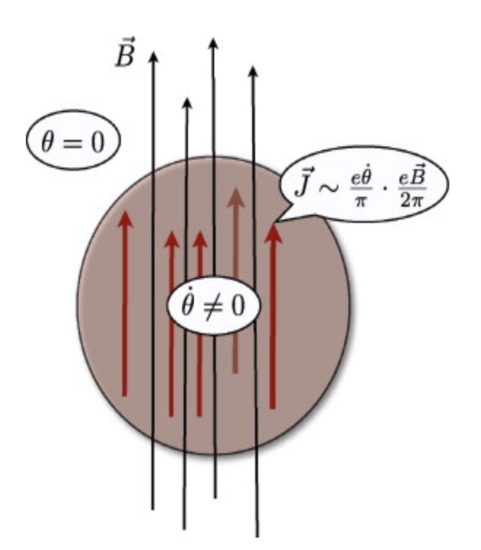
Figure 3.
Chiral magnetic effect—in the case of a strong magnetic field, in the region with , an electric current is induced. Reprinted from [36], with permission from Elsevier.
Considering the chiral chemical potential which is defined as (see Equation (24)), we can represent the induced current as
In Ref. [37], the same result is obtained by calculating the thermodynamic potential for chiral fermions in the case of finite chiral chemical potential and strong magnetic field.
2.2. The Effects of Chiral Chemical Potential on QCD Phase Structure
As the temperature increases, the strong interaction matter will undergo a deconfinement phase transition from hadronic matter to quark–gluon plasma [44,45]. Since the nontrivial gauge field configurations interact with the fermions and flip the helicities of fermions, the chiral charge may be generated during the phase transition. Some studies show that, in heavy-ion collisions, chiral charge density reaches equilibrium shortly after the collision and keep equilibrium for a comparatively long period of time [46,47,48]. Therefore, to better understand the phase transition in heavy-ion collisions, it is necessary to study the effects of chiral imbalance on the QCD phase structure. As mentioned above, we can introduce the chiral chemical potential to mimic the chiral imbalance between right- and left-hand quarks. In terms of Lagrangian, the following term should be added:
By solving the Dirac equation, we can get the energy spectrum of the free fermions
where denotes helicity eigenstates of fermions and . The energy spectrum shows that, after the introduction of chiral chemical potential , the the degeneracy of helicity is relieved. For massless particles and antiparticles, there are some corresponding relations between chirality and helicity eigenstates: right-hand particle—positive helicity, left-hand particle—negative helicity and right-hand antiparticle—negative helicity, left-hand antiparticle—positive helicity. Thus, the chiral chemical potential can make a difference in the numbers of modes with left- and right-hand chirality below the Fermi-surface, so there is a chiral imbalance. In addition, we can obtain the thermodynamic potential density
The chiral charge density can be expressed as
where is the Fermi–Dirac distribution represented as . In the massless limit, the chiral charge density can be simplified as [37]
The vacuum contribution to the chiral charge density at and is non-vanishing. In massless limit, the vacuum contribution is finite; however, for massive fermions, the vacuum contribution is divergent, [48].
In the following, we focus on discussing the effects of the chiral chemical potential on the phase diagram of the strong interaction. Since the introduction of chiral chemical potential does not increase the sign problem, we can study the phase transition of the chiral imbalanced QCD matter by the lattice simulation [49,50,51]. The results of lattice simulation show that the chiral chemical potential plays the role of a catalyst of spontaneous chiral symmetry breaking and enhance the chiral condensate of quarks [50,51,52]. This result also appears in the model analyses [52,53,54,55]. Moreover, the critical temperature of deconfinement phase transition increases with chiral chemical potential increasing [50,51]. In the case of finite chemical potential, the sign problem will occur in the lattice calculation. In order to study the phase diagram at finite chemical potential, we need to apply the effective model, and some of the results we obtained is model dependent. The Nambu–Jona–Lasinio (NJL) model analyses on the effects of chiral chemical potential are provided in Refs. [52,54,56,57]. The results of Refs. [54,56] show that the chiral chemical potential can reduce the chemical potential of deconfinement phase transition at low temperature and finite density. In Ref. [57], different regularization schemes of the NJL model are employed to study the phase transition at finite chiral chemical potential and temperature. At high temperature and low density, in different regularization schemes, the trend of critical temperature changes with chiral chemical potential is different [54,57].
Recently, we proposed a self-consistent mean-field approximation method for the NJL model [58,59,60,61,62]. This method introduces a free parameter to mimic the weight between the direct channels contributions and the exchange channels contributions when applying the mean-field approximation. In addition, the Lagrangian can be written in a more general form:
where denotes the Fierz transformation of the interaction terms. Because the Fierz transformation is a mathematically equivalent transformation, this redefined Lagrangian is equal to original Lagrangian where . The parameter cannot be determined by a priori and should be regarded as a free parameter. In the case of finite chemical potential, the vector channel in the Fierz transformed terms should be taken into consideration [58,63]. Thus, the axial-vector channel in the Fierz transformed terms cannot be ignored when we study the phase transition at finite chiral chemical potential [54]. Within the self-consistent mean field model, we found that the location of CEP in the QCD phase diagram strongly depends on the values of chiral chemical potential. For example, the baryon chemical potential of CEP decreases with increasing the chiral chemical potential [54]. When is larger than and , there has no critical endpoint (CEP) in the QCD phase diagram; however, with the chiral chemical potential increasing, the CEP will reappear [54,58]. Moreover, the temperature of the CEP shows a nonmonotonic dependence on the chiral chemical potential with a long plateau around the maximum [54].
Theoretically, fluctuations of conserved charges (such as charge, baryon number, and strangeness) are expected to be sensitive to the correlation length of the system, which will diverge near the CEP. During the last few decades, the measurements of higher-order cumulants of net-charge [64], net-proton [65,66,67], and net-kaon [68] multiplicity distributions have been carried out in heavy-ion collisions by the STAR experiment in the first phase of beam energy scan (BES-I, 2010–2017) program at Relativistic Heavy Ion Collider (RHIC). The fourth-order net-proton fluctuations exhibit non-monotonic behaviors as a function of , with a 3.1 significance [69]. To further confirm this non-monotonic behavior, RHIC started the second phase of beam energy scan program (BES-II), focusing on the collision energies below 27 GeV. From the year of 2018 to 2020, the STAR experiment has collected the high statistics data of Au+Au collision at = 9.2, 11.5, 14.6, 19.6 and 27 GeV under collider mode and = 3.0–7.7 GeV under a fixed target mode. It will allow us to map the QCD phase diagram with the baryon chemical potential up to ≈ 720 MeV. Current experimental strategies of CEP search are mainly focusing on varying the temperature and baryon chemical potential of the hot dense nuclear matter created in heavy-ion collisions. This theoretical model study could motivate experimentalists to think about the possibility and importance to vary the chiral chemical potential in the future heavy-ion collisions experiment by placing some special experimental selections.
In Refs. [53,70,71,72,73,74], the Polyakov-loop-modified Nambu–Jona–Lasinio models (PNJL) are employed to study the effects of the chiral chemical potential. At high temperature and low density, the results of the PNJL model show that the chiral chemical potential can reduce the critical temperature of phase transition [70,71]. This result is consistent with the calculations of NJL model [57] and linear sigma model coupled to Polyakov loop () [75]. Moreover, the phase diagram on –T plane have a (the critical endpoint on –T plane at ), and the CEP on –T plane can consecutively move to the on the –T plane [70,71]. This conclusion is consistent with the result of the quark–meson model (QM) [71] and [75], but disagrees with the calculation of the NJL model [54], Dyson–Schwinger equations (DSEs) [55,72,76] and lattice simulation [50,51]. In the NJL model and DSEs, the trajectory of CEPs cannot extend to the –T plane, and there is no on –T plane [54,55,72,76]. The contradiction between the PNJL model and lattice calculation about the existence of is resolved in Ref. [72]. If we apply a regularization scheme to suppress the contribution of high-momentum quark modes in the effective potential connected with the PNJL models, the chemical potential of CEP cannot decrease to zero, so there is no .
Within the framework of Dyson–Schwinger equations, the effects of chiral chemical potential on the phase diagram and CEP are studied in Refs. [55,72,76,77,78]. All the studies of DSEs show that there is no on the –T plane. This is consistent with the result of lattice QCD. As the chiral chemical potential increases, the chemical potential of CEP decreases at first, and then keeps constant at large [55,72]. In addition, the lowest chemical potential of CEP is in the range 40∼60 . The temperature of CEP always increases with chiral chemical potential increasing [55,72,76].
Finite-volume effects on the phase diagram should be taken into account when we study the small fireball produced in heavy ion collisions. The finite-volume effects on phase diagram with a chiral chemical potential are studied in Refs. [55,73,74]. It is shown in the PNJL model analyses that the chiral chemical potential can shift the location of CEP significantly but does not change the critical exponents [73]. Moreover, the smaller system size will result in smaller chiral charge density [74]. However, we obtain the opposite result in DSEs. The results of DESs indicate that, in the smaller system size, the chiral charge density becomes larger [55].
2.3. The Effects of Chiral Chemical Potential on Quark Stars
As shown in Ref. [74], at nonzero chiral chemical potential, the chiral charge density rapidly increases with chemical potential in the deconfinement phase. It indicates that the chiral imbalance is more significant in the dense QCD matter. Therefore, neutron stars are a natural object to study the effects of chiral chemical potential because their density and magnetic fields are much higher than those produced in the laboratory. As mentioned above, we can introduce the chiral chemical potential to the equation of state (EOS) to see whether the chiral chemical potential has effects on quark stars.
We applied the self-consistent mean field approximation method of NJL model to study the effects of chiral chemical potential on the phase diagram in Ref. [54]. The Lagrangian of this model is represented as Equation (44). In this subsection, we will discuss this method in more detail and use it to explore the effects of chiral chemical potential on quark stars.
As proposed by Witten [79], strange quark matter might be the ground state of strong interaction matter. However, recent studies demonstrated that up-down quark matter could be more stable than the strange quark matter and the ordinary nuclear matter [62,80]. Accordingly, it has been proposed that the compact stars involved in the binary merger events GW170817 and GW190814 may be the up-down quark stars (nonstrange quark stars) [59,81,82,83,84]. Since theoretical predictions and astronomical observations cannot rule out the existence of non-strange quark stars, we will discuss the influence of chiral chemical potential on quark stars in the two flavor case.
In the case of finite chiral chemical potential and finite chemical potential, the effective Lagrangian of Equation (44) is expressed as
where denotes the Fierz transformation of the interaction terms and can be represented as
If we set , the redefined Lagrangian is reduced to the original Lagrangian
Considering the Fierz transformation is a mathematical identity transformation, the redefined Lagrangian Equation (45) is equal to the original Lagrangian Equation (47). As mentioned above, when we perform the mean field approximation for the effective Lagrangian, the scalar, vector, and axial-vector interaction channels in the Fierz transformed terms should be taken into account. By the mean field approximation and the self-consistent thermodynamic relations, we can obtain the gap equations:
and
where , , are respectively the constituent quark mass, the effective chemical potential, the effective chiral chemical potential, is the Fermi–Dirac distribution function, with denoting the helicity eigenstates of quarks, G and are respectively coupling constant and cut-off parameters which are fixed by fitting the experimental results [63]. We can see that, although the redefined Lagrangian Equation (45) is equal to the original Lagrangian Equation (47) of the NJL model, the introduction of leads to essential modifications of the gap equations. If we set , the gap equations Equations (48) are reduced to the conventional gap equation which contains only the constituent quark mass equation. It indicates that the conventional gap equation obtained from the original Lagrangian where is zero only takes the direct contributions into consideration when performing the mean field approximation. However, at the level of mean field approximation, the exchange contributions from the Fierz transformed term are as important as the direct contributions, and there is no physical reason to ignore the contribution from the exchange channels when we apply the mean field approximation. Therefore, the parameter is necessary to be introduced to mimic the proportion between the direct and exchange contributions. Since the parameter cannot be determined theoretically, and we lack the experimental data at finite density to fix it, is treated as a free parameter.
Because of the electromagnetic repulsion and the electro-weak reaction , the charge neutrality, i.e.,
and the chemical equilibrium relation
should be imposed on the gap equations Equations (48) and (49) when studying the quark star. Solve Equations (48)–(51) at zero temperature simultaneously, then we can obtain the solutions which satisfy the charge neutrality condition and the chemical equilibrium relation. At zero temperature, the pressure and energy density can be expressed as
where B is the bag constant of MIT bag model [59,81,85]. Plugging the solutions we obtained into Equation (52), we can get the EOSs of quark stars. Then, the mass–radius relation of quark star can be obtained by solving the Tolman–Oppenheimer–Volkoff equations with these EOSs,
where G is the gravitational constant and is the total mass within radius r.
Our previous works have investigated the effects of on the EOS and the properties of quark stars [59,81,85]. The larger leads to stiffer EOS and larger maximum mass of quark star. When is larger than 0.9, the results of our self consistent NJL model meet the astronomical observations very well.
According to Ref. [59], when and MeV, the maximum mass of two flavor quark star can reach 2 , and the mass–radius relation is consistent with the observation of neutron star merger GW170817. We plot the mass–radius relation of quark star with different chiral chemical potential at and MeV in Figure 4. Since the global CP violation is very weak in the real world, it is reasonable for us to keep chiral chemical potential below 50 MeV in quark stars. As shown in Figure 4, the chiral chemical potential can significantly reduce the maximum mass of quark stars. The observations of gravitational wave (GW) give the constraint not only on the mass–radius relation but also on the tidal deformability [86]. See Ref. [87] for the calculation method of tidal deformability. The tidal deformabilities of 1.4–solar–mass quark stars at different chiral chemical potential are shown in Table 1. We can see from Table 1 that not only the maximum mass but also the tidal deformability of quark star decrease with chiral chemical potential.
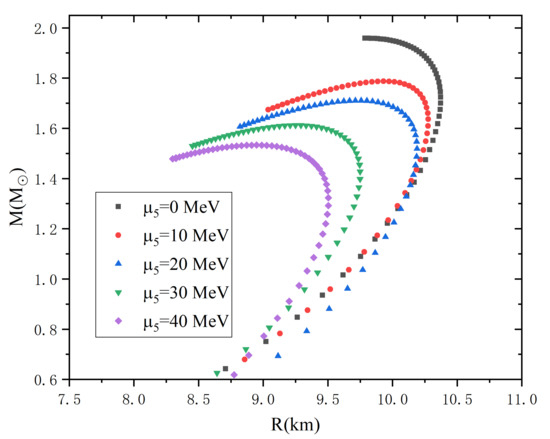
Figure 4.
The mass–radius relation of quark star with different chiral chemical potential at and = 90 MeV.

Table 1.
The maximum mass of quark star with different are shown. In addition, the tidal deformabilities of the 1.4-solar-mass stars are also listed.
The results in Figure 4 and Table 1 indicate that the quark star with smaller mass can have larger chiral chemical potential. For a quark star with mass around , the chiral chemical potential is zero. In contrast, for a quark star with mass around , the chiral chemical potential can be as high as 40 MeV. The chiral imbalance is more obvious in the quark star with smaller mass which means that the effects of CP violation are more easily observed in smaller mass stars. Moreover, among the quark stars with the same mass, those with chiral chemical potential have smaller tidal deformabilities than those without. If we observe a quark star that not only has a small mass but also small tidal deformability, it may indicate that the quark star has large chiral chemical potential. Therefore, it is possible to search for the evidence of CP violation from the astronomical observation of quark stars.
3. Conclusions
In this paper, we have made a brief review for the origin of chiral chemical potential and its physical effects. The problem has been resolved by the realization of the more complex structure of QCD vacuum. Since the nontrivial gauge field configurations can travel between different vacuums, the is not a true symmetry of QCD. Considering the instantons tunneling, the real vacuum should be the –vacuum. In addition, a term that breaks the P and T symmetry should be introduced into the Lagrangian. However, the experimental estimate of the angle is very small, which raises another problem: the strong CP problem. Despite years of efforts, the strong CP problem remains a mystery. Fortunately, the topological fluctuations in the heavy-ion collisions open another door for us to study the strong CP violation. In hot QCD, the sphalerons can leap over the potential barrier and enormously increase the transition rate between different vacuums. This will cause a significant fluctuation of the topological charge of vacuum. Because of the chiral anomaly, this process results in local chiral imbalance. In order to mimic the local CP violation and chiral imbalance, we assume that the angle depends on space-time. In addition, it is equivalent to add the chiral chemical potential term to the Lagrangian if . In the case of a strong magnetic field, the chiral imbalance can induce an electromagnetic current along the magnetic. In addition, a charge separation is generated between the two domain-walls perpendicular to the magnetic field. The influence of chiral chemical potential on the phase diagram includes many aspects. We display the results of lattice simulation and model analyses. The results of the NJL model, self consistent NJL model, PNJL model, and DSEs are discussed in detail in this paper. Some results are model independent. For example, the chiral chemical potential can increase the chiral condensate of quarks, and there is no on the –T plane. Other results may be model dependent, such as the trajectory of CEP. Finally, we discussed the application of the self-consistent mean field approximation method of the NJL model to study the effects of chiral chemical potential on the properties of quark stars. It was found that the chiral chemical potential can reduce not only the maximum mass but also the tidal deformability of quark stars, which indicates that the signal of strong CP violation could be more easily observed in smaller mass stars. For these reasons, the quark stars may be a natural laboratory for testing the destruction of strong interaction CP.
Author Contributions
Conceptualization, L.-K.Y. and H.-S.Z.; formal analysis, L.-K.Y.; writing—original draft preparation, L.-K.Y., X.-F.L., J.S. and H.-S.Z.; writing—review and editing, L.-K.Y., X.-F.L., J.S. and H.-S.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported in part by the National Natural Science Foundation of China (under Grants No. 12075117, No. 11475085, No. 11535005, and No. 11690030) and by the Nation Major State Basic Research and Development of China (2016YFE0129300). X.-F.L. is supported by the National Key Research and Development Program of China (2018YFE0205201) and the National Natural Science Foundation of China (Grants No. 11828501, No. 11575069, No. 11890711, and No. 11861131009). Jorge Segovia is supported by Ministerio Español de Ciencia e Innovación, Grant No. PID2019-107844GB-C22; and Junta de Andalucía, contract Nos. P18-FRJ-1132 and Operativo FEDER Andalucía 2014-2020 UHU-1264517.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hooft, G.T. Symmetry Breaking through Bell-Jackiw Anomalies. Phys. Rev. Lett. Phys. 1976, 37, 8–11. [Google Scholar] [CrossRef]
- Hooft, G.T. Computation of the quantum effects due to a four-dimensional pseudoparticle. Phys. Rev. D 1976, 14, 3432–3450. [Google Scholar] [CrossRef]
- Adler, S.L. Axial-Vector Vertex in Spinor Electrodynamics. Phys. Rev. 1969, 177, 2426–2438. [Google Scholar] [CrossRef]
- Bell, J.S.; Jackiw, R. A PCAC puzzle: π0γγ in the σ-model. Nuovo Cimento A Ser. 1969, 60, 47–61. [Google Scholar] [CrossRef]
- Fujikawa, K. Path-Integral Measure for Gauge-Invariant Fermion Theories. Phys. Rev. Lett. 1979, 42, 1195–1198. [Google Scholar] [CrossRef]
- Crewther, R.J. Effects of Topological Charge in Gauge Theories. Act. Phys. Austriaca Suppl. 1978, 19, 47–153. [Google Scholar]
- Bogomolny, E.B. Stability of Classical Solutions. Sov. J. Nucl. Phys. 1976, 24, 449. [Google Scholar]
- Callan, C.G.; Dashen, R.F.; Gross, D.J. The structure of the gauge theory vacuum. Phys. Lett. B 1976, 63, 334–340. [Google Scholar] [CrossRef]
- Jackiw, R.; Rebbi, C. Vacuum Periodicity in a Yang-Mills Quantum Theory. Phys. Rev. Lett. 1976, 37, 172–175. [Google Scholar] [CrossRef]
- Weinberg, S. The Quantum Theory of Fields; Volume 2: Modern Applications; Cambridge University Press: Cambridge, UK, 2013; pp. 455–461. [Google Scholar]
- Baker, C.A.; Doyle, D.D.; Geltenbort, P.; Green, K.; Van der Grinten, M.G.D.; Harris, P.G.; Iaydjiev, P.; Ivanov, S.N.; May, D.J.R.; Pendlebury, J.M.; et al. Improved Experimental Limit on the Electric Dipole Moment of the Neutron. Phys. Rev. Lett. 2006, 97, 131801. [Google Scholar] [CrossRef]
- Baluni, V. CP-nonconserving effects in quantum chromodynamics. Phys. Rev. D 1979, 19, 2227–2230. [Google Scholar] [CrossRef]
- Crewther, R.; Vecchia, P.D.; Veneziano, G.; Witten, E. Chiral estimate of the electric dipole moment of the neutron in quantum chromodynamics. Phys. Lett. B 1979, 88, 123–127. [Google Scholar] [CrossRef]
- Peccei, R.D.; Quinn, H.R. CP Conservation in the Presence of Pseudoparticles. Phys. Rev. Lett. 1977, 38, 1440–1443. [Google Scholar] [CrossRef]
- Peccei, R.D.; Quinn, H.R. Constraints imposed by CP conservation in the presence of pseudoparticles. Phys. Rev. D 1977, 16, 1791–1797. [Google Scholar] [CrossRef]
- Barr, S.M. Solving the Strong CP Problem without the Peccei–Quinn Symmetry. Phys. Rev. Lett. 1984, 53, 329–332. [Google Scholar] [CrossRef]
- Nelson, A. Naturally weak CP violation. Phys. Lett. B 1984, 136, 387–391. [Google Scholar] [CrossRef]
- Kim, J.E.; Carosi, G. Axions and the Strong CP Problem. Rev. Mod. Phys. 2010, 82, 557–602. [Google Scholar] [CrossRef]
- Wilczek, F. Problem of Strong P and T Invariance in the Presence of Instantons. Phys. Rev. Lett. 1978, 40, 279–282. [Google Scholar] [CrossRef]
- Weinberg, S. A New Light Boson? Phys. Rev. Lett. 1978, 40, 223–226. [Google Scholar] [CrossRef]
- Peccei, R.D. The Strong CP Problem and Axions. In Axions: Theory, Cosmology, and Experimental Searches; Kuster, M., Raffelt, G., Beltrán, B., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 3–17. [Google Scholar]
- Cheng, H.Y. The strong CP problem revisited. Phys. Rep. 1988, 158, 1–89. [Google Scholar] [CrossRef]
- Schwartz, M.D. Quantum Field Theory and the Standard Model; Cambridge University Press: Cambridge, UK, 2014; pp. 609–613. [Google Scholar]
- Bernard, C. Gauge zero modes, instanton determinants, and quantum-chromodynamic calculations. Phys. Rev. D 1979, 19, 3013–3019. [Google Scholar] [CrossRef]
- Pisarski, R.D.; Yaffe, L.G. The density of instantons at finite temperature. Phys. Lett. B 1980, 97, 110–112. [Google Scholar] [CrossRef]
- McLerran, L.; Mottola, E.; Shaposhnikov, M.E. Sphalerons and axion dynamics in high-temperature QCD. Phys. Rev. D 1991, 43, 2027–2035. [Google Scholar] [CrossRef] [PubMed]
- Moore, G.D.; Tassler, M. The sphaleron rate in SU(N) gauge theory. J. High Energy Phys. 2011, 2, 105. [Google Scholar] [CrossRef]
- Kharzeev, D.E.; McLerran, L.D.; Warringa, H.J. The Effects of topological charge change in heavy ion collisions: ‘Event by event P and CP violation’. Nucl. Phys. A 2008, 803, 227–253. [Google Scholar] [CrossRef]
- Kharzeev, D.; Pisarski, R.D.; Tytgat, M.H. Possibility of Spontaneous Parity Violation in Hot QCD. Phys. Rev. Lett. 1998, 81, 512–515. [Google Scholar] [CrossRef]
- Kharzeev, D. Parity violation in hot QCD: Why it can happen, and how to look for it. Phys. Lett. B 2006, 633, 260–264. [Google Scholar] [CrossRef]
- Kharzeev, D.; Krasnitz, A.; Venugopalan, R. Anomalous chirality fluctuations in the initial stage of heavy ion collisions and parity odd bubbles. Phys. Lett. B 2002, 545, 298–306. [Google Scholar] [CrossRef]
- Kharzeev, D.E.; Pisarski, R.D.; Tytgat, M.H. Aspects of parity, CP, and time reversal violation in hot QCD. arXiv 2001, arXiv:2000.12012. [Google Scholar]
- Buckley, K.; Fugleberg, T.; Zhitnitsky, A. Can Induced Θ Vacua be Created in Heavy-Ion Collisions? Phys. Rev. Lett. 2000, 84, 4814–4817. [Google Scholar] [CrossRef]
- Buckley, K.; Fugleberg, T.; Zhitnitsky, A. Induced θ-vacuum states in heavy ion collisions: A possible signature. Phys. Rev. C 2001, 63, 034602. [Google Scholar] [CrossRef]
- Kharzeev, D.E. Chern–Simons current and local parity violation in hot QCD matter. Nucl. Phys. A 2009, 830, 543c–546c. [Google Scholar] [CrossRef]
- Kharzeev, D.E. Topologically induced local P and CP violation in QCD × QED. Ann. Phys. 2010, 325, 205–218. [Google Scholar] [CrossRef]
- Fukushima, K.; Kharzeev, D.E.; Warringa, H.J. Chiral magnetic effect. Phys. Rev. D 2008, 78, 074033. [Google Scholar] [CrossRef]
- Jacobs, P. Measurements of high density matter at RHIC. eConf 2002, C020805, TTH05. [Google Scholar]
- Arsene, I.; Bearden, I.G.; Beavis, D.; Besliu, C.; Budick, B.; Bøggild, H.; Chasman, C.; Christensen, C.H.; Christiansen, P.; Cibor, J.; et al. Quark gluon plasma and color glass condensate at RHIC? The Perspective from the BRAHMS experiment. Nucl. Phys. A 2005, 757, 1–27. [Google Scholar] [CrossRef]
- Adams, J.; Aggarwal, M.M.; Ahammed, Z.; Amonett, J.; Anderson, B.D.; Arkhipkin, D.; Averichev, G.S.; Badyal, S.K.; Bai, Y.; Balewski, J.; et al. Experimental and theoretical challenges in the search for the quark gluon plasma: The STAR Collaboration’s critical assessment of the evidence from RHIC collisions. Nucl. Phys. A 2005, 757, 102–183. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, F. Experimental searches for the chiral magnetic effect in heavy-ion collisions. Prog. Part. Nucl. Phys. 2019, 107, 200–236. [Google Scholar] [CrossRef]
- Wilczek, F. Two applications of axion electrodynamics. Phys. Rev. Lett. 1987, 58, 1799–1802. [Google Scholar] [CrossRef]
- Kharzeev, D.; Zhitnitsky, A. Charge separation induced by P-odd bubbles in QCD matter. Nucl. Phys. A 2007, 797, 67–79. [Google Scholar] [CrossRef]
- Collins, J.C.; Perry, M.J. Superdense Matter: Neutrons or Asymptotically Free Quarks? Phys. Rev. Lett. 1975, 34, 1353–1356. [Google Scholar] [CrossRef]
- Meyer-Ortmanns, H. Phase transitions in quantum chromodynamics. Rev. Mod. Phys. 1996, 68, 473–598. [Google Scholar] [CrossRef]
- Ruggieri, M.; Peng, G.X.; Chernodub, M. Chiral relaxation time at the crossover of quantum chromodynamics. Phys. Rev. D 2016, 94, 054011. [Google Scholar] [CrossRef]
- Ruggieri, M.; Peng, G.X. Quark matter in a parallel electric and magnetic field background: Chiral phase transition and equilibration of chiral density. Phys. Rev. D 2016, 93, 094021. [Google Scholar] [CrossRef]
- Ruggieri, M.; Chernodub, M.N.; Lu, Z.-Y. Topological susceptibility, divergent chiral density, and phase diagram of chirally imbalanced QCD medium at finite temperature. Phys. Rev. D 2020, 102, 014031. [Google Scholar] [CrossRef]
- Yamamoto, A. Chiral Magnetic Effect in Lattice QCD with a Chiral Chemical. Phys. Rev. Lett. 2011, 107, 031601. [Google Scholar] [CrossRef] [PubMed]
- Braguta, V.V.; Goy, V.A.; Ilgenfritz, E.M.; Kotov, A.Y.; Molochkov, A.V.; Müller-Preussker, M.; Petersson, B. Two-Color QCD with Chiral Chemical Potential. J. High Energy Phys. 2015, 2015, 94. [Google Scholar] [CrossRef]
- Braguta, V.V.; Ilgenfritz, E.-M.; Kotov, A.Y.; Petersson, B.; Skinderev, S.A. Study of the QCD phase diagram with a nonzero chiral chemical potential. Phys. Rev. D 2016, 93, 034509. [Google Scholar] [CrossRef]
- Braguta, V.V.; Kotov, A.Y. Catalysis of dynamical chiral symmetry breaking by chiral chemical potential. Phys. Rev. D 2016, 93, 105025. [Google Scholar] [CrossRef]
- Fukushima, K.; Ruggieri, M.; Gatto, R. Chiral magnetic effect in the Polyakov–Nambu–Jona–Lasinio model. Phys. Rev. D 2010, 81, 114031. [Google Scholar] [CrossRef]
- Yang, L.K.; Luo, X.; Zong, H.S. QCD phase diagram in chiral imbalance with self-consistent mean field approximation. Phys. Rev. D 2019, 100, 094012. [Google Scholar] [CrossRef]
- Shi, C.; He, X.-T.; Jia, W.-B.; Wang, Q.-W.; Xu, S.-S.; Zong, H.-S. Chiral transition and the chiral charge density of the hot and dense QCD matter. J. High Energy Phys. 2020, 2020, 122. [Google Scholar] [CrossRef]
- Shi, C.; He, X.-T.; Jia, W.-B.; Wang, Q.-W.; Xu, S.-S.; Zong, H.-S. QCD phase diagram with a chiral chemical potential. Phys. Rev. D 2016, 93, 074037. [Google Scholar]
- Yu, L.; Liu, H.; Huang, M. Effect of the chiral chemical potential on the chiral phase transition in the NJL model with different regularization schemes. Phys. Rev. D 2016, 94, 014026. [Google Scholar] [CrossRef]
- Wang, F.; Cao, Y.; Zong, H. Novel self-consistent mean field approximation and its application in strong interaction phase transitions. Chin. Phys. C 2019, 43, 084102. [Google Scholar] [CrossRef]
- Zhao, T.; Zheng, W.; Wang, F.; Li, C.M.; Yan, Y.; Huang, Y.F.; Zong, H.S. Do current astronomical observations exclude the existence of nonstrange quark stars? Phys. Rev. D 2019, 100, 043018. [Google Scholar] [CrossRef]
- Su, L.-Q.; Shi, C.; Xia, Y.-H.; Zong, H. Color superconductivity in a self-consistent NJL-type model. Phys. Rev. D 2020, 102, 054028. [Google Scholar] [CrossRef]
- Wu, Z.-Q.; Shi, C.; Ping, J.-L.; Zong, H.-S. Contributions of the vector-channel at finite isospin chemical potential with the self-consistent mean field approximation. Phys. Rev. D 2020, 101, 074008. [Google Scholar] [CrossRef]
- Wang, Q.; Zhao, T.; Zong, H. On the stability of two-flavor and three-flavor quark matter in quark stars within the framework of NJL model. Mod. Phys. Lett. A 2020, 2020, 2050321. [Google Scholar] [CrossRef]
- Klevansky, S.P. The Nambu—Jona–Lasinio model of quantum chromodynamics. Rev. Mod. Phys. 1992, 64, 649–708. [Google Scholar] [CrossRef]
- Adamczyk, L.; Adkins, J.K.; Agakishiev, G.; Aggarwal, M.M.; Ahammed, Z.; Alekseev, I.; Alford, J.; Anson, C.D.; Aparin, A.; Arkhipkin, D.; et al. Beam energy dependence of moments of the net-charge multiplicity distributions in Au+Au collisions at RHIC. Phys. Rev. Lett. 2014, 113, 092301. [Google Scholar] [CrossRef] [PubMed]
- Aggarwal, M.M.; Ahammed, Z.; Alakhverdyants, A.V.; Alekseev, I.; Alford, J.; Anderson, B.D.; Arkhipkin, D.; Averichev, G.S.; Balewski, J.; Barnby, L.S.; et al. Higher Moments of Net-proton Multiplicity Distributions at RHIC. Phys. Rev. Lett. 2010, 105, 022302. [Google Scholar] [CrossRef] [PubMed]
- Adamczyk, L.; Adkins, J.K.; Agakishiev, G.; Aggarwal, M.M.; Ahammed, Z.; Alekseev, I.; Alford, J.; Anson, C.D.; Aparin, A.; Arkhipkin, D.; et al. Energy Dependence of Moments of Net-proton Multiplicity Distributions at RHIC. Phys. Rev. Lett. 2014, 112, 032302. [Google Scholar] [CrossRef] [PubMed]
- Luo, X. Exploring the QCD Phase Structure with Beam Energy Scan in Heavy-ion Collisions. Nucl. Phys. A 2016, 956, 75–82. [Google Scholar] [CrossRef]
- Adamczyk, L.; Adams, J.R.; Adkins, J.K.; Agakishiev, G.; Aggarwal, M.M.; Ahammed, Z.; Ajitan, N.N.; Alekseev, I.; Anderson, D.M.; Aoyama, R.; et al. Collision Energy Dependence of Moments of Net-Kaon Multiplicity Distributions at RHIC. Phys. Lett. B 2018, 785, 551–560. [Google Scholar] [CrossRef]
- Adam, J.; Adamczyk, L.; Adams, J.R.; Adkins, J.K.; Agakishiev, G.; Aggarwal, M.M.; Ahammed, Z.; Alekseev, I.; Anderson, D.M.; Aparin, A.; et al. Net-proton number fluctuations and the Quantum Chromodynamics critical point. arXiv 2020, arXiv:2001.02852. [Google Scholar]
- Gatto, R.; Ruggieri, M. Hot quark matter with an axial chemical potential. Phys. Rev. D 2012, 85, 054013. [Google Scholar] [CrossRef]
- Ruggieri, M. Critical end point of quantum chromodynamics detected by chirally imbalanced quark matter. Phys. Rev. D 2011, 84, 014011. [Google Scholar] [CrossRef]
- Cui, Z.-F.; Cloët, I.C.; Lu, Y.; Roberts, C.D.; Schmidt, S.M.; Xu, S.-S.; Zong, H.-S. Critical end point in the presence of a chiral chemical potential. Phys. Rev. D 2016, 94, 071503. [Google Scholar] [CrossRef]
- Pan, Z.; Cui, Z.-F.; Chang, C.-H.; Zong, H.-S. Finite-volume effects on phase transition in the Polyakov-loop extended Nambu–Jona–Lasinio model with a chiral chemical potential. Int. J. Mod. Phys. A 2017, 32, 1750067. [Google Scholar] [CrossRef]
- Liu, R.-L.; Lai, M.-Y.; Shi, C.; Zong, H.-S. Finite volume effects on QCD susceptibilities with a chiral chemical potential. Phys. Rev. D 2020, 102, 014014. [Google Scholar] [CrossRef]
- Chernodub, M.N.; Nedelin, A.S. Phase diagram of chirally imbalanced QCD matter. Phys. Rev. D 2011, 83, 105008. [Google Scholar] [CrossRef]
- Xu, S.-S.; Cui, Z.-F.; Wang, B.; Shi, Y.-M.; Yang, Y.-C.; Zong, H.-S. Chiral phase transition with a chiral chemical potential in the framework of Dyson-Schwinger equations. Phys. Rev. D 2015, 91, 056003. [Google Scholar] [CrossRef]
- Wang, B.; Wang, Y.-L.; Cui, Z.-F.; Zong, H.-S. Effect of the chiral chemical potential on the position of the critical endpoint. Phys. Rev. D 2015, 91, 034017. [Google Scholar] [CrossRef]
- Tian, Y.-L.; Cui, Z.-F.; Wang, B.; Shi, Y.-M.; Yang, Y.-C.; Zong, H.-S. Dyson–Schwinger Equations of Chiral Chemical Potential. Chin. Phys. Lett 2015, 32, 081101. [Google Scholar] [CrossRef]
- Witten, E. Cosmic separation of phases. Phys. Rev. D 1984, 30, 272–285. [Google Scholar] [CrossRef]
- Holdom, B.; Ren, J.; Zhang, C. Quark Matter May Not Be Strange. Phys. Rev. Lett. 2018, 120, 222001. [Google Scholar] [CrossRef]
- Wang, Q.; Shi, C.; Zong, H.-S. Nonstrange quark stars from an NJL model with proper-time regularization. Phys. Rev. D 2019, 100, 123003. [Google Scholar] [CrossRef]
- Zhang, C. Probing up-down quark matter via gravitational waves. Phys. Rev. D 2020, 101, 043003. [Google Scholar] [CrossRef]
- Zhang, C.; Mann, R.B. Unified Interacting Quark Matter and its Astrophysical Implications. arXiv 2020, arXiv:2009.07182. [Google Scholar]
- Cao, Z.; Chen, L.W.; Chu, P.C.; Zhou, Y. GW190814: Circumstantial Evidence for Up-Down Quark Star. arXiv 2020, arXiv:2009.00942. [Google Scholar]
- Li, C.-M.; Zuo, S.-Y.; Yan, Y.; Zhao, Y.-P.; Wang, F.; Huang, Y.-F.; Zong, H.-S. Strange quark stars within proper time regularized (2 + 1)-flavor NJL model. Phys. Rev. D 2020, 101, 063023. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef] [PubMed]
- Hinderer, T.; Lackey, B.D.; Lang, R.N.; Read, J.S. Tidal deformability of neutron stars with realistic equations of state and their gravitational wave signatures in binary inspiral. Phys. Rev. D 2010, 81, 123016. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).