A Superellipse with Deformation and Its Application in Describing the Cross-Sectional Shapes of a Square Bamboo
Abstract
:1. Introduction
2. Materials and Methods
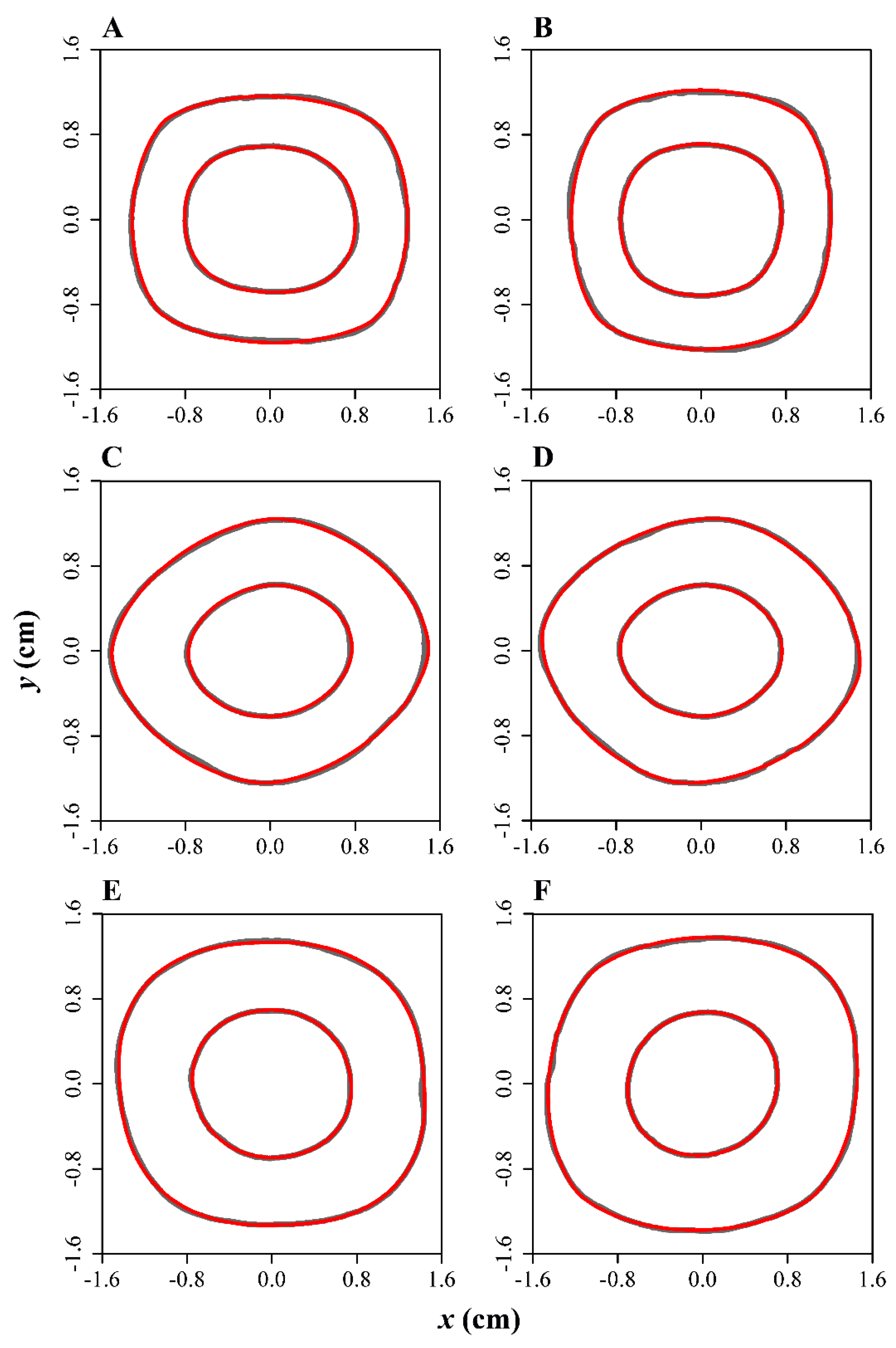
2.1. Cross-Section Sampling and Preparation
2.2. Image Processing and Boundary Data Acquisition
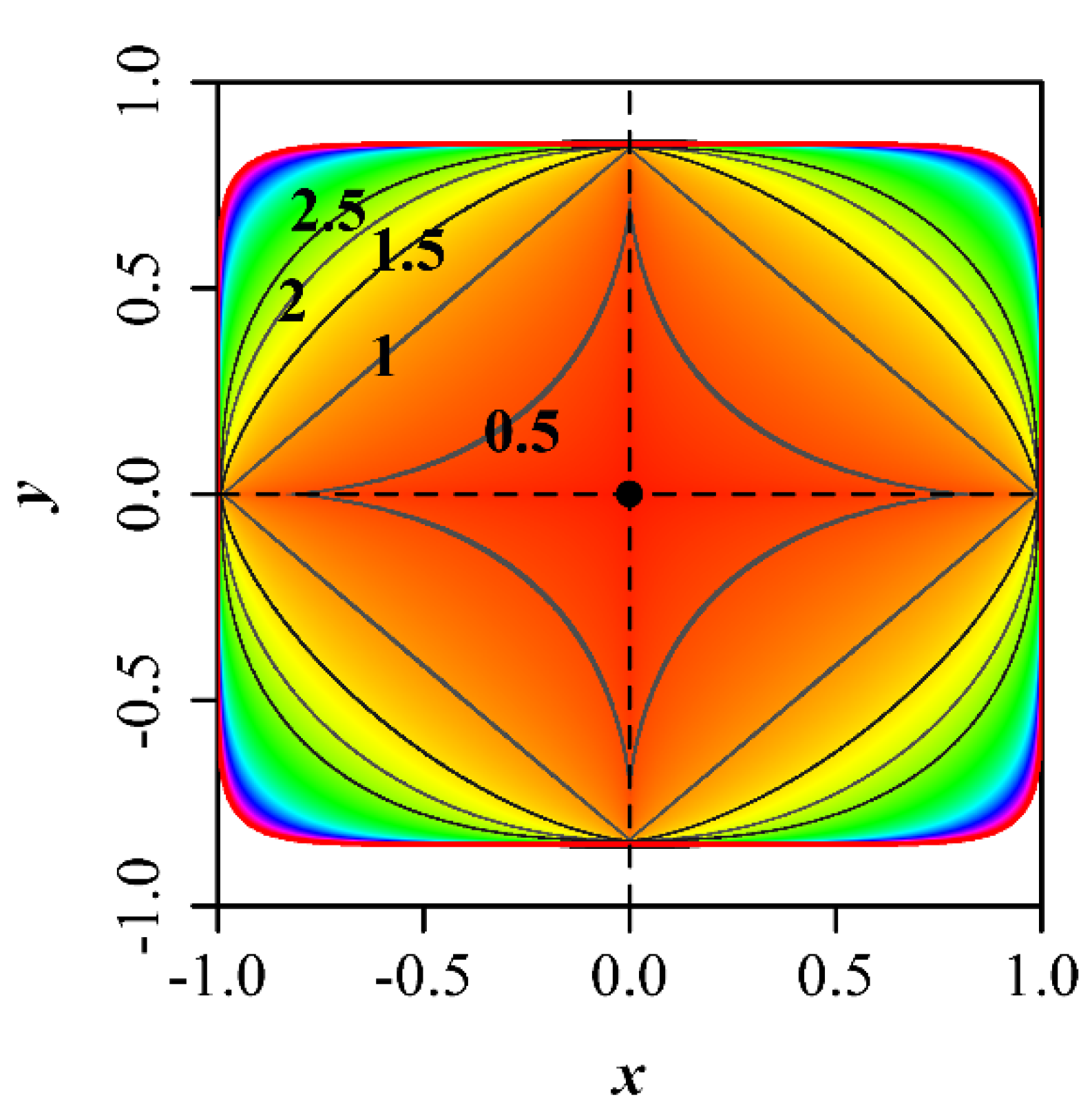
2.3. Fitting the Superellipse Equation and the Introduction of a Deformation Parameter
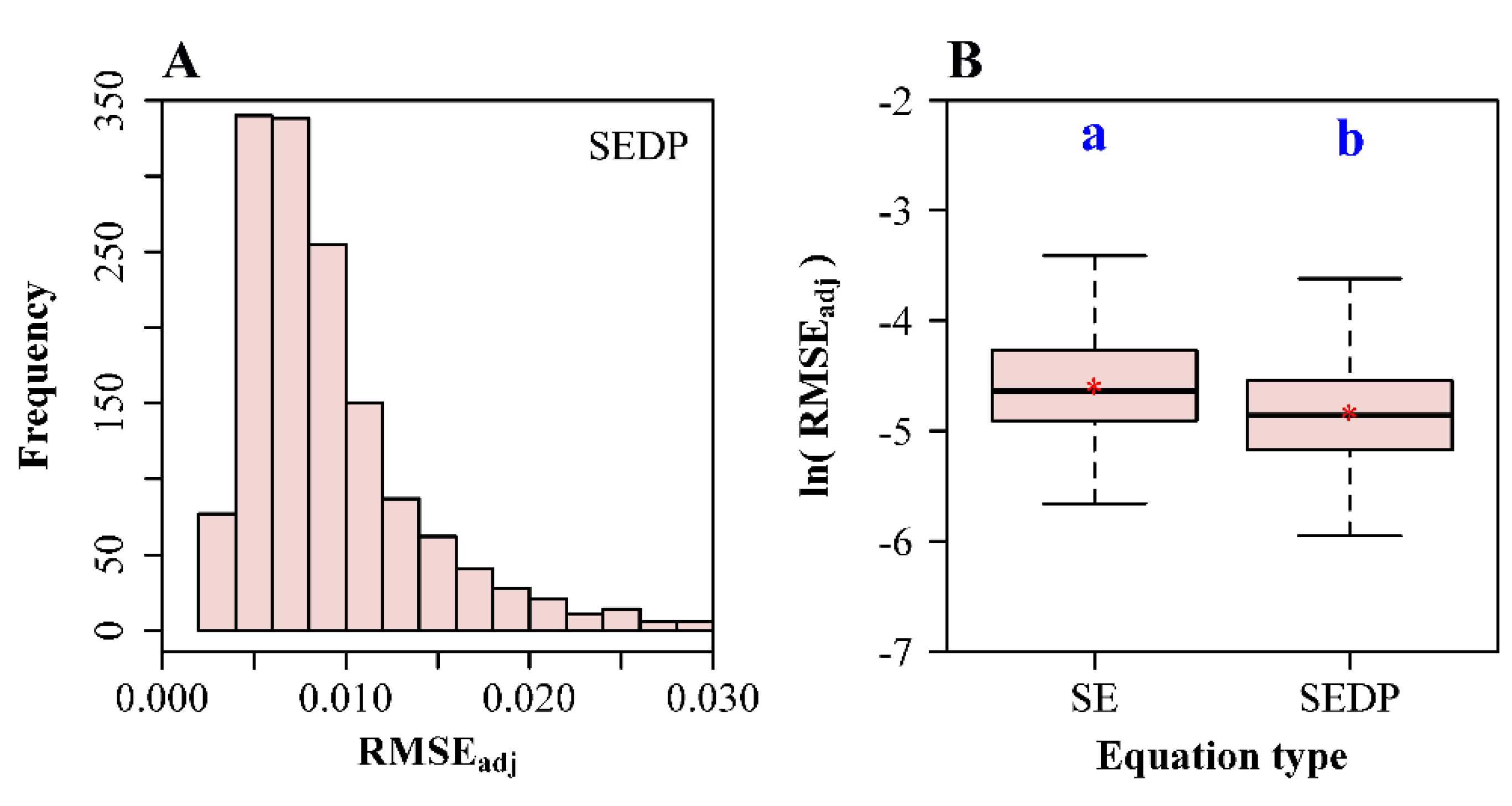
2.4. Analysis of the Fitted Results
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Proof of the Superellipse Equation with the Deformation Parameter w
References
- Lamé, G. Examen des différentes méthodes employées pour résoudre les problèmes de géométrie; V. Courcier: Paris, France, 1818. [Google Scholar]
- Gielis, J. Inventing the Circle: The Geometry of Nature; Geniaal Press: Antwerpen, Belgium, 2003. [Google Scholar]
- Gielis, J. The Geometrical Beauty of Plants; Atlantis Press: Paris, France, 2017. [Google Scholar]
- Shi, P.; Huang, J.; Hui, C.; Grissino-Mayer, H.D.; Tardif, J.; Zhai, L.; Wang, F.; Li, B. Capturing spiral radial growth of conifers using the superellipse to model tree-ring geometric shape. Front. Plant Sci. 2015, 6, 856. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gielis, J. Supervormen in bamboo. Newsletter of the Belgian Bamboo Society 1997, 14, 20–26. [Google Scholar]
- Liese, W.; Köhl, M. Bamboo: The Plant and its Uses; Springer: Heidelberg, Germany, 2015. [Google Scholar]
- Wen, T. The taxonomy and cultivation of Chimonobambusa Makino. J. Amer. Bamboo Soc. 1994, 11, 1–80. [Google Scholar]
- Chen, S.; Li, D.; Zhu, G.; Wu, L.; Lu, S.; Liu, L.; Wang, Z.; Sun, B.; Zhu, Z.; Xia, N.; et al. The Flora of China (Volume 22—Poaceae); Science Press: Beijing, China; Missouri Botanical Garden Press: St Louis, MO, USA, 2006. [Google Scholar]
- Shi, P.; Ratkowsky, D.A.; Li, Y.; Zhang, L.; Lin, S.; Gielis, J. General leaf-area geometric formula exists for plants—Evidence from the simplified Gielis equation. Forests 2018, 9, 714. [Google Scholar] [CrossRef] [Green Version]
- Nelder, J.A.; Mead, R. A simplex method for function minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2019; Available online: https://www.R-project.org/ (accessed on 1 January 2020).
- Wei, H.; Li, X.; Huang, H. Leaf shape simulation of castor bean and its application in nondestructive leaf area estimation. Int. J. Agric. Biol. Eng. 2019, 12, 135–140. [Google Scholar]
- Shi, P.; Ratkowsky, D.A.; Gielis, J. The generalized Gielis geometric equation and its application. Symmetry 2020, 12, 645. [Google Scholar] [CrossRef] [Green Version]
- Ratkowsky, D.A. Handbook of Nonlinear Regression Models; Marcel Dekker: New York, NY, USA, 1990. [Google Scholar]
- Hsu, J.C. Multiple Comparisons: Theory and Methods; Chapman and Hall/CRC: New York, NY, USA, 1996. [Google Scholar]
- Royston, J.P. An extension of Shapiro and Wilk’s W test for normality to large samples. J. R. Stat. Soc. Ser. C Appl. Stat. 1982, 31, 115–124. [Google Scholar] [CrossRef]
- Shi, P.; Liu, M.; Ratkowsky, D.A.; Gielis, J.; Su, J.; Yu, X.; Wang, P.; Zhang, L.; Lin, Z.; Schrader, J. Leaf area-length allometry and its implications in leaf-shape evolution. Trees Struct. Funct. 2019, 33, 1073–1085. [Google Scholar] [CrossRef]
- Yu, X.; Shi, P.; Schrader, J.; Niklas, K.J. Nondestructive estimation of leaf area for 15 species of vines with different leaf shapes. Am. J. Bot. 2020, 107, 1481–1490. [Google Scholar] [CrossRef] [PubMed]
- Weisstein, E. Superellipse. MathWorld. 2003. Available online: https://mathworld.wolfram.com/Superellipse.html (accessed on 1 November 2020).
- Thiselton Dyer, W.T. The Square Bamboo. Nature 1885, 32, 391–392. [Google Scholar] [CrossRef] [Green Version]
- Faisal, T.R.; Abad, E.M.K.; Hristozov, N.; Pasini, D. The impact of tissue morphology, cross-section and turgor pressure on the mechanical properties of the leaf petiole in plants. J. Bionic Eng. 2010, 7, S11–S23. [Google Scholar] [CrossRef]
- Faisal, T.R.; Hristozov, N.; Western, T.L.; Rey, A.; Pasini, D. The twist-to-bend compliance of the Rheum rhabarbarum petiole: Integrated computations and experiments. Comput. Method. Biomec. 2017, 20, 343–354. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tian, F.; Wang, Y.J.; Sandhu, H.S.; Gielis, J.; Shi, P.J. Comparison of seed morphology of two ginkgo cultivars. J. Forest Res. 2020, 31, 751–758. [Google Scholar] [CrossRef]
- Shi, P.; Xu, Q.; Sandhu, H.S.; Gielis, J.; Ding, Y.; Li, H.; Dong, X. Comparison of dwarf bamboos (Indocalamus sp.) leaf parameters to determine relationship between spatial density of plants and total leaf area per plant. Ecol. Evol. 2015, 5, 4578–4589. [Google Scholar] [CrossRef] [PubMed]
- Lin, S.; Zhang, L.; Reddy, G.V.P.; Hui, C.; Gielis, J.; Ding, Y.; Shi, P. A geometrical model for testing bilateral symmetry of bamboo leaf with a simplified Gielis equation. Ecol. Evol. 2016, 6, 6798–6806. [Google Scholar] [CrossRef] [PubMed]
- Shi, P.; Liu, M.; Yu, X.; Gielis, J.; Ratkowsky, D.A. Proportional relationship between leaf area and the product of leaf length and width of four types of special leaf shapes. Forests 2019, 10, 178. [Google Scholar] [CrossRef] [Green Version]
- Wang, P.; Ratkowsky, D.A.; Xiao, X.; Yu, X.; Su, J.; Zhang, L.; Shi, P. Taylor’s power law for leaf bilateral symmetry. Forests 2018, 9, 500. [Google Scholar] [CrossRef] [Green Version]
- Guo, X.; Reddy, G.V.P.; He, J.; Li, J.; Shi, P. Mean-variance relationships of leaf bilateral asymmetry for 35 species of plants and their implications. Glob. Ecol. Conser. 2020, 23, e01152. [Google Scholar] [CrossRef]
- Shi, P.; Niinemets, U.; Hui, C.; Niklas, K.J.; Yu, X.; Holscher, D. Leaf bilateral symmetry and the scaling of the perimeter vs. the surface area in 15 vine species. Forests 2020, 11, 246. [Google Scholar] [CrossRef] [Green Version]
- Thompson, D.W. On Growth and Form; Cambridge University Press: London, UK, 1917. [Google Scholar]



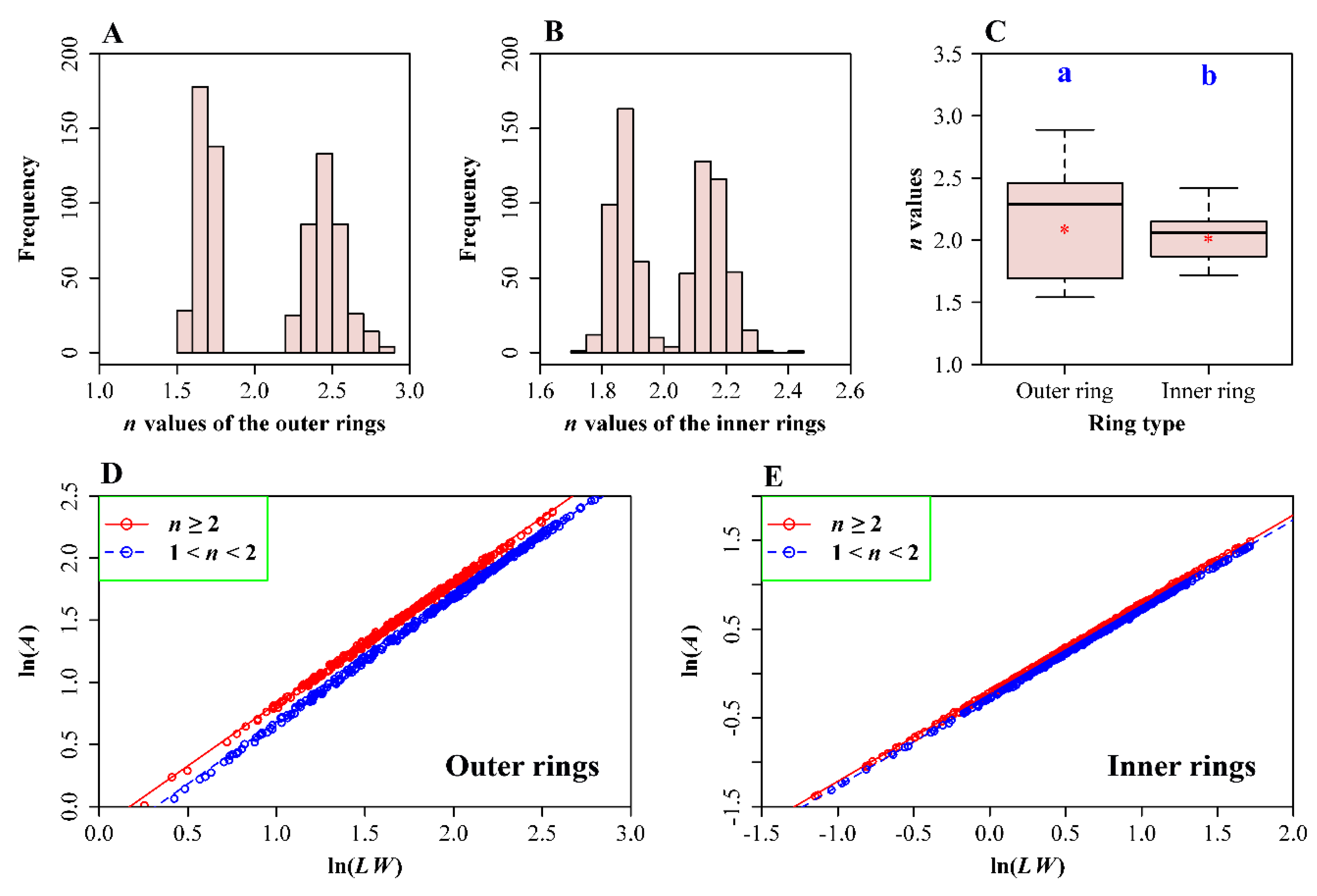
| Ring Type | Data Range | Theoretical Intercept 1 | Estimated Intercept | LCI | UCI | RMSE |
|---|---|---|---|---|---|---|
| Outer | n ≥ 2 | 0.8421 | 0.8246 | 0.8235 | 0.8257 | 0.0134 |
| Outer | n < 2 | 0.7282 | 0.7291 | 0.7279 | 0.7303 | 0.0158 |
| Inner | n ≥ 2 | 0.8071 | 0.7994 | 0.7986 | 0.8001 | 0.0092 |
| Inner | n < 2 | 0.7637 | 0.7600 | 0.7593 | 0.7607 | 0.0087 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, W.; Li, Y.; Niklas, K.J.; Gielis, J.; Ding, Y.; Cao, L.; Shi, P. A Superellipse with Deformation and Its Application in Describing the Cross-Sectional Shapes of a Square Bamboo. Symmetry 2020, 12, 2073. https://doi.org/10.3390/sym12122073
Huang W, Li Y, Niklas KJ, Gielis J, Ding Y, Cao L, Shi P. A Superellipse with Deformation and Its Application in Describing the Cross-Sectional Shapes of a Square Bamboo. Symmetry. 2020; 12(12):2073. https://doi.org/10.3390/sym12122073
Chicago/Turabian StyleHuang, Weiwei, Yueyi Li, Karl J. Niklas, Johan Gielis, Yongyan Ding, Li Cao, and Peijian Shi. 2020. "A Superellipse with Deformation and Its Application in Describing the Cross-Sectional Shapes of a Square Bamboo" Symmetry 12, no. 12: 2073. https://doi.org/10.3390/sym12122073
APA StyleHuang, W., Li, Y., Niklas, K. J., Gielis, J., Ding, Y., Cao, L., & Shi, P. (2020). A Superellipse with Deformation and Its Application in Describing the Cross-Sectional Shapes of a Square Bamboo. Symmetry, 12(12), 2073. https://doi.org/10.3390/sym12122073








