1. Introduction
In [
1], simple rational operators
and
were constructed, reaching the following pointwise approximation error estimates
and
and
Here, C denotes a positive constant independent of n and is the usual modulus of continuity of
We remark that if
in (
1) or
in (
2), such error estimates are not achievable by polynomials, as proved by Gopengauz (see [
1,
2]).
Moreover, in [
1] the authors proved that the exponents
and
in (
1) and (
2), respectively, cannot be equal to 1 (see remark to Corollary 2.5 proposed by Totik [
1]). A crucial key for such estimates is the careful choice of node meshes of algebraic-type.
Zeros of orthogonal polynomials as nodes for rational approximation were examined in [
3], but corresponding results are weaker than (
1) and (
2).
It was an open problem to construct simple rational operators, reaching pointwise approximation error estimates in terms of functions vanishing at any fixed point in
faster than in (
1) and (
2), like
or
On the other hand, it was an unsolved question to get results of convergence and pointwise estimates of the approximation error by the above rational operators, based on exponential-type meshes. In such cases, the main difficulty is to balance the rational nature of above operators with the exponential mesh behavior.
The present paper aims at giving a first successful answer to the above problems, considering easy rational operators based on exponential-type meshes.
In
Section 2, convergence statements and pointwise approximation error estimates, involving functions of type (
3) or (
4), are given in Theorems 1–4.
Then, in
Section 3, we use above operators to construct rational curves by Discrete Fourier Transform (DFT) and design a truncated progressive iterative approximation technique, useful in CAGD modeling.
Recently, parametric Shepard-type curves were studied and properties and algorithms, interesting in CAGD and image processing, were deduced in [
4,
5]. In
Section 3, we study how to transform Shepard-type curves into a different domain using Discrete Fourier Transform through the well-known Fast Fourier Transform algorithm. Theorem 6 presents the inner structure of Shepard-type curves in the form of other Shepard-type curves, known as base Shepard-type curves in the transform form. These base Shepard-type curves have as control points twiddle factors of DFT; hence, the geometry of these curves is determined by the geometry of the corresponding star polygons. The modeling power of such basic Shepard-type curves overcomes the analogous Bézier and B-spline ones, as in original Shepard-type curves case (cf. [
4]). Then, in
Section 3.1, by truncated DFT and the progressive iterative approximation (PIA in short) algorithm introduced in [
4], we deduce a method to construct new Shepard-type curves having good shaping behavior. Indeed, the number of base Fourier functions and the iteration level of PIA algorithm handle modeling the outline of Shepard-type curve, getting as a limit case the Shepard-type interpolating curve.
The proofs of the above results are included in
Section 4. They are based on smart choices of nodes meshes, careful estimates for our operators and suitable matrix formulations of DFT and the PIA algorithm. Finally,
Section 5 shows numerical experiments, illustrating achieved results.
2. Rational Approximation on Exponential-Type Meshes
For
, we introduce the nodes matrix
,
Then, for any function
, we consider the Shepard operator
as
with
and
even. From the definition, we can deduce that
is a positive, linear operator, preserving constants;
is a rational function having degree
, interpolating
f at
,
and is stable in Fejér sense, i.e.,
If the mesh is equispaced on
, and we assume
for example, then
is a symmetric operator, i.e.,
This operator is widely used in classical approximation theory and problems of scattered data interpolation (see, e.g., [
6,
7,
8,
9]).
When the nodes’ mesh is equispaced, direct and converse results for the operator
exist (e.g., [
7,
10]). For nodes mesh of algebraic type, pointwise estimates were obtained in [
1].
The case of nodes exponentially thicker near one fixed point was an open problem. Now we prove that, by nodes exponentially dense,
operator achieves results of convergence and estimates of pointwise approximation error, involving functions of type (
3) and (
4).
To this aim, we assume
and denote by
the usual supremum norm on
of
Moreover,
C denotes a positive constant that can assume different values, even when it appears more times in the same formula. Then let
be the nodes’ matrix. This mesh is exponentially thick near
Then, we consider operator
defined by (
5) based on the nodes matrix
X in (
7). We have
Theorem 1. Let and be the operator defined by (5)–(7). Then Moreover, , , where , and means x vanishing, as . Remark 1. Equation (8) allows us to deduce the uniform convergence of to f, as , . Moreover, estimate (9) gives an answer to the problems presented in Introduction. The thickness of the exponential-type mesh near 0 affects estimate of the error (due to the presence of functions and at the r.h.s. in (9)). As remarked in [
1], the left-end point 0 is not a special point and we can get analogous results for the right-endpoint 1 case, both endpoints case and any interior point case. For example, let
with
given in (
7). Now consider the matrix
,
,
This mesh is exponentially finer near
Moreover, for any
, consider the operator
based on the matrix
We can state
Theorem 2. Let and be the operator defined by (5) and (10). Then Furthermore, , with and Remark 2. Obviously, from (11) we deduce the uniform convergence of to f, as Moreover, error estimate is affected by the mesh thickness near 1, because of functions and at the r.h.s. of (12). Combining the above results, we can consider the matrix
with
n even,
as in (
7). Then, denote by
the operator
based on the matrix
When
n is odd, we can replace
by
We have
Theorem 3. Let and be the operator defined by (5) and (13). Then In addition, with and Remark 3. From (14), we have the uniform convergence of to as Moreover, the mesh thickness near 0 and 1 affects estimate of the error (due to functions and at the r.h.s. of Equation (15)). Hence, Theorem 3 successfully answers the problems posed in the introduction. For example, if and then by (15) which is faster than coming from (1). Additionally for
n even, let
This mesh is thicker near the inner point Denote by the operator based on the matrix If n is odd, we can replace by
We prove
Theorem 4. Let and be the operator defined by (5) and (16). Then Moreover, , with and Remark 4. Equation (17) proves the uniform convergence of to f, as The error estimate is affected by the mesh thickness near , because of functions and at the r.h.s. of (18). Theorem 4 answers to the problems posed in the introduction. For example if and then by (18) which is better than descending from (2). 3. Shepard-Type Curves and Discrete Fourier Transform
Let us first recall some properties of parametric curves of Shepard-type (see [
4]). Let
where
for
where
C is any fixed positive constant, and
is even.
Let
be the control vector. Then the parametric curve of Shepard-type
is defined as
In [
4], some properties of such curves were studied, that are interesting in CAGD. In particular,
is a rational curve that reproduces points and lies within the convex hull of the control polygon
P. Such a curve satisfies the pseudo-local control property; that is, each function
reaches its maximum value close to 1 at
therefore the point
strongly affects the shape of the curve close to
From (
6), Shepard-type curves are symmetric, i.e.,
, with
The choice
makes
a near-interpolating curve of the original control polygon. This fixes the flat spots artifact that affects the original Shepard operator (cf. [
4]).
In [
4], we introduced and investigated a PIA technique for curves of Shepard-type. The PIA process starts with an initial Shepard-type curve; then through iterations, it adjusts the control points at each iteration, resulting in a sequence of fitting curves. The limiting of the curves at different iterations is the Shepard-type curve interpolating the data. In details, given the control vector
P and the basis
,
, defined by (
19), the initial curve is generated as
with
,
. Then the remaining curves of the sequence
, for
, are computed as
with
and
the adjusting vectors given by
The iterative process can be also expressed in matrix form as
with
B the collocation matrix of
basis, i.e.,
We remark that
B is a symmetric, stochastic, diagonally dominant matrix (see [
4]).
We say that the
curve satisfies the PIA property iff
,
. We can state (cf. [
4])
Theorem 5. Curve satisfies the PIA property.
Remark 5. The proof of Theorem 5 is based on the well-known resultwhere M is any nonsingular matrix such that , with being the spectral radius of , I the identity matrix, the i-th power of matrix and the inverse matrix, i.e., Thanks to the PIA property, we can construct a sequence of control polygons that converge to the control polygon generating a Shepard-type interpolating curve. In addition, we can use k as a shape parameter so to model several outlines; the extreme cases are the curve of Shepard-type and the global interpolating curve of Shepard-type. As remarked in [4], the rate of convergence of such a procedure is faster than the Bézier case. Then we recall some preliminaries on Fourier analysis, namely the resulting Fourier Transform. The Fourier Transform is the decomposition of a function into components at higher and higher frequencies. Discrete Fourier Transform (DFT) is the discrete counterpart of the Fourier Transform, yielding an estimate starting from a finite sample. DFT maps an ordered set of
complex number to a different one. Let
be a series of
complex numbers. We assume a periodicity condition that outside the range
the series is extended
periodic, i.e.,
. We denote DFT of this series
The forward transform is defined as
with
known as twiddle factor and
j the solution of
(complex unity).
In practical applications, DFT is computed by the well-known Fast Fourier Transform algorithm.
Now we are ready to analyze Shepard-type curves by DFT.
Theorem 6. Let be the Shepard-type curve defined in (20). We can writewhereis called the “base Shepard-type curve” and In matrix notation, we can writewhere , , and W is the Fourier matrixwith H denoting the Hermitian. Remark 6. From Theorem 6, curve can be expressed as weighted average of base Shepard-type curves, by DFT of the original control points.
It can be easily proved that behaves as a basis for Shepard-type curve by polygon points in transformed form. Thus, the original Shepard-type curves are generated by these base Shepard-type curves.
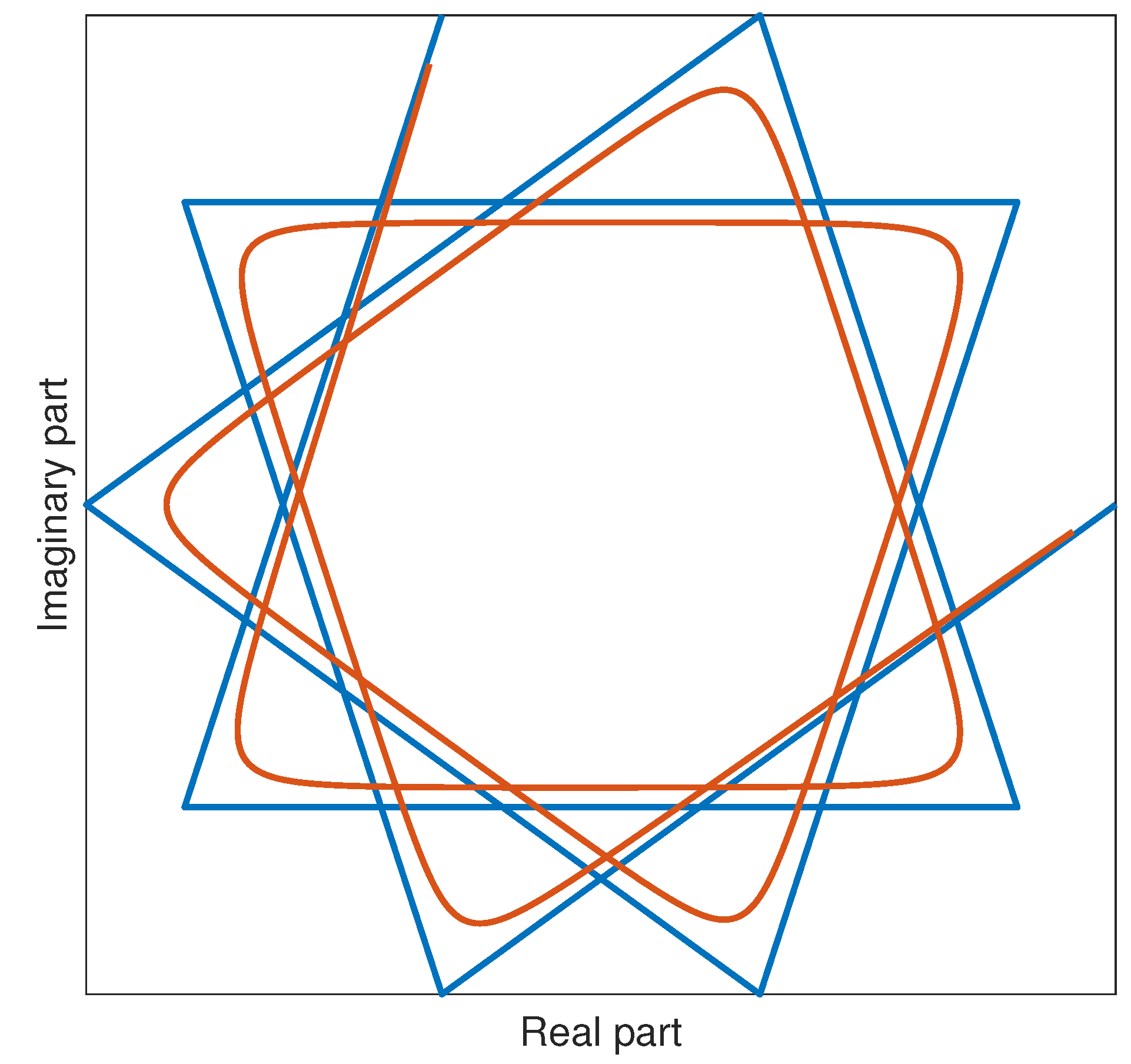
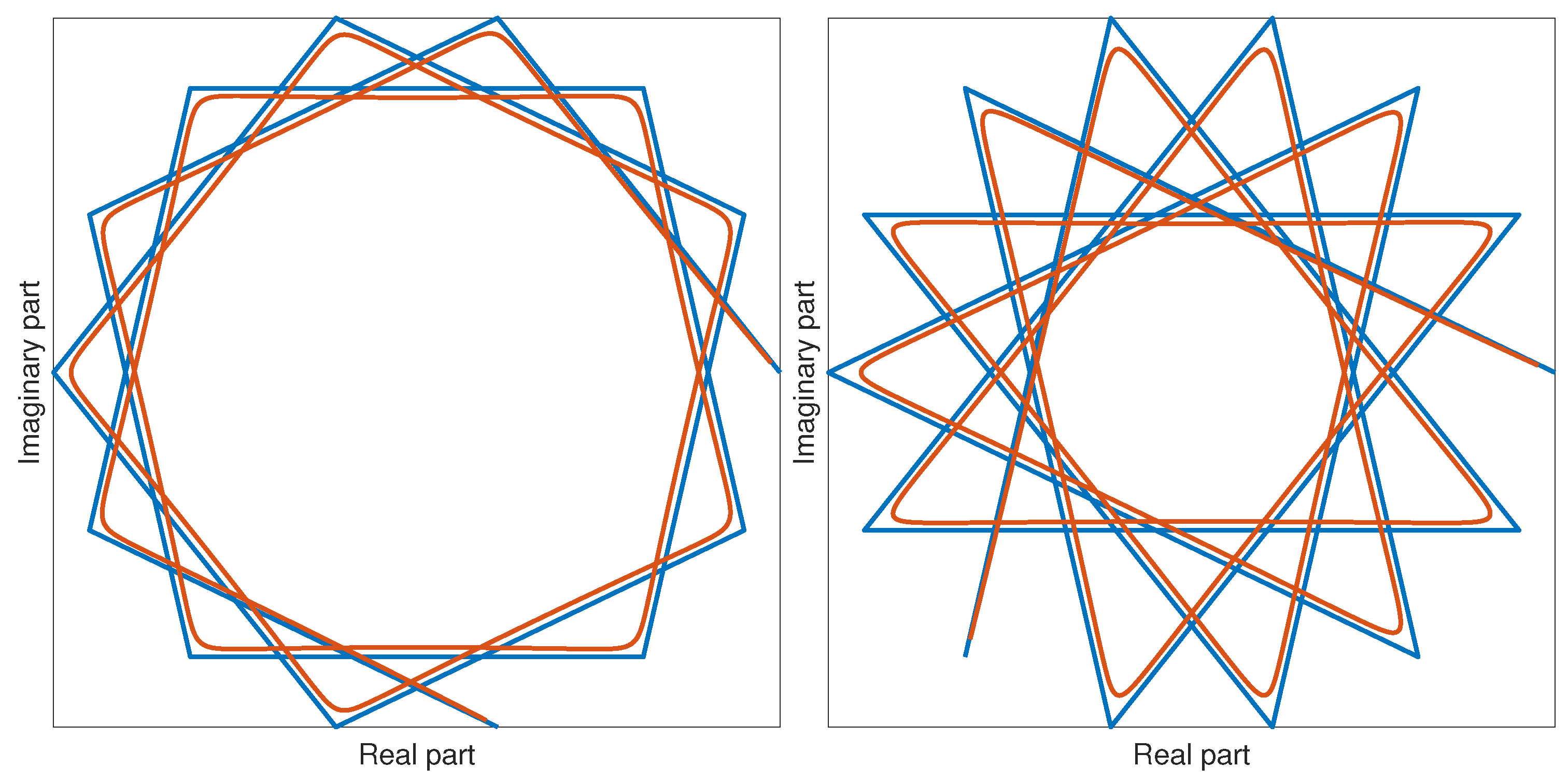
The control points that are obtained for them are , so the corresponding polygon is a regular or star one. The relative base curves of Shepard-type lie in the convex-hull of these regular polygons or star polygons, (cf. [11]). Since obtained Shepard-type curves and are mirror images of each other about axis.
Analogous Fourier analysis for Bézier, B-splines and rational B-splines curves was presented in [12,13], but at lower modeling power than our curves (see Section 5). 3.1. Shepard-Type Curves via DFT and PIA
Consider the global interpolating Shepard-type curve (cf. [
4])
with
such that
i.e., by (
21)
or equivalently
From (
25), (
24) in Theorem 6 and (
26), we can write
Now let us consider only the first
k,
, Fourier basis functions in
W, or in matrix notation
, with index
denoting the truncation procedure. This choice is made in analogy with truncation occurring in some statistical contexts involving FT. Then the truncated interpolating curve of Shepard-type is introduced:
Obviously, if
,
and we get back (
25). Hence, varying
in (
27), we get different curves approaching the interpolating Shepard-type curve.
Representation (
27) suggests to use the above PIA technique (see Theorem 5, (
22) and consequent remark) to construct a method giving a pencil of curves of Shepard-type, modeling the original data points.
We sketch the procedure. In (
27), we replace
V by
with
r being the iteration level. From [
4],
and convergence rate is fast, so a few iterations are enough to go close to
V.
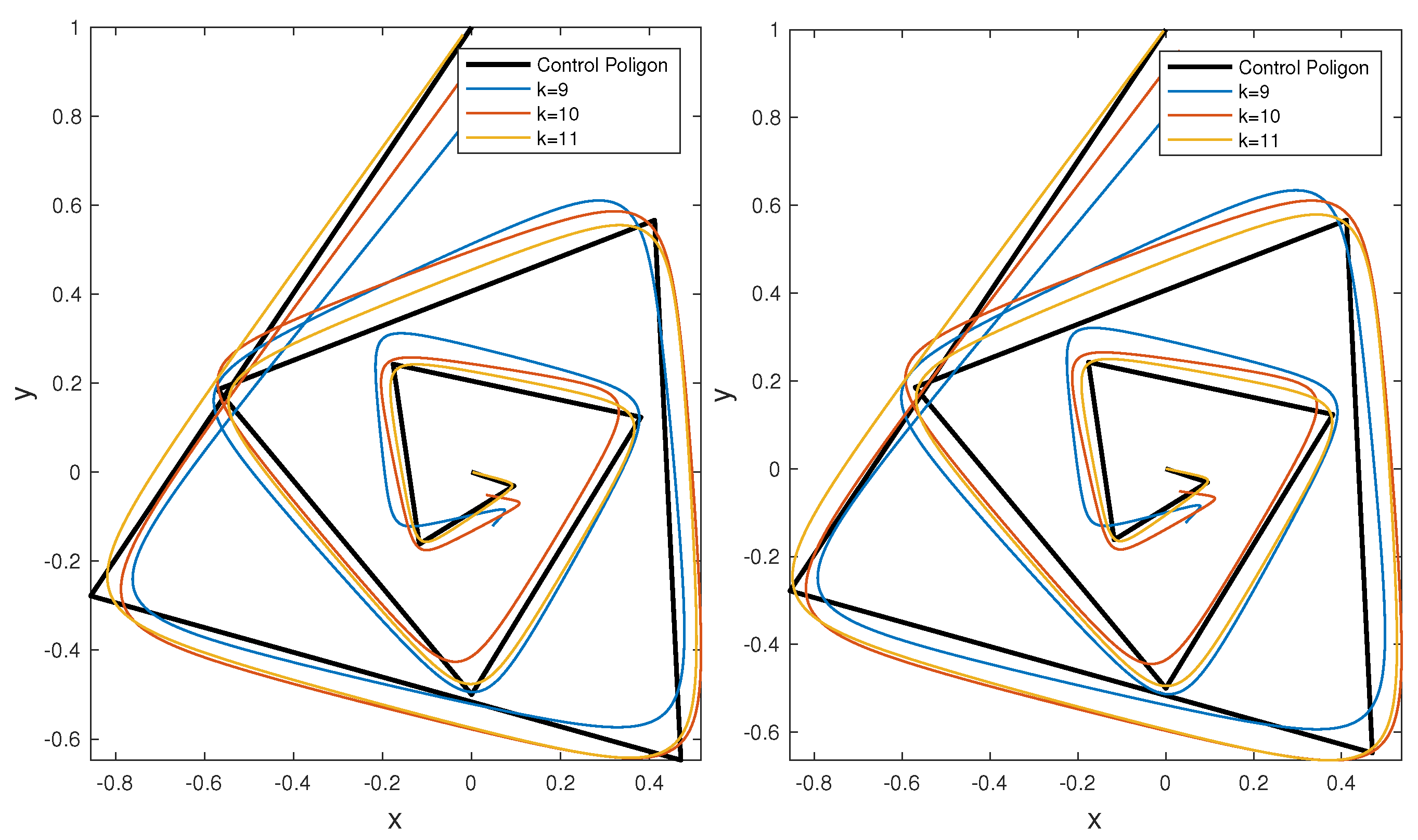
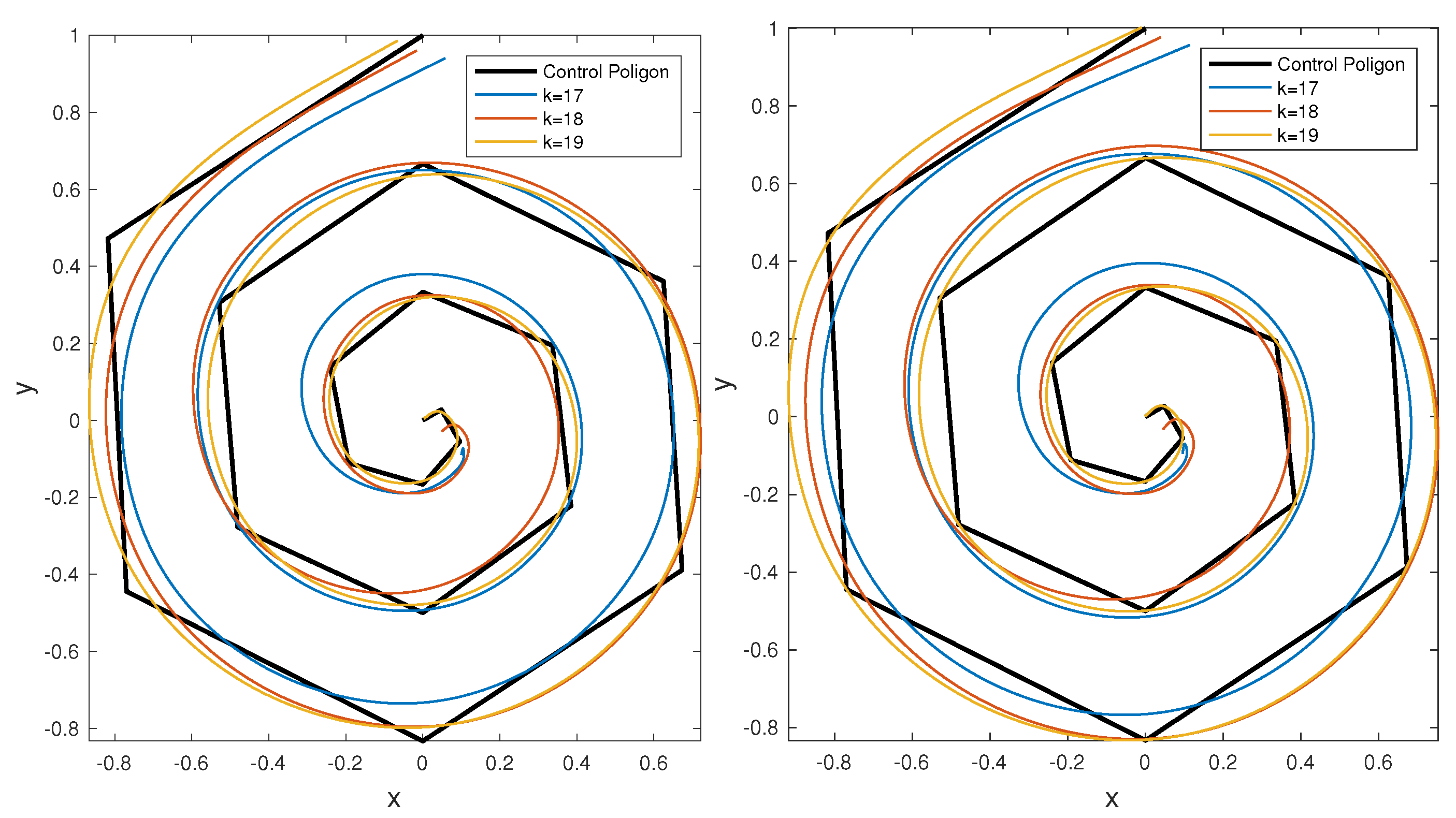
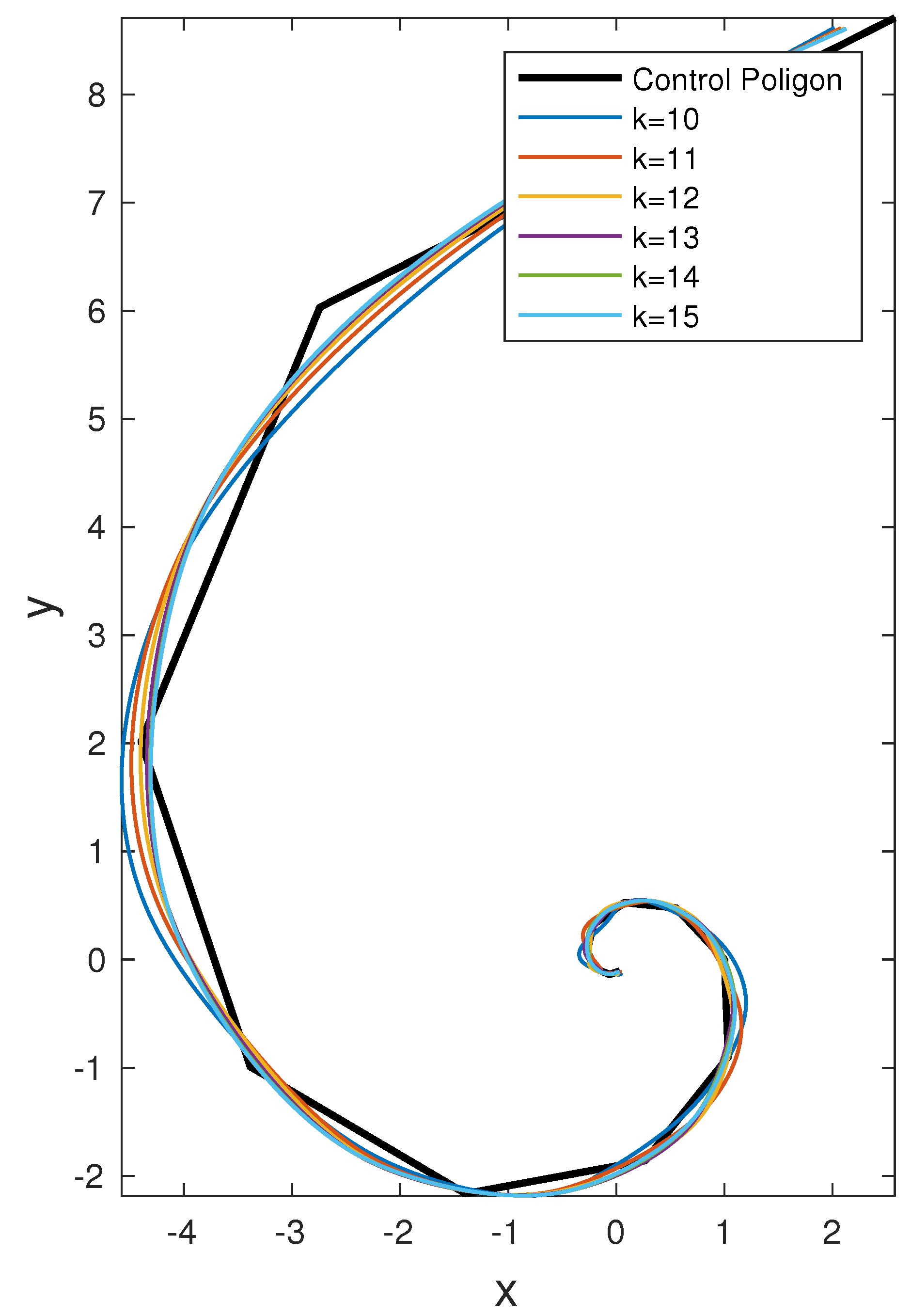
Then playing on two shape parameters, the number
k of basis Fourier functions in (
27) and the iteration level of the PIA algorithm—the index
r in (
28), the designer can get intermediate contours not reachable by original PIA format (see
Section 5).