An Iterative Weighted-Mean Filter for Removal of High-Density Salt-and-Pepper Noise
Abstract
1. Introduction
2. Scheme of the Iterative Weighted-Mean Filter
2.1. Stage 1: Noise Detection
- All pixels in this region have extreme intensity.
- About half of the noise pixels take the intensity 255, so the total number of pixels with an intensity of 255 is greater than the pixels with an intensity of 0. In other words, pixels with an intensity of 255 are the majority.
2.2. Stage 2: Noise Removal
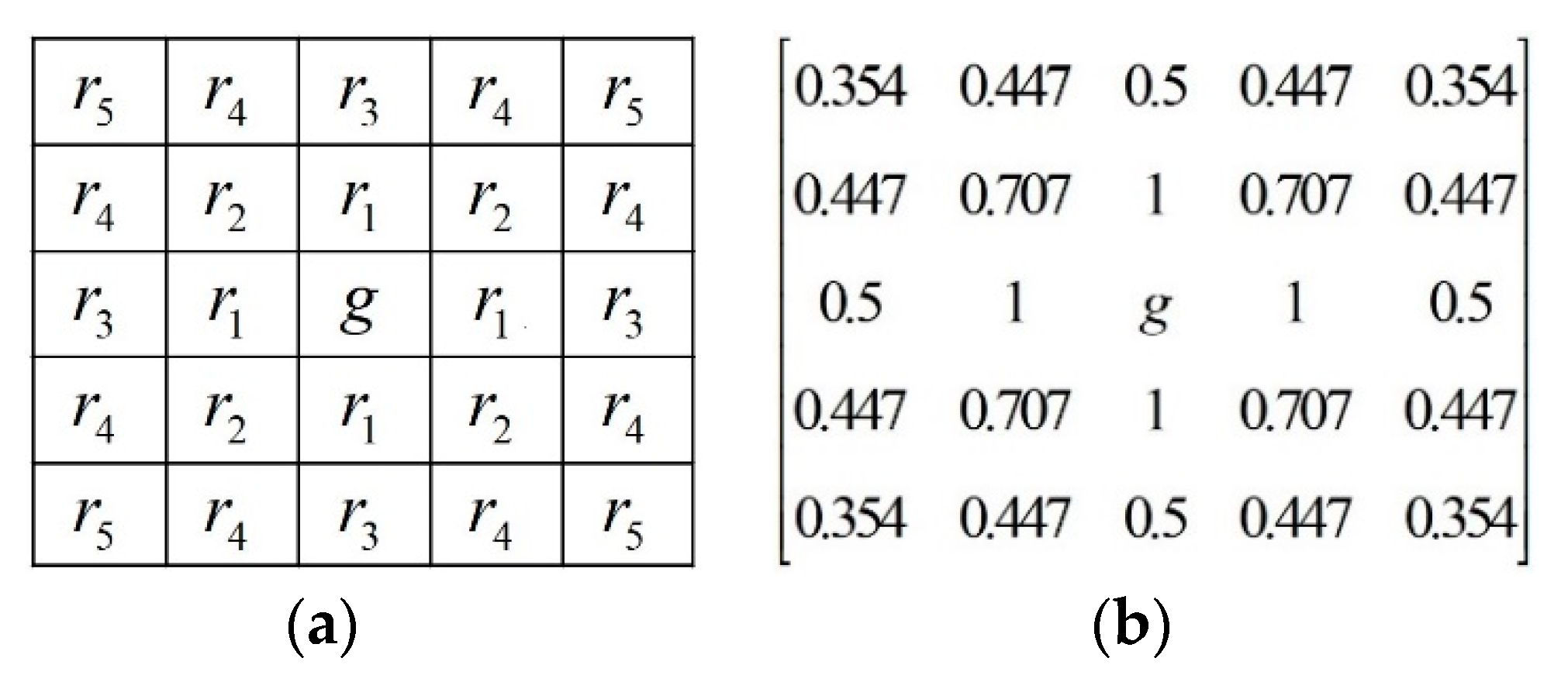
2.2.1. Selection of Filtering Window
- If the number of noise-free pixels in W5(g) is greater than 3, then set W = r1 as the candidate filtering window. If the number of noise-free pixels in W is less than 3, then let W = r1 + r2. By analogy, increase W by ri (r1, r2, ... r5) until the number of noise-free pixels selected exceeds 2.
- If the number of noise-free pixels in W5(g) is 1 or 2, then let W = W5(g).
- If all pixels in W5(g) are noise, then a suitable filtering window cannot be obtained. In this case, the pixel needs to be further detected by method 2 in Section 2.2.2.
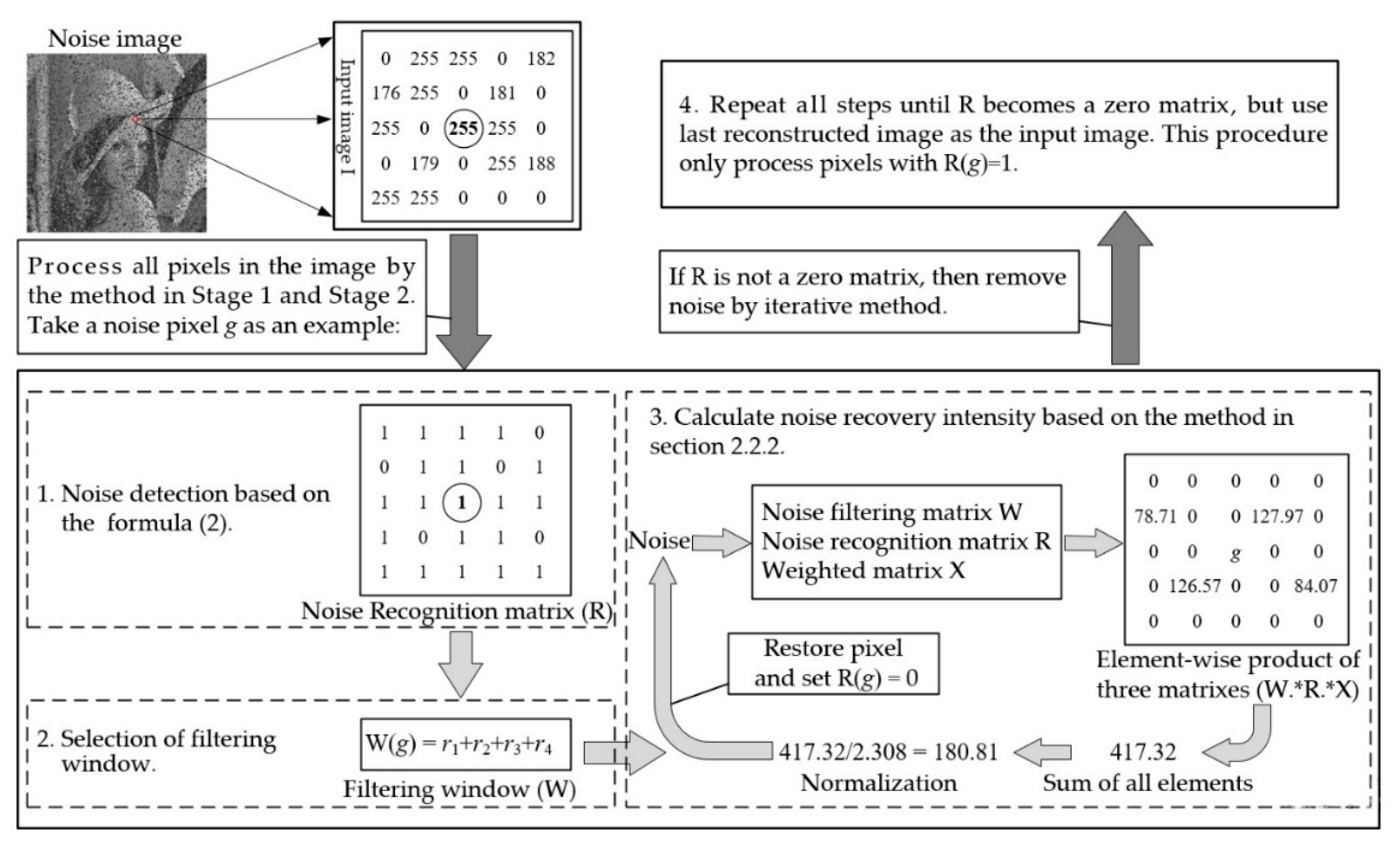
2.2.2. Calculation of Noise Pixels Restored Value
- In the spatial filtering theory, corrupted pixels can be restored using the normalized weighted mean of all pixels in the neighborhood. The noise restored value can be calculated as (3). Replace the noise pixel value with the restored value, and set R(g) = 0.
- 2.
- If g is in the extreme intensity flat regions, then the recovery step is performed according to the formula (5) and set R(g) = 0; otherwise, the pixel is processed in Stage 3.
2.3. Stage 3: Noise Removal by Iterative Approach
- For each pixel g with R(g) = 1, process g by the method proposed in stage 2.
- If R is not a zero matrix, repeat 1 until R becomes a zero matrix, but use the last reconstruct image as the input image. Otherwise, leave it unchanged. If all pixels in the image are noisy pixels, then the procedure should stop.
3. Simulation Results
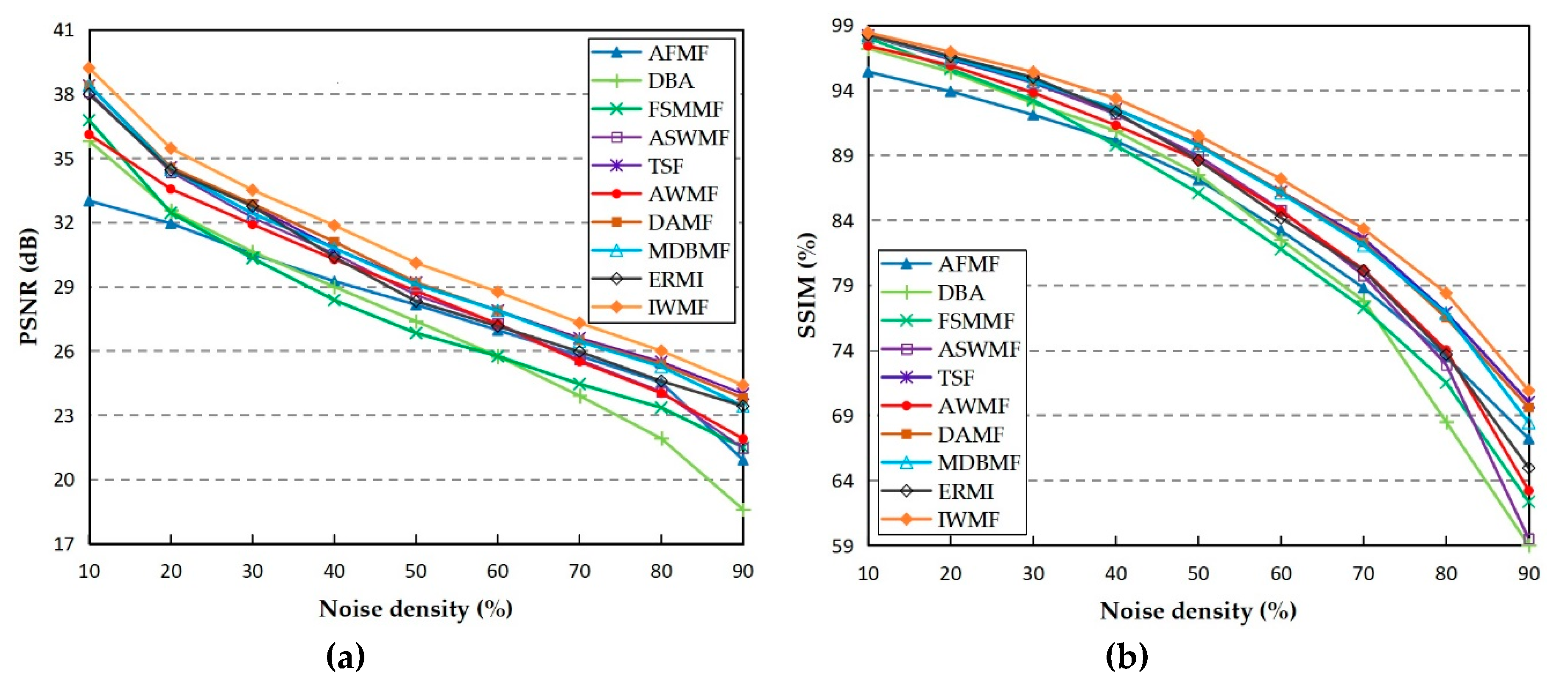
3.1. Evaluate by Visual Perception and Quantitative Measurements
3.2. Evaluate by Computational Time
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sundaramurthy, S. Digital Image Processing, 2nd ed.; Oxford University Press: Oxford, UK, 2016. [Google Scholar]
- Chen, J.Y.; Zhan, Y.W.; Cao, H.Y.; Xiong, G.Q. Iterative grouping median filter for removal of fixed value impulse noise. IET Image Proc. 2019, 13, 946–953. [Google Scholar] [CrossRef]
- Tukey, J.W. Exploratory Data Analysis. J. Am. Stat. Assoc. 1977, 28. [Google Scholar] [CrossRef]
- Bhadouria, V.S.; Ghoshal, D.; Siddiqi, A.H. A new approach for high density saturated impulse noise removal using decision-based coupled window median filter. Signal Image Video Process. 2014, 8, 71–84. [Google Scholar] [CrossRef]
- Charalampidis, D. Steerable Weighted Median Filters. IEEE Trans. Image Process. IEEE Signal Process. Soc. 2010, 19, 882–894. [Google Scholar] [CrossRef]
- Chen, J.; Zhan, Y.; Cao, H. Iterative deviation filter for fixed-valued impulse noise removal. Multimed. Tools Appl. 2020, 79, 23695–23710. [Google Scholar] [CrossRef]
- Chen, J.; Zhan, Y.; Cao, H.; Wu, X. Adaptive probability filter for removing salt and pepper noise. IET Image Proc. 2018, 12, 863–871. [Google Scholar] [CrossRef]
- Dong, Y.; Xu, S. A New Directional Weighted Median Filter for Removal of Random-Valued Impulse Noise. IEEE Signal Process. Lett. 2007, 14, 193–196. [Google Scholar] [CrossRef]
- Erkan, U.; Enginolu, S.; Thanh, D.N.H.; Minh, H.L. Adaptive Frequency Median Filter for the Salt and Pepper Denoising Problem. IET Image Proc. 2020, 14, 1291–1302. [Google Scholar] [CrossRef]
- Erkan, U.; Gokrem, L.; Enginolu, S. Different applied median filter in salt and pepper noise. Comput. Electr. Eng. 2018, 70, 789–798. [Google Scholar] [CrossRef]
- Esakkirajan, S.; Veerakumar, T.; Subramanyam, A.N.; Premchand, C.H. Removal of High Density Salt and Pepper Noise through Modified Decision Based Unsymmetric Trimmed Median Filter. IEEE Signal Process. Lett. 2011, 18, 287–290. [Google Scholar] [CrossRef]
- Faragallah, O.S.; Ibrahem, H.M. Adaptive switching weighted median filter framework for suppressing salt-and-pepper noise. AEU Int. J. Electron. Commun. 2016, 70, 1034–1040. [Google Scholar] [CrossRef]
- Hsieh, M.H.; Cheng, F.C.; Shie, M.C.; Ruan, S.-J. Fast and efficient median filter for removing 1–99% levels of salt-and-pepper noise in images. Eng. Appl. Artif. Intell. 2013, 26, 1333–1338. [Google Scholar] [CrossRef]
- Hwang, H.; Haddad, R.A. Adaptive median filters: New algorithms and results. IEEE Trans. Image Process. 1995, 4, 499–502. [Google Scholar] [CrossRef]
- Ibrahim, H.; Kong, N.S.P.; Ng, T.F. Simple adaptive median filter for the removal of impulse noise from highly corrupted images. IEEE Trans. Consum. Electron. 2008, 54, 1920–1927. [Google Scholar] [CrossRef]
- Khan, S.; Lee, D.H. An adaptive dynamically weighted median filter for impulse noise removal. EURASIP J. Adv. Signal. Process. 2017, 1–4. [Google Scholar] [CrossRef]
- Kunsoth, R.; Biswas, M. Modified decision based median filter for impulse noise removal. In Proceedings of the IEEE International Conference on Wireless Communications, Signal Processing and Networking, Chennai, India, 23–25 March 2016; pp. 1316–1319. [Google Scholar]
- Park, H. Making Joint-Histogram-Based Weighted Median Filter Much Faster. IEICE Trans. Inf. Syst. 2015, 98, 721–725. [Google Scholar] [CrossRef]
- Srinivasan, K.S.; Ebenezer, D. A New Fast and Efficient Decision-Based Algorithm for Removal of High-Density Impulse Noises. IEEE Signal Process. Lett. 2007, 14, 189–192. [Google Scholar] [CrossRef]
- Thanh, D.N.H.; Hai, N.H.; Prasath, S.; Minh, H.L.; Tavares, J.M.R.S. A Two-Stage Filter for High Density Salt and Pepper Denoising. Multimed. Tools Appl. 2020, 79, 21013–21035. [Google Scholar] [CrossRef]
- Erkan, U.; Gokrem, L. A new method based on pixel density in salt and pepper noise removal. Turk. J. Electr. Eng. Comput. Sci. 2018, 26, 162–171. [Google Scholar] [CrossRef]
- Yuan, S.; Tan, Y. Impulse noise removal by a global–local noise detector and adaptive median filter. Signal Process. 2006, 86, 2123–2128. [Google Scholar] [CrossRef]
- Zhang, Z.; Han, D.; Dezert, J.; Yang, Y. A new adaptive switching median filter for impulse noise reduction with pre-detection based on evidential reasoning. Signal Process. 2018, 147, 173–189. [Google Scholar] [CrossRef]
- Goel, N.; Aggarwal, P. Enhanced Modified Decision-Based Unsymmetric Trimmed Adaptive Neighborhood Winsorized Mean Filter for Removing 1–99% Levels of Salt-and-Pepper Noise. Iran. J. Sci. Technol. Trans. Electr. Eng. 2019, 43, 459–468. [Google Scholar] [CrossRef]
- Iqbal, N.; Ali, S.; Khan, I.; Lee, B. Adaptive Edge Preserving Weighted Mean Filter for Removing Random-Valued Impulse Noise. Symmetry 2019, 11. [Google Scholar] [CrossRef]
- Chen, J.; Huang, N.; Xiong, G.; Cao, H.; Xu, Q. Adaptive weighted mean filtering algorithm based on confidence interval. J. Nanjing Univ. Sci. Technol. 2017, 22, 1538–1575. [Google Scholar]
- Nasri, M.; Saryazdi, S.; Nezamabadi-Pour, H. A Fast Adaptive Salt and Pepper Noise Reduction Method in Images. Circuits Syst. Signal Process. 2013, 32, 1839–1875. [Google Scholar] [CrossRef]
- Ramadan, Z.M. Efficient Restoration Method for Images Corrupted with Impulse Noise. Circuits Syst. Signal Process. 2012, 31, 1397–1406. [Google Scholar] [CrossRef]
- Wang, X.; Shen, S.; Shi, G.; Xu, Y.; Zhang, P. Iterative non-local means filter for salt and pepper noise removal. J. Vis. Commun. Image Represent. 2016, 34, 440–450. [Google Scholar] [CrossRef]
- Zhang, P.; Li, F. A New Adaptive Weighted Mean Filter for Removing Salt-and-Pepper Noise. IEEE Signal Process. Lett. 2014, 21, 1280–1283. [Google Scholar] [CrossRef]
- Vijaykumar, V.R.; Santhana Mari, G.; Ebenezer, D. Fast switching based median–mean filter for high density salt and pepper noise removal. EURASIP J. Adv. Signal Process. 2014, 68, 1145–1155. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, K. A switching median–mean filter for removal of high-density impulse noise from digital images. Optik 2015, 126, 956–961. [Google Scholar] [CrossRef]
- The UC Berkeley Dataset. Available online: https://www2.eecs.berkeley.edu/Research/Projects/CS/vision/bsds/BSDS300/html/dataset/images.html (accessed on 31 October 2020).






| Noise Density, % | 10 | 30 | 50 | 70 | 90 | 10 | 30 | 50 | 70 | 90 |
|---|---|---|---|---|---|---|---|---|---|---|
| PSNR (dB) | SSIM (%) | |||||||||
| AFMF | 37.9 | 34.9 | 31.8 | 29.0 | 23.1 | 97.8 | 94.9 | 91.6 | 85.8 | 70.2 |
| DBA | 40.5 | 34.8 | 30.4 | 26.1 | 19.9 | 98.6 | 94.8 | 90.5 | 80.1 | 56.5 |
| ASWMF | 42.2 | 36.1 | 32.3 | 29.0 | 23.8 | 98.9 | 96.3 | 92.3 | 85.7 | 67.2 |
| TSF | 43.2 | 36.8 | 33.0 | 30.2 | 27.1 | 98.9 | 96.5 | 93.1 | 87.9 | 80.2 |
| AWMF | 39.6 | 36.7 | 32.3 | 28.2 | 24.5 | 98.9 | 96.0 | 91.9 | 84.1 | 76.4 |
| DAMF | 43.2 | 36.9 | 33.1 | 30.1 | 27.0 | 99.1 | 96.5 | 93.0 | 87.8 | 80.1 |
| FSMMF | 40.9 | 34.3 | 30.5 | 27.9 | 23.9 | 98.7 | 95.2 | 89.6 | 83.7 | 73.2 |
| ERMI | 42.2 | 36.9 | 31.7 | 29.5 | 25.7 | 99.0 | 96.6 | 91.7 | 86.7 | 75.3 |
| MDBMF | 42.7 | 36.6 | 33.0 | 30.1 | 26.1 | 99.0 | 96.5 | 93.0 | 87.7 | 77.8 |
| IWMF | 43.3 | 37.6 | 34.0 | 31.0 | 27.1 | 99.1 | 96.9 | 93.8 | 89.3 | 80.3 |
| Noise Density, % | 10 | 30 | 50 | 70 | 90 | 10 | 30 | 50 | 70 | 90 |
|---|---|---|---|---|---|---|---|---|---|---|
| PSNR (dB) | SSIM (%) | |||||||||
| AFMF | 37.5 | 36.5 | 32.8 | 30.5 | 24.9 | 96.2 | 97.2 | 94.7 | 89.3 | 78.6 |
| DBA | 40.2 | 34.6 | 31.9 | 27.2 | 20.4 | 98.5 | 95.3 | 86.6 | 80.2 | 70.6 |
| ASWMF | 43.0 | 37.0 | 33.3 | 30.1 | 25.4 | 99.3 | 97.5 | 94.5 | 89.2 | 71.9 |
| TSF | 43.5 | 36.9 | 33.7 | 30.6 | 27.5 | 99.2 | 97.3 | 94.5 | 89.4 | 84.5 |
| AWMF | 40.5 | 35.6 | 31.5 | 26.9 | 25.0 | 99.0 | 96.8 | 94.3 | 89.2 | 71.8 |
| DAMF | 43.5 | 36.9 | 33.8 | 30.4 | 27.3 | 99.3 | 97.3 | 94.7 | 89.2 | 84.3 |
| FSMMF | 41.3 | 34.9 | 31.8 | 29.5 | 26.8 | 99.1 | 96.2 | 92.2 | 87.2 | 78.5 |
| ERMI | 42.1 | 36.7 | 32.5 | 30.1 | 27.8 | 99.2 | 97.4 | 92.9 | 88.6 | 80.7 |
| MDBMF | 42.7 | 36.8 | 33.6 | 30.9 | 27.8 | 99.3 | 97.4 | 94.6 | 90.6 | 83.3 |
| IWMF | 44.0 | 37.9 | 34.8 | 31.7 | 28.5 | 99.5 | 98.0 | 95.8 | 91.9 | 84.5 |
| Noise Density, % | 10 | 30 | 50 | 70 | 90 | 10 | 30 | 50 | 70 | 90 |
|---|---|---|---|---|---|---|---|---|---|---|
| PSNR (dB) | SSIM (%) | |||||||||
| AFMF | 34.3 | 32.1 | 30.7 | 27.1 | 23.5 | 95.3 | 92.9 | 88.0 | 79.8 | 68.2 |
| DBA | 36.1 | 31.2 | 28.1 | 23.5 | 18.9 | 97.2 | 90.1 | 80.6 | 73.2 | 59.9 |
| ASWMF | 38.9 | 33.4 | 30.1 | 27.3 | 23.1 | 98.6 | 95.0 | 89.5 | 81.2 | 60.8 |
| TSF | 39.1 | 33.3 | 30.5 | 28.3 | 25.2 | 98.5 | 95.1 | 89.9 | 83.4 | 71.5 |
| AWMF | 38.0 | 33.2 | 30.1 | 27.4 | 22.5 | 98.4 | 94.5 | 88.5 | 80.2 | 60.0 |
| DAMF | 39.1 | 33.5 | 30.6 | 28.1 | 25.0 | 98.5 | 95.2 | 90.1 | 82.9 | 71.4 |
| FSMMF | 38.1 | 32.0 | 28.8 | 26.6 | 24.4 | 98.3 | 93.4 | 86.3 | 78.1 | 65.5 |
| ERMI | 39.0 | 33.9 | 29.4 | 27.4 | 25.2 | 98.6 | 95.3 | 86.7 | 79.1 | 66.5 |
| MDBMF | 39.1 | 33.6 | 30.5 | 28.0 | 25.1 | 98.6 | 95.1 | 90.0 | 82.9 | 70.6 |
| IWMF | 40.3 | 34.7 | 31.4 | 28.6 | 25.6 | 98.9 | 96.1 | 91.6 | 84.3 | 71.6 |
| Noise Density, % | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 |
|---|---|---|---|---|---|---|---|---|---|
| Time (ms) | |||||||||
| AFMF | 22.44 | 23.61 | 28.97 | 36.16 | 50.77 | 60.25 | 70.97 | 94.59 | 116.6 |
| DBA | 12.07 | 12.66 | 13.25 | 13.25 | 13.31 | 13.25 | 13.31 | 13.42 | 12.84 |
| ASWMF | 7.95 | 19.79 | 21.91 | 22.49 | 25.15 | 28.74 | 33.04 | 34.51 | 29.68 |
| TSF | 2.53 | 6.07 | 7.71 | 7.77 | 8.18 | 8.95 | 9.37 | 7.25 | 7.18 |
| AWMF | 28.38 | 26.62 | 26.21 | 25.79 | 24.79 | 24.85 | 24.44 | 24.03 | 23.67 |
| DAMF | 2.54 | 6.05 | 7.68 | 7.72 | 8.07 | 8.99 | 9.18 | 7.19 | 7.21 |
| FSMMF | 3.59 | 6.12 | 9.54 | 13.61 | 16.37 | 16.93 | 19.14 | 19.91 | 19.96 |
| ERMI | 0.94 | 1.59 | 2.29 | 3.29 | 9.77 | 10.36 | 10.48 | 11.36 | 23.09 |
| MDBMF | 2.29 | 5.59 | 7.42 | 7.01 | 7.95 | 8.54 | 8.66 | 6.18 | 6.01 |
| IWMF | 0.76 | 1.06 | 1.35 | 1.82 | 2.29 | 3.01 | 3.59 | 4.24 | 4.59 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, F.; Huang, M.; Ma, Z.; Li, Y.; Huang, Q. An Iterative Weighted-Mean Filter for Removal of High-Density Salt-and-Pepper Noise. Symmetry 2020, 12, 1990. https://doi.org/10.3390/sym12121990
Chen F, Huang M, Ma Z, Li Y, Huang Q. An Iterative Weighted-Mean Filter for Removal of High-Density Salt-and-Pepper Noise. Symmetry. 2020; 12(12):1990. https://doi.org/10.3390/sym12121990
Chicago/Turabian StyleChen, Fengyu, Minghui Huang, Zhuxi Ma, Yibo Li, and Qianbin Huang. 2020. "An Iterative Weighted-Mean Filter for Removal of High-Density Salt-and-Pepper Noise" Symmetry 12, no. 12: 1990. https://doi.org/10.3390/sym12121990
APA StyleChen, F., Huang, M., Ma, Z., Li, Y., & Huang, Q. (2020). An Iterative Weighted-Mean Filter for Removal of High-Density Salt-and-Pepper Noise. Symmetry, 12(12), 1990. https://doi.org/10.3390/sym12121990




