EEG-Based EMG Estimation of Shoulder Joint for the Power Augmentation System of Upper Limbs
Abstract
1. Introduction
2. A Concept of a Virtual Flexor–Extensor Muscle
3. Materials and Methods
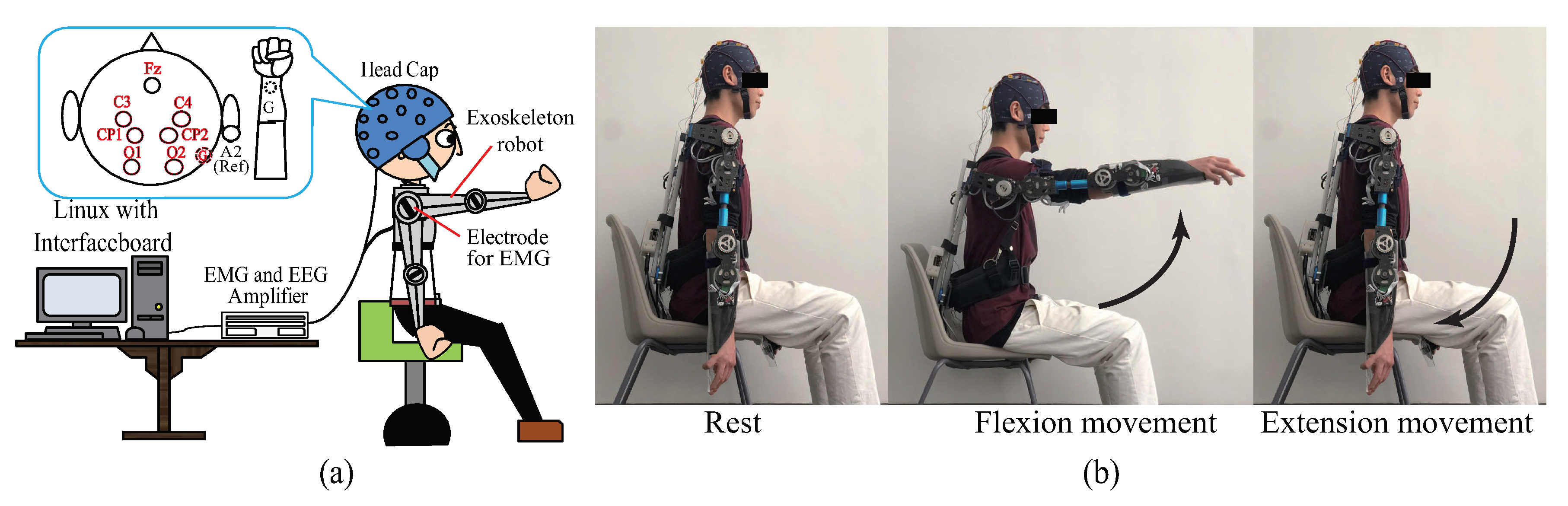
3.1. Experimental Setup
3.2. Task
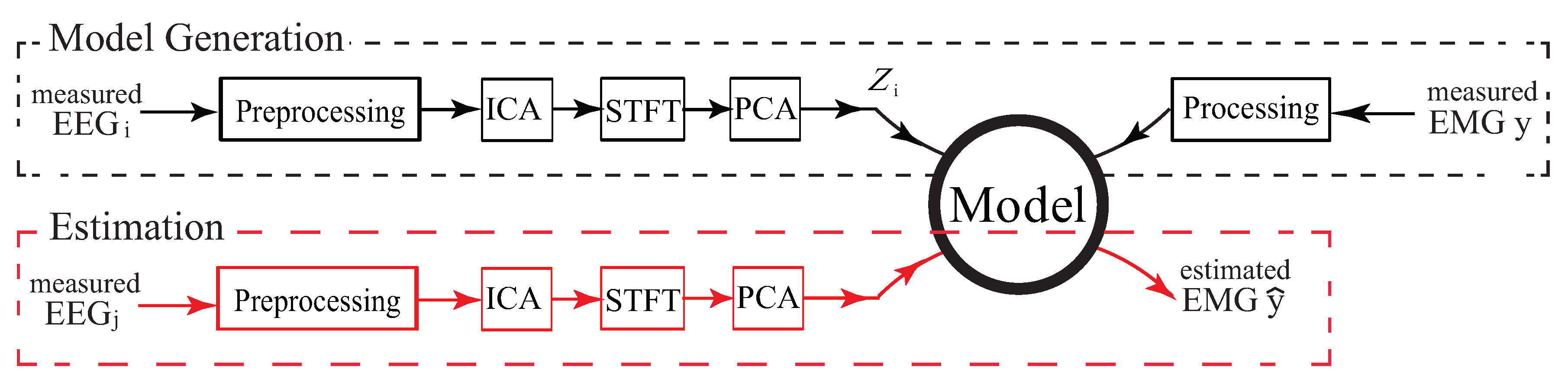
3.3. Model
3.3.1. EEG and EMG Signal Pre-Processing and Independent Component Analysis (ICA)
3.3.2. Feature Extraction by STFT and PCA
3.3.3. PCA-Based EEG—EMG Model
4. Data Analysis and Results
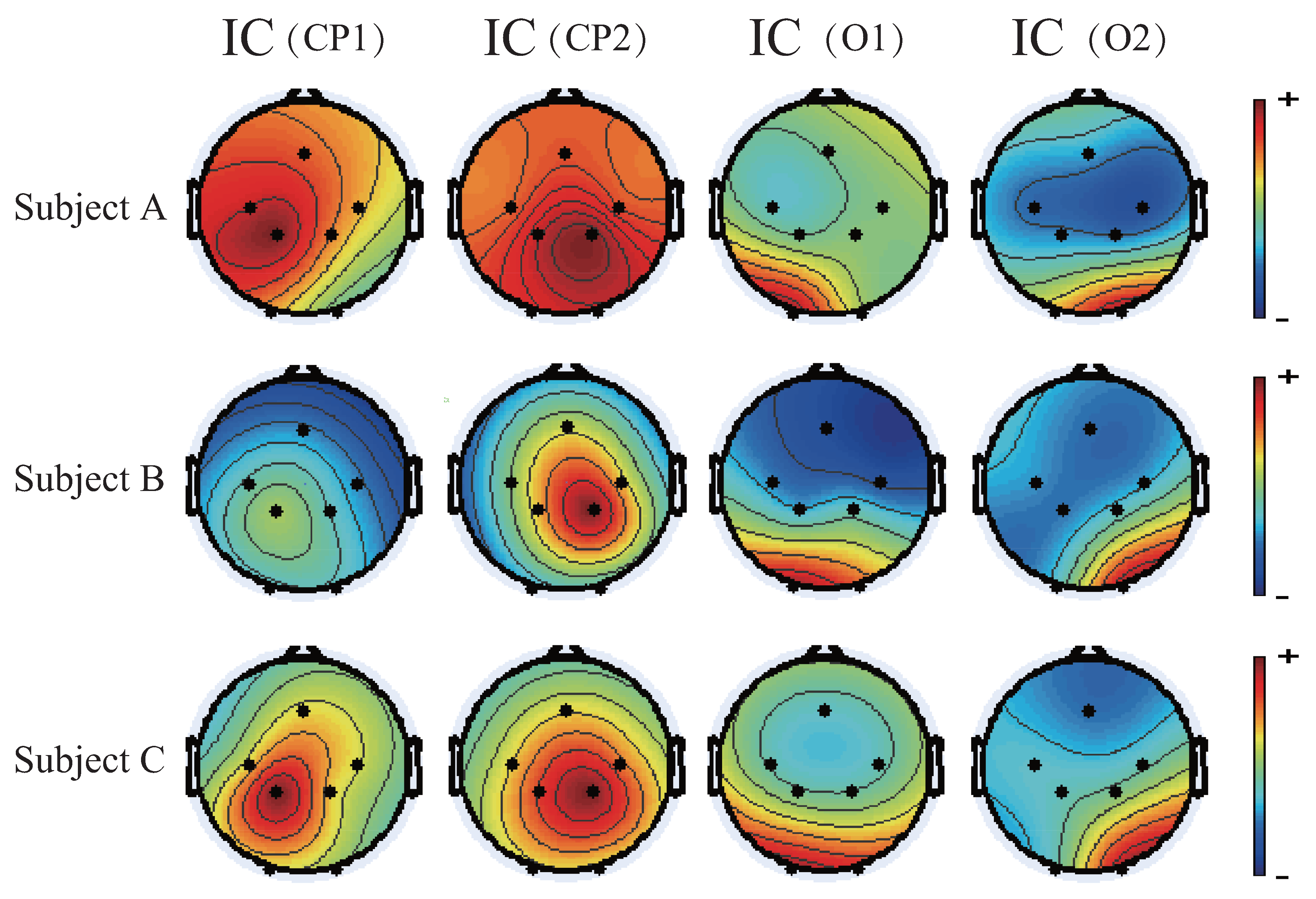
4.1. Motion-Related Independent Components
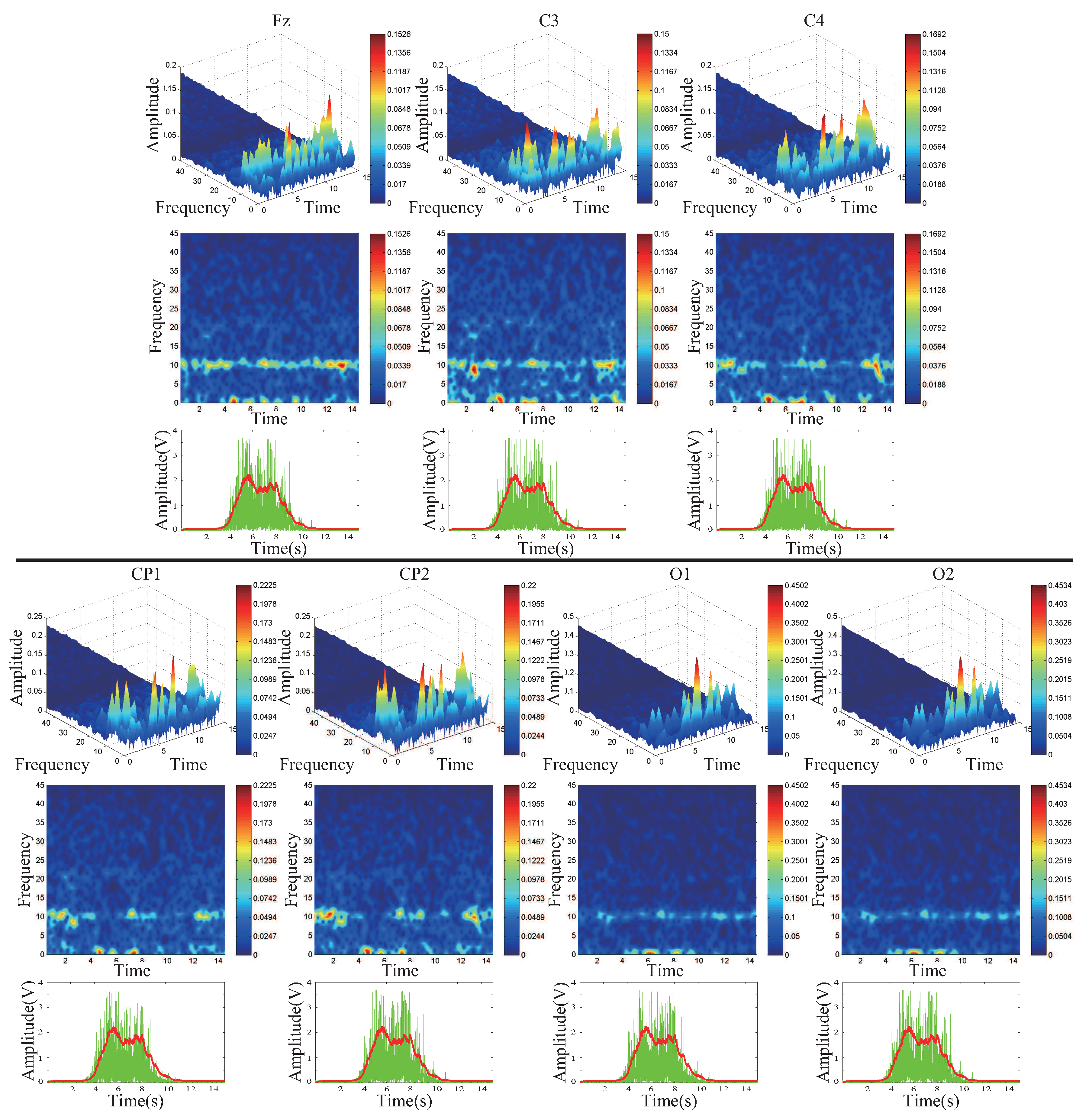
4.2. Feature Extraction by STFT and PCA
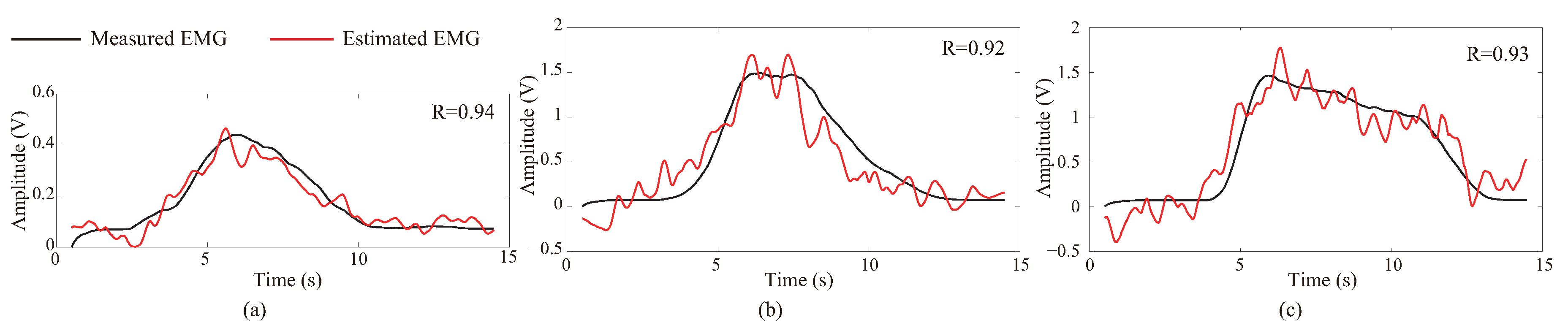
4.3. Results of EMG Estimation
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| BMI | Brain-machine interface |
| EEG | Electroencephalography |
| EMG | Electromyography |
| HAL | Hybrid Assistive Limb |
| fMRI | functional magnetic resonance imaging |
| MEG | magnetoencephalography |
| ICA | Independent component analysis |
| STFT | Short-time Fourier transform |
| PCA | Principal component analysis |
| A/D | Analog/Digital |
| IC | Independent component |
| PC | Principal component |
References
- Herr, H. Exoskeletons and orthoses: Classification, design challenges and future directions. J. Neuroeng. Rehabil. 2009, 6, 1–9. [Google Scholar] [CrossRef]
- Sankai, Y. HAL: Hybrid assistive limb based on cybernics. In Robotics Research; Springer: Berlin/Heidelberg, Germany, 2010; pp. 25–34. [Google Scholar]
- Kiguchi, K.; Hayashi, Y. An EMG-based control for an upper-limb power-assist exoskeleton robot. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2012, 42, 1064–1071. [Google Scholar] [CrossRef] [PubMed]
- Gopura, R.A.; Kiguchi, K.; Li, Y. SUEFUL-7: A 7DOF upper-limb exoskeleton robot with muscle-model-oriented EMG-based control. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, St. Louis, MO, USA, 10–15 October 2009; pp. 1126–1131. [Google Scholar]
- Strausser, K.A.; Kazerooni, H. The development and testing of a human machine interface for a mobile medical exoskeleton. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, 25–30 September 2011; pp. 4911–4916. [Google Scholar]
- Huo, W.; Huang, J.; Wang, Y.; Wu, J.; Cheng, L. Control of upper-limb power-assist exoskeleton based on motion intention recognition. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 2243–2248. [Google Scholar]
- Huang, J.; Huo, W.; Xu, W.; Mohammed, S.; Amirat, Y. Control of upper-limb power-assist exoskeleton using a human-robot interface based on motion intention recognition. IEEE Trans. Autom. Sci. Eng. 2015, 12, 1257–1270. [Google Scholar] [CrossRef]
- Gopura, R.A.R.C.; Kiguchi, K. Development of a 6DOF exoskeleton robot for human upper-limb motion assist. In Proceedings of the 2008 4th International Conference on Information and Automation for Sustainability, Colombo, Sri Lanka, 12–14 December 2008; pp. 13–18. [Google Scholar]
- Lenzi, T.; De Rossi, S.; Vitiello, N.; Carrozza, M. Proportional emg control for upper-limb powered exoskeletons. In Proceedings of the Engineering in Medicine and Biology Society, EMBC, 2011 Annual International Conference of the IEEE, Boston, MA, USA, 30 August–3 September 2011; pp. 628–631. [Google Scholar]
- Lenzi, T.; De Rossi, S.; Vitiello, N.; Chiri, A.; Roccella, S.; Giovacchini, F.; Vecchi, F.; Carrozza, M.C. The neuro-robotics paradigm: NEURARM, NEUROExos, HANDEXOS. In Proceedings of the 2009 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Minneapolis, MN, USA, 3–6 September 2009; pp. 2430–2433. [Google Scholar]
- Gopura, R.D.; Bandara, S.V.; Gunasekara, J.M.P.; Jayawardane, T.S.S. Recent trends in EMG-Based control methods for assistive robots. Electrodiag. New Front. Clin. Res. 2013, 237–268. [Google Scholar] [CrossRef]
- Kiguchi, K.; Tanaka, T.; Fukuda, T. Neuro-fuzzy control of a robotic exoskeleton with EMG signals. IEEE Trans. Fuzzy Syst. 2004, 12, 481–490. [Google Scholar] [CrossRef]
- Tariq, M.; Trivailo, P.M.; Simic, M. EEG-based BCI control schemes for lower-limb assistive-robots. Front. Hum. Neurosci. 2018, 12, 312. [Google Scholar] [CrossRef]
- Tucker, M.R.; Olivier, J.; Pagel, A.; Bleuler, H.; Bouri, M.; Lambercy, O.; del RMillan, J.; Riener, R.; Vallery, H.; Gassert, R. Control strategies for active lower extremity prosthetics and orthotics: A review. J. Neuroeng. Rehabil. 2015, 12, 1. [Google Scholar] [CrossRef]
- Liu, C.; Zhu, C.; Liang, H.; Yoshioka, M.; Murata, Y.; Yu, Y. Development of A Light Wearable Exoskeleton for Upper Extremity Augmentation. In Proceedings of the 2016 23rd International Conference on Mechatronics and Machine Vision in Practice (M2VIP 2016), Nanjing, China, 28–30 November 2016; Volume 11, pp. 1–6. [Google Scholar]
- Huang, H.; Kuiken, T.A.; Lipschutz, R.D. A Strategy for Identifying Locomotion Modes Using Surface Electromyography. IEEE Trans. Biomed. Eng. 2009, 56, 65–73. [Google Scholar] [CrossRef]
- Kuai, H.; Zhong, N. The extensible Data-Brain model: Architecture, applications and directions. J. Comput. Sci. 2020, 101103. [Google Scholar] [CrossRef]
- Lebedev, M.A.; Nicolelis, M.A.L. Brain-machine interfaces: From basic science to neuroprostheses and neurorehabilitation. Physiol. Rev. 2017, 97, 767–837. [Google Scholar] [CrossRef]
- Birbaumer, N. Breaking the silence: Brain–computer interfaces (BCI) for communication and motor control. Psychophysiology 2006, 43, 517–532. [Google Scholar] [CrossRef] [PubMed]
- Paek, A.Y.; Brown, J.D.; Gillespie, R.B.; O’Malley, M.K.; Shewokis, P.A.; Contreras-Vidal, J.L. Reconstructing surface emg from scalp eegs during myoelectric control of a closed looped prosthetic device. In Proceedings of the 2013 35th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Osaka, Japan, 3–7 July 2013; pp. 5602–5605. [Google Scholar]
- Yoshimura, N.; Dasalla, C.S.; Hanakawa, T.; Sato, M.A.; Koike, Y. Reconstruction of flexor and extensor muscle activities from electroencephalography cortical currents. NeuroImage 2012, 59, 1324–1337. [Google Scholar] [CrossRef] [PubMed]
- Nakagome, S.; Luu, T.P.; Brantley, J.A.; Contreras-Vidal, J.L. Prediction of EMG envelopes of multiple terrains over-ground walking from EEG signals using an unscented Kalman filter. In Proceedings of the 2017 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Banff, AB, Canada, 5–8 October 2017; pp. 3175–3178. [Google Scholar]
- Schünke, M.; Schulte, E.; Schumacher, U. Prometheus LernAtlas der Anatomie; Thieme: New York, NY, USA, 2012. [Google Scholar]
- Kiguchi, K.; Fukuda, T. A 3 DOF exoskeleton for upper limb motion assist: Consideration of the effect of bi-articular muscles. In Proceedings of the IEEE International Conference on Robotics and Automation, New Orleans, LA, USA, 26 April–1 May 2004; pp. 2424–2429. [Google Scholar]
- Junius, K.; Moltedo, M.; Cherelle, P.; Rodriguez-Guerrero, C.; Vanderborght, B.; Lefeber, D. Biarticular elements as a contributor to energy efficiency: Biomechanical review and application in bio-inspired robotics. Bioinspir. Biomimetics 2017, 12, 061001. [Google Scholar] [CrossRef] [PubMed]
- Beuchat, N.J.; Chavarriaga, R.; Degallier, S.; del R Millan, J. Offline decoding of upper limb muscle synergies from eeg slow cortical potentials. In Proceedings of the 2013 35th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Osaka, Japan, 3–7 July 2013; pp. 3594–3597. [Google Scholar]
- Wattanaprakornkul, D.; Halaki, M.; Boettcher, C.; Cathers, I.; Ginn, K.A. A comprehensive analysis of muscle recruitment patterns during shoulder flexion: An electromyographic study. Clin. Anat. 2011, 24, 619–626. [Google Scholar] [CrossRef] [PubMed]
- Kronberg, M.; Németh, G.; Broström, L.A. Muscle activity and coordination in the normal shoulder. An electromyographic study. Clin. Orthop. Relat. Res. 1990, 257, 76–85. [Google Scholar]
- Wattanaprakornkul, D.; Cathers, I.; Halaki, M.; Ginn, K.A. The rotator cuff muscles have a direction specific recruitment pattern during shoulder flexion and extension exercises. J. Sci. Med. Sport 2011, 14, 376–382. [Google Scholar] [CrossRef]
- Kuechle, D.K.; Newman, S.R.; Itoi, E.; Morrey, B.F.; An, K.N. Shoulder muscle moment arms during horizontal flexion and elevation. J. Shoulder Elbow Surg. 1997, 6, 429–439. [Google Scholar] [CrossRef]
- Clancy, E.A.; Hogan, N. Relating agonist-antagonist electromyograms to joint torque during isometric, quasiisotonic, nonfatiguing contractions. IEEE Trans. Biomed. Eng. 1997, 41, 1024–1028. [Google Scholar] [CrossRef]
- Hof, A.L.; Van Den Berg, J.W. Linearity between the weighted sum of the EMGs of the human triceps surae and the total torque. J. Biomech. 1977, 10, 529–539. [Google Scholar] [CrossRef]
- Kutch, J.J.; Buchanan, T.S. Human elbow joint torque is linearly encoded in electromyographic signals from multiple muscles. Neurosci. Lett. 2001, 311, 97–100. [Google Scholar] [CrossRef]
- Kizuka, T.; Masuda, T.; Kiryu, T.; Sadoyama, T. Practical Usage of Surface Electromyogram (Biomechanism Library), 1st ed.; Tokyo Denki University Press: Tokyo, Japan, 2006. (In Japanese) [Google Scholar]
- Doležal, J.; Štastný, J.; Sovka, P. Recognition of direction of finger movement from EEG signal using markov models. In Proceedings of the IFMBE Proceedings (Prague), Prague, Czech Republic, 3–9 June 2018; pp. 1727–1983. [Google Scholar]
- Št’astnỳ, J.; Sovka, P.; Stančák, A. EEG signal classification: Introduction to the problem. Radioengineering 2003, 12, 51–55. [Google Scholar]
- Buzsaki, G. Rhythms of the Brain; Oxford University Press: New York, NY, USA, 2006; Available online: https://neurophysics.ucsd.edu/courses/physics_171/Buzsaki%20G.%20Rhythms%20of%20the%20brain.pdf (accessed on 7 October 2020).
- Klimesch, W. EEG alpha and theta oscillations reflect cognitive and memory performance: A review and analysis. Brain Res. Rev. 1999, 29, 169–195. [Google Scholar] [CrossRef]
- Sagara, K.; Tanaka, Y.; Takeichi, H.; Yamashita, S.; Hasegawa, R.; Okabe, T.; Maeda, T. Brain Communication—The Brain and Means of Society Communication; Electronics, Information and Communication Engineers: Tokyo, Japan, 2011. (In Japanese) [Google Scholar]
- Gratton, G.; Coles, M.G.; Donchin, E. A new method for off-line removal of ocular artifact. Electroencephalogr. Clin. Neurophysiol. 1983, 55, 468–484. [Google Scholar] [CrossRef]
- Hillyard, S.A.; Galambos, R. Eye-movement artifact in the CNV. Electroencephalogr. Clin. Neurophysiol. 1970, 28, 173–182. [Google Scholar] [CrossRef]
- Verleger, R.; Gasser, T.; Möcks, J. Correction of EOG artifacts in event-related potentials of EEG: Aspects of reliability and validity. Psychophysiology 1982, 19, 472–480. [Google Scholar] [CrossRef] [PubMed]
- Whitton, J.L.; Lue, F.; Moldofsky, H. A spectral method for removing eye-movement artifacts from the EEG. Electroencephalogr. Clin. Neurophysiol. 1978, 44, 735–741. [Google Scholar] [CrossRef]
- Woestenburg, J.C.; Verbaten, M.N.; Slangen, J.L. The removal of the eye-movement artifact from the EEG by regression analysis in the frequency domain. Biol. Psychol. 1983, 16, 127–147. [Google Scholar] [CrossRef]
- Berg, P.; Scherg, M. Dipole models of eye activity and its application to the removal of eye artifacts from the EEG ad MEG. Clin. Phys. Physiol. Meas. 1991, 12 (Suppl. A), 49–54. [Google Scholar] [CrossRef]
- Berg, P.; Scherg, M. Dipole models of eye movements and blinks. Electroencephalogr. Clin. Neurophysiol. 1991, 79, 36–44. [Google Scholar] [CrossRef]
- Lagerlund, T.D.; Sharbrough, F.W.; Busacker, N.E. Spatial filtering of multichannel electroencephalographic recordings through principal component analysis by singular value decomposition. J. Clin. Neurophysiol. 1997, 14, 73–82. [Google Scholar] [CrossRef]
- Jung, T.P.; Makeig, S.; Humphries, C.; Lee, T.W.; Mckeown, M.J.; Iragui, V.; Sejnowski, T.J. Removing electroencephalographic artifacts by blind source separation. Psychophysiology 2000, 37, 163–178. [Google Scholar] [CrossRef] [PubMed]
- Song, D.; Hendrickson, P.; Marmarelis, V.Z.; Aguayo, J.; He, J.; Loeb, G.E.; Berger, T.W. Predicting EMG with generalized Volterra kernel model. In Proceedings of the 2008 30th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Vancouver, BC, Canada, 20–25 August 2008; pp. 201–204. [Google Scholar]
- Rivera-Alvidrez, Z.; Kalmar, R.S.; Ryu, S.I.; Shenoy, K.V. Low-dimensional neural features predict muscle EMG signals. In Proceedings of the 2010 Annual International Conference of the IEEE Engineering in Medicine and Biology, Buenos Aires, Argentina, 31 August–4 September 2010; pp. 6027–6033. [Google Scholar]
- Zhang, H.; Ma, C.; He, J. Predicting lower limb muscular activity during standing and squatting using spikes of primary motor cortical neurons in monkeys. In Proceedings of the 2010 Annual International Conference of the IEEE Engineering in Medicine and Biology, Buenos Aires, Argentina, 31 August–4 September 2010; pp. 4124–4127. [Google Scholar]
- Flint, R.D.; Ethier, C.; Oby, E.R.; Miller, L.E.; Slutzky, M.W. Local field potentials allow accurate decoding of muscle activity. Neurophysiol 2012, 108, 18–24. [Google Scholar] [CrossRef] [PubMed]
- Ganesh, G.; Burdet, E.; Haruno, M.; Kawato, M. Sparse linear regression for reconstructing muscle activity from human cortical fMRI. NeuroImage 2008, 42, 1463–1472. [Google Scholar] [CrossRef] [PubMed]

| Contribution Ratio of PC1 | Contribution Ratio of PC2 | Cumulative Contribution Ratio (PC1 + PC2) | ||
|---|---|---|---|---|
| Subject A | Max. | 91.2 | 25.0 | 97.6 |
| Min. | 58.3 | 6.23 | 82.0 | |
| Average | 73.7 ± 10.1 | 16.1 ± 6.00 | 89.8 ± 5.26 | |
| Subject B | Max. | 92.1 | 27.4 | 97.5 |
| Min. | 50.6 | 2.93 | 70.0 | |
| Average | 73.5 ± 11.2 | 13.9 ± 6.15 | 87.4 ± 6.32 | |
| Subject C | Max. | 82.7 | 27.6 | 95.2 |
| Min. | 47.6 | 8.41 | 66.0 | |
| Average | 64.0 ± 12.1 | 17.8 ± 5.42 | 81.8 ± 9.01 |
| Correlation Coefficient (R) | Standard Error | |
|---|---|---|
| Subject A | 0.74 | 0.004 |
| Subject B | 0.83 | 0.002 |
| Subject C | 0.77 | 0.002 |
| Reference | Subject | Task | Measurement | Accuracy |
|---|---|---|---|---|
| [49] | Monkeys | Reach to grasp | M1 spike * | r = 0.69 |
| [50] | Monkeys | Center out reach | M1/PMd neuron spikes * | = 0.65 |
| [51] | Monkeys | Stand and squat | M1 Spike | = 0.74 |
| [52] | Monkeys | Reach to grasp the wrist | M1 spike and LFP * | VAF = 0.67 |
| [53] | Humans | Isometric wrist movements | fMRI BOLD response * | = 0.47 |
| [21] | Humans | Isometric wrist | ||
| flexion/extension | Scalp EEG | = 0.55 | ||
| [20] | Humans | Prosthesis control | ||
| with biceps contraction | Scalp EEG | r = 0.59 | ||
| Current Study | Humans | Flexion/extension | r = 0.78 | |
| of shoulder joint | Scalp EEG | ( = 0.61) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, H.; Yu, Y.; Mochida, M.; Liu, C.; Ueda, N.; Li, P.; Zhu, C. EEG-Based EMG Estimation of Shoulder Joint for the Power Augmentation System of Upper Limbs. Symmetry 2020, 12, 1851. https://doi.org/10.3390/sym12111851
Liang H, Yu Y, Mochida M, Liu C, Ueda N, Li P, Zhu C. EEG-Based EMG Estimation of Shoulder Joint for the Power Augmentation System of Upper Limbs. Symmetry. 2020; 12(11):1851. https://doi.org/10.3390/sym12111851
Chicago/Turabian StyleLiang, Hongbo, Yingxin Yu, Mika Mochida, Chang Liu, Naoya Ueda, Peirang Li, and Chi Zhu. 2020. "EEG-Based EMG Estimation of Shoulder Joint for the Power Augmentation System of Upper Limbs" Symmetry 12, no. 11: 1851. https://doi.org/10.3390/sym12111851
APA StyleLiang, H., Yu, Y., Mochida, M., Liu, C., Ueda, N., Li, P., & Zhu, C. (2020). EEG-Based EMG Estimation of Shoulder Joint for the Power Augmentation System of Upper Limbs. Symmetry, 12(11), 1851. https://doi.org/10.3390/sym12111851






