A Novel Strategy for Complete and Phase Robust Synchronizations of Chaotic Nonlinear Systems

Abstract

Our work here is to propose a novel technique by which chaos complete and phase synchronizations can be accomplished via a low-cost scheme. We call the proposed technique a “single-state feedback track synchronization control algorithm”. A single-state feedback track synchronization control algorithm is designed so that both complete and phase synchronizations can be accomplished using the same controller. Complete synchronization between two chaotic systems means complete symmetry between them, but phase synchronization means complete symmetry with a phase shift. In addition, the proposed method is applied to the synchronization of two identical chaotic Lorenz models. The effectiveness and robustness of the proposed algorithm is well illustrated via exhaustive numerical simulation experiments based on the Matlab toolbox of the powerful genetic algorithm. The robustness of the proposed algorithm motivated us to apply this method of synchronization in a secure communication application.

1. Introduction

There are two types of chaotic synchronization [1,2]: chaos phase synchronization (CPS) and chaos complete (or full) synchronization (CS). CPS [3,4,5] is a kind of synchronization by which a chaotic oscillator tunes its internal dynamics’ frequencies according to the effects of an external force or to the behaviors of another selected chaotic system, however, the variations of their amplitudes are still uncorrelated. There is a wide range of distinct systems that demonstrate this type of synchronization in physics, chemistry and biology, in addition to coupled electronic oscillating circuits [3], plasma evacuation tubes driven by wave generators with low amplitude [6], globally paired electrochemical oscillator arrays [7], human visual responses that are phase-locked [8] and the flow of blood to adjacent operational units inside the kidney [9].

Considering simple topology systems (e.g., systems whose attractors are of a spiral type and the Rössler system), the chaotic oscillation’s phase $\varphi \left(t\right)$ is defined, in the polar coordinate framework of a suitable projection level $(x,$$y),$ as an angle where $\varphi \left(t\right)={tan}^{-1}\left(\frac{y}{x}\right)$. Generally, the boundedness of the phase difference between two chaotic models implies chaotic phase synchronization between them [10], while CS is achieved when the phase difference approaches zero as time approaches infinity. Similarly, the amplitude of the chaotic signal can be defined instantaneously as $A={(x^2+y^2)}^{\frac{1}{2}}$. Two chaotic models realize CPS in situations where those amplitudes are linearly independent (uncorrelated) and chaotic. Applying Hilbert transformation is sometimes carried out to obtain a more comprehensive definition of the chaotic signals’ phase [11]. In addition, the phase may be defined as a fraction of a complete period.

Via numerical trials, we can monitor the method by which the frequency spectrum harmonics for an obliged chaotic system approach the controlling frequency in a selected period. The switch from phase synchronization behavior to non-synchronization behavior of a controlled chaotic system is shown via certain changes in the Lyapunov exponent and via certain variations in the shape of the Poincaré map. In theory, the major issue is understanding the regulation of the huge group of unsteady cyclic paths that model the state of chaotic synchronization [12].

The complete synchronization (CS) notion came about through noting [13] that a couple of similar chaotic systems with suitable conditions can synchronize their changes completely, and the status of synchronization can be stabilized under accidental disturbances. This observation has attracted great attention via its possible utilization in safe communication applications that have become very important [14,15]. Theoretically, the great attention on CS is due to the several new ideas and phenomenons it has caused, such as soft attraction [16], puzzled and mixed basins of attraction [17], discontinuous intermittence [18] and bubbling attractors [19]. Specific attention is given to the design of the attraction basin for the state of chaotic synchronization [20] and to establishing necessary and sufficient synchronization conditions [21]. The traditional synchronization condition relying on Lyapunov conditions is not necessary, however it is sufficient. In addition, there is an insufficient alternate case that requires the largest transversal Lyapunov exponent to be negative.

From all of the chaotic systems, the chaotic Lorenz model is commonly selected because it involves numerous characteristics of chaotic behaviors [22,23]. For a real framework, it commonly operates in the required stable work regions. Consequently, the tracking of controlled chaotic models (where states are driven to track certain predetermined reference values) has attracted great interest. In [24], a tracking control method was applied to control the Lorenz model. In [24], the tracking reference values were supposed to obey certain conditions, and this limited its ability to be applied in several real-world cases. In [25], the author suggested a new track control technique to avert the restrictions suggested in [24]. Using fewer sensors in a control strategy is preferred due to lower cost and simple realization.

In [25,26,27], an easy controller with output/state feedback was applied to control a general chaotic model. The studies in [25,27,28] motivated us to propose the single-state feedback track synchronization control technique that is proved in our study here. Furthermore, lack of certainty cannot be avoided in real applications. Consequently, robust control has become a significant aspect of controller design [25,28,29].

Although there is chaos in chaotic systems, they also have symmetrical features. In this research, we show that there is symmetry in the solutions of the chaotic system under study. In addition, synchronization between two chaotic systems means making them symmetrical to each other and this is the main aim of our proposed control strategy. Complete synchronization between two chaotic systems means complete symmetry between them, but phase synchronization means complete symmetry with a phase shift. In this study, based on a genetic algorithm (GA), a novel robust single-state feedback tracking synchronization control of two identical chaotic systems will be proposed. For an alternative approach, the gradient-based (or mathematical programming) method for solving differential-algebraic equation systems, interested readers can refer to [30] and the references cited there.

The main aim of this work is to design a new robust scheme by which two important types of chaotic synchronization (i.e., chaotic complete synchronization and chaotic phase synchronization) can be achieved based on a single-state feedback track synchronization control algorithm using the same controller. In addition, the robustness of the proposed controller is proved using a genetic algorithm. A new secure communication plan is also developed relying on the proposed robust single-state feedback track synchronization method as an application. The track control method is applied only to control chaotic systems [25]. To the best of our knowledge, this is the first time it has been applied in chaos synchronization and it is the first time two types of synchronization using the same controller have been achieved. In addition, phase synchronization is accomplished via a single-state feedback track controller that is less costly than feeding back all system states.

The paper is designed as follows. Following the current section, a novel single-state feedback track synchronization control algorithm is suggested in Section 2. The proposed algorithm is applied to the synchronization of two identical Lorenz chaotic systems in Section 3. A robust single-state feedback track synchronization optimal control design is produced in Section 4. As an application, the proposed robust track synchronization controller is applied to the development of a secure communication scheme in Section 5. Intensive simulation experiments are also presented in Section 3, Section 4 and Section 5. Our conclusions are presented in Section 6.

2. Track Synchronization Algorithm

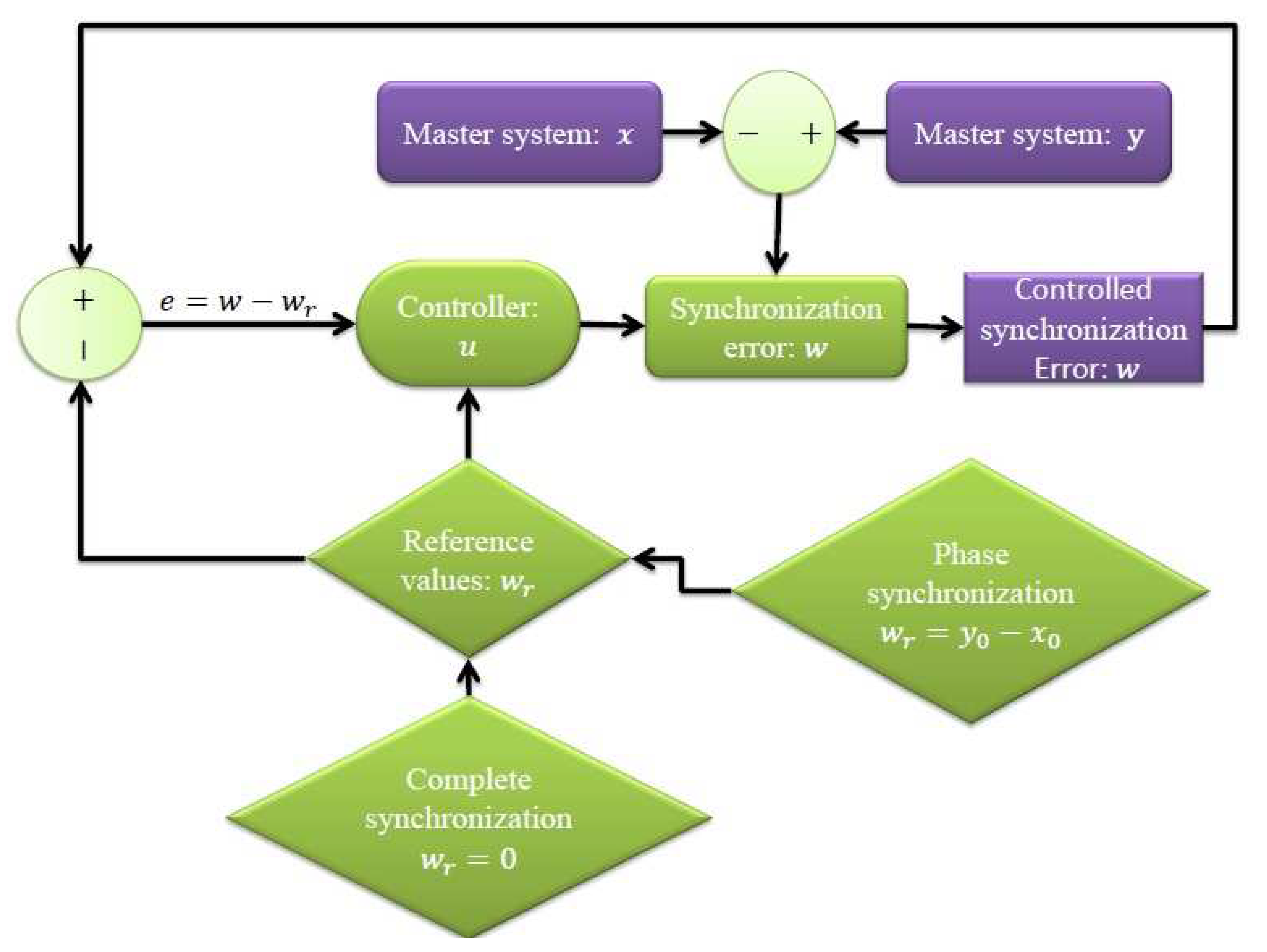
In this section, we propose an algorithm by which the complete and phase synchronization can be done in the same structure (see Figure 1). The main idea of it is to give reference values for the synchronization errors. If the reference values of the synchronization errors are all zero then a complete synchronization is achieved, but if their values are not equal to zero a phase synchronization is achieved. All previous studies on the phase synchronization were done depending on the stability theory only, which needs to feedback all system states, but here we achieve the phase synchronization based on the proposed single-state feedback track synchronization control algorithm.

Let the states of the n-dimensional master and slave systems be denoted by $x_i$ and $y_i+u_i$, respectively, where $u_i$’s are the control signals. The synchronization errors are denoted by $w_i=y_i+u_i-x_i$. This means that we have three systems: master, slave and synchronization errors systems. Our task is to control the synchronization errors system by proposing a controller such that the synchronization errors track predetermined reference values $w_{ir}$.

• Construct the synchronization errors system $w_i=y_i-x_i$.
• Construct the track synchronization control signals $u_i$.
• Construct the track synchronization control errors system $e_i=w_i-w_{ir}$.
• Apply stability criteria to calculate the range of the controller such that the track errors system is asymptotically stable.
• If the reference values $w_{ir}=0$ then a complete synchronization will be reached while a phase synchronization is accomplished if $w_{ir}=y_i\left(0\right)-x_i\left(0\right)$.

Let the master system be denoted by $d{x}_i/dt=f_i\left(x_i\right)$ and the slave synchronized system be denoted by $d{y}_i/dt=f_i\left(y_i\right)+u_i$. Then the synchronization errors system can be constructed as

$$d{w}_i/dt=f_i\left(y_i\right)+u_i-f_i\left(x_i\right)=g_i\left(w_i\right)+u_i,$$

(1)

where $w_i=y_i-x_i$.

The track controller is proposed in such a way that feeding back only one state variable reduces the number of sensors. Assuming that the only measurable state is $w_h$, then the proposed controller takes the form

$$u_i=\left\{\begin{array}{c}k(w_h-w_{hr})-f_h\left(w_{hr}\right)\mathrm{if}i=h,\hfill \\ -f_i\left(w_{ir}\right)\mathrm{otherwise},\hfill \end{array}\right.$$

(2)

where k is the gain of the closed loop track synchronization controller.

By putting $w_i=w_{ir}+e_i$ in the (1), the track error system can be constructed as

$$d{e}_i/dt=H(x,y,k,w_r)$$

(3)

The main task after that is to calculate the value of the controller gain k that ensures that the track synchronization control errors system (3) is asymptotically stable.

In the next section, we apply this proposed method to the synchronization of two identical Lorenz systems.

3. Implementation of the Novel Track Synchronization Controller

In this section, we apply the proposed algorithm to synchronize two identical Lorenz chaotic systems via two types of synchronizations (i.e., complete and phase synchronization) by the same single-state feedback controller which has not been applied before in the literature.

The master and slave systems are selected to be two identical Lorenz systems in the following forms:

$$\begin{array}{ccc}\hfill \frac{d{x}_1}{dt}& =& -\sigma x_1+\sigma x_2,\hfill \\ \hfill \frac{d{x}_2}{dt}& =& r{x}_1-x_2-x_1{x}_3,\hfill \\ \hfill \frac{d{x}_3}{dt}& =& x_1{x}_2-b{x}_3.\hfill \end{array}$$

(4)

And

$$\begin{array}{ccc}\hfill \frac{d{y}_1}{dt}& =& -\sigma y_1+\sigma y_2+u_1,\hfill \\ \hfill \frac{d{y}_2}{dt}& =& r{y}_1-y_2-y_1{y}_3+u_2,\hfill \\ \hfill \frac{d{y}_3}{dt}& =& y_1{y}_2-b{y}_3+u_3.\hfill \end{array}$$

(5)

where the parameters are selected here to be $(\sigma ,b,r)=(10,8/3,28).$

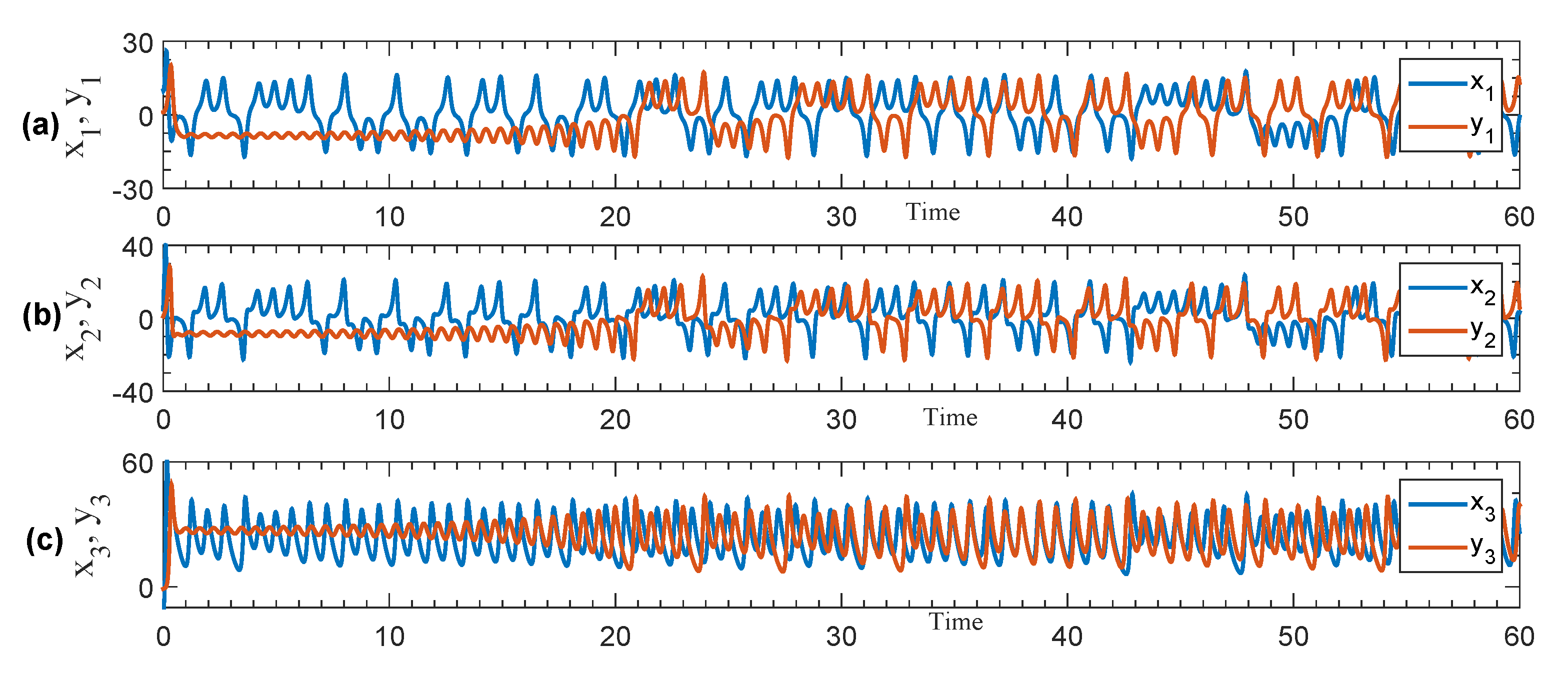
Figure 2 shows the time history of the master and the slave Lorenz chaotic models, where the initial conditions are $x_0=(10,5,-15)$ and $y_0=(1,1,-1)$. The difference between the two systems is clear due to the difference in their initial values.

Let the synchronization errors system be $w_1=y_1-x_1$, $w_2=y_2-x_2$ and $w_3=y_3-x_3$. Then the synchronization errors system can be represented as follows:

$$\begin{array}{ccc}\hfill \frac{d{w}_1}{dt}& =& -\sigma w_1+\sigma w_2+u_1,\hfill \\ \hfill \frac{d{w}_2}{dt}& =& r{w}_1-w_2-x_3{w}_1-y_1{w}_3+u_2,\hfill \\ \hfill \frac{d{w}_3}{dt}& =& x_1{w}_2+y_2{w}_1-b{w}_3+u_3.\hfill \end{array}$$

(6)

Our task here is to control the synchronization errors system using the single-state feedback track control strategy that has not been used before for this purpose. This method enables us to control the synchronization errors to track any predetermined values $w_{ir}$ (reference values) for all $i\in \{1,2,3\}$.

Assume that the only measurable state in the system (6) is $w_2$, then it is the only one that will be used to construct the closed-loop single-state feedback track control as follows.

The single-state feedback track controller is proposed to be

$$\begin{array}{ccc}\hfill u_1& =& \sigma w_{1r}-\sigma w_{2r},\hfill \\ \hfill u_2& =& k(w_2-w_{2r})-r{w}_{1r}+w_{2r}+x_3{w}_{1r}+y_1{w}_{3r},\hfill \\ \hfill u_3& =& -x_1{w}_{2r}-y_2{w}_{1r}+b{w}_{3r}.\hfill \end{array}$$

(7)

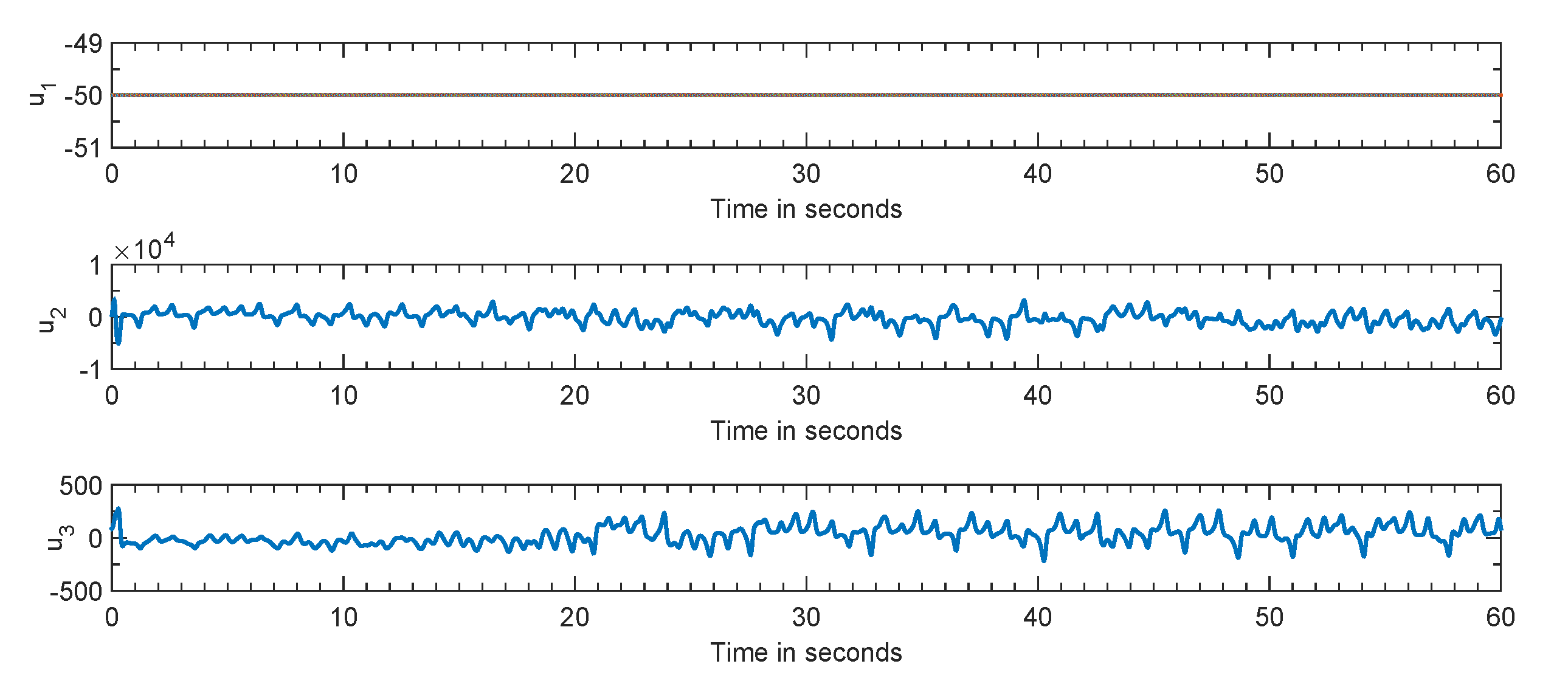
Figure 3 shows the control signals used to derive the synchronization error to follow its selected reference values.

Note that $w_2$ is the only state variable in the synchronization error system which is utilized to formulate the proposed closed-loop feedback and k is the gain of the proposed track controller with single-state feedback.

The single-state feedback closed-loop controlled synchronization error system becomes

$$\begin{array}{ccc}\hfill \frac{d{w}_1}{dt}& =& -\sigma w_1+\sigma w_2+u_1,\hfill \\ \hfill \frac{d{w}_2}{dt}& =& r{w}_1-w_2-x_3{w}_1-y_1{w}_3+u_2,\hfill \\ \hfill \frac{d{w}_3}{dt}& =& x_1{w}_2+y_2{w}_1-b{w}_3+u_3.\hfill \end{array}$$

(8)

Let $e_1=w_1-w_{1r}$, $e_2=w_2-w_{2r}$, $e_3=w_3-w_{3r}.$ Substituting $w_1=w_{1r}+e_1$, $w_2=w_{2r}+e_2$, $w_3=w_{3r}+e_3$ and (7) in (8), the tracking error dynamics of the synchronization error system (6) can be represented as follows:

$$\begin{array}{ccc}\hfill \frac{d{e}_1}{dt}& =& -\sigma e_1+\sigma e_2,\hfill \\ \hfill \frac{d{e}_2}{dt}& =& k{e}_2+r{e}_1-e_2-x_3{e}_1-y_1{e}_3,\hfill \\ \hfill \frac{d{e}_3}{dt}& =& x_1{e}_2+y_2{e}_1-b{e}_3.\hfill \end{array}$$

(9)

It is obvious that the point $E_0=(0,0,0)$ is an equilibrium point of the tracking error system (9) whose Jacobian matrix is calculated and can be written as follows:

$$\left[\begin{array}{ccc}-\sigma & \sigma & 0\\ r-x_3& k-1& -y_1\\ y_2& x_1& -b\end{array}\right]$$

(10)

Our task here is to find the range of synchronization controller gain k that guarantees the stability of all Jacobian matrix (10) eigenvalues, which implies that the tracking synchronization control error dynamics $e_1,e_2$ and $e_3$ will be stable at the equilibrium point $E_0=(0,0,0)$ asymptotically. As a result the synchronization errors $w_1$, $w_2$ and $w_3$ will track their references $w_{1r}$, $w_{2r}$ and $w_{3r}$ respectively. The main task is to determine an appropriate control gain k. Our result is recorded in Theorem 1 as follows.

Theorem 1.

The synchronization error system (6) of the Lorenz synchronized systems (5) with the selected set of parameters via the tracking controller (7) can track any predetermined values$w_{1r}$, $w_{2r}$and$w_{3r}$if the controller gain satisfies

$$\begin{array}{ccc}\hfill k& <& min\{b+\sigma +1,(b\sigma +b+\sigma -\sigma (r-x_3)-x_1{y}_1)/(b+\sigma ),\hfill \\ & & -(b(\sigma (r-x_3)-\sigma )+\sigma (x_1{y}_1+y_1{y}_2))/b\sigma ,\frac{-B-\sqrt[2]{B^2-4AC}}{2A}\}\hfill \end{array}$$

where$A=(b+\sigma )$, $B=(-2\sigma -b^2-{\sigma }^2-2b-2b\sigma +r\sigma -\sigma x_3+x_1{y}_1)$and$C=(b+\sigma +2b\sigma -r\sigma +{\sigma }^2+\sigma x_3-x_1{y}_1+b{\sigma }^2+b^2\sigma -r{\sigma }^2+{\sigma }^2{x}_3+b^2-b{x}_1{y}_1+\sigma y_1{y}_2).$

Proof. 

The Jacobian matrix characteristic Equation (10) is written as follows:

$$a_0{\lambda }^3+a_1{\lambda }^2+a_2\lambda +a_3=0,$$

(11)

where

$$a_0=1,a_1=\left(b-k+\sigma +1\right),$$

$$a_2=\left(b\left(\sigma -k+1\right)-\sigma \left(r-x_3\right)-x_1{y}_1-\sigma \left(k-1\right)\right)$$

and

$$a_3=-\left(b\left(\sigma \left(r-x_3\right)+\sigma \left(k-1\right)\right)+x_1{y}_1\left(k-1\right)+x_1{y}_1\left(\sigma -k+1\right)+\sigma y_1{y}_2\right).$$

By applying the Routh–Hurwitz stability test [31], the eigenvalues of (11) have negative real parts if and only if $a_0=1>0;a_1=\left(b-k+\sigma +1\right)>0$, then

$$k<b+\sigma +1;$$

(12)

$a_2=\left(b\left(\sigma -k+1\right)-\sigma \left(r-x_3\right)-x_1{y}_1-\sigma \left(k-1\right)\right)>0$, then

$$k<(b\sigma +b+\sigma -\sigma (r-x_3)-x_1{y}_1)/(b+\sigma );$$

(13)

$a_3=-\left(b\left(\sigma \left(r-x_3\right)+\sigma \left(k-1\right)\right)+x_1{y}_1\left(k-1\right)+x_1{y}_1\left(\sigma -k+1\right)+\sigma y_1{y}_2\right)>0$, then

$$k<-(b(\sigma (r-x_3)-\sigma )+\sigma (x_1{y}_1+y_1{y}_2))/b\sigma \Rightarrow k\mathrm{is}\mathrm{negative};$$

(14)

$a_1{a}_2-a_0{a}_3>0$, then $k^2(b+\sigma )+k(-2\sigma -b^2-{\sigma }^2-2b-2b\sigma +r\sigma -\sigma x_3+x_1{y}_1)+(b+\sigma +2b\sigma -r\sigma +{\sigma }^2+\sigma x_3-x_1{y}_1+b{\sigma }^2+b^2\sigma -r{\sigma }^2+{\sigma }^2{x}_3+b^2-b{x}_1{y}_1+\sigma y_1{y}_2)>0$, then

$$k<\frac{-B-\sqrt[2]{B^2-4AC}}{2A},$$

(15)

where $A=(b+\sigma )$, $B=(-2\sigma -b^2-{\sigma }^2-2b-2b\sigma +r\sigma -\sigma x_3+x_1{y}_1)$ and $C=(b+\sigma +2b\sigma -r\sigma +{\sigma }^2+\sigma x_3-x_1{y}_1+b{\sigma }^2+b^2\sigma -r{\sigma }^2+{\sigma }^2{x}_3+b^2-b{x}_1{y}_1+\sigma y_1{y}_2).$

From (12) to (15), it easy to conclude that $k<min\{b+\sigma +1,(b\sigma +b+\sigma -\sigma (r-x_3)-x_1{y}_1)/(b+\sigma ),-(b(\sigma (r-x_3)-\sigma )+\sigma (x_1{y}_1+y_1{y}_2))/b\sigma ,\frac{-B-\sqrt[2]{B^2-4AC}}{2A}\}$, which completes the proof. □

Numerical Simulation of Tracking Synchronization of Two Identical Lorenz Systems

In this section, numerical simulation of the proposed tracking synchronization of two identical Lorenz systems is performed in order to demonstrate the above algorithm. Furthermore, we numerically solve systems (4) and (5) with parameters $(\sigma ,b,r)=(10,8/3,28)$ and the initial conditions for the master and slave systems as $x_0=(10,5,-15)$ and $y_0=(1,1,-1)$, respectively. The numerical simulation of the proposed algorithm is executed for two cases of synchronization, namely chaotic complete synchronization and chaotic phase synchronization.

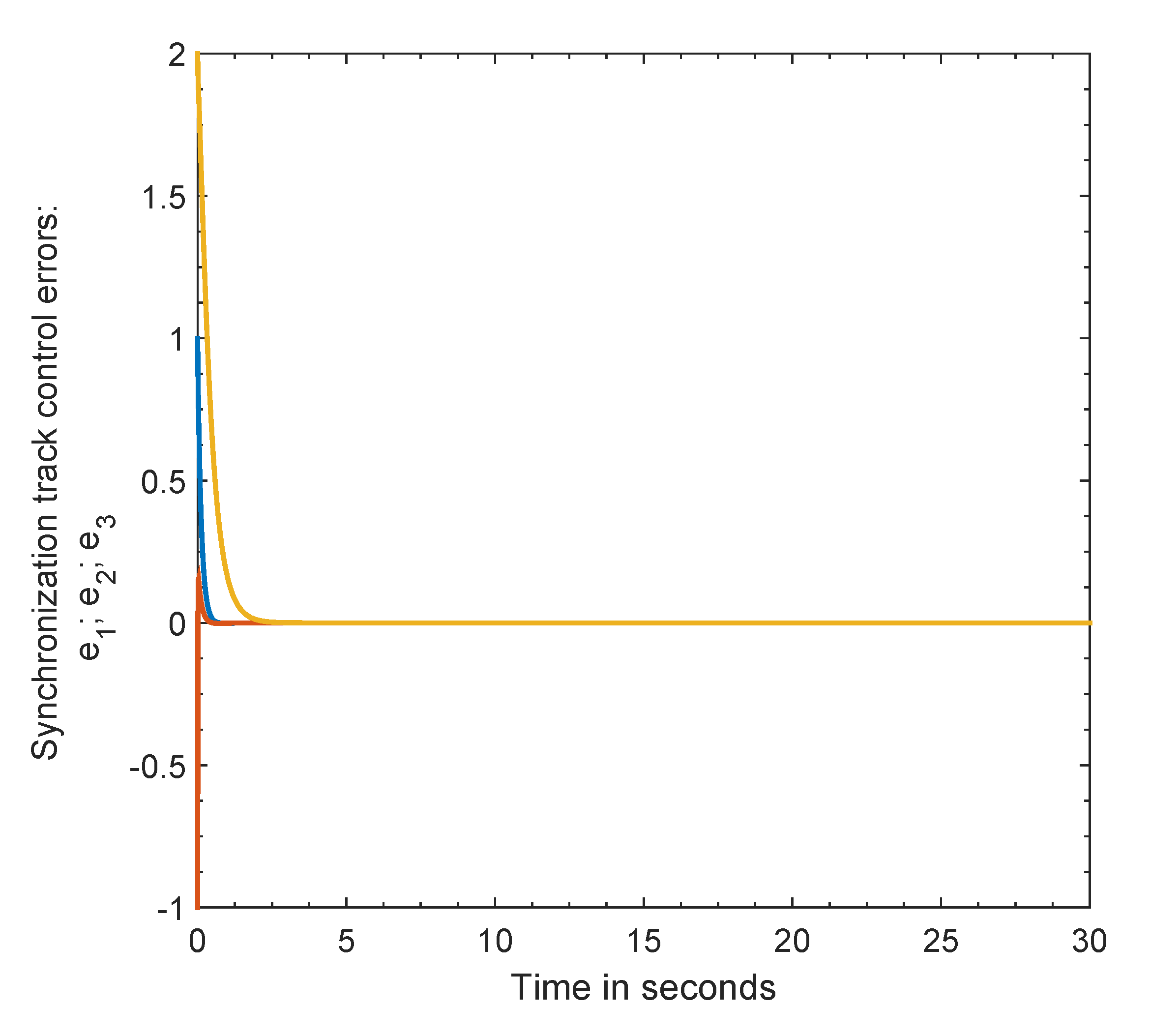
Case 1. Complete synchronization

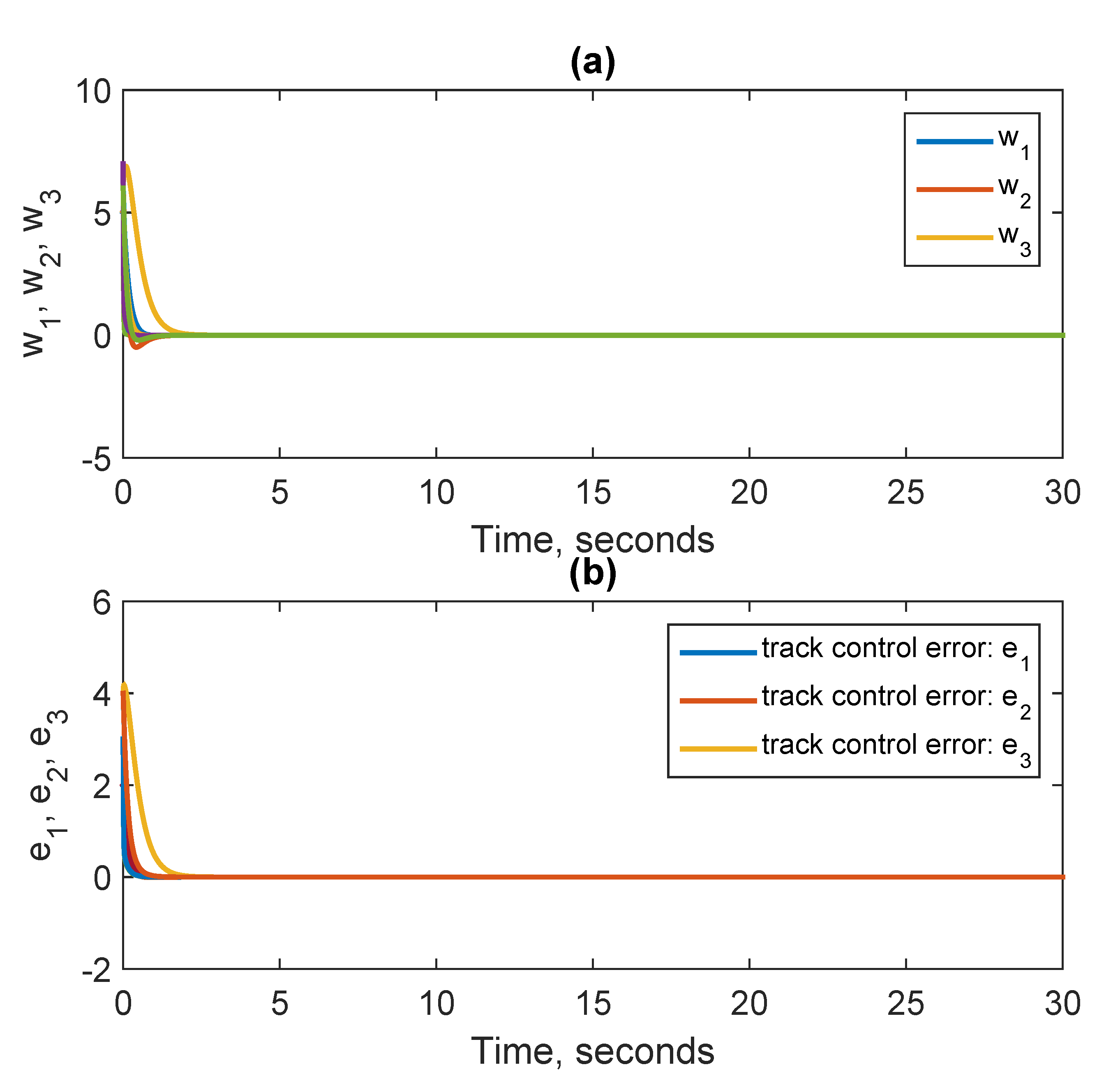
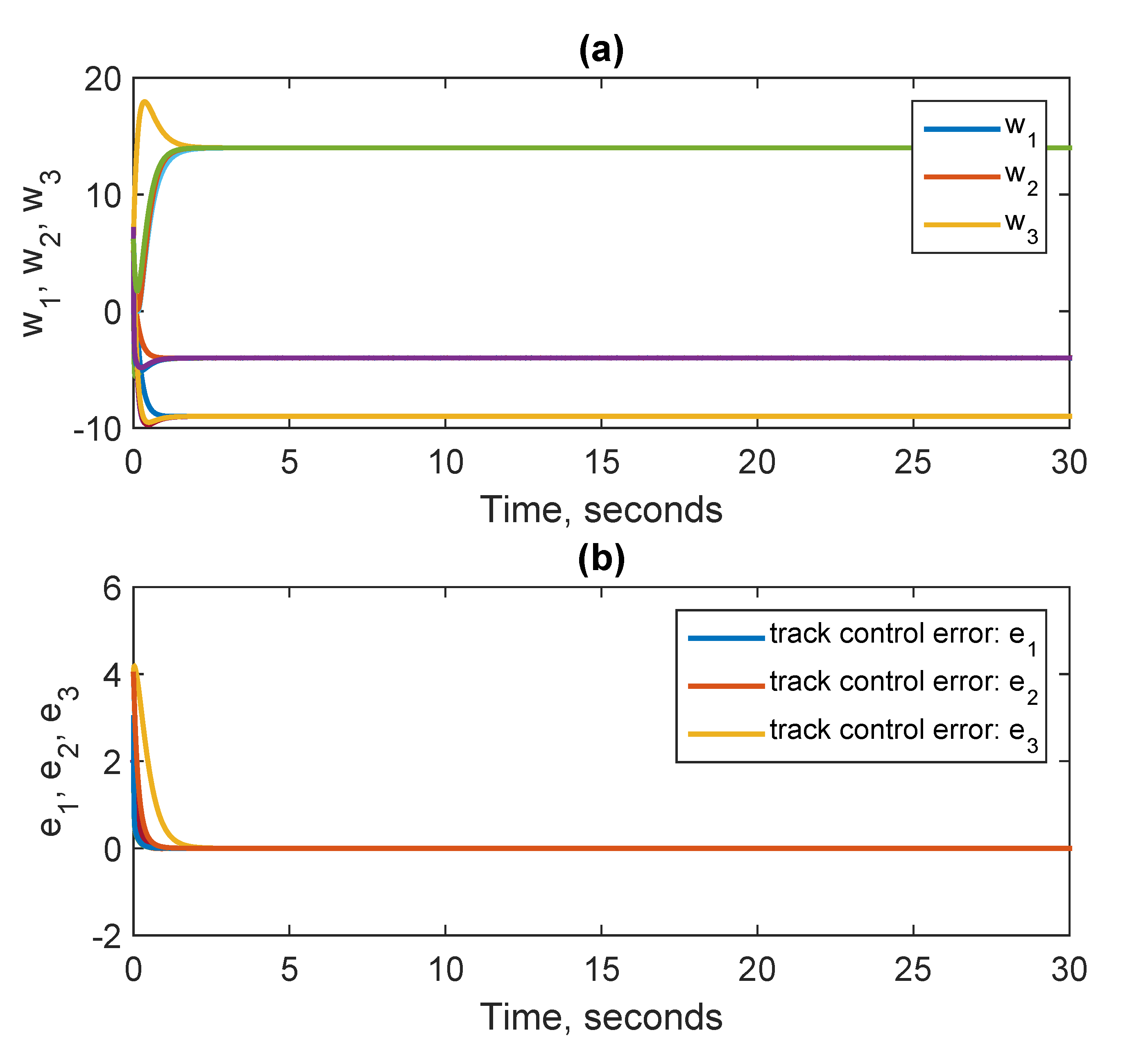
The reference values are adjusted in this case as $(w_{1r},w_{2r},w_{3r})=(0,0,0)$. Figure 4a shows the synchronization errors system. It is clear that the synchronization errors approach zero in a short time. Figure 4b shows the track synchronization control errors, from which it is obvious that the synchronization control errors tend to zero in a short time as predicted from the analytical results. In conclusion, from Figure 4, the chaotic complete synchronization is achieved in a short time.

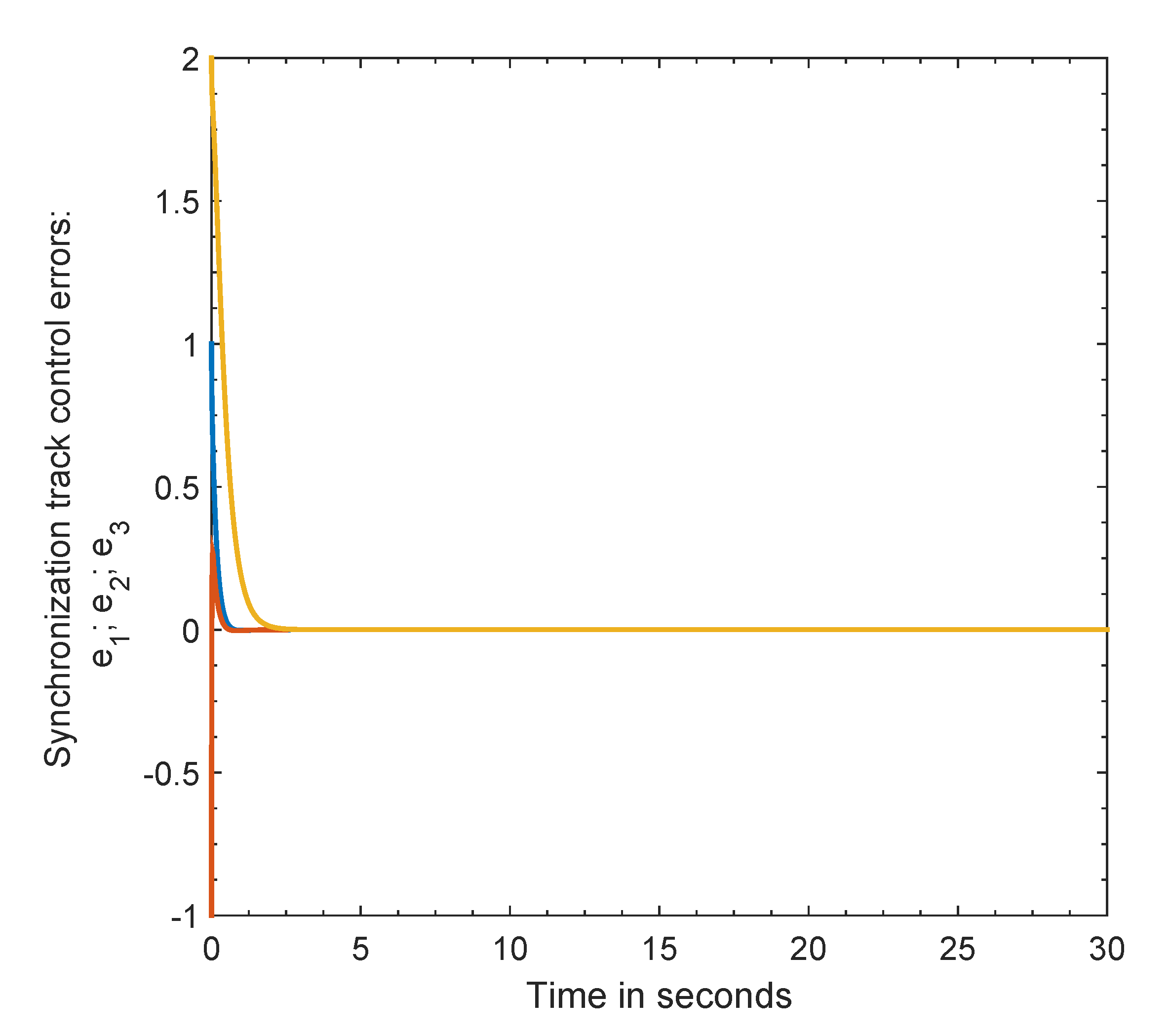
Case 2. Phase synchronization

In this case, the reference values are calculated as $(w_{1r},w_{2r},w_{3r})=(y_{10}-x_{10},y_{20}-x_{20},y_{30}-x_{30})=(-9,-4,14)$. This case is clearly different from the previous one. The reference values depend on the initial conditions of the two systems. It is clear from Figure 5a that the phase synchronization errors are tracking the predetermined reference values. The track synchronization control errors approach zero as shown in Figure 5b as predicted from the analytical results. As a result, Figure 5 proves that the phase synchronization is accomplished quickly.

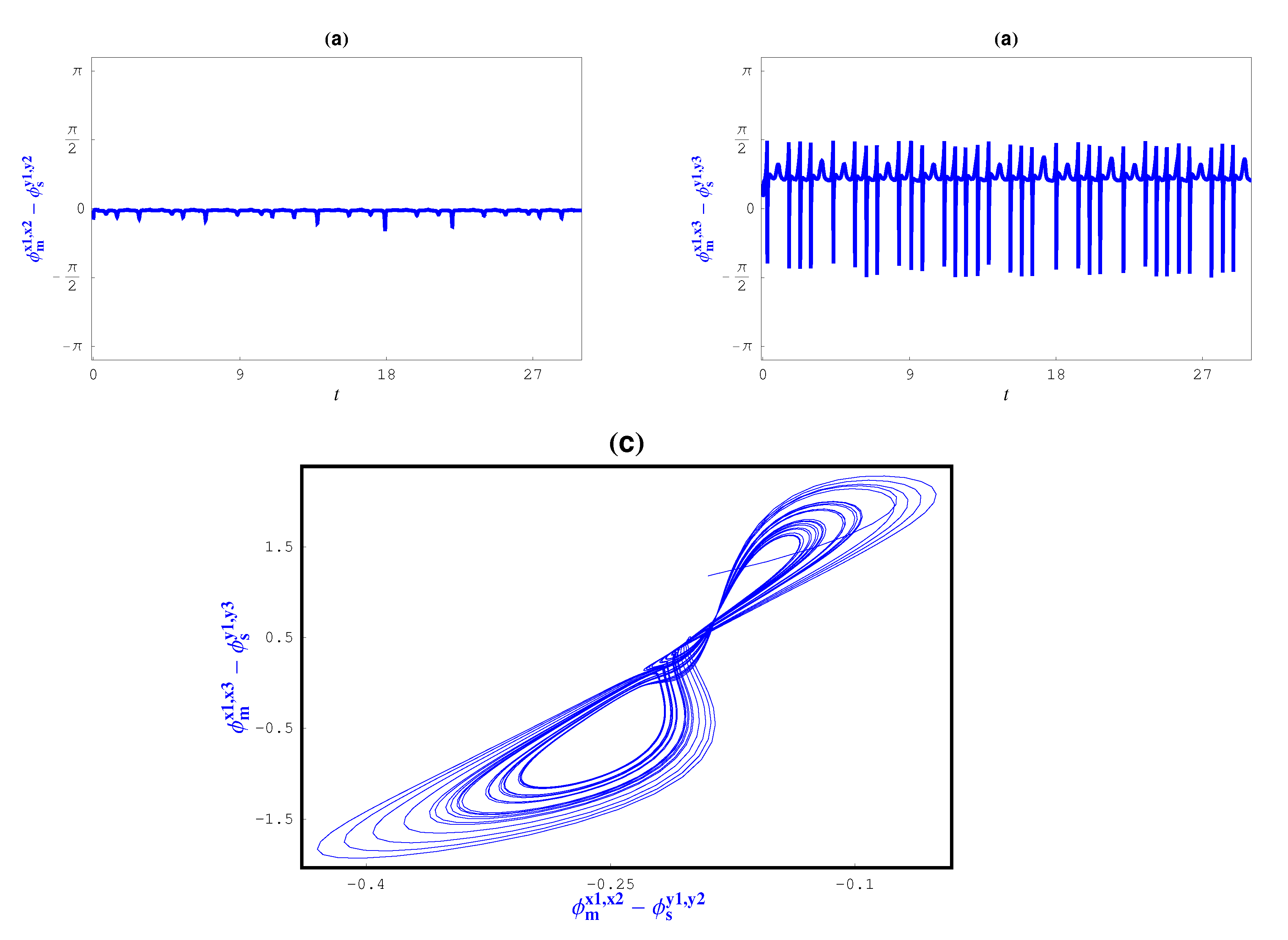
In addition, in this case we will compute the phase difference and the amplitude of the master and slave systems numerically. The phase differences between the master and slave systems can be formed as ${\varphi }_m^{x_l,x_k}-{\varphi }_s^{y_l,y_k},$ $l,k=1,2,3$ and $l\ne k$, where ${\varphi }_m^{x_l,x_k}={tan}^{-1}\left(\frac{x_{km}}{x_{lm}}\right)$ and ${\varphi }_s^{y_l,y_k}={tan}^{-1}\left(\frac{y_{ks}}{y_{ls}}\right)$ are phases of the master and slave systems, respectively. The phase differences ${\varphi }_m^{x_1,x_2}-{\varphi }_s^{y_1,y_2}$ and ${\varphi }_m^{x_1,x_3}-{\varphi }_s^{y_1,y_3}$ in ($x_1,x_2),$ ($x_1,x_3)$ planes, respectively, are computed by and plotted in Figure 6a,b. It is clear the phase differences ${\varphi }_m^{x_1,x_2}-{\varphi }_s^{y_1,y_2}$ and ${\varphi }_m^{x_1,x_3}-{\varphi }_s^{y_1,y_3}$ are finite and fluctuate in a chaotic mode, which implies that CPS is accomplished. Figure 6c displays the relationship ${\varphi }_m^{x_1,x_2}-{\varphi }_s^{y_1,y_2}$ and ${\varphi }_m^{x_1,x_3}-{\varphi }_s^{y_1,y_3}$. As shown, this relationship is a chaotic attractor and this means that ${\varphi }_m^{x_1,x_2}-{\varphi }_s^{y_1,y_2}$ and ${\varphi }_m^{x_1,x_3}-{\varphi }_s^{y_1,y_3}$ change in chaotic style and CPS is active.

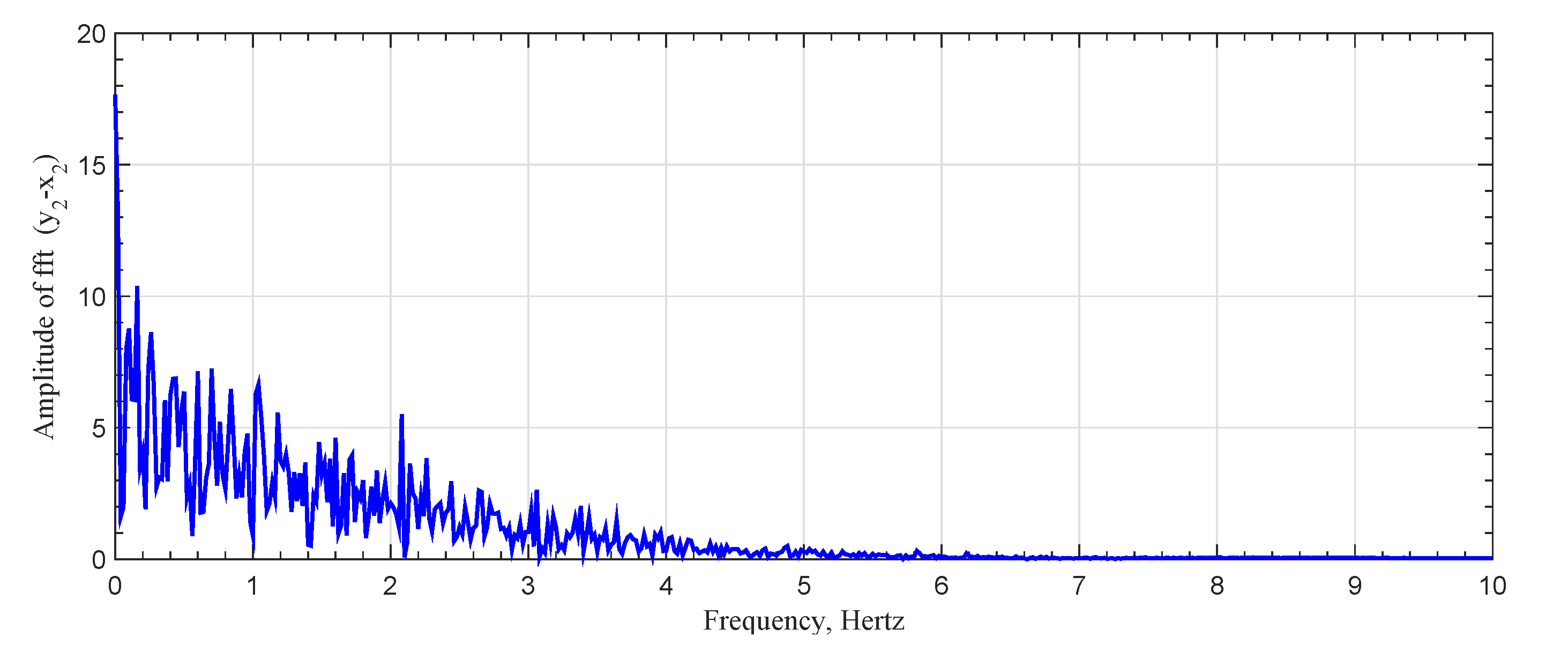
In addition, the master system amplitude in ($x_1,x_2)$ projection is formed as $A_m^{x_1,x_2}=\sqrt{{\left(x_1\right)}^2+{\left(x_2\right)}^2},$ and the same is formed for the slave as $A_s^{y_1,y_2}=\sqrt{{\left(y_1\right)}^2+{\left(y_2\right)}^2}$. In Figure 7a,b, these amplitudes are graphed with respect to t, whilst Figure 2c displays $A_s^{y_1,y_2}$ versus $A_m^{x_1,x_2}$. Figure 7c shows that those amplitudes have a chaotic style and they are linearly independent (uncorrelated). Similar results can be found for the other phase variations and amplitude relationships for the master and slave models on different projection planes.

4. Robust Track Synchronization for Two Identical Lorenz Chaotic Systems

4.1. Designing a Robust Tracking Synchronization Control Algorithm

In a practical environment, there exist certain unavoidable uncertainties. Consequently, it is useful to consider robustness with respect to perturbations in track synchronization control if applied for two identical Lorenz systems. Suppose that the parameters of the model have some perturbations, the uncertain synchronization error system can be represented as

$$\begin{array}{ccc}\hfill \frac{d{w}_1}{dt}& =& -(\sigma +\Delta \sigma )w_1+(\sigma +\Delta \sigma )w_2+u_1,\hfill \\ \hfill \frac{d{w}_2}{dt}& =& (r+\Delta r)w_1-w_2-x_3{w}_1-y_1{w}_3+u_2,\hfill \\ \hfill \frac{d{w}_3}{dt}& =& x_1{w}_2+y_2{w}_1-(b+\Delta b)w_3+u_3.\hfill \end{array}$$

(16)

Let $d_1=\Delta \sigma (w_2-w_1)$, $d_2=\Delta r{w}_1$ and $d_3=-\Delta b{w}_3$. Applying the designed controller whose form is represented in (7) and the model (16), the single-state feedback tracking synchronization control error of the the single-state feedback tracking synchronization error system becomes

$$\begin{array}{ccc}\hfill \frac{d{e}_1}{dt}& =& -\sigma e_1+\sigma e_2+d_1,\hfill \\ \hfill \frac{d{e}_2}{dt}& =& k{e}_2+r{e}_1-e_2-x_3{e}_1-y_1{e}_3+d_2,\hfill \\ \hfill \frac{d{e}_3}{dt}& =& x_1{e}_2+y_2{e}_1-b{e}_3+d_3.\hfill \end{array}$$

(17)

It can be rewritten in matrix form as

$$de/dt=Ae+d$$

(18)

where

$de/dt=\left[\begin{array}{c}\frac{d{e}_1}{dt}\\ \frac{d{e}_2}{dt}\\ \frac{d{e}_3}{dt}\end{array}\right]$, $d=\left[\begin{array}{c}{d}_1\\ d_2\\ d_3\end{array}\right]$ and

$$A=\left[\begin{array}{ccc}-\sigma & \sigma & 0\\ r-x_3& k-1& -y_1\\ y_2& x_1& -b\end{array}\right].$$

(19)

The track control error of the synchronization error system is presented in the frequency-domain as $e\left(s\right)={(sI-A)}^{-1}d\left(s\right)$.

For the robust controller our goal is to choose an appropriate value for the gain k in order to minimize the consequences of disturbance $d.$ From (18) and (19), the effects from $d_2$ can be decreased via choosing an appropriate value for the gain k, whilst the selected value of the gain k has no impact to minimize the consequences of $d_1$ and $d_2$. As a result, we can improve the track synchronization controller as follows:

$$\begin{array}{ccc}\hfill u_1& =& k_1(w_2-w_{2r})+\sigma w_{1r}-\sigma w_{2r},\hfill \\ \hfill u_2& =& k_2(w_2-w_{2r})-r{w}_{1r}+w_{2r}+x_3{w}_{1r}+y_1{w}_{3r},\hfill \\ \hfill u_3& =& k_3(w_2-w_{2r})-x_1{w}_{2r}-y_2{w}_{1r}+b{w}_{3r},\hfill \end{array}$$

(20)

where $k_1$, $k_2$ and $k_3$ are gains of the single-state feedback track synchronization controller.

By utilizing (16) and (20), the closed-loop track synchronization control error dynamics for the synchronization errors system can be represented as follows:

$$\begin{array}{ccc}\hfill \frac{d{e}_1}{dt}& =& -\sigma e_1+(k_1+\sigma )e_2+p_1,\hfill \\ \hfill \frac{d{e}_2}{dt}& =& (r-x_3)e_1+(k_2-1)e_2-y_1{e}_3+p_2,\hfill \\ \hfill \frac{d{e}_3}{dt}& =& y_2{e}_1+(k_3+x_1)e_2-b{e}_3+p_3.\hfill \end{array}$$

(21)

That can be represented in compact matrix form as

$$de/dt=Be+p,$$

(22)

where $e=\left[\begin{array}{c}{e}_1\\ e_2\\ e_3\end{array}\right]$,

$$B=\left[\begin{array}{ccc}-\sigma & k_1+\sigma & 0\\ r-x_3& k_2-1& -y_1\\ y_2& k_{3+}{x}_1& -b\end{array}\right],$$

and $p=\left[\begin{array}{c}{p}_1\\ p_2\\ p_3\end{array}\right]$ where $p_1=\Delta \sigma (w_2-w_1)$, $p_2=\Delta r{w}_1$ and $p_3=-\Delta b{w}_3.$

The Laplace transform of (22) is written as

$$e\left(s\right)={(sI-B)}^{-1}p\left(s\right)$$

(23)

As a consequence of this, it is possible to select appropriate values of the gain $k_1$, $k_2$ and $k_3$ that decrease all disturbance effects. To do this, the following proposed fitness function can be minimized:

$$f=\sum _i{∥\left({(sI-B)}^{-1}\right)∥}_{s_i=j{\omega }_{p_i}}$$

(24)

where $w_{p_i}$ ($i=1,2,\dots$) are the dominant frequencies related to the disturbances. We use the fast Fourier transform (FFT) [32] to determine the dominant frequencies of the $w_2=y_2-x_2$ (that are used for feeding back the tracking controller). Figure 8 shows the FFT of $w_2=y_2-x_2$. We choose the genetic algorithm to minimize the fitness function (24) because of its power as an optimization technique [33].

The optimization process for selecting robust optimal gains $k_1$, $k_2$ and $k_3$ is recorded as follows.

GA Track synchronization control procedure. Select optimal gains $k_1$, $k_2$ and $k_3$ using GA algorithm.

(1)

Determine the dominant frequencies via FFT of the suggested measurable signal $w_2=y_2-x_2.$

(2)

Design the fitness function as in (24).

(3)

The nonlinear constraints are set up as $Re\left({\lambda }_i\right)\le -\theta$, where $\left\{{\lambda }_i\left|det({\lambda }_{i}I-B)=0\right.\right\},$ $i=1$, 2, 3, and $\theta$ is a chosen positive real angle.

(4)

Utilize Matlab’s GA toolbox to search for the optimal gains $(k_1,k_2,k_3)$.

4.2. Numerical Simulation for Robust Track Synchronization Control

Consider the master system (4) and the slave system (5) with $(\sigma ,r,b)=(10,28,8/3)$ where $x_0=(10,5,-15)$ and $y_0=(1,1,-1)$. The disturbances are $p_1=sin\left(2\pi t\right)(w_2-w_1)+noisesignal$, $p_2=sin\left(4\pi t\right)w_1+noisesignal$, and $p_3=sin\left(6\pi t\right)w_3$, where the noise signal is a band-limited white noise signal. The spectrum of $w_2$ can be obtained by FFT as shown in Figure 8. The dominant frequencies are selected as $f{r}_1=0.01$; $f{r}_2=0.02$; $f{r}_3=0.08$; $f{r}_4=0.1$; $f{r}_5=0.16$; $f{r}_6=0.24$; $f{r}_7=0.26$. Consequently, $j{\omega }_{p_i}=2\pi f_i,$ where $i=1,2,3,4,5,6,7$ are utilized for computing the fitness function (24).

Remark 1.

The white noise is computed using the standard deviation of the feedbacked state as $ss=std(y_2-x_2)$. Then compute n such that the signal to noise ratio $snr=20*log10(s/n)$. Give a $snr$ value and compute n, then compute the white noise as $noise=n*\left(randn\right(:,1\left)\right).$

Assume that $\theta =2$ and set the population size and the number of generation equal to 100. The execution of GA optimization is shown in Figure 9. The GA produces the following optimal gains.

$$(k_1,k_2,k_3)=(-0.05,-200,-1),$$

(25)

and the best fitness value is $168.8316$.

Using the optimal gains (25), the tracking synchronization robust controller error dynamics are depicted in Figure 10 and Figure 11. Other testing sets of gain values are used for more testing where $(k_1,k_2,k_3)=(-1,-100,-2)$.

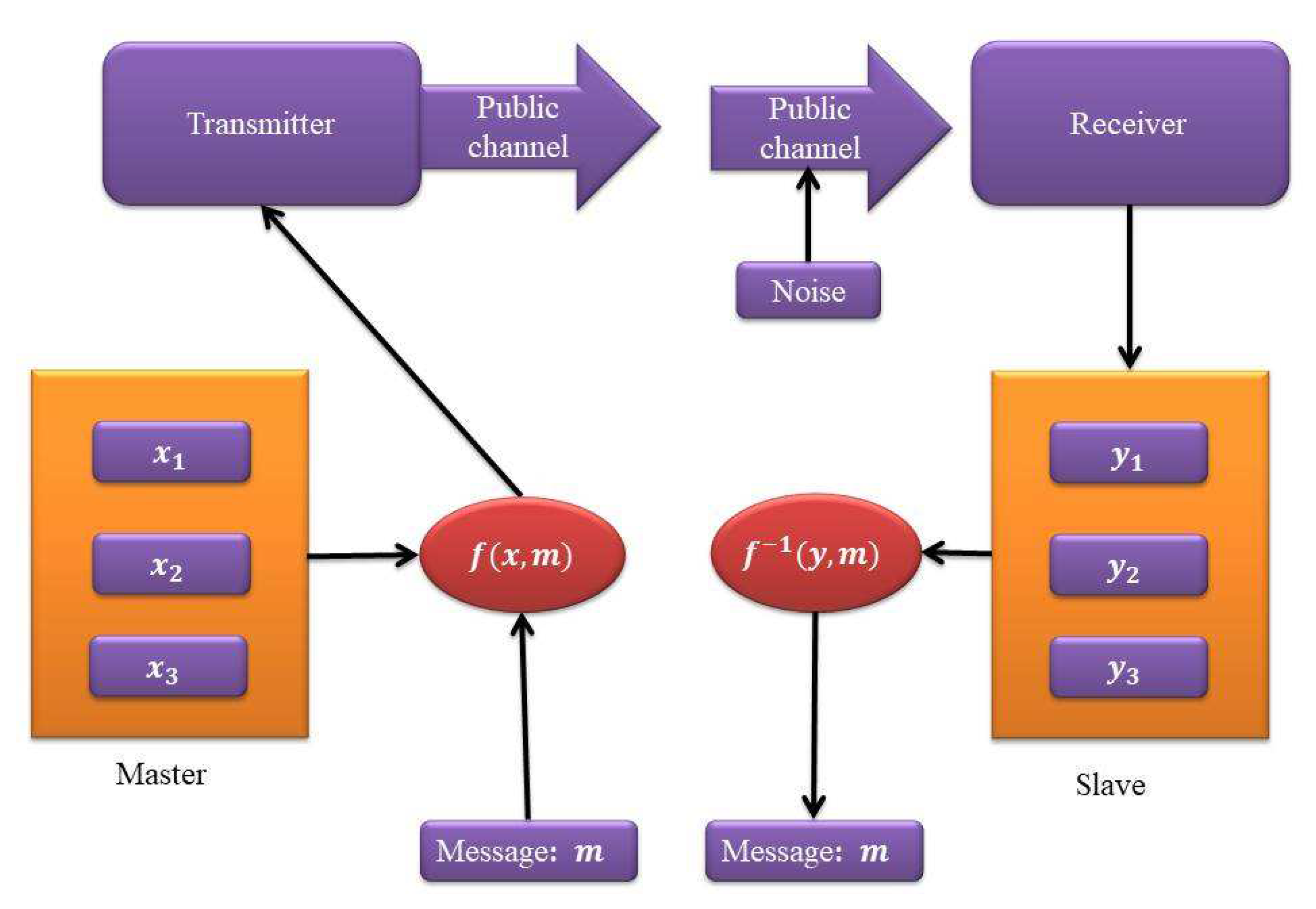
5. Secure Communication Application via Robust Track Synchronization Control Results

Secure communication is an important application of the topic and these types of synchronization have been studied in the literature [34,35,36]. In this section we will take advantage of the results of the robust synchronization that we obtained in order to provide a secure communication application. In Figure 12, we propose a scheme for complete robust synchronization secure communications. As is clear from this scheme, we consider the master and slave systems as transmitter and receiver systems, respectively. The most important thing that distinguishes this scheme from previous plans is the presence of noise when the message is sent from the sending equipment to the receiving equipment, and despite this, the message extraction process occurs successfully. Let the signal of the transmitted data message be denoted by $r\left(t\right)$ and let $\Theta =\Phi (r,x_1,x_2,x_3)$ be a complex invertible mapping that is used to encrypt the signals of the transmitter system in a chaotic manner. Then, combine the encrypted signal $\Theta$ with one (or more) of the three state variables, with any pair of their products or with their product. For illustration purposes, after adding this to the state variable $x_3$ the encrypted message becomes $\Gamma \left(t\right)=\Theta +x_3$. After that, the chaotic carrying signal of the sender device is produced and the encrypted message is transferred to the recipient end. When the message is sent there is strong noise that will intercept the message as well as the signals of the transmitter system. Therefore, if the synchronization used in making this application is not robust, this could affect message extraction. At the receiver side, we construct the controller as proposed in Equation (20). As a result, the synchronization between the drive (master) (4) and the identical controlled (5) frameworks will occur after a certain time $t_s$ and the difference between the master system x and the slave system states y will be zero in a specific period $t_c$ that is a time period longer than the time period $t_s$ ($t_s$ is the time period after which the synchronization process starts). For illustration purposes take $t_c=5$ s, recovering $\Gamma \left(t\right)$ via a straightforward mutation $\Theta =\Gamma \left(t\right)-y_3$ that starts at the receiver end. At the end, the sent data can be retrieved via an inverting operation $r^{*}\left(t\right)={\Phi }^{-1}(y_1,y_2,y_3,\Theta )$ because the nonlinear function $\Phi$ is invertible.

The outputs of the numerical experiments are given in the following lines, where the values of the transmitter framework and receiver framework are adjusted to be as per those in Section 3. 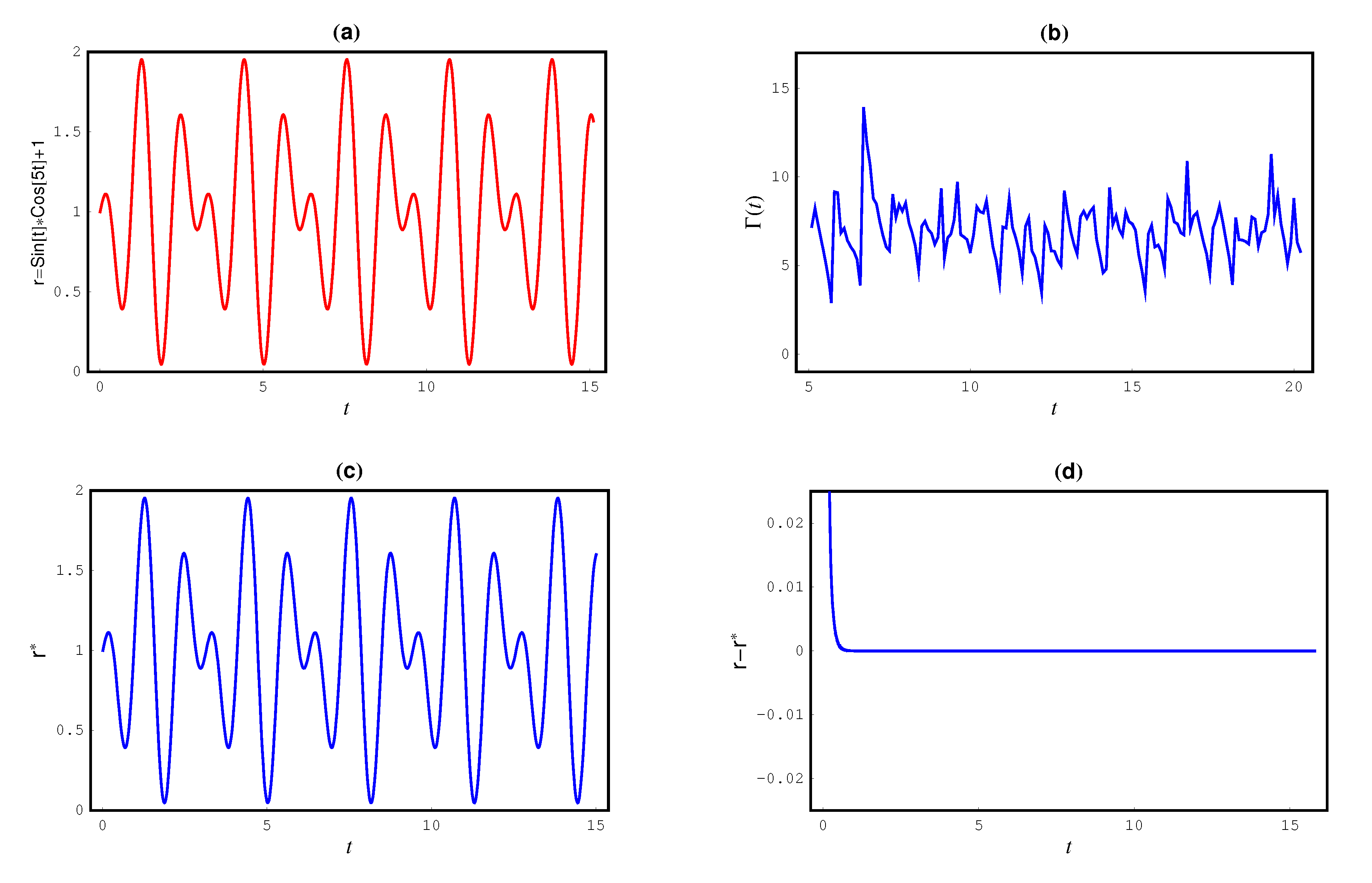For illustration purposes, the invertible function is selected as $\Theta =x_1+r\left(t\right)$ and $r\left(t\right)$ is taken for example as $r\left(t\right)=sin\left(t\right)cos\left(5t\right)+1.$ Suppose that the encrypted signal $\Theta$ is combined with the state variable $x_3⟹\Gamma \left(t\right)=x_1+r\left(t\right)+x_3.$ Figure 13 displays the results of secure communication via chaos synchronization. The sent message $r\left(t\right)$ and the transferred chaos signal $\Gamma \left(t\right)$ are, respectively, displayed in Figure 13a,b. Figure 13c displays the recovered message $r^{*}\left(t\right)=\Gamma \left(t\right)-y_1-y_3$. Figure 13d displays the error between the authentic sent message and the data signal of the retrieved message. It is clear from Figure 13d, that the sent message data signal $r\left(t\right)$ is retrieved exactly after a short transitory time.

6. Conclusions

This study has been suggested to accomplish two types of synchronization between the master and the controlled slave Lorenz chaotic systems via a single-state feedback track controller. In addition, the robustness of the proposed scheme has been proved and the gains of the proposed controller have been determined based on a genetic algorithm. Furthermore, the proposed scheme has been successfully applied to a secure communication system. The experimental results verify that the methods are correct and practical. Finally, we can confirm that this study has made the following contributions.

• Design of a single-state feedback track synchronization controller to accomplish two types of synchronization between two identical Lorenz chaotic systems.
• The complete and phase synchronizations of two identical Lorenz chaotic systems are achieved via the same controller, which has not been done before.
• The single-state feedback strategy is less costly and its realization is simple since it uses fewer sensors.
• The powerful GA algorithm has been combined with our proposed strategy to compute the suitable gains of the proposed synchronization controller.
• More complex chaotic systems will likely require more complex treatment of parameters to fit between systems to achieve a decent measure of synchronization. This can be seen from the condition in Theorem 1 required to measure the degree of synchronization.
• The proposed method has been successfully applied in a secure communication application.