Relationship between the Shear Strength and Microscopic Pore Parameters of Saline Soil with Different Freeze-Thaw Cycles and Salinities
Abstract
1. Introduction
2. Materials and Methods
2.1. Soil Properties and Sample Preparation
2.2. Freeze–Thaw Tests
2.3. Triaxial Tests
2.4. SEM Tests
2.5. Acquisition of Microscopic Parameters
- 1.
- Porosity
- 2.
- Average pore diameter
- 3.
- Average shape coefficient
- 4.
- Surface fluctuation fractal dimension
- 5.
- Orienting probability entropy
3. Results and Discussion
3.1. Shear Strength Characteristic
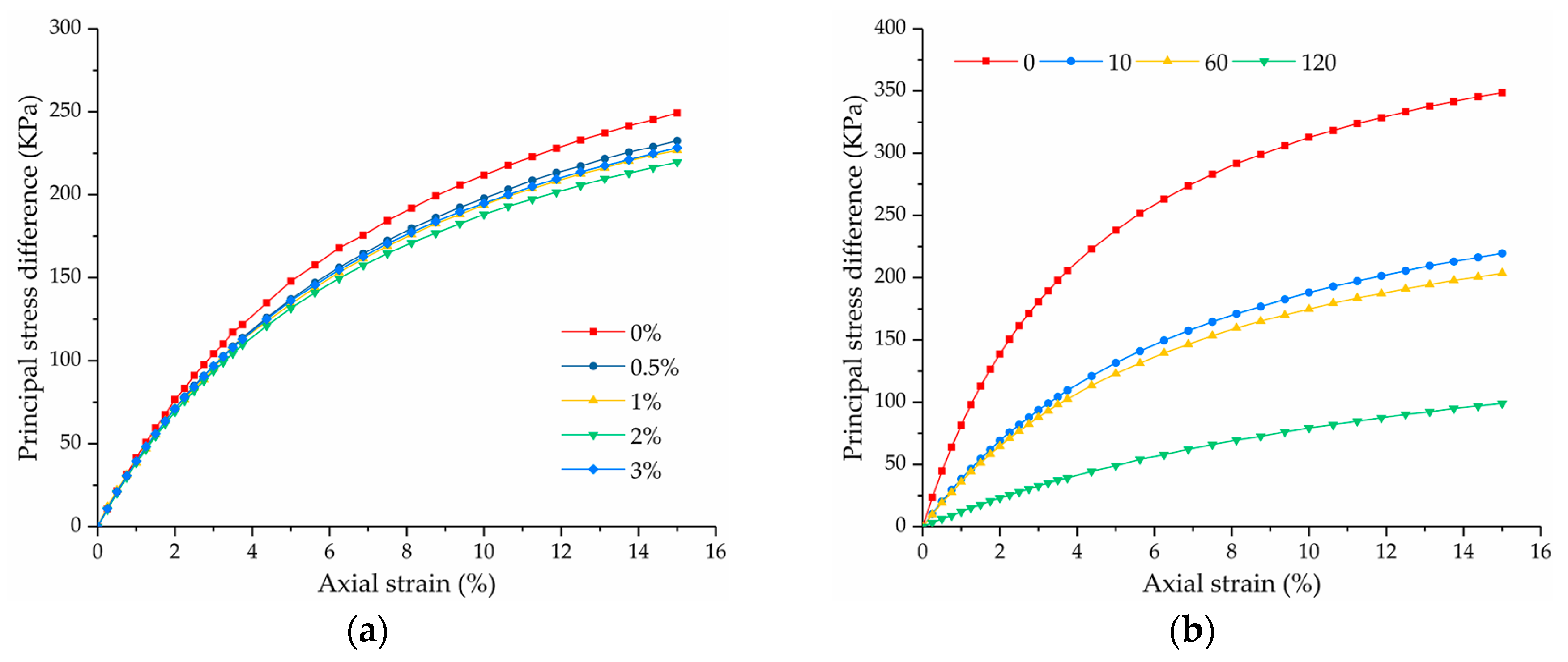
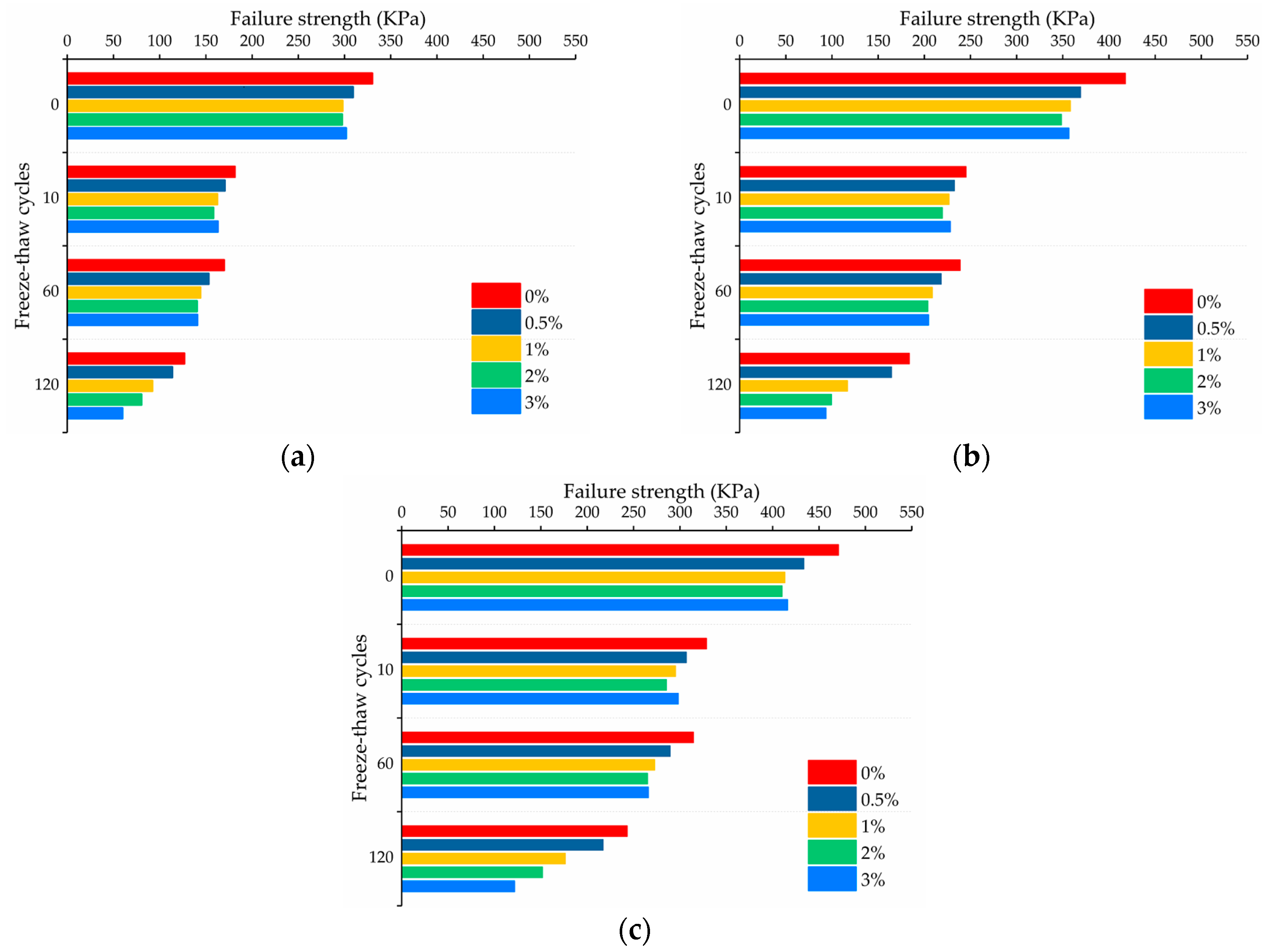
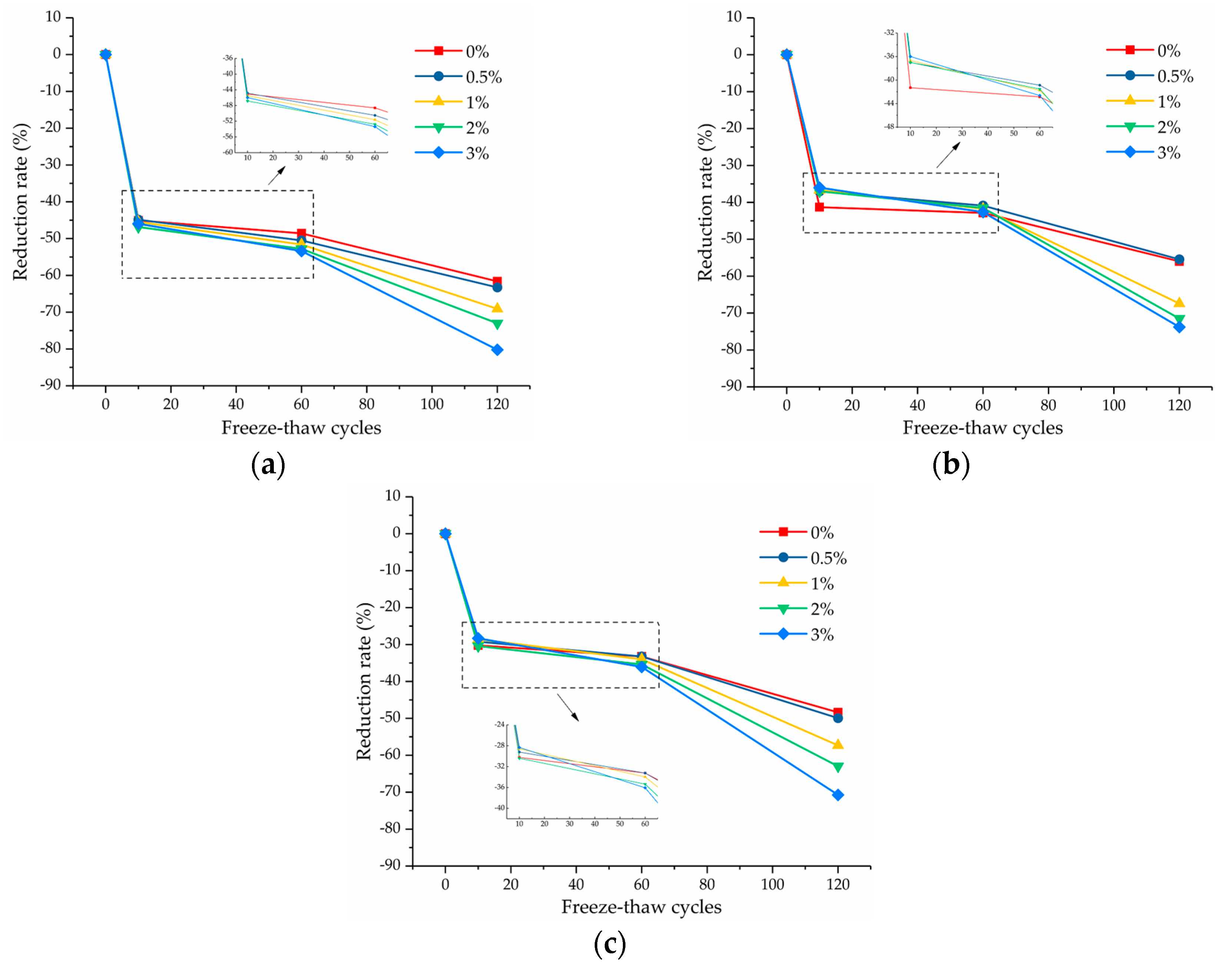
3.1.1. Failure Strength
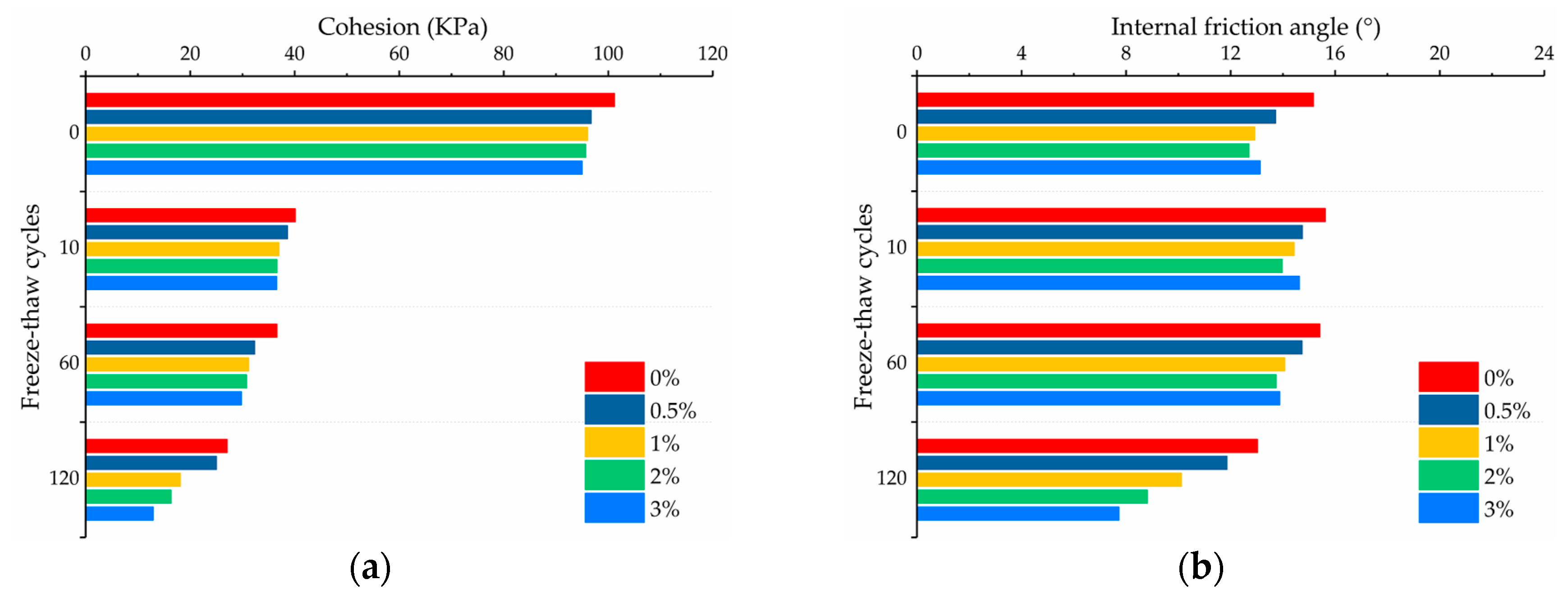
3.1.2. Shear Strength Parameters
3.2. Microstructure Characteristics
3.2.1. General Description of Microstructure of Soil Samples
3.2.2. Porosity
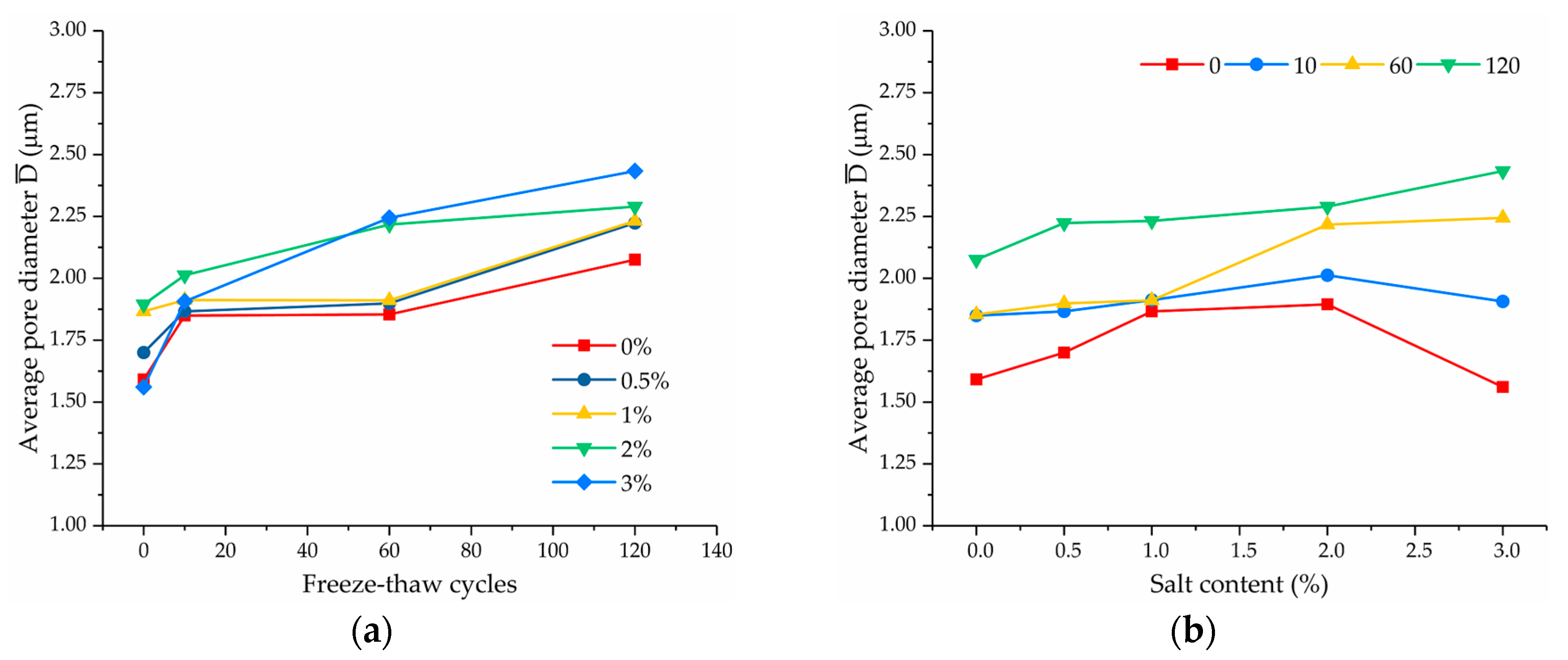
3.2.3. Average Pore Diameter
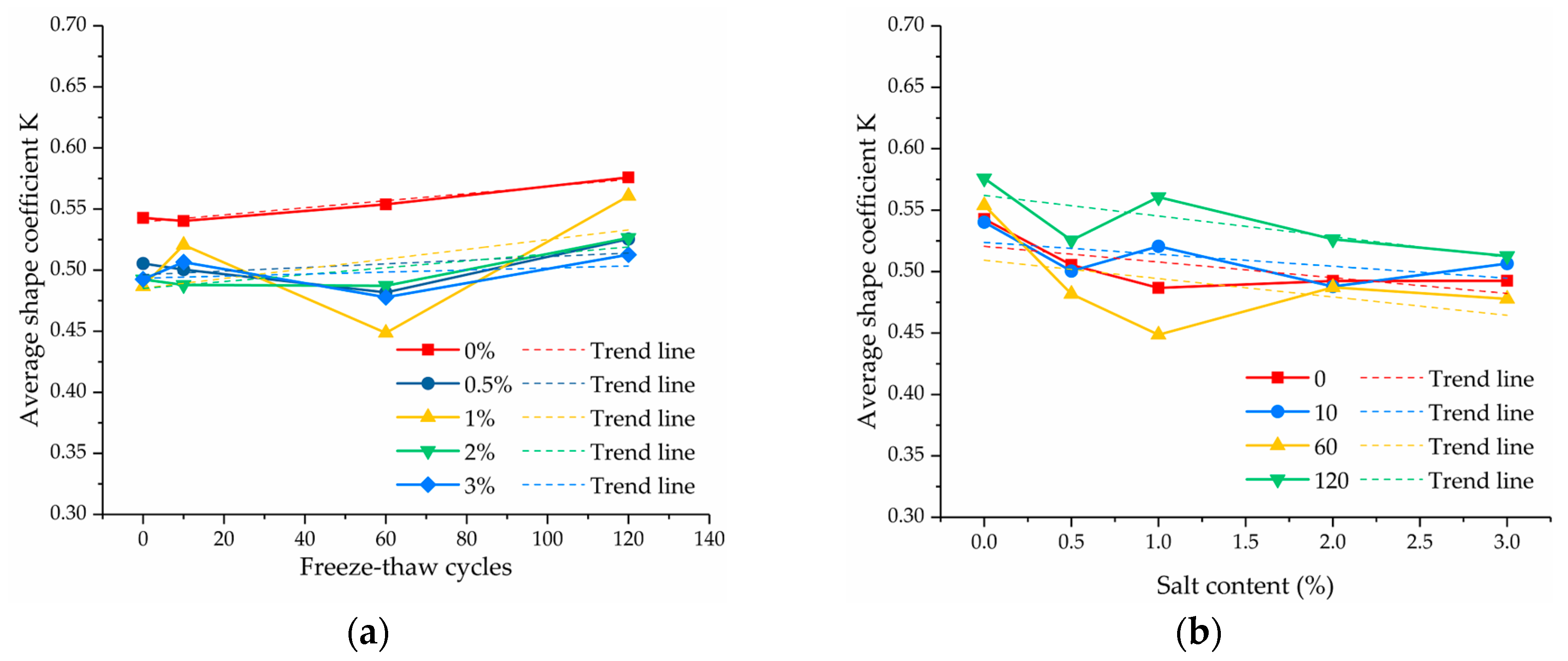
3.2.4. Average Shape Coefficient of Pores
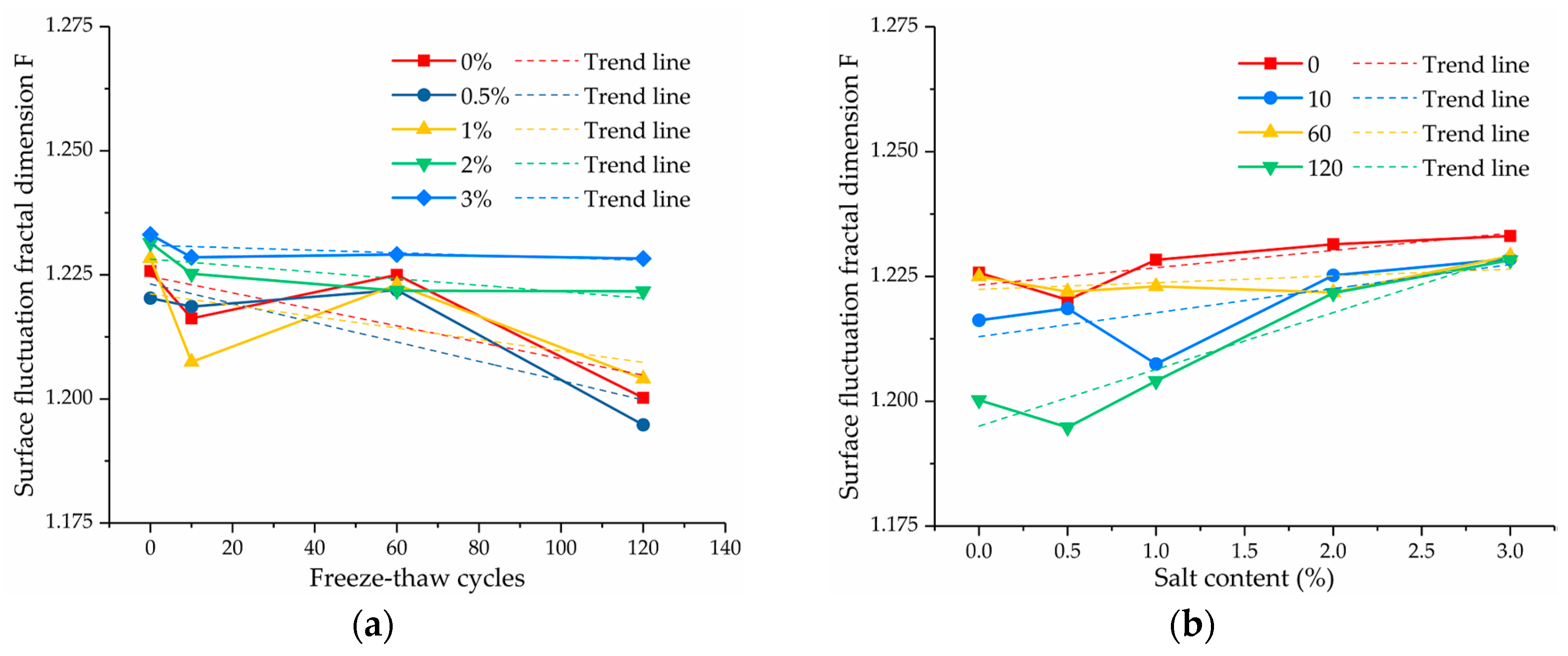
3.2.5. Surface Fluctuation Fractal Dimension of Pores
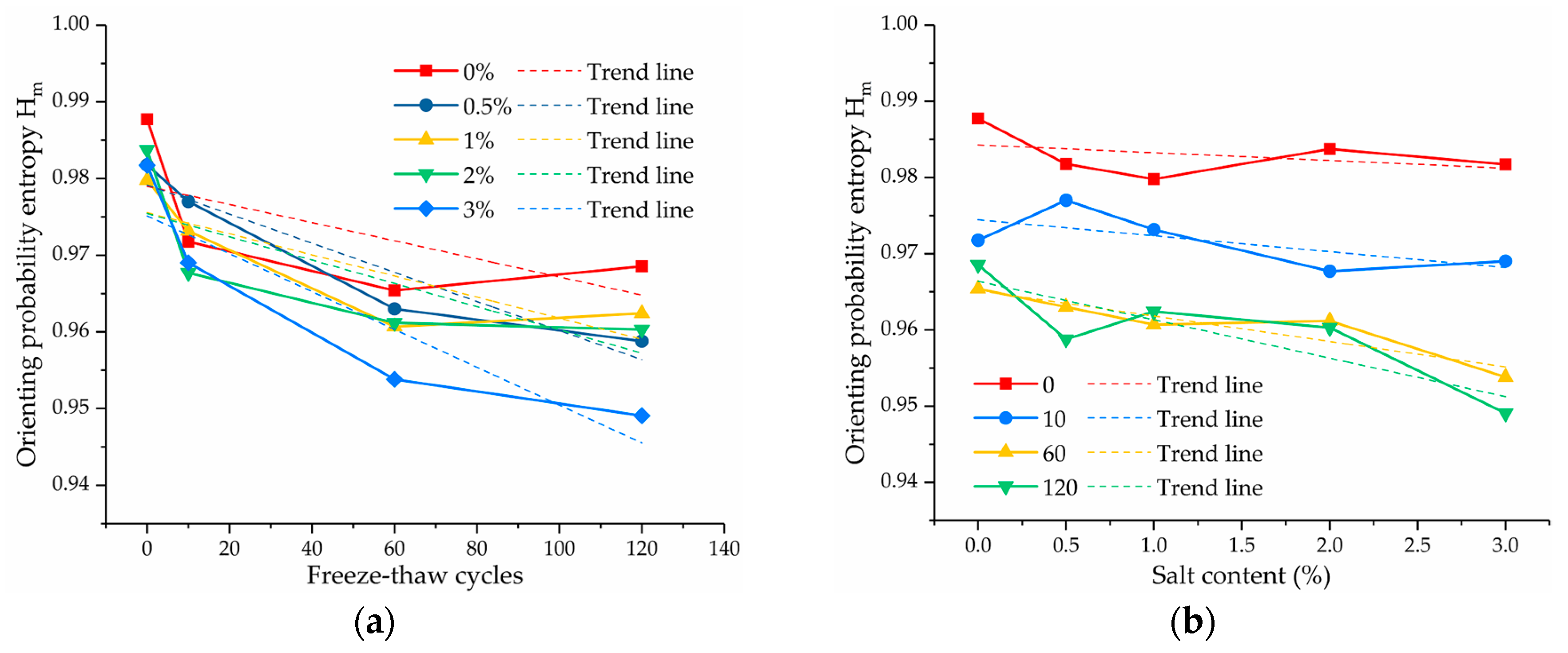
3.2.6. Orienting Probability Entropy of Pores
3.3. Relationship between Failure Strength and Microscopic Pore Parameters
4. Conclusions
- The stress–strain characteristics of soil samples with different salinities and freeze–thaw cycles all belong to the strain–hardening type. The failure strength of the soil samples increased with increasing confining pressure under different experimental conditions. Compared with the salt content, the number of freeze–thaw cycles had a greater influence on the failure strength of the soil samples. As the number of freeze–thaw cycles increased, the failure strength of the soil samples showed a decreasing trend. The decreasing rate was the largest after the first 10 freeze–thaw cycles and tended to be slow in the range of 10–60 freeze–thaw cycles, while the decreasing rate increased again after 120 freeze–thaw cycles. When the number of freeze–thaw cycles was no larger than 60, the failure strength of the soil samples decreased first, then increased with the increasing salt content, but when the number of freeze–thaw cycles was 60–120, the failure strength decreased continuously with the increasing salt content.
- The cohesion of the soil samples decreased with the increase in freeze–thaw cycles, and the decreasing rate was the largest in the first 10 freeze–thaw cycles, which was similar to the variation trend of the failure strength, while the variation of the internal friction angle of the soil samples was relatively small with an increase in freeze–thaw cycles. When the number of freeze–thaw cycles was the same, the variation of the shear strength parameter of the soil samples with salt content was relatively small, the cohesion of the soil samples decreased with the increasing salt content, and the variation trend of the internal friction angle was similar to the failure strength.
- The SEM tests showed that the surface of the soil samples not experiencing freeze–thaw cycles was flat and dense, while after experiencing freeze–thaw cycles, the proportion of pores and fissures in the soil increased, the structure became loose, and the structural change of the soil samples was most obvious in the first 10 freeze–thaw cycles. When the number of freeze–thaw cycles was the same, the agglomeration degree of the soil particles increased as the salt content increased.
- The quantitative analysis results of the microstructure showed that, with the increase in salt content and freeze–thaw cycles, the failure strength of the soil samples was generally negatively correlated with the porosity and average pore diameter, and the orienting probability entropy of the pores showed a decreasing trend overall. The orientation of the pore arrangement became better. However, the variation of the average shape coefficient and surface fluctuation fractal dimension of the pores under different experimental conditions was relatively small.
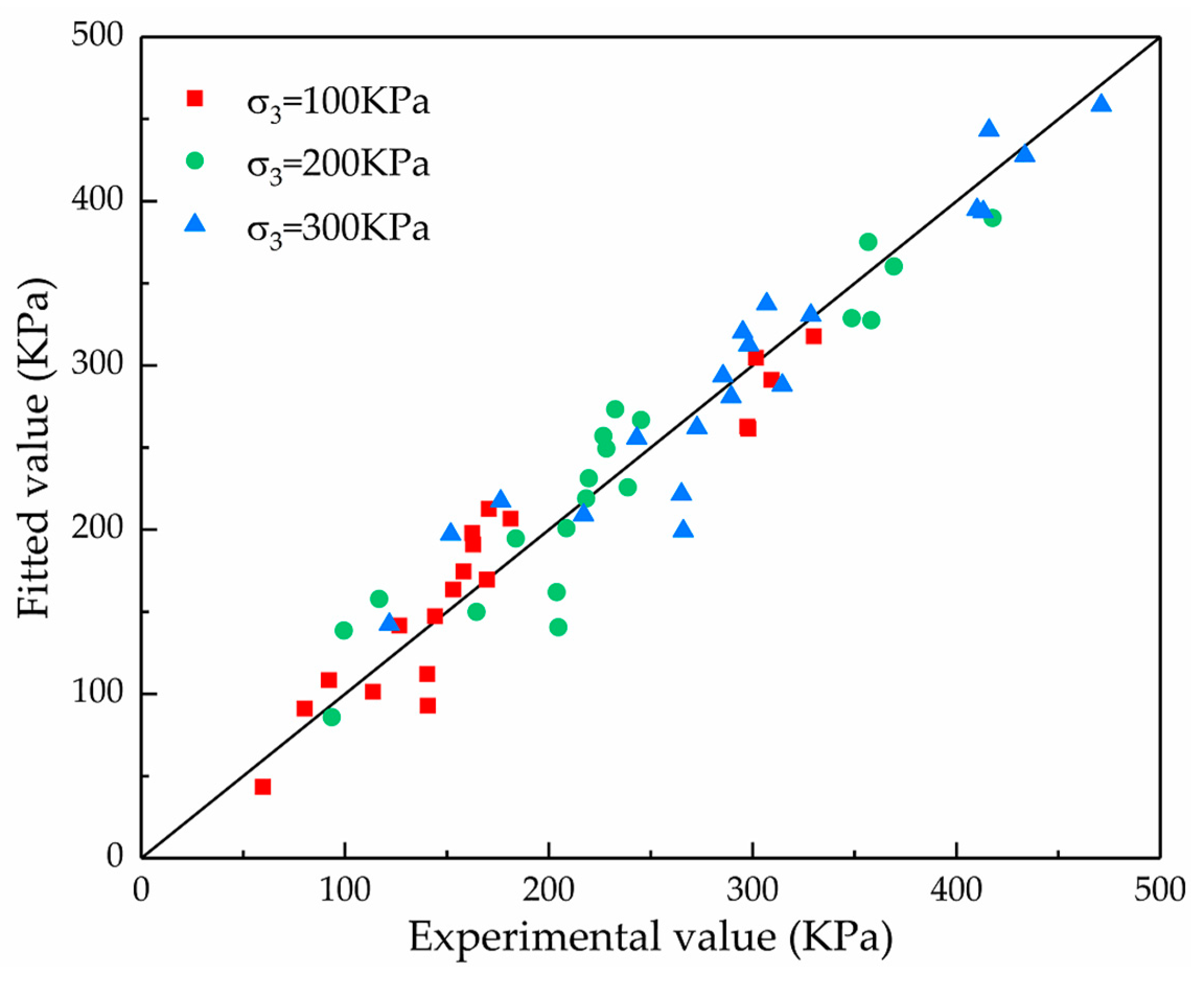
- A reasonable regression model was established to express the relationship between the microscopic pore parameters and failure strengths of the soil samples based on principal component regression analysis. The results showed that the failure strength of the saline soil was mainly affected by the size and orientation of the pores in the soil, while it was affected little by the pore morphology. The failure strength of the soil was negatively correlated with the size of the pores and positively correlated with the orienting probability entropy of the pores.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wei, J.; Shi, B.; Li, J.; Li, S.; He, X. Shear strength of purple soil bunds under different soil water contents and dry densities: A case study in the Three Gorges Reservoir Area, China. Catena 2018, 166, 124–133. [Google Scholar] [CrossRef]
- Wang, J.-J.; Zhang, H.-P.; Tang, S.-C.; Liang, Y. Effects of Particle Size Distribution on Shear Strength of Accumulation Soil. J. Geotech. Geoenvironmental Eng. 2013, 139, 1994–1997. [Google Scholar] [CrossRef]
- Malizia, J.P.; Shakoor, A. Effect of water content and density on strength and deformation behavior of clay soils. Eng. Geol. 2018, 244, 125–131. [Google Scholar] [CrossRef]
- Wang, D.-y.; Ma, W.; Niu, Y.-h.; Chang, X.-x.; Wen, Z. Effects of cyclic freezing and thawing on mechanical properties of Qinghai-Tibet clay. Cold Reg. Sci. Technol. 2007, 48, 34–43. [Google Scholar] [CrossRef]
- Zheng, Y.; Ma, W.; Li, G.; Mu, Y.; Peng, H. Laboratory study on quantitative parameter of structural characteristics of soils considering effect of freeze-thaw cycles. Chin. J. Geotech. Eng. 2016, 38, 1339–1344. [Google Scholar]
- Qi, J.; Vermeer, P.A.; Cheng, G. A review of the influence of freeze-thaw cycles on soil geotechnical properties. Permafr. Periglac. Process. 2006, 17, 245–252. [Google Scholar] [CrossRef]
- Lu, J.; Zhang, M.; Zhang, X.; Pei, W.; Bi, J. Experimental study on the freezing–thawing deformation of a silty clay. Cold Reg. Sci. Technol. 2018, 151, 19–27. [Google Scholar] [CrossRef]
- Han, Y.; Wang, Q.; Kong, Y.; Cheng, S.; Wang, J.; Zhang, X.; Wang, N. Experiments on the initial freezing point of dispersive saline soil. Catena 2018, 171, 681–690. [Google Scholar] [CrossRef]
- Bing, H.; He, P. Experimental investigations on the influence of cyclical freezing and thawing on physical and mechanical properties of saline soil. Environ. Earth Sci. 2011, 64, 431–436. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Q.; Yu, T.; Wang, G.; Wang, W. Numerical Study on the Multifield Mathematical Coupled Model of Hydraulic-Thermal-Salt-Mechanical in Saturated Freezing Saline Soil. Int. J. Geomech. 2018, 18, 04018064. [Google Scholar] [CrossRef]
- Viran, P.A.G.; Binal, A. Effects of repeated freeze-thaw cycles on physico-mechanical properties of cohesive soils. Arab. J. Geosci. 2018, 11, 250. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Q.; Liu, S.; Shangguan, Y.; Fu, H.; Ma, B.; Chen, H.; Yuan, X. Experimental investigation of the geotechnical properties and microstructure of lime-stabilized saline soils under freeze-thaw cycling. Cold Reg. Sci. Technol. 2019, 161, 32–42. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, L. The Microstructure Characters of Saline Soil in Qarhan Salt Lake Area and Its Behaviors of Mechanics and Compressive Strength. Arab. J. Sci. Eng. 2014, 39, 8649–8658. [Google Scholar] [CrossRef]
- Li, M.; Chai, S.; Du, H.; Wang, C. Effect of chlorine salt on the physical and mechanical properties of inshore saline soil treated with lime. Soils Found. 2016, 56, 327–335. [Google Scholar] [CrossRef]
- Yan, C.; Zhang, Z.; Jing, Y. Characteristics of strength and pore distribution of lime-flyash loess under freeze-thaw cycles and dry-wet cycles. Arab. J. Geosci. 2017, 10, 544. [Google Scholar] [CrossRef]
- Tang, Y.-q.; Yan, J.-j. Effect of freeze–thaw on hydraulic conductivity and microstructure of soft soil in Shanghai area. Environ. Earth Sci. 2015, 73, 7679–7690. [Google Scholar] [CrossRef]
- Hu, R.L.; Yeung, M.R.; Lee, C.F.; Wang, S.J. Mechanical behavior and microstructural variation of loess under dynamic compaction. Eng. Geol. 2001, 59, 203–217. [Google Scholar] [CrossRef]
- Qi, J.; Zhang, J.; Zhu, Y. Influence of freezing-thawing on soil structure and its soil mechanics significance. Chin. J. Rock Mech. Eng. 2003, 39, 2690–2694. [Google Scholar]
- Jiang, M.; Zhang, F.; Hu, H.; Cui, Y.; Peng, J. Structural characterization of natural loess and remolded loess under triaxial tests. Eng. Geol. 2014, 181, 249–260. [Google Scholar] [CrossRef]
- Xu, J.; Ren, J.; Wang, Z.; Wang, S.; Yuan, J. Strength behaviors and meso-structural characters of loess after freeze-thaw. Cold Reg. Sci. Technol. 2018, 148, 104–120. [Google Scholar] [CrossRef]
- Wen, B.-P.; Yan, Y.-J. Influence of structure on shear characteristics of the unsaturated loess in Lanzhou, China. Eng. Geol. 2014, 168, 46–58. [Google Scholar] [CrossRef]
- Zhang, Z.; Liang, J.; Huang, Y.; Qiu, G.; Yuan, Q. A study of the relationship between shear strength and microstructure of laterite under drying and wetting cycles. Hydrogeol. Eng. Geol. 2018, 45, 78–85. [Google Scholar]
- Cui, Z.-D.; He, P.-P.; Yang, W.-H. Mechanical properties of a silty clay subjected to freezing–thawing. Cold Reg. Sci. Technol. 2014, 98, 26–34. [Google Scholar] [CrossRef]
- You, Z.; Lai, Y.; Zhang, M.; Liu, E. Quantitative analysis for the effect of microstructure on the mechanical strength of frozen silty clay with different contents of sodium sulfate. Environ. Earth Sci. 2017, 76, 143. [Google Scholar] [CrossRef]
- Aldaood, A.; Bouasker, M.; Al-Mukhtar, M. Impact of freeze–thaw cycles on mechanical behaviour of lime stabilized gypseous soils. Cold Reg. Sci. Technol. 2014, 99, 38–45. [Google Scholar] [CrossRef]
- Roustaei, M.; Eslami, A.; Ghazavi, M. Effects of freeze–thaw cycles on a fiber reinforced fine grained soil in relation to geotechnical parameters. Cold Reg. Sci. Technol. 2015, 120, 127–137. [Google Scholar] [CrossRef]
- Kamei, T.; Ahmed, A.; Shibi, T. Effect of freeze–thaw cycles on durability and strength of very soft clay soil stabilised with recycled Bassanite. Cold Reg. Sci. Technol. 2012, 82, 124–129. [Google Scholar] [CrossRef]
- Zhang, F.; Wang, G.; Kamai, T.; Chen, W.; Zhang, D.; Yang, J. Undrained shear behavior of loess saturated with different concentrations of sodium chloride solution. Eng. Geol. 2013, 155, 69–79. [Google Scholar] [CrossRef]
- Han, Y.; Wang, Q.; Wang, N.; Wang, J.; Zhang, X.; Cheng, S.; Kong, Y. Effect of freeze-thaw cycles on shear strength of saline soil. Cold Reg. Sci. Technol. 2018, 154, 42–53. [Google Scholar] [CrossRef]
- Wang, Q.; Li, C.; Liu, Y.; Sun, D.; Zhang, X.; Ma, B. Mechanical properties of saline soil under the influence of different factors. Fresenius Environ. Bull. 2019, 28, 1366–1373. [Google Scholar]
- Chinese Standard. GB/T50123-1999. Standard for Soil Test Methods; China Planning Press: Beijing, China, 1999. [Google Scholar]
- ASTM. Standard Practice for Classification of Soils for Engineering Purposes (Unified Soil Classification System), D2487-11; ASTM International: West Conshohocken, PA, USA, 2011. [Google Scholar]
- Wang, N.; Wang, Q.; Huo, Z.; Ma, B.; Chen, Y. Influence of salt and compaction on critical water content of frost heaving of saline soil. J. Eng. Geol. 2016, 24, 951–958. [Google Scholar]
- Wang, J.-D.; Li, P.; Ma, Y.; Vanapalli, S.K. Evolution of pore-size distribution of intact loess and remolded loess due to consolidation. J. Soils Sediments 2019, 19, 1226–1238. [Google Scholar] [CrossRef]
- Tang, C.; Shi, B.; Wang, B. Factors affecting analysis of soil microstructure using SEM. Chin. J. Geotech. Eng. 2008, 30, 560–565. [Google Scholar]
- Wang, Q.; Wang, F.; Xiao, S. A quantitative study of the microstructure characteristics of soil and its application to the engineering. J. Chengdu Univ. Technol. 2001, 162, 148–153. [Google Scholar]
- Tarquis, A.M.; McInnes, K.J.; Key, J.R.; Saa, A.; Garcia, M.R.; Diaz, M.C. Multiscaling analysis in a structured clay soil using 2D images. J. Hydrol. 2006, 322, 236–246. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, J.; Yan, H. Quantitative evaluation of microstructure characteristics of cement consolidated soil. Bull. Eng. Geol. Environ. 2013, 72, 233–236. [Google Scholar] [CrossRef]
- Wang, J.; Wang, Q.; Kong, Y.; Han, Y.; Cheng, S. Analysis of the pore structure characteristics of freeze-thawed saline soil with different salinities based on mercury intrusion porosimetry. Environ. Earth Sci. 2020, 79, 161. [Google Scholar] [CrossRef]
- Shi, B. Quantitative Assessment of Changes of Microstructure for Clayey Soil in the Process of Compaction. Chin. J. Geotech. Eng. 1996, 42, 60–65. [Google Scholar]
- Fang, L.; Qi, J.; Ma, W. Freeze-thaw induced changes in soil structure and its relationship with variations in strength. J. Glaciol. Geocryol. 2012, 34, 435–440. [Google Scholar]
- Zhang, Y.; Bing, H.; Yang, C. Influences of freeze-thaw cycles on mechanical properties of silty clay based on SEM and MIP test. Chin. J. Rock Mech. Eng. 2015, 34, 3597–3603. [Google Scholar]
- Zhang, Z.-L.; Cui, Z.-D. Analysis of microscopic pore structures of the silty clay before and after freezing–thawing under the subway vibration loading. Environ. Earth Sci. 2017, 76, 528. [Google Scholar] [CrossRef]
- Liu, R.X.; Kuang, J.; Gong, Q.; Hou, X.L. Principal component regression analysis with spss. Comput. Methods Programs Biomed. 2003, 71, 141–147. [Google Scholar] [CrossRef]
- Alver, A.; Kazan, Z. Prediction of full-scale filtration plant performance using artificial neural networks based on principal component analysis. Sep. Purif. Technol. 2020, 230, 115868. [Google Scholar] [CrossRef]


| Property | Value | Testing Method |
|---|---|---|
| Natural water content (%) | 26.6 | Oven-drying method |
| Natural density (g/cm3) | 1.92 | Cutting ring method |
| Dry density (g/cm3) | 1.517 | |
| Particle size distribution (%) | Combined densimeter and sieve method | |
| Sand (2–0.075 mm) | 2.20 | |
| Silt (0.075–0.005 mm) | 79.55 | |
| Clay (<0.005 mm) | 18.25 | |
| Liquid limit (%) | 43.0 | Liquid-plastic limit joint determination method |
| Plastic limit (%) | 22.0 | |
| Soluble salt content | ||
| Total (%) | 1.42 | Water-bath evaporation |
| Na+ (mmol/100 g) | 3.48 | Flame photometer |
| HCO3− (mmol/100 g) | 1.87 | Neutralization titration |
| SO42− (mmol/100 g) | 1.72 | EDTA complexometry titration |
| Mineral | Quartz | Alkali Feldspar | Plagioclase | Calcite | Illite | Kaolinite |
|---|---|---|---|---|---|---|
| Content (%) | 43 | 12 | 29 | 4 | 7 | 5 |
| 100 kPa | −0.843 | −0.169 | 0.430 | 0.901 | −0.976 |
| 200 kPa | −0.870 | −0.184 | 0.423 | 0.885 | −0.955 |
| 300 kPa | −0.899 | −0.178 | 0.401 | 0.891 | −0.939 |
| 1.000 | −0.856 | 0.827 | |
| −0.856 | 1.000 | −0.902 | |
| 0.827 | −0.902 | 1.000 |
| Confining Pressure | Principal Component Regression Equation | |
|---|---|---|
| 100 kPa | −144.10 + 2612.03 − 276.76 − 2049.38 | 0.901 |
| 200 kPa | −126.40 + 2893.71 − 306.61 − 2232.60 | 0.894 |
| 300 kPa | −131.64 + 3013.52 − 317.64 − 2272.78 | 0.906 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Wang, Q.; Lin, S.; Han, Y.; Cheng, S.; Wang, N. Relationship between the Shear Strength and Microscopic Pore Parameters of Saline Soil with Different Freeze-Thaw Cycles and Salinities. Symmetry 2020, 12, 1709. https://doi.org/10.3390/sym12101709
Wang J, Wang Q, Lin S, Han Y, Cheng S, Wang N. Relationship between the Shear Strength and Microscopic Pore Parameters of Saline Soil with Different Freeze-Thaw Cycles and Salinities. Symmetry. 2020; 12(10):1709. https://doi.org/10.3390/sym12101709
Chicago/Turabian StyleWang, Jiaqi, Qing Wang, Sen Lin, Yan Han, Shukai Cheng, and Ning Wang. 2020. "Relationship between the Shear Strength and Microscopic Pore Parameters of Saline Soil with Different Freeze-Thaw Cycles and Salinities" Symmetry 12, no. 10: 1709. https://doi.org/10.3390/sym12101709
APA StyleWang, J., Wang, Q., Lin, S., Han, Y., Cheng, S., & Wang, N. (2020). Relationship between the Shear Strength and Microscopic Pore Parameters of Saline Soil with Different Freeze-Thaw Cycles and Salinities. Symmetry, 12(10), 1709. https://doi.org/10.3390/sym12101709





