An Alternate Unsupervised Technique Based on Distance Correlation and Shannon Entropy to Estimate λ0-Fuzzy Measure
Abstract
1. Introduction
1.1. Motivation of the Study
1.2. Statement on Contributions
2. Related Works
- Boundary condition infers that the value of the empty set should be zero, whereas the value of the universal set, which has the presence of all attributes, should be one, i.e., and .
- Monotone condition refers to a situation where the addition of any new attribute to a subset will never decline the value of the subset [40], i.e., if then .
- First limitation—All the techniques required the input of some initial data by the decision-makers, mainly concerning the interrelationships held by the decision attributes. Such data cannot be simply furnished by any decision-makers who have incomplete information, or exhibits ambiguity over the nature of the attributes. In short, only fully-informed decision-makers may benefit from these techniques.
- Second limitation—The initial data requirement of the DEMATEL and ISM-based technique is three-fold and two-fold than that of the original technique, respectively. Although the quantity of initial data required by all the three techniques is still manageable when is relatively small, it will grow exponentially as increases. This gives an indication that even a fully-informed decision-maker may struggle to provide the necessary initial data, especially when is sufficiently large, in a consistent and precise manner. For instance, for a problem involving ten attributes, an amount of 45, 90, or 135 initial data is required by the decision-makers should they use the original technique, ISM-based technique, or DEMATEL-based technique, respectively.
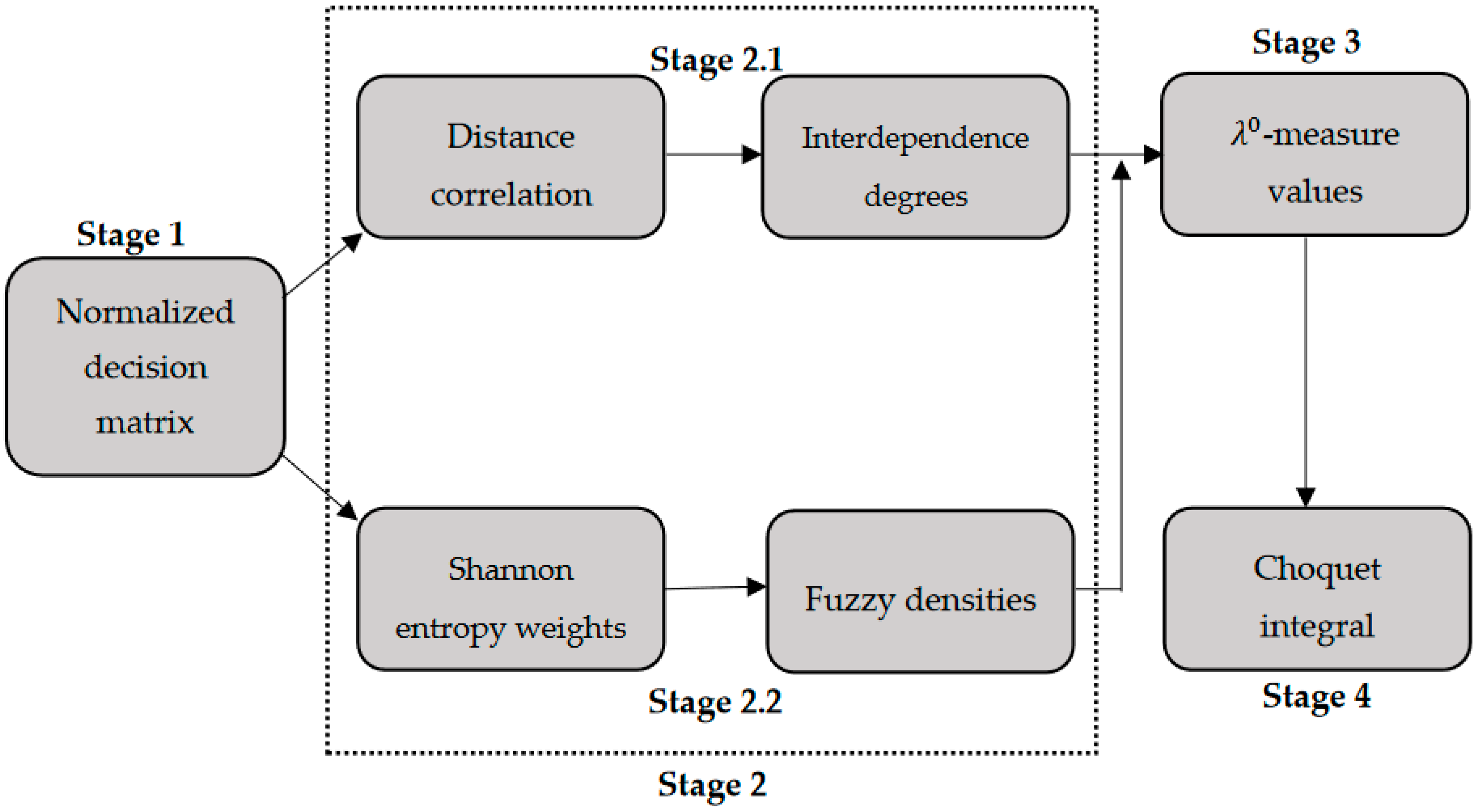
3. The Proposed Technique
- Stage 1—Normalizing the decision matrix.
- Stage 2—Determining the inputs required for estimation.
- ◦
- Stage 2.1—Determining the interdependence degrees using distance correlation.
- ◦
- Stage 2.2—Determining the fuzzy densities with the aid of Shannon entropy weighting method.
- Stage 3—Estimating -measure values.
- Stage 4—Applying Choquet integral.
3.1. Normalizing Decision Matrix (Stage 1)
3.2. Determining the Inputs Required for Estimation (Stage 2)
3.2.1. Determining the Interdependence Degrees using Distance Correlation (Stage 2.1)
- Step 1—The Euclidean distance matrix of attribute was constructed based on the scores associated with all the alternatives under consideration. A similar matrix was constructed for .
- Step 2—The following double-centering steps on each matrix were executed, where the row means, column means, and the overall mean of the elements in each matrix become zero. The row mean from each element was deducted, then the column mean from each element was deducted, and finally, the matrix mean was added to each element.
- Step 3—Multiplication of the double-centered matrices elementwise was performed and the mean value of the elements from the resulted matrix was identified. Mean value is obtained by dividing the sum of elements with the total number of elements. The square root of the mean value is the distance covariance of and i.e., .
- Step 4—Since the distance variance of , , and the distance variance of , then these two values can be calculated by repeating step 1-3 accordingly.
- Step 5—The available , , and were substituted into (6) to compute the distance correlation between and i.e., respectively.
3.2.2. Application of Shannon Entropy Method (Stage 2.2)
3.3. Estimating -Measure Values and Applying Choquet Integral (Stage 3 and 4)
4. An Application to Hospital Website Evaluation Problem
Comparison with Other Techniques
- As the term “supervised” suggests, all the existing supervised techniques, namely the original technique, the DEMATEL-based technique, and ISM-based technique required the input of additional data by the decision-makers for the estimation of -measure values. On the contrary, the PCBU and the proposed unsupervised technique were completely free from such requirement. As such, both techniques may be able to minimize possible biases that are usually tied with the subjective evaluation made by individuals, and thus increases the objectivity of the estimation. However, possible errors in the estimation may present in PCBU due to the inaccurate interdependence degrees that are determined using Pearson correlation coefficients, which is supported by the difference in the aggregated scores derived with the proposed technique and PCBU (refer to Table 8).
- The determination of fuzzy densities in the proposed technique was carried out systematically by considering the entropy weights of attributes. A similar approach was applied to other techniques except for the original technique. The original technique determines the densities by solving a system of inequalities in the absence of any additional inputs on the possible ratio of importance between the attributes.
- Unlike the DEMATEL-based and ISM-based technique, the proposed technique, the original technique, and PCBU failed to express the actual causal relationships represented by the attributes. It was observed that the DEMATEL-based and ISM-based technique portrayed such information via digraphs, and having a better understanding of the causal relationships will be very useful in the perspective of decision-making. For instance, decision-makers can develop a more efficient strategy to improve alternative performance by shifting the focus on the causal attributes than on the effect attributes.
- There were no arithmetic operations involved in the context of the determination of interdependence degrees for the original technique as it was achieved through direct and subjective evaluation by the decision-makers. Meanwhile, in the case of the other two supervised techniques, the interdependence degrees were determined with the help of DEMATEL or ISM method. Thus, complications arise for the calculation process with the increasing number of decision attributes. As for the proposed technique and PCBU, worse complications may even occur as these techniques determined the interdependence degree that was based on the distance correlation and Pearson correlation measures respectively. Therefore, the number of arithmetic operations required can grow rapidly even with a slight increase in both the number of decision alternatives and attributes (i.e., the size of the decision matrix) [81]. Nevertheless, the steps involved in the calculation of Pearson correlation was less complicated than that of the distance correlation. Therefore, it can be concluded that the proposed technique is computationally more demanding as compared to the other four techniques.
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
- Scores with respect to and
| Website/Attribute | ||
| 1 | 0.8730 | |
| 0.3333 | 1 | |
| 0.7843 | 0.6508 | |
| 0 | 0 | |
| 0.0392 | 0.0476 |
- Euclidean distance matrix of
| Website | Row Mean | |||||
| 0 | 0.6667 | 0.2157 | 1.0000 | 0.9608 | 0.5686 | |
| 0.6667 | 0 | 0.4510 | 0.3333 | 0.2941 | 0.3490 | |
| 0.2157 | 0.4510 | 0 | 0.7843 | 0.7451 | 0.4392 | |
| 1.0000 | 0.3333 | 0.7843 | 0 | 0.0392 | 0.4314 | |
| 0.9608 | 0.2941 | 0.7451 | 0.0392 | 0 | 0.4078 | |
| Column mean | 0.5686 | 0.3490 | 0.4392 | 0.4314 | 0.4078 | Mean = 0.4392 |
- Euclidean distance matrix of
| Website | Row Mean | |||||
| 0 | 0.1270 | 0.2222 | 0.8730 | 0.8254 | 0.4095 | |
| 0.1270 | 0 | 0.3492 | 1.0000 | 0.9524 | 0.4857 | |
| 0.2222 | 0.3492 | 0 | 0.6508 | 0.6032 | 0.3651 | |
| 0.8730 | 1.0000 | 0.6508 | 0 | 0.0476 | 0.5143 | |
| 0.8254 | 0.9524 | 0.6032 | 0.0476 | 0 | 0.4857 | |
| Column mean | 0.4095 | 0.4857 | 0.3651 | 0.5143 | 0.4857 | Mean = 0.4521 |
- Double-centered matrix of
| Website | Row Mean | |||||
| −0.6980 | 0.1882 | −0.3529 | 0.4392 | 0.4235 | 0 | |
| 0.1882 | −0.2588 | 0.1020 | −0.0078 | −0.0235 | 0 | |
| −0.3529 | 0.1020 | −0.4392 | 0.3529 | 0.3373 | 0 | |
| 0.4392 | −0.0078 | 0.3529 | −0.4235 | −0.3608 | 0 | |
| 0.4235 | −0.0235 | 0.3373 | −0.3608 | −0.3765 | 0 | |
| Column mean | 0 | 0 | 0 | 0 | 0 | Mean = 0 |
- Double-centered matrix of
| Website | Row Mean | |||||
| −0.3670 | −0.3162 | −0.1003 | 0.4013 | 0.3822 | 0 | |
| −0.3162 | −0.5194 | −0.0495 | 0.4521 | 0.4330 | 0 | |
| −0.1003 | −0.0495 | −0.2781 | 0.2235 | 0.2044 | 0 | |
| 0.4013 | 0.4521 | 0.2235 | −0.5765 | −0.5003 | 0 | |
| 0.3822 | 0.4330 | 0.2044 | −0.5003 | −0.5194 | 0 | |
| Column mean | 0 | 0 | 0 | 0 | 0 | Mean = 0 |
- = = = 0.2966
| Website | |||||
| 0.2562 | −0.0595 | 0.0354 | 0.1762 | 0.1619 | |
| −0.0595 | 0.1344 | −0.0050 | −0.0035 | −0.0102 | |
| 0.0354 | −0.0050 | 0.1221 | 0.0789 | 0.0689 | |
| 0.1762 | −0.0035 | 0.0789 | 0.2442 | 0.1805 | |
| 0.1619 | −0.0102 | 0.0689 | 0.1805 | 0.1955 |
- = = = 0.3401
| Website | |||||
| 0.4873 | 0.0354 | 0.1246 | 0.1929 | 0.1794 | |
| 0.0354 | 0.0670 | 0.0104 | 0.0001 | 0.0006 | |
| 0.1246 | 0.0104 | 0.1929 | 0.1246 | 0.1137 | |
| 0.1929 | 0.0001 | 0.1246 | 0.1794 | 0.1302 | |
| 0.1794 | 0.0006 | 0.1137 | 0.1302 | 0.1417 |
- = = = 0.3683
| Website | |||||
| 0.1347 | 0.1000 | 0.0101 | 0.1610 | 0.1461 | |
| 0.1000 | 0.2697 | 0.0025 | 0.2044 | 0.1875 | |
| 0.0101 | 0.0025 | 0.0773 | 0.0499 | 0.0418 | |
| 0.1610 | 0.2044 | 0.0499 | 0.3324 | 0.2503 | |
| 0.1461 | 0.1875 | 0.0418 | 0.2503 | 0.2697 |
References
- Khameneh, A.Z.; Kılıçman, A.; Kilicman, A. Multi-attribute decision-making based on soft set theory: A systematic review. Soft Comput. 2018, 23, 6899–6920. [Google Scholar] [CrossRef]
- Mardani, A.; Nilashi, M.; Zavadskas, E.K.; Awang, S.R.; Zare, H.; Jamal, N.M. Decision Making Methods Based on Fuzzy Aggregation Operators: Three Decades Review from 1986 to 2017. Int. J. Inf. Technol. Decis. Mak. 2018, 17, 391–466. [Google Scholar] [CrossRef]
- Qin, Y.; Qi, Q.; Scott, P.J.; Jiang, X. Multiple criteria decision making based on weighted Archimedean power partitioned Bonferroni aggregation operators of generalised orthopair membership grades. Soft Comput. 2020, 24, 1–27. [Google Scholar] [CrossRef]
- Krishnan, A.R.; Kasim, M.M.; Abu Bakar, E.M.N.E. A Short Survey on the Usage of Choquet Integral and its Associated Fuzzy Measure in Multiple Attribute Analysis. Procedia Comput. Sci. 2015, 59, 427–434. [Google Scholar] [CrossRef]
- Marichal, J.-L. An axiomatic approach of the discrete Choquet integral as a tool to aggregate interacting criteria. IEEE Trans. Fuzzy Syst. 2000, 8, 800–807. [Google Scholar] [CrossRef]
- Hu, Y.-C.; Chen, H.-C. Choquet integral-based hierarchical networks for evaluating customer service perceptions on fast food stores. Expert Syst. Appl. 2010, 37, 7880–7887. [Google Scholar] [CrossRef]
- Bonferroni, C. Sulle medie multiple di potenze. Boll. dell’Unione Mat. Ital. 1950, 5, 267–270. [Google Scholar]
- Wang, L.; Li, N. Pythagorean fuzzy interaction power Bonferroni mean aggregation operators in multiple attribute decision making. Int. J. Intell. Syst. 2019, 35, 150–183. [Google Scholar] [CrossRef]
- Wang, Z.; Leung, K.-S.; Wong, M.-L.; Fang, J. A new type of nonlinear integrals and the computational algorithm. Fuzzy Sets Syst. 2000, 112, 223–231. [Google Scholar] [CrossRef]
- Mu, Z.; Zeng, S. Some novel intuitionistic fuzzy information fusion methods in decision making with interaction among attributes. Soft Comput. 2018, 23, 10439–10448. [Google Scholar] [CrossRef]
- Choquet, G. Theory of capacities. Ann. de l’Institut Fourier. 1954, 5, 131–295. [Google Scholar] [CrossRef]
- Abdullah, L.; Zulkifli, N.; Liao, H.; Herrera-Viedma, E.; Al-Barakati, A. An interval-valued intuitionistic fuzzy DEMATEL method combined with Choquet integral for sustainable solid waste management. Eng. Appl. Artif. Intell. 2019, 82, 207–215. [Google Scholar] [CrossRef]
- Corrente, S.; Greco, S.; Ishizaka, A. Combining analytical hierarchy process and Choquet integral within non-additive robust ordinal regression. Omega 2016, 61, 2–18. [Google Scholar] [CrossRef]
- Beliakov, G.; Divakov, D. On representation of fuzzy measures for learning Choquet and Sugeno integrals. Knowl. Based Syst. 2020, 189, 105134. [Google Scholar] [CrossRef]
- Pasi, G.; Viviani, M.; Carton, A. A Multi-Criteria Decision Making approach based on the Choquet integral for assessing the credibility of User-Generated Content. Inf. Sci. 2019, 503, 574–588. [Google Scholar] [CrossRef]
- Larbani, M.; Huang, C.Y.; Tzeng, G.H. A novel method for fuzzy measure identification. Int. J. Fuzzy Syst. 2011, 13, 24–34. [Google Scholar]
- Krishnan, A.R.; Aqilah, S.N.; Kasim, M.M.; Nazri, E.M.; Char, A.K. A revised procedure to identify λ 0-measure values for applying Choquet integral in solving multi-attribute decision problems. OPSEARCH 2017, 54, 637–650. [Google Scholar] [CrossRef]
- Krishnan, A.R.; Ab Wahab, S.N.A.; Kasim, M.M.; Abu Bakar, E.M.N.E. An alternate method to determine λ0-measure values prior to applying Choquet integral in a multi-attribute decision making environment. Decis. Sci. Lett. 2019, 8, 193–210. [Google Scholar] [CrossRef]
- Rowley, H.V.; Geschke, A.; Lenzen, M. A practical approach for estimating weights of interacting criteria from profile sets. Fuzzy Sets Syst. 2015, 272, 70–88. [Google Scholar] [CrossRef]
- Krishnan, A.R.; Hamid, R.; Kasim, M.M. An Unsupervised Technique to Estimate λ0-Fuzzy Measure Values and Its Application to Multi-criteria Decision Making. In Proceedings of the 2020 IEEE 7th International Conference on Industrial Engineering and Applications (ICIEA), Bangkok, Thailand, 16–21 April 2020. [Google Scholar]
- Kosorok, M.R. Discussion of: Brownian distance covariance. Ann. Appl. Stat. 2009, 3, 1270–1278. [Google Scholar] [CrossRef]
- Székely, G.J.; Rizzo, M.L.; Bakirov, N.K. Measuring and testing dependence by correlation of distances. Ann. Stat. 2007, 35, 2769–2794. [Google Scholar] [CrossRef]
- Krishnan, A.R.; Kasim, M.M.; Abu Bakar, E.M.N.E. Application of Choquet integral in solving multi-attribute decision making problems. In International Conference on Graphic and Image Processing (ICGIP 2011); SPIE: Bellingham, WA, USA, 2011; Volume 8285, p. 82853L. [Google Scholar]
- Mohd, W.R.W.; Abdullah, L. Choquet integral with respect to maximized L-measure and delta-measure. In AIP Conference Proceedings; American Institute of Physics: College Park, MD, USA, 2017; Volume 1870. [Google Scholar]
- Murillo, J.; Guillaume, S.; Bulacio, P. k-maxitive fuzzy measures: A scalable approach to model interactions. Fuzzy Sets Syst. 2017, 324, 33–48. [Google Scholar] [CrossRef]
- Kojadinovic, I. Estimation of the weights of interacting criteria from the set of profiles by means of information-theoretic functionals. Eur. J. Oper. Res. 2004, 155, 741–751. [Google Scholar] [CrossRef]
- Sugeno, M. Theory of Fuzzy Integrals and Its Applications; Tokyo Institute of Technology: Meguro City, Tokyo, Japan, 1974. [Google Scholar]
- Khan, M.S.A. The Pythagorean fuzzy Einstein Choquet integral operators and their application in group decision making. Comput. Appl. Math. 2019, 38, 128. [Google Scholar] [CrossRef]
- Grabisch, M. k-order additive discrete fuzzy measures and their representation. Fuzzy Sets Syst. 1997, 92, 167–189. [Google Scholar] [CrossRef]
- Wu, J.Z.; Zhang, Q. 2-Order Additive Fuzzy Measures Identification Method Based on Maximum Entropy Principle. Fuzzy Optim. Decis. Mak. 2010, 9, 435–453. [Google Scholar] [CrossRef]
- Zhang, L.; Zhou, P.; Zhou, D. A non-additive multiple criteria analysis method for evaluation of airline service quality. J. Air Transp. Manag. 2015, 47, 154–161. [Google Scholar] [CrossRef]
- Lee, K.M.; Leekwang, H. Identification of λ-fuzzy measure by genetic algorithms. Fuzzy Sets Syst. 1995, 75, 301–309. [Google Scholar] [CrossRef]
- Takahagi, E. On Identification Methods of λ-Fuzzy Measures using Weights and λ. J. Jpn. Soc. Fuzzy Theory Syst. 2000, 12, 665–676. [Google Scholar] [CrossRef]
- Chen, T.-Y.; Wang, J.-C. Identification of -fuzzy measures using sampling design and genetic algorithms. Fuzzy Sets Syst. 2001, 123, 321–341. [Google Scholar] [CrossRef]
- Wang, J.-C.; Chen, T.-Y. Experimental analysis of λ-fuzzy measure identification by evolutionary algorithms. Int. J. Fuzzy Syst. 2005, 7, 1–9. [Google Scholar]
- Feng, C.-M.; Wu, P.-J.; Chia, K.-C. A hybrid fuzzy integral decision-making model for locating manufacturing centers in China: A case study. Eur. J. Oper. Res. 2010, 200, 63–73. [Google Scholar] [CrossRef]
- Krishnan, A.R. A Multi-Attribute Decision Making Procedure Using Fuzzy Numbers and Hybrid Aggregators. Ph.D. Thesis, Universiti Utara Malaysia, Changlun, Malaysia, 2014. [Google Scholar]
- Murofushi, T.; Sugeno, M. A theory of fuzzy measures: Representations, the Choquet integral, and null sets. J. Math. Anal. Appl. 1991, 159, 532–549. [Google Scholar] [CrossRef]
- Jin, L.; Mesiar, R.; Yager, R.R. Derived fuzzy measures and derived Choquet integrals with some properties. IEEE Trans. Fuzzy Syst. 2020, 1. [Google Scholar] [CrossRef]
- Chang, J.-P.; Chen, Z.-S.; Xiong, S.-H.; Zhang, J.; Chin, K.-S. Intuitionistic Fuzzy Multiple Criteria Group Decision Making: A Consolidated Model With Application to Emergency Plan Selection. IEEE Access 2019, 7, 41958–41980. [Google Scholar] [CrossRef]
- Wang, X.-Z.; Wang, X.-J. A new methodology for determining fuzzy densities in the fusion model based on fuzzy integral. In Proceedings of the 2004 International Conference on Machine Learning and Cybernetics (IEEE Cat. No.04EX826), Shanghai, China, 26–29 August 2004; Volume 4, pp. 2028–2031. [Google Scholar]
- Grabisch, M. The application of fuzzy integrals in multicriteria decision making. Eur. J. Oper. Res. 1996, 89, 445–456. [Google Scholar] [CrossRef]
- Szekely, G.J.; Rizzo, M.L. On the uniqueness of distance covariance. Stat. Probab. Lett. 2012, 82, 2278–2282. [Google Scholar] [CrossRef]
- Jahan, A.; Edwards, K. A state-of-the-art survey on the influence of normalization techniques in ranking: Improving the materials selection process in engineering design. Mater. Des. 2015, 65, 335–342. [Google Scholar] [CrossRef]
- Vafaei, N.; Ribeiro, R.A.; Camarinha-Matos, L. Normalization Techniques for Multi-Criteria Decision Making: Analytical Hierarchy Process Case Study. In IFIP Advances in Information and Communication Technology; Springer Nature: Cham, Switzerland, 2016; Volume 470, pp. 261–269. [Google Scholar]
- Weaver, K.F.; Morales, V.; Dunn, S.L.; Godde, K.; Weaver, P.F. An Introduction to Statistical Analysis in Research. In An Introduction to Statistical Analysis in Research; Wiley: Hoboken, NJ, USA, 2017; pp. 435–471. [Google Scholar]
- Edelmann, D.; Fokianos, K.; Pitsillou, M. An Updated Literature Review of Distance Correlation and Its Applications to Time Series. Int. Stat. Rev. 2018, 87, 237–262. [Google Scholar] [CrossRef]
- Shen, C.; Priebe, C.E.; Vogelstein, J.T. From Distance Correlation to Multiscale Graph Correlation. J. Am. Stat. Assoc. 2019, 115, 280–291. [Google Scholar] [CrossRef]
- Understanding Distance Correlation Computations. Available online: https://stats.stackexchange.com/q/183930 (accessed on 20 January 2020).
- Chaudhuri, A.; Hu, W. A fast algorithm for computing distance correlation. Comput. Stat. Data Anal. 2019, 135, 15–24. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Lee, H.-C.; Chang, C.-T. Comparative analysis of MCDM methods for ranking renewable energy sources in Taiwan. Renew. Sustain. Energy Rev. 2018, 92, 883–896. [Google Scholar] [CrossRef]
- Fu, Y.; Wang, M.; Lai, K.K. A Modified Nature Publishing Index via Shannon Entropy. Discret. Dyn. Nat. Soc. 2015. [Google Scholar] [CrossRef]
- Song, Y.; Peng, Y. A MCDM-Based Evaluation Approach for Imbalanced Classification Methods in Financial Risk Prediction. IEEE Access 2019, 7, 84897–84906. [Google Scholar] [CrossRef]
- Zhu, Y.; Tian, D.; Yan, F. Effectiveness of Entropy Weight Method in Decision-Making. Math. Probl. Eng. 2020. [Google Scholar] [CrossRef]
- Dehdasht, G.; Ferwati, M.S.; Zin, R.M.; Abidin, N.Z. A hybrid approach using entropy and TOPSIS to select key drivers for a successful and sustainable lean construction implementation. PLoS ONE 2020, 15, e0228746. [Google Scholar] [CrossRef]
- Huerta, T.R.; Hefner, J.L.; Ford, E.W.; McAlearney, A.S.; Menachemi, N.; Kazley, A.; Vagelatos, A. Hospital Website Rankings in the United States: Expanding Benchmarks and Standards for Effective Consumer Engagement. J. Med. Internet Res. 2014, 16, e64. [Google Scholar] [CrossRef]
- Dickinger, A.; Stangl, B. Website performance and behavioral consequences: A formative measurement approach. J. Bus. Res. 2013, 66, 771–777. [Google Scholar] [CrossRef]
- Abou-Shouk, M.A.; Khalifa, G.S. The influence of website quality dimensions on e-purchasing behaviour and e-loyalty: A comparative study of Egyptian travel agents and hotels. J. Travel Tour. Mark. 2016, 34, 608–623. [Google Scholar] [CrossRef]
- Stringam, B.B.; Gerdes, J. Service gap in hotel website load performance. Int. Hosp. Rev. 2019, 33, 16–29. [Google Scholar] [CrossRef]
- McKinney, V.; Yoon, K.; Zahedi, F. “Mariam” The Measurement of Web-Customer Satisfaction: An Expectation and Disconfirmation Approach. Inf. Syst. Res. 2002, 13, 296–315. [Google Scholar] [CrossRef]
- Wątróbski, J.; Karczmarczyk, A.; Jankowski, J.; Ziemba, P.; Wolski, W. Hierarchical Representation of Website Evaluation Model Using Survey and Perceptual Based Criteria. In Lecture Notes in Business Information Processing; Springer: Cham, Switzerland, 2018; Volume 311, pp. 229–248. [Google Scholar]
- Perçin, S. A combined fuzzy multicriteria decision-making approach for evaluating hospital website quality. J. Multi. Criteria Decis. Anal. 2019, 26, 129–144. [Google Scholar] [CrossRef]
- Lajiun, J. Sabah medical tourism ‘much cheaper’. Borneo Post Online, 14 July 2019. [Google Scholar]
- Qi, S.; Ip, C.; Leung, R.; Law, R.; Law, R. A New Framework on Website Evaluation. In Proceedings of the 2010 International Conference on E-Business and E-Government, Guangzhou, China, 7–9 May 2010; pp. 78–81. [Google Scholar]
- Kumar, A.; Dash, M.K. Using Fuzzy Delphi and Generalized Fuzzy TOPSIS to Evaluate Technological Service Flexibility Dimensions of Internet Malls. Glob. J. Flex. Syst. Manag. 2017, 18, 153–161. [Google Scholar] [CrossRef]
- Ahn, T.; Ryu, S.; Han, I. The impact of Web quality and playfulness on user acceptance of online retailing. Inf. Manag. 2007, 44, 263–275. [Google Scholar] [CrossRef]
- Pandey, D.; Nagpal, R.; Mehrotra, D. Navigational Complexity Metrics of a Website. In Advances in Intelligent Systems and Computing; Springer: Berlin, Germany, 2018; Volume 731, pp. 433–440. [Google Scholar]
- Teng, P.S.; Cai, D.; Walker, V.; Cassidy, T. A study of websites’ layout and user impressions from the perspective of college students. Bull. Jpn. Soc. Sci. Des. 2015, 61, 19–28. [Google Scholar]
- Thielsch, M.T.; Hirschfeld, G. Facets of Website Content. Hum. Comput. Interact. 2018, 34, 279–327. [Google Scholar] [CrossRef]
- Ismailova, R.; Inal, Y. Accessibility evaluation of top university websites: A comparative study of Kyrgyzstan, Azerbaijan, Kazakhstan and Turkey. Univers. Access Inf. Soc. 2017, 17, 437–445. [Google Scholar] [CrossRef]
- Viscomi, R.; Davies, A.; Duran, M. Using WebPageTest: Web Performance Testing for Novices and Power Users; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2016. [Google Scholar]
- Analysis, S. Fuzzy Measure-Choquet Integral Calculation System (λ Fuzzy Measure and Sensitivity Analysis). Available online: http://www.isc.senshu-u.ac.jp/~thc0456/Efuzzyweb/mant2/mant2.html (accessed on 8 February 2020).
- Raji, S.O.; Mahmud, M.; Tap, A.O.M.; Abubakar, A. Usability Evaluation of Hospital Websites in Nigeria: What Affects End Users’ Preferences? In Communications in Computer and Information Science; Springer: Berlin, Germany, 2014; Volume 435, Part I; pp. 430–434. [Google Scholar]
- MacCrimmon, K.R. Decision Making Among Multiple–Attribute Alternatives: A Survey and Consolidated Approach. In Research Memoranda; RAND Corporation: Santa Monica, CA, USA, 1968; Volume 189. [Google Scholar]
- Sears, G.W.; Miller, D.W.; Starr, M.K. Executive decisions and operations research. J. Oper. Res. Soc. 1962, 13. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Turskis, Z.; Antucheviciene, J. Optimization of Weighted Aggregated Sum Product Assessment. Elektron. Ir Elektrotechnika 2012, 122, 3–6. [Google Scholar] [CrossRef]
- Hwang, C.-L.; Yoon, K. Multiple Attribute Decision Making: Methods and Applications; Springer: Berlin, Germany, 1981; Volume 186. [Google Scholar]
- Mathew, M.; Sahu, S.; Upadhyay, A.K. Effect of normalization techniques in robot selection using weighted aggregated sum product assessment. Int. J. Innov. Res. Adv. Stud. 2017, 4, 59–63. [Google Scholar]
- Yalçın, N.; Pehlivan, N.Y. Application of the Fuzzy CODAS Method Based on Fuzzy Envelopes for Hesitant Fuzzy Linguistic Term Sets: A Case Study on a Personnel Selection Problem. Symmetry 2019, 11, 493. [Google Scholar] [CrossRef]
- Huo, X.; Székely, G.J. Fast Computing for Distance Covariance. Technometrics 2016, 58, 435–447. [Google Scholar] [CrossRef]
- Yuhana, U.L.; Fanani, N.Z.; Yuniarno, E.M.; Rochimah, S.; Koczy, L.T.; Purnomo, M.H. Combining Fuzzy Signature and Rough Sets Approach for Predicting the Minimum Passing Level of Competency Achievement. Int. J. Artif. Intell. 2020, 18, 1. [Google Scholar]
- Wong, K.W.; Gedeon, T.; Kóczy, L.T. Fuzzy Signature and Cognitive Modelling for Complex Decision Model. Adv. Intell. Soft Comput. 2007, 42, 380–389. [Google Scholar] [CrossRef]
- Ghorbanzadeh, O.; Moslem, S.; Blaschke, T.; Duleba, S. Sustainable Urban Transport Planning Considering Different Stakeholder Groups by an Interval-AHP Decision Support Model. Sustainability 2018, 11, 9. [Google Scholar] [CrossRef]
- Duleba, S. An ahp-ism approach for considering public preferences in a public transport development decision. Transport 2019, 34, 662–671. [Google Scholar] [CrossRef]
- Ilbahar, E.; Karaşan, A.; Cebi, S.; Kahraman, C. A novel approach to risk assessment for occupational health and safety using Pythagorean fuzzy AHP & fuzzy inference system. Saf. Sci. 2018, 103, 124–136. [Google Scholar] [CrossRef]
- Gündoğdu, F.K.; Kahraman, C. Spherical fuzzy sets and spherical fuzzy TOPSIS method. J. Intell. Fuzzy Syst. 2019, 36, 337–352. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
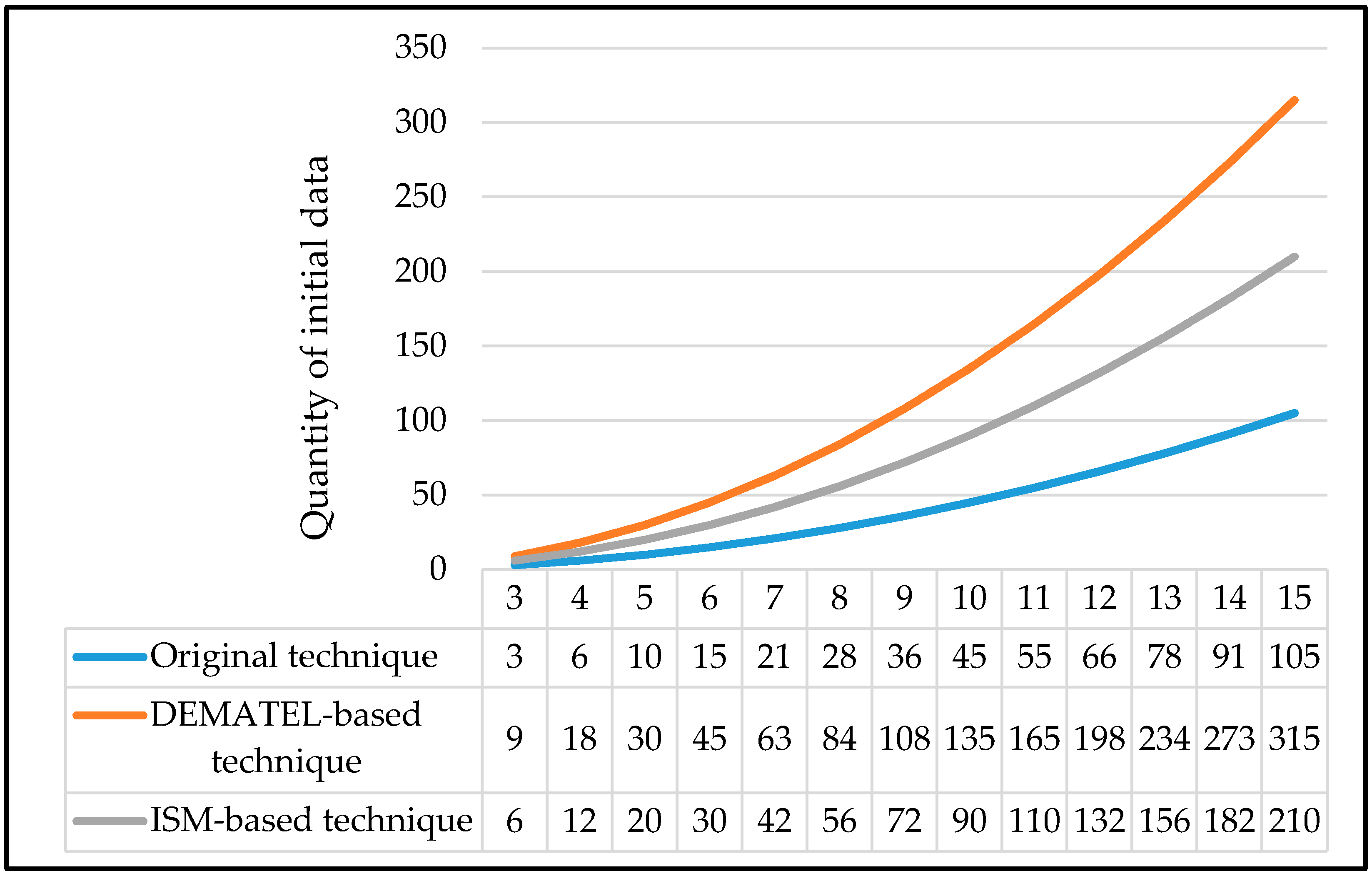
| Technique | Original Technique | DEMATEL Based-Technique | ISM Based-Technique |
|---|---|---|---|
| Type of initial data required | Interdependence degree of each pair of attributes | -Direct influence between every two attributes -Interdependence degree of each pair of attributes | -Contextual relationship between every two attributes -Interdependence degree of each pair of attributes |
| Quantity of initial data required |
| No. | Attribute | Description |
|---|---|---|
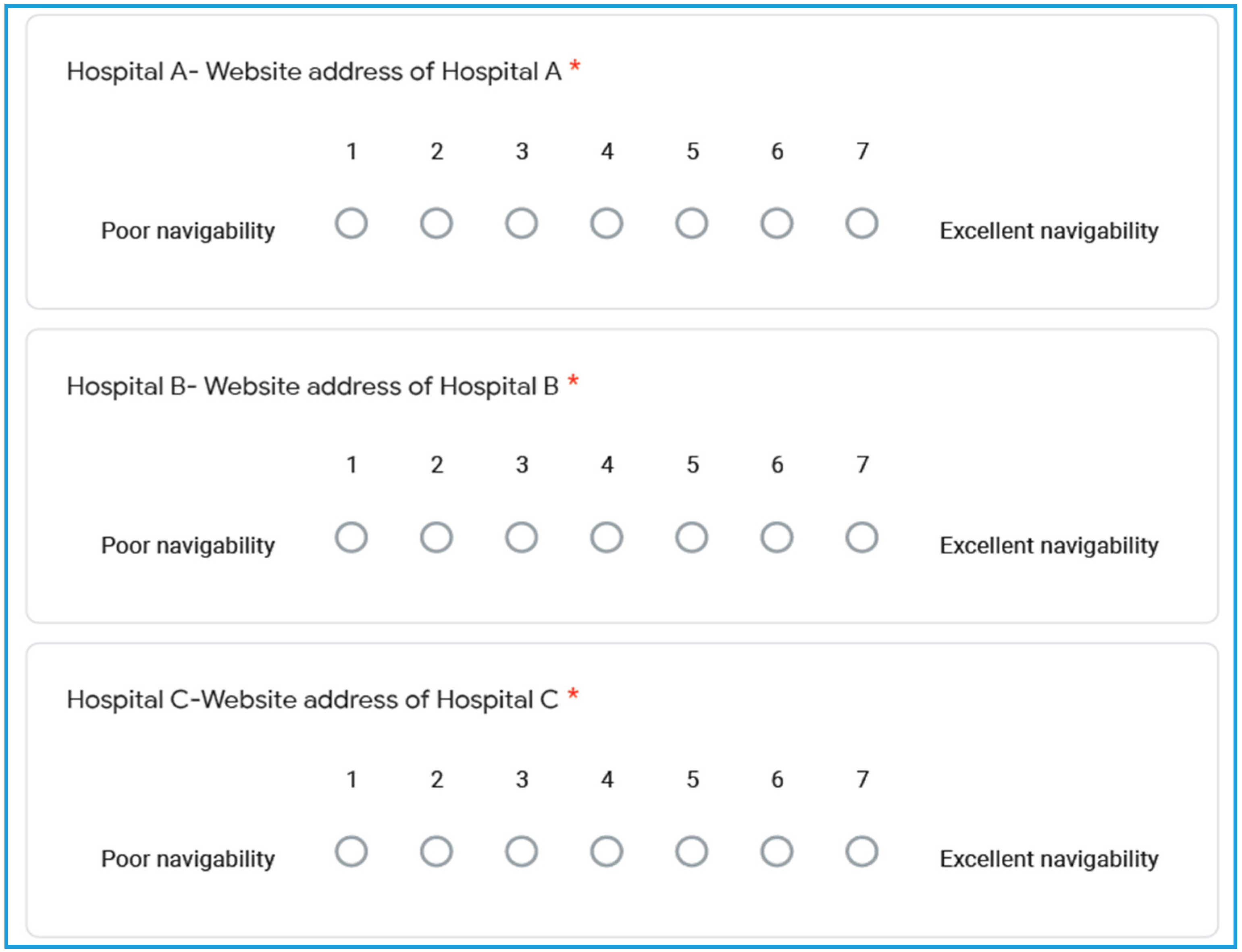
| 1 | Website navigability [68] | The visitors of the website can surf and leave every different page of the website with minimal hassle. The website also provides a clear site map (i.e., list of pages on the website) and efficient keyword search engine that allows the visitors to conveniently search for the desired subject. |
| 2 | Website layout design [69] | The website has a simple but attractive and well-organized layout structure. |
| 3 | Ease of use [58] | Even a new visitor can effortlessly learn to use or operate the website. |
| 4 | Website content [70] | The website provides useful, accurate, up-to-date, and easy-to-understand information to visitors. |
| 5 | Accessibility [71] | There are few indicators for accessibility, but for this study, accessibility is measured based on the download speed of the web page. |
| Decision Matrix | |||||
|---|---|---|---|---|---|
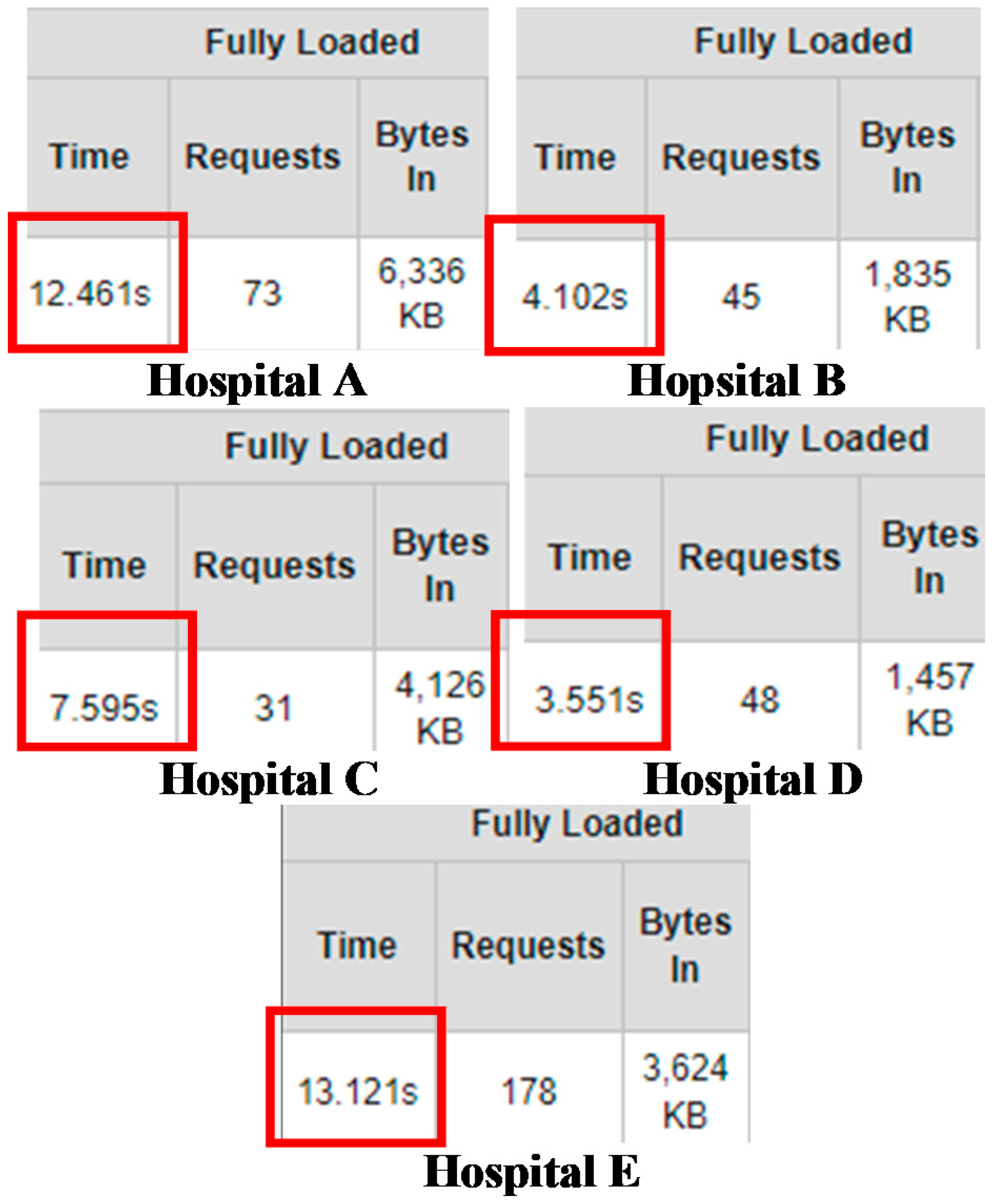
| 5.2451 | 5.3039 | 5.2353 | 5.3529 | 12.4610 | |
| 4.9118 | 5.3824 | 5.0294 | 4.9510 | 4.1020 | |
| 5.1373 | 5.1667 | 5.1078 | 4.9804 | 7.5950 | |
| 4.7451 | 4.7647 | 4.8235 | 4.6373 | 3.5510 | |
| 4.7647 | 4.7941 | 4.6373 | 4.6471 | 13.1210 |
| Normalized Decision Matrix | |||||
|---|---|---|---|---|---|
| 1 | 0.8730 | 1 | 1 | 0.0690 | |
| 0.3333 | 1 | 0.6557 | 0.4384 | 0.9424 | |
| 0.7843 | 0.6508 | 0.7869 | 0.4795 | 0.5774 | |
| 0 | 0 | 0.3115 | 0 | 1 | |
| 0.0392 | 0.0476 | 0 | 0.0137 | 0 |
| , | 0.2966 | 0.3401 | 0.3683 | 0.8381 |
| , | 0.2873 | 0.3401 | 0.2782 | 0.9340 |
| , | 0.2954 | 0.3401 | 0.2964 | 0.9305 |
| , | 0.1835 | 0.3401 | 0.3720 | 0.5158 |
| , | 0.2929 | 0.3683 | 0.2782 | 0.9152 |
| , | 0.2999 | 0.3683 | 0.2964 | 0.9076 |
| , | 0.1268 | 0.3683 | 0.3720 | 0.3426 |
| , | 0.2723 | 0.2782 | 0.2964 | 0.9482 |
| , | 0.1815 | 0.2782 | 0.3720 | 0.5642 |
| , | 0.1684 | 0.2964 | 0.3720 | 0.5071 |
| Attribute | |||||
|---|---|---|---|---|---|
| 0.4248 | 0.3374 | 0.5149 | 0.4801 | 0.3463 | |
| 0.1986 | 0.2288 | 0.1675 | 0.1795 | 0.2257 |
| Subset | Subset | ||
|---|---|---|---|
| {Ø} | 0 | {} | 0.0117 |
| { | 0.0103 | {,} | 0.5378 |
| {} | 0.0118 | {,} | 0.3661 |
| * {,} | 0.8602 | {,,} | 0.8719 |
| {} | 0.0087 | {,} | 0.5846 |
| {,} | 0.9529 | {,,} | 0.9646 |
| {,} | 0.9358 | {,,} | 0.9474 |
| ** {,,} | 0.9648 | {,,,} | 0.9765 |
| {} | 0.0093 | {,} | 0.0210 |
| {,} | 0.9501 | {,,} | 0.9618 |
| {,} | 0.9287 | {,,} | 0.9404 |
| {,,} | 0.9619 | {,,,} | 0.9736 |
| {,} | 0.9662 | {,,} | 0.9779 |
| {,,} | 0.9765 | {,,,} | 0.9882 |
| {,,} | 0.9780 | {,,,} | 0.9897 |
| {,,,} | 0.9883 | {,,,,} | 1 |
| Website | Proposed Technique | WSM | WPM | WASPAS | TOPSIS | PCBU |
|---|---|---|---|---|---|---|
| 1 (0.9876) | 1 (0.7608) | 3 (0.5302) | 3 (0.6456) | 1 (0.9286) | 1 (0.9736) | |
| 3 (0.7489) | 2 (0.6962) | 2 (0.6374) | 1 (0.6668) | 3 (0.4982) | 3 (0.6549) | |
| 2 (0.7732) | 3 (0.6529) | 1 (0.6424) | 2 (0.6476) | 2 (0.6017) | 2 (0.7674) | |
| 4 (0.1901) | 4 (0.2779) | 4 (0) | 4 (0.1389) | 5 (0.1073) | 4 (0.0403) | |
| 5 (0.0352) | 5 (0.0211) | 4 (0) | 5 (0.0106) | 4 (0.3740) | 5 (0.0325) |
| Proposed Technique | WSM | WPM | WASPAS | TOPSIS | PCBU | |
|---|---|---|---|---|---|---|
| Proposed technique | 1 | 0.9000 | 0.6500 | 0.6000 | 0.9000 | 1.0000 |
| WSM | 0.9000 | 1 | 0.5500 | 0.7000 | 0.8000 | 0.9000 |
| WPM | 0.6500 | 0.5500 | 1 | 0.8500 | 0.6500 | 0.6500 |
| WASPAS | 0.6000 | 0.7000 | 0.8500 | 1 | 0.5000 | 0.6000 |
| TOPSIS | 0.9000 | 0.8000 | 0.6500 | 0.5000 | 1 | 0.9000 |
| PCBU | 1.0000 | 0.9000 | 0.6500 | 0.6 | 0.9 | 1 |
| Mean | 0.8417 | 0.8083 | 0.7250 | 0.7083 | 0.7917 | 0.8417 |
| Does the Technique Require Additional Data from the Decision-Makers? | Possible Bias/Error in the Estimated Values | Are the Fuzzy Densities Identified with Extra Inputs? | Does the Technique Explicitly Portray the Causal Relationships Held by the Attributes? | The Calculation Involved in Determining Interdependence Degrees | |
|---|---|---|---|---|---|
| Original technique [16] | Yes (interdependence degree of each pair of attributes) | Yes | No | No | No calculation involved, i.e., direct estimation by decision-makers |
| DEMATEL-based technique [17] | Yes (The direct influence between every two attributes and interdependence degree of each pair of attributes) | Yes | Yes (based on the prominence values determined via DEMATEL) | Yes (via diagraphs) | Influenced by no. of decision attributes |
| ISM-based technique [18] | Yes (Contextual relationship between every two attributes and interdependence degree of each pair of attributes) | Yes | Yes (based on the driving and dependence power determined via ISM) | Yes (via diagraphs) | Influenced by no. of decision attributes |
| PCBU | No | Yes | * Yes (based on the objective weights derived via CRITIC) | No | Influenced by both the decision alternatives and attributes (i.e., the size of decision matrix) |
| Proposed unsupervised technique | * No | * No | * Yes (based on the objective weights derived via Shannon entropy) | ** No | ** Influenced by both the decision alternatives and attributes (i.e., the size of decision matrix) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krishnan, A.R.; Mat Kasim, M.; Hamid, R. An Alternate Unsupervised Technique Based on Distance Correlation and Shannon Entropy to Estimate λ0-Fuzzy Measure. Symmetry 2020, 12, 1708. https://doi.org/10.3390/sym12101708
Krishnan AR, Mat Kasim M, Hamid R. An Alternate Unsupervised Technique Based on Distance Correlation and Shannon Entropy to Estimate λ0-Fuzzy Measure. Symmetry. 2020; 12(10):1708. https://doi.org/10.3390/sym12101708
Chicago/Turabian StyleKrishnan, Anath Rau, Maznah Mat Kasim, and Rizal Hamid. 2020. "An Alternate Unsupervised Technique Based on Distance Correlation and Shannon Entropy to Estimate λ0-Fuzzy Measure" Symmetry 12, no. 10: 1708. https://doi.org/10.3390/sym12101708
APA StyleKrishnan, A. R., Mat Kasim, M., & Hamid, R. (2020). An Alternate Unsupervised Technique Based on Distance Correlation and Shannon Entropy to Estimate λ0-Fuzzy Measure. Symmetry, 12(10), 1708. https://doi.org/10.3390/sym12101708





