Evaluation of the Quality Supervision System for Construction Projects in China Considering the Quality Behavior Risk Transmission

Abstract

In construction projects, improper quality behavior of a participant results in quality behavior risks, which can transmit to the downstream participants and may cause detrimental effects on the quality of the entity finally constructed. Controlling the transmission of quality behavior risks is the key to effectively supervising and ensuring the quality of construction projects. In this study, the effectiveness of the quality supervision system of construction projects in China was investigated by considering the transmission of quality behavior risks. A multi-player evolutionary game model consisting of the players of quality supervision of a government department, upstream participant (UP), and downstream participant (DP) was generated. By using the system dynamics theory, the game model was simulated to determine the stability of the evolutionary system and to evaluate the effectiveness of China’s current quality supervision system under different scenarios. The results showed that there is no evolutionary stable strategy (ESS) in the evolutionary system of the current quality supervision system in China and there are fluctuations in the evolution process. It revealed that high risk exists in the current quality supervision system in China. To resolve the problem of the low efficiency of the current Chinese supervision system, a dynamic penalty and incentive method is developed, which has been proven to be able to effectively control the quality behavior risks in construction projects and hence ensuring the quality of the entity finally constructed.

1. Introduction

Construction projects usually involve many participants, including the employer, survey unit, design unit, supervision unit, construction unit, detection unit, and so on. Complex and changing internal and external environments can generate different quality risk perceptions for the participants [1], because they are commonly influenced by the quality awareness, quality capability, quality risk propensity [2], and the completeness of information [3], which conversely play a significant role in their risk decisions. This will further result in high uncertainty to the quality behavior of the participants. The quality behavior refers to an actual response, or action, to the production quality and management quality of the participants, and is the external reflection of the quality awareness [4]. According to China’s work guideline on the quality supervision of construction projects, the quality behavior represents the activities carried out by the participants, fulfilling the quality responsibility and obligations stipulated by the relevant laws and regulations of the state during the construction. The quality behavior can be divided into two aspects: positive quality behavior and negative quality behavior [4]. The positive quality behavior indicates that the participants adopt the legal and required quality behavior. The negative quality behavior indicates that the quality behavior of the participants is often driven by achieving maximum interest because of the commonly asymmetric information, namely improper quality behavior, which can give rise to quality defects, quality accidents, or even damage to the quality of the entity finally constructed. As a kind of the negative quality behavior, the quality behavior risks can be defined in this study based on the principle of maximum interest; the participants adopt the improper quality behavior from the beginning of project decision-making to a project put into use, which causes deviation to the expected quality targets, finally leading to the possibility of misfunction or even collapse of the project.

During construction, overlapped work interfaces often exist between the participants [5,6], which requires close collaboration between them. Since the work sequences fulfilled by the participants are characterized by strong dependence, the participants become dependent [7]. Owing to these dependencies, quality behavior risks aroused by a participant can transmit to the downstream participants if the participant fails to eliminate the risks. Furthermore, the quality behavior risks aroused by a participant will have a significant impact on the quality performance of the downstream participants [8]. This process is called the transmission of quality behavior risks, and it can evolve during construction, which may cause the entire project to collapse. For example, the design deviations caused by the design unit can critically affect the quality performance of the construction unit in construction projects. Therefore, exploring control solutions to effectively control the transmission of quality behavior risks for reducing quality behavior risks in construction projects is urgent.

The occurrence of the transmission of quality behavior risks depends on whether each participant adopts the positive quality behavior, which has a positive effect on the quality of a project. If a participant adopts illegal and unqualified quality behaviors, it may bring excess profits to itself, while the accumulation and transmission of quality behavior risks caused thereby will inevitably lead to quality problems, quality defects, and even quality accidents during the project. The uncertainty of quality behaviors of the participants highlights the importance of the supervision of quality behavior. At present, the quality supervision of construction projects is dominated by the quality supervision department of government in China. According to China’s work guideline on the quality supervision of construction projects, it is the responsibility of the government to supervise the quality behavior of all participants (e.g., the employer, design unit, detection unit) from the beginning of a project decision-making to a project put into use. However, with the increasing number of construction projects, the government does not have enough human resources to supervise the participants effectively under the current quality supervision system in China. Due to the growing occurrence of quality accidents, some scholars in China have begun to study the existing problems of China’s quality supervision system. One argument has pointed out that the government should improve the intensity of the government supervision to reduce illegal quality behavior during construction [9]. However, others have expressed their disagreement that the government supervision neither has enough supervisors or funding nor follows the market mechanism, and thus, is ineffective as an external constraint means [8,10,11]. The main reason for the ineffective quality supervision system in China is that the different interests of the government and the participants often give rise to conflicts. Although the government in China has enacted a series of laws, regulations, and some incentive policies on improving quality in construction projects, the high incidence of quality defects and quality accidents show that these laws and regulations seem to malfunction, which makes it difficult for the government to develop effective supervision strategies.

The evolutionary game is a dynamic game method based on bounded rationality to study the process of the strategy selection of players, which can simulate a conflict of interest among different players [12,13]. In most existing studies, the evolutionary game has been used to analyze the conflict of interest between the government and the participants. Gao studied how the government supervises the opportunistic behavior of investors in public–private partnership projects during the operation stage and concluded that the government supervision mode depends on its probability of identifying investors’ opportunistic behavior during performance evaluations [9]. Liu analyzed the game relationship between the regulator and the coal-mine participants to explore the effectiveness of coal-mine regulation in China [14]. Fan discussed the optimal supervision strategy of the government to supervise the low-carbon subsidy of enterprises and showed that the overall optimal supervision probability was 0.24 [15]. Guo studied the interactions among the project owner, supervising engineer, and contractor during the construction quality supervision by using the evolutionary game theory [16]. Concerning the government supervision, some scholars focus on stressing the regulatory measures of the government, such as penalty and reward. Generally, punishment is recognized as an effective way to implement social norms [17,18]. However, with the absence of an incentive mechanism [19], it is difficult to reach a cooperation due to the conflict of interests in the quality supervision system. As a result, the illegal and unqualified quality behaviors of the participants cannot be controlled. Thus, a collection of penalty and reward has been put forward to curb the illegal quality behavior. Different combinations of penalty and reward mechanisms have been successfully applied to many areas, such as coal-mine safety regulation [14,20] and railway transportation safety regulation [10].

In light of the above reviews, this paper attempts to study three aspects: (i) previous studies have focused mainly on the different interests and demands among some specific participants, e.g., the employer, supervision unit, and construction unit, while ignoring the dynamic transmission between the upstream and downstream participants. Thus, an upstream participant (UP) and a downstream participant (DP) were abstracted from the participants to investigate the transmission of the quality behavior risks; (ii) considering the inconsistency of interests and the bounded rationality between the participants and the government, an evolutionary game model was established to analyze the dynamic evolution process of the selection of quality behaviors among the government, UP, and DP. Then the game was simulated by using the system dynamics to analyze the stability of the evolutionary system and the effectiveness on controlling the transmission of quality behavior risks under different scenarios; (iii) a dynamic penalty and incentive (DPI) mechanism was developed to restrain the fluctuation of the evolutionary process in the game, and the stability and effectiveness of the DPI mechanism were verified. This research provides theoretical support to the government for controlling the quality behavior risks, implementing effective supervision, and innovating the supervision mode in construction projects.

2. Evolutionary Game Analysis of the Transmission of Quality Behavior Risks

2.1. Game Design and Assumption

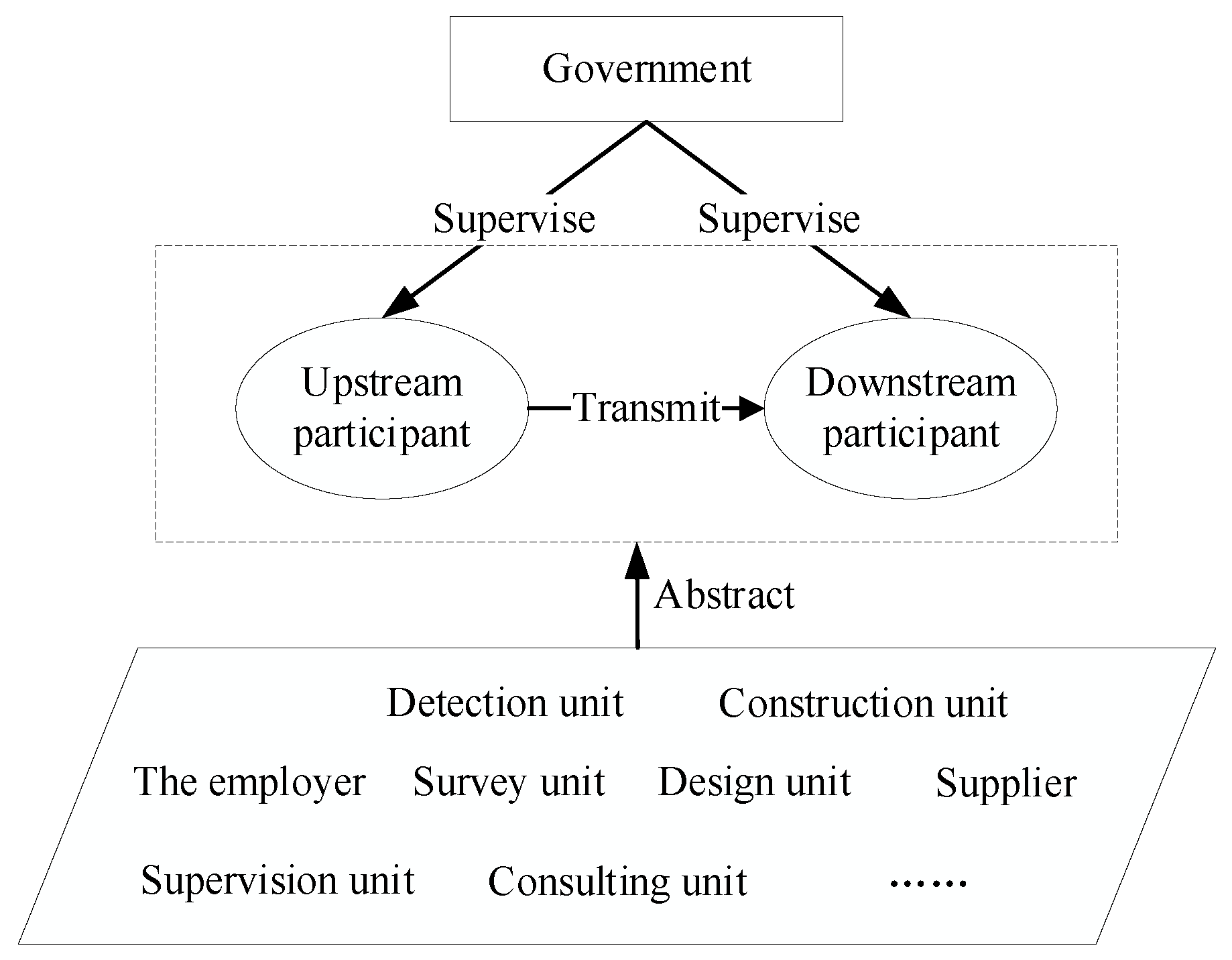
Based on the work sequence of participation in construction projects, the UP and DP are abstracted from the participants to study the transmission of the quality behavior risks, illustrated in Figure 1. Each subject in Figure 1 is a bounded rational economic person, characterized by obtaining maximum profit. The evolutionary game theory has the greatest advantage for analyzing the bounded rationality of players and the dynamic process of games.

Assume that the participants $i \left(i=1,2\right)$, $i=1$ represents UP and $i=2$ represents DP, choosing $y_i \left(0\le y_i\le 1, i=1,2\right)$ as their strategy in the game process, where $y_i$ represents the probability of following the regulations. $y_i=1$ represents the participants following the regulations, and adopting the legal and required quality behavior, and $y_i=0$ represents the participants adopting illegal and unqualified quality behavior. During the construction, $R_i$($R_i>0, i=1,2)$ represents the quality cost when the participants adopt the legal and required quality behavior, namely, the effort on the construction. If the participants choose the illegal and unqualified quality behavior, the extra profits $T_i(T_i>0,i=1,2)$ can be gained, but at the same time, the quality behavior risks resulting from the illegal and unqualified quality behavior will be transmitted to the DPs. The DPs can claim the damages from the quality behavior risks of UPs, and $S\left(S>0\right)$ is the compensation to the DP.

Assume that the government chooses $x \left(0\le x\le 1\right)$ as its strategy in the game process, where $x$ represents the probability of supervising. $x=1$ means that the government invests more labor, money, or material resources, such as purchasing the testing service from the third-party, unannounced inspection, strengthening the training and incentive for the supervisors of government, and so on. $x=0$ represents the government that makes the rules of supervision, and the authority of supervision is delegated to the participants. The government needs to pay a cost $C_p(C_p>0)$ when adopting the positive supervision, and the cost of the negative supervision is so low that it can be ignored in this paper. Assume that the inspection ability of the government is strong enough, once the government adopts positive supervision, the quality behavior of the participants, including the illegal and unqualified behavior and the legal and required behavior, will be discovered. The government imposes fines $F_i(F_i>0,i=1,2)$ on the participants when they adopt the illegal and unqualified quality behavior, e.g., downgrading credit rating. The participants are also rewarded $E_i(E_i>0,i=1,2)$ by the government when they adopt the legal and required quality behavior, e.g., upgrading credit rating.

The participants need to bear the cost of quality behavior risks when adopting the strategy of illegal and unqualified quality behavior. The cost of quality behavior risks refers to the cost of repairing the quality problem and quality defect, which result from quality behavior risks, and the loss incurred from quality accidents [21,22]. If a quality accident occurs, the government will bear joint liability in China. In general, the cost of quality behavior risks borne by both the government and the responsible participant is linearly correlated. Assume that $C_i(C_i>0,i=1,2)$ represents the cost of quality behavior risks borne by the participants, $\alpha C_i$ is the cost of quality behavior risks borne by the government, where $\alpha \left(\alpha \ge 0\right)$ is the transmission coefficient of quality behavior risks. Furthermore, assessing the influence of quality behavior risks commonly depends on the risk effect of the behavior itself, and the reaction time and reaction strength to find and address the problem. This can be reflected in the cost of quality behavior risks, which is the discount coefficient of the cost of quality behavior risks. When the government adopts the strategy of positive supervision, the cost of quality behavior risks borne by the government is $\alpha \beta C_i$, where $\beta (0<\beta \le 1)$ is the discount coefficient of the cost of quality behavior risks.

The variables of the multi-player game are shown in

Table 1. Meanings of the variables in the multi-player game.

Variables	Meanings	Notes
$x$	Ratio of positive supervision	$0\le x\le 1$
$y_i$	Ratio of adopting the legal and required quality behavior	$0\le y_i\le 1, i=1,2$
$C_p$	Cost of positive supervision	$C_p>0$
$R_i$	Quality cost of adopting the legal and required quality behavior	$R_i>0, i=1,2$
$T_i$	Extra profit of adopting the illegal and unqualified quality behavior	$T_i>0,i=1,2$
$F_i$	Penalty	$F_i>0,i=1,2$
$E_i$	Reward	$E_i>0,i=1,2$
$C_i$	Cost of quality behavior risks	$C_i>0,i=1,2$
$\alpha$	Transmission coefficient of cost of quality behavior risks	$\alpha \ge 0$
$s$	Compensation	$s>0$
$\beta$	Discount coefficient of cost of quality behavior risks	$0<\beta \le 1$
$\delta$	Penalty coefficient	$\delta >0$
$\epsilon$	Reward coefficient	$\epsilon >0$

. Based on the above assumptions and analysis, the payoff matrix of the multi-player game can be obtained in

Table 2. Payoff matrix of the multi-player game.

		The Government
		$\mathbf{Positive} \mathbf{Supervision} \left(\mathit{x}\right)$		$\mathbf{Negative} \mathbf{Supervision} \left(1-\mathit{x}\right)$
		DP		DP
Strategy		Adopting the legal and required quality behavior ($y_2)$	Adopting the illegal and unqualified quality behavior ($1-y_2)$	Adopting the legal and required quality behavior ($y_2)$	Adopting the illegal and unqualified quality behavior ($1-y_2)$
UP	Adopting the legal and required quality behavior ($y_1)$	$-C_p-E_1-E_2,$ $-R_1+E_1,$ $-R_2+E_2$	$-C_p+F_2-\alpha \beta C_2-E_1,$ $-R_1+E_1,$ $-R_2+T_2-F_2-\beta C_2-s$	0, $-R_1,$ $-R_2$	$-\alpha C_2,$ $-R_1,$ $-R_2+T_2-C_2-s$
	Adopting the illegal and unqualified quality behavior ($1-y_1)$	$-C_p+F_1-\alpha \beta C_1-E_2,$ $-R_1+T_1-F_1-\beta C_1-s,$ $-R_2+E_2+s$	$-C_p+F_1+F_2-\alpha \beta C_1-\alpha \beta C_2,$ $-R_1+T_1-F_1-\beta C_1-s,$ $-R_2+T_2-F_2-\beta C_2-s$	$-\alpha C_1,$ $-R_1+T_1-C_1-s,$ $-R_2+s$	$-\alpha C_1-\alpha C_2,$ $-R_1+T_1-C_1-s,$ $-R_2+T_2-C_2-s$

.

2.2. Game Solution

According to the evolutionary game theory, replication dynamics is used to represent the learning and evolution mechanism of individuals in the process of the transmission of quality behavior risks. Thus, the expected benefits of the government from positive supervision ($U_x$) and negative supervision ($U_{1-x})$ can be obtained as follows, respectively.

$$\begin{array}{c}{U}_x=y_1{y}_2\left(-C_p-E_1-E_2\right)+\left(1-y_1\right)y_2\left(-C_p+F_1-\alpha \beta C_1-E_2\right)+y_1\left(1-y_2\right)(-C_p+\\ F_2-\alpha \beta C_2-E_1)+(1-y_1)\left(1-y_2\right)\left(-C_p+F_1+F_2-\alpha \beta C_1-\alpha \beta C_2\right)\\ =\left(\alpha \beta C_1-E_1-F_1\right)y_1+\left(\alpha \beta C_2-E_2-F_2\right)y_2-\alpha \beta C_1-\alpha \beta C_2-C_p+F_1+F_2\end{array}$$

(1)

$$\begin{array}{c}{U}_{1-x}=y_1{y}_2\times 0+\left(1-y_1\right)y_2\left(-\alpha C_1\right)+y_1\left(1-y_2\right)\left(-\alpha C_2\right)+(1-y_1)\left(1-y_2\right)\left(-\alpha C_1-\alpha C_2\right)\\ =\alpha C_1{y}_1+\alpha C_2{y}_2-\alpha C_1-\alpha C_2\end{array}$$

(2)

The average expected benefit of the government is shown by Equation (3) below:

$${\overline{U}}_{x, 1-x}=x{U}_x+\left(1-x\right)U_{1-x}$$

(3)

Similarly, the expressions of the expected benefits for the UP are shown by Equations (4) and (5).

$$\begin{array}{c}{U}_{y_1}=x{y}_2\left(-R_1+E_1\right)+x\left(1-y_2\right)\left(-R_1+E_1\right)+\left(1-x\right)y_2\left(-R_1\right)+\left(1-x\right)(1-y_2)\left(-R_1\right)\\ =E_{1}x-R_1\end{array}$$

(4)

$$\begin{array}{c}{U}_{1-y_1}=x{y}_2\left(-R_1+T_1-F_1-\beta C_1-s\right)+x\left(1-y_2\right)\left(-R_1+T_1-F_1-\beta C_1-s\right)+\left(1-x\right)y_2\\ \left(-R_1+T_1-C_1-s\right)+\left(1-x\right)(1-y_2)\left(-R_1+T_1-C_1-s\right)\\ =\left(C_1-F_1-\beta C_1\right)x-R_1+T_1-C_1-s\end{array}$$

(5)

The expressions of the expected benefits for the DP are shown by Equations (6) and (7).

$$\begin{array}{c}{U}_{y_2}=x{y}_1\left(-R_2+E_2\right)+x\left(1-y_1\right)\left(-R_2+E_2+s\right)+\left(1-x\right)y_1\left(-R_2\right)+\left(1-x\right)(1-y_1)\\ \left(-R_2+s\right)=E_{2}x-s{y}_1-R_2+s\end{array}$$

(6)

$$\begin{array}{c}{U}_{1-y_2}=x{y}_1\left(-R_2+T_2-F_2-\beta C_2-s\right)+x\left(1-y_1\right)\left(-R_2+T_2-F_2-\beta C_2-s\right)+\left(1-x\right)y_1\\ \left(-R_2+T_2-C_2-s\right)+\left(1-x\right)(1-y_1)\left(-R_2+T_2-C_2-s\right)\\ =\left(C_2-F_2-\beta C_2\right)x-R_2+T_2-C_2-s\end{array}$$

(7)

According to the replication dynamics, the change rate of $x$ is as follows:

$$\begin{array}{cc}\hfill G\left(x,y_1,y_2\right)=\frac{dx}{dt}& =x\left[U_x-{\overline{U}}_{x, 1-x})\right]=x\left(1-x\right)\left[U_x-U_{1-x}\right]\hfill \\ & =x\left(1-x\right)[\left(\alpha \beta C_1-\alpha C_1-E_1-F_1\right)y_1+\left(\alpha \beta C_2-\alpha C_2-F_2-E_2\right)y_2\hfill \\ & +F_1+F_2-C_p+\left(\alpha -\alpha \beta \right)\left(C_1+C_2\right)]\hfill \end{array}$$

(8)

Similarly, the change rates of $y_1$ and $y_2$ can be obtained as follows, respectively.

$$\begin{gathered} H\left(x,y_1,y_2\right)=\frac{d{y}_1}{dt}=y_1\left[U_{y_1}-{\overline{U}}_{y_1, 1-y_1}\right]=y_1\left(1-y_1\right)\left[U_{y_1}-U_{1-y_1}\right] \\ =y_1\left(1-y_1\right)\left[\left(\beta C_1+F_1+E_1-C_1\right)x-T_1+C_1+s\right] \end{gathered}$$

(9)

$$\begin{gathered} I\left(x,y_1,y_2\right)=\frac{d{y}_2}{dt}=y_2\left[U_{y_2}-{\overline{U}}_{y_2, 1-y_2}\right]=y_2\left(1-y_2\right)\left[U_{y_2}-U_{1-y_2}\right] \\ =y_2\left(1-y_2\right)\left[\left(E_2+F_2-C_2+\beta C_2\right)x-s{y}_1-T_2+C_2+2s\right] \end{gathered}$$

(10)

Equations (8)–(10) reflect the speed of the strategy adjustment of the government, UP, and DP. When the equations are equal to zero, it means that the strategy will not be changed and the game system reaches a relatively stable equilibrium state. Many researchers have followed the method proposed by Friedman to analyze the stability of the equilibrium points by calculating the determinant and trace of the Jacobian matrix of the game [23]. Since this general method requires specific analysis of different parameters in different cases, calculations are tedious and complicated to the multi-player game. Therefore, a computer simulation method is used in this paper to analyze the stability of the complex dynamic multi-player game.

3. The Stability Analysis of the Multi-Player Game System

In the multi-player game, each player learns the behavior of other players by comparing and observing the benefits with others and then adjusts its strategy selection. This process is the feedback behavior in the game. System dynamics (SD) simulation is an effective method to study the feedback behaviors by analyzing the causal relationship and interaction among variables in complex systems [14,16,24]. Using the SD simulation to study the transmission of the quality behavior risks in the construction process can not only show the dynamic process of quality behavior risks in the construction process, but also intuitively illustrate the effectiveness of the strategic selection of the participants on the quality of entity finally constructed in construction projects. Therefore, this section will build an SD model to analyze the stability of the equilibrium points in the multi-player game, which can provide an effective experimental reference for controlling the quality behavior risks and optimizing supervision strategies.

3.1. Building the SD Model

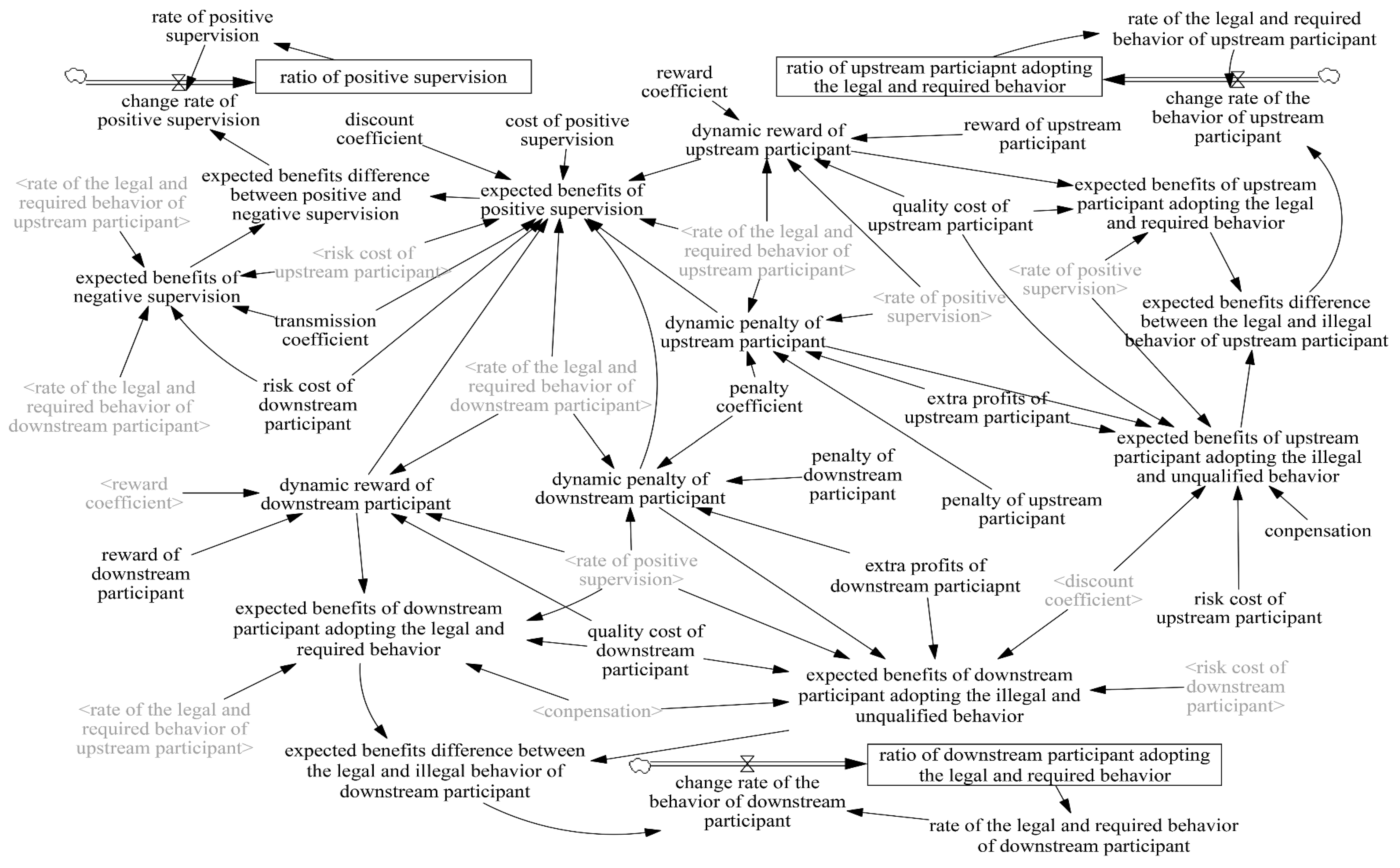
The multi-player evolutionary game SD model is built according to the above game assumptions and analysis by using Vensim PLE 7.2. The SD model of the multi-player game of the transmission of quality behavior risks is shown in Figure 2, including three state variables: the ratio of positive supervision, the ratio of the UP adopting the legal and required quality behavior, and the ratio of the DP adopting the legal and required quality behavior; three rate variables: the change rate of choosing positive supervision, the change rate of the UP adopting the legal and required quality behavior, and the change rate of the DP adopting the legal and required quality behavior; nine auxiliary variables; and fourteen external variables. The auxiliary variables are $U_x$, $U_{1-x}$, $U_x-U_{1-x}$, $U_{y_1}$, $U_{1-y_1}, U_{y_1}-U_{1-y_1},$ $U_{y_2}$, $U_{1-y_2}$, $U_{y_2}-U_{1-y_2}$ and the external variables are shown in Table 1.

The values of the external variables influence the auxiliary variables, and the values of the auxiliary variables influence the rate variables. Then, the state variables will change, which in turn affects the auxiliary variables. Thus, there is a feedback system. Finally, the system will be analyzed using numerical simulation.

3.2. Numerical Simulation

From the above analysis, we obtained some external variables that are supposed to affect the simulation result. To make the results reasonable, an orthogonal experiment was designed to perform the analysis for various values of parameters to reflect more possible situations [25]. Taking three selected variables ($T_1$, $F_1$, and $E_1$) as factors, we made two levels of them for the experiment and then simulated the four experimental plans from the orthogonal array. The factor-level table and orthogonal array are shown in

Table 3. Factor-level table.

Factor	${\mathit{T}}_1$	${\mathit{F}}_1$	${\mathit{E}}_1$
Level	Extra profit of the UP	Penalty of the UP	Reward of the UP
Level 1	8	9	2
Level 2	12	11	3

and

Table 4. Orthogonal array.

Factor	${\mathit{T}}_1$	${\mathit{F}}_1$	${\mathit{E}}_1$
Experiment	Extra profit of the UP	Penalty of the UP	Reward of the UP
1	8	9	2
2	12	9	3
3	12	11	3
4	8	11	2

, respectively.

To analyze the stability of the game, the values of the first experiment were taken as an example. The model setting of the Vensim PLE 7.2 is Initial Time = 0, Final Time = 100, Time Step = 0.03125, Units for Time = Month, and Integration Type: Euler. Through interviews with related people, such as the government supervisor and the project manager, after pretreatment, we determined the initial values of the other external variables, which are shown in

Table 5. Initial values of external variables in the SD model.

Variables	Meanings	Initials Value
$C_p$	Cost of positive supervision	6
$R_1$	Quality cost of the UP adopting the legal and required quality behavior	15
$R_2$	Quality cost of the DP adopting the legal and required quality behavior	13
$T_1$	Extra profit of the UP adopting the illegal and unqualified quality behavior	8
$T_2$	Extra profit of the DP adopting the illegal and unqualified quality behavior	6
$F_1$	Penalty of the UP	9
$F_2$	Penalty of the DP	7
$E_1$	Reward of the UP	2
$E_2$	Reward of the DP	2
$C_1$	Cost of quality behavior risks for the UP	3
$C_2$	Cost of quality behavior risks for the DP	3
$\alpha$	Transmission coefficient of cost of quality behavior risks	0.5
$s$	Compensation	1
$\beta$	Discount coefficient of cost of quality behavior risks	0.6

.

3.2.1. Stability Analysis

In the asymmetric game, the evolutionary stability strategy must be pure strategy [26]. Since the multi-player game in this paper is an asymmetric game, we analyzed the stability of the pure strategies: $Z_1\left(0,0,0\right),Z_2\left(0,1,0\right),Z_3\left(0,0,1\right),Z_4\left(1,0,0\right),Z_5\left(1,1,0\right),Z_6\left(0,1,1\right),Z_7\left(1,0,1\right),$ and $Z_8\left(1,1,1\right)$, which are from $G\left(x,y_1,y_2\right)=0, H\left(x,y_1,y_2\right)=0, \mathrm{and} I\left(x,y_1,y_2\right)=0$ in Equations (10)–(12). 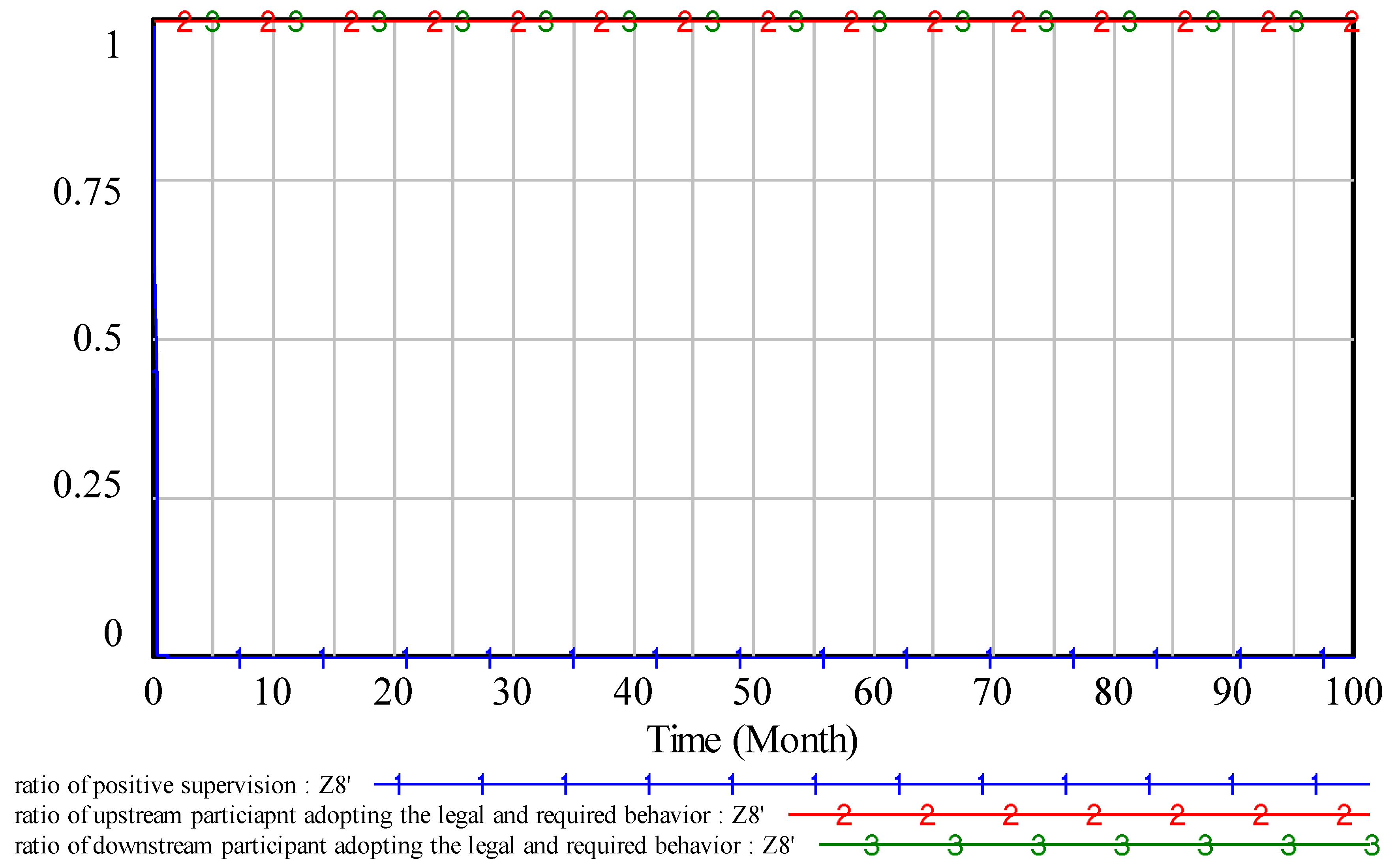The simulation results of $Z_1~Z_8$ show that the multi-player game reaches a relative equilibrium state and no player has any change in their strategy. Taking one of the initial pure strategy equilibrium points, $Z_8=\left(1,1,1\right)$, as an example, the evolution process under the initial strategy $Z_8$ is shown in Figure 3. Curve 1 represents the ratio of positive supervision, namely, $x$, curve 2 represents the ratio of the UP adopting the legal and required quality behavior, namely, $y_1$, and curve 3 represents the ratio of the DP adopting the legal and required quality behavior, namely, $y_2$.

In practice, the value of $x$ is close to 1, the more resources that the government invests in supervision, and the higher the supervision cost. The values of $y_1$ and $y_2$ are close to 1, the upstream and DPs are more willing to adopt the legal and required quality behavior. From the perspective of cost-benefit of the quality supervision in construction projects, the lower the supervision cost is and the higher the legal and required quality behavior ratio are, the higher the quality supervision efficiency.

The simulation results of $Z_8$ show that none of the three curves fluctuate. This phenomenon can be explained as follows. During the process of supervision, if the three players choose the above strategies at the beginning, none of them will change. However, this state only represents the decision process at this point. This balance may be broken when a few individuals in a group are disturbed by external factors and slight changes in other players’ strategies. To verify the stability of $Z_8$, assume that the initial strategy $x$ is slightly mutated from 1 to 0.99; the evolution process under $Z_8{}^{\prime }$= (0.99,1,1) is shown in Figure 4.

As shown in Figure 4, the equilibrium state of $Z_8$ is unsteady. Specifically, the quality behavior of the UP and the DP has not been affected by changing the ratio of positive supervision. The equilibrium state is evolved from $Z_8$ to $Z_6$ after changing $x$. This phenomenon can be explained as follows. Although only a few individuals in the group of the government mutate their initial strategies, this mutation can get better benefits, namely, they decrease their supervision cost and the participants follow the legal and required quality behavior. This further leads to the fact that the other individuals in the group of the government constantly adjust their strategies for better benefits. Once a slight change happens in an initial strategy, the equilibrium state of the game will be broken. This conclusion is also applied to other pure strategies. There is no evolutionary stable strategy in the multi-player game.

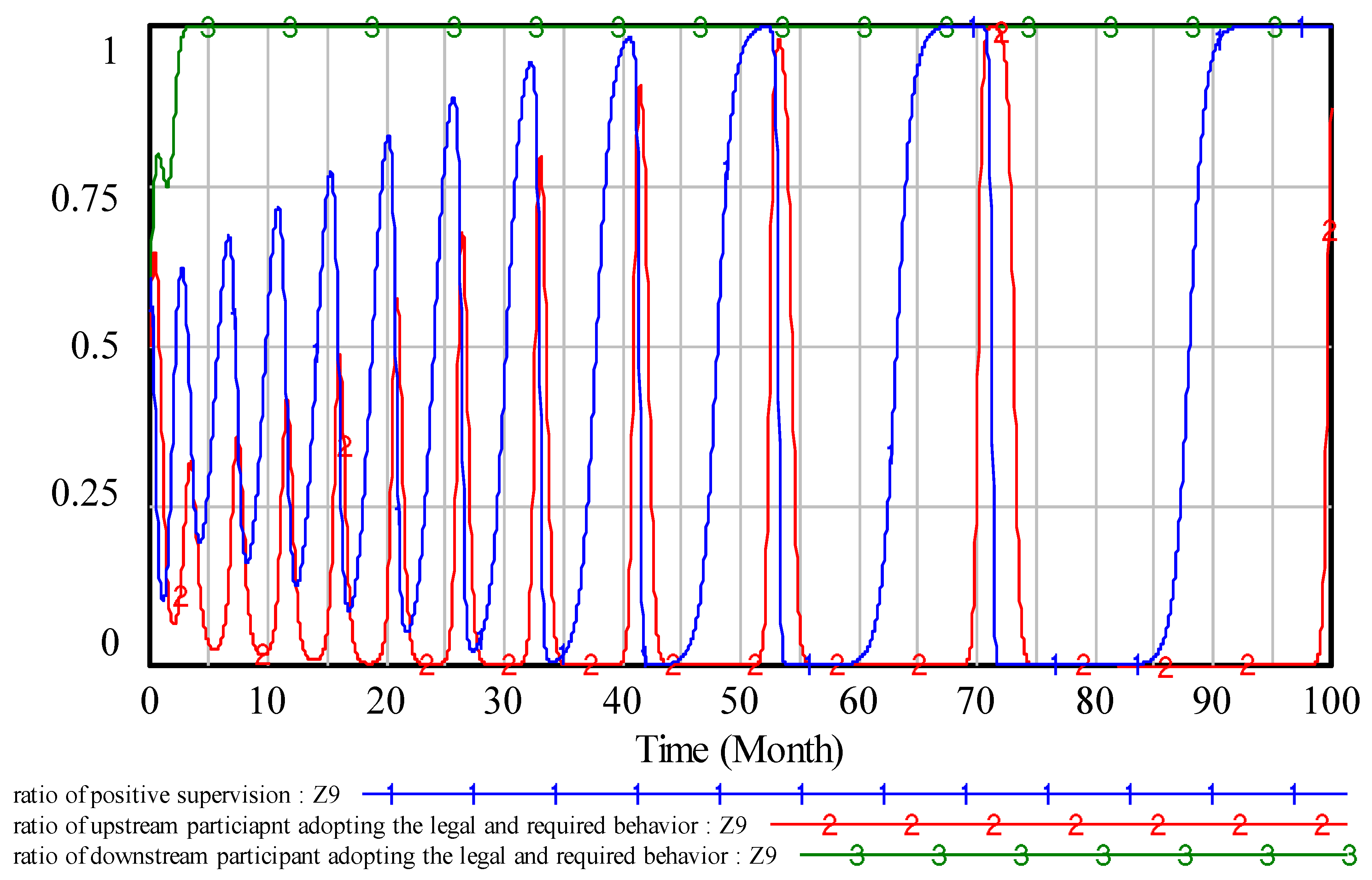
Furthermore, more general initial strategies should be simulated close to the actual condition. Since the government pays more attention to the social and ecological impacts of a project and its reputation loss in addition to the economic benefits, it will tend to be more perceptive than the participants for the consequences of quality behavior risks in construction projects. As a result, we input $Z_9\left(0.6,0.5,0.5\right)$ in the model. 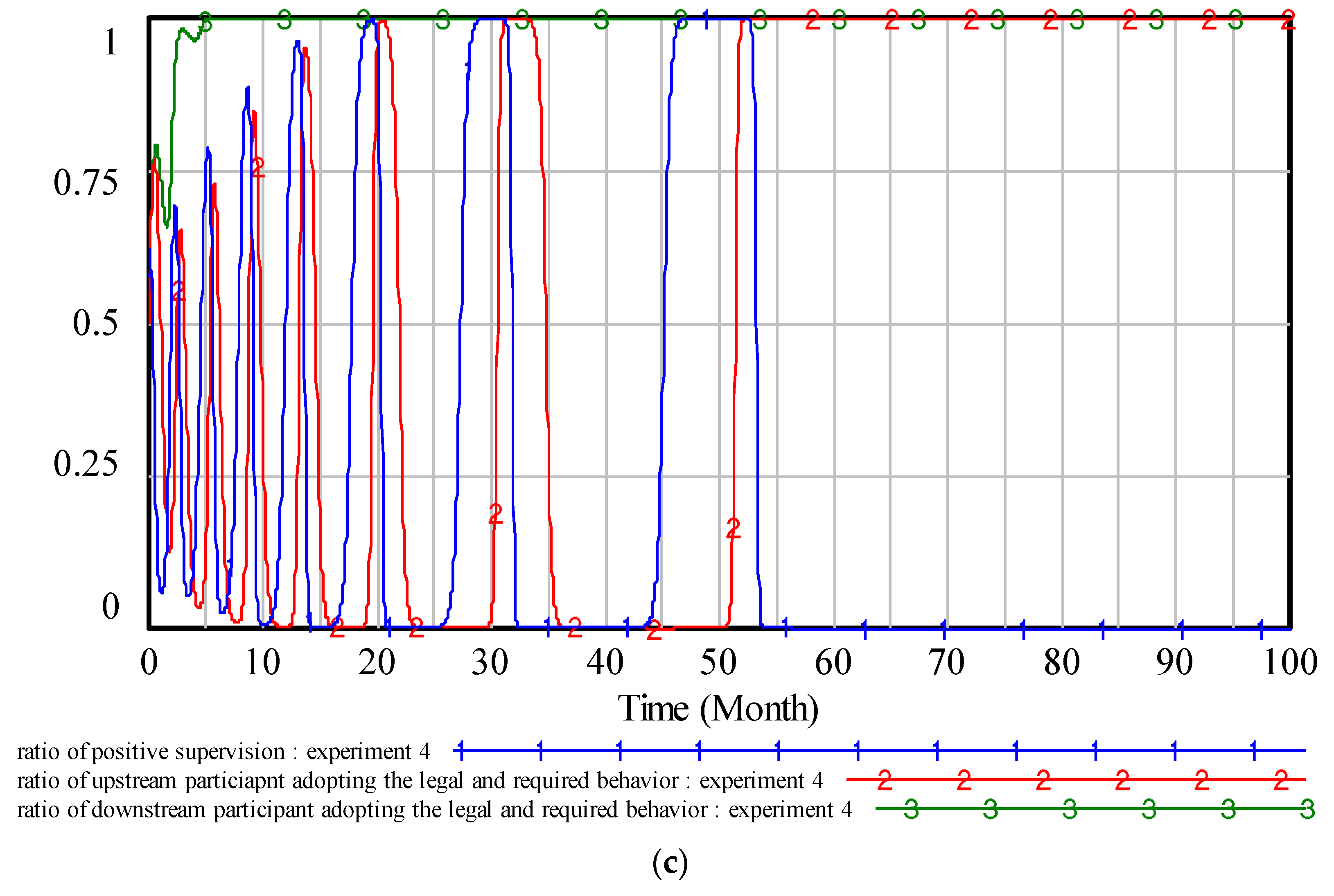The result of $Z_9$ cannot reach an ESS, which is shown in Figure 5. Curves 1 and 2 fluctuate sharply. By observing the fluctuation laws of curves 1 and 2, the amplitude of the fluctuation becomes bigger and bigger. The bigger the amplitude is, the higher the quality behavior risk for the construction projects is. There is an alternating push–pull relationship between the government ratio and the UP ratio. This phenomenon can be explained as follows. When the ratio of the UP is low, the possibility of the quality behavior risks aroused by the UP inspected by the government is high, and the government will increase their supervision ratio to force the participant to adopt the legal and required quality behavior. When the ratio of the UP increases to a certain extent, the government will relax their supervision to save money, which in turn makes the UPs decrease their investment in construction to get more profits. This is the main reason for the high occurrence probability of quality accidents in construction projects in China. This process forms the fluctuations between the government and the UP. It shows that the current supervision of the government can have an impact on supervising the quality behavior of the UP. However, this approach does not prevent or eliminate the quality behavior risks in construction projects. When curve 2 is closed or equal to 0, the risks can be transmitted, evolved, and finally a quality accident may happen if the participant cannot eliminate them. The shortage of human resources and limited funding in the government supervision department make it more difficult for the government to deal with the actual problems.

Another phenomenon can be seen in Figure 5, where the DP seems immune to the interaction of the other players and adopts the legal and required quality behavior almost all the time. It can be explained as follows. The interplay between the UP and the government produces a deterrent effect on the DP. By comparing the price and profit of adopting the illegal and unqualified quality behavior of the UP, the strategy of the DP will be adjusted and the legal and required quality behavior will be chosen.

3.2.2. Analysis of Different Rewards and Penalties

It is generally acknowledged by scholars that the government increasing the number of penalties or rewards is an effective measure to control illegal behavior during construction [9,10,20]. In this section, the penalty and the reward will be changed respectively to investigate the influence of the changes on the multi-player game. When changing the number of penalties or rewards, other parameters remain fixed.

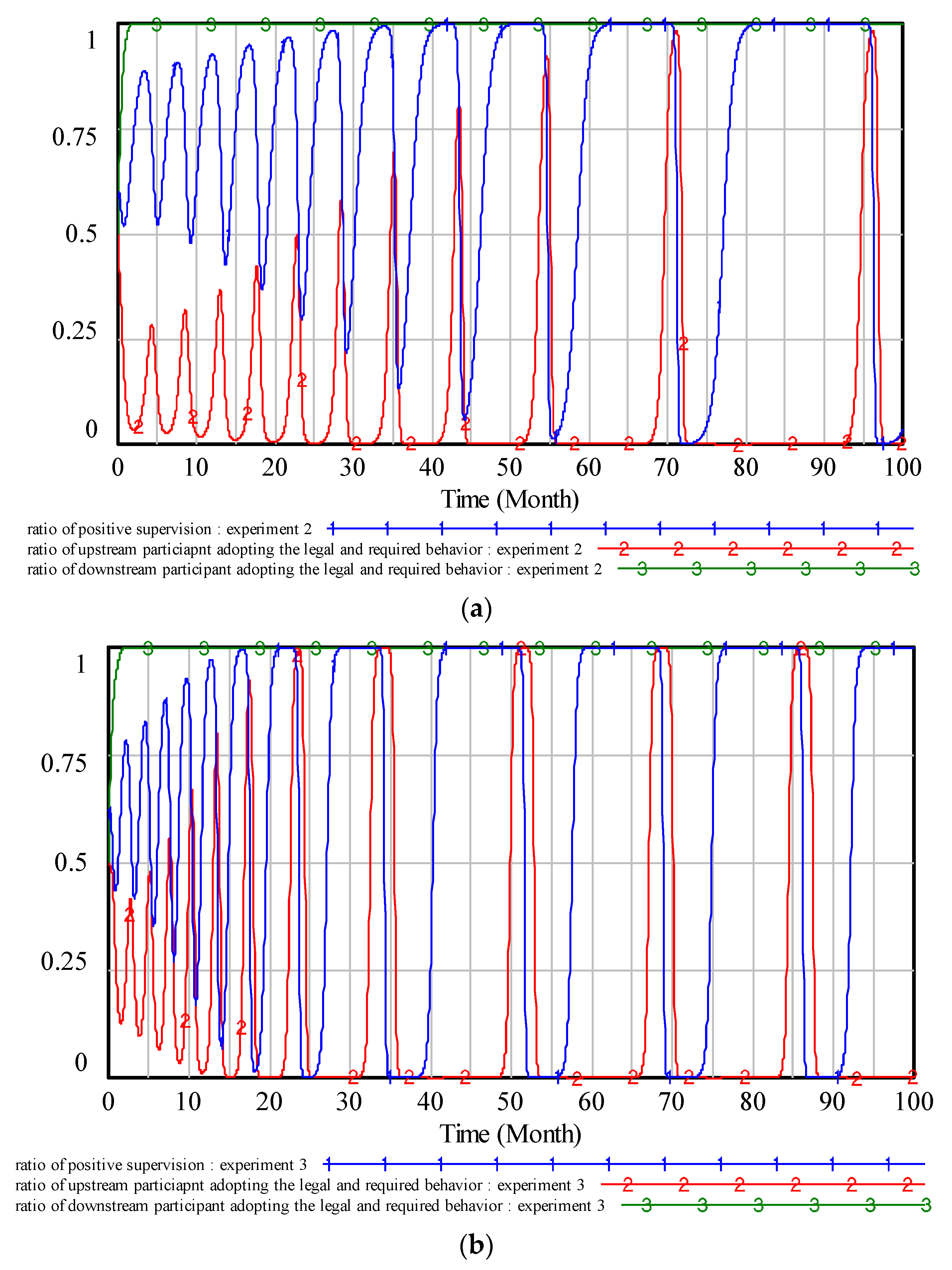
Scenario 1. Changing the Penalties of the Participants

We changed the penalties $(F_1,F_2)$ from (9,7) to (7,5) or (11,9). For an initial strategy of $Z_9\left(0.6,0.5,0.5\right)$, the evolution process is shown in Figure 6. Figure 6a,b show the evolution process when the penalties ($F_1,F_2)$ are (7,5) and (11,9), respectively.

Comparing Figure 5 with Figure 6a, after the government decreased the penalties of the UP and the DP to (7,5), the UP adjusted its strategy rapidly to choose the illegal and unqualified quality behavior. Simultaneously, the DP adjusted its strategy from the stable legal behavior to fluctuation. The ratios of the behaviors show that the occurrence probability of a quality accident is higher. Therefore, decreasing the penalty proves that the quality behavior risks are more serious.

Comparing Figure 5 with Figure 6b, after the government increased the penalties of the UP and the DP to (11,9), the multi-player game model gradually reached a pure strategy at (0,1,1). This point is a perfect state for quality supervision in construction projects. In current China, the government is devoted to exploring a mode of quality supervision that can reduce regulation and maximize participants’ behavior. However, in the Section 4, we proved that the pure strategy is unstable.

Scenario 2. Changing the Rewards of the Participants

We changed the rewards $\left(E_1,E_2\right)$ from (2,2) to (1,1) or (3,3). For an initial strategy of $Z_9\left(0.6,0.5,0.5\right)$, the evolution process is shown in Figure 7. Figure 7a,b show the evolution process when the rewards $\left(E_1,E_2\right)$ are (1,1) and (3,3), respectively.

Comparing Figure 5 with Figure 7a, after the government decreased the rewards of the UP and the DP to (1,1), the fluctuation frequency of the ratio of the UP increases. The quality behavior of the UP became more unpredictable. It is detrimental for the government to supervise. Comparing Figure 5 with Figure 7b, after the government increased the rewards of the UP and the DP to (3,3), the amplitude of the fluctuation of the ratio of UP gradually increases, which can raise the uncertainty of the game system. The results show that changing the rewards of the participants cannot reduce the fluctuations and an ESS in the system is never reached.

In conclusion, there is no ESS in the current multi-player game system from the set of values of the orthogonal experiment. Changing the penalties and the rewards of the participants respectively under the strategy of $Z_9$ shows that the fluctuation cannot be dampened. The simulation results of the model (Figure 5, Figure 6b and Figure 7) prove that there is an alternating push–pull relationship between the government and the UP. The government urges the UP to improve the legal and required quality behavior. With the relaxed supervision, the ratio of the legal and required quality behavior decreases, which in turn prompts the government to strengthen its supervision. However, the simulation results show that changing the penalty or the reward cannot retrain the fluctuation, which means the supervision of the government is not efficient to the UP. Based on the deterrent effect, controlling the quality behavior of the UP is more important than the DP. Moreover, the ratio of the legal and required quality behavior of the UP is too low, which may increase the probability of quality problems, quality defects, and even quality accidents.

In the other experiment, for an initial strategy of $Z_9\left(0.6,0.5,0.5\right)$, the simulations of the other three combinations of factors present similar results with the above experiment, which are shown in Figure 8a–c. Although the levels of extra profit, penalty, and reward of the UP have been changed from low to high, the game system is still unstable. It can be deduced from this phenomenon that it makes no sense to mechanically adjust the levels of the variables to reduce the quality behavior risks in the current quality supervision system. Thus, it is urgent for the government to design an incentive mechanism for the participants to control the risks in construction projects, since the DP can also become the UP for other participants. The following study will continue to use the first set of values to keep consistency.

3.3. Analysis of the Dynamic Penalty and Incentive (DPI) Mechanism

Many research trials have proven that relating the penalty and reward to the actions of the players can effectively control the fluctuations in the evolutionary game [10,27,28]. This article attempts to introduce a dynamic penalty and incentive mechanism, including a dynamic penalty and dynamic reward. The dynamic penalty correlates with the ratio of the illegal and unqualified quality behavior, the extra profits, and the ratio of positive supervision. The dynamic reward correlates with the ratio of the legal and required quality behavior, the quality cost, and the ratio of positive supervision. We use $F_i^{\prime }, E_i^{\prime } \left(i=1,2\right)$ to represent the penalty and the reward in the system, respectively. The equations are as follows:

$$F_1^{\prime }=\delta F_1\left(1-y_1\right)+\delta \frac{T_1}{x}$$

(11)

$$F_2^{\prime }=\delta F_2\left(1-y_2\right)+\delta \frac{T_2}{x}$$

(12)

$$E_1^{\prime }=\epsilon E_1{y}_1+\epsilon \frac{x}{R_1}$$

(13)

$$E_2^{\prime }=\epsilon E_2{y}_2+\epsilon \frac{x}{R_2}$$

(14)

where $\delta$ is the penalty coefficient, and $\epsilon$ is the reward coefficient.

We replace $F_i, E_i\left(i=1,2\right)$ with $F_i^{\prime }, E_i^{\prime } \left(i=1,2\right)$. Thus, the SD model of the multi-player game under the DPI mechanism is shown in Figure 9.

Based on the initial values in Table 5, assuming that the values of $\delta$ and $\epsilon$ are set to 1 [27], for an initial strategy of $Z_9\left(0.6,0.5,0.5\right)$, the evolution process is shown in Figure 10.

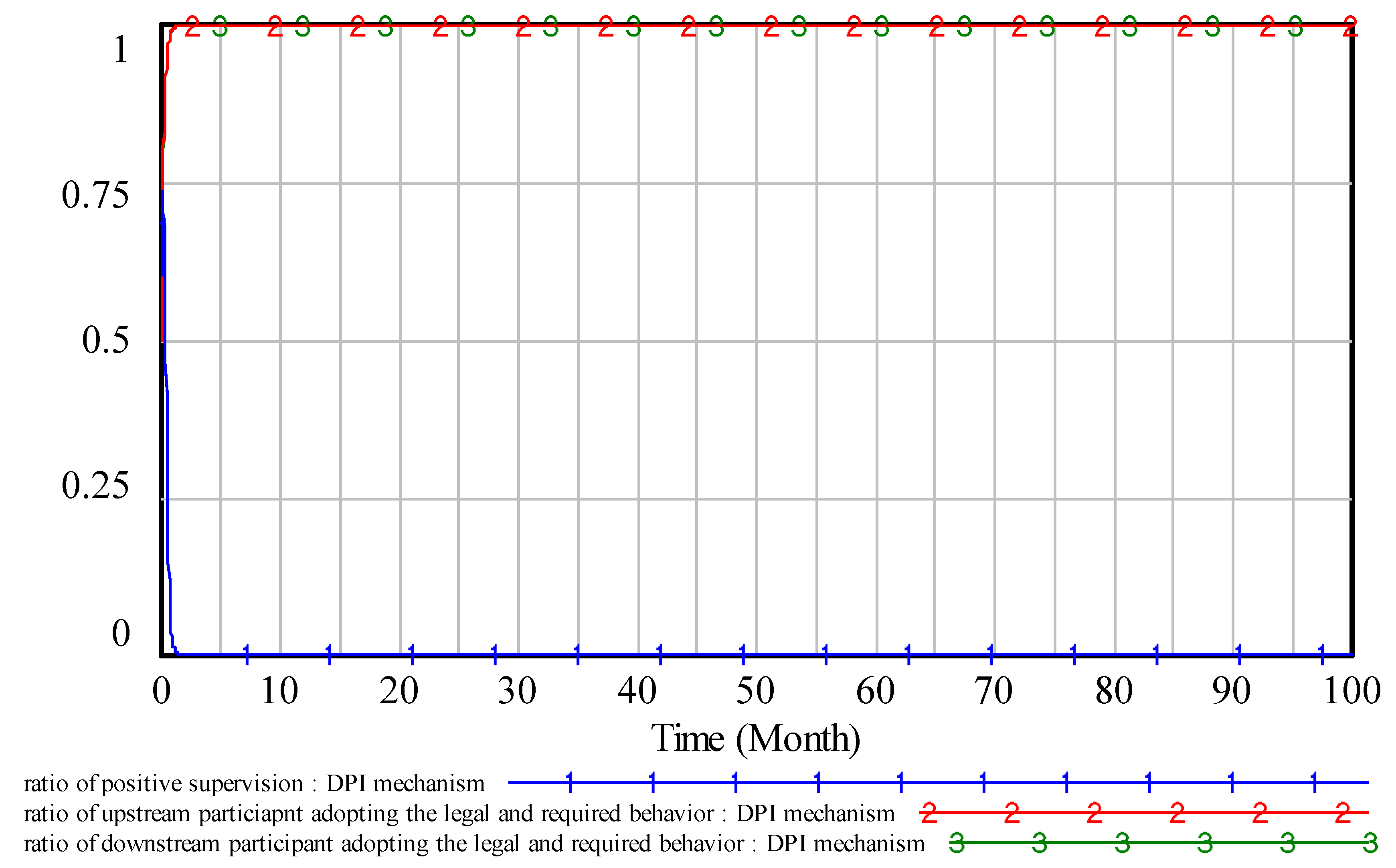
As shown in Figure 10, curves 1, 2, and 3 reach a steady state rapidly. The equilibrium strategy of the multi-player game system is $Z^{\ast }$ (0,1,1). To analyze the stability of $Z^{\ast }$, $Z_{10}\left(0.1,0.1,0.1\right)$ and $Z_{11}\left(0.9,0.9,0.9\right)$, which are shown in Figure 11a,b, respectively, are considered as the initial strategies.

As we can see in Figure 11, no matter the initial strategy under a high ratio or a low ratio, the system keeps stable and converges to $Z^{\ast }$ (0,1,1). The results show that this stable state is unaffected by an initial strategy. The DPI mechanism can effectively dampen the fluctuation of the evolutionary process. Compared with the current incentive mechanism, the designing incentive mechanism can further improve the ratio of the legal and required quality behavior of the participants and reduce the ratio of positive supervision. This does not mean that the government is not important under the DPI mechanism. The government still needs to do the top-level design, such as making the incentive mechanism. Furthermore, the government is trying to innovate a market-oriented quality supervision mode that can achieve a lower investment and a higher ratio of the legal quality behavior in construction projects. The DPI mechanism meets this requirement perfectly.

The stability of $Z^{\ast }$ was analyzed by computer simulation. In this part, we used the characteristic values of the Jacobian matrix to verify the simulation result. It turns out that the characteristic value is less than zero in the Jacobian matrix, which indicates that the equilibrium solution is the ESS. We first put the DPI mechanism into Equations (8)–(10). Then the Jacobian matrix of the multi-player game can be obtained below:

$$J=\left|\begin{array}{ccc}\frac{\partial G\left(x,y_1,y_2\right)}{\partial x}& \frac{\partial G\left(x,y_1,y_2\right)}{\partial y_1}& \frac{\partial G\left(x,y_1,y_2\right)}{\partial y_2}\\ \frac{\partial H\left(x,y_1,y_2\right)}{\partial x}& \frac{\partial H\left(x,y_1,y_2\right)}{\partial y_1}& \frac{\partial H\left(x,y_1,y_2\right)}{\partial y_2}\\ \frac{\partial I\left(x,y_1,y_2\right)}{\partial x}& \frac{\partial I\left(x,y_1,y_2\right)}{\partial y_1}& \frac{\partial I\left(x,y_1,y_2\right)}{\partial y_2}\end{array}\right|$$

(15)

Its characteristic values are as follows: ${\rho }_1=\frac{\partial G\left(x,y_1,y_2\right)}{\partial x}=\left(2x-1\right)\left(\frac{28}{195}x+13\right)+\frac{28}{195}x\left(x-1\right)$, ${\rho }_2=\frac{\partial H\left(x,y_1,y_2\right)}{\partial y_1}=-\frac{16}{5}x-\frac{1}{15}{x}^2-3$, ${\rho }_3=\frac{\partial I\left(x,y_1,y_2\right)}{\partial y_2}=-\frac{11}{5}x-\frac{1}{13}{x}^2-3$. According to the stability theory proposed by Lyapunov, for the strategy of $Z^{\ast }$(0,1,1), because $x\ne 0$ in the DPI mechanism, set $x\to 0$, ${\rho }_1=\underset{x\to 0}{\lim }\left(2x-1\right)\left(\frac{28}{195}x+13\right)+\frac{28}{195}x\left(x-1\right)=-13<0, {\rho }_2=\underset{x\to 0}{\lim }-\frac{16}{5}x-\frac{1}{15}{x}^2-3=-3<0, {\rho }_3=\underset{x\to 0}{\lim }-\frac{11}{5}x-\frac{1}{13}{x}^2-3=-3<0.$

The results show that all characteristic values are less than zero, so the $Z^{\ast }$ is the ESS, which is consistent with the computer simulation results.

The above results demonstrate the effectiveness and stability of the DPI mechanism in the multi-player game. The government can reduce its direct supervision cost by making the game rule in the quality supervision system. As mentioned earlier, this fits in the reform of the quality supervision of China, that the supervisory authority is decentralizing to the market and the supervision relationship is shifting from microcosmic to macroscopic. As the number of construction projects continues to expand, it would be impossible to rely on the government with limited funding and a shortage of supervisors to supervise the participants. As a result, the government only inspects a small part. Therefore, the ratio of positive supervision is not high in reality. The simulation results of the model fit this situation. Under the fixed incentive mechanism, there is a risk of fluctuations in the multi-player game, and the designing DPI mechanism can restrain such fluctuations effectively. Furthermore, the simulation results of the DPI mechanism show its advantage to stabilize and improve the ratio of the legal and required quality behavior of the participants. It can optimize the quality supervision system of construction projects in China.

4. Conclusions

Improper quality behavior results in quality behavior risks of the participants in construction projects. The quality behavior risks of a participant can be transmitted to the downstream participant if the participant fails to eliminate the risks. The government, with a shortage of supervisors and limited funding, cannot supervise the participants efficiently. To address the transmission of quality behavior risks in construction projects, this paper abstracts the participants as UP and DP. The evolutionary multi-player game in China’s quality supervision system, including the government, UP, and DP, was investigated in this research. Then, the multi-player game was simulated by the SD model to intuitively analyze the stability of the game. The influence of changing the penalties and rewards of the participants on the evolution process was explored. A DPI mechanism was developed to deal with the fluctuations in the game. The conclusions are made as follows:

(1)

In the current incentive mechanism, the evolutionary process of the multi-player game system fluctuates and it cannot reach an ESS, which means high risk exists in the current quality supervision system of construction projects in China. This is the main reason for the high occurrence probability of quality accidents in construction projects in China. A reasonable penalty and reward mechanism has a significant impact on the strategy selections of the participants. The penalty is low, resulting in all participants adopting the illegal and unqualified quality behavior. High penalty finally converges to a pure strategy, which is unstable. Excessively high reward and low reward can worsen the amplitude and frequency of the fluctuations of the multi-player game, which can raise the uncertainty of the game system and is detrimental for the government to supervise.

(2)

The simulation results show that there is an alternating push–pull relationship between the government and the UP, the government urges the UP to improve the legal and required quality behavior. With the relaxed supervision, the ratio of the legal and required quality behavior decreases, which in turn prompts the government to strengthen its supervision. But the results show that the supervision efficiency is not good. With the deterrent effect produced by the interplay between the government and the UP, the DP keeps the legal and required quality behavior. Under the transmission of the quality behavior risks, setting high priority to UP is conducive to control the risks, namely, hinder the transmission.

(3)

The DPI mechanism can effectively restrain the fluctuation of the evolutionary process to control the quality behavior risks. The system rapidly reaches an ESS where the government has its lowest supervision cost and the participants have their highest quality responsibility to ensure quality. It can be deduced that the introduction of the DPI mechanism in the quality supervision of construction projects can help stabilize and improve the ratio of the legal and required quality behavior of the participants.

To implement the DPI mechanism and improve the efficiency of the quality supervision system, several policy recommendations are proposed below by the authors for the government.

(1)

The DPI mechanism requires a wholesome and robust supervision system. The government should devote some time to enable the implementation of the DPI mechanism, such as, establishment of perfect laws and rules, scientific division of responsibilities, clear regulatory boundaries and standards.

(2)

The dynamic red lists and black lists of the participants can be adopted to stimulate the participants to choose legal and required quality behavior during the supervision. This requires the government to strengthen the information integration of violations and improve the update speed of the information. Dynamic and automatic detection techniques also need to be introduced, such as building information modeling.

There are some limitations to this article. This paper considers the effectiveness of the government supervision on controlling the quality behavior risks in construction projects. The supervision of the government is divided into positive supervision and negative supervision in this paper. The positive supervision contains several approaches, such as purchasing the testing service from a third-party, unannounced inspection, strengthening the training, and incentives for the supervisors of government. The supervision cost and the efficiency among these approaches should be different. However, this paper does not consider the difference. Therefore, the effectiveness of different approaches of positive supervision on controlling the quality behavior risks can be explored in future research. In addition, the simulation result of the DPI mechanism shows that the ratio of positive supervision is equal to zero. Though we explain the phenomenon that zero supervision means the government should do some top-level design during the supervision, the optimal intensity of the supervision is not considered. Thus, the optimal intensity of the supervision in the quality supervision system can be further investigated.