Abstract
Hand pose estimation from 3D data is a key challenge in computer vision as well as an essential step for human–computer interaction. A lot of deep learning-based hand pose estimation methods have made significant progress but give less consideration to the inner interactions of input data, especially when consuming hand point clouds. Therefore, this paper proposes an end-to-end capsule-based hand pose estimation network (Capsule-HandNet), which processes hand point clouds directly with the consideration of structural relationships among local parts, including symmetry, junction, relative location, etc. Firstly, an encoder is adopted in Capsule-HandNet to extract multi-level features into the latent capsule by dynamic routing. The latent capsule represents the structural relationship information of the hand point cloud explicitly. Then, a decoder recovers a point cloud to fit the input hand point cloud via a latent capsule. This auto-encoder procedure is designed to ensure the effectiveness of the latent capsule. Finally, the hand pose is regressed from the combined feature, which consists of the global feature and the latent capsule. The Capsule-HandNet is evaluated on public hand pose datasets under the metrics of the mean error and the fraction of frames. The mean joint errors of Capsule-HandNet on MSRA and ICVL datasets reach 8.85 mm and 7.49 mm, respectively, and Capsule-HandNet outperforms the state-of-the-art methods on most thresholds under the fraction of frames metric. The experimental results demonstrate the effectiveness of Capsule-HandNet for 3D hand pose estimation.
1. Introduction
Along with the development of depth cameras, interaction based on hand poses plays an important role in human–computer interaction [1,2] and has extensive application scenarios. Thus, hand pose estimation from depth images has drawn growing research interest in recent years. With the development of deep neural networks in the field of computer vision and the emergence of large hand pose datasets [3,4,5], many 3D hand pose estimation methods have been applied and improved based on Convolutional Neural Networks (CNNs) [6,7,8,9,10,11,12,13,14]. A class of methods [6,14] project depth images onto multi-views and apply multi-view CNNs to regress the heat maps of these multi-views. Unfortunately, multi-view CNNs cannot fully exploit 3D spatial information in a hand depth image. In order to utilize the spatial information, a depth image, a typical type of 3D data, is fed into 3D CNN after being rasterized into 3D voxels [7,10]. However, due to the sparsity of 3D point clouds, most of the voxels are often not occupied by any points. Therefore, these 3D CNN-based methods not only waste the calculation of 3D convolution, but also distract the neural network from learning effective features. In this situation, many studies on point cloud processing have started to focus on consuming point clouds directly to tackle the spatial information loss problems [8,9].
Most of the hand pose estimation methods mentioned above mainly focus on acquiring global or local features without explicitly representing the structural relationships among local parts. However, the geometrical and locational relations, including symmetry, junction, relative location, etc., are of great significance for certain tasks such as hand pose estimation. To aim for this, some studies try to endow the object features with structural relationship information. For example, the concept of a capsule with a dynamic routing mechanism is proposed to realize this idea [15,16]. The capsule is a vector to present geometrical and locational information. The lower-level capsules deliver their outputs to higher-level capsules in training. The corresponding higher-level capsule will be activated while an object has the desired structures. Hence, the capsule contains structural relationship information after training.
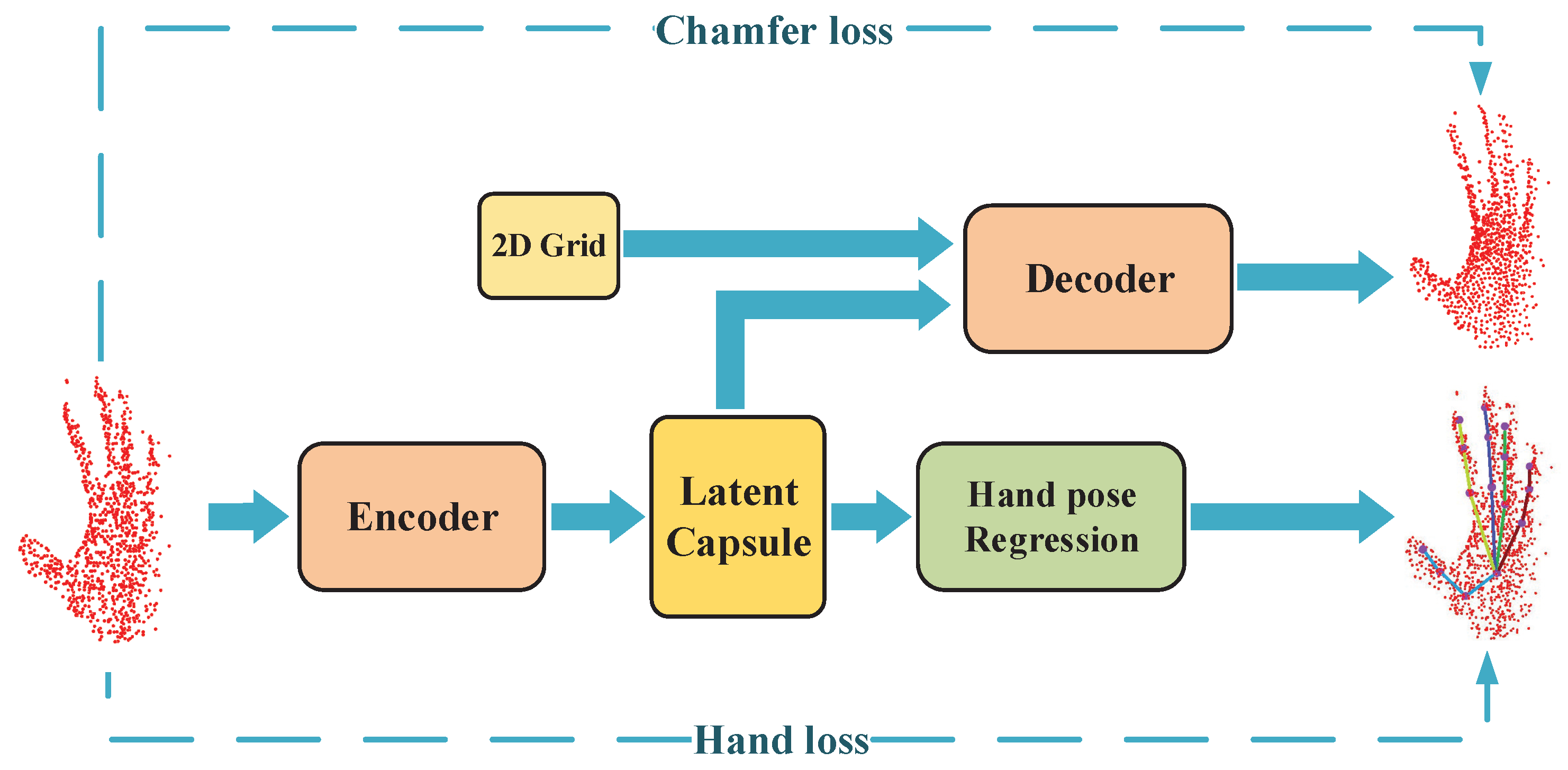
This paper proposes an end-to-end capsule-based network for hand pose estimation from hand point clouds, namely Capsule-HandNet. More importantly, inspired by [15,16], the capsule and the unsupervised dynamic routing mechanism are adopted in Capsule-HandNet, which represents the structural relationships among local parts of hand point clouds explicitly. As shown in Figure 1, Capsule-HandNet, which consists of two main phases: the auto-encoder phase and the hand pose regression phase takes point clouds as input and outputs hand poses. Specifically, the auto-encoder phase is a symmetric evaluation, which is designed to optimize the latent capsule before the hand pose regression. In this phase, the encoder uses dynamic routing to encode the hand point cloud into a latent capsule while the decoder uses the latent capsule to recover the hand point cloud with random 2D grids. Additionally, a symmetric Chamfer distance metric is adopted to optimize the auto-encoder. The smaller the error between the recovered object and the input point cloud is, the better representation ability the latent capsule has. In the hand pose regression phase, a hand pose regression network is attached after the latent capsule to estimate the regression of hand joints. The network is optimized by both Chamfer loss and hand pose loss in the training phase. Finally, the accurate hand pose can be learned from the latent capsule.
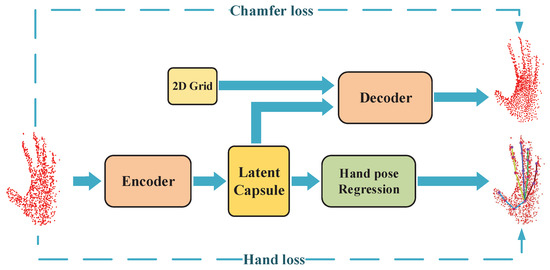
Figure 1.
Overview of the proposed Capsule-HandNet for 3D hand pose estimation.
Capsule-HandNet has the following characteristics:
- (1)
- A capsule and dynamic routing based mechanism is first employed for hand pose estimation, which enable the network to learn the structural relationships among the local parts of the hand point cloud.
- (2)
- The hand feature is embedded into a lower-dimensional latent capsule, from which superior results can be obtained by a simple regressor.
- (3)
- An auto-encoder with a symmetric Chamfer distance metric is designed for hand feature optimization to acquire an effective latent capsule.
- (4)
- An end-to-end network is adopted to avoid extra transformation and a complicated intermediate modeling process for the hand point cloud, which reduces unnecessary 3D information loss and workload.
The remainder of this paper is organized as follows. Section 2 briefly describes the existing approaches related to our work, including deep learning of point clouds and hand pose estimation. Section 3 presents the detailed design of Capsule-HandNet with a thorough description of every component. Section 4 presents the performance of Capsule-HandNet on public datasets with comprehensive evaluation protocols and comparisons with state-of-the-art methods. Finally, Section 5 draws the conclusions and discusses future works.
2. Related Work
Most of the recent studies on hand pose estimation have been based on deep neural networks. Hand poses can be regressed from both 2D images and depth images (point clouds). Due to the data’s characteristics, there are a lot of advantages for hand pose estimation based on depth images (point cloud). The proposed Capsule-HandNet is a deep learning network consuming hand point clouds. Therefore, recent approaches to the deep learning of point clouds and hand pose estimation are briefly summarized and analyzed in the following subsection.
2.1. Deeping Learning on Point Cloud
Due to the irregular format of point clouds, it is difficult to feed point cloud into conventional 2D CNNs directly [17]. Therefore, some methods process 3D point cloud data into other data structures, such as multi-view methods [6,18,19,20], voxelization methods [7,10,21,22] and other geometric form-based methods [23,24]. However, these methods require a large memory size, but suffer from low resolution.
In order to reduce the preprocessing of point clouds, Qi et al. first proposed PointNet [25], which takes point clouds as direct inputs. PointNet uses T-Net to achieve the effective alignment of features, and applies a max-pooling symmetric function to extract order-independent global features. In order to extract the local structures and features of the point cloud, Qi et al. propose PointNet++ [26], based on PointNet, in which the local features are up-sampled into higher levels hierarchically.
In recent years, several studies have explored local structures to enhance feature learning [27,28,29] or project irregular points into a regular space to apply traditional CNN [30,31]. Considering the importance of the local characteristics of point clouds, other recent methods such as self-organizing networks (SO-Net) [29], similarity group proposal networks (SGPN) [32] and PointCNN [33] combine the spatial distribution of the inputted point clouds. However, they fail to fully exploit the structural relations among local sub-clouds. To solve this problem, Zhao et al. [16] made improvements to the 2D capsule network [15] to design a 3D capsule network that respects the structural relationships of the parts of the point cloud. Inspired by the 3D capsule network, this paper designed a capsule-based network for feature extraction and pose regression from hand point clouds.
2.2. Hand Pose Estimation
The task of hand pose estimation is to acquire hand joints or hand shapes from 2D or 3D hand data such as 2D images, depth images, point clouds, etc. The studies of hand pose estimation from 3D data have made great progress in recent years, along with the development of depth sensors [34,35]. These studies are mainly based on three models, which are generative models [35,36,37,38,39], discriminative models [5,10,11,12,40,41] and hybrid models, separately [42,43,44]. Generally, hand pose estimation methods can be divided into three categories: generative methods [35,36,37,38,39], discriminative methods [5,10,11,12,40,41] and hybrid methods [42,43,44]. Generation methods select the most suitable hand model for the observations among the generated hand models. Discriminant methods learn to map from the depth image to the hand pose. Hybrid methods are the combination of generative methods and discriminative methods. In this section, we mainly discuss discrimination methods based on deep neural networks.
Tompson et al. [5] first apply CNN to hand pose estimation. They use CNN to extract features and generate heatmaps for joint positions and then apply Inverse Kinetics to get the hand pose in the heatmap. However, this method can only predict the 2D position of the hand joints and the 3D spatial information of the point cloud will be lost in the 2D heatmap. In a later work, Zhou et al. [45] apply CNN to get the hand joint angles and regress 3D hand poses through embedded kinematic layers. Ge et al. [7] transform point clouds into 3D volumes and use 3D-CNN to regress the 3D hand pose. Choi et al. [46] use geometric features as additional inputs to estimate 3D hand poses. However, none of these methods directly take the point cloud as the input of the neural network. Ge et al. [8] propose Hand-PointNet, which regresses 3D hand poses from hand point clouds directly, and design a fingertip thinning network to refine fingertip positions. Inspired by So-net [29], Chen et al. [13] propose SO-HandNet, which uses unannotated data to obtain accurate 3D hand pose estimations in a semi-supervised manner. The above studies make a positive contribution to discriminant-based hand pose estimation. However, the structural relationship information in hand point clouds is not fully utilized in most of these methods. In this paper, the proposed Capsule-HandNet exploits the structural relationships in hand point clouds based on a capsule and dynamic routing.
3. Methodology
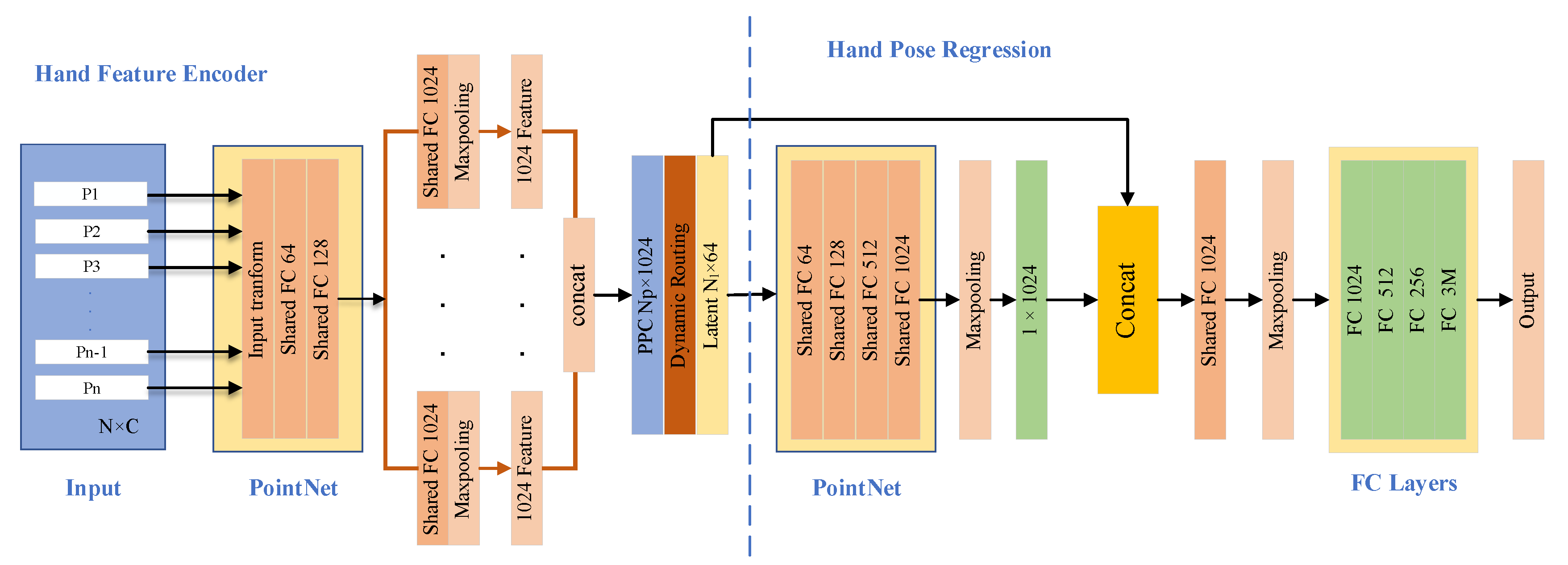
This paper proposes an end-to-end hand pose estimation network which takes hand point clouds as inputs and outputs locations of 3D hand joints based on structural relationship information. As shown in Figure 2, first of all, a set of 3D points are transformed from the hand depth image and are normalized in an Oriented Bounding Box (OBB) [47]. The hand feature encoder takes the standardized hand point clouds as inputs and uses PointNet [25] to extract features from it. Then, these features are sent into multiple independent convolutional layers. After max-pooling, these features are concatenated to the primary point capsules (PPC). Finally, dynamic routing is used to cluster the PPC into the latent capsule. Symmetrically, a feature decoder is utilized to recover the hand point cloud to enhance the representation of the latent capsule. The decoder recovers hand point sets from the latent capsule. The decoder endows the latent capsules with random 2D grids and applies MLPs to generate multiple point patches. Finally, these patches are aggregated to get the hand point cloud. To estimate the hand pose, the hand pose regression takes the latent capsule as an input and aggregates a global representation by PointNet and max-pooling. Then, the combined feature is sent into FC layers to regress the hand pose. The implementation details of Capsule-HandNet, including the preprocessing of hand point clouds, the mechanism of capsule-based hand feature extraction, the latent capsule auto-encoder and hand pose regression are introduced in the following sections.
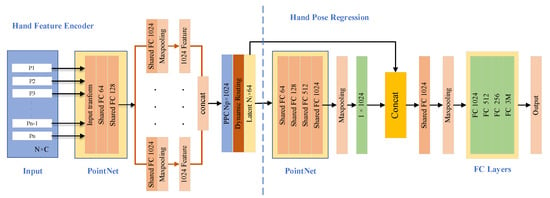
Figure 2.
The architecture of Capsule-HandNet.
3.1. Hand Point Cloud Preprocessing
Because of the diversity in the orientation of hands, it is necessary to normalize the hand point clouds to a canonical coordinate system. The input point clouds are sampled to N points first, where N is set as 1024. Similar to PointNet [25], the sampled 3D point cloud is normalized by the OBB. The OBB Coordinate System (OBB C.S) is determined by principal component analysis on the 3D coordinates of the input point and is aligned with the eigenvectors of the covariance matrix of the input points. Then, the original point locations in the camera coordinate system are transformed to normalized OBB C.S, where the orientation of point clouds is more consistent.
3.2. Capsule and Dynamic Routing
The concept of capsule was first proposed by Hinton [15] and has been widely used in 2D and 3D deep learning [16]. Generally, the capsule is a set of vectors. The length of a capsule represents the probability of the existence of an entity, and the direction represents the instantiated parameters, such as hand position, size, direction and shape. The forward propagation of the capsule network is actually the propagation from the lower-level capsule to the higher-level capsule. Each lower-level capsule delivers learned and predicted data to the higher-level capsule. If multiple predictions agree, the higher-level capsule becomes active. This process is called dynamic routing. With dynamic routing iteration, the information learned by high-level capsules becomes more and more accurate. When applying a capsule network to hand point clouds, Capsule-HandNet takes hand point clouds as inputs and extract features with MLP. The extracted features are max-pooled and concatenated to form the primary point capsule (PPC). Finally, the PPC is clustered into the final latent capsules with dynamic routing.
3.3. Hand Pose Estimation Network
Capsule-HandNet takes a set of normalized points X = = as inputs and outputs the regressed hand joints J = = , where h is the coordinates of hand points, n is the normal 3D surface, j is the coordinate of the m-th joint, N is the number of input points, and M is the number of hand joints.
Hand pose latent capsule: In this network, the latent capsule is a high-level representation of the hand feature. As shown in Figure 2, the normalized N×C input point cloud is mapped to high dimensional space by PointNet [25]. The N multiple independent convolutional layers make sure of the diversity of hand feature learning. After max-pooling multiple features to a 1024-dim global latent vector space, the squash function [15], a special non-linear activation function, is adopted to ensure the length of the output vector representing the probability of the hand feature. The output vector is called capsule and the squash function is denoted as
where v is the capsule output and s is the vector input. Then, these representations are concatenated into a set of N×1024 vectors named PPC. Finally, the unsupervised dynamic routing is used to embed the PPC into the latent capsule (N×64). With the guidance of dynamic routing, the latent capsule reflects the structural relationships among the hand parts.
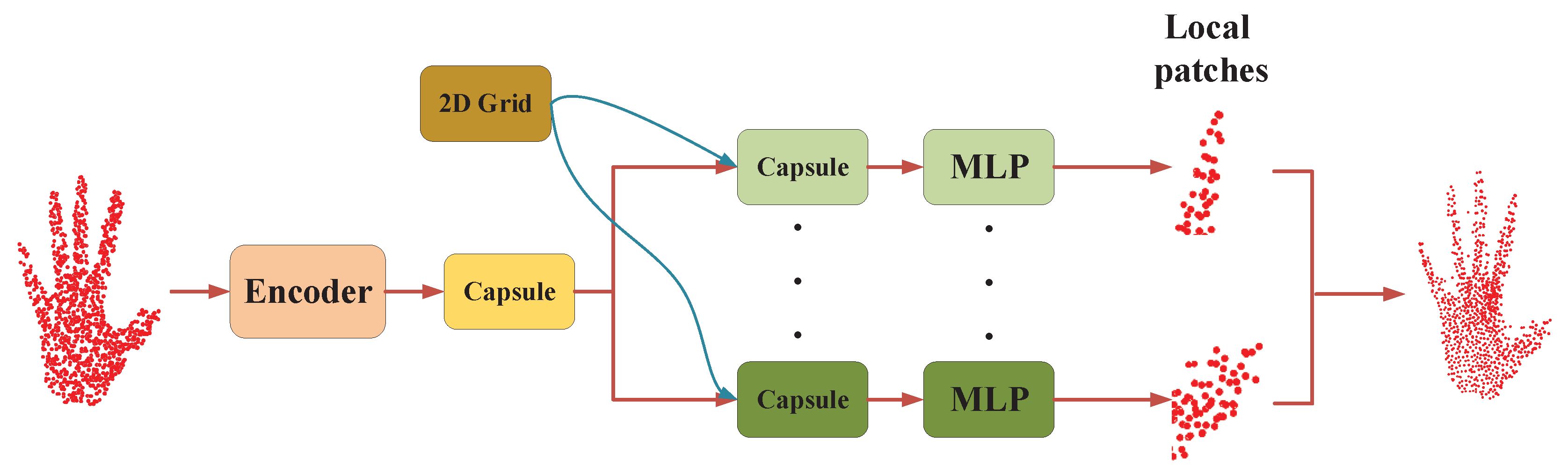
Latent capsule auto-encoder: An auto-encoder procedure is designed in the network to enhance the latent capsule for hand pose regression, as shown in Figure 3. The 1024-dim features are extracted from the input point cloud by PointNet [25]-based layers and are concatenated to generate the PPC. Then, the latent capsule is clustered by dynamic routing. This process can be seen as a encoding process of the hand feature. To improve the performance of the encoder, a decoder is designed symmetrically. As in Figure 3, the decoder takes the latent capsule as an input and employs MLP to reconstruct a patch of points. Different from employing a single MLP to recover points in PointNet, the latent capsule is duplicated m times and is appended with a unique randomly 2D grid [48]. Each grid can be folded to the special 3D object surface of a local area with independent MLPs. Finally, the output patches are glued together to form the whole hand point cloud. Since the size of the recovered object is not required to be the same as the input in Capsule-HandNet, the Chamfer distance [16] and Hausdorff distance [49] are applicable as the metrics for comparing two shapes in this case. Hence, a symmetric Chamfer distance metric is adopted as the loss function for network optimization to minimize the gap between the recovered object and original point cloud, denoted as
where is the input hand point cloud and is the recovered object. With this auto-encoder process, the latent capsule can be optimized before the following regression phase.
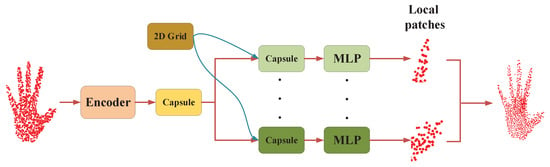
Figure 3.
The architecture of the auto-encoder in Capsule-HandNet.
Hand pose regression: As shown in Figure 2, to estimate the hand pose, the latent capsule is mapped to a 1024-dim higher dimensional space. Then, a max-pooling layer is employed to get the global feature. Since the latent capsule represents multiple features that are learned from PPC, the global feature is duplicated N times to ensure that it is concatenated with the latent capsule. The N×1088 combined features are forwarded into a shared, fully connected layer to ensure each channel is the same size. Then, max-pooling is applied to fuse the redundant information. Finally, a set of fully connected layers are adopted to regress the hand pose. In the training phase, Euclidean distance is employed for the network optimization to minimize the hand joint loss. The objective function is denoted as
where X is the input of the normalized point cloud; G is the ground truth of hand joints; x is the i-th input of normalized point cloud; g is the corresponding ground truth of hand joint; F represents the hand pose regression network; F(x) is the predicted coordinate of hand joint; N is the number of input points; is the regularization strength; represents the network parameter.
4. Experiments
In this section, several experiments are conducted to evaluate the performance of Capsule-HandNet. At first, the datasets and settings of the experiments are introduced. Then, the results of evaluations on public datasets and comparisons with state-of-the-arts are reported. After that, some ablation studies are designed to analyze the impact of components in Capsule-HandNet. Moreover, the runtime and model size of Capsule-HandNet are reported. The training and testing program was implemented in Pytorch, and the corresponding code is available from our community site (https://github.com/djzgroup/Capsule-HandNet).
4.1. Datasets and Settings
Experiments for Capsule-HandNet are conducted on two commonly used datasets for hand posed estimation: the ICVL dataset [3] and the MSRA dataset [4]. The ICVL dataset contains about 24 K frames (about 22 K training frames and 1.6 K testing frames) collected from 10 subjects captured by depth camera. The ground truth of the hand pose in each frame is indicated by 16 annotated hand joints (1 palm joint and 15 finger joints, 3 joints per finger). The MSRA dataset contains about 76 K frames. These frames are collected from 9 subjects and there are 17 gestures for each subject. The ground truth of the hand pose in each frame is indicated by 21 annotated hand joints (1 palm joint and 20 finger joints, 4 joints per finger). The Capsule-Handnet is trained on 8 subjects and is tested on the remaining subject.
The performance of Capsule-HandNet is evaluated by two commonly used metrics for the hand pose estimation task: the mean per-joint error and the fraction of frames. Mean per-joint error indicates the mean error between each joint and corresponding ground truth as well as the mean error of all joints. The fraction of good frames is a stricter metric. This indicates the proportion of frames whose errors are within a certain threshold. The threshold means the maximum error allowed for the ground truth.
Implementation settings: For network settings, the number of sampled points is 1024 and the size of PPC is 16 × 1024. The size for the latent capsule is set at 64 × 64. For training the network, an Adam optimizer is employed with an initial learning rate of 0.0001, a batch size of 32 and a regularization strength of 0.0005.
Experimental configuration: The hardware environment of experiments is Intel Core i5-10500 + RTX 2080TI + 32 GB RAM, and the software environment is Ubuntu16.04 x64 + CUDA 10.1 + cuDNN 7.4 + Python3.6.
4.2. Comparisons with State-of-the-Art Methods
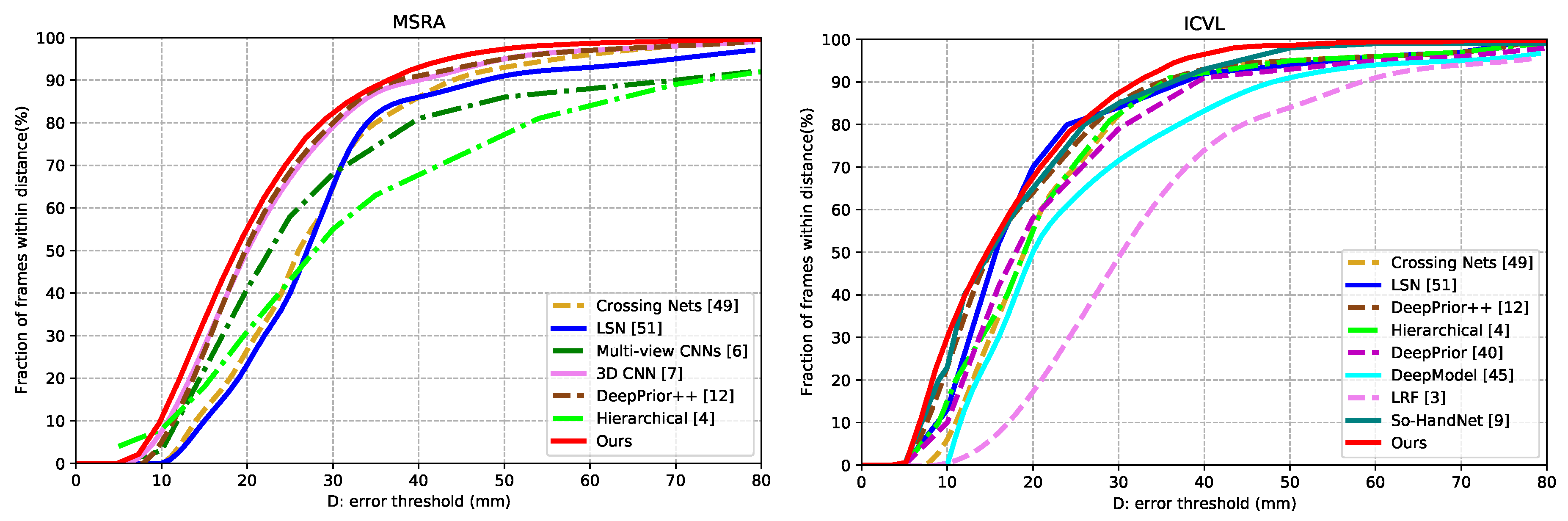
Capsule-HandNet is compared with some of the state-of-the-art methods, including multi-view CNNs [6], LRF [3], the Deep Model [45], DeepPrior [40], DeepPrior++ [12], Crossing Nets [50], HBE [51], 3D CNN [7], V2V PoseNet [10], So-HandNet [9], LSN [52], Hierarchical [4], REN [53]. The fraction of frames and the per-joint mean error distances of different methods in MSRA and ICVL datasets are presented in Figure 4 and Figure 5, respectively. The results of some methods are obtained from trained models available online [3,9,12,40,52,53] and others are cited from corresponding papers [4,6,7,10,45,50,51].
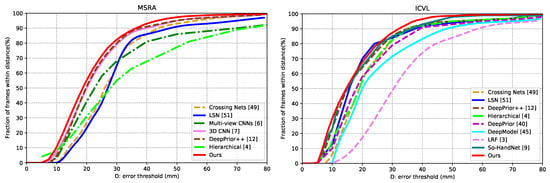
Figure 4.
Comparisons of fraction of frames on MSRA (left) and ICVL (right) datasets.
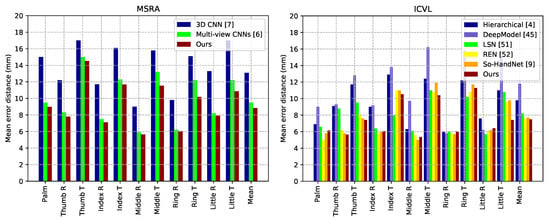
Figure 5.
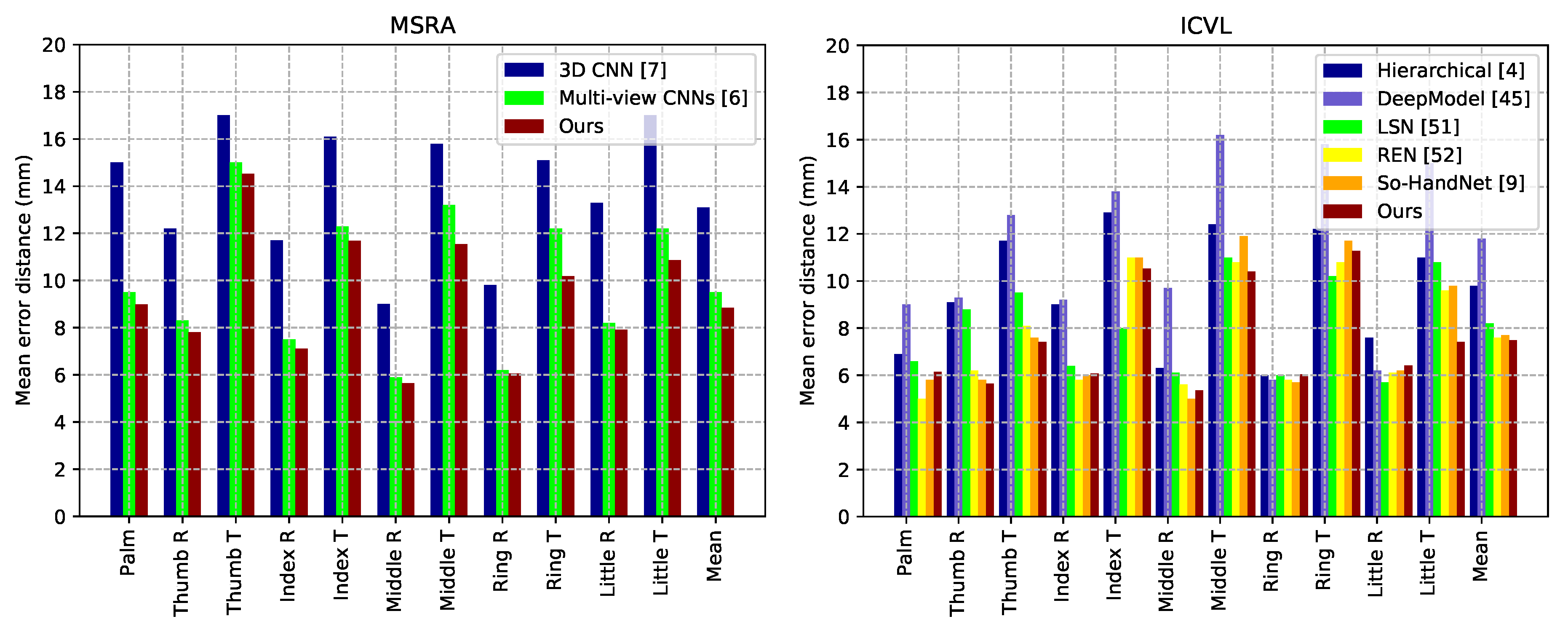
Comparisons of per-joint mean error and overall mean error on MSRA (left) and ICVL (right) datasets (R: root, T: tip).
For the MSRA dataset, as shown in Table 1, the proposed Capsule-HandNet achieves a low mean joint error on the test dataset of 8.85 mm. Compared to other methods, Capsule-HandNet shows a large improvement, except for V2V-PoseNet [10]. Considering that [10] is a voxel-based method, our method is more advantageous in terms of runtime (details about the runtime of our method are discussed in Section 4.4). Figure 4 (left) shows the proportion of good frames over different error thresholds in the MSRA dateset. Our method outperforms other methods in most of the error thresholds. When the error threshold is between 15mm and 20mm, our method is about 10% to 20% better than other methods.

Table 1.
Comparisons with state-of-the-art methods on the MSRA dataset.
For the ICVL dataset, as shown in Table 2, the mean joint errors of other methods are from 7.6 mm to 12.6 mm, which are larger than the 7.49 mm of Capsule-HandNet. As shown in Figure 4 (right), our method outperforms other methods on most error thresholds. In particular, on the thresholds from 30 mm to 50 mm, the performance of our method is obviously superior.

Table 2.
Comparisons with state-of-the-art methods on the ICVL dataset.
For the mean error distances shown in Figure 5, on both MSRA and ICVL datasets, our method achieves the smallest mean error distances for most of the hand joints. Specifically, Capsule-HandNet outperforms the multi-view method [6] and the 3D CNN [7] method on the MSRA dataset. On the ICVL dataset, Capsule-HandNet also outperforms or is on par with other methods on the whole. Compared to errors in finger root joints, errors in the tips are larger.
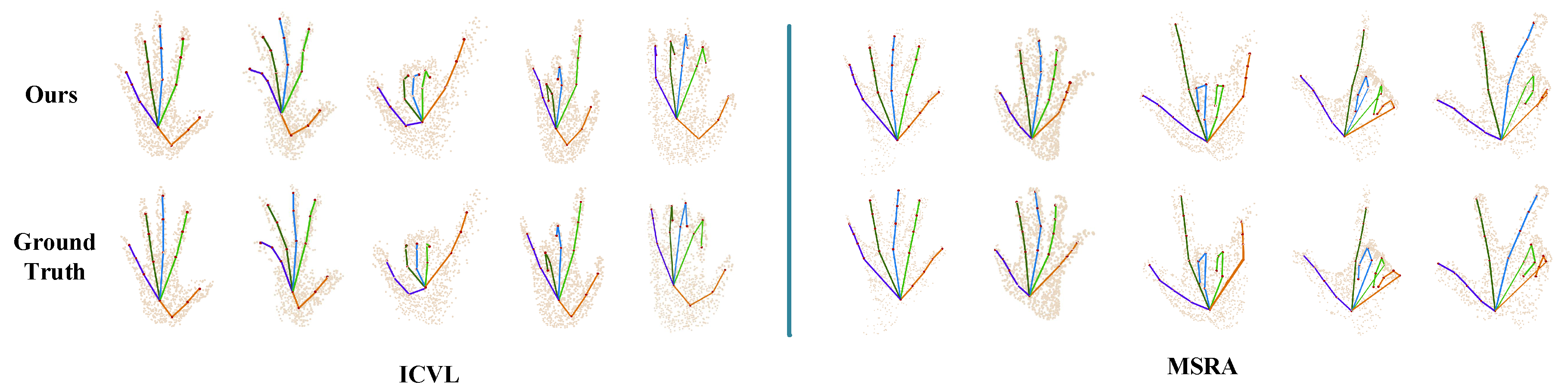
Figure 6 shows the visualization results of Capsule-HandNet on ICVL (left) and MSRA (right) datasets. The 3D hand joint locations estimated by Capsule-HandNet are very close to the ground truth, as shown in the figure, which demonstrates that the network is able to deal with complicated hand structures and obtain accurate hand joints.
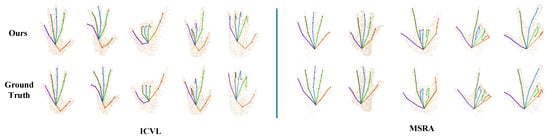
Figure 6.
Qualitative results for ICVL (left) and MSRA (right) datasets.
4.3. Ablation Study
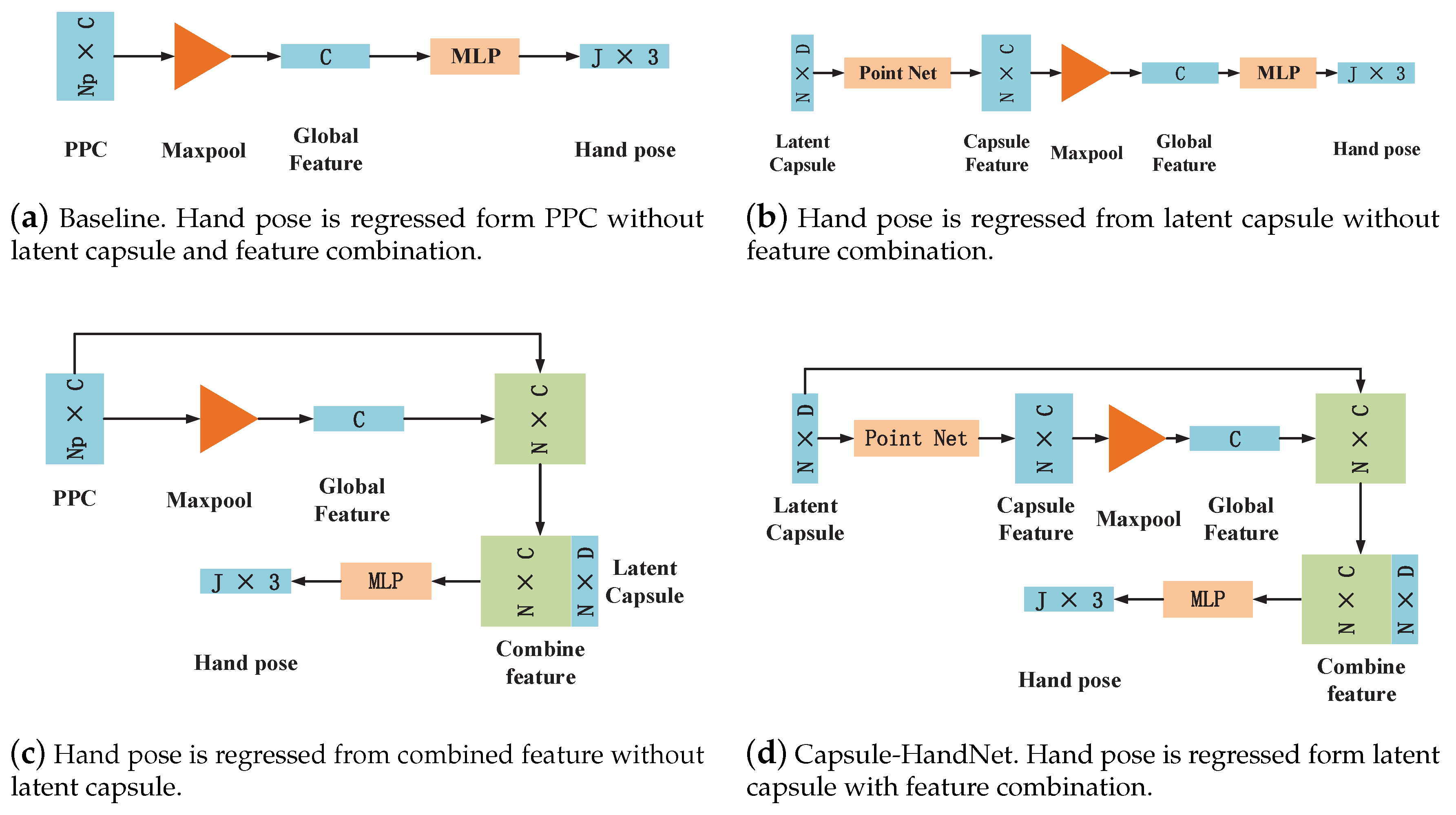
In this section, extensive experiments are designed to show the impacts of critical components in Capsule-HandNet. Figure 7 shows varied strategies for hand pose estimation to demonstrate the impacts of the latent capsule and feature combination in the regression phase, respectively. All ablation studies are conducted on both the MSRA and ICVL datasets.
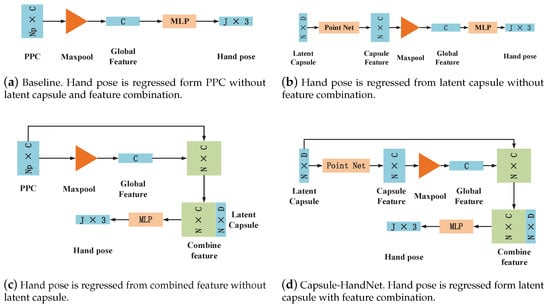
Figure 7.
Strategies of hand joints regression for ablation studies.
(a) Baseline: A baseline is designed to demonstrate the performance of a network in which both the latent capsule and feature combination are ablated from Capsule-HandNet. As shown in Figure 7a, the global feature is obtained from PPC and is used to regress hand poses directly.
(b) Impact of feature combination: In the hand feature encoding stage, the latent capsule, which represents hand features, is obtained. Then, the global feature vector is duplicated to be concatenated with the latent capsule in the regression stage. To evaluate the impact of the feature combination, in the ablation study, the global feature is extracted from the latent capsule and is used to regress the hand pose directly without the combination process, as shown in Figure 7b.
(c) Impact of latent capsule: The latent capsule is the key component of Capsule-Hand Net. It is clustered from PPC by dynamic routing. To verify the impact of the latent capsule, in the ablation study, hand poses are regressed from PPC directly, without the generation of a latent capsule (the feature combination is retained), as shown in Figure 7c.
(d) Capsule-HandNet:Figure 7d shows the simplified framework of Capsule-HandNet, which contains modules of the latent capsule and feature combinations.
The results of the ablation studies are shown in Table 3. When the network is without latent capsule and feature combinations (baseline), the mean joint error is 13.50 mm on the MSRA dataset and 9.85 mm on the ICVL dataset. The mean joint error with the latent capsule decreases by 2.29 mm and 4.27 mm compared to no latent capsule strategies, respectively, which is a significant improvement. Compared with strategies that only utilize global features, feature combination improves the performance of the network significantly. Both components have obvious positive impacts on Capsule-HandNet.

Table 3.
Ablation study of ICVL dataset and MSRA dateset.
4.4. Runtime and Model Size
The experimental results using a single GPU (RTX 2080TI) show that Capsule-HandNet achieves an outstanding performance with a runtime speed of 223.7fps, which indicates that this network has advantages for real-time applications. The testing time of Capsule-HandNet is 12.21 ms on average. Specifically, the hand feature encoding time is 6.705 ms and the hand pose regression time is 5.535 ms. In addition, since the hand feature encoder of Capsule-HandNet needs multiple MLP networks to extract potential capsules, the size of the encoder is relatively large—264MB. The size of the hand pose regression network is 12 MB in total.
5. Conclusions
In this paper, a novel network is proposed for 3D hand pose estimation from point clouds. The proposed network, namely Capsule-HandNet, is the first work that exploits the structural relations among local parts for hand pose estimation via a capsule. In the network, hand features are encoded into a latent capsule and an auto-encoder is designed to optimize the latent capsule by recovering the inputted hand point cloud. The generation of a capsule by dynamic routing explicitly extracts the structural relationship information from the hand point cloud. With the latent capsule, accurate 3D hand poses can be regressed from combined features by a simple regressor in Capsule-HandNet. Experiments are conducted on public datasets and the results show that Capsule-HandNet achieves a superior performance, which demonstrates that hand features with structural relationship information are beneficial for 3D hand pose estimation. Capsule-HandNet could be adopted for many applications related to hand pose recognition, such as gesture interactions for remote controls, human computer interactions in virtual environments and virtual reality, etc. In future, we plan to optimize our network [8,54,55], deploy our network in more scenarios, such as human pose estimation [56] and video object processing [57,58], and make the network adapt to diverse types of 3D data [59].
Author Contributions
Y.W. and S.M. conceived and designed the algorithm and the experiments. S.M. analyzed the data. S.M. wrote the manuscript. D.Z. supervised the research. Y.W. and D.Z. provided suggestions for the proposed method and its evaluation and assisted in the preparation of the manuscript. J.S. collected and organized the literature. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China under grants 61802355 and 61702350.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rautaray, S.S.; Agrawal, A. Vision based hand gesture recognition for human computer interaction: A survey. Artif. Intell. Rev. 2015, 43, 1–54. [Google Scholar] [CrossRef]
- Deng, Y.; Gao, F.; Chen, H. Angle Estimation for Knee Joint Movement Based on PCA-RELM Algorithm. Symmetry 2020, 12, 130. [Google Scholar] [CrossRef]
- Tang, D.; Jin Chang, H.; Tejani, A.; Kim, T.K. Latent regression forest: Structured estimation of 3d articulated hand posture. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 3786–3793. [Google Scholar]
- Sun, X.; Wei, Y.; Liang, S.; Tang, X.; Sun, J. Cascaded hand pose regression. In Proceedings of the IEEE conference on computer vision and pattern recognition, Boston, MA, USA, 7–12 June 2015; pp. 824–832. [Google Scholar]
- Tompson, J.; Stein, M.; Lecun, Y.; Perlin, K. Real-time continuous pose recovery of human hands using convolutional networks. ACM Trans. Graph. (ToG) 2014, 33, 169. [Google Scholar] [CrossRef]
- Ge, L.; Liang, H.; Yuan, J.; Thalmann, D. Robust 3d hand pose estimation in single depth images: From single-view cnn to multi-view cnns. In Proceedings of the IEEE conference on computer vision and pattern recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 3593–3601. [Google Scholar]
- Ge, L.; Liang, H.; Yuan, J.; Thalmann, D. 3d convolutional neural networks for efficient and robust hand pose estimation from single depth images. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1991–2000. [Google Scholar]
- Ge, L.; Cai, Y.; Weng, J.; Yuan, J. Hand pointnet: 3d hand pose estimation using point sets. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 8417–8426. [Google Scholar]
- Chen, Y.; Tu, Z.; Ge, L.; Zhang, D.; Chen, R.; Yuan, J. So-handnet: Self-organizing network for 3d hand pose estimation with semi-supervised learning. In Proceedings of the IEEE International Conference on Computer Vision, Seoul, Korea, 27 October–3 November 2019; pp. 6961–6970. [Google Scholar]
- Moon, G.; Yong Chang, J.; Mu Lee, K. V2v-posenet: Voxel-to-voxel prediction network for accurate 3d hand and human pose estimation from a single depth map. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 5079–5088. [Google Scholar]
- Chen, X.; Wang, G.; Zhang, C.; Kim, T.K.; Ji, X. Shpr-net: Deep semantic hand pose regression from point clouds. IEEE Access 2018, 6, 43425–43439. [Google Scholar] [CrossRef]
- Oberweger, M.; Lepetit, V. Deepprior++: Improving fast and accurate 3d hand pose estimation. In Proceedings of the IEEE International Conference on Computer Vision Workshops, Venice, Italy, 22–29 October 2017; pp. 585–594. [Google Scholar]
- Chen, X.; Wang, G.; Guo, H.; Zhang, C. Pose guided structured region ensemble network for cascaded hand pose estimation. Neurocomputing 2020, 395, 138–149. [Google Scholar] [CrossRef]
- Poier, G.; Schinagl, D.; Bischof, H. Learning pose specific representations by predicting different views. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 60–69. [Google Scholar]
- Sabour, S.; Frosst, N.; Hinton, G.E. Dynamic routing between capsules. In Advances in Neural Information Processing Systems; 2017; pp. 3856–3866. Available online: http://papers.nips.cc/paper/6975-dynamic-routing-between-capsules (accessed on 2 October 2020).
- Zhao, Y.; Birdal, T.; Deng, H.; Tombari, F. 3D point capsule networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–21 June 2019; pp. 1009–1018. [Google Scholar]
- Zhang, D.; He, F.; Tu, Z.; Zou, L.; Chen, Y. Pointwise geometric and semantic learning network on 3D point clouds. Integr. Comput. Aided Eng. 2020, 27, 57–75. [Google Scholar] [CrossRef]
- Qi, C.R.; Su, H.; Nießner, M.; Dai, A.; Yan, M.; Guibas, L.J. Volumetric and multi-view cnns for object classification on 3d data. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 5648–5656. [Google Scholar]
- He, X.; Zhou, Y.; Zhou, Z.; Bai, S.; Bai, X. Triplet-center loss for multi-view 3d object retrieval. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 1945–1954. [Google Scholar]
- Yu, T.; Meng, J.; Yuan, J. Multi-view harmonized bilinear network for 3d object recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 186–194. [Google Scholar]
- Wu, Z.; Song, S.; Khosla, A.; Yu, F.; Zhang, L.; Tang, X.; Xiao, J. 3d shapenets: A deep representation for volumetric shapes. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1912–1920. [Google Scholar]
- Maturana, D.; Scherer, S. Voxnet: A 3d convolutional neural network for real-time object recognition. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 922–928. [Google Scholar]
- Landrieu, L.; Simonovsky, M. Large-scale point cloud semantic segmentation with superpoint graphs. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 4558–4567. [Google Scholar]
- Prokudin, S.; Lassner, C.; Romero, J. Efficient learning on point clouds with basis point sets. In Proceedings of the IEEE International Conference on Computer Vision Workshops, Seoul, Korea, 27–28 October 2019. [Google Scholar]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. Pointnet: Deep learning on point sets for 3d classification and segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 652–660. [Google Scholar]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. Pointnet++: Deep hierarchical feature learning on point sets in a metric space. In Advances in Neural Information Processing Systems; 2017; pp. 5099–5108. Available online: http://papers.nips.cc/paper/7095-pointnet-deep-hierarchical-feature-learning-on-point-se (accessed on 2 October 2020).
- Liu, Y.; Fan, B.; Meng, G.; Lu, J.; Xiang, S.; Pan, C. Densepoint: Learning densely contextual representation for efficient point cloud processing. In Proceedings of the IEEE International Conference on Computer Vision, Seoul, Korea, 27 October–3 November 2019; pp. 5239–5248. [Google Scholar]
- Liu, Y.; Fan, B.; Xiang, S.; Pan, C. Relation-shape convolutional neural network for point cloud analysis. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–21 June 2019; pp. 8895–8904. [Google Scholar]
- Li, J.; Chen, B.M.; Hee Lee, G. So-net: Self-organizing network for point cloud analysis. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 9397–9406. [Google Scholar]
- Thomas, H.; Qi, C.R.; Deschaud, J.E.; Marcotegui, B.; Goulette, F.; Guibas, L.J. Kpconv: Flexible and deformable convolution for point clouds. In Proceedings of the IEEE International Conference on Computer Vision, Seoul, Korea, 27 October–3 November 2019; pp. 6411–6420. [Google Scholar]
- Mao, J.; Wang, X.; Li, H. Interpolated convolutional networks for 3d point cloud understanding. In Proceedings of the IEEE International Conference on Computer Vision, Seoul, Korea, 27 October–3 November 2019; pp. 1578–1587. [Google Scholar]
- Wang, W.; Yu, R.; Huang, Q.; Neumann, U. Sgpn: Similarity group proposal network for 3d point cloud instance segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 2569–2578. [Google Scholar]
- Li, Y.; Bu, R.; Sun, M.; Wu, W.; Di, X.; Chen, B. Pointcnn: Convolution on x-transformed points. In Advances in Neural Information Processing Systems; 2018; pp. 820–830. Available online: http://papers.nips.cc/paper/7362-pointcnn-convolution-on-x-transformed-points (accessed on 2 October 2020).
- Zhang, Z. Microsoft kinect sensor and its effect. IEEE Multimed. 2012, 19, 4–10. [Google Scholar] [CrossRef]
- Keselman, L.; Iselin Woodfill, J.; Grunnet-Jepsen, A.; Bhowmik, A. Intel realsense stereoscopic depth cameras. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, HI, USA, 21–26 July 2017; pp. 1–10. [Google Scholar]
- Romero, J.; Tzionas, D.; Black, M.J. Embodied hands: Modeling and capturing hands and bodies together. ACM Trans. Graph. (ToG) 2017, 36, 245. [Google Scholar] [CrossRef]
- Tkach, A.; Tagliasacchi, A.; Remelli, E.; Pauly, M.; Fitzgibbon, A. Online generative model personalization for hand tracking. ACM Trans. Graph. (ToG) 2017, 36, 243. [Google Scholar] [CrossRef]
- Khamis, S.; Taylor, J.; Shotton, J.; Keskin, C.; Izadi, S.; Fitzgibbon, A. Learning an efficient model of hand shape variation from depth images. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 2540–2548. [Google Scholar]
- Remelli, E.; Tkach, A.; Tagliasacchi, A.; Pauly, M. Low-dimensionality calibration through local anisotropic scaling for robust hand model personalization. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2535–2543. [Google Scholar]
- Oberweger, M.; Wohlhart, P.; Lepetit, V. Hands deep in deep learning for hand pose estimation. arXiv 2015, arXiv:1502.06807. [Google Scholar]
- Deng, X.; Yang, S.; Zhang, Y.; Tan, P.; Chang, L.; Wang, H. Hand3d: Hand pose estimation using 3d neural network. arXiv 2017, arXiv:1704.02224. [Google Scholar]
- Oberweger, M.; Wohlhart, P.; Lepetit, V. Training a feedback loop for hand pose estimation. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 3316–3324. [Google Scholar]
- Sharp, T.; Keskin, C.; Robertson, D.; Taylor, J.; Shotton, J.; Kim, D.; Rhemann, C.; Leichter, I.; Vinnikov, A.; Wei, Y.; et al. Accurate, robust, and flexible real-time hand tracking. In Proceedings of the 33rd Annual ACM Conference on Human Factors in Computing Systems, Seoul, Korea, 18–23 April 2015; pp. 3633–3642. [Google Scholar]
- Ye, Q.; Yuan, S.; Kim, T.K. Spatial attention deep net with partial pso for hierarchical hybrid hand pose estimation. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 8–16 October 2016; Springer: Cham, Switzerland, 2016; pp. 346–361. [Google Scholar]
- Zhou, X.; Wan, Q.; Zhang, W.; Xue, X.; Wei, Y. Model-based deep hand pose estimation. arXiv 2016, arXiv:1606.06854. [Google Scholar]
- Choi, C.; Kim, S.; Ramani, K. Learning hand articulations by hallucinating heat distribution. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 3104–3113. [Google Scholar]
- Zhang, D.; Zhang, Z.; Zou, L.; Xie, Z.; He, F.; Wu, Y.; Tu, Z. Part-based visual tracking with spatially regularized correlation filters. Vis. Comput. 2020, 36, 509–527. [Google Scholar] [CrossRef]
- Yang, Y.; Feng, C.; Shen, Y.; Tian, D. Foldingnet: Point cloud auto-encoder via deep grid deformation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 206–215. [Google Scholar]
- Zhang, D.; He, F.; Han, S.; Zou, L.; Wu, Y.; Chen, Y. An efficient approach to directly compute the exact Hausdorff distance for 3D point sets. Integr. Comput. Aided Eng. 2017, 24, 261–277. [Google Scholar] [CrossRef]
- Wan, C.; Probst, T.; Van Gool, L.; Yao, A. Crossing nets: Combining gans and vaes with a shared latent space for hand pose estimation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 680–689. [Google Scholar]
- Zhou, Y.; Lu, J.; Du, K.; Lin, X.; Sun, Y.; Ma, X. Hbe: Hand branch ensemble network for real-time 3d hand pose estimation. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 501–516. [Google Scholar]
- Wan, C.; Yao, A.; Van Gool, L. Hand pose estimation from local surface normals. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; pp. 554–569. [Google Scholar]
- Guo, H.; Wang, G.; Chen, X.; Zhang, C.; Qiao, F.; Yang, H. Region ensemble network: Improving convolutional network for hand pose estimation. In Proceedings of the 2017 IEEE International Conference on Image Processing (ICIP), Beijing, China, 17–20 September 2017; pp. 4512–4516. [Google Scholar]
- Pan, Y.; He, F.; Yu, H. A novel enhanced collaborative autoencoder with knowledge distillation for top-N recommender systems. Neurocomputing 2019, 332, 137–148. [Google Scholar] [CrossRef]
- Zhang, D.; Luo, M.; He, F. Reconstructed similarity for faster GANs-based word translation to mitigate hubness. Neurocomputing 2019, 362, 83–93. [Google Scholar] [CrossRef]
- Sun, J.; Wang, M.; Zhao, X.; Zhang, D. Multi-View Pose Generator Based on Deep Learning for Monocular 3D Human Pose Estimation. Symmetry 2020, 12, 1116. [Google Scholar] [CrossRef]
- Guo, M.; Zhang, D.; Sun, J.; Wu, Y. Symmetry Encoder-Decoder Network with Attention Mechanism for Fast Video Object Segmentation. Symmetry 2019, 11, 1006. [Google Scholar] [CrossRef]
- Zhang, D.; He, L.; Tu, Z.; Han, F.; Zhang, S.; Yang, B. Learning motion representation for real-time spatio-temporal action localization. Pattern Recognit. 2020, 103, 107312. [Google Scholar] [CrossRef]
- Liang, Y.; He, F.; Zeng, X. 3D mesh simplification with feature preservation based on Whale Optimization Algorithm and Differential Evolution. Integr. Comput. Aided Eng. 2020, 1–19, Preprint. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).