Eliciting Correlated Weights for Multi-Criteria Group Decision Making with Generalized Canonical Correlation Analysis

Abstract

The proper solution of a multi-criteria group decision making (MCGDM) problem usually involves a series of critical issues that are to be dealt with, among which two are noteworthy, namely how to assign weights to the (possibly distinct) judgment criteria used by the different decision makers (DMs) and how to reach a satisfactory level of agreement between their individual decisions. Here we present a novel methodology to address these issues in an integrated and robust way, referred to as the canonical multi-criteria group decision making (CMCGDM) approach. CMCGDM is based on a generalized version of canonical correlation analysis (GCCA), which is employed for simultaneously computing the criteria weights that are associated with all DMs. Because the elicited weights maximize the linear correlation between all criteria at once, it is expected that the consensus measured between the DMs takes place in a more natural way, not necessitating the creation and combination of separate rankings for the different groups of criteria. CMCGDM also makes use of an extended version of TOPSIS, a multi-criteria technique that considers the symmetry of the distances to the positive and negative ideal solutions. The practical usefulness of the proposed approach is demonstrated through two revisited examples that were taken from the literature as well as other simulated cases. The achieved results reveal that CMCGDM is indeed a promising approach, being more robust to the problem of ranking irregularities than the extended version of TOPSIS when applied without GCCA.

1. Introduction

Multi-criteria group decision making (MCGDM) is usually described as the process of selecting the best alternative(s) from a given set of viable options that are based on the opinions that are provided by multiple domain experts, frequently referred to as decision makers (DMs), concerning multiple judgment criteria [1,2]. In recent years, a number of MCGDM techniques have been proposed and widely applied in many distinct fields, such as sustainable development [3,4], personnel evaluation [5], social network analysis [6], software selection [7,8], supplier selection [9,10], and economics [11].

Among others, Herrera-Viedma et al. [12] have argued that solving a group decision making (GDM) problem usually involves the carrying out of two complementary processes: a consensus reaching process (generally guided by a moderator), which refers to how to obtain, via one or more stages of negotiation, the maximum degree of agreement between the experts; and, a selection process, which achieves the final solution via the aggregation of the experts’ individual preferences over the different alternatives available. Various approaches have been developed so far to help undertaking these processes, especially the latter, in different circumstances; for instance, by addressing dynamic sets of alternatives [13] and criteria [14], changes of preferences [15] and opinions [16,17], as well as differences in the knowledge level between the accessible DMs [18,19].

Specifically concerning the modelling of the DMs’ preferences, the assignment of weights to their evaluation criteria turns out to be a crucial task to be accomplished, since the final decision that is delivered by a given MCGDM method usually depends on such weights to a large extent. However, properly calibrating criteria weights in multi-criteria decision making is a hard task to pursue, even when considering the single DM setting [20]. This task becomes even more relevant (and harder to attempt) when different criteria are adopted by different DMs. In this regard, Fan et al. [21] recently pointed out that research concerning this more complex scenario is still relatively scarce in the literature and, thus, developed a method for tackling MCGDM with different evaluation criteria sets.

Based on these considerations, this paper investigates a novel GDM approach that is aimed to address, in an integrated manner, both the elicitation of the DMs’ preferences and the consensus of their individual decisions. The approach, which is referred to as canonical multi-criteria group decision making (CMCGDM, for short), can also deal with MCGDM problems having different criteria sets for different DMs and makes use of a generalized version of canonical correlation analysis (CCA) [22] to automatically compute the values of criteria weights.

In a nutshell, the goal of CCA is to maximize the linear correlation between two sets of variables, so as to yield a novel set of canonical variates, which, in turn, may replace the original ones. This procedure involves computing the weights for both sets of original variables that result in the highest possible correlation between the canonical variates [23]. Although the standard CCA only handles two sets of variables, there are extensions that handle more, such as the generalized CCA (GCCA) version that was proposed by Kettenring [24].

CMCGDM also adopts the extended version of TOPSIS (technique for order preference by similarity solution) [25] that was proposed by Shih et al. [26], which is specific for MCGDM. The practical usefulness of CMCGDM is demonstrated by revisiting two examples, one on a human resource selection [26] and the other on a machine acquisition [21]. The results achieved in these examples and other simulated cases reveal that CMCGDM is indeed a promising approach, being more robust to cope with the ranking irregularity problem [27] than the extended TOPSIS for GDM without using GCCA.

In short, the main contributions of this paper are: to show that GCCA is a viable approach to eliciting weights in the MCGDM context; to prove that CMCGDM is more robust for dealing with the problem of classification irregularity than the extended TOPSIS without using GCCA, and that it does it in a straightforward way without the need for changes in the extended TOPSIS procedure; and, to be able to reach the group’s consensus by reconciling the different canonical weights that were provided by the GCCA.

The rest of this paper is organized as follows. In Section 2 and Section 3, we review the main aspects that are related to standard MCGDM and GCCA. In Section 4, we present the main steps comprising the new CMCGDM methodology and point out some of its relevant properties. In Section 5 and Section 6, we evaluate CMCGDM on the examples considered by Shih et al. [26] and Fan et al. [21], whereas, in Section 7, we compare GCCA with other well-known criteria weighting methods on several simulated cases. Finally, Section 8 concludes the paper and brings some remarks on future work.

2. Multi-Criteria Group Decision Making

Briefly stated, MCGDM refers to the process of making decisions in group when there are multiple (but a finite list of) alternative solutions that are available to the decision problem in hand. In addition, the group of DMs assess the pros and cons of these alternatives by taking multiple (usually conflicting) judgment criteria into account [1,2]. Formally, an MCGDM problem with M alternatives, N criteria, and K DMs can be formulated by defining K decision matrices of the form:

$$\begin{array}{cc}\hfill {\mathcal{D}}^k& ={\left(x_{ij}^k\right)}_{M\times n_k}=\begin{array}{c}{A}_1\\ A_2\\ .\\ .\\ .\\ A_M\end{array}\left(\begin{array}{cccccc}{c}_1^k& c_2^k& & & & c_{n_k}^k\\ x_{11}^k& x_{12}^k& .& .& .& x_{1n_k}^k\\ x_{21}^k& x_{22}^k& .& .& .& x_{2n_k}^k\\ .& .& .& .& .& .\\ .& .& .& .& .& .\\ .& .& .& .& .& .\\ x_{M1}^k& x_{M2}^k& .& .& .& x_{M{n}_k}^k\end{array}\right)\hfill \\ \hfill w^k& =(w_1^k,w_2^k,\dots ,w_{n_k}^k),k=1,\dots ,K,\hfill \end{array}$$

(1)

where $A=\{A_1,A_2,\dots ,A_M\}$ denotes the set of feasible alternatives, $C^k=\{c_1^k,c_2^k,\dots ,c_{n_k}^k\}$ represents the $n_k$ evaluation criteria that are associated with the k-th DM, $x_{ij}^k$ is the performance rating of alternative $A_i$ under criterion $c_j^k$ ($j=1,\dots ,n_k$), and $w_j^k$ stands for the weight of this criterion. Notice that $0\le w_j^k\le 1$ and ${\sum }_{j=1}^{n_k}{w}_j^k=1$. On the other hand, the K criteria sets may be equal, partially overlap, or be completely disjoint, in which case ${\sum }_k{n}_k=N$. Each criterion can be classified as either a benefit (“the higher, the better”) or cost (“the lower, the better”) criterion.

Several multi-criteria methods have been proposed or extended in order to cope with different variants of the MCGDM problem. In the sequel, we focus on the extended version of TOPSIS that was proposed by Shih et al. [26], which was adopted in the development of CMCGDM. Afterwards, we overview some of the most well-known methods used to compute criteria weights in TOPSIS, formalizing these methods in the context of GDM.

2.1. Extended TOPSIS for GDM

TOPSIS [25] is a well-known multi-criteria method, which is based on the notion that the chosen alternative should have the closest distance to a positive ideal solution (PIS) and the farthest distance to a negative ideal solution (NIS). A crucial assumption of this compensatory method is that the decision criteria are either monotonically increasing or decreasing [28]. The variant that was conceived by Shih et al. [26] keeps this assumption, but extends the scope of the method in order to acknowledge the existence of several DMs.

The main steps of the extended TOPSIS for GDM are:

Step 1: 

compose the decision matrix ${\mathcal{D}}^k$ for the k-th DM—refer to Equation (1).

Step 2: 

compute the normalized decision matrix ${\mathcal{R}}^k=\left[r_{ij}^k\right],i=1,\dots ,M,j=1,\dots ,n_k$, for the k-th DM. For this purpose, the vector normalization scheme is usually employed [29]:

$$r_{ij}^k=\frac{x_{ij}^k}{\sqrt{{\sum }_{i=1}^M{\left(x_{ij}^k\right)}^2}},i=1,\dots ,M;j=1,\dots ,n_k.$$

(2)

Step 3: 

calculate the positive ideal solution $V^{k+}$ and the negative ideal solution $V^{k-}$ for the k-th DM, as follows:

$$\begin{array}{c}\hfill V^{k+}=\left\{v_1^{k+},\dots ,v_{n_k}^{k+}\right\}=\left\{\left(\underset{i}{\max }\left\{r_{ij}^k\right\}\right|j\in J_1),\left(\underset{i}{\min }\left\{r_{ij}^k\right\}\right|j\in J_2)\right\},\end{array}$$

(3)

$$\begin{array}{c}\hfill V^{k-}=\left\{v_1^{k-},\dots ,v_{n_k}^{v-}\right\}=\left\{\left(\underset{i}{\min }\left\{r_{ij}^k\right\}\right|j\in J_1),\left(\underset{i}{\max }\left\{r_{ij}^k\right\}\right|j\in J_2)\right\},\end{array}$$

(4)

where $J_1$ and $J_2$ are the sets of benefit and cost criteria, respectively.

Step 4: 

assign a weight vector $w^k=(w_1^k,w_2^k,\dots ,w_{n_k}^k)$ to the criteria set of the k-th DM, such that ${\sum }_{j=1}^{n_k}{w}_j^k=1$.

Step 5: 

compute the overall separation of a given alternative from the set of positive and negative ideal solutions. Here, two substeps should be performed. The first considers the PIS and NIS that are associated with each DM separately, while the second aggregates the measurements for the whole group.

Substep 5a: 

compute the distances $S_i^{k+}$ and $S_i^{k-}$ of the i-th alternative, $i=1,\dots ,M$, to the pair of PIS and NIS associated with the k-th DM, $k=1,\dots ,K$. Here, we have considered the Euclidean distance:

$$S_i^{k+}=\sqrt{{\displaystyle \sum _{j=1}^{n_k}}{w}_j^k{(r_{ij}^k-v_j^{k+})}^2},i=1,\dots ,M,$$

(5)

$$S_i^{k-}=\sqrt{{\displaystyle \sum _{j=1}^{n_k}}{w}_j^k{(r_{ij}^k-v_j^{k-})}^2},i=1,\dots ,M,$$

(6)

where $r_{ij}^k$, $v_j^{k+}$ and $v_j^{k-}$ are defined in Equations (2), (3) and (4), respectively.

Substep 5b: 

compute the overall separation measures $\overline{S_i^{+}}$ and $\overline{S_i^{-}}$ for each alternative. For this purpose, one should calculate the geometric mean over the K values of $S_i^{k+}$ (5) and $S_i^{k-}$ (6) to yield:

$$\overline{S_i^{+}}={\left({\displaystyle \prod _{k=1}^K}{S}_i^{k+}\right)}^{\frac{1}{K}},i=1,\dots ,M,$$

(7)

and

$$\overline{S_i^{-}}={\left({\displaystyle \prod _{k=1}^K}{S}_i^{k-}\right)}^{\frac{1}{K}},i=1,\dots ,M.$$

(8)

Step 6: 

compute $\overline{C_i^{*}}$, the overall relative closeness of the i-th alternative $A_i$, $i=1,\dots ,M$, to the K positive ideal solutions, which can be expressed as:

$$\overline{C_i^{*}}=\frac{\overline{S_i^{-}}}{S_i^{+}+S_i^{-}},i=1,\dots ,M,$$

(9)

where $0\le \overline{C_i^{*}}\le 1$, and $\overline{S_i^{+}}$ and $\overline{S_i^{-}}$ are defined, respectively, in Equations (7) and (8). Hence, the alternatives can be ranked from the best (higher values of closeness) to worst.

2.2. Objective Methods for Criteria Weighting

In the literature, different methods have been proposed in order to ascertain the relevance of the different decision criteria [30]. In this section, we review the following: Entropy [31], Statistical Variance, Standard Deviation [32], CRITIC [33], DEMATEL [34], and DEMATEL-based ANP [35]. However, other promising methods could be considered, such as CSW-DEA [36,37,38], nonlinear programming methods [39], and swing-weighting [40], just to name a few.

Weighting methods, in particular, attach cardinal or ordinal values directly to the criteria, so as to reflect their relative importance. Wang et al. [41] classify the weighting methods into three categories: subjective, objective, and combination methods. The first determine the weights based on the subjective preferences of the DMs, whereas the second make use of mathematical models without any consideration of the DM’s preferences. Combination methods are hybrids of the former, including, for instance, multiplication and additive synthesis. In the following, we review some of the most well-known methods of this class because the use of GCCA for computing the criteria weights in the context of CMCGDM can be regarded as an objective method.

2.2.1. Entropy Method

In short, entropy is a measure of uncertainty in information, as formulated in probability theory [31]. Entropy also means that some information cannot be recovered or is lost, like noise in a message. Accordingly, the higher the entropy E of a system, the lower its information content I. In fact, $E=1-I,E\in [0,1]$.

When applied to multi-criteria decision making, this concept can be used to quantitatively measure the capacity of a given criterion to discriminate the quality of different alternatives. High discrimination corresponds to low entropy and, thus, better information content. Conversely, low discrimination corresponds to high entropy and worse information. One particular advantage of using entropy as a criterion weight measure is that it weakens the bad effects from abnormal values (outliers), which makes the result of evaluation more accurate and reasonable.

When this procedure is applied to all criteria at once, it is possible to rank them according to their significance: the higher the information content I of a criterion, the more relevant it is comparatively. It is worthy noticing that these weights can be used for the assessment of alternatives, since they are built based on the dispersion (discrimination) of the alternatives’ performance values. Consequently, they are totally objective (unbiased), not depending upon the specific DM doing the analysis.

When considering the GDM context, in order to calculate the criteria weights $w_j^k$ via the entropy method, the decision matrix ${\mathcal{D}}^k$ (1) should be first normalized to yield the probabilities $p_{ij}^k$, as given by

$$p_{ij}^k=\frac{x_{ij}^k}{{\sum }_{i=1}^M{x}_{ij}^k},i=1,\dots ,M,j=1,\dots ,n_k,$$

(10)

and then the following equations should be calculated:

$$E_j^k=-\left({\displaystyle \sum _{i=1}^M}{p}_{ij}^k\log \left(p_{ij}^k\right)/\log \left(M\right)\right),j=1,\dots ,n_k,$$

(11)

$$w_j^k=\frac{1-E_j^k}{{\sum }_{j^{\prime }=1}^{n_k}(1-E_{j^{\prime }}^k)},j=1,\dots ,n_k,$$

(12)

where $\log (·)$ denotes the logarithm function, and $E_j^k$ and $w_j^k$ are, respectively, the entropy and weight values that are associated with the j-th criterion of the k-th DM. As discussed above, the higher the value of $E_j^k$, the lower is the value of $w_j^k$.

2.2.2. Statistical Variance Method

In statistics, variance is defined as the expectation of the squared deviation of a random variable from its mean. In other words, it measures how far a set of quantitative observations are spread out from their average value. Studying variance allows for one to quantify how much variability is in a probability distribution. If the outcomes of the distribution vary wildly, then it will have a large variance. Otherwise, if the variance is null (it is always non-negative), then the random variable takes a single constant value, which is exactly its expected value.

Based on the above considerations, statistical variance can be used in multi-criteria decision making in order to assess the capability of the judgment criteria to discriminate between the different alternatives available. The larger the variance of a given criterion (viewed as a random variable), the more dispersed are the performance values of the alternatives, which allows the DM to have better judgement on their good/bad characteristics. In this way, the higher the variance, the higher should be the relative weight of a criterion.

In this method, the statistical variance of information is first calculated for the j-th criterion of the k-th DM based on the original score values:

$$V_j^k=\frac{1}{M-1}{\displaystyle \sum _{i=1}^M}{(x_{ij}^k-\overline{x_j^k})}^2,$$

(13)

where $V_j^k$ is the statistical variance of the j-th criterion of the k-th DM and $\overline{x_j^k}$ is the average value of the original score values $x_{ij}^k$.

Subsequently, the weights are obtained via a simple normalization, so that they lie in $[0,1]$:

$$w_j^k=\frac{V_j^k}{{\sum }_{j^{\prime }=1}^{n_k}{V}_{j^{\prime }}^k},j=1,\dots ,n_k.$$

(14)

2.2.3. Standard Deviation Method

Because the standard deviation (SD) is defined as the positive square root of the statistical variance, it can also be regarded as a measure of dispersion around the mean of a data set. However, calculating the variance involves squaring deviations, so it does not have the same unit of measurement as the original observations. This negative feature is not shared by SD, whose values are in the same unit of the original scale. On the other hand, both variance and SD can be greatly affected if the mean gives a poor measure of central tendency, which can happen due to the presence of outliers. A single outlier can raise the standard deviation and, thus, distort the picture of spread.

In the context of multi-criteria decision making, the SD measure can be used to assign a small weight to a criterion if it shows similar values across the alternatives; otherwise, the criteria with larger deviations should be assigned the larger weights. If all available alternatives score almost equally with respect to a given criterion, then such a criterion will be regarded as unimportant by most experts and, thus, could be removed from the analysis.

Formally, the SD method determines the weights of the criteria in terms of their SDs, according to the following equations [32]:

$${\sigma }_j^k=\sqrt{\frac{{\sum }_{i=1}^M{(x_{ij}^k-\overline{x_j^k})}^2}{M-1}},j=1,\dots ,n_k,$$

(15)

$$w_j^k=\frac{{\sigma }_j^k}{{\sum }_{j^{\prime }=1}^{n_k}{\sigma }_{j^{\prime }}^k},j=1,\dots ,n_k,$$

(16)

where $\overline{x_j^k}$ and ${\sigma }_j^k$ are, respectively, the mean and SD values that are associated with the j-th criterion of the k-th DM.

Although the computation of variance and SD is similar, their differences are rather significant. By employing squared deviations, variance gives more weight to those criteria whose performance values are more spread around their average. Besides, the sum of square root values used in the denominator of Equation (16) yields a different normalization factor than the one adopted in Equation (14), which, in turn, is based on a sum of squared values. As a result, the rankings of alternatives that are produced by these measures need not be the same. In any case, both statistical measures are sensitive to a wide variation between the measurement scales of the different criteria. Of course, such a drawback is more aggravated in variance, due to the squared deviations. Entropy, in contrast, is robust to criteria scaling.

2.2.4. Criteria Importance through Inter-Criteria Correlation

The CRITIC (criteria importance through intercriteria correlation) method, as proposed by Diakoulaki et al. [33], uses correlation analysis to detect contrasts and dependencies between the criteria. Contrary to the other methods discussed so far, CRITIC was specifically conceived for the multi-criteria decision making domain, performing a detailed investigation of the decision matrix for extracting judicious information that is available in the evaluation criteria as well as their mutual/contrastive relationships. According to this method, objective weights are derived in order to quantify the intrinsic information of each evaluation criterion, while using both its standard deviation and its correlation (as calculated by Pearson correlation) with the other criteria. This way, both contrast and conflict intensity contained in the structure of the decision problem are captured by this method.

Consider the decision matrix of the k-th DM, as given in Equation (1). In order to calculate each weight $w_j^k$, the following symbols are used: $r_{ij}^k$ is the normalized performance measure of the i-th alternative with respect to the j-th criterion, $c_j^k$ denotes the quantity of contrastive information contained in the j-th criterion, ${\sigma }_j^k$ stands for the standard deviation of the j-th criterion, and ${\rho }_{j{j}^{\prime }}^k$ denotes the value of the Pearson correlation coefficient between the j-th and $j^{\prime }$-th criteria. Based on these notations, the steps of the CRITIC method are given as follows [32]:

Step 1: 

the score values associated with benefit/cost criteria are first normalized using Equations (17) and (18), respectively.

$$r_{ij}^k=\frac{x_{ij}^k-\min \left(x_{ij}^k\right)}{\max \left(x_{ij}^k\right)-\min \left(x_{ij}^k\right)},i=1,\dots ,M;j=1,\dots ,n_k,(\mathrm{benefit}\mathrm{criteria})$$

(17)

$$r_{ij}^k=\frac{\max \left(x_{ij}^k\right)-x_{ij}^k}{\max \left(x_{ij}^k\right)-\min \left(x_{ij}^k\right)},i=1,\dots ,M;j=1,\dots ,n_k,(\cos \mathrm{t}\mathrm{criteria})$$

(18)

Step 2: 

the correlation between each pair of criteria is calculated via Equation (19).

$${\rho }_{j{j}^{\prime }}^k=\frac{{\displaystyle \sum _{i=1}^M}(r_{ij}^k-\overline{r_j^k})(r_{i{j}^{\prime }}^k-\overline{r_{j^{\prime }}^k})}{\sqrt{{\displaystyle \sum _{i=1}^M}{(r_{ij}-\overline{r_j^k})}^2}·\sqrt{{\displaystyle \sum _{i=1}^M}{(r_{i{j}^{\prime }}^k-\overline{r_{j^{\prime }}^k})}^2}},j,j^{\prime }=1,\dots ,n_k$$

(19)

Step 3: 

finally, Equations (20) and (21) are employed for producing the weights.

$$w_j^k=\frac{c_j^k}{{\displaystyle \sum _{j^{\prime }=1}^{n_k}}{c}_{j^{\prime }}},j=1,\dots ,n_k,$$

(20)

$$c_j^k={\sigma }_j^k{\displaystyle \sum _{j=1}^{n_k}}(1-{\rho }_{jk}^k),j=1,\dots ,n_k.$$

(21)

2.3. DEMATEL

Decision Making Trial and Evaluation Laboratory (DEMATEL) was elaborated as a procedure for solving problems of identifying cause-and-effect relationships [34]. With time, this method has been well adapted for use in multi-criteria decision making. This way, some authors discuss the use of DEMATEL in order to determine the significance of the criteria [42,43,44]. This section describes the approach that was proposed by Kobryń [42], whose formulation was adapted for several DMs.

First, the direct-influence matrix is created for each DM, which is a square matrix whose size is equal to the number of alternatives/criteria. For this purpose, we have adopted a four-degree scale to express the influence of the i-th criterion on the j-th criterion, where: 0—no influence, 1—medium influence, …, 4—maximum influence [45]. Besides, in the direct-influence matrix ${\mathbf{B}}^k$ of the k-th DM, $k=1,\dots ,K$, the elements on the main diagonal are null, while non-zero elements $b_{ij}^k(i\ne j)$ reflect the impact of the i-th criterion on the j-th criterion:

$${\mathbf{B}}^k=\left(\begin{array}{cccc}0& b_{12}^k& \dots & b_{1n_k}^k\\ b_{21}^k& 0& \dots & b_{2n_k}^k\\ \dots & \dots & \dots & \dots \\ b_{n_{k}1}^k& b_{n_{k}2}^k& \dots & 0\end{array}\right).$$

(22)

Matrix (22) is then normalized, as follows:

$${\widehat{\mathbf{B}}}^k={\mathbf{B}}^k\frac{1}{\underset{i}{\max }\left({\displaystyle \sum _{j=1}^{n_k}}{b}_{ij}^k\right)}.$$

(23)

From (23), we calculate the total-influence matrix (${\mathbf{T}}^k$), as described by

$${\mathbf{T}}^k={\widehat{\mathbf{B}}}^k{(\mathbf{I}-{\widehat{\mathbf{B}}}^k)}^{-1},$$

(24)

where $\mathbf{I}$ is the $n_k\times n_k$ identity matrix.

Subsequently, two vectors of indicators are determined based on ${\mathbf{T}}^k$ to express a relation between the criteria, covering both direct and indirect influences. They are defined as importance indicator vector (${\mathbf{t}}^{k+}$) and relation indicator vector (${\mathbf{t}}^{k-}$), whose components are given as follows:

$$t_i^{k+}={\displaystyle \sum _{j=1}^{n_k}{t}_{ij}^k+\sum _{j=1}^{n_k}{t}_{ji}^k},$$

(25)

$$t_i^{k-}={\displaystyle \sum _{j=1}^{n_k}{t}_{ij}^k-\sum _{j=1}^{n_k}{t}_{ji}^k}.$$

(26)

From Equations (25) and (26), the weights are determined as proportional to the average value ($t_i^{k_{av}}$) of the appropriate pair of indicators $t_i^{k+}$ and $t_i^{k-}$, given as follows:

$$t_i^{k_{av}}=\frac{1}{2}(t_i^{k+}+t_i^{k-}).$$

(27)

Next, the equation below can be used to calculate each normalized weight:

$$w_i^k=\frac{t_i^{k_{av}}}{{\displaystyle \sum _{j=1}^{n_k}}{t}_j^{k_{av}}}.$$

(28)

It is necessary to correct the weight values calculated from Equation (28), as no criterion can be assigned to zero weight. The key issue is to determine the correction value $\delta$, and the final decision should belong to the decision-maker [42]. The value $\delta$ should be as small as possible and as such Kobryń [42] suggests setting $\delta \le \underset{i}{\min }{w}_i^k$, if $w_i^k>0$. The values $w_i^{k_{cor}}$ and $w_i^{k_{norm}}$ are given as follows:

$$w_i^{k_{cor}}=w_i^k+\delta ,$$

(29)

$$w_i^{k_{norm}}=\frac{w_i^{k_{cor}}}{{\displaystyle \sum _{j=1}^{n_k}}{w}_j^{k_{cor}}}.$$

(30)

2.4. DEMATEL-Based ANP (DANP)

The DANP method was proposed by Yang et al. [35]. It consists in forming a matrix ${\mathbf{S}}^k$, which is similar to the Analytic of Network Process (ANP) [46], on the basis of the modified total-influence matrix ${\mathbf{T}}^k$ (24), representing the outcome of the application of DEMATEL [47]. The components of ${\mathbf{S}}^k$ should be given as:

$$s_{ij}^k=\frac{t_{ji}^k}{{\displaystyle \sum _{w=1}^{n_k}}{t}_{jw}^k},\forall i,j=1,2,\dots ,n_k,$$

(31)

where $n_k$ is the number of interrelated criteria adopted by the k-th DM, $t_{ji}^k$ denotes the element of the matrix ${\mathbf{T}}^k$ depicting the total influence of the j-th criterion on the i-th criterion, and $s_{ij}^k$ represents a component of the matrix ${\mathbf{S}}^k$.

Next, the matrix ${\mathbf{S}}_{\mathtt{lim}}^k$ is determined based on matrix ${\mathbf{S}}^k$, while using the procedure characteristic for ANP, as follows:

$${\mathbf{S}}_{\mathtt{lim}}^k=\underset{w\to \infty }{\lim }{\mathbf{S}}^w.$$

(32)

The matrix ${\mathbf{S}}_{\mathtt{lim}}^k$ consists of $n_k$ identical columns. The elements of the individual columns depict the normalized weights of the criteria.

3. Generalized Canonical Correlation Analysis

In multivariate statistical analysis, data usually consist of multiple variables measured on a set of observations [48]. In this context, CCA comprises a family of statistical techniques that model the linear relationships between two (or more) sets of variables [22,49]. More specifically, in CCA, the variables of an observation can be partitioned into two or more sets, with each one regarded as a view of the data [22].

Like principal component analysis (PCA) and linear discriminant analysis (LDA) [48,49], CCA can reduce the dimensionality of the original variables, since only a few factor pairs are normally needed to represent the relevant information. Besides, CCA is invariant to any affine transformation of the input variables [50]. Another appealing property is that CCA does not assume a priori the direction of the relationship between the variable sets. This is in contrast to regression methods, which have to designate an independent and a dependent data set [51]. Finally, CCA characterizes relationships between data sets in an interpretable way, a property that is not displayed by other common correlation methods, which simply quantify the similarity between data sets [51].

Formally, given two zero-mean data sets $\mathbf{X}=({\mathbf{x}}_{\mathbf{1}},{\mathbf{x}}_{\mathbf{2}},\dots ,{\mathbf{x}}_{\mathbf{n}})\in {\mathbb{R}}^{d\times n}$ and $\mathbf{Y}=({\mathbf{y}}_{\mathbf{1}},{\mathbf{y}}_{\mathbf{2}},\dots ,{\mathbf{y}}_{\mathbf{m}})\in {\mathbb{R}}^{d\times m}$, with ${\mathbf{x}}_i$ and ${\mathbf{y}}_i$ denoting d-dimensional column vectors, standard CCA finds a canonical coordinate space that maximizes correlations between the projections of the two variable sets onto that space [51]. Associated with the j-th dimension of this new space, there is a pair of projection weight vectors, ${\mathbf{a}}_j=(a_{1j},a_{2j},\dots ,a_{nj})$ and ${\mathbf{b}}_j=(b_{1j},b_{2j},\dots ,b_{mj})$, named canonical weights. The resulting projections of variable sets $\mathbf{X}$ and $\mathbf{Y}$ onto the j-th dimension of the canonical space comprise a pair of d-dimensional vectors, ${\mathbf{u}}_j=\langle {\mathbf{a}}_j,\mathbf{X}\rangle$ and ${\mathbf{v}}_j=\langle {\mathbf{b}}_j,\mathbf{Y}\rangle$, which are called canonical variates. Here, $\langle ·,·\rangle$ denotes the inner (projection) product operator. CCA maximizes the linear correlations between each pair of canonical variates, as given by

$${\rho }_j=\max \left\{\frac{\langle {\mathbf{u}}_j,{\mathbf{v}}_j\rangle }{\parallel {\mathbf{u}}_j\parallel ·\parallel {\mathbf{v}}_j\parallel }\right\},$$

(33)

where $\parallel {\mathbf{u}}_j\parallel$ denotes the norm of vector ${\mathbf{u}}_j$.

More precisely, $r=\min (n,m)$ pairs of projection vectors are generated, so that the correlation ${\rho }_1$ between ${\mathbf{u}}_1$ and ${\mathbf{v}}_1$ is maximum, the correlation ${\rho }_2$ between ${\mathbf{u}}_2$ and ${\mathbf{v}}_2$ is maximum, subject to the constraint that the canonical variates ${\mathbf{u}}_2$ and ${\mathbf{v}}_2$ are orthogonal to ${\mathbf{u}}_1$ and ${\mathbf{v}}_1$, respectively, and so on and so forth, up to the point that the correlation ${\rho }_r$ between ${\mathbf{u}}_r$ and ${\mathbf{v}}_r$ is maximum, provided that they correlate with neither ${\mathbf{u}}_1,{\mathbf{u}}_2,\dots ,{\mathbf{u}}_{r-1}$ nor ${\mathbf{v}}_1,{\mathbf{v}}_2,\dots ,{\mathbf{v}}_{r-1}$, respectively. The symmetry of the correlation matrices guarantees orthogonality.

To accomplish this, CCA solves the following optimization problem [51]:

$$\rho =\max \left\{\frac{{\mathbf{a}}^T{\mathbf{C}}_{XY}\mathbf{b}}{\sqrt{\parallel {\mathbf{a}}^T{\mathbf{C}}_{XX}\mathbf{a}\parallel ·\parallel {\mathbf{b}}^T{\mathbf{C}}_{YY}\mathbf{b}\parallel }}\right\},$$

(34)

where $\rho$ represents the maximum value of the canonical correlation vector, ${\mathbf{C}}_{XY}$ denotes the sample covariance of the two variable sets, $\mathbf{X}$ and $\mathbf{Y}$, and ${\mathbf{C}}_{XX}$ and ${\mathbf{C}}_{YY}$ are their autocovariances.

The objective function (34) has infinite solutions if no restriction is imposed on weights $\mathbf{a}$ and $\mathbf{b}$. However, the size of the canonical weights can be constrained, such that ${\mathbf{a}}^T{\mathbf{C}}_{XX}\mathbf{a}=1$ and ${\mathbf{b}}^T{\mathbf{C}}_{YY}\mathbf{b}=1$ [49]. This leads to the following Lagrangian [22,51]:

$$L(\lambda ,\mathbf{a},\mathbf{b})={\mathbf{a}}^T{\mathbf{C}}_{XY}\mathbf{b}-\frac{{\lambda }_X}{2}({\mathbf{a}}^T{\mathbf{C}}_{XX}\mathbf{a}-1)-\frac{{\lambda }_Y}{2}({\mathbf{b}}^T{\mathbf{C}}_{YY}\mathbf{b}-1),$$

(35)

which, in turn, can be formulated as the following generalized eigenvalue problem:

$$\begin{array}{c}\hfill \left(\begin{array}{cc}0& {\mathbf{C}}_{XY}\\ {\mathbf{C}}_{YX}& 0\end{array}\right)\left(\begin{array}{c}a\\ b\end{array}\right)={\rho }^2\left(\begin{array}{cc}{\mathbf{C}}_{XX}& 0\\ 0& {\mathbf{C}}_{YY}\end{array}\right).\end{array}$$

(36)

Several variants of CCA have been proposed along the years, among which those that extend the correlation analysis to encompass more than two sets of variables [22]. These extensions, which are typically referred to as GCCA, aim at generating a series of components (variates) that maximize the association between the multiple variable sets. For instance, when considering the availability of three views on the data, the generalized eigenvalue problem that is defined in (36) can be simply extended, as follows [24,51]:

$$\begin{array}{c}\hfill \left(\begin{array}{ccc}0& {\mathbf{C}}_{XY}& {\mathbf{C}}_{XZ}\\ {\mathbf{C}}_{YX}& 0& {\mathbf{C}}_{YZ}\\ {\mathbf{C}}_{ZX}& {\mathbf{C}}_{ZY}& 0\end{array}\right)\left(\begin{array}{c}\mathbf{a}\\ \mathbf{b}\\ \mathbf{c}\end{array}\right)={\rho }^2\left(\begin{array}{ccc}{\mathbf{C}}_{XX}& 0& 0\\ 0& {\mathbf{C}}_{YY}& 0\\ 0& 0& {\mathbf{C}}_{ZZ}\end{array}\right).\end{array}$$

(37)

The fact that the sets of variables may differ significantly is an interesting property of this extended formulation. Hence, the number of variables in each set does not need to be the same. We argue that this feature is interesting for the MCGDM context, particularly in those circumstances when the DMs make use of different judgment criteria.

4. A Canonical Multi-Criteria Group Decision Making Approach

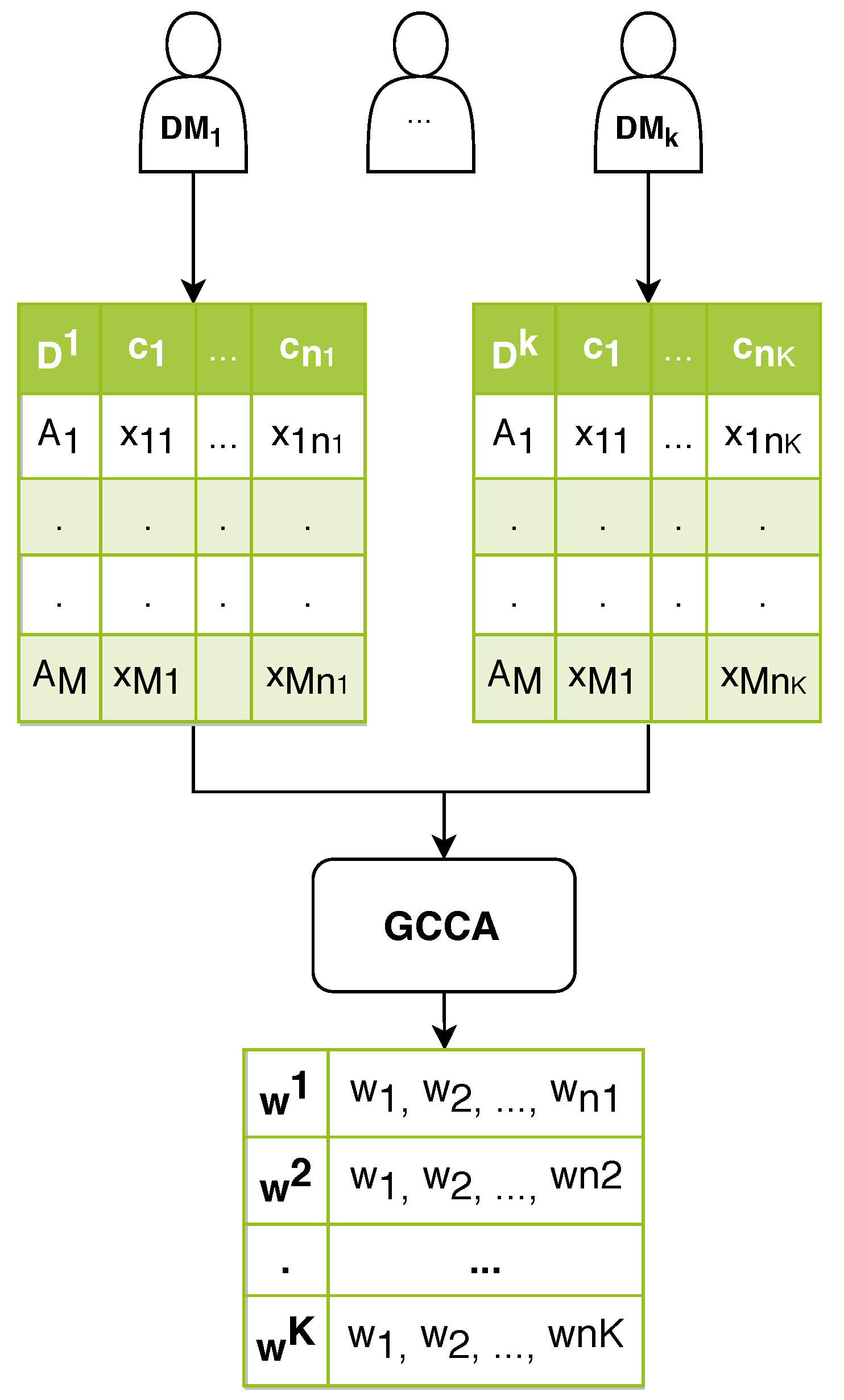
By drawing a parallel between GCCA and MCGDM, one can note that methods pertaining to both areas operate on numerical values arranged in two-dimensional (data/decision) matrices. While, in GCCA, there is a set of data instances (rows) represented by two or more variable sets (columns), in MCGDM one has a set of solution alternatives (rows), each assessed in accordance with two or more sets of criteria (columns). By establishing this correspondence, it is possible to make use of GCCA’s functionalities to automatically compute the values of the criteria weights used in MCGDM.

Assume that K decision matrices are available, with ${\mathcal{D}}^k$ pertaining to the k-th DM, $k=1,\dots ,K$. GCCA is directly applied to all K matrices at once, yielding the criteria weights ${\mathbf{w}}^k$ that are related to each matrix (refer to Figure 1). These weights are the canonical weights that are associated with the first dimension of the canonical space. To bring about the consensus decision between the DMs, CMCGDM employs the same steps of the extended TOPSIS variant proposed by Shih et al. [26] (see Section 2.1), with some minor modifications. More specifically, while the computation of $V^{k+}$ and $V^{k-}$ (Equations (3) and (4)) in the third step now takes into account the positive/negative signs of the canonical weights as calculated by GCCA (i.e., before they are normalized), in the fifth step the computation of $S_i^{k+}$ and $S_i^{k-}$ (Equations (5) and (6)) makes use of the normalized weights.

We claim that the above methodology is useful for capturing the intrinsic relationships between the DMs’ beliefs regarding the relative performance of the different alternatives. Usually, the weights of the criteria adopted by all DMs are separately calculated for each DM (sometimes via an unrelated methodology, such as in [52]) and, then, the group consensus is achieved by somehow reconciling the different weights adopted by the different DMs. In the case of CMCGDM, because the canonical weights maximize the correlation between the different decision matrices simultaneously, it is expected that the consensus between the experts can be captured more naturally and effectively, bringing about a more reliable ranking of the available alternatives. In this case, the canonical correlation index can be interpreted as a sort of consensus indicator between the DMs’ opinions.

When considering the more complicated setting where different groups of criteria are used by different DMs, our method can work well, even when the sets of criteria are completely disjoint (that is, with no overlap). Moreover, instead of generating separate rankings of alternatives for all criteria subsets, which are then aggregated to compose the final ranking by solving a specific optimization problem, such as in the approach that was proposed by Fan et al. [21], our methodology seems to be more straightforward, not demanding intermediary rankings for different criteria sets.

Another good property of CMCGDM is that it allows for one to interpret each criterion according to the sign of its associated canonical weight, taking the role played by the other criteria as reference. While positively weighted criteria can be considered as benefit ones, those with negative weights can be regarded as cost criteria.

In order to further clarify this important property, consider a fictitious MCGDM problem that involves four DMs and eight alternatives, each of which is evaluated via five judgment criteria, shared by all DMs.

Table 1. Fictitious multi-criteria group decision making (MCGDM) problem—non-normalized generalized version of canonical correlation analysis (GCCA) weights.

Criteria	DM1	DM2	DM3	DM4
C1	−0.0116	−0.0081	−0.0105	0.0071
C2	−0.0122	−0.0063	0.0037	0.0033
C3	−0.0049	−0.0123	−0.0053	−0.0184
C4	−0.0123	−0.0132	0.0015	−0.0167
C5	0.0148	0.0157	−0.0229	0.0004

and

Table 2. Fictitious MCGDM problem—normalized GCCA weights.

Criteria	DM1	DM2	DM3	DM4
C1	0.0218	0.1227	0.1528	0.3769
C2	0.0025	0.1652	0.3284	0.3201
C3	0.2107	0.0206	0.2173	0.0000
C4	0.0000	0.0000	0.3014	0.0250
C5	0.7650	0.6915	0.0000	0.2780

show the criteria weights as elicited by GCCA, either before or after normalization is applied. As one can notice, for the first and second DMs, all criteria, except the last one, should be interpreted as of the cost type, since their weights are negative. For the fourth DM, in contrast, the number of benefit criteria is larger. Therefore, the interpretation is contextualized for each DM. Although the non-normalized weights are small in magnitude, they were induced by GCCA so as to maximize the correlation between the DMs’ decision matrices (not shown in this example). After normalization is applied, the magnitude of the criteria weights is rescaled, so that the more relevant ones are more noticeable (they are highlighted in Table 2).

Another good property of CMCGDM is that GCCA is invariant to any affine transformation of the input variables (criteria values), as mentioned before. Besides, like entropy, GCCA is robust against the problem of criteria scaling. By another perspective, the use of GCCA renders our approach flexible enough to allow the dynamic (re)calibration of the criteria weights once the sets of alternatives or criteria change over time. GCCA could be used without modification, even when the number of DMs is allowed to change. However, this important property will not be further explored in this paper and it should be investigated in future work.

We argue that these fine properties are not shared by other popular criteria weighting methods, such as those that are reviewed in Section 2.2. In fact, these methods were not conceived to elicit the weights of different groups of criteria based on the intrinsic relations between the DMs’ preferences (decision matrices). Moreover, as we will show in Section 7, the adopted MCGDM method becomes more resilient to the problem of ranking irregularity [27] when using GCCA in place of the aforementioned criteria weighting methods.

5. Example on Human Resource Selection

To demonstrate the utility of the proposed CMCGDM approach (our implementation uses the Python package Pyrcca [51] for GCCA, which is hosted in http://github.com/gallantlab/pyrcca), we first present in this section the same example considered by Shih et al. [26], which is about the recruitment of an on-line manager by a firm. Subsequently, we compare the performance displayed by the CMCGDM approach with that delivered by the extended TOPSIS version, as originally proposed by Shih et al. [26] (that is, without using GCCA to generate the criteria weights). This is done by considering how resilient each method is to the ranking irregularity problem.

According to the example, the human resource department of the firm coordinates some knowledge tests (namely, language, professional, and safety rule tests), skill tests (namely, professional and computer tests), and interviews (namely, panel and one-on-one interviews) with the candidates. In all, 17 qualified candidates are on the list, whereas four recruiters (DMs) are responsible for conducting the selection. The decision matrix that was used for the decision process is split in

Table 3. Decision matrix (objective criteria) for the first example, adapted from ([26] [Table 6a]).

No.	Candidates	Objective Criteria
		Knowledge Tests			Skill Tests
		Language Test	Professional Test	Safety Rule Test	Professional Skills	Computer Skills
1	James B. Wang	80	70	87	77	76
2	Carol L. Lee	85	65	76	80	75
3	Kenney C. Wu	78	90	72	80	75
4	Robert M. Liang	75	84	69	85	65
5	Sophia M. Cheng	84	67	60	75	85
6	Lily M. Pai	85	78	82	81	79
7	Abon C. Hsieh	77	83	74	70	71
8	Frank K. Yang	78	82	72	80	78
9	Ted C. Yang	85	90	80	88	90
10	Sue B. Ho	89	75	79	67	77
11	Vincent C. Chen	65	55	68	62	70
12	Rosemary I. Lin	70	64	65	65	60
13	Ruby J. Huang	95	80	70	75	70
14	George K. Wu	70	80	79	80	85
15	Philip C. Tsai	60	78	87	70	66
16	Michael S. Liao	92	85	88	90	85
17	Michelle C. Lin	86	87	80	70	72

and

Table 4. Decision matrix (subjective criteria) for the first example, adapted from ([26] [Table 6b]).

No.	Subjective Criteria
	DM #1		DM #2		DM #3		DM #4
	Panel Interview	1-on-1 Interview	Panel Interview	1-on-1 Interview	Panel Interview	1-on-1 Interview	Panel Interview	1-on-1 Interview
1	80	75	85	80	75	70	90	85
2	65	75	60	70	70	77	60	70
3	90	85	80	85	80	90	90	95
4	65	70	55	60	68	72	62	72
5	75	80	75	80	50	55	70	75
6	80	80	75	85	77	82	75	75
7	65	70	70	60	65	72	67	75
8	70	60	75	65	75	67	82	85
9	80	85	95	85	90	85	90	92
10	70	75	75	80	68	78	65	70
11	50	60	62	65	60	65	65	70
12	60	65	65	75	50	60	45	50
13	75	75	80	80	65	75	70	75
14	80	70	75	72	80	70	75	75
15	70	65	75	70	65	70	60	65
16	90	95	92	90	85	80	88	90
17	80	85	70	75	75	80	70	75

, according to the type of judgment criteria (objective vs subjective). Notice that the $K=4$ criteria sets are the same for all DMs, and all criteria are regarded as of the benefit type. Moreover, all of the DMs share the same score values for the objective criteria, only changing their assessment on the two subjective criteria. In addition, the normalized criteria weights elicited by the DMs themselves (as originally used in [26]) are shown in

Table 5. Original criteria weights for the first example, adapted from ([26] [Table 6b]).

No.	Criteria	The Weights of the Group
		DM #1	DM #2	DM #3	DM #4
	Knowledge tests
1	Language test	0.066	0.042	0.060	0.047
2	Professional test	0.196	0.112	0.134	0.109
3	Safety rule test	0.066	0.082	0.051	0.037
	Skill tests
4	Professional skills	0.130	0.176	0.167	0.133
5	Computer skills	0.130	0.118	0.100	0.081
	Interviews
6	Panel interview	0.216	0.215	0.203	0.267
7	1-on-1 interview	0.196	0.215	0.285	0.326
	Sum	1	1	1	1

, whereas the canonical weights that are generated by GCCA (normalized or not) are displayed in

Table 6. Criteria weights (non-normalized values in parentheses) for the first example, as elicited by GCCA.

No.	Criteria	The Weights of the Group
		DM #1	DM #2	DM #3	DM #4
	Knowledge tests
1	Language test	0.2665 (0.0003)	0.1661 (−0.0001)	0.1668 (0.0014)	0.1251 (0.0005)
2	Professional test	0.0000 (−0.0119)	0.0383 (−0.0092)	0.0156 (−0.0107)	0.0104 (−0.0109)
3	Safety rule test	0.2368 (−0.0011)	0.0626 (−0.0075)	0.1927 (0.0035)	0.1827 (0.0062)
	Skill tests
4	Professional skills	0.2057 (−0.0025)	0.1885 (0.0015)	0.0875 (−0.0049)	0.1470 (0.0027)
5	Computer skills	0.0503 (−0.0096)	0.2984 (0.0093)	0.0798 (−0.0056)	0.2033 (0.0083)
	Interviews
6	Panel interview	0.1266 (−0.0061)	0.2101 (0.0030)	0.2985 (0.0119)	0.2157 (0.0095)
7	1-on-1 interview	0.1142 (−0.0067)	0.0360 (−0.0094)	0.1590 (0.0008)	0.1158 (−0.0004)
	Sum	1	1	1	1

.

According to Wang and Triantaphyllou [27], an intriguing problem that may happen with different decision-making methods is that of generating disparate outcomes (rankings) when submitted to the same decision problem instance. Consequently, it is natural to raise the question of how to properly assess the performance of such methods. Because it is practically impossible to know which is the best alternative solution for a given decision problem, in [53] some tests capturing different ranking irregularities are discussed as a way for assessing the performance of multi-criteria methods in general:

Test #1: 

the best alternative selected should not alter when a non-optimal alternative is added or removed from the problem (assuming that the relative importance of each criterion remains unchanged) [54].

Test #2: 

the best alternative selected should not change if a non-optimal alternative is replaced by a worse one [27,55].

Test #3: 

the final ranking of the alternatives should not violate the transitivity property if a non-optimal alternative is added to (or removed from) the problem [27,55].

Table 7. Assessment of the extended TOPSIS [26] on the ranking irregularity tests—first example.

Extended TOPSIS		Test #1–Addition		Test #1–Removal		Test #2
Rank	Score	Rank	Score	Rank	Score	Rank	Score
A16	0.8960	A16	0.8956	A16	0.8963	A16	0.8960
A9	0.8797	A9	0.8797	A9	0.8797	A9	0.8797
A3	0.7860	A3	0.7862	A3	0.7859	A3	0.7860
A6	0.6611	A6	0.6611	A6	0.6611	A6	0.6611
A1	0.6272	A1	0.6259	A14	0.5925	A14	0.5924
A14	0.5924	A1	0.6259	A17	0.5915	A17	0.5919
A17	0.5920	A17	0.5925	A8	0.5700	A8	0.5701
A8	0.5701	A14	0.5924	A13	0.5565	A13	0.5568
A13	0.5568	A8	0.5701	A10	0.5079	A10	0.5080
A10	0.5080	A13	0.5571	A5	0.4660	A5	0.4660
A5	0.4660	A10	0.5082	A7	0.4516	A4	0.4524
A4	0.4527	A5	0.4659	A4	0.4514	A7	0.4522
A7	0.4523	A4	0.4538	A2	0.4401	A2	0.4404
A2	0.4404	A7	0.4530	A15	0.4092	A1	0.4224
A15	0.4091	A2	0.4406	A11	0.2101	A15	0.4091
A11	0.2097	A15	0.4091	A12	0.1673	A11	0.2097
A12	0.1678	A11	0.2093	----	----	A12	0.1677
----	----	A12	0.1682	----	----	----	----

brings the ranking of the alternatives delivered by the extended TOPSIS, as reported in [26], as well as the results of the application of the three ranking irregularity tests that are described above.

Table 8. Assessment of the CMCGDM approach on the ranking irregularity tests–first example.

CMCGDM		Test #1–Addition		Test #1–Removal		Test #2
Rank	Score	Rank	Score	Rank	Score	Rank	Score
A16	0.9016	A16	0.9013	A16	0.9018	A16	0.9016
A9	0.8797	A9	0.8799	A9	0.8794	A9	0.8796
A3	0.7230	A3	0.7231	A3	0.7228	A3	0.7230
A6	0.6720	A6	0.6719	A6	0.6722	A6	0.6721
A14	0.6608	A14	0.6608	A14	0.6608	A14	0.6608
A1	0.5964	A1	0.5954	A8	0.5854	A8	0.5855
A8	0.5855	A1	0.5954	A5	0.5491	A5	0.5495
A5	0.5495	A8	0.5855	A2	0.5170	A2	0.5173
A2	0.5173	A5	0.5499	A17	0.4813	A17	0.4811
A17	0.4811	A2	0.5176	A13	0.4778	A13	0.4779
A13	0.4779	A17	0.4810	A4	0.4699	A4	0.4705
A4	0.4706	A13	0.4781	A10	0.4634	A10	0.4632
A10	0.4632	A4	0.4713	A7	0.3956	A7	0.3957
A7	0.3957	A10	0.4630	A15	0.3627	A1	0.3627
A15	0.3620	A7	0.3958	A11	0.2259	A15	0.3621
A11	0.2254	A15	0.3615	A12	0.1408	A11	0.2255
A12	0.1409	A11	0.2250	----	----	A12	0.1409
----	----	A12	0.1410	----	----	----	----

follows the same layout, but it relates to the extended TOPSIS with criteria weights estimated by GCCA (i.e., CMCGDM approach). In both tables, the second and third columns show the new rankings of the alternatives (and their associated scores) that result when an irrelevant alternative is added or removed, respectively, to the alternative set, whereas the last column exhibits the ranking that results from the replacement of a non-optimal alternative by a worse one. Those cases where the transitivity property is violated (Test #3) are indicated by shadowed alternatives.

The extended TOPSIS, using the weights given in Table 5, could pass well Tests #1 and #2, but failed to respect the transitivity requirement, since there is a ranking position change between alternatives A14 and A17 (A4 and A7) when an irrelevant alternative (namely, A1) is duplicated (removed) during the application of Test #1, as one can readily observe from Table 7. On the other hand, the proposed CMCGDM approach could get through all of the three ranking irregularity tests without generating any ranking inconsistencies.

6. Example on Machine Acquisition

In this section, we conduct the same previous analysis on a second example, taken from [21]. In this example, there are different criteria sets that are associated with different DMs. The decision problem relates to the acquisition of a novel machine by a given manufacturing company. There are seven products (alternatives) under analysis by the manufacture department (DM #1) and the financial department (DM #2). The last alternative was introduced by us in order to turn the decision problem a bit more complex. The criteria concerned by DM #1 include $C_1$: positioning accuracy (mm), $C_2$: maximum load (kg), $C_3$: mean time to failure (h), $C_4$: degree of standardization of parts, $C_5$: reliable service life (h), and $C_6$: delivery time (month). The criteria concerned by DM #2 include $C_7$: price ($) and $C_8$: down payment ratio (percent), as well as $C_5$ and $C_6$.

The second, sixth, seventh, and eighth are cost criteria, while the others are benefit criteria. The weights of the criteria that are concerned by DM #1 are $(0.3,0.2,0.1,0.05,0.2,0.15,0,0)$, whereas those of the criteria concerned by DM #2 are $(0,0,0,0,0.25,0.15,0.45,0.15)$. The example, as proposed by Fan et al. [21], assumes that such weights were somehow calculated by the DMs themselves.

Table 9. Decision matrix associated with DM #1 for the second example, adapted from ([21] [Table 2]).

	C1	C2	C3	C4	C5	C6
A1	0.05	500	850	8.6	30,500	1.5
A2	0.01	550	925	8.2	26,500	2.0
A3	0.008	600	960	9.0	28,500	3.0
A4	0.008	450	720	9.2	25,800	2.0
A5	0.015	400	650	8.0	24,000	1.5
A6	0.012	480	710	8.4	23,500	1.0
A7	0.017	505	691	8.0	30,100	1.3

and

Table 10. Decision matrix associated with DM #2 for the second example, adapted from ([21] [Table 2]).

	C5	C6	C7	C8
A1	30,500	1.5	530,000	50
A2	26,500	2.0	420,000	40
A3	28,500	3.0	450,000	35
A4	25,800	2.0	480,000	40
A5	24,000	1.5	380,000	30
A6	23,500	1.0	40,000	60
A7	30,100	1.3	392,000	57

bring the decision matrices that are associated with each DM, respectively, whereas

Table 11. Assessment of the extended TOPSIS [26] on the ranking irregularity tests—second example.

Extended TOPSIS		Test #1–Addition		Test #1–Removal		Test #2
Rank	Score	Rank	Score	Rank	Score	Rank	Score
A1	1.0000	A1	1.0000	A1	1.0000	A1	1.0000
A3	0.5892	A3	0.5816	A3	0.5984	A3	0.5908
A4	0.5265	A4	0.5189	A4	0.5357	A4	0.5281
A2	0.4741	A7	0.4682	A7	0.4704	A7	0.4694
A7	0.4691	A2	0.4667	A5	0.4011	A5	0.4004
A5	0.4002	A2	0.4667	A6	0.0000	A2	0.3748
A6	0.0000	A5	0.3996	----	----	A6	0.0000
----	----	A6	0.0000	----	----	----	----

and

Table 12. Assessment of the CMCGDM approach on the ranking irregularity tests–second example.

CMCGDM		Test #1–Addition		Test #1–Removal		Test #2
Rank	Score	Rank	Score	Rank	Score	Rank	Score
A3	0.8455	A3	0.8425	A3	0.8521	A3	0.8478
A4	0.5798	A4	0.5784	A4	0.5800	A4	0.5798
A2	0.5582	A2	0.5581	A1	0.4529	A2	0.4631
A1	0.4578	A2	0.5581	A5	0.3574	A1	0.4577
A5	0.3600	A1	0.4627	A7	0.2919	A5	0.3581
A7	0.2965	A5	0.3581	A6	0.0000	A7	0.2936
A6	0.0000	A7	0.2942	----	----	A6	0.0000
----	----	A6	0.0000	----	----	----	----

bring the results of the application of the three ranking irregularity tests described in the previous section. The layouts of these tables are the same of Table 7 and Table 8. As before, the extended TOPSIS could not keep up well with the transitivity requisite when a mid-ranked alternative (namely, A2) is duplicated. CMCGDM, in turn, could produce rankings showing no inconsistencies according to all ranking irregularity tests.

7. Simulated Cases

In the previous sections, the criteria weights that were used in the comparative analysis were set up either by the DMs themselves or via GCCA. In this section, we enlarge the assessment by also considering the objective criteria weighting methods that are discussed in Section 2.2. The idea is to study, via several simulated cases, how the choice of the weighting method affects the behavior of the extended TOPSIS that was proposed by Shih et al. [26] with respect to the ranking irregularity problem.

The simulations were performed by following the guidelines that were provided in [27,53,56]. According to these authors, the simulations comprise a reasonable expedient to conduct controllable and reproducible experiments in order to have a better understanding of the pros and cons of different multi-criteria decision making methods. By this means, these methods can be deeply assessed by considering different samples and amounts of parameters, numbers of criteria and alternatives, as well as distinct ways to assign weights to the criteria and scores to the alternatives. In our investigation, the main parameters considered along the simulations were the following:

• number of DMs: $\{5,7,10\}$;
• number of criteria: 7;
• number of alternatives: $\{17,19,21,23,25,27,30\}$;
• scores of the alternatives: randomly generated by a uniform distribution in the range [0–100];
• criteria weighting approach: GCCA and the methods described in Section 2.2;
• number of trials: 100 for each parameter configuration, thereby yielding 6300 different decision problem instances; and,
• performance criteria: the three irregularity tests described in Section 5.

Table 13. Assessment of the different criteria weighting methods on the ranking irregularity tests—simulated cases.

		Test #3	Test #3	Test #3
Dist.	Method	Addition	Removal	Replacement	Test #1	Test #2	Total Test #3
uniform	GCCA	11,737	13,226	2727	231	11	27,690
	Entropy	12,504	12,753	2640	246	31	27,897
	Std	12,504	12,753	2640	246	31	27,897
	DEMATEL	12,741	12,837	2626	252	17	28,204
	DEMATEL-ANP	12,145	13,592	2766	283	25	28,503
	CRITIC	12,411	13,276	2869	218	16	28,556
	VarProc	12,366	13,313	3059	183	23	28,738

Note: VarProc refers to the statistical variance procedure; Std refers to the standard deviation method.

shows the results that were delivered by extended TOPSIS when configured with the different criteria weighting methods (it is worthy reminding that extended TOPSIS using GCCA refers to the CMCGDM approach). The third and fourth columns of this table indicate the number of problem instances (out of 6300) for which the transitivity requirement was violated when an unimportant alternative was inserted or removed, respectively. The fifth column does the same transitivity test, but it refers to those simulation trials where a non-optimal alternative was replaced by a worse one. Conversely, the sixth and seventh columns express the number of cases where the best alternative solution was altered either by adding/removing an irrelevant alternative or by replacing a non-optimal alternative by a worse one. Finally, the last column indicates the aggregated sum of the values in the third, fourth, and fifth columns. As one can notice, using GCCA to elicit the criteria weights has usually achieved better performance than the other contestant methods, lagging behind the statistical variance procedure and CRITIC when the best alternative solutions were altered after adding irrelevant alternatives.

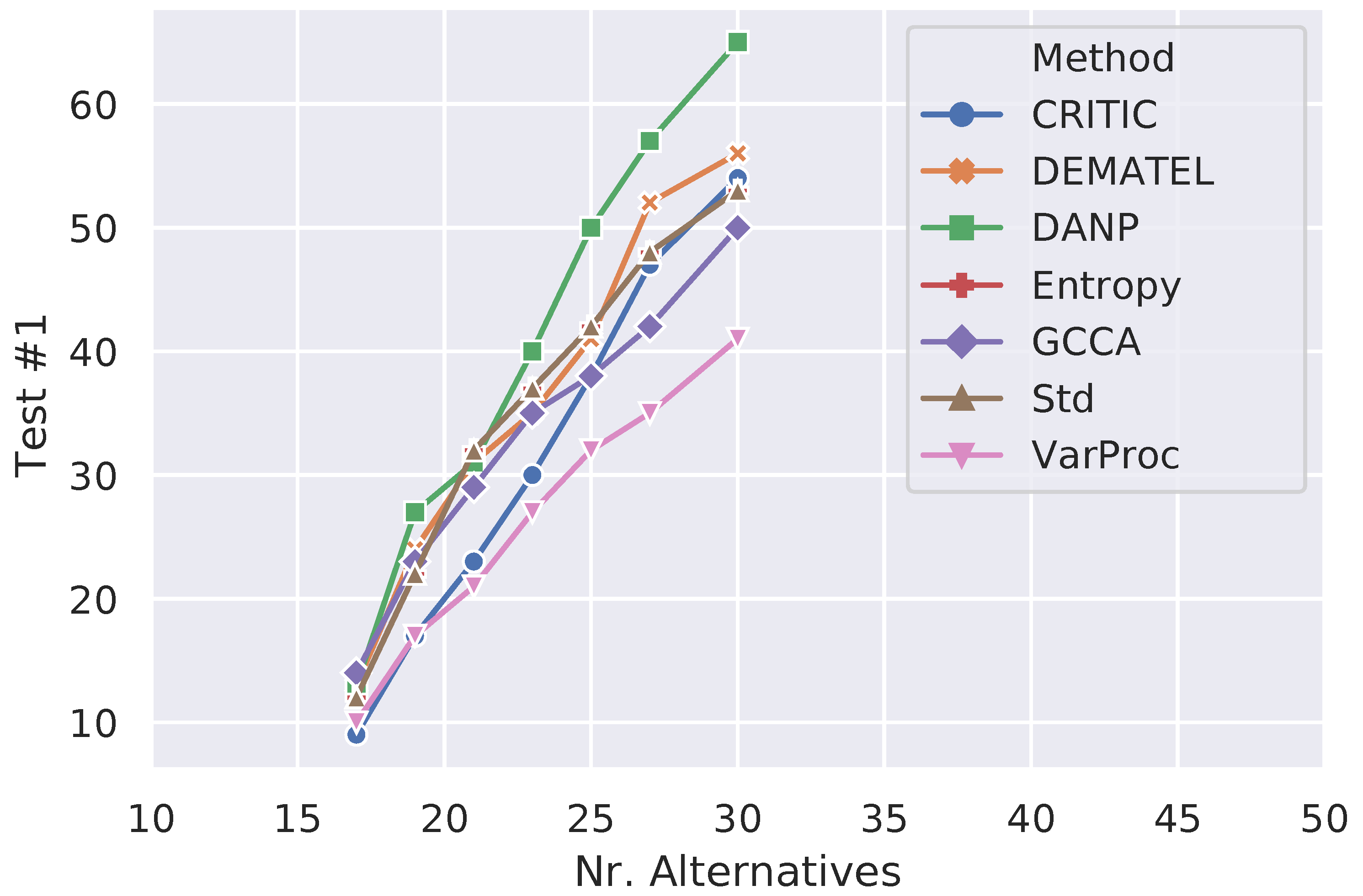
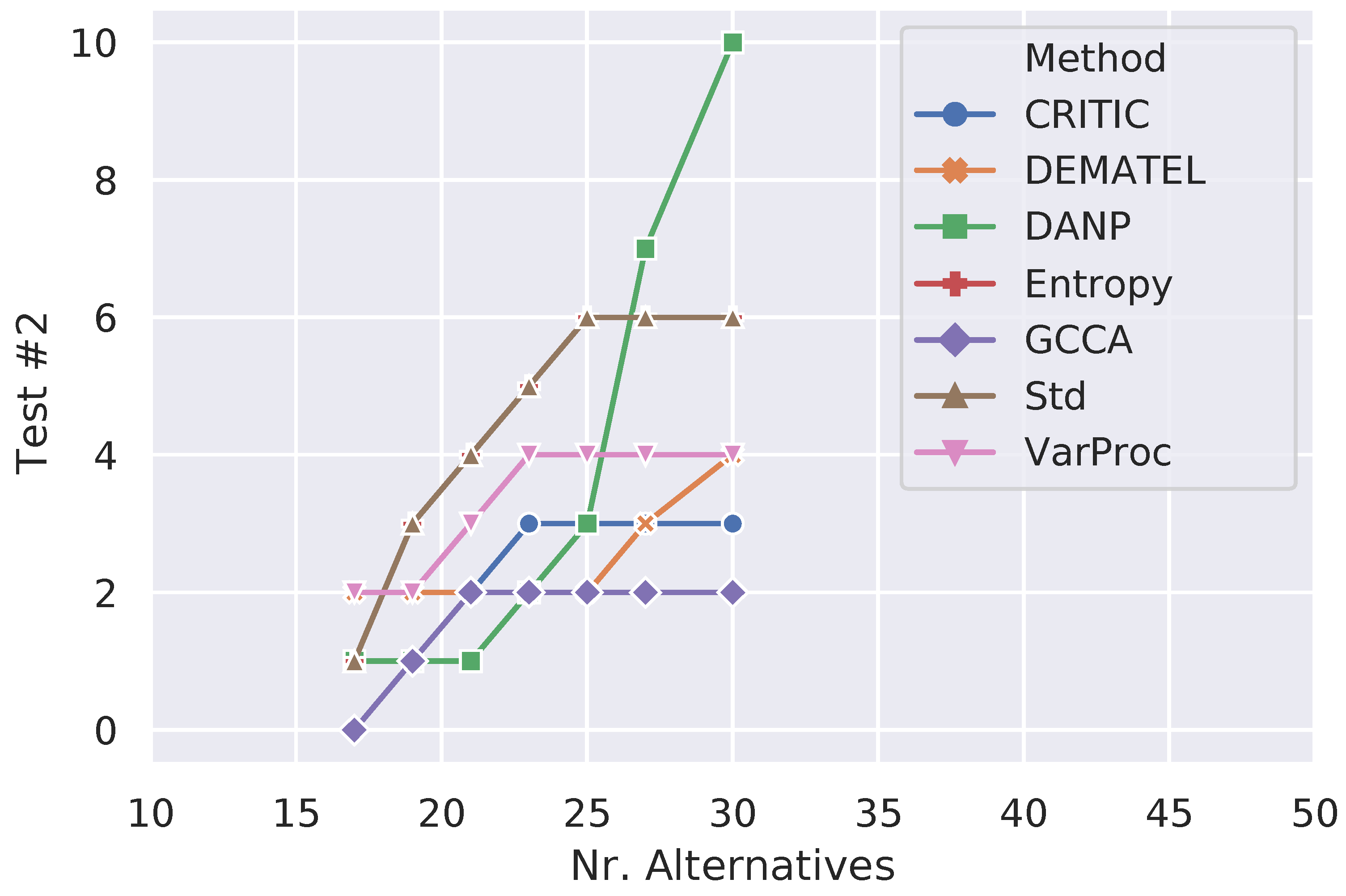
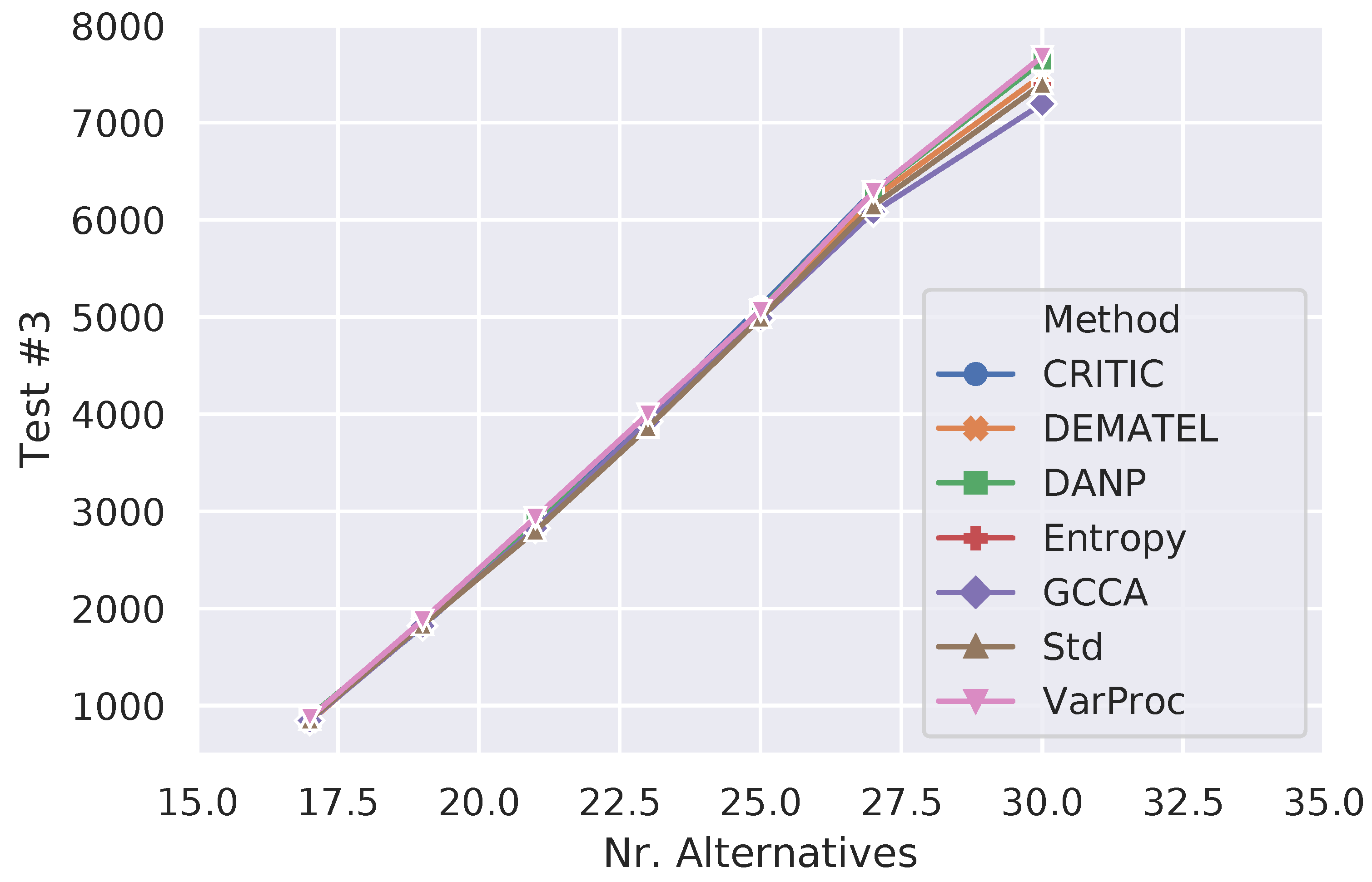
Figure 2, Figure 3 and Figure 4 show how the number of failure cases varied for each type of irregularity test when the number of alternatives increased from 17 (minimum) to 30 (maximum) in order to better understand the performance of the different criteria weighting methods across the simulations. Considering Figure 2 (Test #1), one can notice that GCCA’s overall performance falls short of CRITIC and VarProc, although, after the 25 mark, it is only surpassed by VarProc. While the number of test failures caused by DANP grew up steadily, the increase of this number for GCCA is less accentuated in the range of 25 to 30 alternatives. Regarding Figure 3 (Test #2), the overall performance of GCCA is much better than all other methods and its stability from the 21 mark is remarkable. In general, all methods (except DANP) show a reasonable resilience to the conditions imposed by this test. Finally, Figure 4 informs how the different methods handled the transitivity requirement (Test #3). The values correspond to the aggregated cases, as shown in the last column of Table 13. All methods displayed a similar monotonically increasing behavior in terms of number of failed trials; however, the performance of GCCA was usually better, regardless of the number of alternatives.

8. Final Remarks

In this paper, we introduced a novel GDM approach, CMCGDM, which adopts GCCA to automatically elicit the weights of the (possibly distinct) criteria used by the different DMs. By maximizing the correlation between the DMs’ decision matrices, we argue that the elicited weights can better reflect the consensus between the DMs’ preferences regarding the various alternatives. CMCGDM also makes use of the extended version of TOPSIS conceived by Shih et al. [26], which is specific for MCGDM. We revisited two examples taken from the literature and performed a series of simulations considering popular criteria weighting methods to demonstrate the usefulness of CMCGDM. Overall, the results revealed that CMCGDM is a promising approach, being more resilient to the ranking irregularity problem than the extended TOPSIS without using GCCA.

As future work, we plan to extend CMCGDM to work with other GDM methods available in the literature as well as with uncertain criteria, such as those that involve fuzzy, interval, incomplete, or random values [1,14,57]. We also plan to compare CMCGDM with other methods for eliciting criteria weights, such as CSW-DEA [36,37], nonlinear programming methods [39], and swing-weighting [40]. We shall also investigate the use of GCCA to recalibrate the criteria weights in dynamic settings, particularly in those circumstances where the sets of alternatives or criteria are allowed to change over time [58]. Finally, the use of non-linear versions of CCA (such as those that employ kernels [22]) seems to be a good theme to explore.