Viscosity Approximation Methods for a General Variational Inequality System and Fixed Point Problems in Banach Spaces

Abstract

In Banach spaces, we study the problem of solving a more general variational inequality system for an asymptotically non-expansive mapping. We give a new viscosity approximation scheme to find a common element. Some strong convergence theorems of the proposed iterative method are obtained. A numerical experiment is given to show the implementation and efficiency of our main theorem. Our results presented in this paper generalize and complement many recent ones.

1. Introduction

Throughout this paper, let X be a real Banach space and $E\subset X$ be a nonempty subset. Let $T:E\to E$ be a mapping, the set of fixed points of T is denoted by $F(T)$. If there exists a sequence $\{k_n\}\subset [1,\infty )$ with ${lim}_{n\to \infty }{k}_n=1$ such that

$$\parallel T^n\xi -T^n\eta \parallel \le k_n\parallel \xi -\eta \parallel ,\forall \xi ,\eta \in E,$$

then T is said to be asymptotically nonexpansive. T is uniformly asymptotically regular, if ${lim}_{n\to \infty }\parallel T^{n+1}\xi -T^n\xi \parallel =0,\forall \xi \in E$. If $k_n\equiv 1$, then T is said to be nonexpansive. Recall that T is known as a contractive mapping on E if there exists a constant $\rho \in (0,1)$ such that $\parallel T\xi -T\eta \parallel \le \rho \parallel \xi -\eta \parallel ,\forall \xi ,\eta \in E$.

An operator $A:E\to X$ is called accretive if there exists $j(\xi -\eta )\in J(\xi -\eta )$ such that

$$⟨A\xi -A\eta ,j(\xi -\eta )⟩\ge 0,\forall \xi ,\eta \in E,$$

where $J:X\to 2^{X^{*}}$ is the normalized duality mapping on X. An operator $A:E\to X$ is called $\alpha$-inverse strongly accretive if for $\alpha >0$ and $j(\xi -\eta )\in J(\xi -\eta )$, we have

$$⟨A\xi -A\eta ,j(\xi -\eta )⟩\ge {\alpha \parallel A\xi -A\eta \parallel }^2,\forall \xi ,\eta \in E.$$

For any $ϵ\in (0,2]$, we denote the the modulus of convexity ${\delta }_X(ϵ)>0$ of X as follows:

$${\delta }_X(ϵ)=inf\{1-\frac{1}{2}\parallel \xi +\eta \parallel :\parallel \xi \parallel ,\parallel \eta \parallel \le 1,\parallel \xi -\eta \parallel \ge ϵ\}.$$

X is said to be uniformly convex if ${\delta }_X(0)=0$. Let ${\rho }_X$ be the modulus of smoothness of X defined by:

$${\rho }_X(s)=sup\{\frac{\parallel \xi +s\eta \parallel +\parallel \xi -s\eta \parallel }{2}-1:\parallel \xi \parallel =1,\parallel \eta \parallel =1\}.$$

A Banach space X is said to be uniformly smooth if ${lim}_{n\to \infty }{\rho }_X(s)/s=0$. Moreover, X is uniformly smooth if and only if the norm of X is uniformly Fréchet differentiable.

A mapping $Q:X\to E$ is called sunny if Q has the following property:

$$Q(s\xi +(1-s)Q\xi )=Q\xi ,\xi \in X,s\ge 0,$$

whenever $s\xi +(1-s)Q\xi \in X$. A mapping $Q:X\to E$ is said to be a retraction if $Q\xi =\xi$ for all $\xi \in E$. It is well known that a sunny nonexpansive retraction is also sunny and nonexpansive.

Variational inequality theory has played a significant role in nonlinear analysis and the optimization problem. Many iterative methods have been used to solve variational inequality problems due to the applications in some branches of applied science, convex optimization, mathematical physics, and operator studies, see [1,2,3,4,5,6,7,8,9] and the references therein. In fact, the classical variational inequality problem in Banach spaces is to find $q\in E$ such that

$$⟨Aq,j(x-q)⟩\ge 0,\forall x\in E.$$

In 2010, Yao et al. [10] proposed a system to find $(u,v)\in E\times E$ such that:

$$\left\{\begin{array}{cc}\hfill & ⟨Av+u-v,j(x-u)⟩\ge 0,\forall x\in E,\hfill \\ \hfill & ⟨Bu+v-u,j(x-v)⟩\ge 0,\forall x\in E,\hfill \end{array}\right.$$

which is called the general variational inequality system in Banach spaces. They proved a strong convergence result of the following sequence to a solution of the variational inequality system:

$$\left\{\begin{array}{cc}\hfill & y_n=Q_E(x_n-B{x}_n),\hfill \\ \hfill & x_{n+1}={\alpha }_{n}u+{\beta }_n{x}_n+{\gamma }_n{Q}_E(y_n-A{y}_n),\hfill \end{array}\right.$$

where $Q_E$ is the sunny nonexpansive retract from X onto E.

Recently, many authors have focused their efforts on studying generalized variational inequality systems with variational inequality constraints, see [11,12,13,14,15,16,17] and the references therein. Especially, in 2019, Ceng et al. [11] studied a general system of variational inequalities in Banach spaces:

$$\left\{\begin{array}{cc}\hfill & ⟨\lambda Av+u-v,j(x-u)⟩\ge 0,\forall x\in E,\hfill \\ \hfill & ⟨\mu Bu+v-u,j(x-v)⟩\ge 0,\forall x\in E,\hfill \end{array}\right.$$

(1)

and they considered an implicit composite extra-gradient-like iterative algorithm for countable family Lipschitzian pseudo-contractive mappings and proved strong convergence results in Banach spaces. Cai et al. [14] showed the following viscosity iteration method for the strict pseudo-contraction and non-expansive mapping:

$$\left\{\begin{array}{cc}\hfill & y_n={\alpha }_{n}f(x_n)+(1-{\alpha }_n)x_n,\hfill \\ \hfill & u_n=Q_E(y_n-\mu B{y}_n),\hfill \\ \hfill & z_n=Q_E(u_n-\lambda A{u}_n),\hfill \\ \hfill & x_{n+1}={\beta }_n{x}_n+(1-{\beta }_n)T_{\alpha }{z}_n,\hfill \end{array}\right.$$

where $T_{\alpha }x=\alpha x+(1-\alpha )Tx$. They proved that $x_n$ converges strongly to a common element of the fixed point set and the set of solutions of the problem (1).

Inspired and motivated by the work of researchers, we consider the following problem about the general variational inequality system in Banach spaces:

$$\left\{\begin{array}{cc}\hfill & ⟨(I-\lambda A)(t{x}^{†}+(1-t)y^{†})-x^{†},j(x-x^{†})⟩\le 0,\forall x\in E,\hfill \\ \hfill & ⟨(I-\mu B)x^{†}-y^{†},j(x-y^{†})⟩\le 0,\forall x\in E.\hfill \end{array}\right.$$

(2)

When $t=0$, this is the general system of variational inequalities (1). We present a viscosity iterative algorithm for the general variational inequality system (2) and an asymptotically nonexpansive mapping. Let $\{x_n\}$ be a sequence generated by $x_0\in E$ and:

$$\left\{\begin{array}{cc}\hfill & w_n=Q_E(I-\mu B)x_n,\hfill \\ \hfill & z_n=Q_E(I-\lambda A)(t{x}_n+(1-t)w_n),\hfill \\ \hfill & u_n={\delta }_n{x}_n+(1-{\delta }_n)z_n,\hfill \\ \hfill & x_{n+1}={\alpha }_{n}f(x_n)+{\beta }_n{x}_n+{\gamma }_n{T}^n{u}_n.\hfill \end{array}\right.$$

(3)

Then, the strong convergence theorem of this iterative scheme in Banach spaces is proven. Finally, we give the numerical experiments to show the implementation and efficiency of our main theorem. We study this viscosity approximation method to find a common element of the fixed point set of an asymptotically nonexpansive mapping and the set of solutions of the general variational inequality system in Banach spaces. Our results presented in this paper generalize and complement many recent ones [3,5,6,9,10,12,13,14,17].

2. Preliminaries

In this section, we recall some lemmas which are needed in the proof of our main results.

Lemma 1

([18]). Let X be a smooth Banach space. Assume that $Q:X\to E$ is a retract and J is the normalized duality mapping on X. Then the following statements are equivalent:

(a) Q is sunny and nonexpansive;

(b) ${\parallel Q\xi -Q\eta \parallel }^2\le ⟨\xi -\eta ,J(Q\xi -Q\eta )⟩,\forall \xi ,\eta \in X$;

(c) $⟨\xi -Q\xi ,J(\eta -Q\xi )⟩\le 0,\forall \xi \in X,\eta \in E$.

Lemma 2

([19]). Suppose that $\{v_n\}$ is a sequence of nonnegative real numbers satisfying:

$$v_{n+1}\le (1-b_n)v_n+b_n{\sigma }_n,\forall n\ge 0,$$

where $\{b_n\}\subset (0,1)$ and ${\sigma }_n\subset R$ satisfying the following conditions:

(i) ${lim}_{n\to \infty }{b}_n=0$ and ${\sum }_{n=0}^{\infty }{b}_n=+\infty ;$

(ii) either ${lim\; sup}_{n\to \infty }{\sigma }_n\le 0$ or ${\sum }_{n=0}^{\infty }|b_n{\sigma }_n|<+\infty .$

Then ${lim}_{n\to \infty }{v}_n=0$.

Lemma 3

([14]). Let X be a real Banach space. Let $\varnothing \ne E\subset X$ be a closed convex subset. If the operator $A:E\to X$ is α-inverse strongly accretive, then we have:

$${\parallel (I-\lambda A)\xi -(I-\lambda A)\eta \parallel }^2\le {\parallel \xi -\eta \parallel }^2-\lambda (2\alpha -c\lambda ){\parallel A\xi -A\eta \parallel }^2,$$

where $\lambda >0$. If $0<\lambda <\frac{2\alpha }{c}$, then $I-\lambda A$ is nonexpansive.

Lemma 4

([20]). Let X be a real Banach space and $\{x_n\}$, $\{y_n\}$ be two bounded sequences of X. Let $\{{\beta }_n\}$ be a sequence in $[0,1]$with $0<{lim\; inf}_{n\to \infty }{\beta }_n\le {lim\; sup}_{n\to \infty }{\beta }_n<1$ . If $x_{n+1}=(1-{\beta }_n)x_n+{\beta }_n{p}_n$ for all $n\ge 0$ and ${lim\; sup}_{n\to \infty }(\parallel p_{n+1}-p_n\parallel -\parallel x_{n+1}-x_n\parallel )\le 0$ , then ${lim}_{n\to \infty }\parallel p_n-x_n\parallel =0$.

Lemma 5

([21]). Let X be a real Banach space. Let $\varnothing \ne E\subset X$ be a closed convex subset. And let $T:E\to E$ be an asymptotically nonexpansive mapping with a fixed point. Suppose that X admits a weakly sequentially continuous duality mapping. Then the mapping $I-T$ is demiclosed at zero, i.e., where I is the identity mapping, i.e., if $x_n\rightharpoonup x$ and $\parallel x_n-T{x}_n\parallel \to 0$, then $x=Tx$.

Lemma 6

([22]). Let X be a real Banach space. Let $\varnothing \ne E\subset X$ be a closed convex subset and $T:E\to E$ be a nonexpansive mapping with $F(T)\ne \varnothing$. Let $f:E\to E$ be a contractive mapping. Then the sequence $x_s$ defined by $x_s=sf(x_s)+(1-s)T{x}_s,s\in (0,1)$ converges strongly to a point in $F(T)$. Suppose $Q:{\mathsf{\Pi }}_c\to F(T)$ by $Q(f)={lim}_{s\to 0}{x}_s,f\in {\mathsf{\Pi }}_c$, then $Q(f)$ solves the variational inequality

$$⟨(I-f)Q(f),j(Q(f)-p)⟩\le 0,\forall p\in F(T).$$

Lemma 7

([23]). Let $r>0$. If X is a real smooth and uniformly convex Banach space, then there exists a continuous, strictly increasing and convex function $g:[0,2r]\to R,g(0)=0$ such that $g(\parallel x-y\parallel )\le {\parallel x\parallel }^2-2⟨x,j(y)⟩+{\parallel y\parallel }^2$ for all $x,y\in B_r$.

Lemma 8.

Let X be a real Banach space. Let $\varnothing \ne E\subset X$ be a closed convex subset and $A,B:E\to X$ be two nonlinear mappings. Suppose that $Q_E$ is a sunny nonexpansive retraction. For $\forall \lambda ,\mu >0$ and $t\in [0,1]$, then the following assertions are equivalent:

(a) $(x^{†},y^{†})\in E\times E$ is a solution of problem (2);

(b) Let $\mathsf{\Psi }:E\to E$ be a mapping defined by

$$\mathsf{\Psi }(x)=Q_E(I-\lambda A)[tx+(1-t)Q_E(I-\mu B)x],$$

then let $x^{†}$ be the fixed point of Ψ, that is $x^{†}=\mathsf{\Psi }{x}^{†}$.

where $x^{†}=Q_E(I-\lambda A)[t{x}^{†}+(1-t)y^{†}]$, $y^{†}=Q_E(I-\mu B)x^{†}$. Assume that $A,B:E\to X$ are α-inverse strongly accretive operator and β-inverse strongly operator, respectively. If $0<\lambda <\frac{2\alpha }{c}$, $0<\mu <\frac{2\beta }{c}$, then Ψ is nonexpansive.

Proof. 

From Lemma 1 and the definition of the sunny nonexpansive retraction, we have that (2) is equivalent to

$$\left\{\begin{array}{cc}\hfill & x^{†}=Q_E(I-\lambda A)[t{x}^{†}+(1-t)y^{†}];\hfill \\ \hfill & y^{†}=Q_E(I-\mu B)x^{†},\hfill \end{array}\right.$$

which is a solution of problem (2). Hence $x^{†}=Q_E(I-\lambda A)[t{x}^{†}+(1-t)Q_E(I-\mu B)x^{†}]=\mathsf{\Psi }(x^{†})$. From Lemma 3, for any $x,y\in E$, we find

$$\begin{array}{cc}\hfill \parallel \mathsf{\Psi }(x)-\mathsf{\Psi }(y)\parallel & =\parallel Q_E(I-\lambda A)[tx+(1-t)Q_E(I-\mu B)x]-Q_E(I-\lambda A)[ty+(1-t)Q_E(I-\mu B)y]\parallel \hfill \\ \hfill & \le \parallel (I-\lambda A)[tx+(1-t)Q_E(I-\mu B)x]-(I-\lambda A)[ty+(1-t)Q_E(I-\mu B)y]\parallel \hfill \\ \hfill & \le \parallel tx+(1-t)Q_E(I-\mu B)x-ty-(1-t)Q_E(I-\mu B)y\parallel \hfill \\ \hfill & \le t\parallel x-y\parallel +(1-t)\parallel x-y\parallel \hfill \\ \hfill & =\parallel x-y\parallel .\hfill \end{array}$$

Thus, Ψ is nonexpansive. □

3. Main Results

Theorem 1.

Let X be a uniformly convex and uniformly smooth Banach space. Let $\varnothing \ne E\subset X$ be a closed convex subset. Suppose that $Q_E:X\to E$ is a sunny nonexpansive retraction and $T:E\to E$ is an asymptotically nonexpansive mapping satisfying the uniformly asymptotically regular condition. And $A,B:E\to X$ are an α-inverse strongly accretive operator and β-inverse strongly accretive operator, respectively. Let $f:E\to E$ be a contraction with coefficient $\rho \in (0,1)$ and Ψ be defined by Lemma 8. Assume that $\mathsf{\Omega }=F(T)\bigcap F(\mathsf{\Psi })\ne \varnothing$. Suppose that $\{{\alpha }_n\},\{{\beta }_n\},\{{\gamma }_n\},\{{\delta }_n\}\subset (0,1)$, the sequence $\{x_n\}$ defined by (3) satisfies the following conditions:

$$\begin{array}{cc}\hfill & (i){\alpha }_n+{\beta }_n+{\gamma }_n=1,\underset{n\to \infty }{lim}{\alpha }_n=0,{\mathsf{\Sigma }}_{n=0}^{\infty }{\alpha }_n=\infty ,k_n-1=ϵ{\alpha }_n,0<ϵ<1-\rho ;\hfill \\ \hfill & (ii)0<\underset{n\to \infty }{lim\; inf}{\beta }_n\le \underset{n\to \infty }{lim\; sup}{\beta }_n<1,\underset{n\to \infty }{lim}|{\delta }_{n+1}-{\delta }_n|=0;\hfill \\ \hfill & (iii)0\le t<1,0<\lambda <\frac{2\alpha }{c},0<\mu <\frac{2\beta }{c};\hfill \\ \hfill & (iv){\beta }_n+{\gamma }_n{k}_n^2<1.\hfill \end{array}$$

Then $\{x_n\}$ converges strongly to an element $x^{†}\in \mathsf{\Omega }$ which solves the variational inequality:

$$⟨(I-f)x^{†},j(x^{†}-p)⟩\le 0,\forall p\in \mathsf{\Omega }.$$

Proof. 

Let $x^{†}\in \mathsf{\Omega }$, from Lemma 8, we have $x^{†}=Q_E(I-\lambda A)[t{x}^{†}+(1-t)y^{†}]$, $y^{†}=Q_E(I-\mu B)x^{†}$. It follows from (3) that

$$\begin{array}{cc}\hfill \parallel u_n-x^{†}\parallel & =\parallel {\delta }_n{x}_n+(1-{\delta }_n)z_n-x^{†}\parallel \hfill \\ \hfill & \le {\delta }_n\parallel x_n-x^{†}\parallel +(1-{\delta }_n)\parallel z_n-x^{†}\parallel \hfill \\ \hfill & ={\delta }_n\parallel x_n-x^{†}\parallel +(1-{\delta }_n)\parallel \mathsf{\Psi }(x_n)-x^{†}\parallel \hfill \\ \hfill & \le {\delta }_n\parallel x_n-x^{†}\parallel +(1-{\delta }_n)\parallel x_n-x^{†}\parallel \hfill \\ \hfill & =\parallel x_n-x^{†}\parallel .\hfill \end{array}$$

Then we compute:

$$\begin{array}{cc}\hfill & \parallel x_{n+1}-x^{†}\parallel \hfill \\ \hfill & =\parallel {\alpha }_{n}f(x_n)+{\beta }_n{x}_n+{\gamma }_n{T}^n{u}_n-x^{†}\parallel \hfill \\ \hfill & =\parallel {\alpha }_n(f(x_n)-f(x^{†}))+{\alpha }_n(f(x^{†})-x^{†})+{\beta }_n(x_n-x^{†})+{\gamma }_n(T^n{u}_n-x^{†})\parallel \hfill \\ \hfill & \le {\alpha }_n\parallel f(x_n)-f(x^{†})\parallel +{\alpha }_n\parallel f(x^{†})-x^{†}\parallel +{\beta }_n\parallel x_n-x^{†}\parallel +{\gamma }_n\parallel T^n{u}_n-x^{†}\parallel \hfill \\ \hfill & \le {\alpha }_n\rho \parallel x_n-x^{†}\parallel +{\alpha }_n\parallel f(x^{†})-x^{†}\parallel +{\beta }_n\parallel x_n-x^{†}\parallel +{\gamma }_n{k}_n\parallel u_n-x^{†}\parallel \hfill \\ \hfill & =({\alpha }_n\rho +{\beta }_n+{\gamma }_n{k}_n)\parallel x_n-x^{†}\parallel +{\alpha }_n\parallel f(x^{†})-x^{†}\parallel \hfill \\ \hfill & \le [1-(1-\rho -ϵ){\alpha }_n]\parallel x_n-x^{†}\parallel +{\alpha }_n\parallel f(x^{†})-x^{†}\parallel \hfill \\ \hfill & \le max\{\parallel x_n-x^{†}\parallel ,\frac{1}{1-\rho -ϵ}\parallel f(x^{†})-x^{†}\parallel \},\hfill \end{array}$$

which implies that $x_n$ is bounded, and so are $z_n$, $u_n$, $f(x_n)$, $T^n{u}_n$.

From (3) and Lemma 8, we observe that

$$\begin{array}{cc}\hfill & \parallel z_{n+1}-z_n\parallel \hfill \\ \hfill & =\parallel Q_E(I-\lambda A)(t{x}_{n+1}+(1-t)w_{n+1})-Q_E(I-\lambda A)(t{x}_n+(1-t)w_n)\parallel \hfill \\ \hfill & =\parallel Q_E(I-\lambda A)(t{x}_{n+1}+(1-t)Q_E(I-\mu B)x_{n+1})-Q_E(I-\lambda A)(t{x}_n+(1-t)Q_E(I-\mu B)x_n)\parallel \hfill \\ \hfill & =\parallel \mathsf{\Psi }(x_{n+1})-\mathsf{\Psi }(x_n)\parallel \le \parallel x_{n+1}-x_n\parallel ,\hfill \end{array}$$

then

$$\begin{array}{cc}\hfill \parallel u_{n+1}-u_n\parallel & =\parallel {\delta }_{n+1}{x}_{n+1}+(1-{\delta }_{n+1})z_{n+1}-{\delta }_n{x}_n-(1-{\delta }_n)z_n\parallel \hfill \\ \hfill & =\parallel {\delta }_{n+1}(x_{n+1}-x_n)+({\delta }_{n+1}-{\delta }_n)x_n+(1-{\delta }_{n+1})(z_{n+1}-z_n)-({\delta }_{n+1}-{\delta }_n)z_n\parallel \hfill \\ \hfill & \le {\delta }_{n+1}\parallel x_{n+1}-x_n\parallel +|{\delta }_{n+1}-{\delta }_n|\parallel x_n-z_n\parallel +(1-{\delta }_{n+1})\parallel z_{n+1}-z_n\parallel \hfill \\ \hfill & \le \parallel x_{n+1}-x_n\parallel +|{\delta }_{n+1}-{\delta }_n|\parallel x_n-z_n\parallel .\hfill \end{array}$$

Set $p_n=\frac{x_{n+1}-{\beta }_n{x}_n}{1-{\beta }_n},foralln\ge 0$, we obtain

$$\begin{array}{cc}\hfill p_{n+1}-p_n& =\frac{x_{n+2}-{\beta }_{n+1}{x}_{n+1}}{1-{\beta }_{n+1}}-\frac{x_{n+1}-{\beta }_n{x}_n}{1-{\beta }_n}\hfill \\ \hfill & =\frac{{\alpha }_{n+1}f(x_{n+1})+{\gamma }_{n+1}{T}^{n+1}{u}_{n+1}}{1-{\beta }_{n+1}}-\frac{{\alpha }_{n}f(x_n)+{\gamma }_n{T}^n{u}_n}{1-{\beta }_n}\hfill \\ \hfill & =\frac{{\alpha }_{n+1}f(x_{n+1})+(1-{\beta }_{n+1}-{\alpha }_{n+1})T^{n+1}{u}_{n+1}}{1-{\beta }_{n+1}}-\frac{{\alpha }_{n}f(x_n)+(1-{\alpha }_n-{\beta }_n)T^n{u}_n}{1-{\beta }_n}\hfill \\ \hfill & =\frac{{\alpha }_{n+1}}{1-{\beta }_{n+1}}[f(x_{n+1})-f(x_n)]+(\frac{{\alpha }_{n+1}}{1-{\beta }_{n+1}}-\frac{{\alpha }_n}{1-{\beta }_n})f(x_n)\hfill \\ \hfill & -(\frac{{\alpha }_{n+1}}{1-{\beta }_{n+1}}-\frac{{\alpha }_n}{1-{\beta }_n})T^n{u}_n-\frac{{\alpha }_{n+1}}{1-{\beta }_{n+1}}(T^{n+1}{u}_{n+1}-T^n{u}_n)+T^{n+1}{u}_{n+1}-T^n{u}_n\hfill \\ \hfill & =\frac{{\alpha }_{n+1}}{1-{\beta }_{n+1}}[f(x_{n+1})-f(x_n)]+(\frac{{\alpha }_{n+1}}{1-{\beta }_{n+1}}-\frac{{\alpha }_n}{1-{\beta }_n})[f(x_n)-T^n{u}_n]\hfill \\ \hfill & +(1-\frac{{\alpha }_{n+1}}{1-{\beta }_{n+1}})[T^{n+1}{u}_{n+1}-T^{n+1}{u}_n]+(1-\frac{{\alpha }_{n+1}}{1-{\beta }_{n+1}})[T^{n+1}{u}_n-T^n{u}_n].\hfill \end{array}$$

Thus,

$$\begin{array}{cc}\hfill \parallel p_{n+1}-p_n\parallel & \le \frac{\rho {\alpha }_{n+1}}{1-{\beta }_{n+1}}\parallel x_{n+1}-x_n\parallel +|\frac{{\alpha }_{n+1}}{1-{\beta }_{n+1}}-\frac{{\alpha }_n}{1-{\beta }_n}|M\hfill \\ \hfill & +\frac{{\gamma }_{n+1}}{1-{\beta }_{n+1}}\underset{x\in E}{sup}\parallel T^{n+1}{u}_n-T^n{u}_n\parallel +(1-\frac{{\alpha }_{n+1}}{1-{\beta }_{n+1}})k_{n+1}\parallel u_{n+1}-u_n\parallel \hfill \\ \hfill & \le [\frac{\rho {\alpha }_{n+1}}{1-{\beta }_{n+1}}+(1-\frac{{\alpha }_{n+1}}{1-{\beta }_{n+1}})k_{n+1}]\parallel x_{n+1}-x_n\parallel +|\frac{{\alpha }_{n+1}}{1-{\beta }_{n+1}}-\frac{{\alpha }_n}{1-{\beta }_n}|M\hfill \\ \hfill & +\frac{{\gamma }_{n+1}}{1-{\beta }_{n+1}}\underset{x\in E}{sup}\parallel T^{n+1}{u}_n-T^n{u}_n\parallel +\frac{{\gamma }_{n+1}}{1-{\beta }_{n+1}}{k}_{n+1}|{\delta }_{n+1}-{\delta }_n|M\hfill \\ \hfill & \le [1-\frac{{\alpha }_{n+1}(1-\rho -ϵ)}{1-{\beta }_{n+1}}]\parallel x_{n+1}-x_n\parallel +|\frac{{\alpha }_{n+1}}{1-{\beta }_{n+1}}-\frac{{\alpha }_n}{1-{\beta }_n}|M\hfill \\ \hfill & +\frac{{\gamma }_{n+1}}{1-{\beta }_{n+1}}\underset{x\in E}{sup}\parallel T^{n+1}{u}_n-T^n{u}_n\parallel +\frac{{\gamma }_{n+1}}{1-{\beta }_{n+1}}{k}_{n+1}|{\delta }_{n+1}-{\delta }_n|M,\hfill \end{array}$$

where $M>0$ is a constant satisfies:

$$\begin{array}{cc}\hfill M& \ge \{su{p}_{n\ge 0}\parallel x_n-z_n\parallel ,su{p}_{n\ge 0}\parallel f(x_n)-T^n{u}_n\parallel \}.\hfill \end{array}$$

By $(i)$, $(ii)$ , we can find,

$$\underset{n\to \infty }{lim\; sup}(\parallel p_{n+1}-p_n\parallel -\parallel x_{n+1}-x_n\parallel )\le 0.$$

Applying Lemma 4, we have

$$\underset{n\to \infty }{lim}\parallel p_n-x_n\parallel =0.$$

We know that

$$p_n-x_n=\frac{x_{n+1}-x_n}{1-{\beta }_n},$$

and we obtain

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}\parallel x_{n+1}-x_n\parallel =0.\end{array}$$

(4)

Next, we show that ${lim}_{n\to \infty }\parallel x_n-\mathsf{\Psi }{x}_n\parallel =0$ and ${lim}_{n\to \infty }\parallel x_n-T{x}_n\parallel =0$.

From (3), Lemma 3, and the non-expansiveness of $Q_E$, we have

$$\begin{array}{cc}\hfill \parallel w_n-y^{†}{\parallel }^2& =\parallel Q_E(I-\mu B)x_n-Q_E(I-\mu B)x^{†}{\parallel }^2\hfill \\ \hfill & \le \parallel (I-\mu B)x_n-(I-\mu B)x^{†}{\parallel }^2\hfill \\ \hfill & \le \parallel x_n-x^{†}{\parallel }^2-\mu (2\beta -c\mu ){\parallel B{x}_n-B{x}^{†}\parallel }^2.\hfill \end{array}$$

Then

$$\begin{array}{cc}\hfill & \parallel z_n-x^{†}{\parallel }^2\hfill \\ \hfill & =\parallel Q_E(I-\lambda A)[t{x}_n+(1-t)w_n]-Q_E(I-\lambda A)[t{x}^{†}+(1-t)y^{†}]{\parallel }^2\hfill \\ \hfill & \le \parallel (I-\lambda A)[t{x}_n+(1-t)w_n]-(I-\lambda A)[t{x}^{†}+(1-t)y^{†}]{\parallel }^2\hfill \\ \hfill & \le \parallel t{x}_n+(1-t)w_n-(t{x}^{†}+(1-t)y^{†}){\parallel }^2-\lambda (2\alpha -c\lambda ){\parallel A(t{x}_n+(1-t)w_n)-A(t{x}^{†}+(1-t)y^{†})\parallel }^2\hfill \\ \hfill & \le t\parallel x_n-x^{†}{\parallel }^2+(1-t)\parallel w_n-y^{†}{\parallel }^2-\lambda (2\alpha -c\lambda ){\parallel A(t{x}_n+(1-t)w_n)-A(t{x}^{†}+(1-t)y^{†})\parallel }^2\hfill \\ \hfill & \le \parallel x_n-x^{†}{\parallel }^2-(1-t)\mu (2\beta -c\mu ){\parallel B{x}_n-B{x}^{†}\parallel }^2\hfill \\ \hfill & -\lambda (2\alpha -c\lambda )\parallel A(t{x}_n+(1-t)w_n)-A(t{x}^{†}+(1-t)y^{†}){\parallel }^2,\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill & \parallel u_n-x^{†}{\parallel }^2\hfill \\ \hfill & =\parallel {\delta }_n{x}_n+(1-{\delta }_n)z_n-x^{†}{\parallel }^2\hfill \\ \hfill & \le {\delta }_n\parallel x_n-x^{†}{\parallel }^2+(1-{\delta }_n){\parallel z_n-x^{†}\parallel }^2\hfill \\ \hfill & \le \parallel x_n-x^{†}{\parallel }^2-(1-{\delta }_n)(1-t)\mu (2\beta -c\mu ){\parallel B{x}_n-B{x}^{†}\parallel }^2\hfill \\ \hfill & -(1-{\delta }_n)\lambda (2\alpha -c\lambda ){\parallel A(t{x}_n+(1-t)w_n)-A(t{x}^{†}+(1-t)y^{†})\parallel }^2.\hfill \end{array}$$

Moreover, we know that

$$\begin{array}{cc}\hfill & \parallel x_{n+1}-x^{†}{\parallel }^2\hfill \\ \hfill & =\parallel {\alpha }_{n}f(x_n)+{\beta }_n{x}_n+{\gamma }_n{T}^n{u}_n-x^{†}{\parallel }^2\hfill \\ \hfill & \le {\alpha }_n\parallel f(x_n)-x^{†}{\parallel }^2+{\beta }_n\parallel x_n-x^{†}{\parallel }^2+{\gamma }_n{\parallel T^n{u}_n-x^{†}\parallel }^2\hfill \\ \hfill & \le {\alpha }_n\parallel f(x_n)-x^{†}{\parallel }^2+{\beta }_n\parallel x_n-x^{†}{\parallel }^2+{\gamma }_n{k}_n^2{\parallel u_n-x^{†}\parallel }^2\hfill \\ \hfill & \le {\alpha }_n\parallel f(x_n)-x^{†}{\parallel }^2+{\beta }_n\parallel x_n-x^{†}{\parallel }^2+{\gamma }_n{k}_n^2{\parallel x_n-x^{†}\parallel }^2\hfill \\ \hfill & -{\gamma }_n{k}_n^2(1-{\delta }_n)(1-t)\mu (2\beta -c\mu ){\parallel B{x}_n-B{x}^{†}\parallel }^2\hfill \\ \hfill & -{\gamma }_n{k}_n^2(1-{\delta }_n)\lambda (2\alpha -c\lambda ){\parallel A(t{x}_n+(1-t)w_n)-A(t{x}^{†}+(1-t)y^{†})\parallel }^2,\hfill \end{array}$$

which implies that

$$\begin{array}{cc}\hfill & {\gamma }_n{k}_n^2(1-{\delta }_n)(1-t)\mu (2\beta -c\mu ){\parallel B{x}_n-B{x}^{†}\parallel }^2\hfill \\ \hfill & +{\gamma }_n{k}_n^2(1-{\delta }_n)\lambda (2\alpha -c\lambda ){\parallel A(t{x}_n+(1-t)w_n)-A(t{x}^{†}+(1-t)y^{†})\parallel }^2\hfill \\ \hfill & \le {\alpha }_n\parallel f(x_n)-x^{†}{\parallel }^2+({\beta }_n+{\gamma }_n{k}_n^2)\parallel x_n-x^{†}{\parallel }^2-{\parallel x_{n+1}-x^{†}\parallel }^2\hfill \\ \hfill & \le {\alpha }_n\parallel f(x_n)-x^{†}{\parallel }^2+\parallel x_n-x^{†}{\parallel }^2-{\parallel x_{n+1}-x^{†}\parallel }^2\hfill \\ \hfill & \le {\alpha }_n\parallel f(x_n)-x^{†}{\parallel }^2+\parallel x_n-x_{n+1}\parallel (\parallel x_n-x^{†}\parallel +\parallel x_{n+1}-x^{†}\parallel ).\hfill \end{array}$$

By the conditions $(i)$, $(ii)$, and (4), we deduce

$$\begin{array}{cc}\hfill & \underset{n\to \infty }{lim}\parallel B{x}_n-B{x}^{†}\parallel =0\hfill \\ \hfill & \underset{n\to \infty }{lim}\parallel A(t{x}_n+(1-t)w_n)-A(t{x}^{†}+(1-t)y^{†})\parallel =0.\hfill \end{array}$$

(5)

Applying Lemmas 1 and 7 to find

$$\begin{array}{cc}\hfill \parallel w_n-y^{†}{\parallel }^2& =\parallel Q_E(I-\mu B)x_n-Q_E(I-\mu B)x^{†}{\parallel }^2\hfill \\ \hfill & \le ⟨(I-\mu B)x_n-(I-\mu B)x^{†},j(w_n-y^{†})⟩\hfill \\ \hfill & \le ⟨x_n-x^{†},j(w_n-y^{†})⟩-\mu ⟨B{x}_n-B{x}^{†},j(w_n-y^{†})⟩\hfill \\ \hfill & \le \frac{1}{2}[\parallel x_n-x^{†}{\parallel }^2+\parallel w_n-y^{†}{\parallel }^2-g(\parallel x_n-x^{†}-(w_n-y^{†})\parallel )]-\mu ⟨B{x}_n-B{x}^{†},j(w_n-y^{†})⟩.\hfill \end{array}$$

Hence, we have

$$\begin{array}{cc}\hfill \parallel w_n-y^{†}{\parallel }^2& \le \parallel x_n-x^{†}{\parallel }^2-g(\parallel x_n-x^{†}-(w_n-y^{†})\parallel )-2\mu ⟨B{x}_n-B{x}^{†},j(w_n-y^{†})⟩.\hfill \end{array}$$

Further, we estimate

$$\begin{array}{cc}\hfill \parallel z_n-x^{†}{\parallel }^2& =\parallel Q_E(I-\lambda A)[t{x}_n+(1-t)w_n]-Q_E(I-\lambda A)[t{x}^{†}+(1-t)y^{†}]{\parallel }^2\hfill \\ \hfill & \le ⟨(I-\lambda A)[t{x}_n+(1-t)w_n]-(I-\lambda A)[t{x}^{†}+(1-t)y^{†}],j(z_n-x^{†})⟩\hfill \\ \hfill & \le ⟨t{x}_n+(1-t)w_n-(t{x}^{†}+(1-t)y^{†}),j(z_n-x^{†})⟩\hfill \\ \hfill & -\lambda ⟨A(t{x}_n+(1-t)w_n)-A(t{x}^{†}+(1-t)y^{†}),j(z_n-x^{†})⟩\hfill \\ \hfill & \le t⟨x_n-x^{†},j(z_n-x^{†})⟩+(1-t)⟨w_n-y^{†},j(z_n-x^{†})⟩\hfill \\ \hfill & -\lambda ⟨A(t{x}_n+(1-t)w_n)-A(t{x}^{†}+(1-t)y^{†}),j(z_n-x^{†})⟩\hfill \\ \hfill & \le \frac{t}{2}[\parallel x_n-x^{†}{\parallel }^2+\parallel z_n-x^{†}{\parallel }^2-g(\parallel x_n-z_n\parallel )]\hfill \\ \hfill & +\frac{1-t}{2}[\parallel w_n-y^{†}{\parallel }^2+\parallel z_n-x^{†}{\parallel }^2-g(\parallel w_n-y^{†}-(z_n-x^{†})\parallel )]\hfill \\ \hfill & -\lambda ⟨A(t{x}_n+(1-t)w_n)-A(t{x}^{†}+(1-t)y^{†}),j(z_n-x^{†})⟩,\hfill \end{array}$$

noting that $0\le t<1$, so

$$\begin{array}{cc}\hfill \parallel z_n-x^{†}{\parallel }^2& \le t\parallel x_n-x^{†}{\parallel }^2+(1-t)\parallel w_n-y^{†}{\parallel }^2-tg(\parallel x_n-z_n\parallel )\hfill \\ \hfill & -(1-t)g(\parallel w_n-y^{†}-(z_n-x^{†})\parallel )\hfill \\ \hfill & -2\lambda ⟨A(t{x}_n+(1-t)w_n)-A(t{x}^{†}+(1-t)y^{†}),j(z_n-x^{†})⟩\hfill \\ \hfill & \le \parallel x_n-x^{†}{\parallel }^2-(1-t)g(\parallel x_n-x^{†}-(w_n-y^{†})\parallel )\hfill \\ \hfill & -2\mu (1-t)⟨B{x}_n-B{x}^{†},j(w_n-y^{†})⟩\hfill \\ \hfill & -(1-t)g(\parallel w_n-y^{†}-(z_n-x^{†})\parallel )\hfill \\ \hfill & -2\lambda ⟨A(t{x}_n+(1-t)w_n)-A(t{x}^{†}+(1-t)y^{†}),j(z_n-x^{†})⟩\hfill \\ \hfill & \le \parallel x_n-x^{†}{\parallel }^2-(1-t)g(\parallel x_n-x^{†}-(w_n-y^{†})\parallel )\hfill \\ \hfill & -2\mu (1-t)\parallel B{x}_n-B{x}^{†}\parallel \parallel w_n-y^{†}\parallel \hfill \\ \hfill & -(1-t)g(\parallel w_n-y^{†}-(z_n-x^{†})\parallel )\hfill \\ \hfill & -2\lambda \parallel A(t{x}_n+(1-t)w_n)-A(t{x}^{†}+(1-t)y^{†})\parallel \parallel z_n-x^{†}\parallel ,\hfill \end{array}$$

then

$$\begin{array}{cc}\hfill & \parallel u_n-x^{†}{\parallel }^2\hfill \\ \hfill & \le {\delta }_n\parallel x_n-x^{†}{\parallel }^2+(1-{\delta }_n){\parallel z_n-x^{†}\parallel }^2\hfill \\ \hfill & \le \parallel x_n-x^{†}{\parallel }^2-(1-{\delta }_n)(1-t)g(\parallel x_n-x^{†}-(w_n-y^{†})\parallel )\hfill \\ \hfill & -2\mu (1-{\delta }_n)(1-t)\parallel B{x}_n-B{x}^{†}\parallel \parallel w_n-y^{†}\parallel \hfill \\ \hfill & -(1-t)(1-{\delta }_n)g(\parallel w_n-y^{†}-(z_n-x^{†})\parallel )\hfill \\ \hfill & -2\lambda (1-{\delta }_n)\parallel A(t{x}_n+(1-t)w_n)-A(t{x}^{†}+(1-t)y^{†})\parallel \parallel z_n-x^{†}\parallel .\hfill \end{array}$$

We know that

$$\begin{array}{cc}\hfill & \parallel x_{n+1}-x^{†}{\parallel }^2\hfill \\ \hfill & \le {\alpha }_n\parallel f(x_n)-x^{†}{\parallel }^2+{\beta }_n\parallel x_n-x^{†}{\parallel }^2+{\gamma }_n{k}_n^2{\parallel u_n-x^{†}\parallel }^2\hfill \\ \hfill & \le {\alpha }_n\parallel f(x_n)-x^{†}{\parallel }^2+{\beta }_n\parallel x_n-x^{†}{\parallel }^2+{\gamma }_n{k}_n^2{\parallel x_n-x^{†}\parallel }^2\hfill \\ \hfill & -(1-{\delta }_n)(1-t){\gamma }_n{k}_n^{2}g(\parallel x_n-x^{†}-(w_n-y^{†})\parallel )\hfill \\ \hfill & -2\mu (1-{\delta }_n)(1-t){\gamma }_n{k}_n^2\parallel B{x}_n-B{x}^{†}\parallel \parallel w_n-y^{†}\parallel \hfill \\ \hfill & -(1-t)(1-{\delta }_n){\gamma }_n{k}_n^{2}g(\parallel w_n-y^{†}-(z_n-x^{†})\parallel )\hfill \\ \hfill & -2\lambda (1-{\delta }_n){\gamma }_n{k}_n^2\parallel A(t{x}_n+(1-t)w_n)-A(t{x}^{†}+(1-t)y^{†})\parallel \parallel z_n-x^{†}\parallel \hfill \\ \hfill & \le {\alpha }_n\parallel f(x_n)-x^{†}{\parallel }^2+{\parallel x_n-x^{†}\parallel }^2\hfill \\ \hfill & -(1-{\delta }_n)(1-t){\gamma }_n{k}_n^{2}g(\parallel x_n-x^{†}-(w_n-y^{†})\parallel )\hfill \\ \hfill & -2\mu (1-{\delta }_n)(1-t){\gamma }_n{k}_n^2\parallel B{x}_n-B{x}^{†}\parallel \parallel w_n-y^{†}\parallel \hfill \\ \hfill & -(1-t)(1-{\delta }_n){\gamma }_n{k}_n^{2}g(\parallel w_n-y^{†}-(z_n-x^{†})\parallel )\hfill \\ \hfill & -2\lambda (1-{\delta }_n){\gamma }_n{k}_n^2\parallel A(t{x}_n+(1-t)w_n)-A(t{x}^{†}+(1-t)y^{†})\parallel \parallel z_n-x^{†}\parallel ,\hfill \end{array}$$

which implies that

$$\begin{array}{cc}\hfill & (1-{\delta }_n)(1-t){\gamma }_n{k}_n^{2}g(\parallel x_n-x^{†}-(w_n-y^{†})\parallel )\hfill \\ \hfill & +(1-t)(1-{\delta }_n){\gamma }_n{k}_n^{2}g(\parallel w_n-y^{†}-(z_n-x^{†})\parallel )\hfill \\ \hfill & \le {\alpha }_n\parallel f(x_n)-x^{†}{\parallel }^2+\parallel x_n-x^{†}{\parallel }^2-{\parallel x_{n+1}-x^{†}\parallel }^2\hfill \\ \hfill & -2\mu (1-{\delta }_n)(1-t){\gamma }_n{k}_n^2\parallel B{x}_n-B{x}^{†}\parallel \parallel w_n-y^{†}\parallel \hfill \\ \hfill & -2\lambda (1-{\delta }_n){\gamma }_n{k}_n^2\parallel A(t{x}_n+(1-t)w_n)-A(t{x}^{†}+(1-t)y^{†})\parallel \parallel z_n-x^{†}\parallel \hfill \\ \hfill & \le {\alpha }_n\parallel f(x_n)-x^{†}{\parallel }^2+\parallel x_n-x_{n+1}\parallel (\parallel x_n-x^{†}\parallel +\parallel x_{n+1}-x^{†}\parallel )\hfill \\ \hfill & -2\mu (1-{\delta }_n)(1-t){\gamma }_n{k}_n^2\parallel B{x}_n-B{x}^{†}\parallel \parallel w_n-y^{†}\parallel \hfill \\ \hfill & -2\lambda (1-{\delta }_n){\gamma }_n{k}_n^2\parallel A(t{x}_n+(1-t)w_n)-A(t{x}^{†}+(1-t)y^{†})\parallel \parallel z_n-x^{†}\parallel .\hfill \end{array}$$

It follows from (4), (5), condition $(i)$, $(iii)$, and the properties of g, that we have

$$\begin{array}{cc}\hfill & \underset{n\to \infty }{lim}\parallel x_n-x^{†}-(w_n-y^{†})\parallel =0;\hfill \\ \hfill & \underset{n\to \infty }{lim}\parallel w_n-y^{†}-(z_n-x^{†})\parallel =0.\hfill \end{array}$$

So,

$$\begin{array}{cc}\hfill & \parallel x_n-z_{{}_n}\parallel \hfill \\ \hfill & \le \parallel x_n-x^{†}-(w_n-y^{†})\parallel +\parallel w_n-y^{†}-(z_n-x^{†})\parallel \hfill \\ \hfill & \to 0.\hfill \end{array}$$

(6)

We can obtain

$$\begin{array}{c}\hfill \parallel x_n-\mathsf{\Psi }(x_n)\parallel =\parallel x_n-z_n\parallel \to 0,n\to \infty .\end{array}$$

(7)

Moreover, we have

$$\begin{array}{cc}\hfill & \parallel x_{n+1}-T^n{u}_n\parallel \hfill \\ \hfill & =\parallel {\alpha }_{n}f(x_n)+{\beta }_n{x}_n-{\alpha }_n{T}^n{u}_n-{\beta }_n{T}^n{u}_n\parallel \hfill \\ \hfill & =\parallel {\alpha }_n[f(x_n)-T^n{u}_n]+{\beta }_n[x_n-T^n{u}_n]\parallel \hfill \\ \hfill & \le {\beta }_n\parallel x_n-x_{n+1}\parallel +{\beta }_n\parallel x_{n+1}-T^n{u}_n\parallel +{\alpha }_n\parallel f(x_n)-T^n{u}_n\parallel ,\hfill \end{array}$$

which implies that

$$(1-{\beta }_n)\parallel x_{n+1}-T^n{u}_n\parallel \le {\beta }_n\parallel x_n-x_{n+1}\parallel +{\alpha }_n\parallel f(x_n)-T^n{u}_n\parallel .$$

Therefore

$$\parallel x_{n+1}-T^n{u}_n\parallel \le \frac{{\beta }_n}{1-{\beta }_n}\parallel x_n-x_{n+1}\parallel +\frac{{\alpha }_n}{1-{\beta }_n}\parallel f(x_n)-T^n{u}_n\parallel .$$

From conditions $(i)$, $(ii)$, and (4), we find

$$\begin{array}{c}\hfill \parallel x_{n+1}-T^n{u}_n\parallel \to 0,(n\to \infty ).\end{array}$$

(8)

We obtain

$$\begin{array}{cc}\hfill \parallel x_n-T^n{x}_n\parallel & =\parallel x_n-x_{n+1}+x_{n+1}-T^n{u}_n+T^n{u}_n-T^n{x}_n\parallel \hfill \\ \hfill & \le \parallel x_n-x_{n+1}\parallel +\parallel x_{n+1}-T^n{u}_n\parallel +k_n\parallel u_n-x_n\parallel \hfill \\ \hfill & \le \parallel x_n-x_{n+1}\parallel +\parallel x_{n+1}-T^n{u}_n\parallel +k_n(1-{\delta }_n)\parallel z_n-x_n\parallel .\hfill \end{array}$$

By (4), (6), and (8), we have

$$\begin{array}{c}\hfill \parallel x_n-T^n{x}_n\parallel \to 0,n\to \infty .\end{array}$$

(9)

Since T is an asymptotically nonexpansive mapping, we have

$$\begin{array}{cc}\hfill \parallel x_n-T{x}_n\parallel & =\parallel x_n-x_{n+1}+x_{n+1}-T^{n+1}{x}_{n+1}+T^{n+1}{x}_{n+1}-T^{n+1}{x}_n+T^{n+1}{x}_n-T{x}_n\parallel \hfill \\ \hfill & \le \parallel x_n-x_{n+1}\parallel +\parallel x_{n+1}-T^{n+1}{x}_{n+1}\parallel +\parallel T^{n+1}{x}_{n+1}-T^{n+1}{x}_n\parallel +\parallel T^{n+1}{x}_n-T{x}_n\parallel \hfill \\ \hfill & \le \parallel x_n-x_{n+1}\parallel +\parallel x_{n+1}-T^{n+1}{x}_{n+1}\parallel +k_{n+1}\parallel x_{n+1}-x_n\parallel +k_1\parallel T^n{x}_n-x_n\parallel \hfill \\ \hfill & \le (1+k_{n+1})\parallel x_n-x_{n+1}\parallel +\parallel x_{n+1}-T^{n+1}{x}_{n+1}\parallel +k_1\parallel T^n{x}_n-x_n\parallel .\hfill \end{array}$$

By (4) and (9), we have

$$\begin{array}{c}\hfill \parallel x_n-T{x}_n\parallel \to 0,n\to \infty .\end{array}$$

(10)

Since E is a uniformly smooth Banach space and $x_n$ is bounded, there exists a subsequence of $x_n$ which converges weakly to $\omega$. We know that $\mathsf{\Psi }$ is nonexpansive by Lemma 8. From (7) and Lemma 5, we deduce $\omega \in F(\mathsf{\Psi })$. It follows (10) and Lemma 5, and we deduce $w\in F(T)$. Therefore, $\omega \in \mathsf{\Omega }$. From Lemma 6, the following holds:

$$⟨(I-f)x^{†},j(x^{†}-\omega )⟩\le 0,\forall \omega \in \mathsf{\Omega }.$$

Further, noticing that j is the weakly sequential continuous duality mapping, we have

$$\begin{array}{c}\hfill limsu{p}_{n\to \infty }⟨(I-f)x^{†},j(x^{†}-x_n)⟩=\underset{k\to \infty }{lim}⟨(I-f)x^{†},j(x^{†}-x_{n_k})⟩=⟨(I-f)x^{†},j(x^{†}-\omega )⟩\le 0.\end{array}$$

(11)

Finally, we observe

$$\begin{array}{cc}\hfill \parallel x_{n+1}-x^{†}{\parallel }^2& =⟨x_{n+1}-x^{†},j(x_{n+1}-x^{†})⟩\hfill \\ \hfill & =⟨{\alpha }_n(f(x_n)-x^{†})+{\beta }_n(x_n-x^{†})+{\gamma }_n(T^n{u}_n-x^{†}),j(x_{n+1}-x^{†})⟩\hfill \\ \hfill & \le {\alpha }_n⟨f(x_n)-f(x^{†}),j(x_{n+1}-x^{†})⟩+{\beta }_n⟨x_n-x^{†},j(x_{n+1}-x^{†})⟩\hfill \\ \hfill & +{\gamma }_n⟨T^n{u}_n-x^{†},j(x_{n+1}-x^{†})⟩+{\alpha }_n⟨f(x^{†})-x^{†},j(x_{n+1}-x^{†})⟩\hfill \\ \hfill & \le {\alpha }_n\rho \parallel x_n-x^{†}\parallel \parallel x_{n+1}-x^{†}\parallel +{\beta }_n\parallel x_n-x^{†}\parallel \parallel x_{n+1}-x^{†}\parallel \hfill \\ \hfill & +{\gamma }_n{k}_n\parallel u_n-x^{†}\parallel \parallel x_{n+1}-x^{†}\parallel +{\alpha }_n⟨f(x^{†})-x^{†},j(x_{n+1}-x^{†})⟩\hfill \\ \hfill & \le {\alpha }_n\rho \parallel x_n-x^{†}\parallel \parallel x_{n+1}-x^{†}\parallel +{\beta }_n\parallel x_n-x^{†}\parallel \parallel x_{n+1}-x^{†}\parallel \hfill \\ \hfill & +{\gamma }_n{k}_n\parallel x_n-x^{†}\parallel \parallel x_{n+1}-x^{†}\parallel +{\alpha }_n⟨f(x^{†})-x^{†},j(x_{n+1}-x^{†})⟩\hfill \\ \hfill & =[{\alpha }_n\rho +{\beta }_n+{\gamma }_n{k}_n]\parallel x_n-x^{†}\parallel \parallel x_{n+1}-x^{†}\parallel +{\alpha }_n⟨f(x^{†})-x^{†},j(x_{n+1}-x^{†})⟩\hfill \\ \hfill & \le \frac{{\alpha }_n\rho +{\beta }_n+{\gamma }_n{k}_n}{2}(\parallel x_n-x^{†}{\parallel }^2+\parallel x_{n+1}-x^{†}{\parallel }^2)+{\alpha }_n⟨f(x^{†})-x^{†},j(x_{n+1}-x^{†})⟩,\hfill \end{array}$$

which implies

$$\begin{array}{cc}\hfill & \parallel x_{n+1}-x^{†}{\parallel }^2\hfill \\ \hfill & \le \frac{{\alpha }_n\rho +{\beta }_n+{\gamma }_n{k}_n}{2-{\alpha }_n\rho -{\beta }_n-{\gamma }_n{k}_n}{\parallel x_n-x^{†}\parallel }^2+\frac{2{\alpha }_n}{2-{\alpha }_n\rho -{\beta }_n-{\gamma }_n{k}_n}⟨f(x^{†})-x^{†},j(x_{n+1}-x^{†})⟩\hfill \\ \hfill & =[1-\frac{2(1-{\alpha }_n\rho -{\beta }_n-{\gamma }_n{k}_n)}{2-{\alpha }_n\rho -{\beta }_n-{\gamma }_n{k}_n}]{\parallel x_n-x^{†}\parallel }^2+\frac{2{\alpha }_n}{2-{\alpha }_n\rho -{\beta }_n-{\gamma }_n{k}_n}⟨f(x^{†})-x^{†},j(x_{n+1}-x^{†})⟩\hfill \\ \hfill & \le [1-\frac{2{\alpha }_n((1-\rho -ϵ)}{2-{\alpha }_n\rho -{\beta }_n-{\gamma }_n{k}_n}]{\parallel x_n-x^{†}\parallel }^2+\frac{2{\alpha }_n}{2-{\alpha }_n\rho -{\beta }_n-{\gamma }_n{k}_n}⟨f(x^{†})-x^{†},j(x_{n+1}-x^{†})⟩.\hfill \end{array}$$

(12)

We have $b_n=\frac{2{\alpha }_n((1-\rho -ϵ)}{2-{\alpha }_n\rho -{\beta }_n-{\gamma }_n{k}_n}$ and ${\sigma }_n=\frac{⟨f(x^{†})-x^{†},j(x_{n+1}-x^{†})⟩}{1-\rho -ϵ}$, then by the condition $(i)$ and (11), we have

$$\begin{array}{cc}\hfill & \sum _{n=0}^{\infty }{b}_n=\sum _{n=0}^{\infty }\frac{2{\alpha }_n((1-\rho -ϵ)}{2-{\alpha }_n\rho -{\beta }_n-{\gamma }_n{k}_n}\ge \sum _{n=0}^{\infty }{\alpha }_n((1-\rho -ϵ)=+\infty \hfill \\ \hfill & \underset{n\to \infty }{lim\; sup}{\sigma }_n=\underset{n\to \infty }{lim\; sup}\frac{⟨f(x^{†})-x^{†},j(x_{n+1}-x^{†})⟩}{1-\rho -ϵ}\le 0.\hfill \end{array}$$

Thus, applying Lemma 2 to (12), we have ${lim}_{n\to \infty }\parallel x_n-x^{†}\parallel =0$ . This completes the proof. □

Corollary 1.

Let H be a real Hilbert space. Let $\varnothing \ne K\subset H$ be a closed convex subset. Suppose that $T:K\to K$ is a nonexpansive mapping. Let $A,B:K\to H$ be α-inverse strongly monotone operator and β-inverse strongly monotone operator. Let $f:K\to K$ be a contraction with coefficient $\rho \in (0,1)$ and Ψ be defined by Lemma 8. Assume that $\mathsf{\Omega }=F(T)\bigcap F(\mathsf{\Psi })\ne \varnothing$. Suppose $\{{\alpha }_n\},\{{\beta }_n\},\{{\gamma }_n\},\{{\delta }_n\}\subset (0,1)$. If the sequence $\{x_n\}$ is generated in the following manner:

$$\left\{\begin{array}{cc}\hfill & w_n=P_K(I-\mu B)x_n,\hfill \\ \hfill & z_n=P_K(I-\lambda A)(t{x}_n+(1-t)w_n),\hfill \\ \hfill & u_n={\delta }_n{x}_n+(1-{\delta }_n)z_n,\hfill \\ \hfill & x_{n+1}={\alpha }_{n}f(x_n)+{\beta }_n{x}_n+{\gamma }_{n}T{u}_n.\hfill \end{array}\right.$$

satisfying the following conditions:

$$\begin{array}{cc}\hfill & (i){\alpha }_n+{\beta }_n+{\gamma }_n=1,\underset{n\to \infty }{lim}{\alpha }_n=0,{\mathsf{\Sigma }}_{n=0}^{\infty }{\alpha }_n=\infty ;\hfill \\ \hfill & (ii)0<\underset{n\to \infty }{lim\; inf}{\beta }_n\le \underset{n\to \infty }{lim\; sup}{\beta }_n<1,\underset{n\to \infty }{lim}|{\delta }_{n+1}-{\delta }_n|=0;\hfill \\ \hfill & (iii)0\le t<1,0<\lambda <\frac{2\alpha }{c},0<\mu <\frac{2\beta }{c}.\hfill \end{array}$$

Then $\{x_n\}$ converges strongly to $x^{†}\in \mathsf{\Omega }$ which solves the variational inequality:

$$⟨(I-f)x^{†},x^{†}-p⟩\le 0,\forall p\in \mathsf{\Omega }.$$

Proof. 

In Theorem 1, we put $k_n\equiv 1$ for each $n\in N$ and replace Banach space X with Hilbert space H. □

Corollary 2.

Let X be a uniformly convex and uniformly smooth Banach space. Let $\varnothing \ne E\subset X$ be a closed convex subset. Suppose that $Q_E:X\to E$ is a sunny nonexpansive retraction and $T:E\to E$ is an asymptotically nonexpansive mapping satisfying the uniformly asymptotically regular condition, and $A,B:E\to X$ are an α-inverse strongly accretive operator and β-inverse strongly accretive operator, respectively. Let $f:E\to E$ be a contraction with coefficient $\rho \in (0,1)$ and Ψ be defined by Lemma 8. Assume that $\mathsf{\Omega }=F(T)\bigcap F(\mathsf{\Psi })\ne \varnothing$. Suppose $\{{\alpha }_n\},\{{\beta }_n\},\{{\gamma }_n\},\{{\delta }_n\}\subset (0,1)$. If the sequence $\{x_n\}$ generated by the following manner:

$$\left\{\begin{array}{cc}\hfill & w_n=Q_E(I-\mu B)x_n,\hfill \\ \hfill & z_n=Q_E(I-\lambda A)w_n,\hfill \\ \hfill & u_n={\delta }_n{x}_n+(1-{\delta }_n)z_n,\hfill \\ \hfill & x_{n+1}={\alpha }_{n}f(x_n)+{\beta }_n{x}_n+{\gamma }_n{T}^n{u}_n.\hfill \end{array}\right.$$

satisfies the following conditions:

$$\begin{array}{cc}\hfill & (i){\alpha }_n+{\beta }_n+{\gamma }_n=1,\underset{n\to \infty }{lim}{\alpha }_n=0,{\mathsf{\Sigma }}_{n=0}^{\infty }{\alpha }_n=\infty ,k_n-1=ϵ{\alpha }_n,0<ϵ<1-\rho ;\hfill \\ \hfill & (ii)0<\underset{n\to \infty }{lim\; inf}{\beta }_n\le \underset{n\to \infty }{lim\; sup}{\beta }_n<1,\underset{n\to \infty }{lim}|{\delta }_{n+1}-{\delta }_n|=0;\hfill \\ \hfill & (iii)0<\lambda <\frac{2\alpha }{c},0<\mu <\frac{2\beta }{c};\hfill \\ \hfill & (iv){\beta }_n+{\gamma }_n{k}_n^2<1,\hfill \end{array}$$

then $\{x_n\}$ converges strongly to an element $x^{†}\in \mathsf{\Omega }$, which is also the solution of the variational inequality:

$$⟨(I-f)x^{†},j(x^{†}-p)⟩\le 0,\forall p\in \mathsf{\Omega }.$$

Proof. 

In Theorem 1, if $t\equiv 0$, then we obtain the corollary. If $f=u$ and T is a nonexpansive mapping, it is the main result of Qin et al. [6]. □

4. Numerical Examples

In this section, we provide a numerical example to support the validity and feasibility of our proposed algorithm. The results are performed on a personal computer with Intel(R) Core(TM) i7-4710MQ CPU @ 2.50 GHz and RAM 8.00 GB.

Example 1.

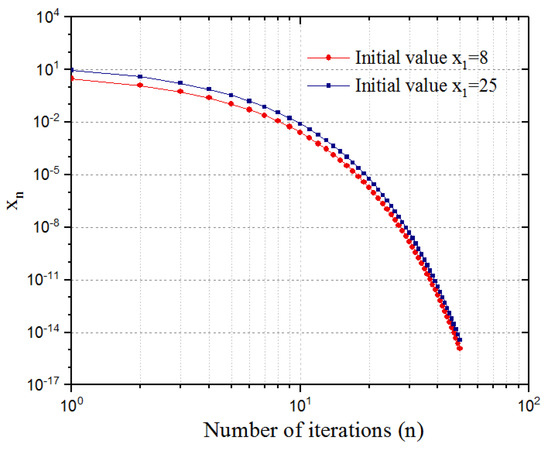
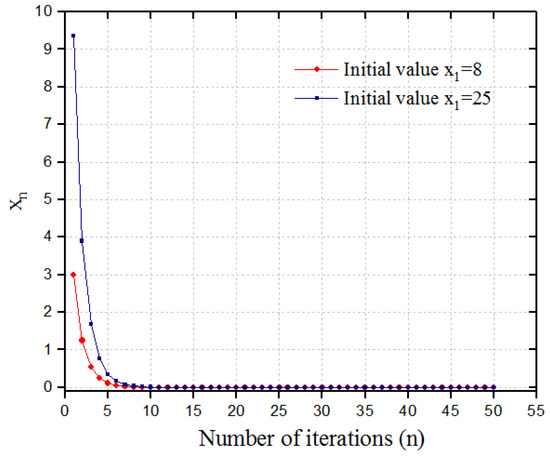
In the real number field R, we put $Bx=\frac{1}{6}x$ and $Ax=\frac{1}{4}x$ where $x\in R$. Let $k_n=1+\frac{1}{12n}$, ${\delta }_n=1-\frac{1}{3n}$, ${\alpha }_n=\frac{1}{3n}$, ${\beta }_n=\frac{1}{2}-\frac{1}{3n}$ and ${\gamma }_n=\frac{1}{2}$ for all $n\in N$. We take $t=\frac{1}{4}$, $\mu =3$, $\lambda =2$. Let T and f be defined by $Tx=\frac{1}{4}x$, $f(x)=\frac{1}{3}x$. This implies that $ϵ=\frac{1}{4}$ and $\rho =\frac{1}{3}$. Then, starting $x_1=8$ and $x_1=25$ in (3). We have

$$x_{n+1}=\frac{144n+144n\times {(\frac{1}{4})}^n-33\times {(\frac{1}{4})}^n-64}{288n}{x}_n.$$

We obtain the following numerical results, as shown in Figure 1 and Figure 2.

Figure 1. Exponential coordinate iteration.

Figure 2. Real coordinate iteration.

Remark 1.

First of all, the parameters in Example 1 satisfy the conditions (i)–($iv$) in Theorem 1, which shows that the coefficients in our Theorem 1 are obtained. From Figure 1, we can see the convergence value of the iterative sequence when the initial values are $x_1=8$ and $x_1=25$, respectively. From Figure 2, we can observe the convergence speed of the iterative algorithm. Figure 1 and Figure 2 show that $\{x_n\}$ converges strongly to 0, where $F(T)\bigcap F(\mathsf{\Psi })=0$. The convergence of $\{x_n\}$ in Example 1 shows the implementation and efficiency of our proposed algorithm.

5. Conclusions

In this paper, we provide a viscosity approximation method for a general variational inequality system and fixed point problems in Banach spaces. Some strong convergence theorems are obtained and the numerical experiments can be guaranteed by Theorem 1. We give an extension to the general variational inequality system in Banach spaces and we generalize the Hilbert spaces to Banach spaces, and the nonexpansive mapping to the asymptotically nonexpansive mappings of Imnang [5] and Cai et al. [14], for the fixed point problem and variational inequality problem. In Theorem 1, if $t=0$ ${\delta }_n=0$ in Hilbert spaces, this is the main results of Ceng et al. [3]. The results and methods presented here also include some corresponding recent results of [6,9,10,12,13,14,17] as special cases.