Research on Spectrum Optimization Technology for a Wireless Communication System
Abstract
1. Introduction
2. General Function Model with the Minimal Spectral Energy Leakage
3. Limitations of the General Function Model
4. Solution and Analysis of Signal with High-Quality Spectrum Characteristics
4.1. Numerical Solution of Signal with High-Quality Spectral Characteristics
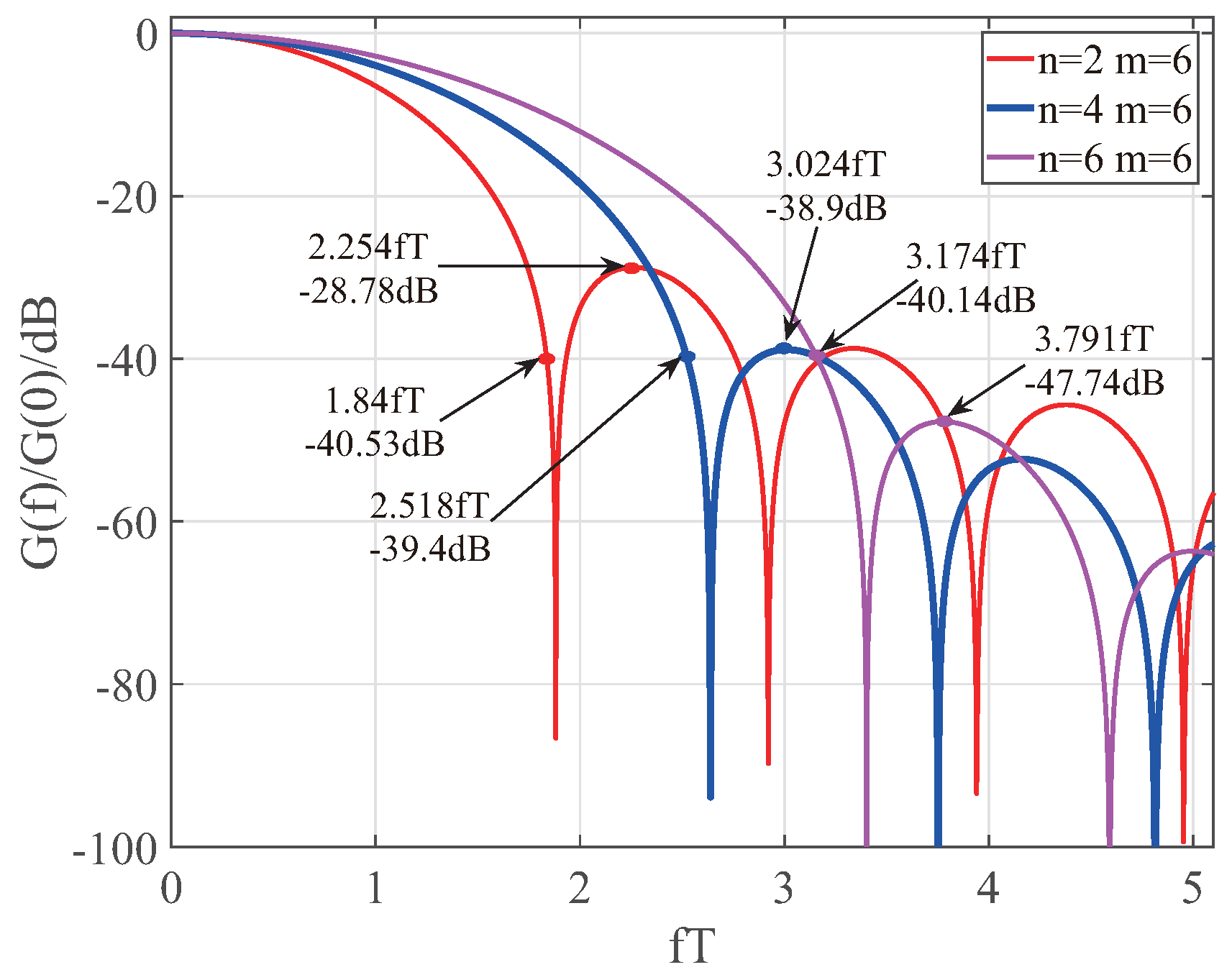
4.2. Comparative Analysis of Energy Spectrum under Different Constraints
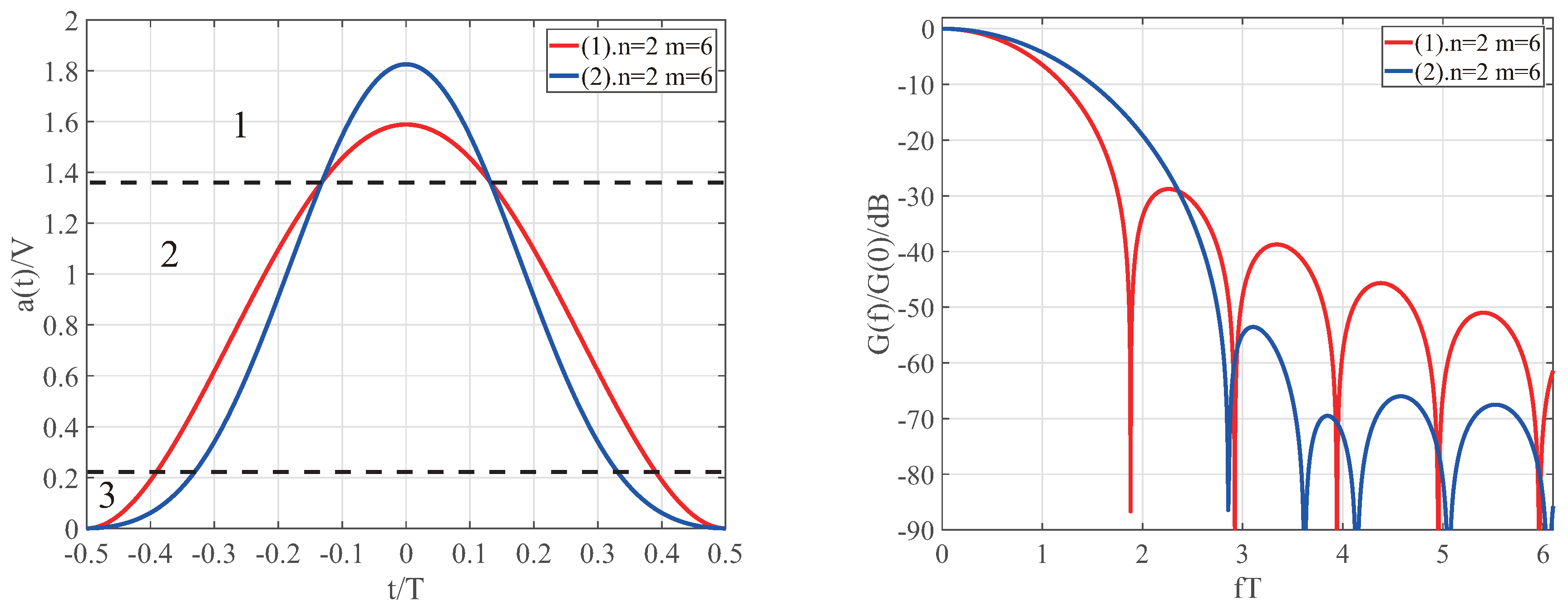
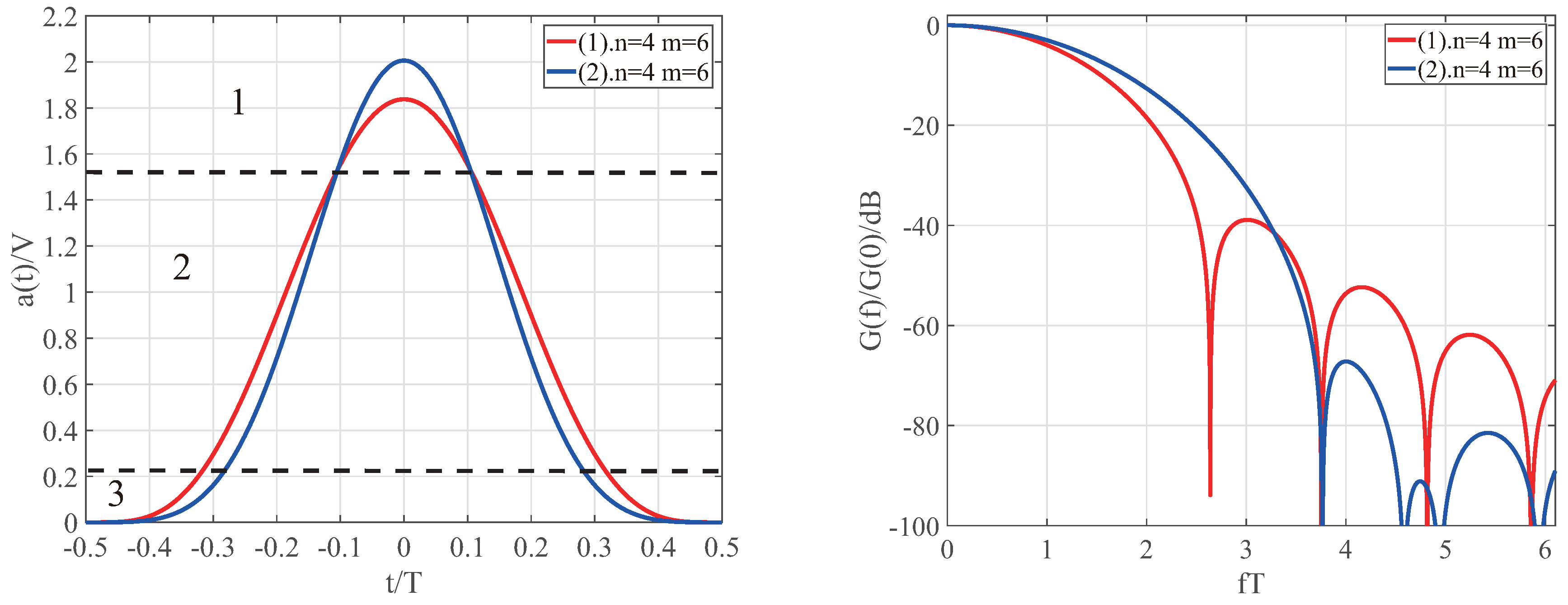
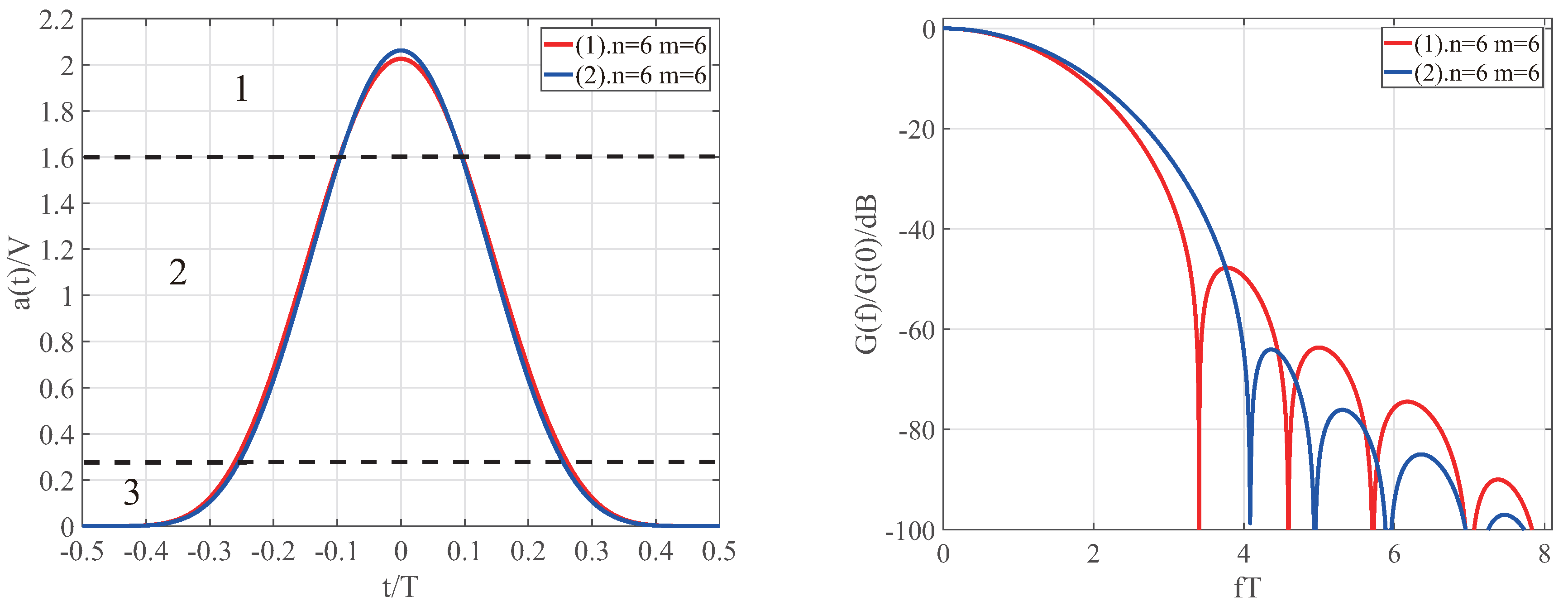
4.3. Spectral Analysis of Signals with Additional Frequency-Domain Restrictions
4.4. Comparative Analysis of Spectral Characteristics under Different Constraints at n = 2
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Han, S.H.; Lee, J.H. An overview of peak-to-average power ratio reduction techniques for multicarrier transmission. IEEE Trans. Wirel. Commun. 2005, 12, 56–65. [Google Scholar] [CrossRef]
- Sahin, A.; Guvene, I.; Sian, H. A Survey on Multicarrier Communications: Prototype Filters, Lattice Structures, and Implementation Aspects. IEEE Commun. Surv. Tutor. 2014, 16, 1312–1338. [Google Scholar] [CrossRef]
- Chevalier, P.; Pipon, F. New insights into optimal widely linear array receivers for the demodulation of BPSK, MSK, and GMSK signals corrupted by noncircular interferences-application to SAIC. IEEE Trans. Signal Process. 2006, 54, 870–883. [Google Scholar] [CrossRef]
- Shen, Z.; Andrews, J.G.; Evans, B.L. Adaptive resource allocation in multiuser OFDM systems with proportional rate constraints. IEEE Trans. Wirel. Commun. 2005, 4, 2726–2737. [Google Scholar] [CrossRef]
- Wu, Q.; Li, Y.; Zakharov, Y.V.; Xue, W.; Shi, W. A Kernel Affine Projection-Like Algorithm in Reproducing Kernel Hilbert Space. IEEE Trans. Circuits Syst. II Express Briefs 2019, 14, 1–5. [Google Scholar] [CrossRef]
- Armstrong, J. OFDM for Optical Communications. J. Lightw. Technol. 2009, 27, 189–204. [Google Scholar] [CrossRef]
- Jang, J.; Lee, K.B. Transmit power adaptation for multiuser OFDM systems. IEEE J. Sel. Areas Commun. 2003, 21, 171–178. [Google Scholar] [CrossRef]
- Farhang-Boroujeny, B. OFDM Versus Filter Bank Multicarrier. IEEE Commun. Mag. 2011, 28, 92–112. [Google Scholar] [CrossRef]
- Siohan, P.; Siclet, C.; Lacaille, N. Analysis and design of OFDM/OQAM systems based on filterbank theory. IEEE Trans. Signal Process. 2002, 50, 1170–1183. [Google Scholar] [CrossRef]
- Mesleh, R.Y.; Haas, H.; Sinanovic, S.; Ahn, C.W.; Yun, S. Spatial Modulation. IEEE Trans. Veh. Technol. 2008, 57, 2228–2241. [Google Scholar] [CrossRef]
- Michailow, N.; Mendes, L.; Matthé, M.; Gaspar, I.; Festag, A.; Fettweis, G. Robust WHT-GFDM for the Next Generation of Wireless Networks. IEEE Commun. Lett. 2015, 19, 106–109. [Google Scholar] [CrossRef]
- Tao, Y.; Liu, L.; Liu, S.; Zhang, Z. A survey: Several technologies of non-orthogonal transmission for 5G. China Commun. 2015, 12, 1–15. [Google Scholar] [CrossRef]
- Farhang, A.; Marchetti, N.; Doyle, L.E. Low-Complexity Modem Design for GFDM. IEEE Trans. Signal Process. 2016, 64, 1507–1518. [Google Scholar] [CrossRef]
- Matthé, M.; Mendes, L.L.; Fettweis, G. Generalized Frequency Division Multiplexing in a Gabor Transform Setting. IEEE Commun. Lett. 2014, 18, 1379–1382. [Google Scholar] [CrossRef]
- Qu, D.; Lu, S.; Jiang, T. Multi-Block Joint Optimization for the Peak-to-Average Power Ratio Reduction of FBMC-OQAM Signals. IEEE Trans. Signal Process. 2013, 61, 1605–1613. [Google Scholar] [CrossRef]
- Ihalainen, T.; Ikhlef, A.; Louveaux, J.; Renfors, M. Channel Equalization for Multi-Antenna FBMC/OQAM Receivers. IEEE Trans. Veh. Technol. 2011, 60, 2070–2085. [Google Scholar] [CrossRef]
- Michailow, N.; Matthe, M.; Gaspar, I.S.; Caldevilla, A.N.; Mendes, L.L.; Festag, A.; Fettweis, G. Generalized Frequency Division Multiplexing for 5th Generation Cellular Networks. IEEE Trans. Commun. 2014, 62, 3045–3061. [Google Scholar] [CrossRef]
- Saeedi-Sourck, H.; Wu, Y.; Bergmans, J.W.M.; Sadri, S.; Farhang-Boroujeny, B. Sensitivity analysis of offset QAM multicarrier systems to residual carrier frequency and timing offsets. Signal Process. 2011, 91, 1604–1612. [Google Scholar] [CrossRef]
- Zhang, L.; Xiao, P.; Zafar, A.; Quddus, A.; Tafazolli, R. FBMC System: An Insight Into Doubly Dispersive Channel Impact. IEEE Trans. Veh. Technol. 2016, 66, 3942–3956. [Google Scholar] [CrossRef]
- Caus, M.; Pérez-Neira, A.I. Multi-Stream Transmission for Highly Frequency Selective Channels in MIMO-FBMC/OQAM Systems. IEEE Trans. Signal Process. 2013, 62, 786–796. [Google Scholar] [CrossRef]
- Zhang, D.; Matthé, M.; Mendes, L.L.; Fettweis, G. A Study on the Link Level Performance of Advanced Multicarrier Waveforms Under MIMO Wireless Communication Channels. IEEE Trans. Wirel. Commun. 2017, 16, 2350–2365. [Google Scholar] [CrossRef]
- Xu, Y.; Xue, W.; Shang, W. A Pan-Function Model for the Utilization of Bandwidth Improvement and PAPR Reduction. Math. Probl. Eng. 2014, 2014. [Google Scholar] [CrossRef]

| m | ||||||||
|---|---|---|---|---|---|---|---|---|
| 3 | 1.5478 | 0.8877 | 0.1163 | 0.0025 | - | - | - | - |
| 4 | 1.5280 | 0.9011 | 0.1438 | 0.0052 | −0.0015 | - | - | - |
| 5 | 1.5252 | 0.9038 | 0.1413 | −0.0004 | −0.0003 | 0.0002 | - | - |
| 6 | 1.5077 | 0.9155 | 0.1585 | −0.0029 | 0.0003 | −0.00002 | −0.00001 | - |
| 7 | 1.4769 | 0.9339 | 0.1931 | −0.0022 | 0.0002 | 0.00001 | 0.00002 | 0.00002 |
| m | ||||||||
|---|---|---|---|---|---|---|---|---|
| 4 | 1.4479 | 0.9540 | 0.2256 | −0.0027 | 0.0017 | - | - | - |
| 5 | 1.3873 | 0.9687 | 0.3059 | 0.0319 | −0.0008 | −0.0018 | - | - |
| 6 | 1.3812 | 0.9727 | 0.3127 | 0.0301 | −0.0006 | −0.00004 | 0.00004 | - |
| 7 | 1.3597 | 0.9782 | 0.3391 | 0.0393 | −0.0013 | 0.0001 | −0.00001 | −0.000002 |
| m | ||||||||
|---|---|---|---|---|---|---|---|---|
| 5 | 1.331 | 0.9857 | 0.3844 | 0.0592 | −0.0007 | 0.0003 | - | - |
| 6 | 1.3279 | 0.9843 | 0.3841 | 0.0598 | −0.0004 | 0.0002 | −0.00007 | - |
| 7 | 1.3269 | 0.9875 | 0.3842 | 0.0596 | −0.0003 | 0.0002 | −0.00006 | 0.00002 |
| n | the Number of Lines | m | |
|---|---|---|---|
| 2 | Figure 2, line 1 | 6 | 1.470202 |
| Figure 2, line 2 | 1.780325 | ||
| 4 | Figure 3, line 1 | 1.855372 | |
| Figure 3, line 2 | 2.242426 | ||
| 6 | Figure 4, line 1 | 2.197020 | |
| Figure 4, line 2 | 2.309111 |
| m | −40 dB Spectrum Bandwidth | −60 dB Spectrum Bandwidth | |
|---|---|---|---|
| 5 | 1.466991 | 3.533 fT | 7.614 fT |
| 6 | 1.470202 | ||
| 7 | 1.466096 |
| m | −40 dB Spectrum bandwidth | −60 dB Spectrum bandwidth | |
|---|---|---|---|
| 5 | 1.744317 | 2.57 fT | 4.647 fT |
| 6 | 1.780325 | 2.61 fT | 3.39 fT |
| 7 | 1.860039 | 2.722 fT | 3.716 fT |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, M.; Xue, W.; Jia, P.; Makarov, S.B.; Li, B. Research on Spectrum Optimization Technology for a Wireless Communication System. Symmetry 2020, 12, 34. https://doi.org/10.3390/sym12010034
Liu M, Xue W, Jia P, Makarov SB, Li B. Research on Spectrum Optimization Technology for a Wireless Communication System. Symmetry. 2020; 12(1):34. https://doi.org/10.3390/sym12010034
Chicago/Turabian StyleLiu, Mingxin, Wei Xue, Peisong Jia, Sergey B. Makarov, and Beiming Li. 2020. "Research on Spectrum Optimization Technology for a Wireless Communication System" Symmetry 12, no. 1: 34. https://doi.org/10.3390/sym12010034
APA StyleLiu, M., Xue, W., Jia, P., Makarov, S. B., & Li, B. (2020). Research on Spectrum Optimization Technology for a Wireless Communication System. Symmetry, 12(1), 34. https://doi.org/10.3390/sym12010034





