Abstract
Lightweight stream ciphers have attracted significant attention in the last two decades due to their security implementations in small devices with limited hardware. With low-power computation abilities, these devices consume less power, thus reducing costs. New directions in ultra-lightweight cryptosystem design include optimizing lightweight cryptosystems to work with a low number of gate equivalents (GEs); without affecting security, these designs consume less power via scaled-down versions of the Mutual Irregular Clocking KEYstream generator—version 2-(MICKEY 2.0) cipher. This study aims to obtain a scaled-down version of the MICKEY 2.0 cipher by modifying its internal state design via reducing shift registers and modifying the controlling bit positions to assure the ciphers’ pseudo-randomness. We measured these changes using the National Institutes of Standards and Testing (NIST) test suites, investigating the speed and power consumption of the proposed scaled-down version named MICKEY 2.0.85. The (85) refers to the new modified bit-lengths of each MICKEY 2.0 register. The results show that it is faster, requires less power, and needs fewer GEs. The proposed variant will enhance the security of applications, such asRadio-frequency identification (RFID) technology, sensor networks, and in Internet of things (IoT) in general. It also will enhance research on the optimization of existing lightweight cryptosystems.
1. Introduction
The need to implement lightweight, synchronous encryption algorithms that are suitable for RFID technology is significantly growing. These algorithms are important factors in the cost reduction in small and limited-sized devices and in ensuring financial efficiency in the use of smaller microcontrollers. Moreover, encryption methods need to be tested, as demonstrated in the tests performed for MICKEY 2.0 [1], and scaled-down variants should be proposed with standard randomness tests to ensure security. We introduced a further optimized version of MICKEY 2.0, which is suitable for implementation in real-life applications that require smaller ship sizes with less memory and power consumption (MICKEY 2.0.85). Then, we evaluated its performance to demonstrate its resistance against possible statistical attacks.
Obtaining a scaled-down version of MICKEY 2.0 while maintaining its security is challenging. To achieve this, the objective is to reduce the internal state to save the number of gate equivalents (GEs), and to use the National Institutes of Standards and Testing (NIST) test suite [2] to test the keystream sequences that are sufficiently large in length and number.
Lightweight cryptosystems aim to provide security for devices with specific restraints, such as small memory size and lower computing power and power consumption. Currently, the most effective and widely used cryptosystems, such as Advanced Encryption Standard (AES) [3], require greater computation ability as well as greater ship sizes. The non-lightweight ciphers have slower speed and low throughput [4,5]. Lightweight cryptosystems provide solutions for issues raised by implementing AES, for example, encryption speed and power consumption.
Lightweight stream ciphers, for example, present a more secure solution for small devices, such as microcontrollers and RFID components, namely, RFID tags and RFID readers. Security is needed for small components in important technology, such as sensor networks and IoT technology [6,7,8].
Ciphers such as Trivium has been investigated to design scaled-down versions to suit small technology, such as the Micro-Trivium designed by [9]. However, our proposed MICKEY 2.0 cipher variants consume less power and require fewer GEs than other ciphers. This is discussed in more detail in Section 6.3.
Considering the importance of applying a NIST candidate cipher to hardware [10] demonstrated how NIST can be used as a standard evaluation tool for ciphers. Moreover, their study discussed the hardware design and evaluations standardized by NIST for lightweight ciphers and investigated ACE and WAGE Ciphers. Additional details on the implementation of microcontrollers can be found in [11].
We chose to reduce the power consumption and increase the processing speed by reducing the number of bits in the internal registers (and corresponding driving data structures). The novel discovery is that the overall randomness of the keystream generated was actually slightly better than the MICKEY 2.0 algorithm. This indicated that the additional bits in MICKEY 2.0 were adding power consumption and time without providing additional value.
We propose a MICKEY 2.0 variant to reduce the power consumption and the number of GEs without compromising security. By optimizing and testing the proposed variant with the NIST test suite for the pseudo-randomness comparison between MICKEY 2.0 and MICKEY 1.0, and performing a preliminary cryptanalysis, the security level for this variant appears to be as good as, or slightly better than, MICKEY 2.0. Additionally, its performance in terms of security, speed, and power consumption is measured.
The main contributions of this paper to existing lightweight encryption methods are as follows:
- We propose a new MICKEY 2.0 cipher variant, called MICKEY 2.0.85. This variant has been tested for pseudo-randomness, which, to the best of our knowledge, has never been done before.
- We presented a reduction method for MICKEY 2.0, which resulted in fewer GES for MICKEY 2.0.85.
- We propose a new variant (MICKEY 2.0.85), which is 23% faster and consumes 16% less power than MICKEY 2.0 while maintaining similar pseudo-randomness test results.
- We performed two common cryptanalysis processes, each of which shows the lighter variant to be at least as resistant to attacks as its less efficient predecessor.
This paper is organized as follows. The background and an overview of the MICKEY algorithm are provided in Section 2. The study methodology is presented in Section 3. Section 4 presents an overview of the related work on symmetric encryption and lightweight encryption, in addition to the scaled-down version of the Trivium. Section 5 provides an illustrated description of the MICKEY 2.0 scaled-down methodology. Section 6 describes the utilization of the results and analysis of the following aspects: (1) the NIST test suite to test the pseudo-randomness of MICKEY 2.0 and MICKEY 2.0.85, (2) the speed test performance, and (3) the power consumption tests with the number of GEs. Section 7 contains our cryptanalysis results. Section 8 provides an overall discussion, and Section 9 concludes the paper, along with suggestions for possible future work.
2. Background
MICKEY 2.0 is a lightweight stream cipher designed for hardware implementation and can also be implemented in software applications. The following section provides an overview of how the MICKEY 2.0 cipher works. Additional details can be found in [1].
2.1. MICKEY 2.0 Family of Ciphers
The MICKEY 2.0 cipher family generates a keystream using two internal registers. These registers are used to determine the value (1 or 0) for any given bit position within the keystream.
In general, a keystream is intended to be XORed with a plaintext message to generate ciphertext. Ideally, the keystream should be random enough to mask any statistical patterns within the plaintext and to be irreversible so that the key cannot be derived.
The original MICKEY algorithm (MICKEY 1.0) was vulnerable to statistical attacks. Not surprisingly, MICKEY 1.0 failed all but one of the NIST randomness tests. The MICKEY 2.0 cipher is an improved version of MICKEY 1.0 [12]. The MICKEY 2.0 cipher has two registers, R (linear register) and S (nonlinear register). These registers are initialized by merging an 80-bit key and an 80-bit initialization vector (IV).
As the keystream is generated, the ‘clock’ is advanced along both the linear (R) and nonlinear (S) registers based on the state of the internal control structures, which include R_TAPS, COMP0, COMP1, FB0, and FB1. For simplicity, we will focus on the scaled-down process. The full design description can be found in [1].
The keystream generation process begins with initialization. Both registers (linear and nonlinear) are initialized with all zeros in all their bits. Then, using the key/IV pair, they are loaded by calling the normal keystream clocking function.
As the keystream is being generated, the registers are advanced, generating pseudo-random bits until the keystream reaches the desired number of bits.
The diagram below (Figure 1) illustrates the relationship between the linear and nonlinear registers. Section 5.1 contains detailed flowcharts of the MICKEY family Algorithms.
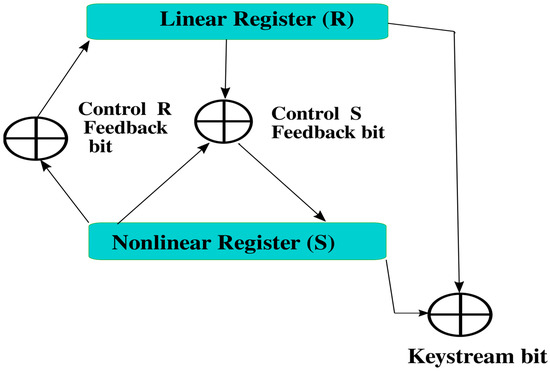
Figure 1.
MICKEY family cipher structure.
2.2. MICKEY Algorithm Keystream Generation
This study aims to reduce the power requirements and increase the performance of the MICKEY algorithm by reducing the size of the internal state. MICKEY 2.0 has a 200-bit internal state (100 bits for each register). The proposed scaled-down variant has a 170-bit internal state (85 bits for each register). While it is no surprise that reducing the number of bits reduces power consumption and increases speed, we have shown, using the NIST testing suite, that this increase in speed and reduction in power does not affect the randomness of the keystream, in fact, Mikey 2.0.85 is slightly more random than MICKEY 2.0
2.3. Algorithm Overview
In the MICKEY Algorithm, each clock function changes the state of the linear register or the nonlinear register or both. Depending on the current state of the registers, previous input, and the values of the internal control structures, each advancement of the clock either XORs the specified register state or shifts it. This uses a ‘feedback’ (prior input) and ‘control’ (internal data structure) mechanism to make the register state changes unpredictable.
GEs can be used to specify the complexity of the electronic circuits. In general, the more GEs an algorithm requires, the slower it is, and the more power it uses [13]. Appendix A and Appendix B describe GEs and how they were determined for both MICKEY 2 and Mikey 2.0.85.
2.4. Internal State: Data Structure Details
The internal states of the algorithms were altered by advancing the clock based on the following driving data structures: R_TAPS, S_TAG/COMP0, COMP1, FB1, and FB0. We will refer to these as “The State Drivers” or “Internal Drivers”. For simplicity, we have focused on the scaled-down process. The full design description can be found in [1].
3. Methods
This paper aims to find the scaled-down version of MICKEY 2.0, which can be faster, smaller, and with less power consumption.
Hypothesis
It is possible to create a faster and more efficient algorithm by revising MICKEY 2.0 to use smaller internal state while maintaining randomness.
We conduct our study using the following methods:
- By reducing the number of bits for both registers, the number of gates (XOR, AND, and MUX) will be reduced given that the number of iterations within the loops will decrease. Therefore, the cipher will have less GEs.The reduction methods should be implemented carefully because they affect the security due to their effect on the pseudo-randomness for the generated keystream.The bits removed from each register were selected, and pseudo-randomness tests were performed.
- NIST randomness consisting of a 15-test suite is a standard statistical test that can be implemented on the keystream generated by the targeted cipher to evaluate the cipher strength. The comparison of these results with existing and popular ciphers is an important measurement to provide a good indicator that the proposed ciphers are sufficient for use.
- Power consumption is estimated by a Xilinx Power Estimator (XPE) [14], which is designed to estimate the power consumption. Interested readers can refer to the following studies using this method [15].
- The cipher performance in terms of encryption speed was tested by running the cipher 10 times and calculating the average speed.
4. Related Work
Lightweight ciphers are considered efficient and optimal solutions for the IoT because they provide security to small devices connected to networks. In addition, symmetric cryptography was shown to help with decreasing the devices’ power consumption, which allows more small devices to be connected within the networks [16].
AES, which is the preferred standard cryptosystem, can be implemented in a wide range of applications. However, for constrained and small devices, the author in [17] compared lightweight cryptosystems and showed that MICKEY 2.0 is simpler to use as well as stronger compared to other ciphers, such as F-FCSR-H v2, Grain, and Trivium.
To improve the AES cipher’s speed, the author in [4] introduced an optimized version called LEX and argued that the speed could be increased by 2.5 times. The principle was to make the AES block cipher mimic the stream cipher through a leak extraction, which was a complex approach. However, the authors in [18] introduced an attack that used bytes from the keystream using one key with different IVs, which led to the recovery of the secret key. Thus, the LEX cipher was discarded from the eSTREAM project [19]. In addition, recent improved attacks can be seen in [20].
To optimize the DES block cipher, the authors in [20] introduced the DESL cipher. They aimed to improve the nonlinear property in the DES cipher and showed that the DESL cipher needs 20% fewer GEs. However, the number of GEs is still large, and the implementation performance of the RFID tags requires fewer GEs.
In the Trivium cipher study of [9], the authors attempted to generalize an internal state structure to select the best parameters for making the cipher smaller by reducing the required number of GEs while maintaining a high level of security performance. In general, a high level of cipher security depends on the number of nonlinear components that are involved. The authors’ model was thus designed to try to observe and maintain the internal state’s nonlinear properties. The authors also compared their version with other ciphers in terms of power consumption and the number of GEs. Their objective was to make their scaled-down Trivium cipher (Micro-Trivium) suitable for low-cost RFID tags.
The MICKEY cipher’s first version (MICKEY 1.0) [12] was optimized because it was vulnerable to attack, as shown in [21]. The authors showed its weakness by applying the time memory data trade (TMD) and finding a group of weak keys. The entropy was reduced by increasing the clocks. The MICKEY 1.0 designers introduced the new version (MICKEY 2.0) of the cipher [1] to address the weakness issues. Moreover, in MICKEY 2.0, the state of each register (R and S) increased in size to 100 bits from 80 bits in the original MICKEY 1.0, and the control of the bit tap positions was altered.
In [22], after comparison of the throughput of the lightweight ciphers to the throughput per area calculation, the authors found the following results: MICKEY 2.0 = 2.554 Mbps, Trivium = 2.186 Mbps, Grain V1 = 0.558 Mbps, ZUC = 1.074 Mbps, and E0 = 1.338 Mbps. These results confirmed that MICKEY 2.0 has the best throughput among the ciphers investigated.
A survey study [23] on embedded systems was accomplished by implementing lightweight ciphers(LWC) ciphers, which indicated that MICKEY 2.0 showed more resistance to fault analysis attacks because it requires 214.7 faults and needs 65 (key, IV) pairs compared to Trivium, which only needs two faults with 240 keystream bits for internal state recovery. This difference is attributed to the design complexity comparison with Trivium and Grain ciphers. Therefore, MICKEY 2.0 is a valuable choice for further optimization for implementation in embedded systems.
A new design based on a stream cipher using a feedback with carry shift register (FCSR), and two linear feedback shift registers was introduced. To evaluate this new design, the authors in [24] used the NIST randomness tests suite to test the applicability of their design to devices such as mobile phones. However, the RFID technology requires a different approach. In our study, we compared the secure MICKEY 2.0 cipher with the proposed MICKEY 2.0.85 cipher to ensure security.
Another new design consisting of two nonlinear feedback shift registers with target implementation on small devices was found to have a good pseudo-randomness appearance based on the implementation of NIST statistical tests in cryptographic applications [25].
In summary, a lightweight cryptosystem is needed to ensure the security of RFID tags, considering that RFID tags’ design specifications require high throughput with low-power consumption and low-level computation. Therefore, in this paper, we propose a new MICKEY 2.0 variant consisting of fewer GEs to address these challenges.
5. Algorithm Reduction Methodology
The algorithm reduction process aims to reduce the power and processing requirements of the MICKEY 2.0 algorithm without compromising security. We intend to determine if even a small reduction in the internal register size (resulting in a reduction in the required processing time) could result in a nontrivial reduction of resource requirements.
To do so, we decided to reduce the number of bits used in the internal registers. We selected each register’s size target at 85 bits. We designated this reduced algorithm for MICKEY 2.0.85 because it resulted from many alterations, modifications, and testing to obtain the optimal trade-off between size, power consumption, and pseudo-randomness. We have tested multiple alterations and variations of registered lengths and bits positions in testing for pseudo-randomness. We achieved the optimal length of the registers and controlling tap positions for our scaled-down variant in the following optimal setting:
5.1. Reduction Optimal Setting
Registers R and S in MICKEY 2.0 each have 100 bits. For MICKEY 2.0.85, each of the two internal state registers need to be reduced to 85 bits. As a general rule of security, the internal state should be at least twice the key size (160 bits) [26]. This implied to us that the number of bits in MICKEY 2.0 may be excessive (providing no additional randomness, but consuming extra resources). Therefore, we set the internal state for MICKEY 2.0.85 to 170 bits. The data structures representing the internal state for each version were reduced to the appropriate number of bits.
5.1.1. Overview
Removal of Bits from R_taps: Fifteen bits were removed from the R_taps for MICKEY 2.0.85.
To reduce the size of the Internal Control Data Structures, we removed bits from the State Drivers so that each one matched the appropriate bit count while still assuring that the clocking output was pseudo-random.
The initializations and loop counts were reduced to the appropriate values depending on the bit count.
To test the scaled-down cipher, we executed the NIST test suite on the keystreams generated for MICKEY 2.0, MICKEY 1.0, and MICKEY 2.0.85. A large number of sequences were generated to compare the randomness of MICKEY 1.0, MICKEY 2.0, and MICKEY 2.0.85. This ensured that the randomness of keystreams for the proposed variant was highly comparable to the randomness of MICKEY 2.0. Section 5 describes this process in detail.
One of the objectives of this algorithm was to reduce the number of GEs. Appendix A explains in detail how the GEs were counted.
The following section explains the logic behind the MICKEY algorithm.
CLOCK_KG invokes CLOCK_R and CLOCK_S for the purpose of determining the appropriate XOR bit for each bit position within the generated keystream. See the detailed logic below, with the flow chart Figure 2.
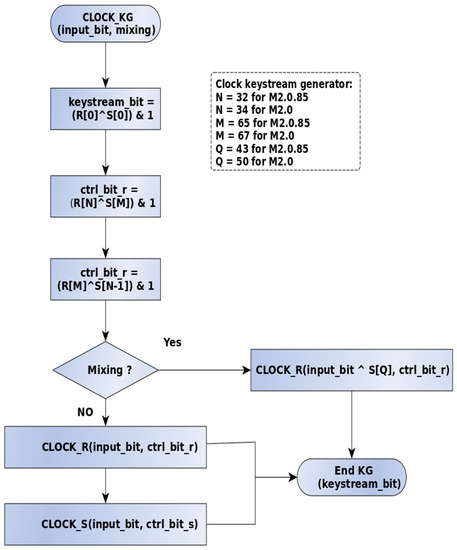
Figure 2.
Flowchart for overall MICKEY logic.
Details of Figure 2: The CLOCK_KG function generates a keystream bit by XORing the first bit of the Linear Register (R[0]) with the first bit of the Nonlinear Register (S[0]).
It advances the bit values of each register by invoking both CLOCK_R and CLOCK_S.
“Mixing Mode” is used in initialization. CLOCK_R is used to “randomize” R by “mixing” the 80-bit key and the 80-bit IV.
Following the lead of MICKEY 2.0 in MICKEY 2.0.85. The values of N, M, and Q were selected to be “spread out” through the Linear and Nonlinear registers.
The logic for advancing the linear register, CLOCK_R, is shown in Figure 3.
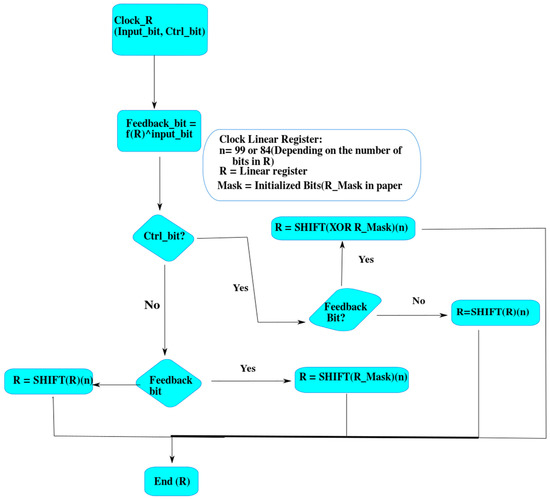
Figure 3.
Flowchart for linear register logic.
Details of Figure 3: The linear register drives the pseudo-randomness.
The CLOCK_R function advances the linear register according to the logic shown in the accompanying flowchart.
The function CLOCK_R advances the position of the linear register and determines whether or not the ‘current’ XOR mask bit is 1 or 0 based on previous operations and the R_MASK.
We reduced the number of bits in R and the R_MASK (Taps) and arranged them as defined in Section 5.1.2.
With the nonlinear register (S), shown in Figure 4, the correspondence between bit and position is more arbitrary, but it is driven by the state of the linear register. The State Drivers (COMP0, COMP1, FB0, and FB1) are also arbitrary (random) bits.
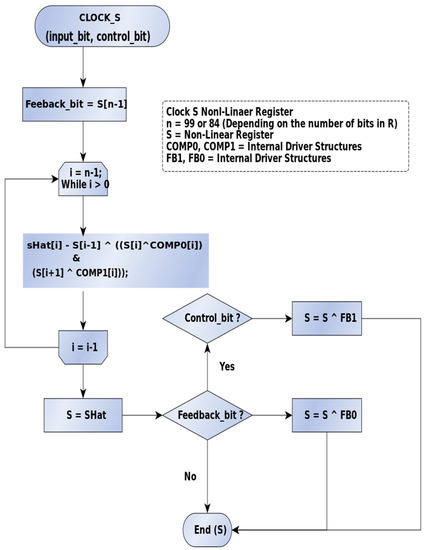
Figure 4.
Flowchart for nonlinear register logic.
Description of Figure 4: The function CLOCK_S advances the position of the nonlinear register. Using four internal and random structures (COMP0, COMP1, FB0, and FB1), the ‘current’ bit position is far more nonlinear.
The purpose of the nonlinear register is to add unpredictability to the bits generated by the linear register.
Exactly which internal structure is used, FB0 or FB1, is determined by the control bit and by using COMP0 and COMP1 to randomize the register.
The bit arrangements for FB0, FB1, COMP0, and COMP1 were experimentally determined for appropriate randomness. See Section 5.1.2 for details of the actual arrangements.
The success of the randomness depends on the initial state of the internal driving structures. The bits in MICKEY 2.0 were selected by the designers to assure randomness. We selected and adjusted the bits in MICKEY 2.0.85 for the same reason. These bits were selected experimentally, specifically eschewing a function to avoid predictability. We tried several other bit arrangements that failed NIST randomness tests.
5.1.2. Internal State Drivers
The purpose of the Internal Drivers in MICKEY 2.0 and MICKEY 2.0.85 is to obscure the relationship between the IV, the key, and the keystream. To understand the bit selection, MICKEY 2.0 refers to [1]. For MICKEY 2.0.85, we selected the bits experimentally specifically avoiding functions and patterns to increase the randomness as measured by the NIST suite. When we discovered a combination that compared favorably to the original algorithm, we settled on the bits specified below.
The following lists show which bit positions within each internal driving structure are initially set to 1 for both MICKEY 2.0 and MICKEY 2.0.85. (The operations described above and depicted in Figure 2, Figure 3 and Figure 4 make use of these data structures.)
R Registers Taps (R_MASK)
MICKEY 2.0
{0,1,3,4,5,6,9,12,13,16,19,20,21,22,25,28,37,38,41,42,45,46,50,52,54,56,58,60,61,63,64,65,66,67,71,72, 79,80,81,82,87,88,89,90,91,92,94,95,96,97}
MICKEY 2.0.85
{0,1,3,4,5,6,9,12,13,16,19,20,21,24,25,2837,38,41,42,45,46,51,53,55,5658,59,60,61,62,66,67,72,73,74,75,76,77,79,80,81,82}
COMP0
MICKEY 2.0
{4,5,9,11,12,13,14,16,19,21,23,25,27,29,30,32,35,43,45,47,49,54,56,59,60,61,62,65,67,69,70,71,72,73,74,75,76,77,79,81,82,83,84,85,86,88,90,97,98}
MICKEY 2.0.85
{4,5,9,11,12,13,14,16,19,21,23,25,27,29,30,32,35,43,45,47,49,50,51,52,55,57,59,60,61,62,63,64,66,67,68,69,70,71,73,75,82,83}
COMP1
MICKEY 2.0
{1,3,4,7,9,10,11,12,15,17,21,22,24,26,27,28,30,31,32,33,37,38,40,42,43,44,49,53,55,56,57,61,62,63,64,65,66,68,70,71,72,74,75,76,77,81,86,87,88,92,95,96}
MICKEY 2.0.85
{1,3,4,7,9,10,11,12,15,17,21,22,24,26,27,28,30,31,32,33,37,38,40,42,43,44,49,55,56,57,61,62,63,64,65,66,68,70,71,72,74,77,80,81}
FB0
MICKEY 2.0
{0,1,2,3,5,7,8,9,10,11,12,13,14,17,19,20,21,22,23,24,25,26,27,28,31,32,39,40,41,44,47,49,51,54,56,57,58,59,61,63,65,75,76,78,82,83,85,86,87,90,91,92,95,96}
MICKEY 2.0.85
{0,1,2,3,5,7,8,9,10,11,12,13,14,17,19,20,21,22,23,24,29,30,31,34,37,39,41,44,46,47,48,49,51,53,55,67,68,70,71,72,75,76,77,80,81}
FB1
MICKEY 2.0
{0,1,2,4,5,6,11,12,13,15,18,19,23,26,27,30,32,33,37,38,44,45,47,48,52,56,59,62,64,65,67,69,72,74,78,79,80,81,83,84,85,86,87,94,99}
MICKEY 2.0.85
{0,1,24,5,6,11,12,13,15,18,19,23,26,27,30,32,33,37,38,44,45,47,48,52,56,59,62,64,56,66,68,69,70,71,72,79,84}
6. Results and Analysis
This section presents the results and analysis based on the randomness tests, algorithm performance testing, and power consumption.
6.1. NIST Randomness Test Suite
The NIST has created a statistical test suite [2] to test the randomness and pseudo-randomness for the proposed encryption algorithms. This suite consists of a series of 15 tests (in the form of a C program) that can be used to determine the randomness of a bitstream. We ran these tests on MICKEY 1.0, MICKEY 2.0, and MICKEY 2.0.85. For the (key, IV) pairs, we used 10 bytes for the keys and the same for the IV string, as randomly generated by Random.org.
NIST tests are important in the software evaluation of the lightweight ciphers used in IoT in terms of cryptographical pseudo-randomness. Hence, the NIST randomness tests were implemented for hardware evaluations and for software security evaluations [27].
To evaluate different lightweight encryption methods, including the eSTREAM cipher finalist [28], used the NIST tests with 100 sequences generated with the length of 106 bits. By contrast, we used a larger number of sequences.
As expected, MICKEY 1.0 did not appear to be random for most tests and was therefore vulnerable to statistical attacks. We observed that MICKEY 1.0 becomes less random as the message size increases. MICKEY 2.0 was substantially more random compared to MICKEY 1.0. More importantly, it stayed random as the message size increased. MICKEY 2.0.85 was nearly identical in randomness to MICKEY 2.0, and it maintained its randomness as the message size increased.
The use of a smaller internal state size may be justified given that the security level did not weaken the algorithm in this context.
To compare the NIST test results for both MICKEY 2.0.85 and MICKEY 2.0, we selected true random numbers generated by a physical source by choosing the same pair (Key, IV) to generate the keystreams for both ciphers. We repeated the process after changing both (Key, IV) pairs generated 410 sequences for each cipher. Each sequence had a length of bits. We ran the NIST test suite for both ciphers to ensure that MICKEY 2.0.85 had the same level of security as MICKEY 2.0 This demonstrates that MICKEY 2.0.85 has a slightly better success rate than MICKEY 2.0. Table 1 shows the results of the MICKEY 2.0.85 tests. Table 2 shows the results of MICKEY 2.0 tests. Note that MICKEY 1.0 failed all but one test.

Table 1.
MICKEY 2.0.85, 410 sequences, each sequence with a length of bits.

Table 2.
MICKEY 2.0, 410 sequences, each sequence with a length of bits.
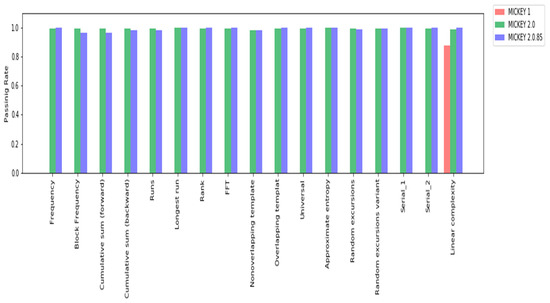
Figure 5.
Histogram for NIST test results for each MICKEY algorithm.
Furthermore, to conduct more extensive tests on MICKEY 2.0.85, we generated 1350 sequences each with lengths of bits. The NIST results are provided in Table 3.

Table 3.
MICKEY 2.0.85, 1350 sequences, each sequence with a length of bits.
6.2. Algorithm Performance Testing
A series of performance tests were conducted by measuring the time for encryption in microseconds. In our tests, we used an Intel i3 processor with a speed of 2.53 GHz. On average, the MICKEY 2.0.85 variant was 23.36% faster than MICKEY 2.0. Given that speed improvement represents a reduction in the overall processing required, this result is favorable because, in low-power technologies, such as microcontrollers, RFID technologies, and other IoT technologies, even seemingly small improvements can be significant.
The following process was used to measure the performance of each algorithm variant. We created a plaintext, random string of 39,900 bytes. We used the same string as the input on all tests. We created a random 10-byte IV and a random 10-byte key. The same IV and key were used on all tests.
We created a main function in C that:
- Measured the start time,
- Initialized and encrypted the plaintext string,
- Measured the end time,
- Calculated the difference.
We ran each test 10 times for each variant, and we computed the average elapsed time. We then compared the average encryption time of each variant to MICKEY 2.0.
Table 4 shows the results of the tests.

Table 4.
Improvement in the encryption speed for MICKEY 2.0.85 compared to MICKEY 2.0.
6.3. Power Consumption Comparison
We used XPE to estimate the power consumption for MICKEY 2.0 and our proposed variants and compared that estimate with both Trivium and Micro-Trivium. Table 5 shows that MICKEY 2.0.85 consumed less power than Micro-Trivium. The values of Trivium and Micro-Trivium were obtained from the results in [9].

Table 5.
Number of GEs and power consumption for the MICKEY 2.0 cipher and its proposed scaled-down variants in comparison to existing ciphers.
The relationship between the number of GEs and the power consumption (for all four ciphers in Table 5) is explained by the polynomial of degree of 3 as given below:
where = number of GEs and = power consumption.
The score for the estimated value of the power is 1.0, and for MICKEY 2.0 and MICKEY 2.0.85, this is given by the linear model as follows:
The score for the estimated value of the power is also 1.0; therefore, we have highly accurate models.
7. Cryptanalysis
Generally speaking, codebreaking consists of finding meaningful information in “random noise”. In theory, the more random a ciphertext is, the harder it is to extract meaningful patterns that match the plaintext. The fact that MICKEY 2.0.85 is slightly “more” random that MICKEY 2.0, while not conclusive, is indicative of equal or better security.
We subjected MICKEY 2.0.85 to several experimental attacks.
7.1. Repeated Key AKA Many Time Pad Attack
It is considered a cryptographic best practice to never reuse a key. When this practice is not followed, the messages are subject to a “many time pad” (MTP) attack (also known as a “Reused Key” attack). Stream ciphers (such as these) in which a keystream is XORed with plaintext are particularly vulnerable to MTP attacks. If a key is reused, one can produce plaintext from ciphertext given a sufficiently large number of intercepted messages. While “sufficiently large” is always variable, it is also almost always feasible.
In our attack simulations, we reused the same key and IV on a series of plaintext files (with lengths of between 56 K-Bits and 96 K-Bits) using both MICKEY 2.0 and MICKEY 2.0.85. We ran a Python program that performed a series of XOR operations on each message, to derive a keystream candidate. This keystream candidate was XORed with the first ciphertext message to produce a plaintext candidate. To determine the effectiveness of the attack, we measured the Levenshtein Distance [29], as a percentage of the original message size, between the plaintext candidate and the actual plain text. A Levenshtein difference percentage of 0% is identical, whereas a Levenshtein difference percentage of 100% is totally dissimilar.
The results are seen in Figure 6. The data show that, for the same number of intercepts on the same text, with the same keys and IV, MICKEY 2.0.85 is virtually identical to MTP attack resistance as MICKEY 2.0.
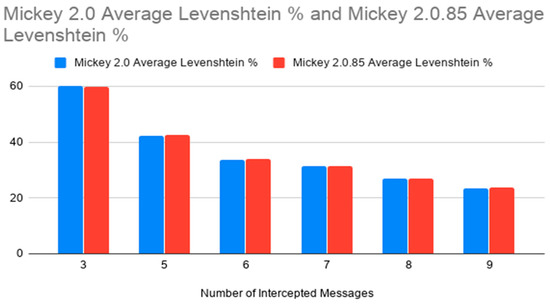
Figure 6.
Levenshtein Similarity based on the number of intercepted messages.
7.2. Cosine Similarity Analysis
Cosine similarity [30] is used in comparing how close a pair of plaintext and ciphertexts are. It is a proportion of similitude between two non-zero vectors of an internal item space. It quantifies the cosine of the point between the two vectors. It is thus suitable to be used to measure how similar two documents or entities are in multidimensional space. The smaller the angle between the vectors, the higher the cosine similarity. Thus, any two vectors are very similar if the angle between them in space is close to zero.
The vector representations of the plaintext and the ciphertext pair are obtained by converting the hexadecimal string values to the individual bytes array. The ciphertext bytes are directly used as the numerical representations.
The cosine similarity values are computed for the blocks of ciphers on an encryption mechanism and average to give a singular measure. This mean cosine similarity is then used to compared against other encryption mechanism Figure 7 shows the cosine similarity between two vectors.
Figure 7.
Cosine similarity between two vectors X1 and X2.
Cosine similarity = 1 − Cosine distance
Table 6 shows the detailed results of our Cosine similarity tests. MICKEY 2.0.85 has a relatively smaller level of similarity and thus has more randomness.

Table 6.
Cosine similarity for MICKEY 2.0 and MICKEY 2.0.85.
8. Discussion
As a rule, no new (or modified) cryptographic algorithm should be generally accepted until it has undergone extensive cryptanalysis by researchers other than its developers. (The assumption is being that had the developers known about a weakness it would have been addressed). “New” should not be assumed to mean “improved”.
What makes MICKEY 2.0.85 worthy of further consideration is the potential power saving and speed improvement. In a resource-constrained environment, a power savings of 16% and a speed increase of 23% is not trivial.
Scaled-down variants of the MICKEY 2.0 cipher have been proposed, and the reduction methods and their results have been provided. MICKEY 2.0 ciphered the eSTREAM project and showed greater resistance to attacks compared to other ciphers. MICKEY 2.0 also provided a strong combination of performance, throughput, security, and power consumption.
Optimizing the security of existing lightweight ciphers, such as RC4, for certain implementation similar to [31] in Android phone devices is promising, even if RC4 was published in 1994. In our study, we optimized a secure cipher, ensuring its suitability for IoT, including smartphones and RFID technology.
Table 5 shows that the proposed MICKEY 2.0 variant, MICKEY 2.0.85, requires fewer GEs and has less power consumption. However, the NIST test suite showed that the passing rates of the proposed variants were similar or even slightly better than those of MICKEY 2.0, which indicates good statistical and pseudo-randomness properties. MICKEY 1.0 was very weak and failed most of the NIST tests. Furthermore, MICKEY 2.0.85 is a better competitor with Micro-Trivium in power consumption and number of GEs, as shown in Table 5.
In addition to the NIST randomness test, we performed a Repeated Key Attack and a Cosine Similarity Analysis between the plaintext and ciphertext of both MICKEY 2.0 and MICKEY 2.0.85. In all cases, MICKEY 2.0.85 performed as well, or slightly better than MICKEY 2.0, while consuming less power and taking less time. Since MICKEY 2.0 is a popular stream cipher, the potential for the use of a smaller, faster, and more efficient lightweight algorithm is quite large.
The scaled-down version for the MICKEY 2.0 ciphers provides new encryption tools for small devices, such as RFID tags, allowing implementation flexibility and optimization based on the devices’ specific designs. Given that the number of GEs is reduced, the MICKEY 2.0 variants may be used for smaller RFID tags and devices that require low-power consumption. The proposed ciphers provide good security levels with reduced power consumption and faster performance (Table 4), which will be reflected in their implementation costs.
For security in IoT applications, such as blockchain, this study provided a solution for blockchains in smart cities to enhance the chain speed and security and to optimize smart contracts to reduce the cost and implementation time [32]. For further research on the authentication using RFID and Near Field-Communication (NFC) and the implementation in the field of healthcare to maintain security of medical data and management, please refer to [33,34,35,36].
The results showed that the MICKEY 2.0.85 cipher performed well with regard to speed and battery consumption. It further showed good pseudorandomness according to the NIST randomness test suite. The MICKEY 2.0.85 cipher therefore provided security and will reduce the overall implementation costs of IoT technology.
Further tests may measure the level of resistance of the proposed variants against different kinds of attacks and optimize their implementation within targeted applications. Moreover, their performance may be studied using different applications. Further reductions in the MICKEY 2.0 R and S registers, up to 80 bits each, may be considered, and the results may be compared with MICKEY 1.0 and MICKEY 2.0. Finally, the controlling tap positions may be changed until the best version is identified and passes the NIST tests at a high rate.
9. Conclusions and Future Work
We have shown that Mikey 2.0.85 uses 16% less power and executes 23% faster than the MICKEY 2.0 version and provides slightly better randomness. We have also shown that it is as resistant to several standard attacks as MICKEY 2.0.
MICKEY 2.0 cipher optimization was made possible through the reduction in the R and S registers and the internal state modifications to fix the security problems in MICKEY 1.0. Lightweight ciphers have been significantly investigated because of their considerable security for small devices.
Lightweight cryptosystems provide a good trade of security and performance in constrained devices with limited resources, such as computation and power consumption.
The MICKEY 2.0 cipher is an efficient, secure encryption cipher among lightweight cryptosystems, which is suitable for small hardware devices. Our proposed scaled-down variant MICKEY 2.0.85 provided similar levels of security when tested by the NIST tests suite for pseudo-randomness comparison with MICKEY 2.0. MICKEY 2.0.85 showed a good passing result similar to MICKEY 2.0. Nevertheless, its speed performance improved by 23.36% faster than MICKEY 2.0. Furthermore, the number of GEs was reduced by 12.45% for MICKEY 2.0.85, and the power consumption was decreased by 16.202%.
Future work should focus on three main areas. First, the MICKEY 2.0 internal state should be reduced to between 170 bits and 160 bits because, to maintain security, the internal state should be at least twice the key size, which is 80 bits in MICKEY 2.0. These new parameters should be tested.
Second, another interesting direction would be to use a 160-bit internal state with slightly increased S register size (to be a bit larger than the R register) and test it for pseudo-randomness.
Finally, the production of devices that require less power consumption, mating high throughput with smaller sizes to be suitable for implementing lightweight cryptosystems with optimal performance is an industrial concern. When tackling RFID tags, for example, the application requires security even though lightweight ciphers are available. However, to achieve better performance and low-power consumption, which is reflected in the overall cost, optimizing existing lightweight ciphers, and testing and measuring their security levels remains a vital task.
Author Contributions
A.A.: the general ideas and main concepts, methodology, simulations, analysis, computations, and writing. B.S.: guidance, comments, analysis validation, revision, and editing. D.E.B.: implementation testing, error corrections, and editing. All authors have read and agreed to the published version of the manuscript.
Funding
Tabuk University, Saudi Arabia PhD scholarship for the first author.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. How GEs Are Counted
Gate Equivalents (GEs) are the unit used to measure the complexity of the electronic circuit [13]. The following operations were typically used to compute GEs.

Table A1.
Number of GEs for a given logical gate; see [13].
Table A1.
Number of GEs for a given logical gate; see [13].
| Gate | Number of Gate Equivalents |
|---|---|
| NOT | 1 |
| AND | 2 |
| OR | 2 |
| XOR | 3 |
| NAND | 1 |
| NOR | 1 |
| XNOR | 3 |
| MUX | 3 |
One of the objectives of this algorithm was to reduce the number of GEs. The following points summarize how the reduction was accomplished with a focus on those algorithm features used for reduction and indicates the kind of gate it represents. This enabled us to count the number of GEs.
CLOCK_R: 1: Initialization of the Internal Register (Single XOR)
CLOCK_R 2: Loop (Conditional) Feedback Bit Logically Assigns Linear Register Bit (Within Loop)
MICKEY 2.0: for i = 0 to 99
MICKEY 2.0.85: for i = 0 to 84
CLOCK_R 3: Linear (R_MASK) Logic to Invert Bit (Single XOR) (Within Loop)
MICKEY 2.0: for i = 0 to 99
MICKEY 2.0.85: for i = 0 to 84
CLOCK_R 4: Multiple Related Operation (Single MUX)—Conditionally executed based on control bit.
CLOCK_R 5: Multiple Related Operation (Single MUX)—Conditionally executed based on feedback bit.
CLOCK_S: 1 Initialization of Internal (Nonlinear) Register (Single XOR)
MICKEY 2.0: For i = 0 to 99:
MICKEY 2.0.85: For i = 0 to 84
CLOCK_S: 2, CLOCK_S: 3: Bitwise operations on internal structures 3 XORs and One AND (gates)
CLOCK_S: 4: Conditional Logic on Feedback and Control Bit (Single MUX)
MICKEY 2.0: For i = 0 to 99:
MICKEY 2.0.85: For i = 0 to 84
CLOCK_S: 5: Change Nonlinear Register (Single XOR)
CLOCK_KG: 1–5: Simple Initializations: (4 XOR, 1 AND)
The IV and key were used along with the internal masks to initialize the registers in the function ECRYPT_keysetup, ECRYPT_ivsetup. The idea is that, by arbitrarily mixing the bits of the key and the IV, the initial state of both the linear and nonlinear registers will be unpredictable.
MICKEY 2.0: IV_i 1: For i = 0 to 79: Initialize on IV (Single MUX)
MICKEY 2.0: IV 2: For i = 0 to 80: Initialize on Key (Single MUX)
Therefore, the MICKEY Algorithm works as follows:
MICKEY 2.0: Process (Single MUX to represent Logic):
- Initialize the internal state using: IV, key, and CLOCK_KG (which uses CLOCK_R and CLOCK_S) to mix in the IV and KEY bits based on the internal driver structures(R_MASK and COMP0, COMP1, FB0, FB1)
- For each bit in the message invoke CLOCK_KG
- a
- CLOCK_KG invokes CLOCK_R, which advances the linear bit and masks it with R_MASK to determine its final value.
- b
- CLOCK_KG also invokes CLOCK_S, which may or may not advance the nonlinear bit depending on the linear position and the values of (COMP0, COMP1, FB0, and FB1)
- c
- CLOCK_KG determines the keystream bit by XORing the current linear and nonlinear registers and ANDs them with 1.
- d
- Ciphertext Generation: The current plaintext message bit is XORed with the current Keystream bit, which becomes the ciphertext output.
Appendix B. GE Comparison between MICKEY Family Algorithms
Table A2. shows the total GE number for MICKEY 2.0 and MICKEY 2.0.85 based on logical gate XOR, AND and MUX count, for each CLOCK_R, CLOCK_S,CLOCK_KG,ECRYPT_IVs setup and Encrypt_process functions.

Table A2.
GE Comparison between MICKEY Family Algorithms.
Table A2.
GE Comparison between MICKEY Family Algorithms.
| Function | Operation | GE Multiplier | MICKEY 2.0 Count | MICKEY 2.0.85 Count | ||
|---|---|---|---|---|---|---|
| Number | GE | Number | GE | |||
| CLOCK_R | XOR | 3 | 401 | 1203 | 341 | 1023 |
| MUX | 3 | 2 | 6 | 2 | 6 | |
| CLOCK_S | XOR | 3 | 400 | 1200 | 340 | 1020 |
| AND | 2 | 100 | 200 | 85 | 170 | |
| MUX | 3 | 2 | 6 | 2 | 6 | |
| CLOCK_KG | XOR | 3 | 4 | 12 | 4 | 12 |
| ECRYPT_IVs setup | MUX | 3 | 160 | 480 | 160 | 480 |
| Encrypt_process | MUX | 3 | 8 | 24 | 8 | 24 |
| Total GE | 3131 | 2741 | ||||
References
- Babbage, S.; Dodd, M. The stream cipher MICKEY 2.0, ECRYPTStream Cipher, EU ECRYPT Netw., Denmark, U.K., Tech. Rep., 2006. Available online: https://www.ecrypt.eu.org/stream/index.html (accessed on 10 October 2019).
- Rukhin, A.; Soto, J.; Nechvatal, J.; Smid, M.; Barker, E. A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications; Booz-Allen and Hamilton Inc.: Mclean, VA, USA; Tysons Corner, VA, USA, 2001. [Google Scholar]
- NIST. Announcing the Advanced Encryption Standard (AES); Federal Information Processing Standards Publication: Gaithersburg, MA, USA, 2001; Volume 197, p. 33.
- Biryukov, A. The Design of a Stream Cipher LEX. In Proceedings of the International Workshop on Selected Areas in Cryptography, Montreal, QC, Canada, 17–18 August 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 67–75. [Google Scholar]
- Maitra, S.; Yelamarthi, K. Rapidly Deployable IoT Architecture with Data Security: Implementation and Experimental Evaluation. Sensors 2019, 19, 2484. [Google Scholar] [CrossRef] [PubMed]
- Rangra, A.; Sehgal, V.K.; Shukla, S. A Novel Approach of Cloud Based Scheduling Using Deep-Learning Approach in E-Commerce Domain. Int. J. Inf. Syst. Model. Des. (IJISMD) 2019, 10, 59–75. [Google Scholar] [CrossRef]
- Chakraborty, R.S.; Mathew, J.; Vasilakos, A.V. Security and Fault Tolerance in Internet of Things; Springer International Publishing: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Randhawa, R.H.; Hameed, A.; Mian, A.N. Energy efficient cross-layer approach for object security of CoAP for IoT devices. Ad Hoc Netw. 2019, 92, 101761. [Google Scholar] [CrossRef]
- Zhang, S.; Chen, G. Micro-Trivium: A lightweight algorithm designed for radio frequency identification systems. Int. J. Distrib. Sens. Netw. 2017, 13. [Google Scholar] [CrossRef]
- Rezvani, B.; Diehl, W. Hardware Implementations of NIST Lightweight Cryptographic Candidates: A First Look; Report 2019/824; Cryptology ePrint Archive: Blacksburg, VA, USA, 2019. [Google Scholar]
- Aagaard, M.D.; Sattarov, M.; Zidaric, N. Hardware design and analysis of the ACE and WAGE ciphers. arXiv 2019, arXiv:1909.12338. [Google Scholar]
- Babbage, S.; Dodd, M. The Stream Cipher MICKEY (Version 1); ECRYPT Stream Cipher Project Report, 2006. Available online: https://www.ecrypt.eu.org/stream/ciphers/mickey/mickey.pdf (accessed on 10 October 2019).
- Kaeslin, H. Digital Integrated Circuit Design: From VLSI Architectures to CMOS Fabrication; Cambridge University Press, University Printing House: Cambridge, UK, 2008. [Google Scholar]
- Xilinx. Xilinx Power Estimator (XPE). Available online: https://www.xilinx.com/products/technology/power/xpe.html (accessed on 12 October 2019).
- Verma, G.; Khare, V.; Kumar, M. More precise FPGA power estimation and validation tool (FPEV_tool) for low power applications. Wirel. Pers. Commun. 2019, 106, 2237–2246. [Google Scholar] [CrossRef]
- Katagi, M.; Moriai, S. Lightweight Cryptography for the Internet of Things; Sony Corporation: Tokyo, Japan, 2008; pp. 7–10. Available online: http://dx.doi.org/10.1016/j.istr.2012.10.005 (accessed on 12 October 2019).
- Preneel, B. Stream Ciphers: Past, Present and Future; ISCISC, 2010. Available online: https://securewww.esat.kuleuven.be/cosic/publications (accessed on 12 October 2019).
- Dunkelman, O.; Keller, N. A New Attack on the LEX Stream Cipher. In Proceedings of the International Conference on the Theory and Application of Cryptology and Information Security, Melbourne, Australia, 7–11 December 2008; Springer: Berlin/Heidelberg, Germany, 2008; pp. 539–556. [Google Scholar]
- ECRYPT II. The eSTREAM Portfolio. Available online: http://www.ecrypt.eu.org/stream (accessed on 6 August 2019).
- Liu, Y.; Shi, Y.; Gu, D.; Dai, B.; Zhao, F.; Li, W.; Liu, Z.; Zeng, Z. Improved impossible differential cryptanalysis of large-block Rijndael. Sci. China Inf. Sci. 2019, 62, 32101. [Google Scholar] [CrossRef]
- Leander, G.; Paar, C.; Poschmann, A.; Schramm, K. New Lightweight DES Variants. In Proceedings of the Fast Software Encryption, Luxembourg, 26–28 March 2007; Springer: Berlin/Heidelberg, Germany, 2007; pp. 196–210. [Google Scholar]
- Hong, J.; Kim, W. TMD-Tradeoff and State Entropy Loss Considerations of Stream Cipher MICKEY. Available online: http://eprint.iacr.org/2005/257 (accessed on 20 October 2019).
- Kitsos, P.; Sklavos, N.; Provelengios, G.; Skodras, A.N. FPGA-based performance analysis of stream ciphers ZUC, snow3g, grain V1, MICKEY V2, Trivium and E0. Microprocess. Microsyst. 2013, 37, 235–245. [Google Scholar] [CrossRef]
- Manifavas, C.; Hatzivasilis, G.; Fysarakis, K.; Papaefstathiou, Y. A survey of lightweight stream ciphers for embedded systems. Secur. Commun. Netw. 2016, 9, 1226–1246. [Google Scholar] [CrossRef]
- Yerukala, N.; Padmavathi, G.; Nalla, V.; Prasad, V.K. LFL-A New Stream Cipher for Secure Communications. In Proceedings of the 2018 IEEE International Conference on Computational Intelligence and Computing Research (ICCIC), Madurai, India, 13–15 December 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–5. [Google Scholar]
- Polak, I.; Boryczka, M. Tabu Search in revealing the internal state of RC4+ cipher. Appl. Soft Comput. 2019, 77, 509–519. [Google Scholar] [CrossRef]
- Kara, O.; Esgin, M.F. On analysis of lightweight stream ciphers with keyed update. IEEE Trans. Comput. 2018, 68, 99–110. [Google Scholar] [CrossRef]
- Qasaimeh, M.; Al-Qassas, R.S.; Tedmori, S. Software randomness analysis and evaluation of lightweight ciphers: The prospective for IoT security. Multimed. Tools Appl. 2018, 77, 18415–18449. [Google Scholar] [CrossRef]
- Parikh, N.; Singh, G.; Sundaresan, N. Query suggestion with large scale data. In Handbook of Statistics; Elsevier: Amsterdam, The Netherlands, 2013; Volume 31, pp. 493–518. [Google Scholar]
- Liu, D.; Chen, X.; Peng, D. Some cosine similarity measures and distance measures between q-rung orthopair fuzzy sets. Int. J. Intell. Syst. 2019, 34, 1572–1587. [Google Scholar] [CrossRef]
- Gorbenko, I.; Kuznetsov, A.; Gorbenko, Y.; Vdovenko, S.; Tymchenko, V.; Lutsenko, M. Studies on statistical analysis and performance evaluation for some stream ciphers. Int. J. Comput. 2019, 18, 82–88. [Google Scholar]
- Rifki, R.; Septiarini, A.; Hatta, H.R. Cryptography using random Rc4 stream cipher on SMS for android-based smartphones. Int. J. Adv. Comput. Sci. Appl. 2018, 9, 89–93. [Google Scholar] [CrossRef]
- Hussein, D.M.; Taha, M.H.N.; Khalifa, N.E.M. A blockchain technology evolution between business process management (BPM) and internet-of-things (IoT). Int. J. Adv. Comput. Sci. Appl. 2018, 9, 442–450. [Google Scholar] [CrossRef]
- Abidin, Z.Z.; Zakaria, N.; Harum, N.; Baharon, M.; Hong, E.-S.; Abas, Z.A.; Ayop, Z.; Ariff, N.M. Crypt-tag authentication in NFC implementation for medicine data management. Int. J. Adv. Comput. Sci. Appl. 2018, 9, 93–100. [Google Scholar] [CrossRef]
- Yeh, K.H.; Lo, N.W.; Wang, C.K. A robust NFC-based personalized IPTV service system. Multimed. Tools Appl. 2018, 77, 5129–5148. [Google Scholar] [CrossRef]
- Wan, X.F.; Zheng, T.; Cui, J.; Zhang, F.; Ma, Z.Q.; Yang, Y. Near Field Communication-based Agricultural Management Service Systems for Family Farms. Sensors 2019, 19, 4406. [Google Scholar] [CrossRef] [PubMed]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).