Solitonic Fixed Point Attractors in the Complex Ginzburg–Landau Equation for Associative Memories
Abstract
1. Introduction
2. The Complex Ginzburg–Landau Equation
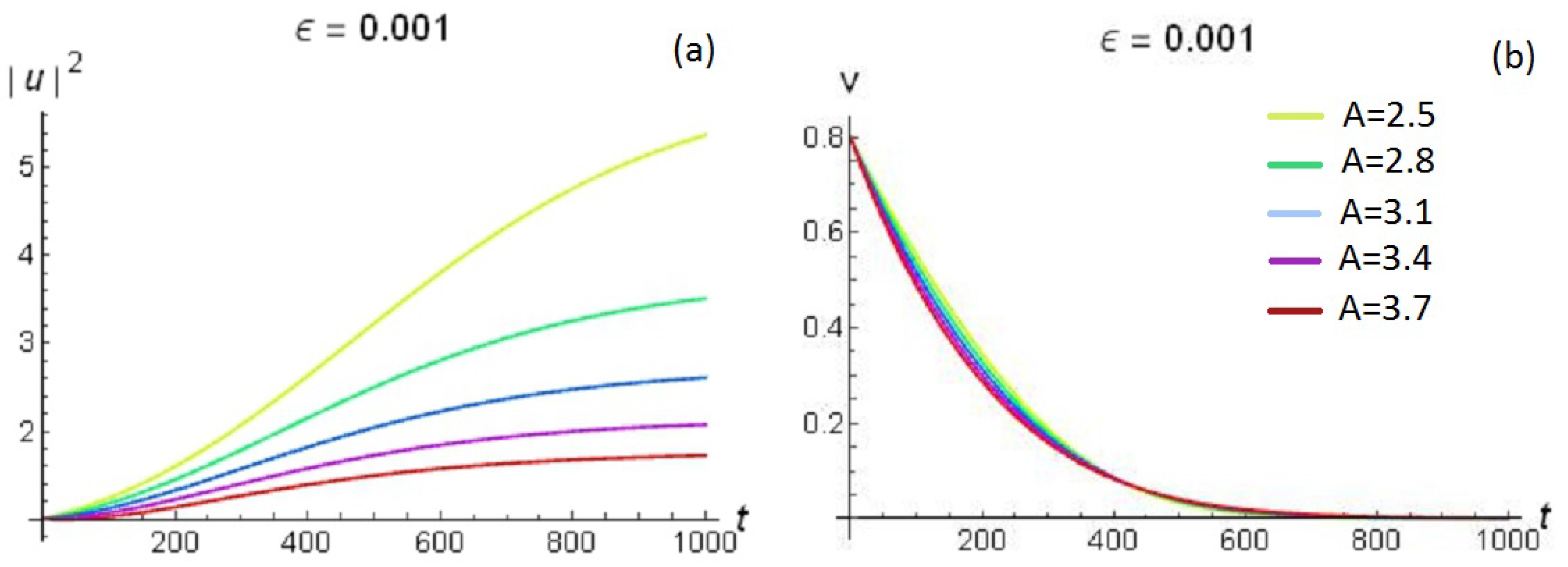
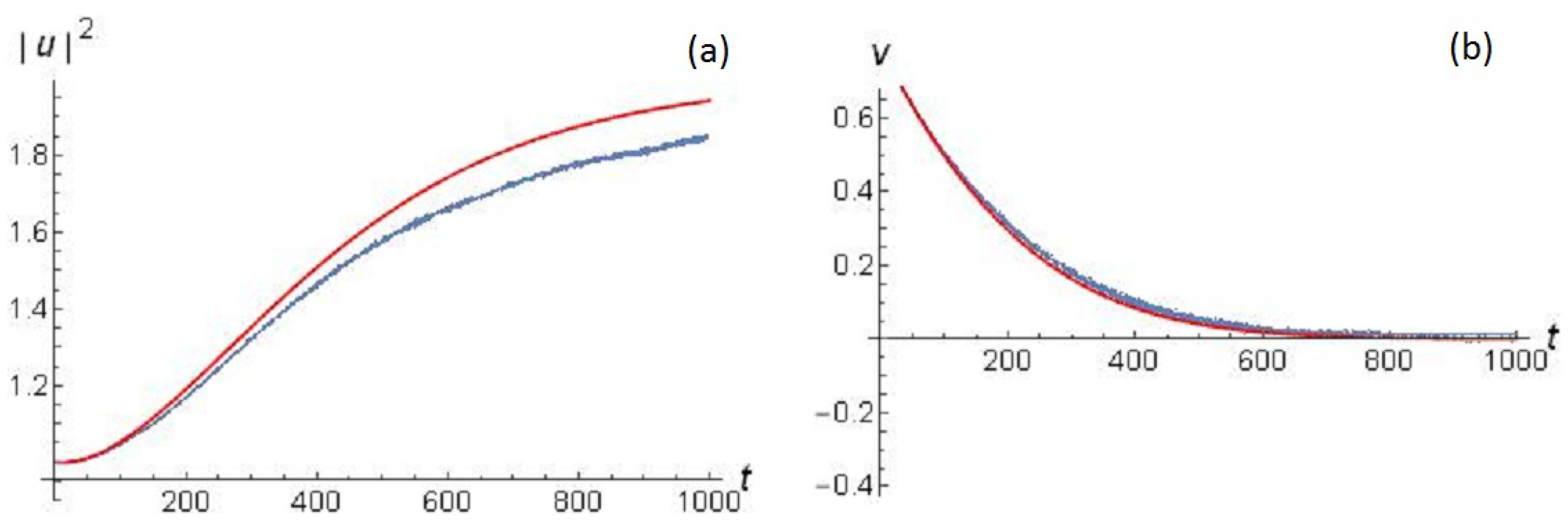
3. Solitonic Fixed Point Attractors
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Monroe, D. Neuromorphic Computing Gets Ready For the (Really) Big Time. Commun. ACM 2014, 57, 13–15. [Google Scholar] [CrossRef]
- Zhao, W.S.; Agnus, G.; Derycke, V.; Filoramo, A.; Bourgoin, J.P.; Gamrat, C. Nanotube devices based crossbar architecture: Toward neuromorphic computing. Nanotechnology 2010, 21, 175202. [Google Scholar] [CrossRef] [PubMed]
- Mead, C. Neuromorphic electronic systems. Proc. IEEE 1990, 78, 1629–1636. [Google Scholar] [CrossRef]
- Sheridan, P.M.; Cai, F.; Du, C.; Zhang, Z.; Lu, W.D. Sparse coding with memristor networks. Nat. Nanotechnol. 2017, 12, 784–789. [Google Scholar] [CrossRef] [PubMed]
- Sebastian, A.; Tuma, T.; Papandreou, N.; Le Gallo, M.; Kull, L.; Parnell, T.; Eleftheriou, E. Temporal correlation detection using computational phase-change memory. Nat. Commun. 2017, 8, 1115. [Google Scholar] [CrossRef] [PubMed]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Preskill, J. Quantum Computing in the NISQ era and beyond. Quantum 2018, 2, 79. [Google Scholar] [CrossRef]
- Lamata, L.; Sanz, M.; Solano, E. Quantum Machine Learning and Bioinspired Quantum Technologies. Adv. Quantum Technol. 2019, 2, 1900075. [Google Scholar] [CrossRef]
- Hopfield, J.J. Neural Networks and Physical Systems with Emergent Collective Computational Abilities. Proc. Natl. Acad. Sci. USA 1982, 79, 2554–2558. [Google Scholar] [CrossRef]
- Izhikevich, E. Dynamical Systems in Neuroscience: The Geometry of Excitability and Bursting; The MIT Press: Cambridge, MA, USA, 2007. [Google Scholar]
- Strogatz, S. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology and Chemistry; Perseus: New York, NY, USA, 2001. [Google Scholar]
- Hertz, J.; Krogh, A.; Palmer, R.G. Introduction to the Theory of Neural Computation; Addison-Wesley: Redwood City, CA, USA, 1991. [Google Scholar]
- Behera, L.; Kar, I.; Elitzur, A. A Recurrent Quantum Neural Network Model to Describe Eye Tracking of Moving Targets. Found. Phys. Lett. 2005, 18, 357–370. [Google Scholar] [CrossRef]
- Onorato, M.; Proment, D.; Clauss, G.; Klein, M. Rogue Waves: From Nonlinear Schrödinger Breather Solutions to Sea-Keeping Test. PLoS ONE 2013, 8, e54629. [Google Scholar] [CrossRef]
- Pitaevskii, L.; Stringari, S. Bose-Einstein Condensation; Clarendon: Oxford, UK, 2003. [Google Scholar]
- Falkovich, G. Fluid Mechanics (A Short Course for Physicists); Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Dalfovo, F.; Giorgini, S.; Pitaevskii, L.P.; Stringari, S. Theory of Bose-Einstein condensation in trapped gases. Rev. Mod. Phys. 1999, 71, 463–512. [Google Scholar] [CrossRef]
- Bagnato, V.S.; Frantzeskakis, D.J.; Kevrekidis, P.G.; Malomed, B.A.; Mihalache, D. Bose-Einstein condensation: Twenty years after. arXiv 2015, arXiv:1502.06328. [Google Scholar]
- Campbell, R.; Oppo, G.-L. Stationary and traveling solitons via local dissipation in Bose-Einstein condensates in ring optical lattices. Phys. Rev. A 2016, 94, 043626. [Google Scholar] [CrossRef]
- Byrnes, T.; Kim, N.Y.; Yamamoto, Y. Exciton–polariton condensates. Nat. Phys. 2014, 10, 803–813. [Google Scholar] [CrossRef]
- Wouters, M.; Carusotto, I. Excitations in a nonequilibrium Bose-Einstein condensate of exciton polaritons. Phys. Rev. Lett. 2007, 99, 140402. [Google Scholar] [CrossRef] [PubMed]
- Amo, A.; Pigeon, S.; Sanvitto, D.; Sala, V.; Hivet, R.; Carusotto, I.; Pisanello, F.; Leménager, G.; Houdré, R.; Giacobino, E.; et al. Polariton superfluids reveal quantum hydrodynamic solitons. Science 2011, 332, 1167–1170. [Google Scholar] [CrossRef]
- Sich, M.; Krizhanovskii, D.; Skolnick, M.; Gorbach, A.V.; Hartley, R.; Skryabin, D.V.; Cerda-Méndez, E.; Biermann, K.; Hey, R.; Santos, P. Observation of bright polariton solitons in a semiconductor microcavity. Nat. Photonics 2012, 6, 50. [Google Scholar] [CrossRef]
- Egorov, O.; Skryabin, D.V.; Yulin, A.; Lederer, F. Bright cavity polariton solitons. Phys. Rev. Lett. 2009, 102, 153904. [Google Scholar] [CrossRef]
- Grelu, P.; Akhmediev, N. Dissipative solitons for mode-locked lasers. Nat. Photonics 2012, 6, 84–92. [Google Scholar] [CrossRef]
- Wright, L.G.; Christodoulides, D.N.; Wise, F.W. Spatiotemporal mode-locking in multimode fiber lasers. Science 2017, 358, 94–97. [Google Scholar] [CrossRef]
- Gustave, F.; Radwell, N.; McIntyre, C.; Toomey, J.P.; Kane, D.M.; Barland, S.; Firth, V.J.; Oppo, G.-L.; Ackemann, T. Observation of Mode-Locked Spatial Laser Solitons. Phys. Rev. Lett. 2017, 118, 044102. [Google Scholar] [CrossRef]
- Kippenberg, T.J.; Gaeta, A.L.; Lipson, M.; Gorodetsky, M.L. Dissipative Kerr solitons in optical microresonators. Science 2018, 361, eaan8083. [Google Scholar] [CrossRef]
- Suh, M.G.; Yang, Q.F.; Yang, K.Y.; Yi, X.; Vahala, K.J. Microresonator soliton dual-comb spectroscopy. Science 2016, 354, 600–603. [Google Scholar] [CrossRef] [PubMed]
- Stone, J.R.; Briles, T.C.; Drake, T.E.; Spencer, D.T.; Carlson, D.R.; Diddams, S.A.; Papp, S.B. Thermal and Nonlinear Dissipative-Soliton Dynamics in Kerr-Microresonator Frequency Combs. Phys. Rev. Lett. 2018, 121. [Google Scholar] [CrossRef] [PubMed]
- Byrnes, T.; Yan, K.; Yamamoto, Y. Accelerated optimization problem search using Bose-Einstein condensation. New J. Phys. 2011, 13, 113025. [Google Scholar] [CrossRef]
- Byrnes, T.; Koyama, S.; Yan, K.; Yamamoto, Y. Neural networks using two-component Bose-Einstein condensates. Sci. Rep. 2013, 3, 2531. [Google Scholar] [CrossRef] [PubMed]
- Byrnes, T.; Rosseau, D.; Khosla, M.; Pyrkov, A.; Thomasen, A.; Mukai, T.; Koyama, S.; Abdelrahman, A.; Ilo-Okeke, E. Macroscopic quantum information processing using spin coherent states. Opt. Commun. 2015, 337, 102–109. [Google Scholar] [CrossRef]
- Pyrkov, A.N.; Byrnes, T. Entanglement generation in quantum networks of Bose-Einstein condensates. New J. Phys. 2013, 15, 093019. [Google Scholar] [CrossRef]
- Pyrkov, A.N.; Byrnes, T. Full-Bloch-sphere teleportation of spinor Bose-Einstein condensates and spin ensembles. Phys. Rev. A 2014, 90, 062336. [Google Scholar] [CrossRef]
- Byrnes, T.; Wen, K.; Yamamoto, Y. Macroscopic quantum computation using Bose-Einstein condensates. Phys. Rev. A 2012, 85, 040306. [Google Scholar] [CrossRef]
- Gross, C. Spin squeezing, entanglement and quantum metrology with Bose-Einstein condensates. J. Phys. B At. Mol. Phys. 2012. [Google Scholar] [CrossRef]
- Pyrkov, A.N.; Byrnes, T. Quantum information transfer between two-component Bose-Einstein condensates connected by optical fiber. Proc. SPIE 2013, 8700, 87001E. [Google Scholar] [CrossRef]
- Pyrkov, A.N.; Byrnes, T. Quantum information processing with macroscopic two-component Bose-Einstein condensates. In Proceedings of the International Conference on Micro- and Nano-Electronics 2018, Zvenigorod, Russia, 1–5 October 2018. [Google Scholar] [CrossRef]
- Hecht, T. Quantum Computation with Bose-Einstein Condensates. Master’s Thesis, Technische Universität München, München, Germany, 2004. [Google Scholar]
- Aranson, I.S.; Kramer, L. The world of the complex Ginzburg-Landau equation. Rev. Mod. Phys. 2002, 74, 99–143. [Google Scholar] [CrossRef]
- Bender, C.M.; Boettcher, S. Real Spectra in Non-Hermitian Hamiltonians Having PT-Symmetry. Phys. Rev. Lett. 1998, 80, 5243–5246. [Google Scholar] [CrossRef]
- Kartashov, Y.V.; Malomed, B.A.; Torner, L. Unbreakable PT symmetry of solitons supported by inhomogeneous defocusing nonlinearity. Opt. Lett. 2014, 39, 5641. [Google Scholar] [CrossRef]
- Chen, Y.; Yan, Z.; Mihalache, D.; Malomed, B.A. Families of stable solitons and excitations in the PT-symmetric nonlinear Schrödinger equations with position-dependent effective masses. Sci. Rep. 2017, 7, 1257. [Google Scholar] [CrossRef]
- Bender, C.M. Making sense of non-Hermitian Hamiltonians. Rep. Progress Phys. 2007, 70, 947–1018. [Google Scholar] [CrossRef]
- Longhi, S. Bloch Oscillations in Complex Crystals with PT Symmetry. Phys. Rev. Lett. 2009, 103, 123601. [Google Scholar] [CrossRef]
- Guo, A. Observation of PT-Symmetry Breaking in Complex Optical Potentials. Phys. Rev. Lett. 2009, 103, 093902. [Google Scholar] [CrossRef]
- Ruter, C.E.; Makris, K.G.; El-Ganainy, R.; Christodoulides, D.N.; Segev, M.; Kip, D. Observation of parity–time symmetry in optics. Nat. Phys. 2010, 6, 192. [Google Scholar] [CrossRef]
- Regensburger, A.; Bersch, C.; Miri, M.A.; Onishchukov, G.; Christodoulides, D.N.; Peschel, U. Parity–time synthetic photonic lattices. Nature 2012, 488, 7410. [Google Scholar] [CrossRef] [PubMed]
- Hodaei, H.; Miri, M.A.; Heinrich, M.; Christodoulides, D.N.; Khajavikhan, M. Parity-time-symmetric microring lasers. Science 2014, 346, 975. [Google Scholar] [CrossRef] [PubMed]
- Wimmer, M.; Regensburger, A.; Miri, M.A.; Bersch, C.; Christodoulides, D.N.; Peschel, U. Observation of optical solitons in PT-symmetric lattices. Nat. Commun. 2015, 6, 8782. [Google Scholar] [CrossRef] [PubMed]
- Kivshar, Y.S.; Malomed, B.A. Dynamics of solitons in nearly integrable systems. Rev. Mod. Phys. 1989, 61, 763–915. [Google Scholar] [CrossRef]
- Malomed, B.A.; Mihalache, D.; Wise, F.; Torner, L. Spatiotemporal optical solitons. J. Opt. B Quantum Semiclassical Opt. 2005, 7, R53–R72. [Google Scholar] [CrossRef]
- Mihalache, D. Multidimensional localized structures in optical and matter-wave media: A topical survey of recent literature. Rom. Rep. Phys. 2017, 69, 403. [Google Scholar]
- Malomed, B.A. Evolution of nonsoliton and “quasi-classical” wavetrains in nonlinear Schrödinger and Korteweg-de Vries equations with dissipative perturbations. Phys. D Nonlinear Phenom. 1987, 29, 155–172. [Google Scholar] [CrossRef]
- Malomed, B.A. Bound solitons in the nonlinear Schrödinger–Ginzburg-Landau equation. Phys. Rev. A 1991, 44, 6954–6957. [Google Scholar] [CrossRef]
- Cherny, V.V.; Byrnes, T.; Pyrkov, A.N. Nontrivial Attractors of the Perturbed Nonlinear Schrödinger Equation: Applications to Associative Memory and Pattern Recognition. Adv. Quantum Technol. 2019, 2, 1800087. [Google Scholar] [CrossRef]
- García-Morales, V.; Krischer, K. The complex Ginzburg-Landau equation: An introduction. Contemp. Phys. 2012, 53, 79–95. [Google Scholar] [CrossRef]
- Leblond, H. Dissipative solitons: The finite bandwidth of gain as a viscous friction. Phys. Rev. A 2016, 93, 013830. [Google Scholar] [CrossRef]
- Pérez-García, V.M.; Michinel, H.; Herrero, H. Bose-Einstein solitons in highly asymmetric traps. Phys. Rev. A 1998, 57, 3837–3842. [Google Scholar] [CrossRef]
- Reinhardt, W.P.; Clark, C.W. Soliton dynamics in the collisions of Bose - Einstein condensates: an analogue of the Josephson effect. J. Phys. B At. Mol. Phys. 1997, 30, L785–L789. [Google Scholar] [CrossRef]
- Burger, S.; Bongs, K.; Dettmer, S.; Ertmer, W.; Sengstock, K.; Sanpera, A.; Shlyapnikov, G.V.; Lewenstein, M. Dark Solitons in Bose-Einstein Condensates. Phys. Rev. Lett. 1999, 83, 5198–5201. [Google Scholar] [CrossRef]
- Denschlag, J.; Simsarian, J.E.; Feder, D.L.; Clark, C.W.; Collins, L.A.; Cubizolles, J.; Deng, L.; Hagley, E.W.; Helmerson, K.; Reinhardt, W.P.; et al. Generating Solitons by Phase Engineering of a Bose-Einstein Condensate. Science 2000, 287, 97–101. [Google Scholar] [CrossRef]
- Dutton, Z.; Budde, M.; Slowe, C.; Vestergaard Hau, L. Observation of Quantum Shock Waves Created with Ultra- Compressed Slow Light Pulses in a Bose-Einstein Condensate. Science 2001, 293, 663–668. [Google Scholar] [CrossRef]
- Chin, C.; Grimm, R.; Julienne, P.; Tiesinga, E. Feshbach resonances in ultracold gases. Rev. Mod. Phys. 2010, 82, 1225–1286. [Google Scholar] [CrossRef]
- Khaykovich, L.; Schreck, F.; Ferrari, G.; Bourdel, T.; Cubizolles, J.; Carr, L.D.; Castin, Y.; Salomon, C. Formation of a Matter-Wave Bright Soliton. Science 2002, 296, 1290–1293. [Google Scholar] [CrossRef]
- Strecker, K.E.; Partridge, G.B.; Truscott, A.G.; Hulet, R.G. Formation and propagation of matter-wave soliton trains. Nature 2002, 417, 150–153. [Google Scholar] [CrossRef]
- Byrnes, T.; Recher, P.; Yamamoto, Y. Mott transitions of exciton polaritons and indirect excitons in a periodic potential. Phys. Rev. B 2010, 81, 205312. [Google Scholar] [CrossRef]
- Byrnes, T.; Kolmakov, G.V.; Kezerashvili, R.Y.; Yamamoto, Y. Effective interaction and condensation of dipolaritons in coupled quantum wells. Phys. Rev. B 2014, 90, 125314. [Google Scholar] [CrossRef]
- Tsarev, D.V.; Arakelian, S.M.; Ray-Kuang Lee, Y.L.C.; Alodjants, A.P. Quantum metrology beyond Heisenberg limit with entangled matter wave solitons. Opt. Express 2018, 26, 19583–19595. [Google Scholar] [CrossRef] [PubMed]
- Malomed, B.A. Multidimensional solitons: Well-established results and novel findings. Eur. Phys. J. Spec. Top. 2016, 225. [Google Scholar] [CrossRef]
- Soto-Crespo, J.M.; Akhmediev, N.; Grelu, P.; Belhache, F. Quantized separations of phase-locked soliton pairs in fiber lasers. Opt. Lett. 2003, 28, 1757–1759. [Google Scholar] [CrossRef]
- Komarov, A.; Komarov, K.; Leblond, H.; Sanchez, F. Spectral-selective management of dissipative solitons in passive mode-locked fibre lasers. J. Opt. A Pure Appl. Opt. 2007, 9, 1149–1156. [Google Scholar] [CrossRef]
- Tang, D.Y.; Man, W.S.; Tam, H.Y.; Drummond, P.D. Observation of bound states of solitons in a passively mode-locked fiber laser. Phys. Rev. A 2001, 64, 033814. [Google Scholar] [CrossRef]
- Chouli, S.; Grelu, P. Rains of solitons in a fiber laser. Opt. Express 2009, 17, 11776. [Google Scholar] [CrossRef]
- Ben Braham, F.; Semaan, G.; Bahloul, F.; Salhi, M.; Sanchez, F. Experimental optimization of dissipative soliton resonance square pulses in all anomalous passively mode-locked fiber laser. J. Opt. 2017, 19, 105501. [Google Scholar] [CrossRef]
- Scott, A. Nonlinear Science: Emergence and Dynamics; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pyrkov, A.N.; Byrnes, T.; Cherny, V.V. Solitonic Fixed Point Attractors in the Complex Ginzburg–Landau Equation for Associative Memories. Symmetry 2020, 12, 24. https://doi.org/10.3390/sym12010024
Pyrkov AN, Byrnes T, Cherny VV. Solitonic Fixed Point Attractors in the Complex Ginzburg–Landau Equation for Associative Memories. Symmetry. 2020; 12(1):24. https://doi.org/10.3390/sym12010024
Chicago/Turabian StylePyrkov, Alexey N., Tim Byrnes, and Valentin V. Cherny. 2020. "Solitonic Fixed Point Attractors in the Complex Ginzburg–Landau Equation for Associative Memories" Symmetry 12, no. 1: 24. https://doi.org/10.3390/sym12010024
APA StylePyrkov, A. N., Byrnes, T., & Cherny, V. V. (2020). Solitonic Fixed Point Attractors in the Complex Ginzburg–Landau Equation for Associative Memories. Symmetry, 12(1), 24. https://doi.org/10.3390/sym12010024




