Soliton Solutions of Mathematical Physics Models Using the Exponential Function Technique
Abstract
1. Introduction
2. Groundwork for Conformable Derivative
3. Presentation of Exp-Function Method for Nonlinear Conformable Pdes
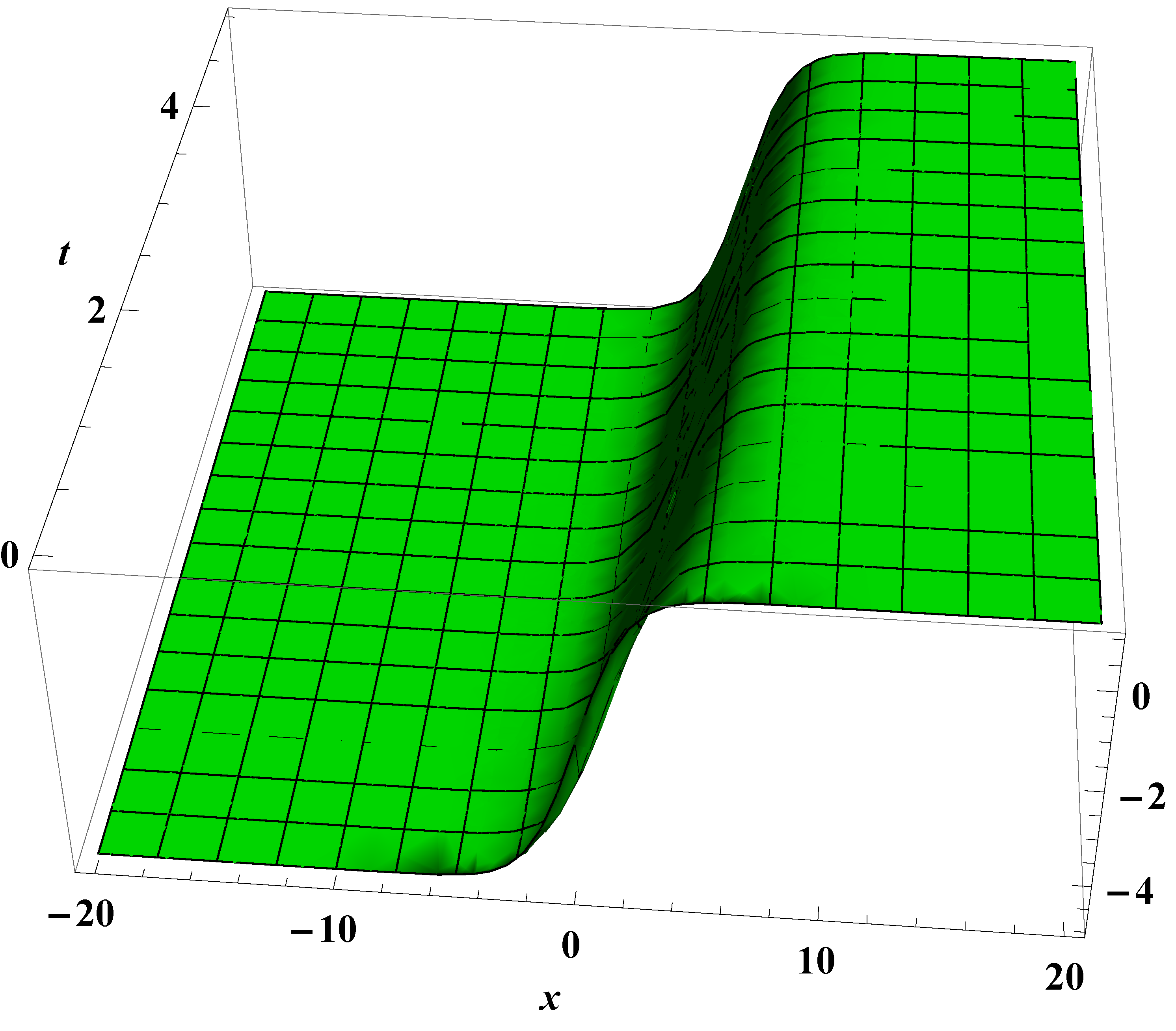
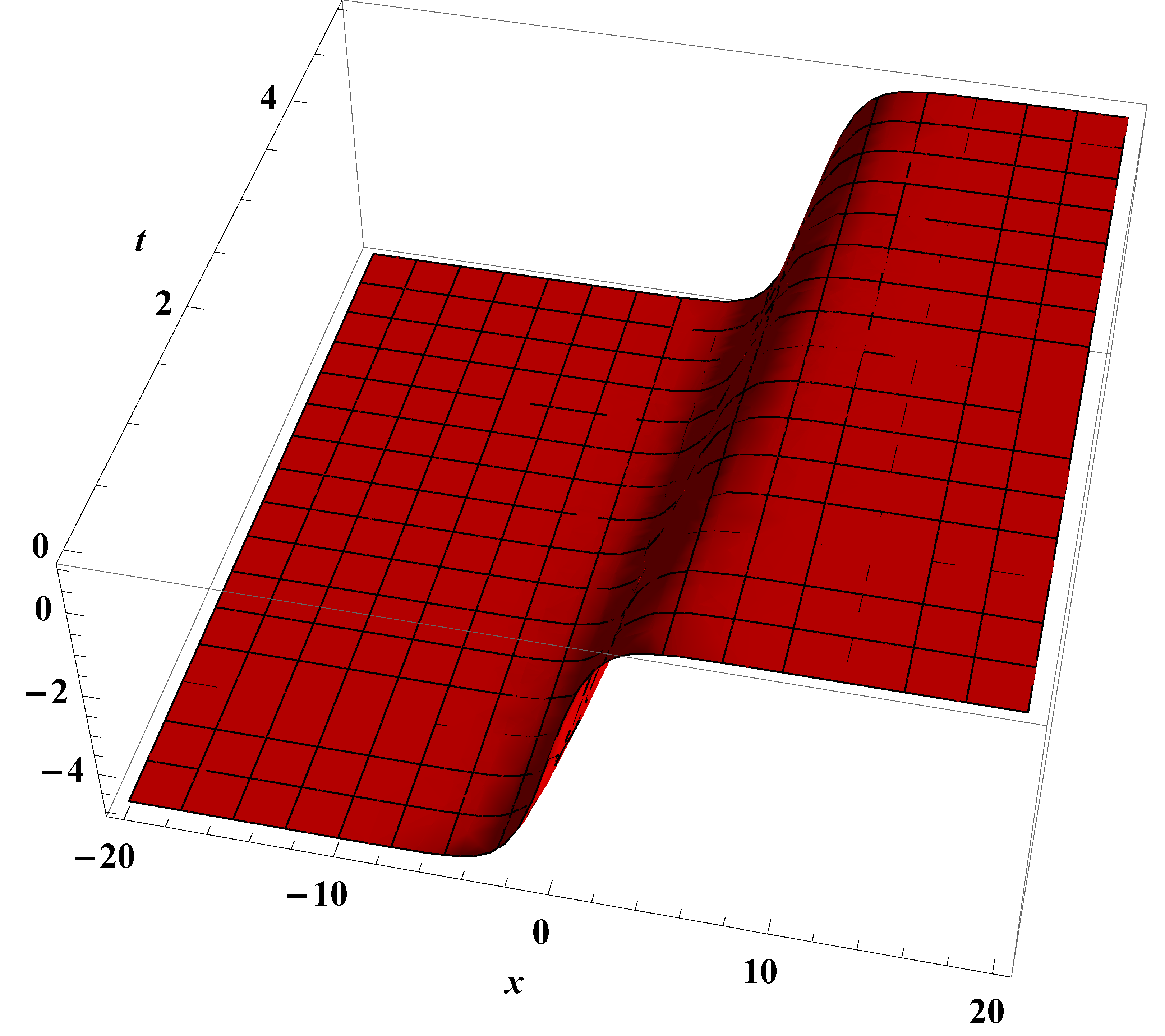
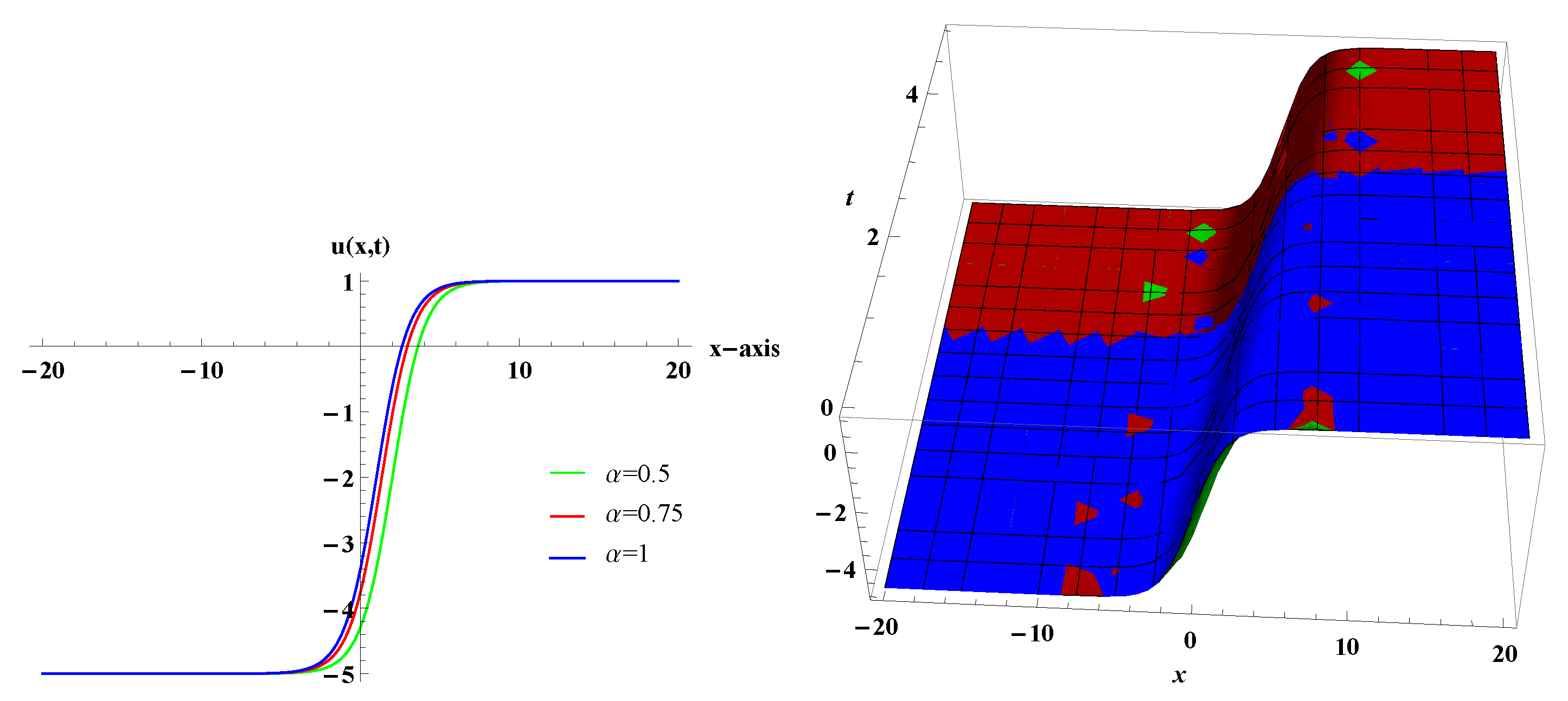
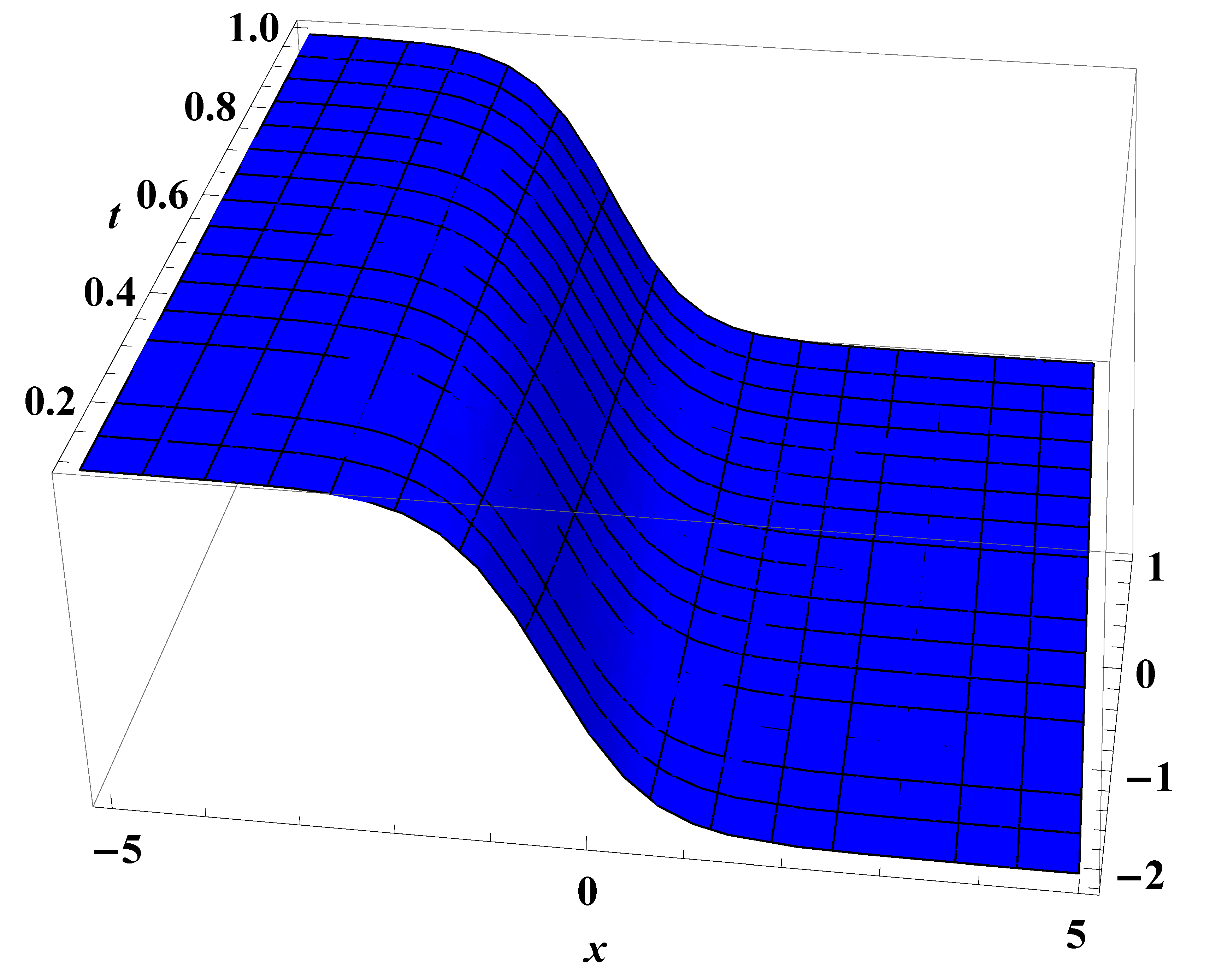
4. Exact Solutions of Burger’S Equation, Equation and Kdv Equation
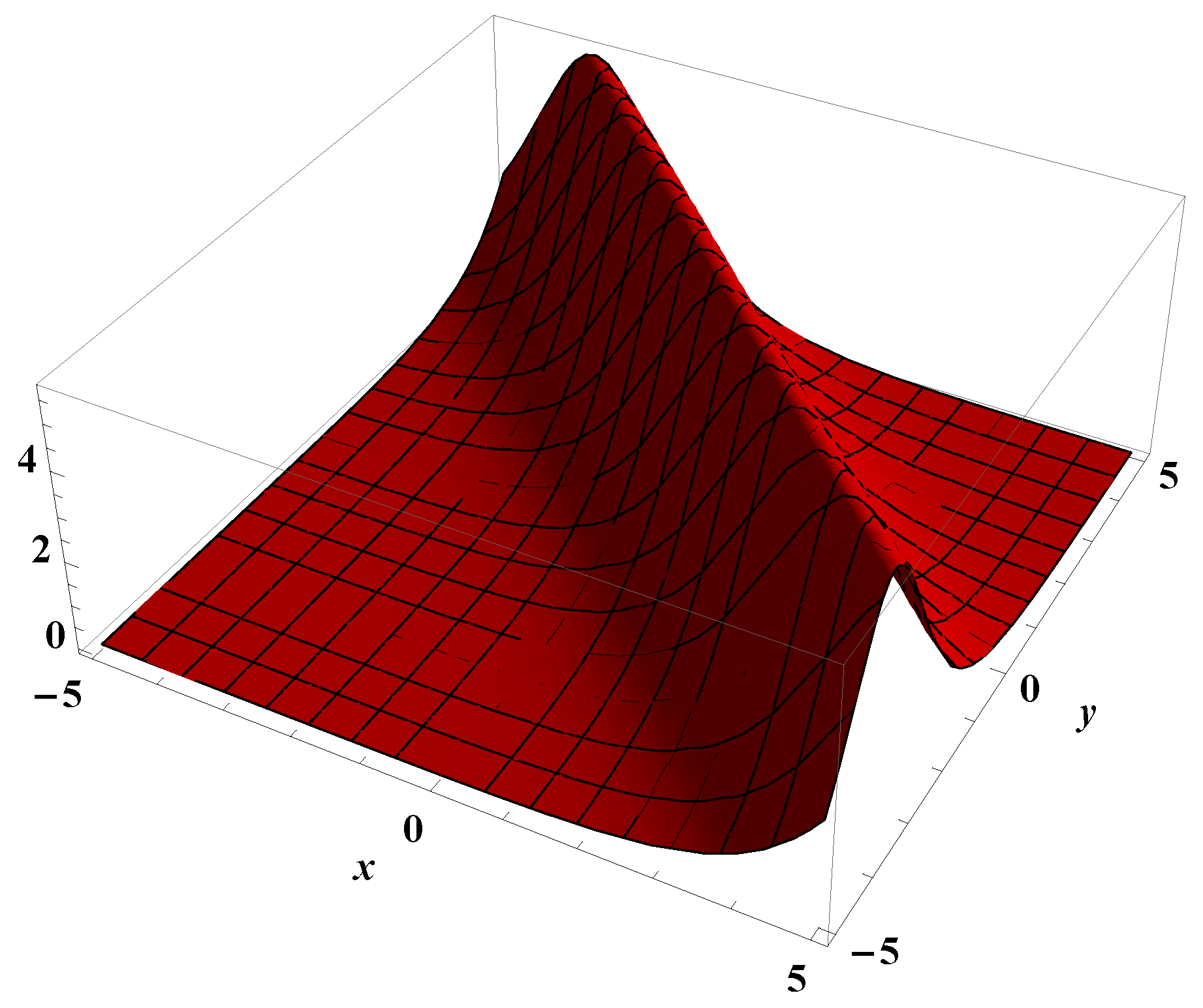
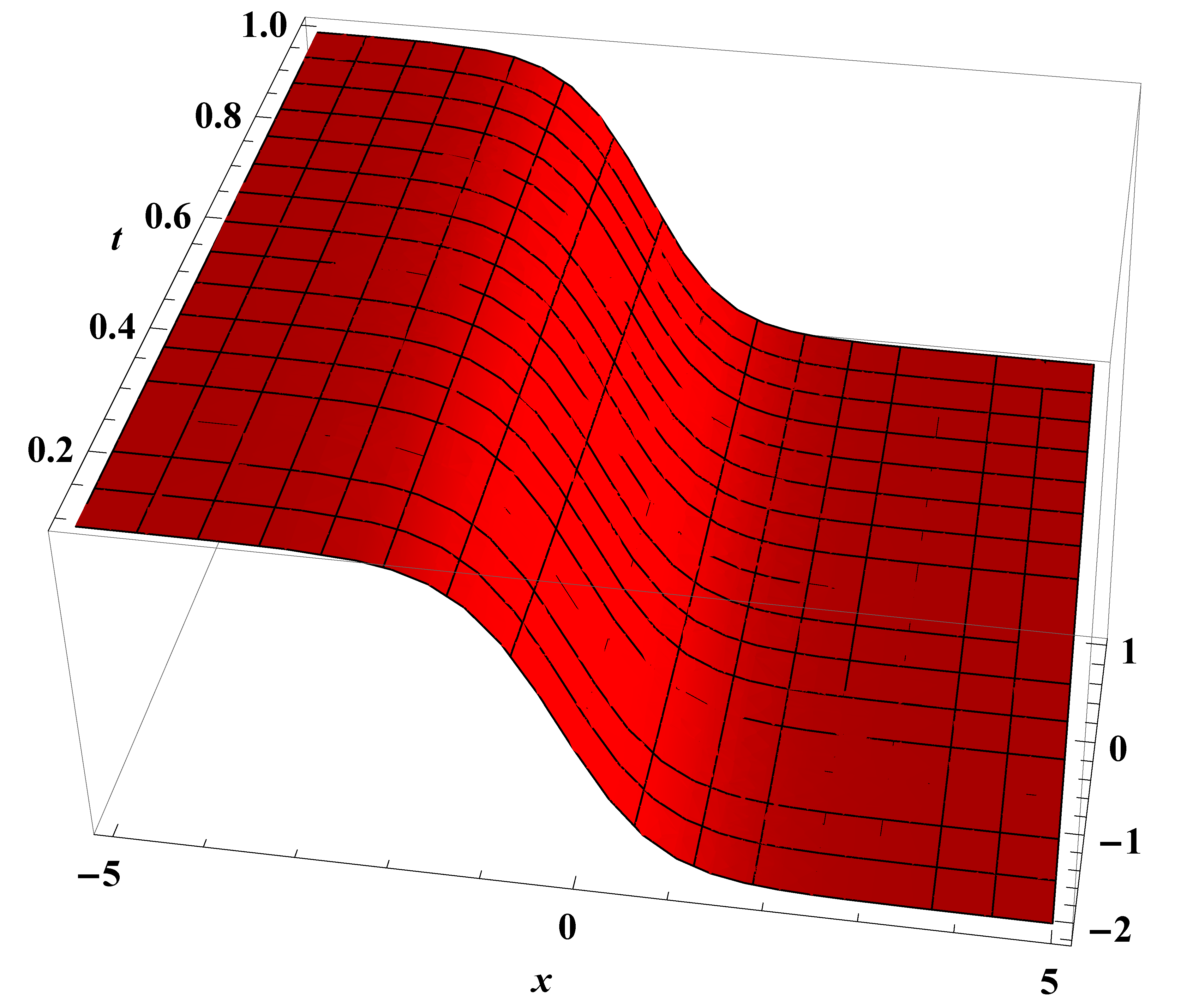
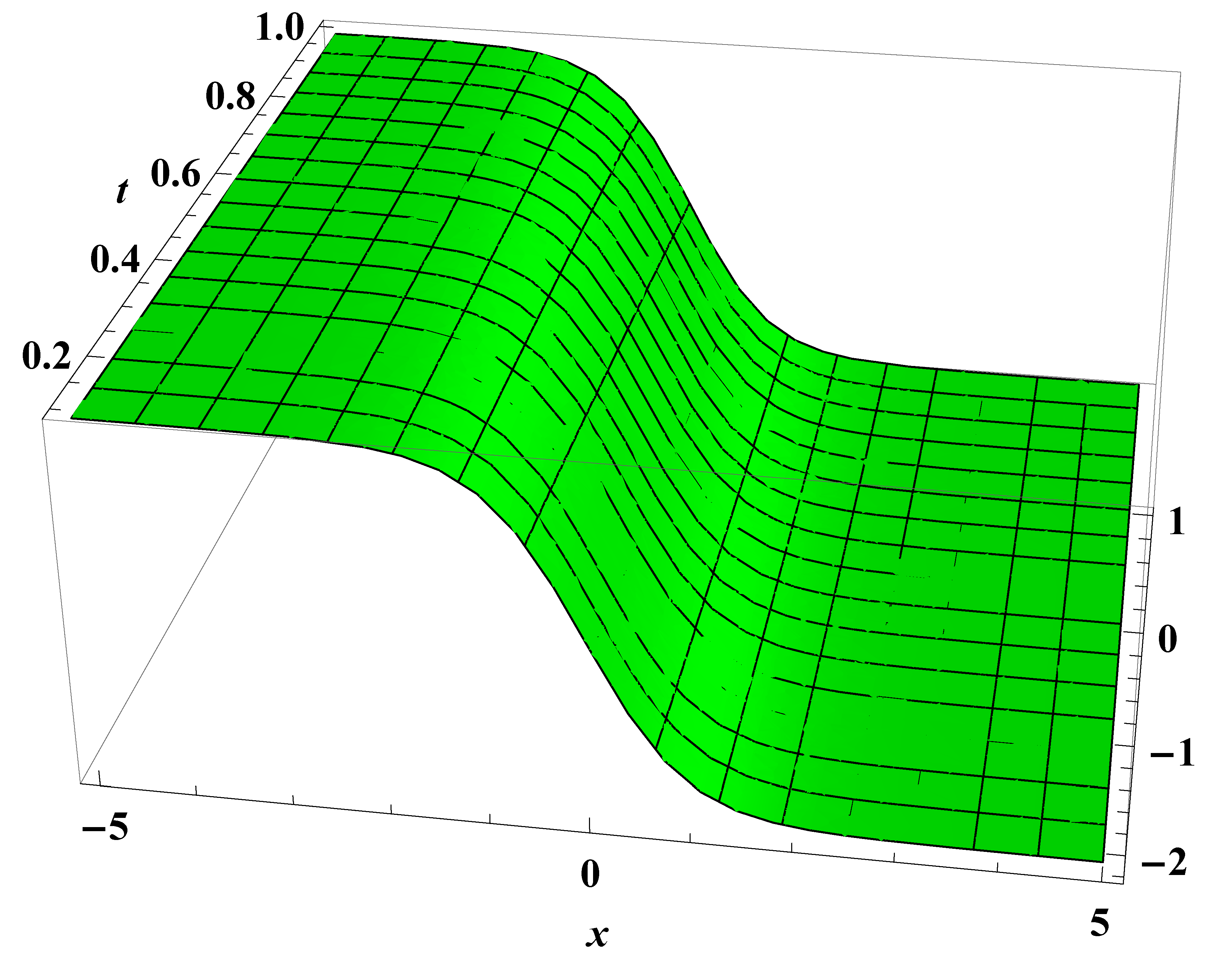
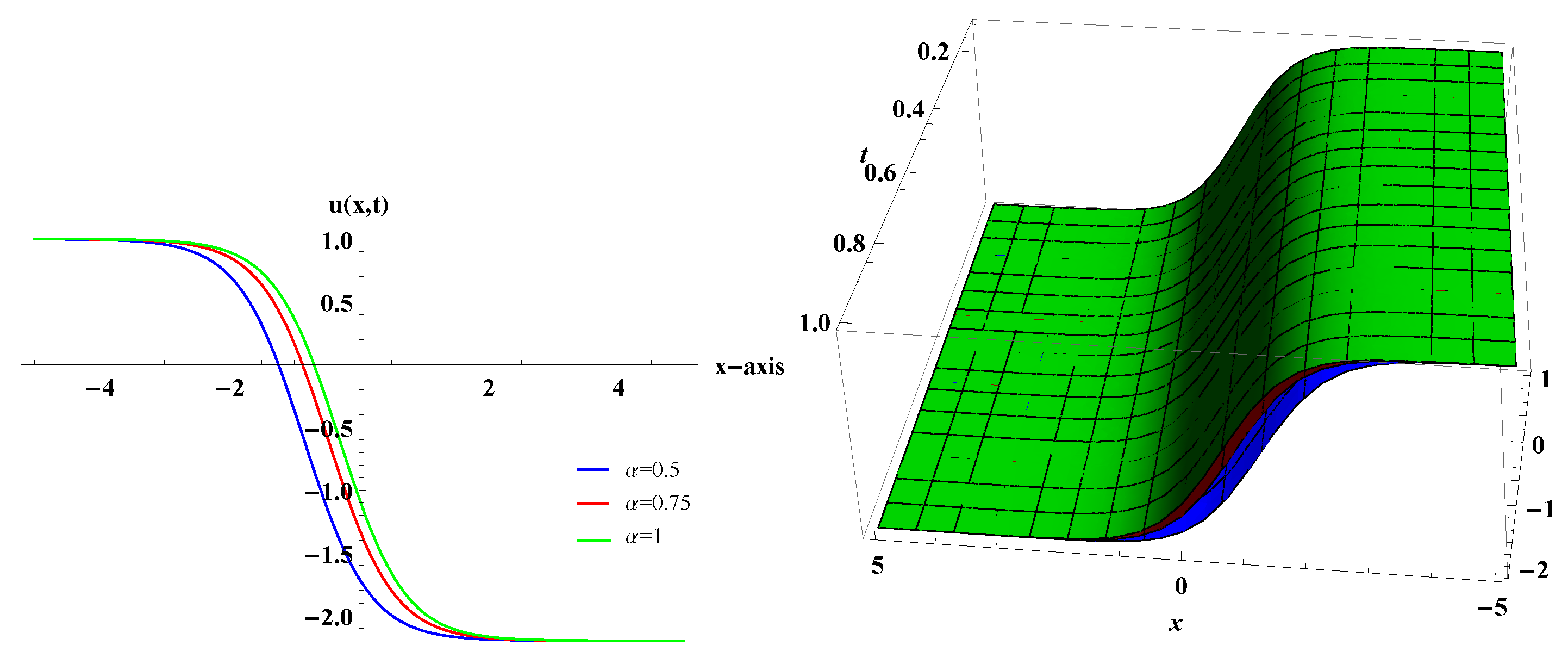
4.1. Exact Solutions of Conformable Equation
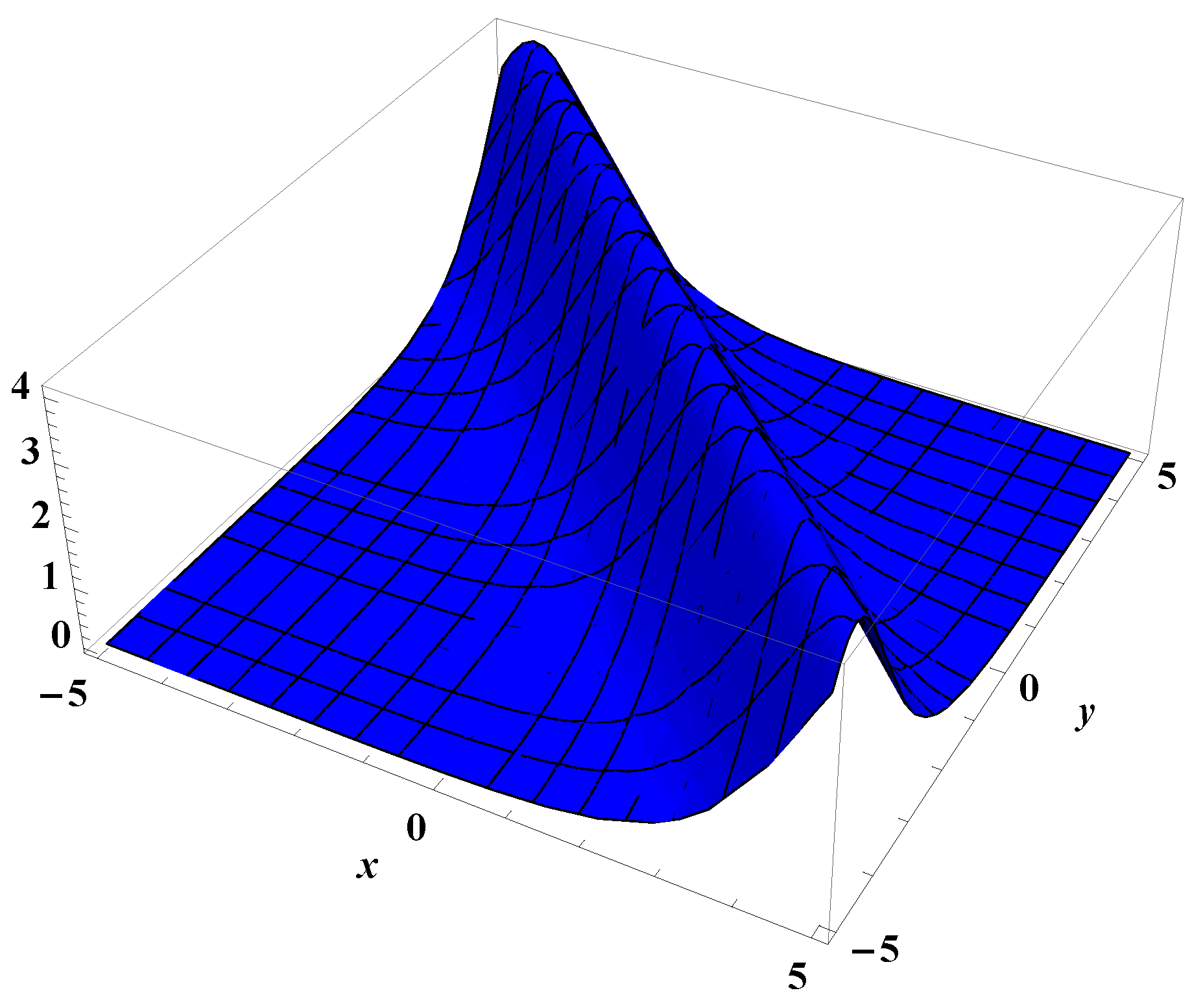
4.2. Exact Solution of Conformable Kdv Equation
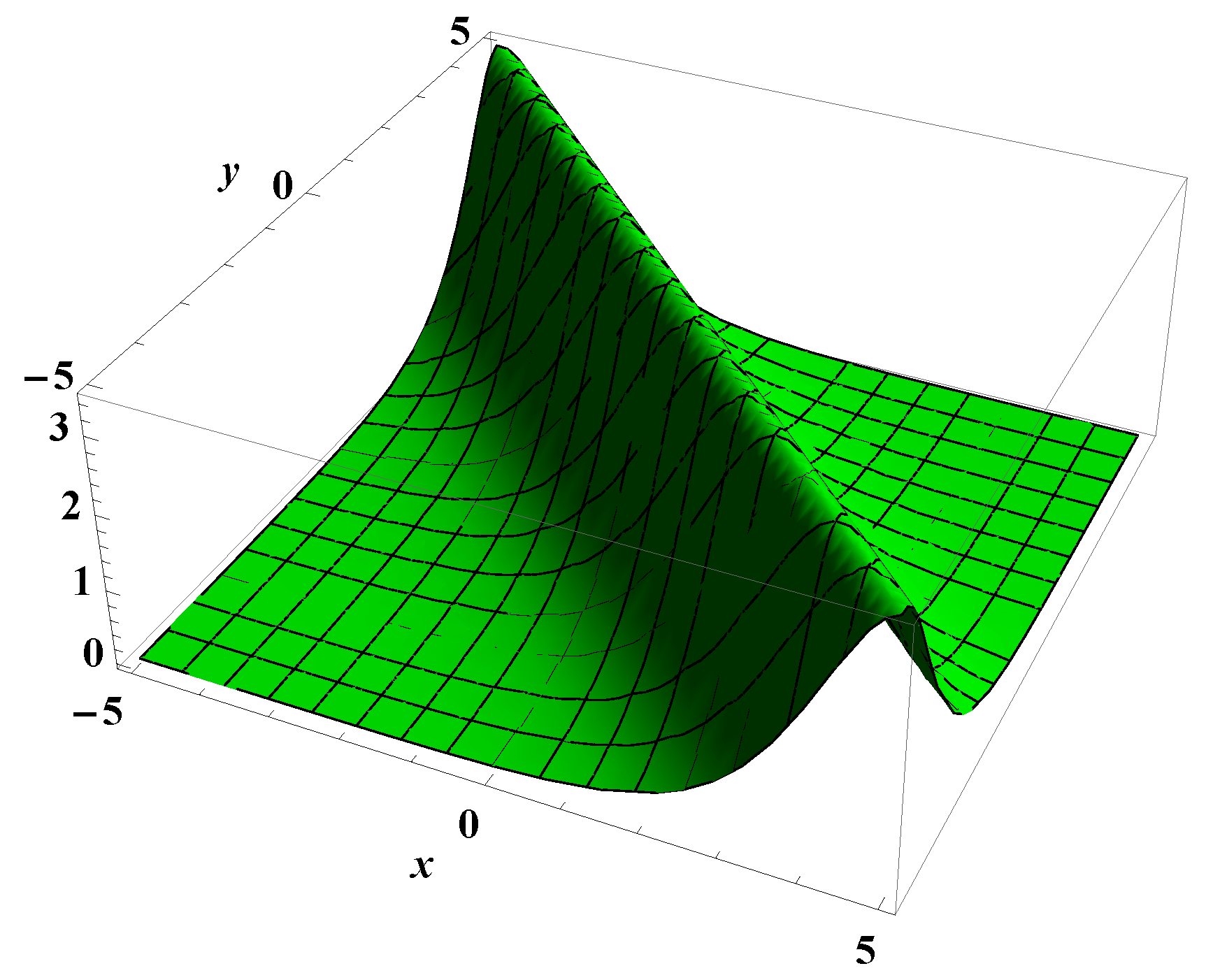
4.3. Exact Solution of Conformable Burgers Equation
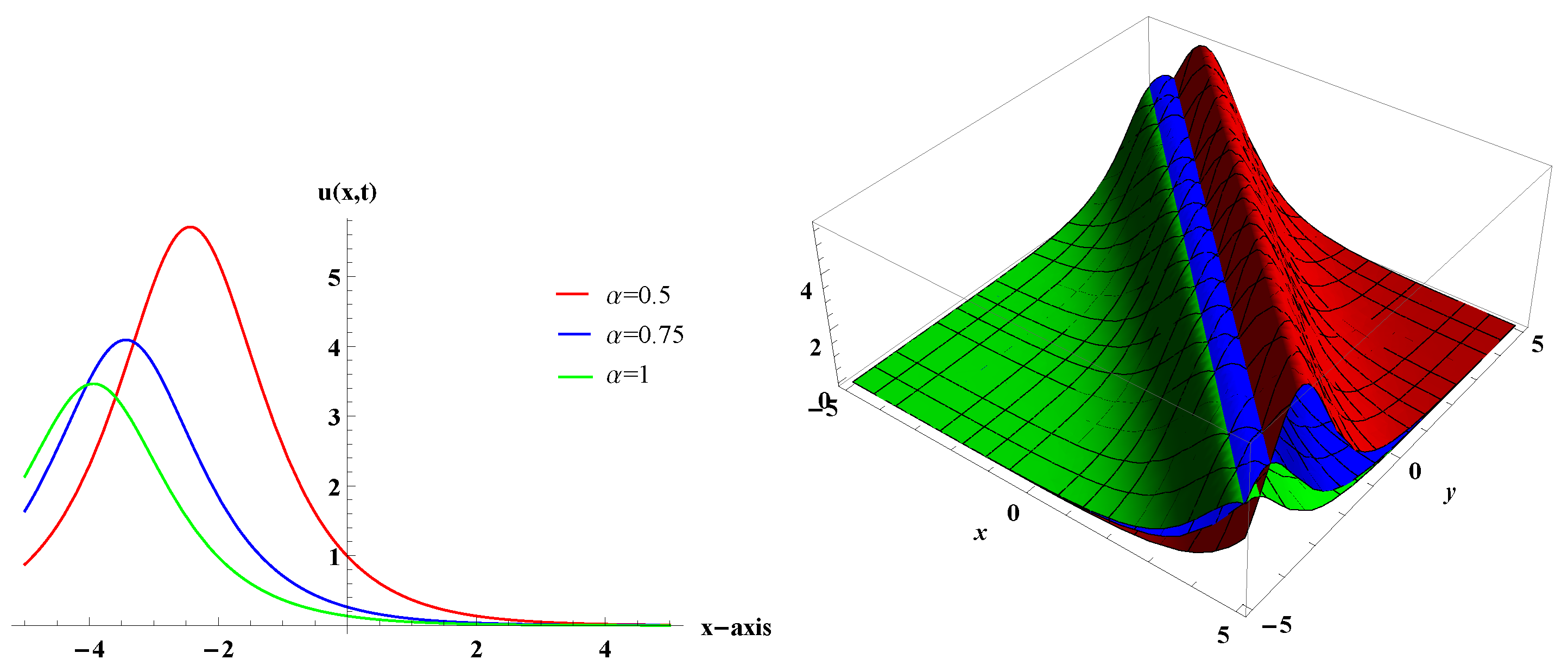
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Vinogradov, A.M. What are symmetries of nonlinear PDEs and what are they themselves? arXiv 2013, arXiv:1308.5861. [Google Scholar]
- Aliyu, A.; Inc, M.; Yusuf, A.; Baleanu, D. Symmetry analysis, explicit solutions, and conservation laws of a sixth-order nonlinear ramani equation. Symmetry 2018, 10, 341. [Google Scholar] [CrossRef]
- Steudel, H. Olver, PJ, Applications of Lie Groups to Differential Equations. Berlin-Heidelberg-New York-Tokyo, Springer Verlag 1986. XXVI, 497 S., DM 158,–. ISBN 3-540-96250-6 (Graduate Texts in Mathematics 107). J. Appl. Math. Mech. 1987, 67, 579. [Google Scholar] [CrossRef]
- Lou, S.Y.; Hu, X.; Chen, Y. Nonlocal symmetries related to Backlund transformation and their applications. J. Phys. A Math. Theor. 2012, 45, 155209. [Google Scholar] [CrossRef]
- Buhe, E.; Bluman, G.W. Symmetry reductions, exact solutions, and conservation laws of the generalized Zakharov equations. J. Math. Phys. 2015, 56, 101501. [Google Scholar] [CrossRef]
- Gao, B. Symmetry analysis and explicit power series solutions of the Boussinesq Whitham Broer Kaup equation. Waves Random Complex Media 2017, 27, 700–710. [Google Scholar] [CrossRef]
- Feng, L.L.; Tian, S.F.; Zhang, T.T.; Zhou, J. Lie symmetries, conservation laws and analytical solutions for two-component integrable equations. Chin. J. Phys. 2017, 55, 996–1010. [Google Scholar] [CrossRef]
- Sahoo, S.; Ray, S.S. Improved fractional sub-equation method for (3 + 1)-dimensional generalized fractional KdV-ZK equations. Comput. Math. Appl. 2015, 70, 158–166. [Google Scholar] [CrossRef]
- Guo, S.; Mei, L.; Li, Y.; Sun, Y. The improved fractional sub-equation method and its applications to the space-time fractional differential equations in fluid mechanics. Phys. Lett. A 2012, 376, 407–411. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, H.Q. Fractional sub-equation method and its applications to nonlinear fractional PDEs. Phys. Lett. A 2011, 375, 1069–1073. [Google Scholar] [CrossRef]
- Kaplan, M.; Akbulut, A.; Bekir, A. Solving space-time fractional differential equations by using modified simple equation method. Commun. Theor. Phys. 2016, 65, 563. [Google Scholar] [CrossRef]
- Kaplan, M.; Bekir, A. Construction of exact solutions to the space-time fractional differential equations via new approach. Optik 2017, 132, 1–8. [Google Scholar] [CrossRef]
- Kaplan, M.; Bekir, A. A novel analytical method for time-fractional differential equations. Optik 2016, 127, 8209–8214. [Google Scholar] [CrossRef]
- Yildirim, A.; Mohyud-Din, S.T. Analytical approach to space-and time-fractional burgers equations. Chin. Phys. Lett. 2010, 27, 090501. [Google Scholar] [CrossRef]
- Tauseef Mohyud-Din, S.; Yildirim, A.; Yülüklü, E. Homotopy analysis method for space-and time-fractional KdV equation. Int. J. Numer. Methods Heat Fluid Flow 2012, 22, 928–941. [Google Scholar] [CrossRef]
- Feng, Z. On explicit exact solutions to the compound Burgers-KdV equation. Phys. Lett. A 2002, 293, 57–66. [Google Scholar] [CrossRef]
- Javeed, S.; Saif, S.; Waheed, A.; Baleanu, D. Exact solutions of fractional mBBM equation and coupled system of fractional Boussinesq-Burgers. Results Phys. 2018, 9, 1275–1281. [Google Scholar] [CrossRef]
- Shakeel, M.; Mohyud-Din, S.T. Improved (G′/G)-expansion and extended tanh methods for (2 + 1)-dimensional Calogero Bogoyavlenskii Schiff equation. Alex. Eng. J. 2015, 54, 27–33. [Google Scholar] [CrossRef]
- Guner, O.; Atik, H.; Kayyrzhanovich, A.A. New exact solution for space-time fractional differential equations via (G′/G)-expansion method. Optik 2017, 130, 696–701. [Google Scholar] [CrossRef]
- Ekici, M. Soliton and other solutions of nonlinear time fractional parabolic equations using extended (G′/G)-expansion method. Optik 2017, 130, 1312–1319. [Google Scholar] [CrossRef]
- Inc, M.; Inan, I.E.; Ugurlu, Y. New applications of the functional variable method. Optik 2017, 136, 374–381. [Google Scholar] [CrossRef]
- Djoudi, W.; Zerarka, A. Exact structures for the KdV-mKdV equation with variable coefficients via the functional variable method. Optik 2016, 127, 9621–9626. [Google Scholar] [CrossRef]
- Liu, H.Z.; Zhang, T. A note on the improved tan(ϕ(ξ)/2)-expansion method. Optik 2017, 131, 273–278. [Google Scholar] [CrossRef]
- Manafian, J.; Lakestani, M. Optical soliton solutions for the Gerdjikov Ivanov model via tan(ϕ/2)-expansion method. Optik 2016, 127, 9603–9620. [Google Scholar] [CrossRef]
- He, J.H.; Wu, X.H. Exp-function method for nonlinear wave equations. Chaos Solitons Fractals 2006, 30, 700–708. [Google Scholar] [CrossRef]
- Aslan, I. On the application of the Exp-function method to the KP equation for N-soliton solutions. Appl. Math. Comput. 2012, 219, 2825–2828. [Google Scholar] [CrossRef][Green Version]
- Navickas, Z.; Ragulskis, M.; Listopadskis, N.; Telksnys, T. Comments on Soliton solutions to fractional-order nonlinear differential equations based on the exp-function method. Optik 2017, 132, 223–231. [Google Scholar] [CrossRef]
- Navickas, Z.; Telksnys, T.; Ragulskis, M. Comments on The exp-function method and generalized solitary solutions. Comput. Math. Appl. 2015, 69, 798–803. [Google Scholar] [CrossRef]
- Khalil, R.; Al Horani, M.; Yousef, A.; Sababheh, M. A new definition of fractional derivative. J. Comput. Appl. Math. 2014, 264, 65–70. [Google Scholar] [CrossRef]
- Abdeljawad, T. On conformable fractional calculus. J. Comput. Appl. Math. 2015, 279, 57–66. [Google Scholar] [CrossRef]
- Batarfi, H.; Losada, J.; Nieto, J.J.; Shammakh, W. Three-point boundary value problems for conformable fractional differential equations. J. Funct. Spaces 2015, 2015, 706383. [Google Scholar] [CrossRef]
- He, J.H.; Abdou, M.A. New periodic solutions for nonlinear evolution equations using Exp-function method. Chaos Solitons Fractals 2007, 34, 1421–1429. [Google Scholar] [CrossRef]
- Ebaid, A. An improvement on the Exp-function method when balancing the highest order linear and nonlinear terms. J. Math. Anal. Appl. 2012, 392, 1–5. [Google Scholar] [CrossRef]
- Navickas, Z.; Ragulskis, M.; Bikulciene, L. Be careful with the Exp-function method-additional remarks. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 3874–3886. [Google Scholar] [CrossRef]
- Wazwaz, A.-M. New sets of solitary wave solutions to the kdv, mkdv, and the generalized kdv equations. Commun. Nonlinear Sci. Numer. Simul. 2008, 13, 331–339. [Google Scholar] [CrossRef]
- Wang, M.L.; Zhou, Y.B.; Li, Z.B. Application of a homogeneous balance method to exact solutions of nonlinear equations in mathematical physics. Phys. Lett. A 1996, 216, 67–75. [Google Scholar] [CrossRef]
- Kudryashov, N.A.; Loguinova, N.B. Be careful with the Exp-function method. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 1881–1890. [Google Scholar] [CrossRef]
- Kudryashov, N.A. Seven common errors in finding exact solutions of nonlinear differential equations. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 3507–3529. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Javeed, S.; Saleem Alimgeer, K.; Nawaz, S.; Waheed, A.; Suleman, M.; Baleanu, D.; Atif, M. Soliton Solutions of Mathematical Physics Models Using the Exponential Function Technique. Symmetry 2020, 12, 176. https://doi.org/10.3390/sym12010176
Javeed S, Saleem Alimgeer K, Nawaz S, Waheed A, Suleman M, Baleanu D, Atif M. Soliton Solutions of Mathematical Physics Models Using the Exponential Function Technique. Symmetry. 2020; 12(1):176. https://doi.org/10.3390/sym12010176
Chicago/Turabian StyleJaveed, Shumaila, Khurram Saleem Alimgeer, Sidra Nawaz, Asif Waheed, Muhammad Suleman, Dumitru Baleanu, and M. Atif. 2020. "Soliton Solutions of Mathematical Physics Models Using the Exponential Function Technique" Symmetry 12, no. 1: 176. https://doi.org/10.3390/sym12010176
APA StyleJaveed, S., Saleem Alimgeer, K., Nawaz, S., Waheed, A., Suleman, M., Baleanu, D., & Atif, M. (2020). Soliton Solutions of Mathematical Physics Models Using the Exponential Function Technique. Symmetry, 12(1), 176. https://doi.org/10.3390/sym12010176





