On Neutrosophic Extended Triplet LA-hypergroups and Strong Pure LA-semihypergroups
Abstract
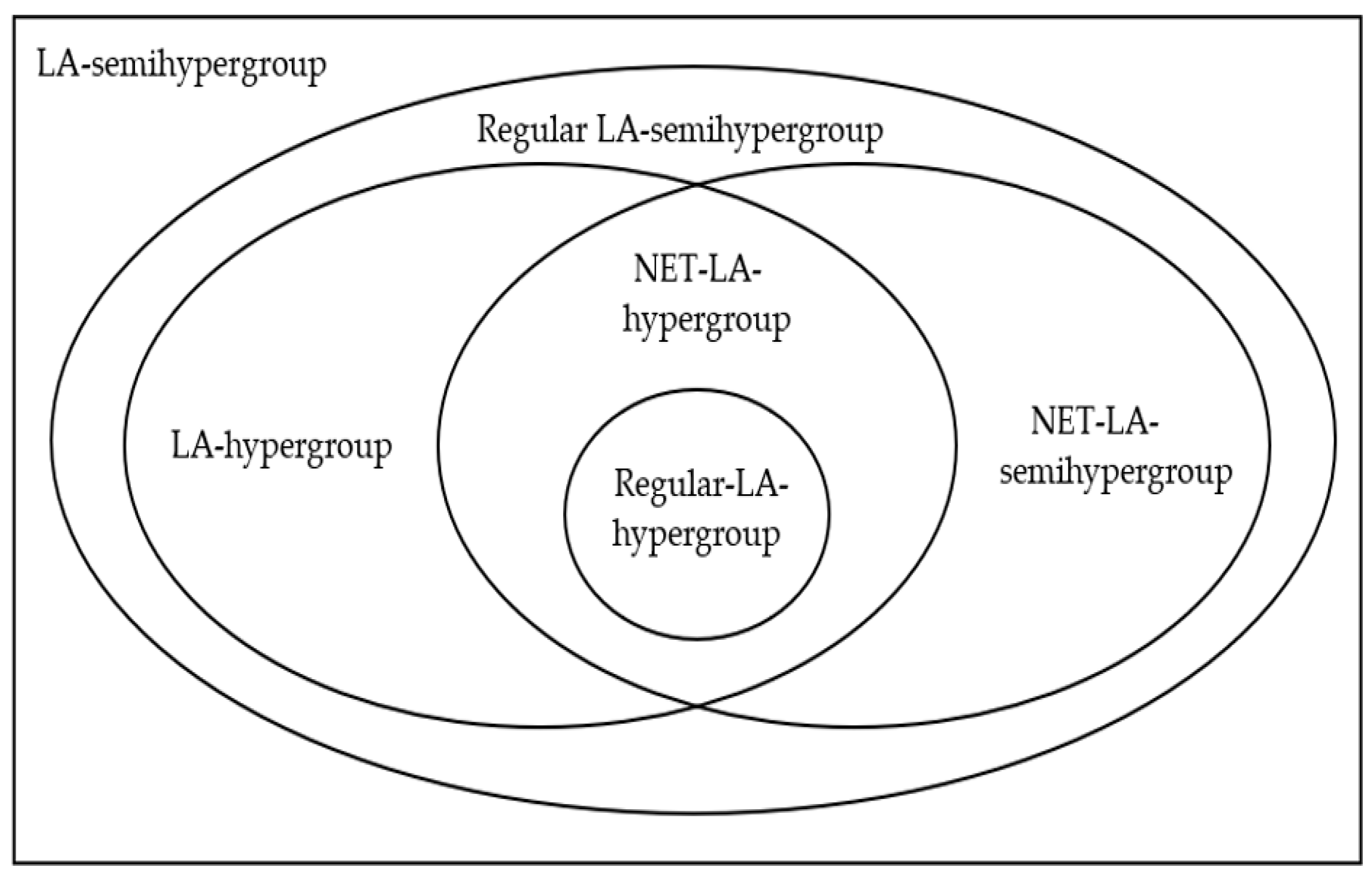
1. Introduction and Preliminaries
- (a)
- T ⊆ H, T ≠;
- (b)
- m ◦ n ⊆ T for all m, n ∈ T;
- (c)
- (H, ◦) is an LA-semihypergroup.
- (a)
- a left identity, if a ∈ e ◦ a for each a ∈ H;
- (b)
- a right identity, if a ∈ a ◦ e for each a ∈ H;
- (c)
- an identity, if a ∈ (e ◦ a) ∩ (a ◦ e) for each a ∈ H;
- (d)
- a pure left identity, if a = e ◦ a for each a ∈ H;
- (e)
- a pure right identity, if a = a ◦ e for each a ∈ H;
- (f)
- a pure identity, if a = (e ◦ a) ∩ (a ◦ e) for each a ∈ H;
- (g)
- a scalar identity, if a = e ◦ a = a ◦ e for each a ∈ H.
- (a)
- (H, ◦) is an LA-hypergroup;
- (b)
- There exists e ∈ H such that e is identity of (H, ◦) ;
- (c)
- Every element a ∈ H has at least one inverse.
2. Neutrosophic Extended Triplet LA-Semihypergroups and Neutrosophic Extended Triplet LA-Hypergroups
- (a)
- a left neutrosophic extended triplet LA-semihypergroup (LNET-LA-semihypergroup) if to any givena ∈ L, there are p ∈ L and q ∈ L, in such a way that
- (b)
- a right neutrosophic extended triplet LA-semihypergroup (RNET-LA-semihypergroup), if to any given a ∈ L, there are s ∈ L and t ∈ L, in such a way that
- (c)
- a neutrosophic extended triplet LA-semihypergroup (NET-LA-semihypergroup), if to any given a ∈ L, there are m ∈ L and n ∈ L, in such a way that
| Python program 1 Verification of LA-semihypergroup 1 |
| 1: T = [ [[0],[0],[0]], [[0], [1], [0]], [[0], [0], [0,2]] ] |
| 2: count = 0 |
| 3: for x in range(3): |
| 4: for y in range(3): |
| 5: for z in range(3): |
| 6: T1 = T[x][y] |
| 7: T2 = set() |
| 8: k1 = len(T1)S3 = set(T[neut_t][t]) |
| 9: for m in range(k1) |
| 10: T2 = set(T[T1[m]][z]).union(T2) |
| 11: T3 = T[z][y] |
| 12: T4 = set() |
| 13: k2 = len(T3) |
| 14: for n in range(k2): |
| 15: T4 = set(T[T3[n]][x]).union(T4) |
| 16: if T2 = = T4:Ifif |
| 17: count += 1 18: while count = = 3**3: |
| 19: print(‘{} is an LA-semihypergroup’.format(T)) 20: break |
| Python program 2 Verification of NET-LA-semihypergroup 1 |
| 1: T = [ [[0],[0],[0]], [[0], [1], [0]], [[0], [0], [0,2]] ] |
| 2: test = [[] |
| 3: for t in range(3): |
| 4: for neut_t in range(3): |
| 5: for anti_t in range(3): |
| 6: S1 = set(T[t][neut_t]) |
| 7: S2 = set(T[t][anti_t]) |
| 8: S3 = set(T[neut_t][t]) |
| 9: S4 = set(T[anti_t][t]) |
| 10: S5 = set(list([t])) |
| 11: S6 = set(list([neut_t])) |
| 12: if S5.issubset(S1 & S3) and S6.issubset(S2 & S4): |
| 13: test.append([t, neut_t, anti_t]) |
| 14: test2 = test |
| 15: test1 = set([test2[i][0] for i in range(len(test2))]) |
| 16: if test1 == set([x for x in range(3)]): |
| 17: print('{0} is an Net-LA-semihypergroup and hyper neutrosophic-triplet are {1}'.format(T, test2)) |
| Python program 3 Verification of LA-semihypergroup 2 |
| 1: T = [ [[0],[0],[0],[0,1,2,3]], [[0], [0], [0],[0,1,2,3]], [[0], [0], [0,1],[2,3]], [[1,2,3],[0,1,2,3],[2,3],[0,3]] ] |
| 2: count = 0 |
| 3: for x in range(4): |
| 4: for y in range(4): |
| 5: for z in range(4): |
| 6: T1 = T[x][y] |
| 7: T2 = set() |
| 8: k1 = len(T1)S3 = set(T[neut_t][t]) |
| 9: for m in range(k1) |
| 10: T2 = set(T[T1[m]][z]).union(T2) |
| 11: T3 = T[z][y] |
| 12: T4 = set() |
| 13: k2 = len(T3) |
| 14: for n in range(k2): |
| 15: T4 = set(T[T3[n]][x]).union(T4) |
| 16: if T2 = = T4:Ifif |
| 17: count += 1 18: while count = = 4**3: |
| 19: print(‘( T,∗) is an LA-semihypergroup.’) 20: break |
| Python program 4 Verification of NET-LA-semihypergroup 2 |
| 1: T = [ [[0],[0],[0],[0,1,2,3]], [[0], [0], [0],[0,1,2,3]], [[0], [0], [0,1],[2,3]], [[1,2,3],[0,1,2,3],[2,3],[0,3]] ] |
| 2: test = [[] |
| 3: for t in range(4): |
| 4: for neut_t in range(4): |
| 5: for anti_t in range(4): |
| 6: S1 = set(T[t][neut_t]) |
| 7: S2 = set(T[t][anti_t]) |
| 8: S3 = set(T[neut_t][t]) |
| 9: S4 = set(T[anti_t][t]) |
| 10: S5 = set(list([t])) |
| 11: S6 = set(list([neut_t])) |
| 12: if S5.issubset(S1 & S3) and S6.issubset(S2 & S4): |
| 13: test.append([t, neut_t, anti_t]) |
| 14: test2 = test |
| 15: test1 = set([test2[i][0] for i in range(len(test2))]) |
| 16: if test1 == set([x for x in range(3)]): |
| 17: print('(T,∗) is an NET-LA-semihypergroup and hyper neutrosophic-triplet are {}'.format(test2). |
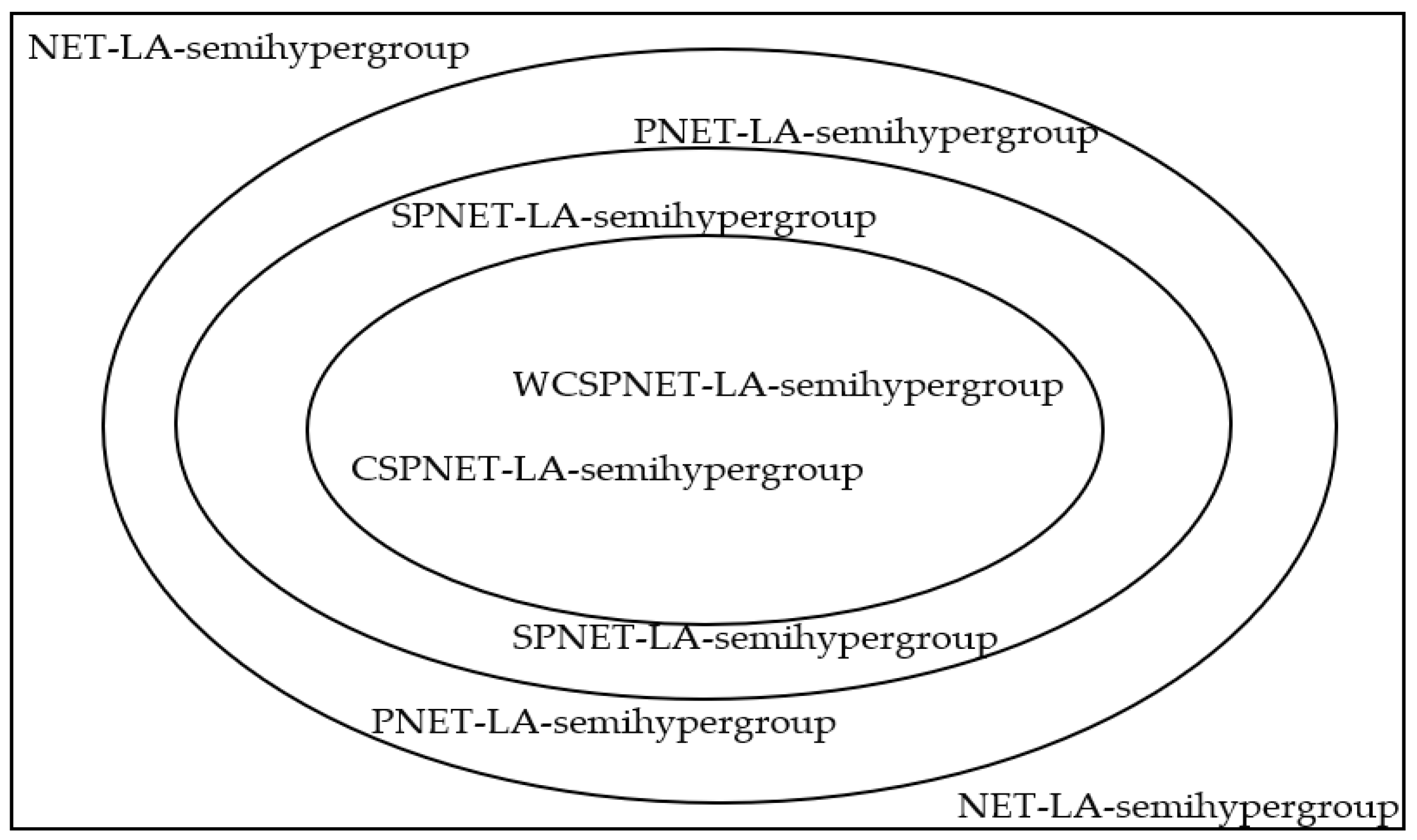
3. Strong Pure Neutrosophic Extended Triplet LA-Semihypergroups (SPNET-LA-Semihypergroups)
- (a)
- a pure left neutrosophic extended triplet LA-semihypergroup (PLNET-LA-semihypergroup), if to any given a ∈ L, there are p ∈ L and q ∈ L, in such a way thata = p ∗ a and p = q ∗ a
- (b)
- a pure right neutrosophic extended triplet LA-semihypergroup (PRNET-LA-semihypergroup), if to any given a ∈ L, there are s ∈ L and t ∈ L, in such a way thata = a ∗ s and s = a ∗ t
- (c)
- a pure neutrosophic extended triplet LA-semihypergroup (PNET-LA-semihypergroup), if to any given a ∈ L, there are m ∈ L and n ∈ L, in such a way thata = (m ∗ a) ∩ (a ∗ m) and m = (n ∗ a) ∩ (a ∗ n)
- (d)
- a strong pure neutrosophic extended triplet LA-semihypergroup (SPNET-LA-semihypergroup), if to any given a ∈ L, there are m ∈ L and n ∈ L, in such a way thata = m ∗ a = a ∗ m and m = n ∗ a = a ∗ n
- (1)
- if s ∈, then s is unique and s∗ s = s;
- (2)
- if s = neut(a), then neut(s) = s and s∈;
- (3)
- if s = neut(a), t ∈, r ∈, then r∗ t ⊆;
- (4)
- if s = neut(a), t ∈, then s∗ t ⊆;
- (5)
- if p = neut(a), s = neut(b), q ∈,t ∈and |a∗ b|=| p∗ s| = 1, then
- (6)
- if s = neut(a) = neut(b), q ∈, t ∈and |a∗ b| = 1, then
- (7)
- if neut(a) = neut(b), then a ∗ b = b ∗ a;
- (8)
- then s ∗ b = s ∗ c if b ∗ a = c ∗ a, where s = neut(a);
- (9)
- if s = neut(a), q, t ∈, then s∗ q = s∗ t.
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kazim, M.A.; Naseeruddin, N. On almost semigroups. Aligarh Bull. Math. 1972, 2, 1–7. [Google Scholar]
- Marty, F. Sur Une Generalization de la Notion de Groupe. In Proceedings of the 8th Congres des Mathematicians Scandinaves, Stockholm, Sweden, 14–18 August 1934; pp. 45–49. [Google Scholar]
- Vougiouklis, T. Hyperstructures and Their Representations; Hadronic Press: Palm Harbor, FL, USA, 1994. [Google Scholar]
- Howie, J.M. Fundamentals of Semigroup Theory; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Corsini, P.; Leoreanu, V. Applications of Hyperstructure Theory; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Davvaz, B. Semihypergroup Theory; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Hila, K.; Dine, J. On hyperideals in left almost semihypergroups. ISRN Algebra 2011, 2011, 953124. [Google Scholar] [CrossRef]
- Yaqoob, N.; Corsini, P.; Yousafzai, F. On intra-regular left almost semihypergroups with pure left identity. J. Math. 2013, 2013, 510790. [Google Scholar] [CrossRef]
- Amjad, V.; Hila, K.; Yousafzai, F. Generalized hyperideals in locally associative left almost semihypergroups. N. Y. J. Math. 2014, 20, 1063–1076. [Google Scholar]
- Yaqoob, N.; Gulistan, M. Partially ordered left almost semihypergroups. J. Egypt. Math. Soc. 2015, 23, 231–235. [Google Scholar] [CrossRef]
- Yousafzai, F.; Hila, K.; Corsini, P.; Zeb, A. Existence of non-associative algebraic hyperstructures and related problems. Afr. Mat. 2015, 26, 981–995. [Google Scholar] [CrossRef]
- Rehman, I.; Yaqoob, N.; Nawaz, S. Hyperideals and hypersystems in LA-hyperrings. Songklanakarin J. Sci. Technol. 2017, 39, 651–657. [Google Scholar]
- Nawaz, S.; Rehman, I.; Gulistan, M. On left almost semihyperrings. Int. J. Anal. Appl. 2018, 16, 528–541. [Google Scholar]
- Smarandache, F.; Ali, M. Neutrosophic triplet group. Neural Comput. Appl. 2018, 29, 595–601. [Google Scholar] [CrossRef]
- Gulistan, M.; Nawaz, S.; Hassan, N. Neutrosophic Triplet Non-Associative Semihypergroups with Application. Symmetry 2018, 10, 613. [Google Scholar] [CrossRef]
- Smarandache, F. Neutrosophic Perspectives: Triplets, Duplets, Multisets, Hybrid Operators, Modal Logic, Hedge Algebras. And Applications; Pons Publishing House: Brussels, Belgium, 2017. [Google Scholar]
- Zhang, X.H.; Hu, Q.Q.; Smarandache, F.; An, X.G. On neutrosophic triplet groups: Basic properties, NT-subgroups, and some notes. Symmetry 2018, 10, 289. [Google Scholar] [CrossRef]
- Jaíyéolá, T.G.; Smarandache, F. Some sesults on neutrosophic triplet group and their applications. Symmetry 2018, 10, 202. [Google Scholar] [CrossRef]
- Zhang, X.H.; Wu, X.Y.; Mao, X.Y.; Smarandache, F.; Park, C. On neutrosophic extended triplet groups (Loops) and Abel-Grassmann’s Groupoids (AG-Groupoids). J. Intell. Fuzzy Syst. 2019, 37, 5743–5753. [Google Scholar] [CrossRef]
- Wu, X.Y.; Zhang, X.H. The decomposition theorems of AG-neutrosophic extended triplet loops and strong AG-(l, l)-loops. Mathematics 2019, 7, 268. [Google Scholar] [CrossRef]
- Ma, Y.C.; Zhang, X.H.; Yang, X.F.; Zhou, X. Generalized neutrosophic extended triplet group. Symmetry 2019, 11, 327. [Google Scholar] [CrossRef]
- Zhang, X.H.; Wang, X.J.; Smarandache, F.; Jaíyéolá, T.G.; Lian, T.Y. Singular neutrosophic extended triplet groups and generalized groups. Cogn. Syst. Res. 2019, 57, 32–40. [Google Scholar] [CrossRef]
- Zhang, X.H.; Samarandache, F.; Ma, Y.C. Neutrosophic Extended Triplet Semihypergroups and Regular Hypergroups. Symmetry 2019, 11, 1217. [Google Scholar] [CrossRef]
- Zhang, X.H.; Mao, X.Y.; Wu, Y.T.; Zhai, X.H. Neutrosophic filters in pseudo-BCI algebras. Int. J. Uncertain. Quan. 2018, 8, 511–526. [Google Scholar] [CrossRef]
- Zhang, X.H.; Borzooei, R.A.; Jun, Y.B. Q-filters of quantum B-algebras and basic implication algebras. Symmetry 2018, 10, 573. [Google Scholar] [CrossRef]
- An, X.G.; Zhang, X.H.; Ma, Y.C. Generalized Abel-Grassmann’s Neutrosophic Extended Triplet Loop. Mathematics 2019, 7, 1206. [Google Scholar] [CrossRef]





| ∗ | 0 | 1 | 2 |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 2 | 0 | 0 | {0, 2} |
| ∗ | 0 | 1 | 2 |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 |
| 2 | 0 | 0 | {0, 1} |
| ∗ | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | {0,1,2,3} |
| 1 | 0 | 0 | 0 | {0,1,2,3} |
| 2 | 0 | 0 | {0,1} | {2,3} |
| 3 | {1,2,3} | {0,1,2,3} | {2,3} | {0,3} |
| ∗ | 0 | 1 | 2 |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | {0, 1} |
| 2 | 0 | {0, 1} | {2} |
| ∗ | 0 | 1 | 2 |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 0 | 2 | 2 |
| 2 | 0 | {0,1,2} | {0,1,2} |
| ∗ | 0 | 1 | 2 |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 2 | 0 | 0 | {0 ,2} |
| ∗ | 0 | 1 | 2 |
|---|---|---|---|
| 0 | 0 | {0,1,2} | {0,1,2} |
| 1 | 0 | {0 ,2} | {1 ,2} |
| 2 | {0,1,2} | {0 ,2} | {0,1,2} |
| ∗ | 0 | 1 | 2 |
|---|---|---|---|
| 0 | {1,2} | {0,1,2} | {0,1,2} |
| 1 | {0,1,2} | {0,2} | {0,2} |
| 2 | {0,1} | {1,2} | {0,1} |
| ∗ | 0 | 1 | 2 |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 0 | 2 | 2 |
| 2 | 0 | {1,2} | {1,2} |
| ∗ | 0 | 1 | 2 |
|---|---|---|---|
| 0 | 0 | {0, 1, 2} | {0, 1, 2} |
| 1 | 2 | 2 | { 1, 2} |
| 2 | {0, 1, 2} | {0, 2} | {0, 1, 2} |
| ∗ | 0 | 1 | 2 |
|---|---|---|---|
| 0 | 0 | 1 | {0,1,2} |
| 1 | 1 | 0 | {0,1,2} |
| 2 | {0,1,2} | {0,1,2} | 2 |
| ∗ | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| 0 | 0 | 1 | {0, 1, 2} | 0 | 4 |
| 1 | 1 | 0 | {0, 1, 2} | 1 | 4 |
| 2 | {0, 1, 2} | {0, 1, 2} | 2 | {0, 1, 2} | 4 |
| 3 | 0 | 1 | {0, 1, 2} | 3 | 4 |
| 4 | 4 | 4 | 4 | 4 | 4 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, M.; Smarandache, F.; Zhang, X. On Neutrosophic Extended Triplet LA-hypergroups and Strong Pure LA-semihypergroups. Symmetry 2020, 12, 163. https://doi.org/10.3390/sym12010163
Hu M, Smarandache F, Zhang X. On Neutrosophic Extended Triplet LA-hypergroups and Strong Pure LA-semihypergroups. Symmetry. 2020; 12(1):163. https://doi.org/10.3390/sym12010163
Chicago/Turabian StyleHu, Minghao, Florentin Smarandache, and Xiaohong Zhang. 2020. "On Neutrosophic Extended Triplet LA-hypergroups and Strong Pure LA-semihypergroups" Symmetry 12, no. 1: 163. https://doi.org/10.3390/sym12010163
APA StyleHu, M., Smarandache, F., & Zhang, X. (2020). On Neutrosophic Extended Triplet LA-hypergroups and Strong Pure LA-semihypergroups. Symmetry, 12(1), 163. https://doi.org/10.3390/sym12010163







