Classification of Kidney Cancer Data Using Cost-Sensitive Hybrid Deep Learning Approach
Abstract
1. Introduction
2. Materials and Methods
2.1. Dataset
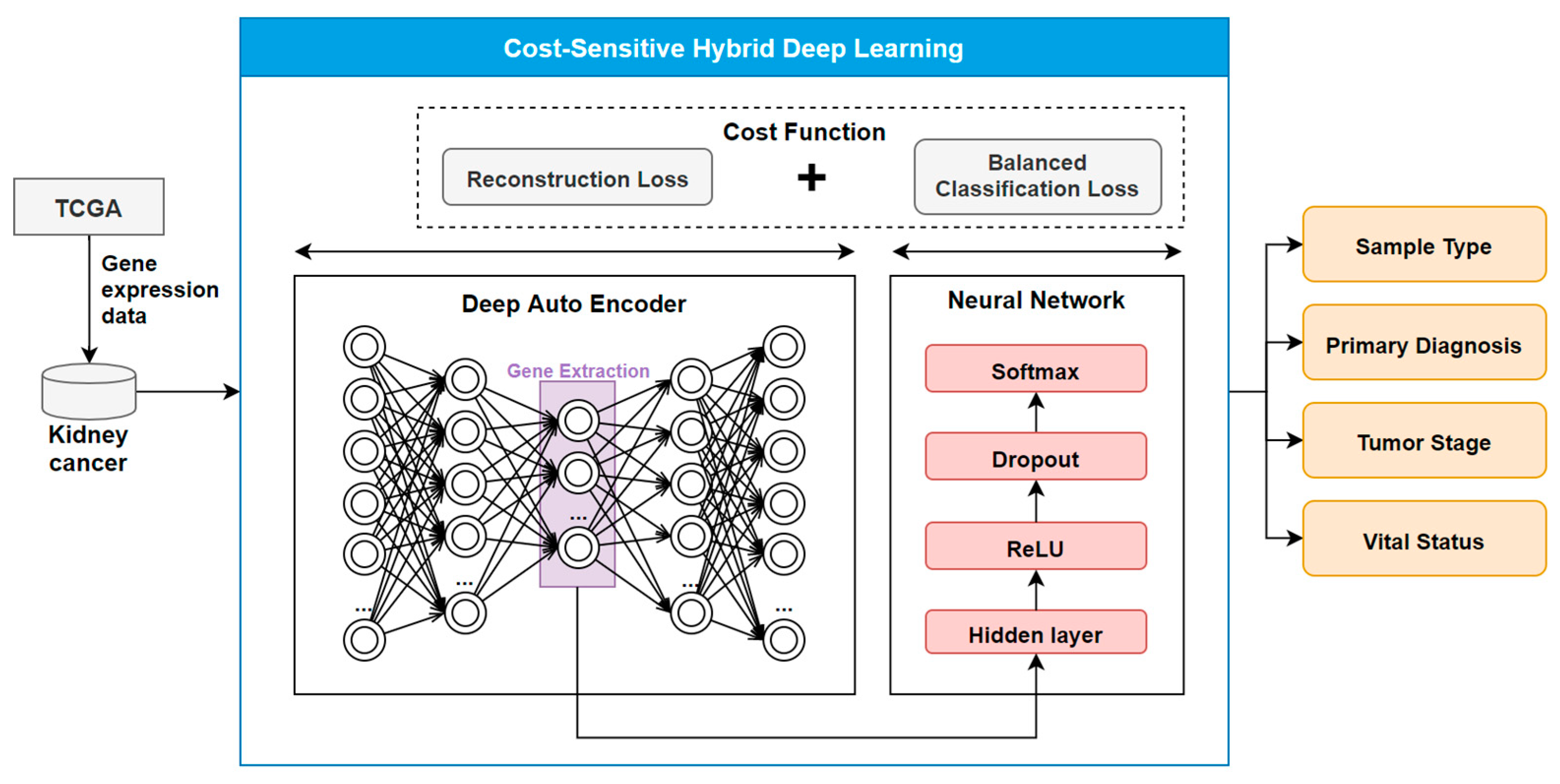
2.2. The COST-HDL Approach
2.2.1. Extracting Deep Features from Gene Biomarkers
2.2.2. Constructing Prognose Prediction Models
2.2.3. Training the Models
3. Results
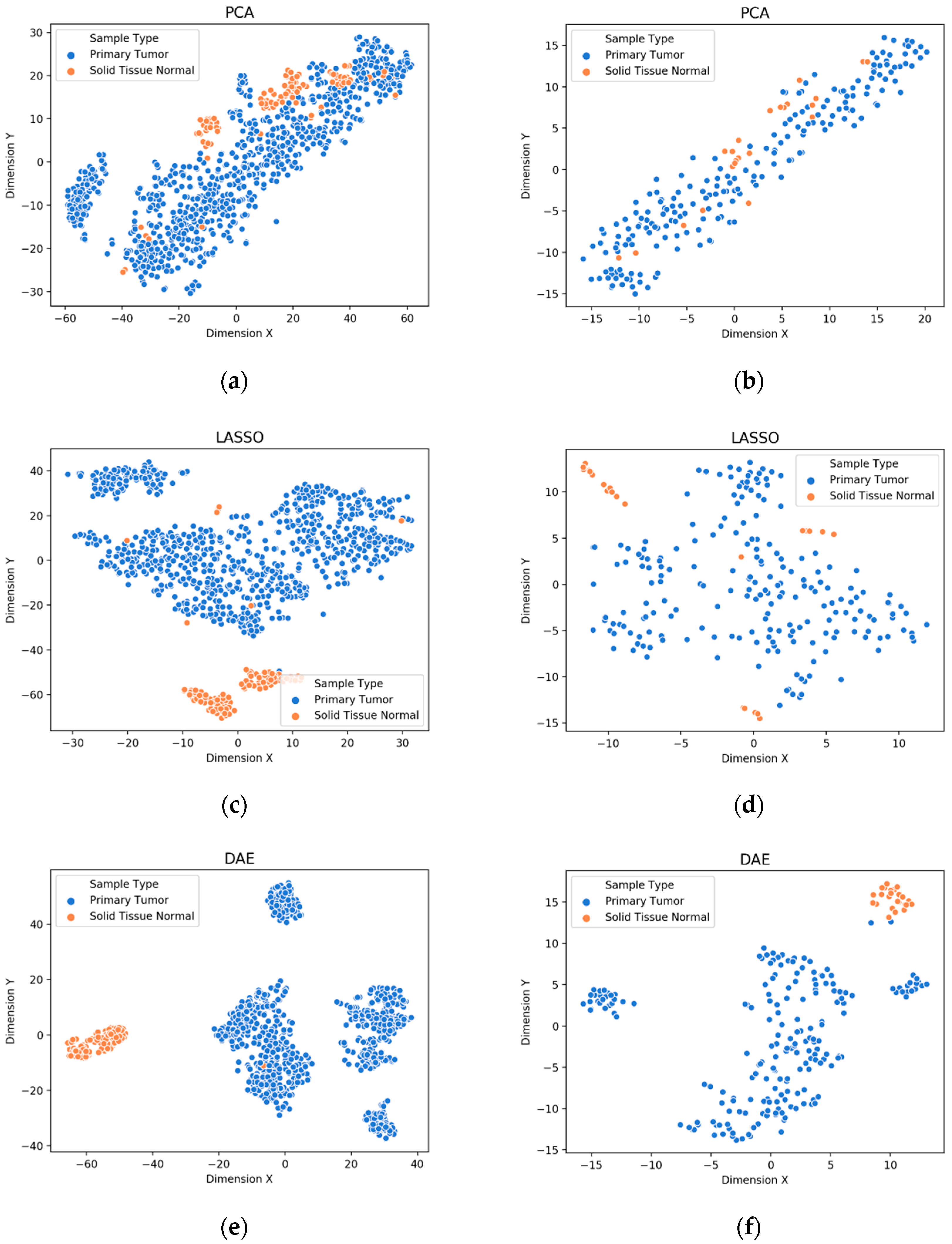
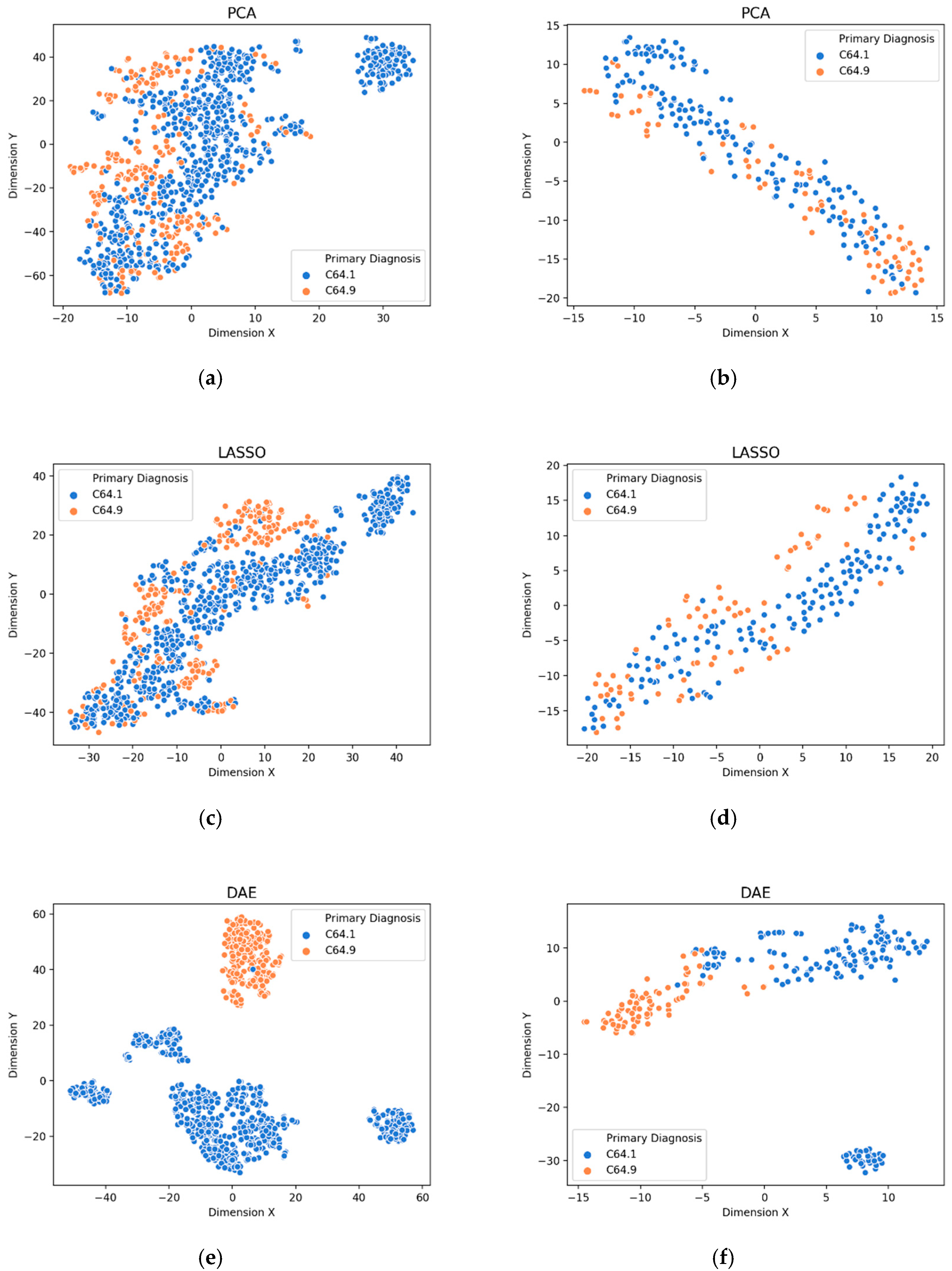
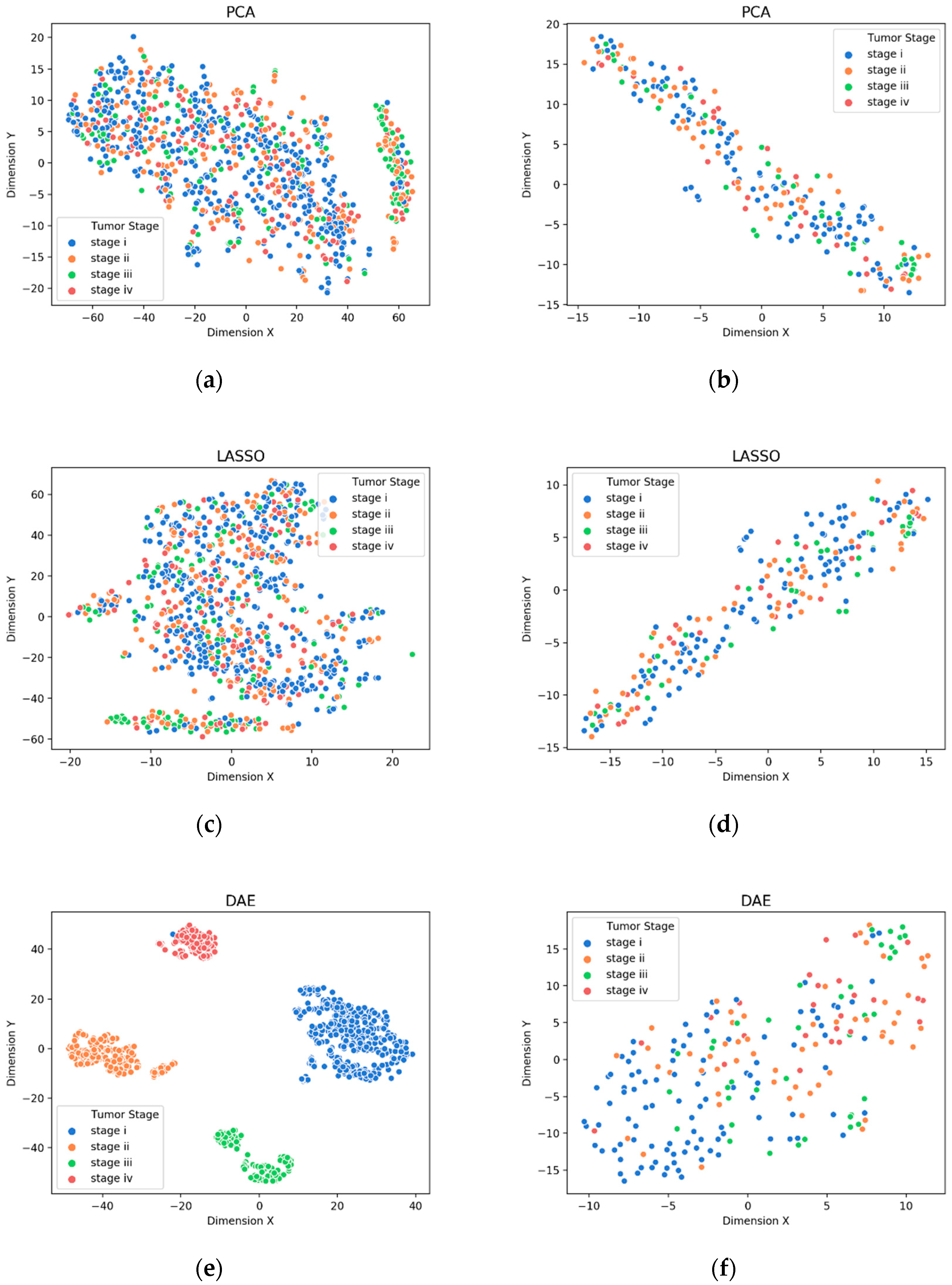
3.1. Visualization of Feature Extraction
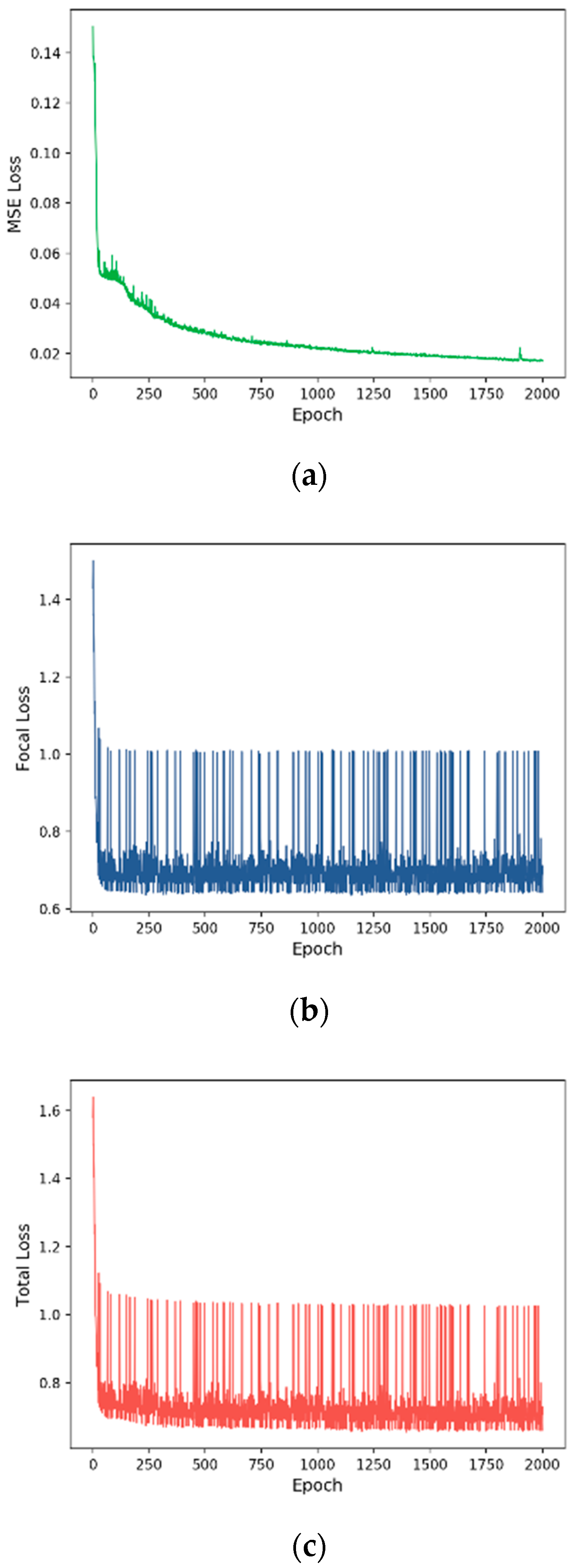
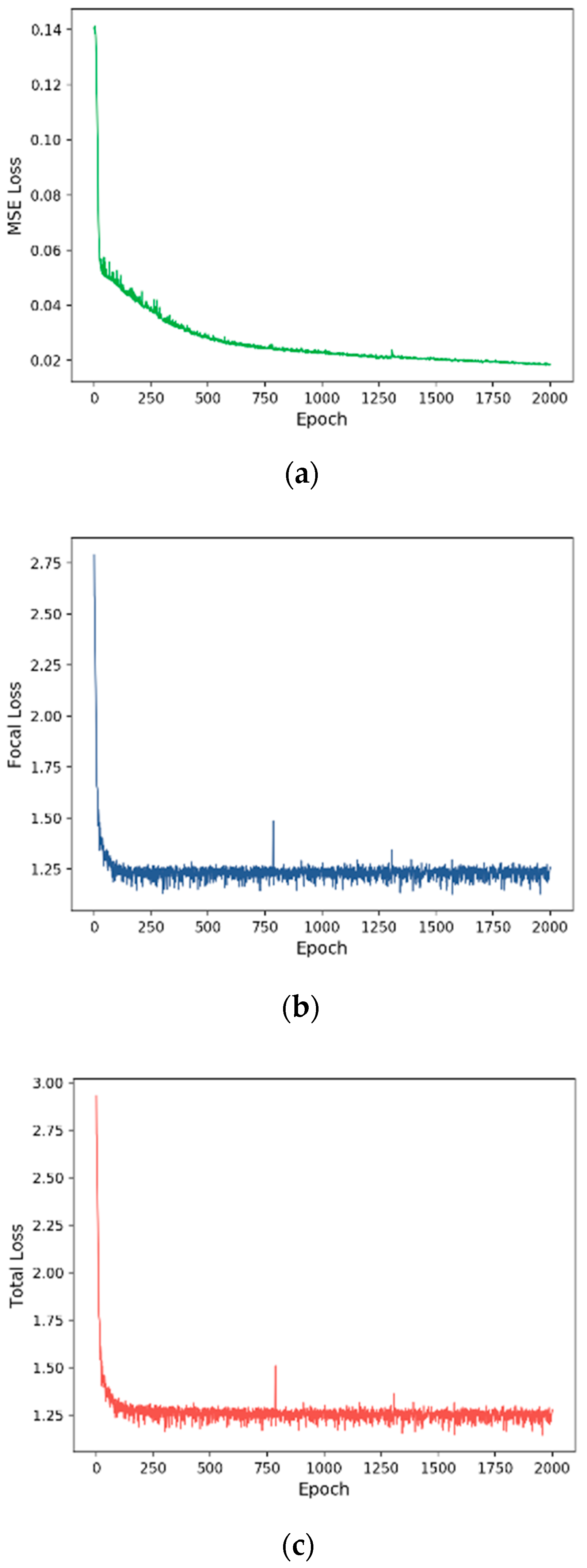
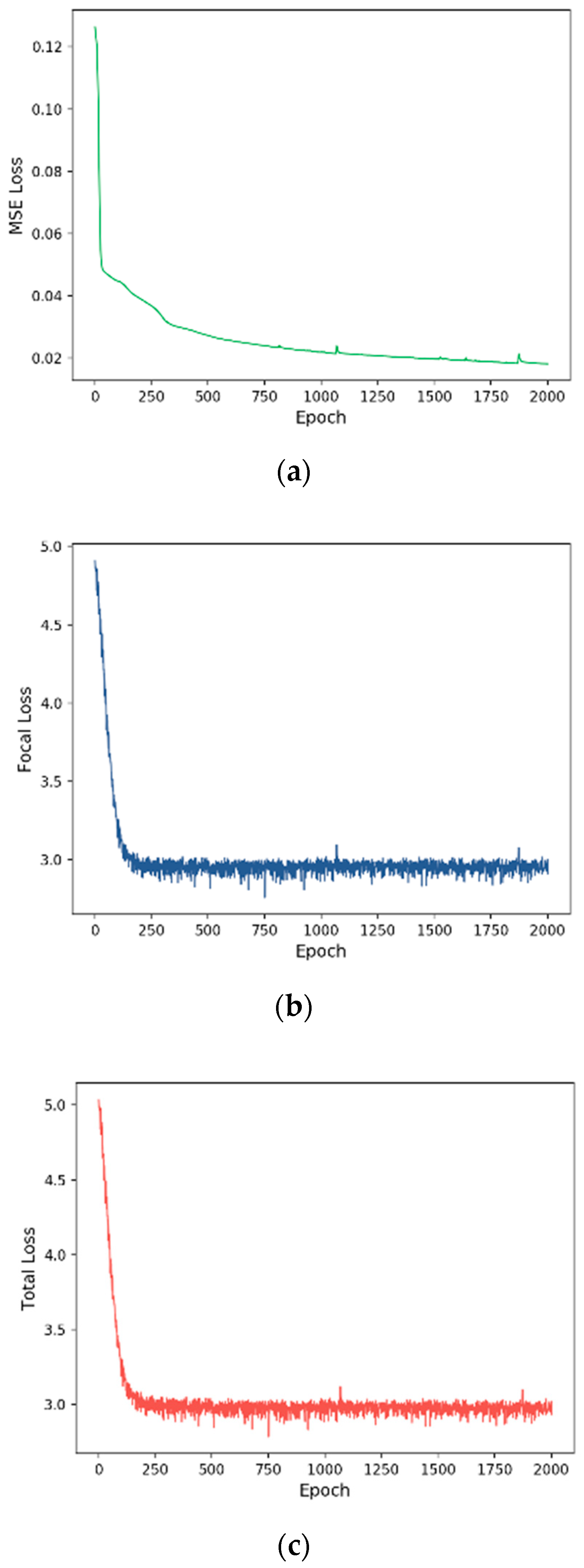
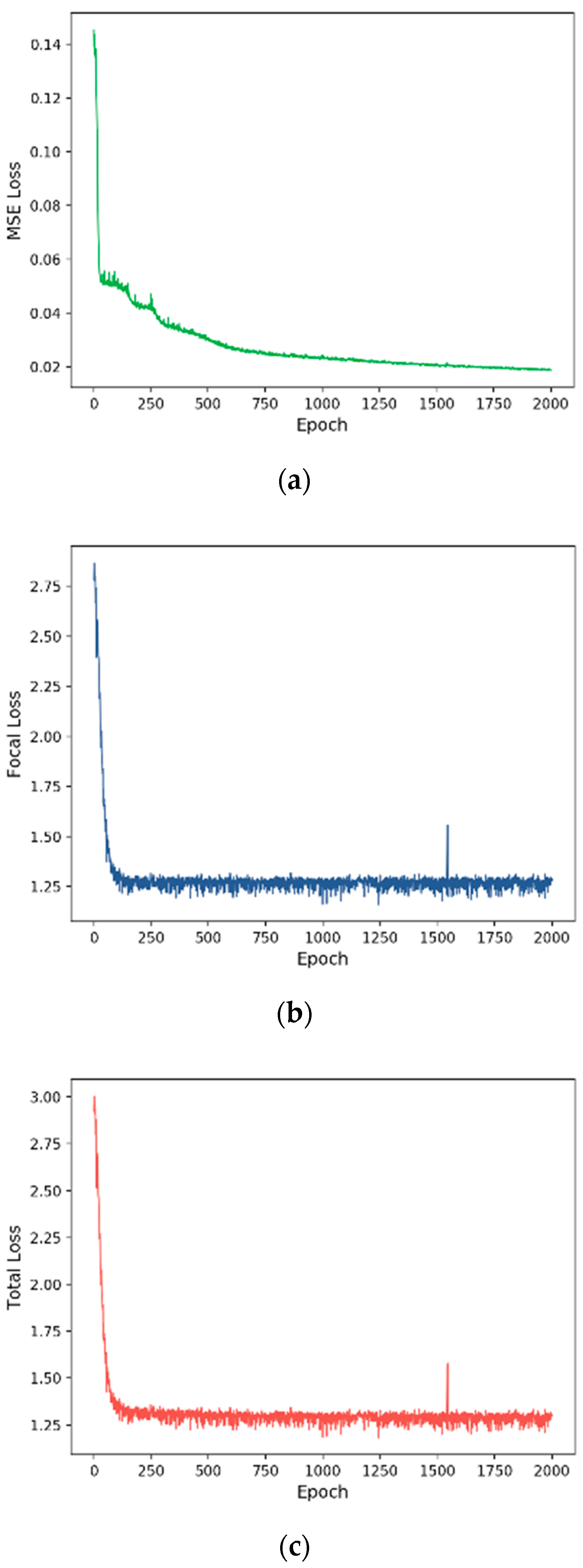
3.2. Training Process
3.3. Evaluation of Prognose Prediction Models
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Xiong, H.Y.; Alipanahi, B.; Lee, L.J.; Bretschneider, H.; Merico, D.; Yuen, R.K.C.; Hua, Y.; Gueroussov, S.; Najafabadi, H.S.; Hughes, T.R.; et al. The human splicing code reveals new insights into the genetic determinants of disease. Science 2015, 347, 1254806. [Google Scholar] [CrossRef] [PubMed]
- Korean National Cancer Center. Available online: https://www.ncc.re.kr (accessed on 23 November 2019).
- Câmara, N.O.S.; Iseki, K.; Kramer, H.; Liu, Z.H.; Sharma, K. Kidney disease and obesity: Epidemiology, mechanisms and treatment. Nat. Rev. Nephrol. 2017, 13, 181–190. [Google Scholar] [CrossRef] [PubMed]
- D’Angelo, G.; Pilla, R.; Tascini, C.; Rampone, S. A proposal for distinguishing between bacterial and viral meningitis using genetic programming and decision trees. Soft Comput. 2019, 23, 11775–11791. [Google Scholar] [CrossRef]
- Bejnordi, B.E.; Veta, M.; Van Diest, P.J.; Van Ginneken, B.; Karssemeijer, N.; Litjens, G.; Van Der Laak, J.A.W.M.; Hermsen, M.; Manson, Q.F.; Balkenhol, M.; et al. Diagnostic assessment of deep learning algorithms for detection of lymph node metastases in women with breast cancer. JAMA 2017, 318, 2199–2210. [Google Scholar] [CrossRef] [PubMed]
- Amgad, M.; Elfandy, H.; Hussein, H.; Atteya, L.A.; Elsebaie, M.A.; Abo Elnasr, L.S.; Sakr, R.A.; Salem, H.S.; Ismail, A.F.; Saad, A.M.; et al. Structured crowdsourcing enables convolutional segmentation of histology images. Bioinformatics 2019, 35, 3461–3467. [Google Scholar] [CrossRef] [PubMed]
- Kim, B.J.; Kim, S.H. Prediction of inherited genomic susceptibility to 20 common cancer types by a supervised machine-learning method. Proc. Natl. Acad. Sci. USA 2018, 115, 1322–1327. [Google Scholar] [CrossRef]
- Chen, Y.; Li, Y.; Narayan, R.; Subramanian, A.; Xie, X. Gene expression inference with deep learning. Bioinformatics 2016, 32, 1832–1839. [Google Scholar] [CrossRef]
- Ferroni, P.; Zanzotto, F.M.; Riondino, S.; Scarpato, N.; Guadagni, F.; Roselli, M. Breast cancer prognosis using a machine learning approach. Cancers 2019, 11, 328. [Google Scholar] [CrossRef]
- Chen, M.; Hao, Y.; Hwang, K.; Wang, L.; Wang, L. Disease prediction by machine learning over big data from healthcare communities. IEEE Access 2017, 5, 8869–8879. [Google Scholar] [CrossRef]
- Muhamed Ali, A.; Zhuang, H.; Ibrahim, A.; Rehman, O.; Huang, M.; Wu, A. A machine learning approach for the classification of kidney cancer subtypes using miRNA genome data. Appl. Sci. 2018, 8, 2422. [Google Scholar] [CrossRef]
- Aljouie, A.; Patel, N.; Roshan, U. Cross-validation and cross-study validation of kidney cancer with machine learning and whole exome sequences from the National Cancer Institute. In Proceedings of the 2018 IEEE Conference on Computational Intelligence in Bioinformatics and Computational Biology (CIBCB), St. Louis, MO, USA, 30 May–2 June 2018; pp. 1–6. [Google Scholar]
- Ing, N.; Huang, F.; Conley, A.; You, S.; Ma, Z.; Klimov, S.; Ohe, C.; Yuan, X.; Amin, M.B.; Figlin, R.; et al. A novel machine learning approach reveals latent vascular phenotypes predictive of renal cancer outcome. Sci. Rep. 2017, 7, 13190. [Google Scholar] [CrossRef]
- Kourou, K.; Exarchos, T.P.; Exarchos, K.P.; Karamouzis, M.V.; Fotiadis, D.I. Machine learning applications in cancer prognosis and prediction. Comput. Struct. Biotechnol. J. 2015, 13, 8–17. [Google Scholar] [CrossRef] [PubMed]
- Wolf, F.A.; Angerer, P.; Theis, F.J. SCANPY: Large-scale single-cell gene expression data analysis. Genome Biol. 2018, 19, 15. [Google Scholar] [CrossRef]
- Libbrecht, M.; Noble, W. Machine learning applications in genetics and genomics. Nat. Rev. Genet. 2015, 16, 321–332. [Google Scholar] [CrossRef]
- Zeng, W.Z.D.; Glicksberg, B.S.; Li, Y.; Chen, B. Selecting precise reference normal tissue samples for cancer research using a deep learning approach. BMC Med. Genomics 2019, 12, 21. [Google Scholar] [CrossRef]
- Danaee, P.; Ghaeini, R.; Hendrix, D.A. A deep learning approach for cancer detection and relevant gene identification. Pac. Symp. Biocomput. 2017, 2017, 219–229. [Google Scholar]
- Kim, B.H.; Yu, K.; Lee, P.C. Cancer classification of single-cell gene expression data by neural network. Bioinformatics 2019. [Google Scholar] [CrossRef]
- Xie, R.; Wen, J.; Quitadamo, A.; Cheng, J.; Shi, X. A deep auto-encoder model for gene expression prediction. BMC Genomics 2017, 18, 845. [Google Scholar] [CrossRef] [PubMed]
- Gupta, A.; Wang, H.; Ganapathiraju, M. Learning structure in gene expression data using deep architectures, with an application to gene clustering. In Proceedings of the 2015 IEEE International Conference on Bioinformatics and Biomedicine (BIBM), Washington, DC, USA, 9–12 November 2015; pp. 1328–1335. [Google Scholar]
- Genomic Data Commons Data Portal. Available online: https://portal.gdc.cancer.gov (accessed on 23 November 2019).
- Wang, H.; Li, B.; Leng, C. Shrinkage tuning parameter selection with a diverging number of parameters. J. R. Stat. Soc. Ser. B Stat. Methodol. 2009, 71, 671–683. [Google Scholar] [CrossRef]
- Mortazavi, A.; Williams, B.A.; McCue, K.; Schaeffer, L.; Wold, B. Mapping and quantifying mammalian transcriptomes by RNA-Seq. Nat. Methods 2008, 5, 621. [Google Scholar] [CrossRef]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Nair, V.; Hinton, G.E. Rectified linear units improve restricted boltzmann machines. In Proceedings of the 27th International Conference on Machine Learning (ICML 2010), Haifa, Israel, 21–24 June 2010; pp. 807–814. [Google Scholar]
- Grave, E.; Joulin, A.; Cissé, M.; Jégou, H. Efficient softmax approximation for GPUs. In Proceedings of the 34th International Conference on Machine Learning (ICML 2017), Sydney, Australia, 6–11 August 2017; Volume 70, pp. 1302–1310. [Google Scholar]
- Lin, T.Y.; Goyal, P.; Girshick, R.; He, K.; Dollár, P. Focal loss for dense object detection. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2980–2988. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- PyTorch. Available online: https://pytorch.org (accessed on 23 November 2019).
- Wold, S.; Esbensen, K.; Geladi, P. Principal component analysis. Chemom. Intell. Lab. Syst. 1987, 2, 37–52. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B Methodol. 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Saeys, Y.; Inza, I.; Larrañaga, P. A review of feature selection techniques in bioinformatics. Bioinformatics 2007, 23, 2507–2517. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Maaten, L.V.D.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Goldberger, J.; Hinton, G.E.; Roweis, S.T.; Salakhutdinov, R.R. Neighbourhood components analysis. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 5–8 December 2005; pp. 513–520. [Google Scholar]
- Tang, Y. Deep learning using linear support vector machines. arXiv 2013, arXiv:1306.0239. [Google Scholar]
- Scholkopf, B.; Smola, A.J. Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond; MIT Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Dreiseitl, S.; Ohno-Machado, L. Logistic regression and artificial neural network classification models: A methodology review. J. Biomed. Inform. 2002, 35, 352–359. [Google Scholar] [CrossRef]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
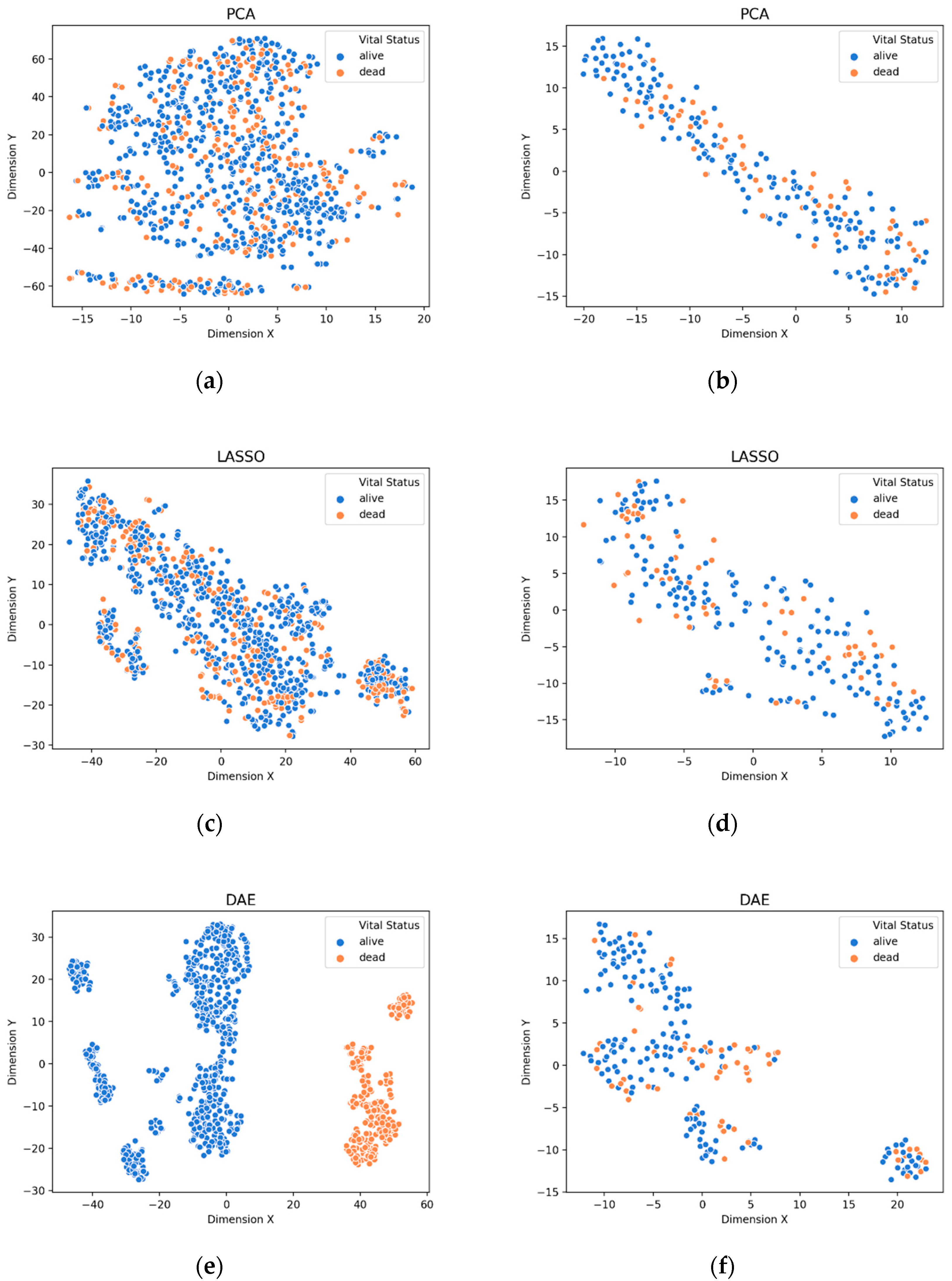
| Prognosis | # Gene | # Sample | Class Type | Total | Train | Test |
|---|---|---|---|---|---|---|
| Sample Type | 58,404 | 1149 | Primary Tumor | 1010 | 805 | 205 |
| Solid Tissue Normal | 139 | 114 | 25 | |||
| Primary Diagnosis | 58,409 | 1157 | C64.9 | 836 | 679 | 157 |
| C64.1 | 321 | 246 | 75 | |||
| Tumor Stage | 60,483 | 1118 | Stage-I | 528 | 424 | 104 |
| Stage-II | 183 | 145 | 38 | |||
| Stage-III | 261 | 204 | 57 | |||
| Stage-IV | 146 | 121 | 25 | |||
| Vital Status | 58,412 | 1157 | Alive | 835 | 664 | 171 |
| Dead | 322 | 261 | 61 |
| Prognosis | # Features |
|---|---|
| Sample Type | 100 |
| Primary Diagnosis | 100 |
| Tumor Stage | 100 |
| Vital Status | 100 |
| Prognosis | # Features |
|---|---|
| Sample Type | 100 |
| Primary Diagnosis | 100 |
| Tumor Stage | 100 |
| Vital Status | 100 |
| Prognosis | # Gene Biomarkers |
|---|---|
| Sample Type | 22 |
| Primary Diagnosis | 77 |
| Tumor Stage | 263 |
| Vital Status | 139 |
| Prognosis | Loss | Accuracy | Precision | Recall | F1-Score |
|---|---|---|---|---|---|
| Sample Type | MSE | 89.13 | 44.57 | 50.00 | 47.13 |
| Focal | 99.57 | 99.76 | 98.00 | 98.86 | |
| Total | 100.00 | 100.00 | 100.00 | 100.00 | |
| Primary Diagnosis | MSE | 62.93 | 43.86 | 47.89 | 42.63 |
| Focal | 96.55 | 97.13 | 95.01 | 95.97 | |
| Total | 96.98 | 97.43 | 95.68 | 96.49 | |
| Tumor Stage | MSE | 12.05 | 7.92 | 26.32 | 7.31 |
| Focal | 54.46 | 45.15 | 45.05 | 43.76 | |
| Total | 56.70 | 49.41 | 46.14 | 46.68 | |
| Vital Status | MSE | 73.71 | 36.85 | 50.00 | 42.43 |
| Focal | 76.29 | 69.00 | 67.05 | 67.83 | |
| Total | 76.72 | 69.78 | 68.92 | 69.32 |
| Classifier | Feature | Sampling | Accuracy | Precision | Recall | F1-Score |
|---|---|---|---|---|---|---|
| KNN | PCA | No | 98.70 | 99.28 | 94.00 | 96.45 |
| Yes | 96.52 | 88.46 | 96.29 | 91.87 | ||
| LASSO | No | 98.70 | 97.43 | 95.76 | 96.57 | |
| Yes | 99.57 | 98.08 | 99.76 | 98.90 | ||
| Linear SVM | PCA | No | 97.39 | 90.32 | 98.54 | 93.90 |
| Yes | 97.83 | 91.67 | 98.78 | 94.84 | ||
| LASSO | No | 99.13 | 96.30 | 99.51 | 97.83 | |
| Yes | 98.70 | 94.64 | 99.27 | 96.80 | ||
| Kernel SVM | PCA | No | 89.13 | 44.57 | 50.00 | 47.13 |
| Yes | 89.13 | 44.57 | 50.00 | 47.13 | ||
| LASSO | No | 89.13 | 44.57 | 50.00 | 47.13 | |
| Yes | 89.13 | 44.57 | 50.00 | 47.13 | ||
| RF | PCA | No | 95.65 | 97.67 | 80.00 | 86.31 |
| Yes | 97.39 | 98.58 | 88.00 | 92.46 | ||
| LASSO | No | 99.13 | 99.52 | 96.00 | 97.67 | |
| Yes | 100.00 | 100.00 | 100.00 | 100.00 | ||
| NN | PCA | No | 98.26 | 95.51 | 95.51 | 95.51 |
| Yes | 98.26 | 95.51 | 95.51 | 95.51 | ||
| LASSO | No | 99.13 | 96.30 | 99.51 | 97.83 | |
| Yes | 99.57 | 98.08 | 99.76 | 98.90 | ||
| COST-HDL | 100.00 | 100.00 | 100.00 | 100.00 | ||
| Classifier | Feature | Sampling | Accuracy | Precision | Recall | F1-Score |
|---|---|---|---|---|---|---|
| KNN | PCA | No | 87.07 | 87.01 | 82.79 | 84.40 |
| Yes | 84.91 | 82.82 | 82.59 | 82.70 | ||
| LASSO | No | 88.79 | 90.21 | 84.06 | 86.24 | |
| Yes | 89.66 | 90.35 | 85.74 | 87.52 | ||
| Linear SVM | PCA | No | 88.79 | 86.67 | 89.28 | 87.67 |
| Yes | 92.67 | 91.32 | 92.15 | 91.71 | ||
| LASSO | No | 94.40 | 94.03 | 93.07 | 93.53 | |
| Yes | 95.69 | 95.37 | 94.73 | 95.04 | ||
| Kernel SVM | PCA | No | 67.67 | 33.84 | 50.00 | 40.36 |
| Yes | 67.67 | 33.84 | 50.00 | 40.36 | ||
| LASSO | No | 67.67 | 33.84 | 50.00 | 40.36 | |
| Yes | 67.67 | 33.84 | 50.00 | 40.36 | ||
| RF | PCA | No | 90.52 | 93.85 | 85.33 | 88.13 |
| Yes | 94.83 | 96.45 | 92.00 | 93.81 | ||
| LASSO | No | 92.24 | 94.24 | 88.35 | 90.56 | |
| Yes | 94.40 | 94.75 | 92.38 | 93.43 | ||
| NN | PCA | No | 89.22 | 88.50 | 86.47 | 87.36 |
| Yes | 88.36 | 87.76 | 85.13 | 86.25 | ||
| LASSO | No | 92.24 | 91.65 | 90.44 | 91.01 | |
| Yes | 92.24 | 92.73 | 89.39 | 90.79 | ||
| COST-HDL | 96.98 | 97.43 | 95.68 | 96.49 | ||
| Classifier | Feature | Sampling | Accuracy | Precision | Recall | F1-Score |
|---|---|---|---|---|---|---|
| KNN | PCA | No | 47.77 | 38.39 | 33.62 | 32.66 |
| Yes | 41.07 | 33.60 | 33.14 | 32.91 | ||
| LASSO | No | 45.09 | 32.25 | 30.07 | 28.96 | |
| Yes | 40.18 | 34.27 | 35.24 | 34.13 | ||
| Linear SVM | PCA | No | 29.91 | 27.61 | 27.15 | 24.73 |
| Yes | 26.34 | 39.21 | 32.28 | 25.64 | ||
| LASSO | No | 40.62 | 37.24 | 40.47 | 34.28 | |
| Yes | 50.00 | 43.01 | 38.21 | 36.61 | ||
| Kernel SVM | PCA | No | 46.43 | 11.61 | 25.00 | 15.85 |
| Yes | 46.43 | 11.61 | 25.00 | 15.85 | ||
| LASSO | No | 46.43 | 11.61 | 25.00 | 15.85 | |
| Yes | 46.43 | 11.61 | 25.00 | 15.85 | ||
| RF | PCA | No | 51.34 | 51.20 | 33.43 | 32.12 |
| Yes | 54.46 | 48.20 | 44.30 | 44.77 | ||
| LASSO | No | 55.36 | 55.87 | 39.11 | 39.07 | |
| Yes | 53.12 | 45.43 | 45.56 | 44.47 | ||
| NN | PCA | No | 46.88 | 38.89 | 38.65 | 38.75 |
| Yes | 47.32 | 40.36 | 40.81 | 40.45 | ||
| LASSO | No | 41.52 | 35.67 | 35.33 | 35.23 | |
| Yes | 45.54 | 38.23 | 37.98 | 38.01 | ||
| COST-HDL | 56.70 | 49.41 | 46.14 | 46.68 | ||
| Classifier | Feature | Sampling | Accuracy | Precision | Recall | F1-Score |
|---|---|---|---|---|---|---|
| KNN | PCA | No | 70.69 | 57.64 | 54.81 | 54.64 |
| Yes | 65.09 | 54.75 | 54.70 | 54.72 | ||
| LASSO | No | 66.38 | 51.15 | 50.83 | 50.29 | |
| Yes | 65.52 | 55.10 | 54.99 | 55.04 | ||
| Linear SVM | PCA | No | 64.66 | 57.54 | 58.62 | 57.71 |
| Yes | 58.19 | 52.62 | 53.18 | 52.05 | ||
| LASSO | No | 73.71 | 63.48 | 57.38 | 57.60 | |
| Yes | 72.84 | 62.39 | 58.38 | 58.94 | ||
| Kernel SVM | PCA | No | 73.71 | 36.85 | 50.00 | 42.43 |
| Yes | 73.71 | 36.85 | 50.00 | 42.43 | ||
| LASSO | No | 73.71 | 36.85 | 50.00 | 42.43 | |
| Yes | 73.71 | 36.85 | 50.00 | 42.43 | ||
| RF | PCA | No | 73.71 | 62.50 | 53.16 | 50.42 |
| Yes | 70.26 | 58.66 | 56.62 | 56.95 | ||
| LASSO | No | 75.00 | 66.56 | 58.79 | 59.33 | |
| Yes | 73.28 | 65.73 | 66.05 | 65.88 | ||
| NN | PCA | No | 62.07 | 53.38 | 53.71 | 53.41 |
| Yes | 58.62 | 53.68 | 54.53 | 53.04 | ||
| LASSO | No | 61.21 | 54.86 | 55.76 | 54.69 | |
| Yes | 58.19 | 54.23 | 55.29 | 53.31 | ||
| COST-HDL | 76.72 | 69.78 | 68.92 | 69.32 | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shon, H.S.; Batbaatar, E.; Kim, K.O.; Cha, E.J.; Kim, K.-A. Classification of Kidney Cancer Data Using Cost-Sensitive Hybrid Deep Learning Approach. Symmetry 2020, 12, 154. https://doi.org/10.3390/sym12010154
Shon HS, Batbaatar E, Kim KO, Cha EJ, Kim K-A. Classification of Kidney Cancer Data Using Cost-Sensitive Hybrid Deep Learning Approach. Symmetry. 2020; 12(1):154. https://doi.org/10.3390/sym12010154
Chicago/Turabian StyleShon, Ho Sun, Erdenebileg Batbaatar, Kyoung Ok Kim, Eun Jong Cha, and Kyung-Ah Kim. 2020. "Classification of Kidney Cancer Data Using Cost-Sensitive Hybrid Deep Learning Approach" Symmetry 12, no. 1: 154. https://doi.org/10.3390/sym12010154
APA StyleShon, H. S., Batbaatar, E., Kim, K. O., Cha, E. J., & Kim, K.-A. (2020). Classification of Kidney Cancer Data Using Cost-Sensitive Hybrid Deep Learning Approach. Symmetry, 12(1), 154. https://doi.org/10.3390/sym12010154






