Doubly Charged Higgs Bosons and Spontaneous Symmetry Breaking at eV and TeV Scales
Abstract
1. Introduction
1.1. Theoretical Introduction to HTM and LRSM
1.1.1. HTM
1.1.2. LRSM
1.2. LFV Bounds on the Triplets VEV
2. A Case Study: Benchmark Points for the Scenario with GeV in HTM and LRSM
3. Results and Discussion
3.1. Limits on the Triplet VEV
3.2. Doubly Charged Scalar Particles Decays within the LRSM and HTM
3.2.1. HTM
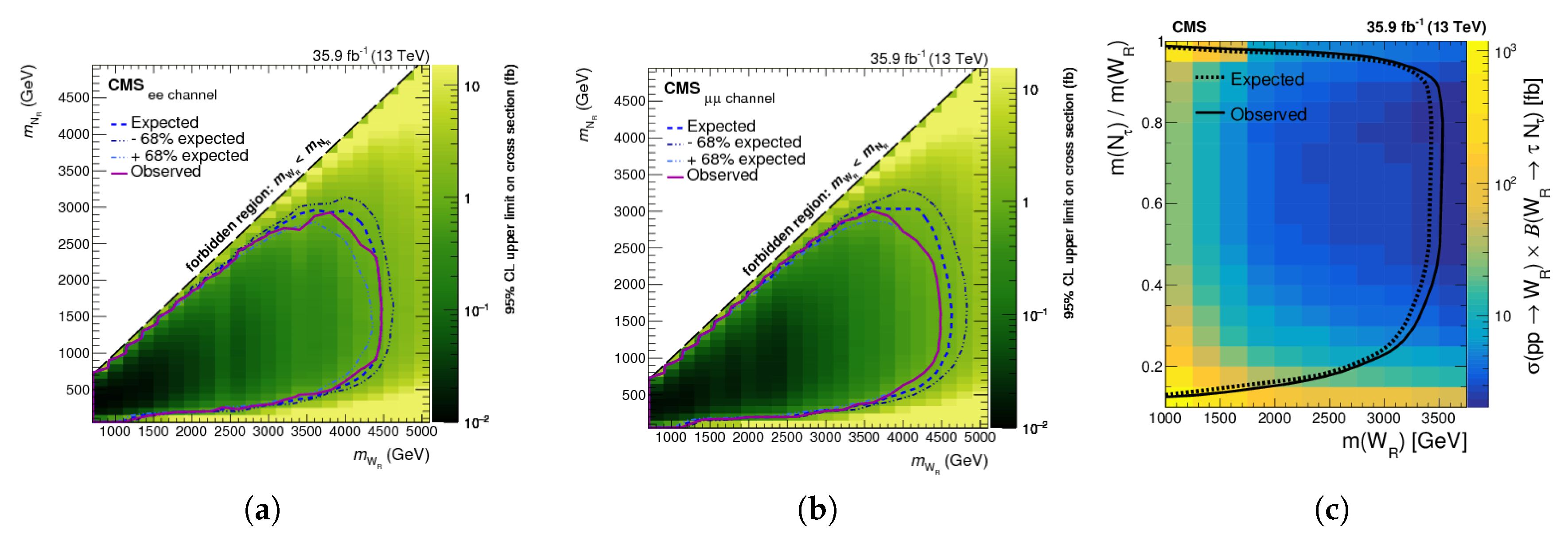
3.2.2. LRSM
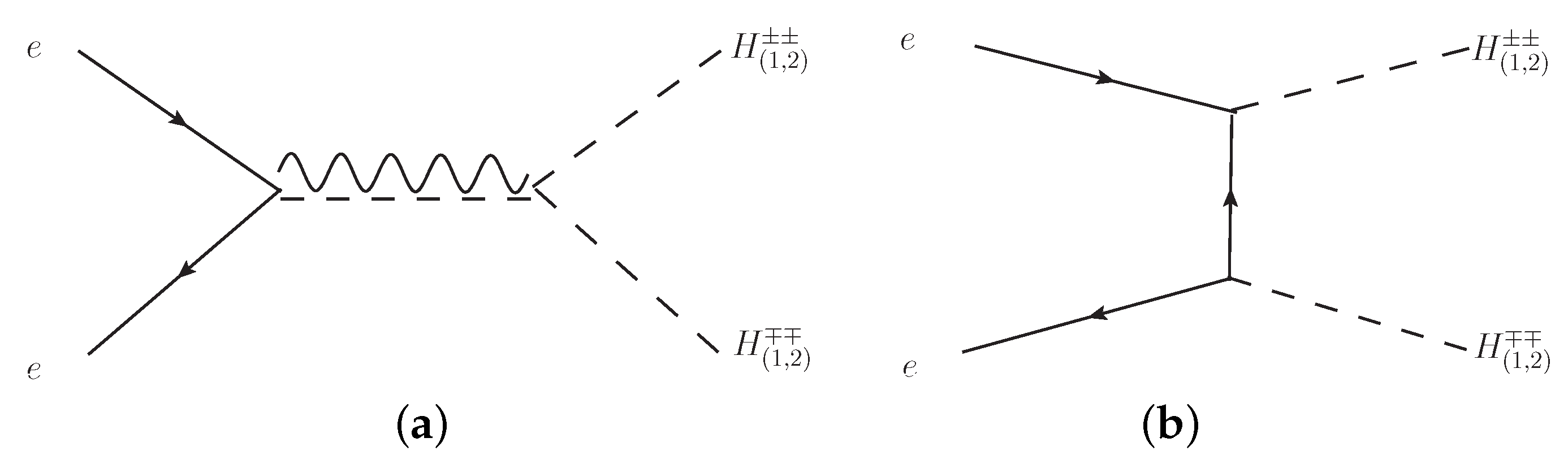
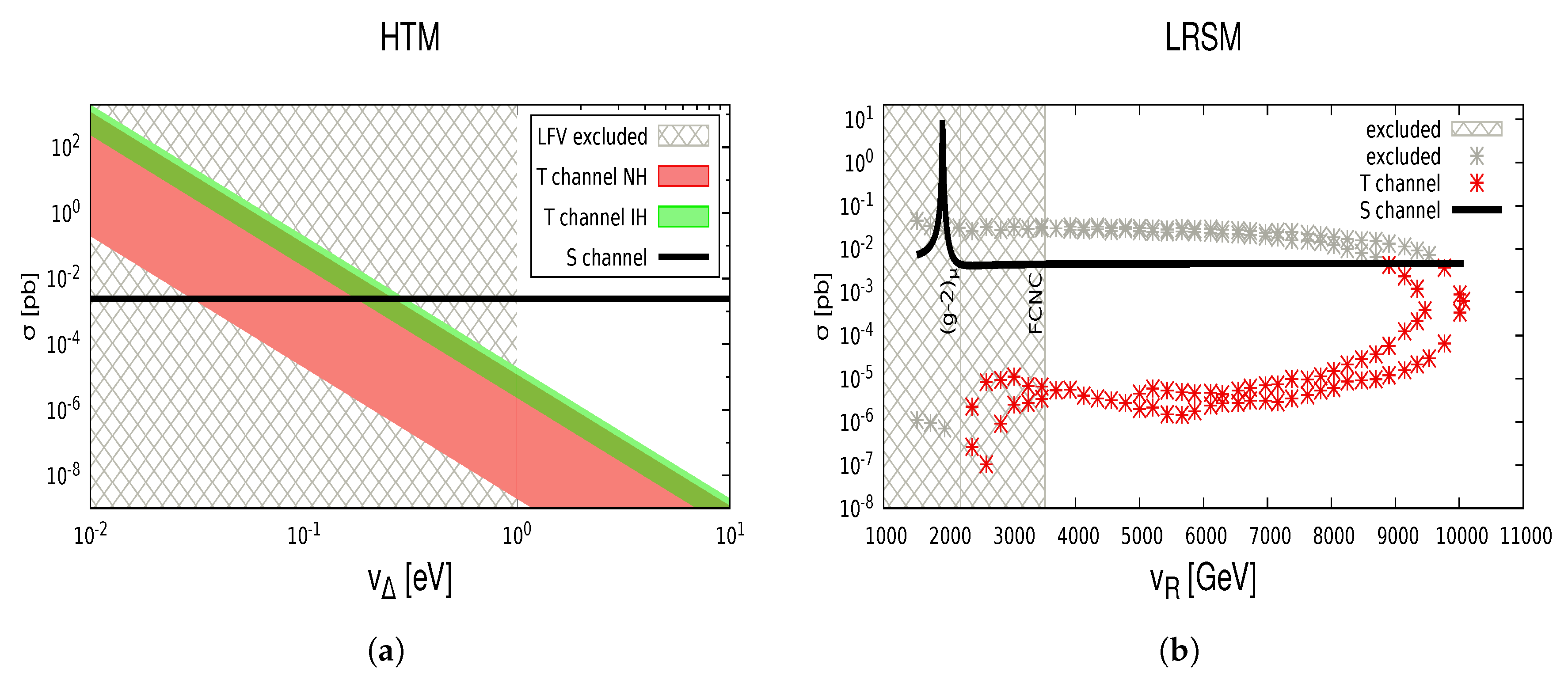
3.3. Doubly Charged Scalar Particles’ Pair Production at Future High Energies
4. Summary and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| SM | Standard Model |
| HTM | Higgs Triplet Model |
| LRSM | left–right Symmetric Model |
| VEV | Vacuum Expectation Value |
| NH | Normal Hierarchy of neutrino masses |
| IH | Inverted Hierarchy of neutrino masses |
| LNV | Lepton Number Violation |
| LFV | Lepton flavor Violation |
Appendix A
Appendix A.1. Scalar Particles within the HTM
Appendix A.2. The Mass Spectrum in LRSM
References
- Aad, G.; Abajyan, T.; Abbott, B.; Abdallah, J.; Khalek, S.A.; Abdelalim, A.A.; Abdinov, O.; Aben, R.; Abi, B.; Abolins, M.; et al. Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC. Phys. Lett. 2012, B716, 1–29. [Google Scholar] [CrossRef]
- Chatrchyan, S.; Khachatryan, V.; Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Aguilo, E.; Bergauer, T.; Dragicevic, M.; Erö, J.; Fabjan, C.; et al. Observation of a New Boson at a Mass of 125 GeV with the CMS Experiment at the LHC. Phys. Lett. 2012, B716, 30–61. [Google Scholar] [CrossRef]
- Campanario, F.; Czyż, H.; Gluza, J.; Jeliński, T.; Rodrigo, G.; Tracz, S.; Zhuridov, D. Standard model radiative corrections in the pion form factor measurements do not explain the aμ anomaly. Phys. Rev. 2019, D100, 076004. [Google Scholar] [CrossRef]
- Contino, R.; Curtin, D.; Katz, A.; Mangano, M.L.; Panico, G.; Ramsey-Musolf, M.J.; Zanderighi, G.; Anastasiou, C.; Astill, W.; Bambhaniya, G.; et al. Physics at a 100 TeV pp collider: Higgs and EW symmetry breaking studies. CERN Yellow Rep. 2017, 255–440. [Google Scholar] [CrossRef]
- Golling, T.; Hance, M.; Harris, P.; Mangano, M.L.; McCullough, M.; Moortgat, F.; Schwaller, P.; Torre, R.; Agrawal, P.; Alves, D.S.M.; et al. Physics at a 100 TeV pp collider: beyond the Standard Model phenomena. CERN Yellow Rep. 2017, 441–634. [Google Scholar] [CrossRef]
- Fukuyama, T.; Sugiyama, H.; Tsumura, K. Constraints from muon g-2 and LFV processes in the Higgs Triplet Model. J. High Energy Phys. 2010, 03, 044. [Google Scholar] [CrossRef]
- Mohapatra, R.N.; Pati, J.C. A Natural left–right Symmetry. Phys. Rev. 1975, D11, 2558. [Google Scholar] [CrossRef]
- Deshpande, N.G.; Gunion, J.F.; Kayser, B.; Olness, F.I. left–right symmetric electroweak models with triplet Higgs. Phys. Rev. 1991, D44, 837–858. [Google Scholar] [CrossRef]
- Duka, P.; Gluza, J.; Zralek, M. Quantization and renormalization of the manifest left–right symmetric model of electroweak interactions. Ann. Phys. 2000, 280, 336–408. [Google Scholar] [CrossRef]
- Chakrabortty, J.; Ghosh, P.; Mondal, S.; Srivastava, T. Reconciling (g-2)μ and charged lepton flavor violating processes through a doubly charged scalar. Phys. Rev. 2016, D93, 115004. [Google Scholar] [CrossRef]
- Baldini, A.M.; Bao, Y.; Baracchini, E.; Bemporad, C.; Berg, F.; Biasotti, M.; Boca, G.; Cascella, M.; Cattaneo, P.W.; Cavoto, G.; et al. Search for the lepton flavor violating decay μ+→e+γ with the full dataset of the MEG experiment. Eur. Phys. J. 2016, C76, 434. [Google Scholar] [CrossRef]
- Aubert, B.; Karyotakis, Y.; Lees, J.P.; Poireau, V.; Prencipe, E.; Prudent, X.; Tisser, V.; Tico, J.G.; Grauges, E.; Martinelli, M.; et al. Searches for Lepton Flavor Violation in the Decays τ± → e±γ and τ± → μ±γ. Phys. Rev. Lett. 2010, 104, 021802. [Google Scholar] [CrossRef]
- Bellgardt, U.; Otter, G.; Eichler, R.; Felawka, L.; Niebuhr, C.; Walter, H.K.; Bertl, W.; Lordong, N.; Martino, J.; Egli, S.; et al. Search for the Decay μ+→e+e+e-. Nucl. Phys. 1988, B299, 1–6. [Google Scholar] [CrossRef]
- Hayasaka, K.; Inami, K.; Miyazaki, Y.; Arinstein, K.; Aulchenko, V.; Aushev, T.; Bakich, A.M.; Bay, A.; Belous, K.; Bhardwaj, V.; et al. Search for Lepton Flavor Violating Tau Decays into Three Leptons with 719 Million Produced Tau+Tau- Pairs. Phys. Lett. 2010, B687, 139–143. [Google Scholar] [CrossRef]
- Bertl, W.H.; Engfer, R.; Hermes, E.A.; Kurz, G.; Kozlowski, T.; Kuth, J.; Otter, G.; Rosenbaum, F.; Ryskulov, N.M.; Van Der Schaaf, A.; et al. A Search for muon to electron conversion in muonic gold. Eur. Phys. J. 2006, C47, 337–346. [Google Scholar] [CrossRef]
- Dinh, D.N.; Ibarra, A.; Molinaro, E.; Petcov, S.T. The μ − e Conversion in Nuclei, μ → eγ, μ → 3e Decays and TeV Scale See-Saw Scenarios of Neutrino Mass Generation. J. High Energy Phys. 2012, 8, 125. [Google Scholar] [CrossRef]
- Hisano, J.; Moroi, T.; Tobe, K.; Yamaguchi, M. Lepton flavor violation via right-handed neutrino Yukawa couplings in supersymmetric standard model. Phys. Rev. 1996, D53, 2442–2459. [Google Scholar] [CrossRef]
- Kitano, R.; Koike, M.; Okada, Y. Detailed calculation of lepton flavor violating muon electron conversion rate for various nuclei. Phys. Rev. 2002, D66, 096002. [Google Scholar] [CrossRef]
- Moore, S.R.; Whisnant, K.; Young, B.L. Second Order Corrections to the Muon Anomalous Magnetic Moment in Alternative Electroweak Models. Phys. Rev. 1985, D31, 105. [Google Scholar] [CrossRef]
- Leveille, J.P. The Second Order Weak Correction to (G-2) of the Muon in Arbitrary Gauge Models. Nucl. Phys. 1978, B137, 63–76. [Google Scholar] [CrossRef]
- Aaboud, M.; Aad, G.; Abbott, B.; Abdinov, O.; Abeloos, B.; Abidi, S.H.; AbouZeid, O.S.; Abraham, N.L.; Abramowicz, H.; Abreu, H.; et al. Search for doubly charged Higgs boson production in multi-lepton final states with the ATLAS detector using proton-proton collisions at = 13 TeV. arXiv 2017, arXiv:1710.09748. [Google Scholar] [CrossRef] [PubMed]
- Garayoa, J.; Schwetz, T. Neutrino mass hierarchy and Majorana CP phases within the Higgs triplet model at the LHC. J. High Energy Phys. 2008, 3, 9. [Google Scholar] [CrossRef]
- Esteban, I.; Gonzalez-Garcia, M.; Maltoni, M.; Martinez-Soler, I.; Schwetz, T. Updated fit to three neutrino mixing: exploring the accelerator-reactor complementarity. J. High Energy Phys. 2017, 1, 87. [Google Scholar] [CrossRef]
- NuFIT. 2017. Available online: http://www.nu-fit.org/ (accessed on 10 January 2018).
- Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Ambrogi, F.; Asilar, E.; Bergauer, T.; Brstetter, J.; Brondolin, E.; Dragicevic, M.; Ero, J.; et al. Search for a heavy right-handed W boson and a heavy neutrino in events with two same-flavor leptons and two jets at = 13 TeV. J. High Energy Phys. 2018, 5, 148. [Google Scholar] [CrossRef]
- Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Ambrogi, F.; Asilar, E.; Bergauer, T.; Brstetter, J.; Dragicevic, M.; Erö, J.; Del Valle, A.E.; et al. Search for heavy neutrinos and third-generation leptoquarks in hadronic states of two τ leptons and two jets in proton-proton collisions at = 13 TeV. J. High Energy Phys. 2019, 3, 170. [Google Scholar] [CrossRef]
- Das, D.; Santamaria, A. Updated scalar sector constraints in Higgs triplet model. Phys. Rev. 2016, D94, 015015. [Google Scholar] [CrossRef]
- Bonilla, C.; Fonseca, R.M.; Valle, J.W.F. Consistency of the triplet seesaw model revisited. Phys. Rev. 2015, D92, 075028. [Google Scholar] [CrossRef]
- Arhrib, A.; Benbrik, R.; Chabab, M.; Moultaka, G.; Peyranere, M.C.; Rahili, L.; Ramadan, J. The Higgs Potential in the Type II Seesaw Model. Phys. Rev. 2011, D84, 095005. [Google Scholar] [CrossRef]
- Krauss, M.E.; Staub, F. Unitarity constraints in triplet extensions beyond the large s limit. arXiv 2018, arXiv:1805.07309. [Google Scholar] [CrossRef]
- Lavoura, L.; Li, L.F. Making the small oblique parameters large. Phys. Rev. 1994, D49, 1409–1416. [Google Scholar] [CrossRef]
- Chun, E.J.; Lee, H.M.; Sharma, P. Vacuum Stability, Perturbativity, EWPD and Higgs-to-diphoton rate in Type II Seesaw Models. J. High Energy Phys. 2012, 11, 106. [Google Scholar] [CrossRef]
- Akeroyd, A.G.; Moretti, S. Enhancement of H to gamma gamma from doubly charged scalars in the Higgs Triplet Model. Phys. Rev. 2012, D86, 035015. [Google Scholar] [CrossRef]
- Shen, J.F.; Bi, Y.P.; Li, Z.X. Pair production of scalars at the ILC in the Higgs triplet model under the non-degenerate case. EPL Europhys. Lett. 2015, 112, 31002. [Google Scholar] [CrossRef]
- Alwall, J.; Frederix, R.; Frixione, S.; Hirschi, V.; Maltoni, F.; Mattelaer, O.; Shao, H.S.; Stelzer, T.; Torrielli, P.; Zaro, M. The automated computation of tree-level and next-to-leading order differential cross-sections, and their matching to parton shower simulations. J. High Energy Phys. 2014, 7, 79. [Google Scholar] [CrossRef]
- Rizzo, T.G. Tests of the fermion and Higgs multiplet structure of the SU(2)×U(1) model. Phys. Rev. D 1980, 21, 1404–1409. [Google Scholar] [CrossRef]
- Czakon, M.; Gluza, J.; Jegerlehner, F.; Zralek, M. Confronting electroweak precision measurements with new physics models. Eur. Phys. J. 2000, C13, 275–281. [Google Scholar] [CrossRef]
- Gunion, J.F.; Grifols, J.; Mendez, A.; Kayser, B.; Olness, F.I. Higgs Bosons in left–right Symmetric Models. Phys. Rev. 1989, D40, 1546. [Google Scholar] [CrossRef]
- Ade, P.A.R.; Aghanim, N.; Armitage-Caplan, C.; Arnaud, M.; Ashdown, M.; Atrio-Barela, F.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; et al. Planck 2013 results. XVI. Cosmological parameters. Astron. Astrophys. 2014, 571, A16. [Google Scholar] [CrossRef]
- Fileviez Perez, P.; Han, T.; Huang, G.Y.; Li, T.; Wang, K. Neutrino Masses and the CERN LHC: Testing Type II Seesaw. Phys. Rev. 2008, D78, 015018. [Google Scholar] [CrossRef]
- Tanabashi, M.; Hagiwara, K.; Hikasa, K.; Nakamura, K.; Sumino, Y.; Takahashi, F.; Tanaka, J.; Agashe, K.; Aielli, G.; Amsler, C.; et al. Review of Particle Physics. Phys. Rev. 2018, D98, 030001. [Google Scholar] [CrossRef]
- Czakon, M.; Gluza, J.; Zralek, M. Low-energy physics and left–right symmetry: Bounds on the model parameters. Phys. Lett. 1999, B458, 355–360. [Google Scholar] [CrossRef]
- CLIC—Compact Linear International Collider Project, CERN. Available online: http://clic-study.web.cern.ch/ (accessed on 1 December 2019).
- Adli, E. Plasma Wakefield Linear Colliders—Opportunities and Challenges. Philos. Trans. R. Soc. 2019, 337. [Google Scholar] [CrossRef] [PubMed]
- Nomura, T.; Okada, H.; Yokoya, H. Discriminating leptonic Yukawa interactions with doubly charged scalar at the ILC. Nucl. Phys. 2018, B929, 193–206. [Google Scholar] [CrossRef]
- Dev, P.S.B.; Ramsey-Musolf, M.J.; Zhang, Y. Doubly-Charged Scalars in the Type-II Seesaw Mechanism: Fundamental Symmetry Tests and High-Energy Searches. Phys. Rev. 2018, D98, 055013. [Google Scholar] [CrossRef]
- Bhupal Dev, P.S.; Zhang, Y. Displaced vertex signatures of doubly charged scalars in the type-II seesaw and its left–right extensions. J. High Energy Phys. 2018, 10, 199. [Google Scholar] [CrossRef]
- Antusch, S.; Fischer, O.; Hammad, A.; Scherb, C. Low scale type II seesaw: Present constraints and prospects for displaced vertex searches. J. High Energy Phys. 2019, 02, 157. [Google Scholar] [CrossRef]
- Acosta, D.; Adelman, J.; Affolder, T.; Akimoto, T.; Albrow, M.G.; Ambrose, D.; Amerio, S.; Amidei, D.; Anastassov, A.; Anikeev, K.; et al. Search for long-lived doubly-charged Higgs bosons in p collisions at = 1.96 TeV. Phys. Rev. Lett. 2005, 95, 071801. [Google Scholar] [CrossRef]
- Khachatryan, V.; Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Asilar, E.; Bergauer, T.; Brstetter, J.; Brondolin, E.; Dragicevic, M.; Erö, J.; et al. Search for long-lived charged particles in proton-proton collisions at = 13 TeV. Phys. Rev. 2016, D94, 112004. [Google Scholar] [CrossRef]
- Aad, G.; Abbott, B.; Abdallah, J.; Abdinov, O.; Aben, R.; Abolins, M.; AbouZeid, O.S.; Abramowicz, H.; Abreu, H.; Abreu, R.; et al. Search for heavy long-lived multi-charged particles in pp collisions at = 8 TeV using the ATLAS detector. Eur. Phys. J. 2015, C75, 362. [Google Scholar] [CrossRef]
- Aad, G.; Abajyan, T.; Abbott, B.; Abdallah, J.; Khalek, S.A.; Abdelalim, A.A.; Abdinov, O.; Aben, R.; Abi, B.; Abolins, M.; et al. Search for long-lived, multi-charged particles in pp collisions at = 7 TeV using the ATLAS detector. Phys. Lett. 2013, B722, 305–323. [Google Scholar] [CrossRef]
- Abada, A.; Abbrescia, M.; AbdusSalam, S.S.; Abdyukhanov, I.; Fernez, J.A.; Abramov, A.; Aburaia, M.; Acar, A.O.; Adzic, P.R.; Agrawal, P.; et al. FCC-hh: The Hadron Collider. Eur. Phys. J. ST 2019, 228, 755–1107. [Google Scholar] [CrossRef]
- Pospelov, M.E. FCNC in left–right symmetric theories and constraints on the right-handed scale. Phys. Rev. 1997, D56, 259–264. [Google Scholar] [CrossRef]
- Chakrabortty, J.; Gluza, J.; Jelinski, T.; Srivastava, T. Theoretical constraints on masses of heavy particles in left–right Symmetric Models. Phys. Lett. 2016, B759, 361–368. [Google Scholar] [CrossRef]

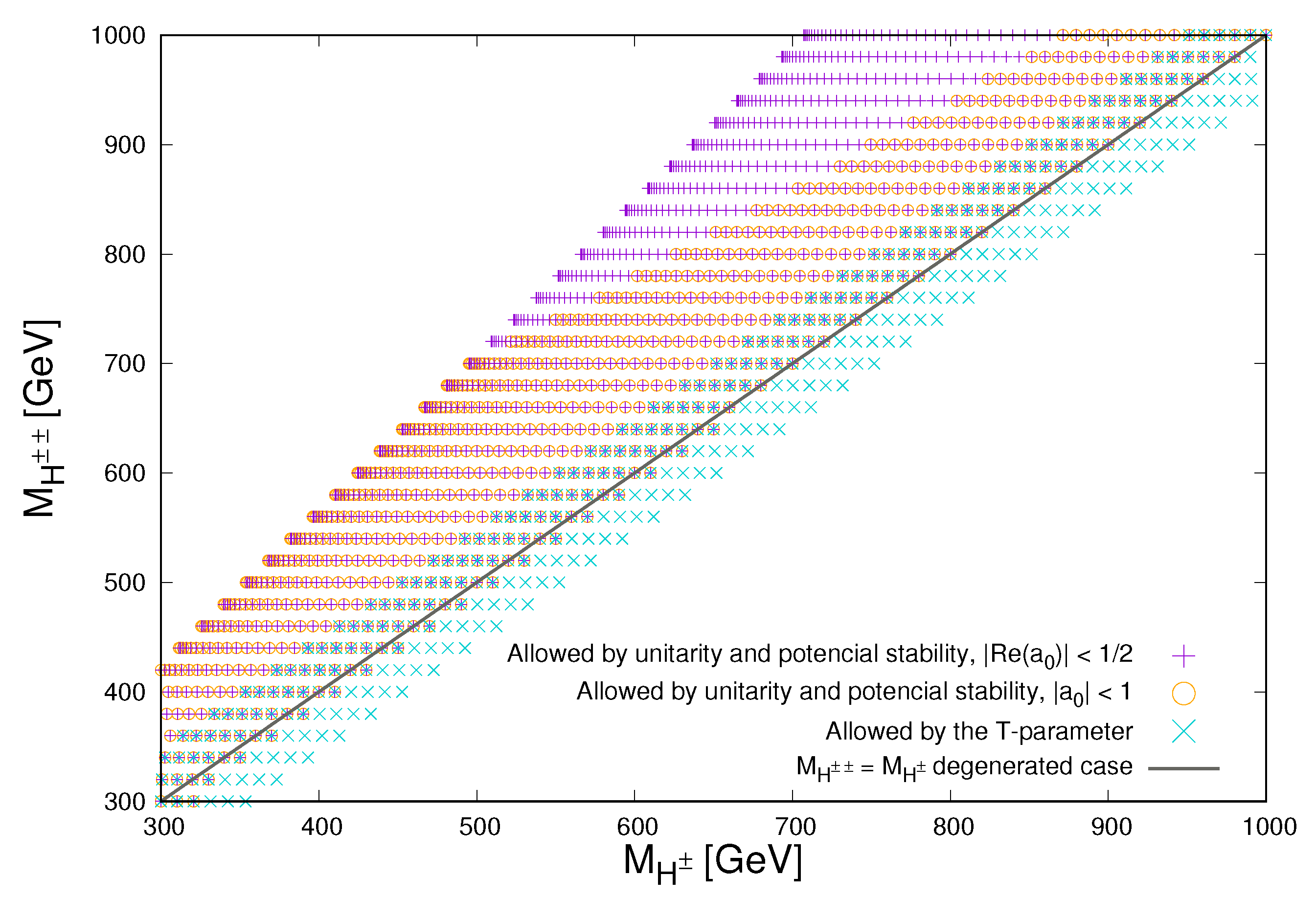
| Process: | Diagrams: | Limits: |
|---|---|---|
| Radiative decay: | 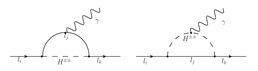 | [11] [12] [12] |
| Three body decay: |  | [13] [14] |
| conversion: | 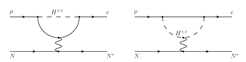 | [15] |
| HTM | |
| LRSM | |
| NH | IH | |
|---|---|---|
| min [eV] | 0.93 | 1.07 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gluza, J.; Kordiaczyńska, M.; Srivastava, T. Doubly Charged Higgs Bosons and Spontaneous Symmetry Breaking at eV and TeV Scales. Symmetry 2020, 12, 153. https://doi.org/10.3390/sym12010153
Gluza J, Kordiaczyńska M, Srivastava T. Doubly Charged Higgs Bosons and Spontaneous Symmetry Breaking at eV and TeV Scales. Symmetry. 2020; 12(1):153. https://doi.org/10.3390/sym12010153
Chicago/Turabian StyleGluza, Janusz, Magdalena Kordiaczyńska, and Tripurari Srivastava. 2020. "Doubly Charged Higgs Bosons and Spontaneous Symmetry Breaking at eV and TeV Scales" Symmetry 12, no. 1: 153. https://doi.org/10.3390/sym12010153
APA StyleGluza, J., Kordiaczyńska, M., & Srivastava, T. (2020). Doubly Charged Higgs Bosons and Spontaneous Symmetry Breaking at eV and TeV Scales. Symmetry, 12(1), 153. https://doi.org/10.3390/sym12010153






