Multidimensional Interpolation Decoupling Strategy for CD Basis Weight of Papermaking Process
Abstract
1. Introduction
2. Experimental
2.1. Materials
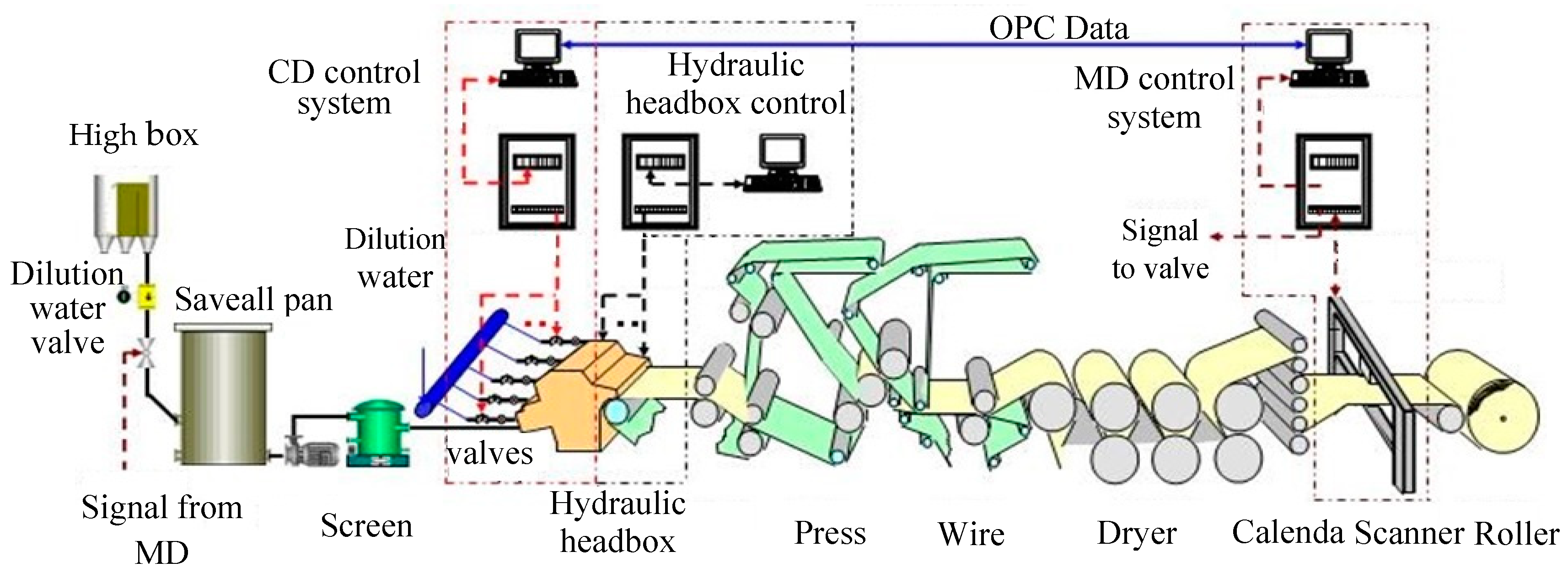
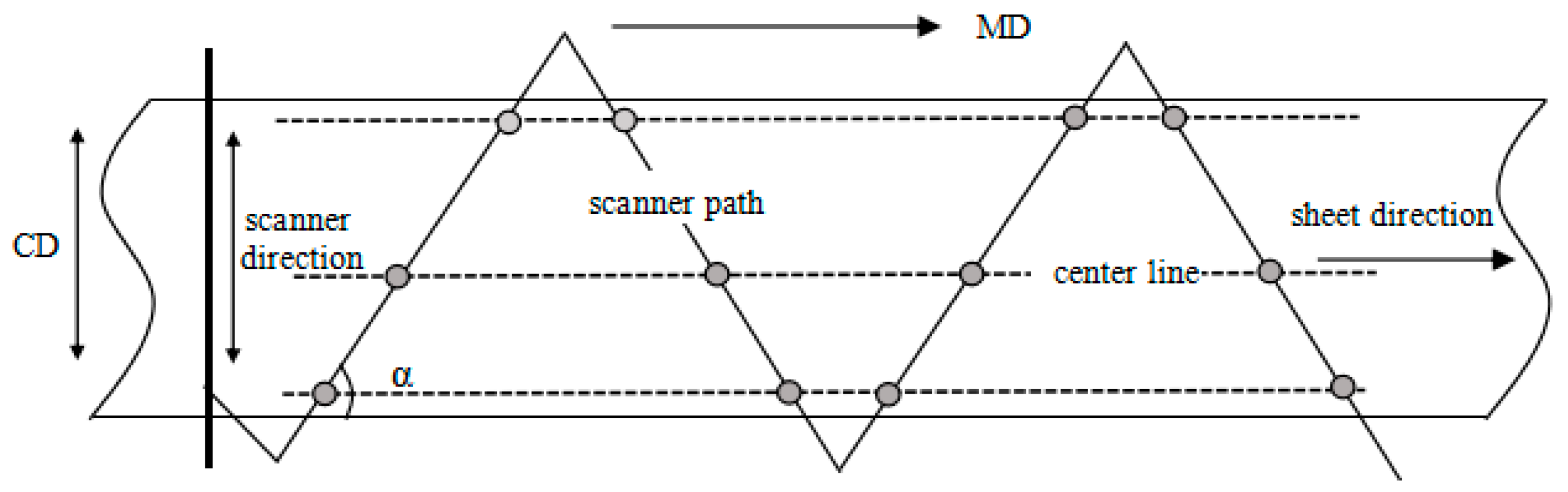
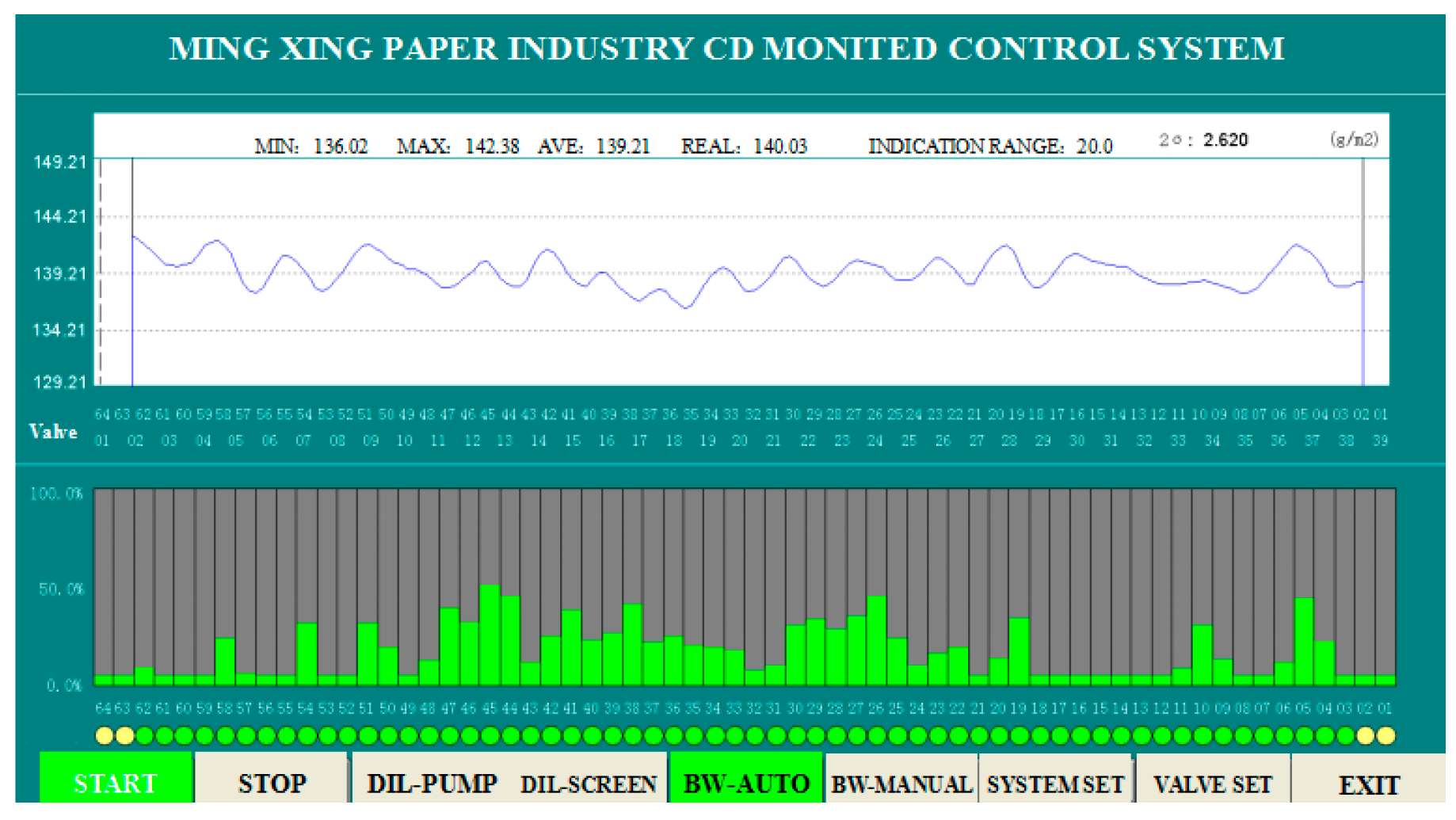
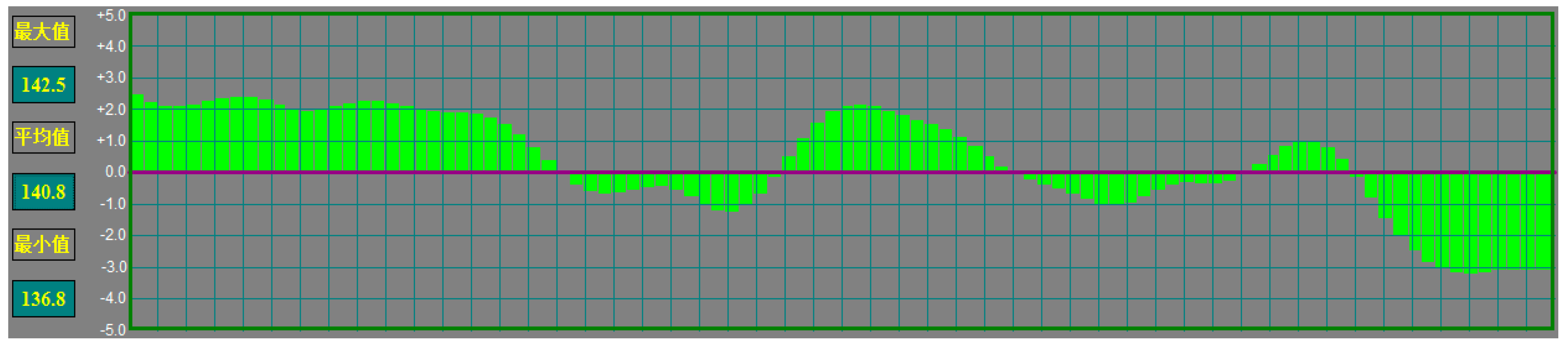
2.2. Measuring Method of the Process Data
3. Modeling and Block Decomposition of CD Control System
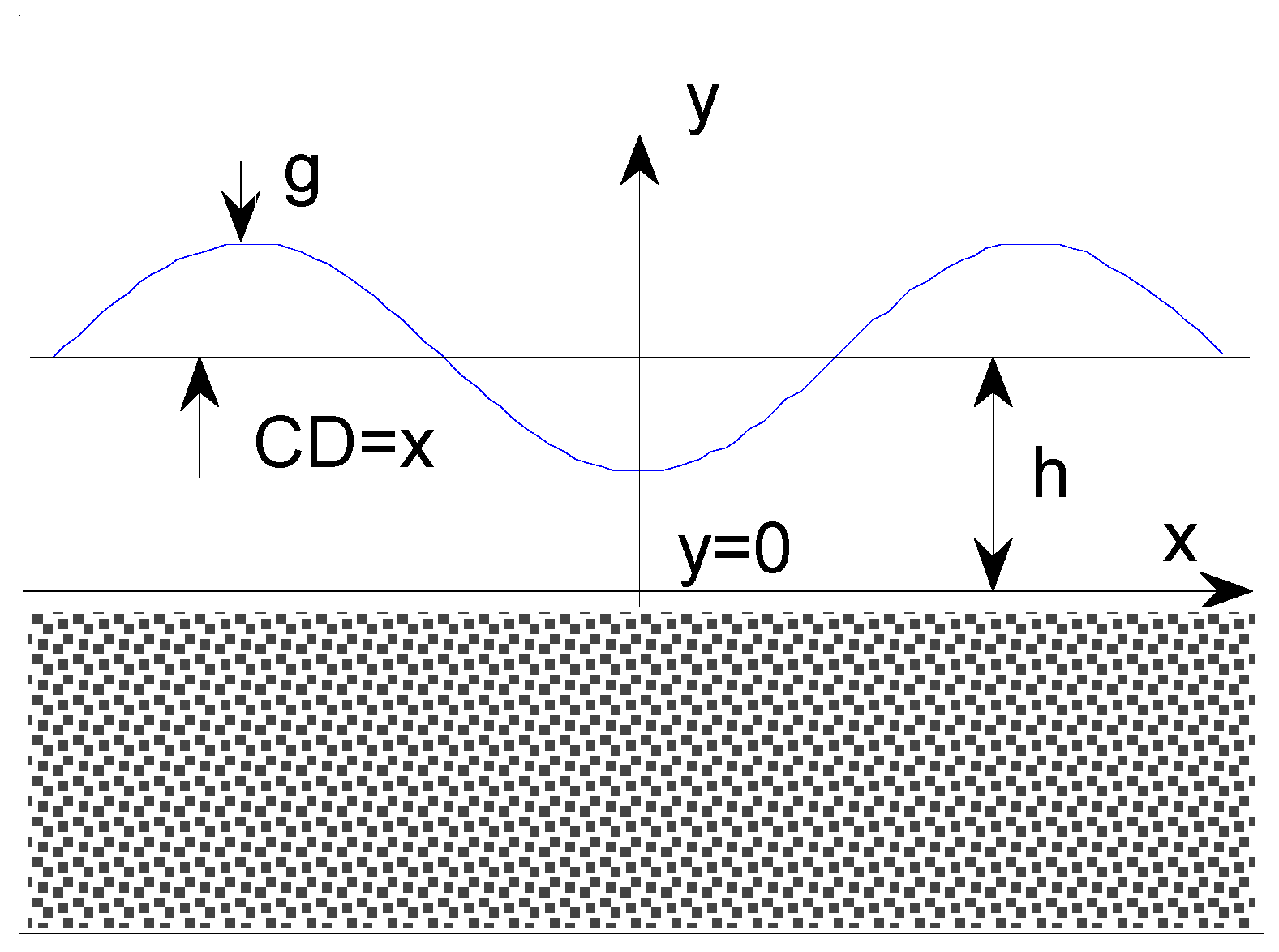
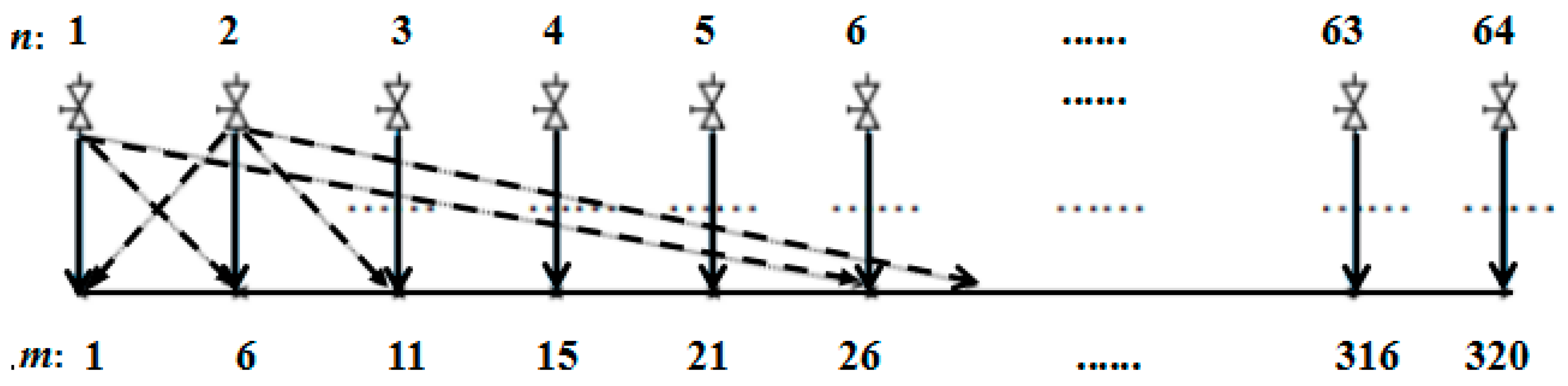
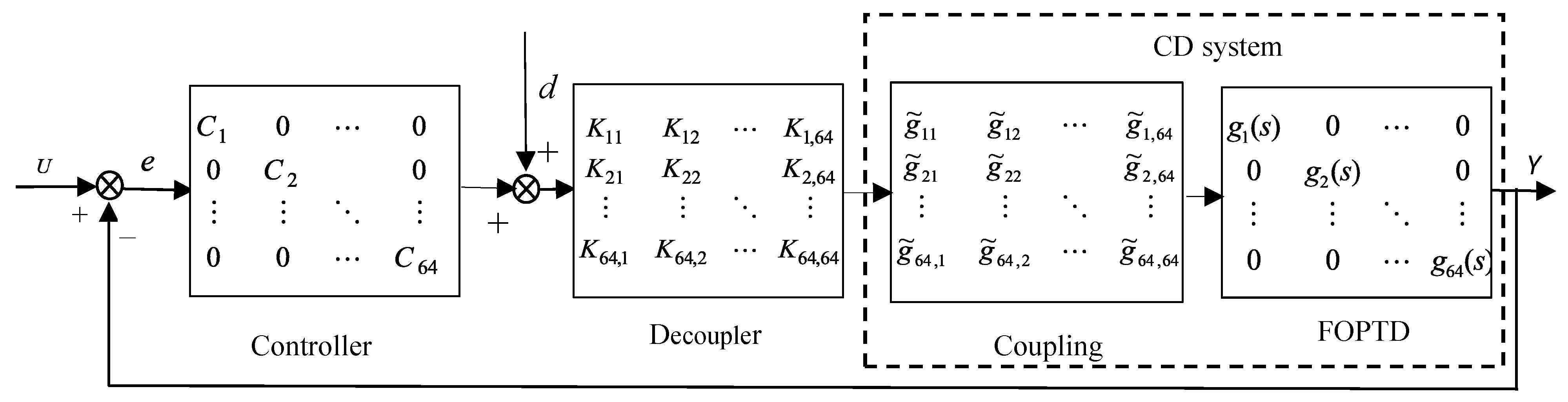
3.1. Modeling of CD Control System
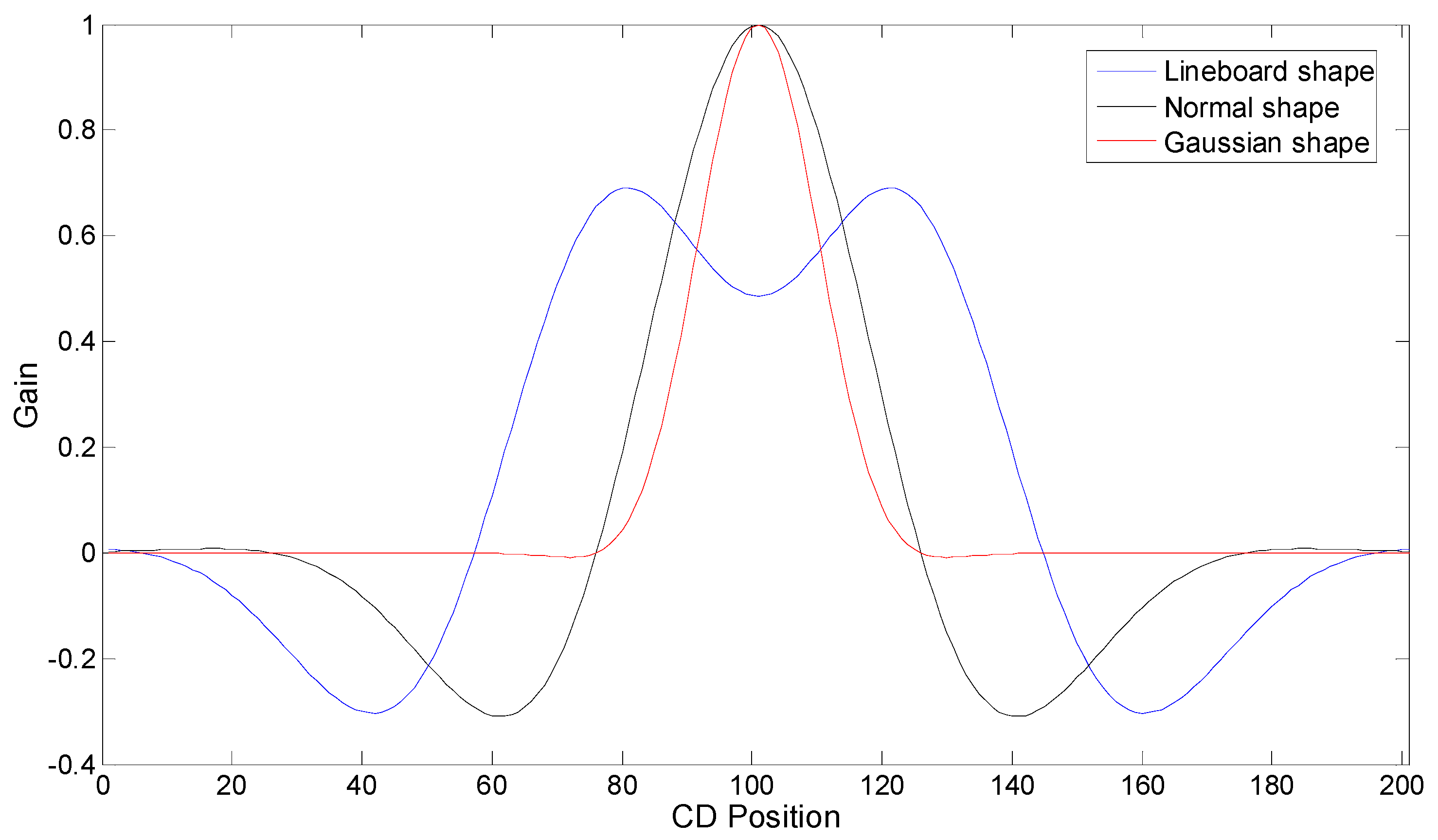
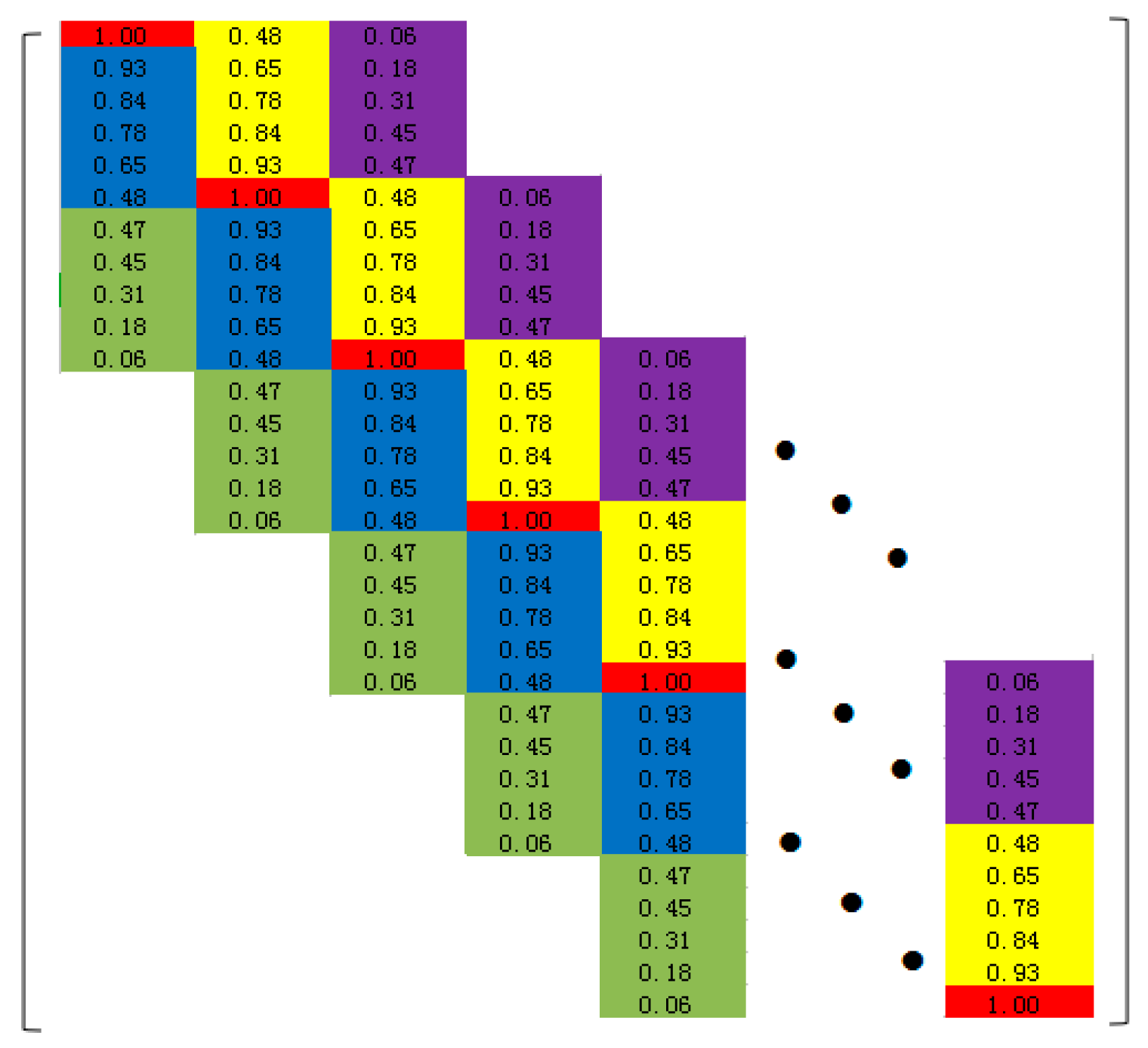
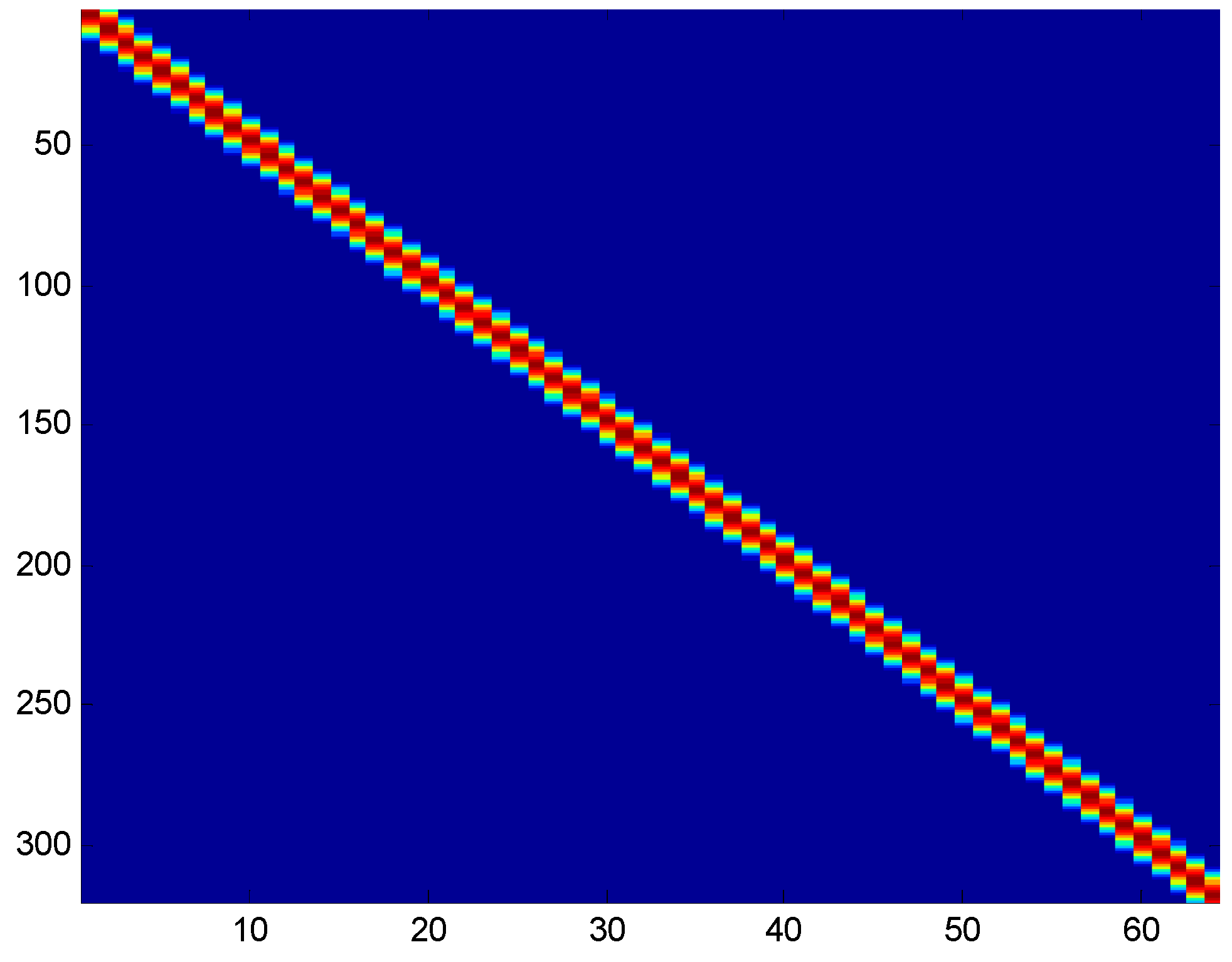
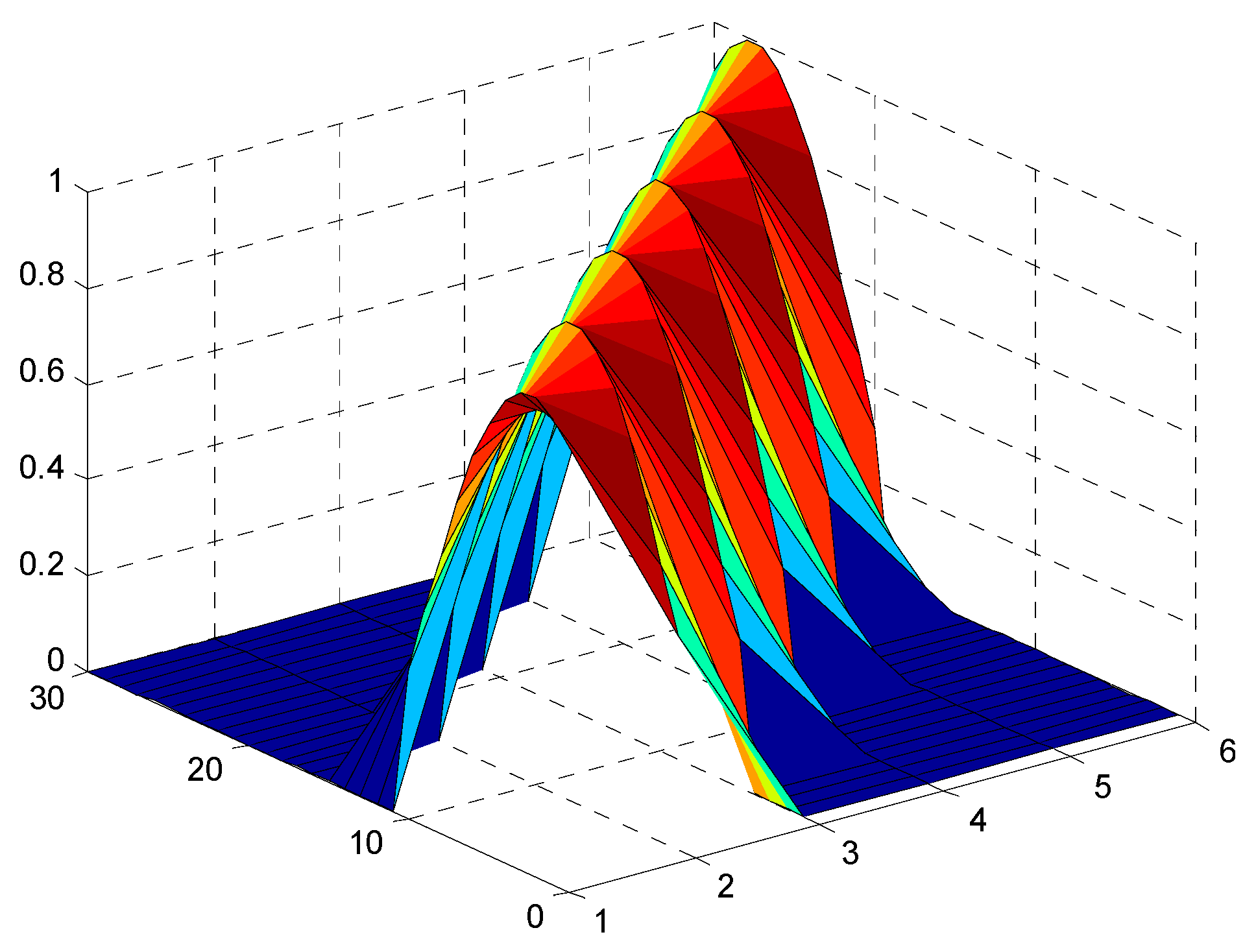
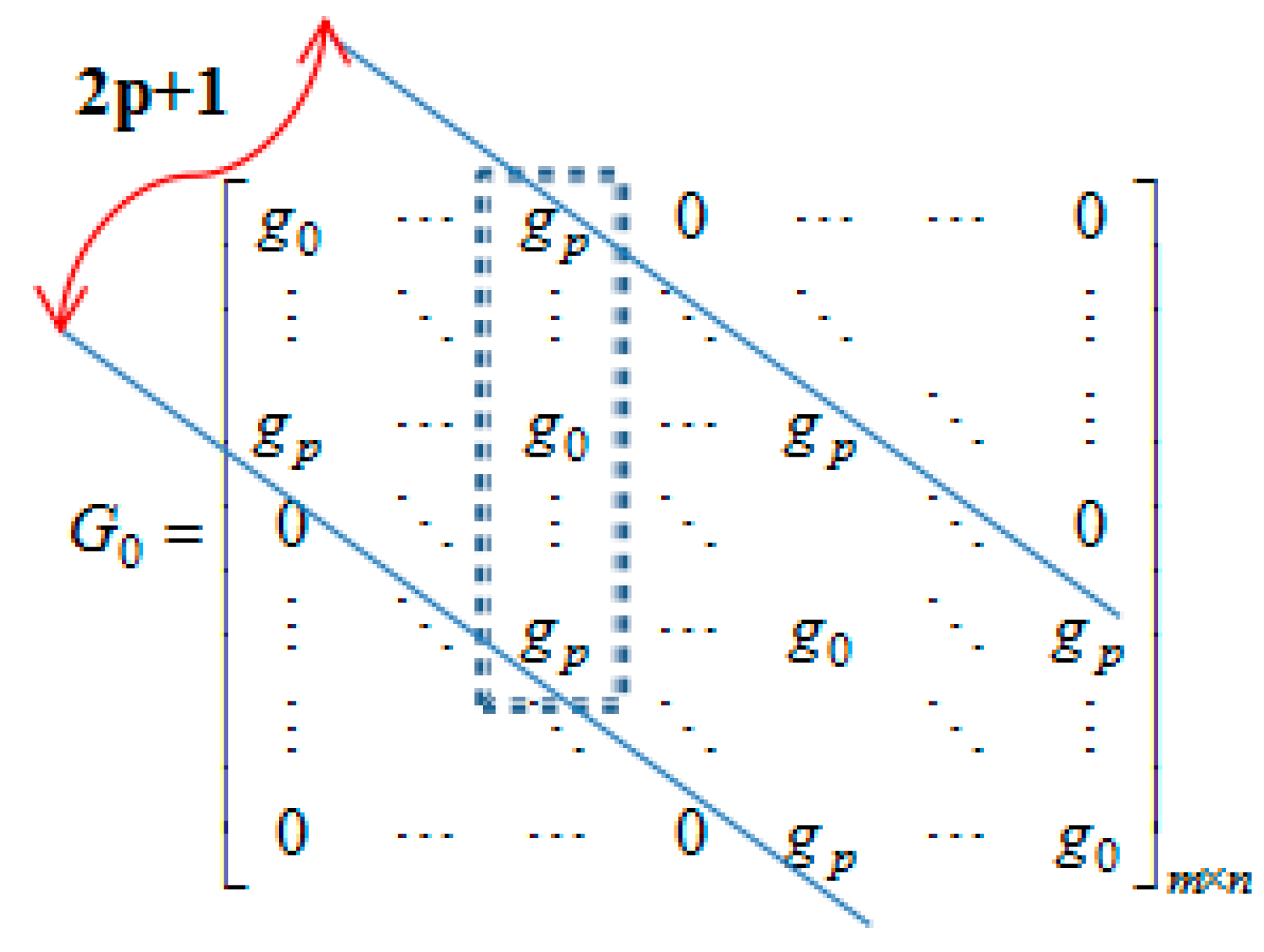
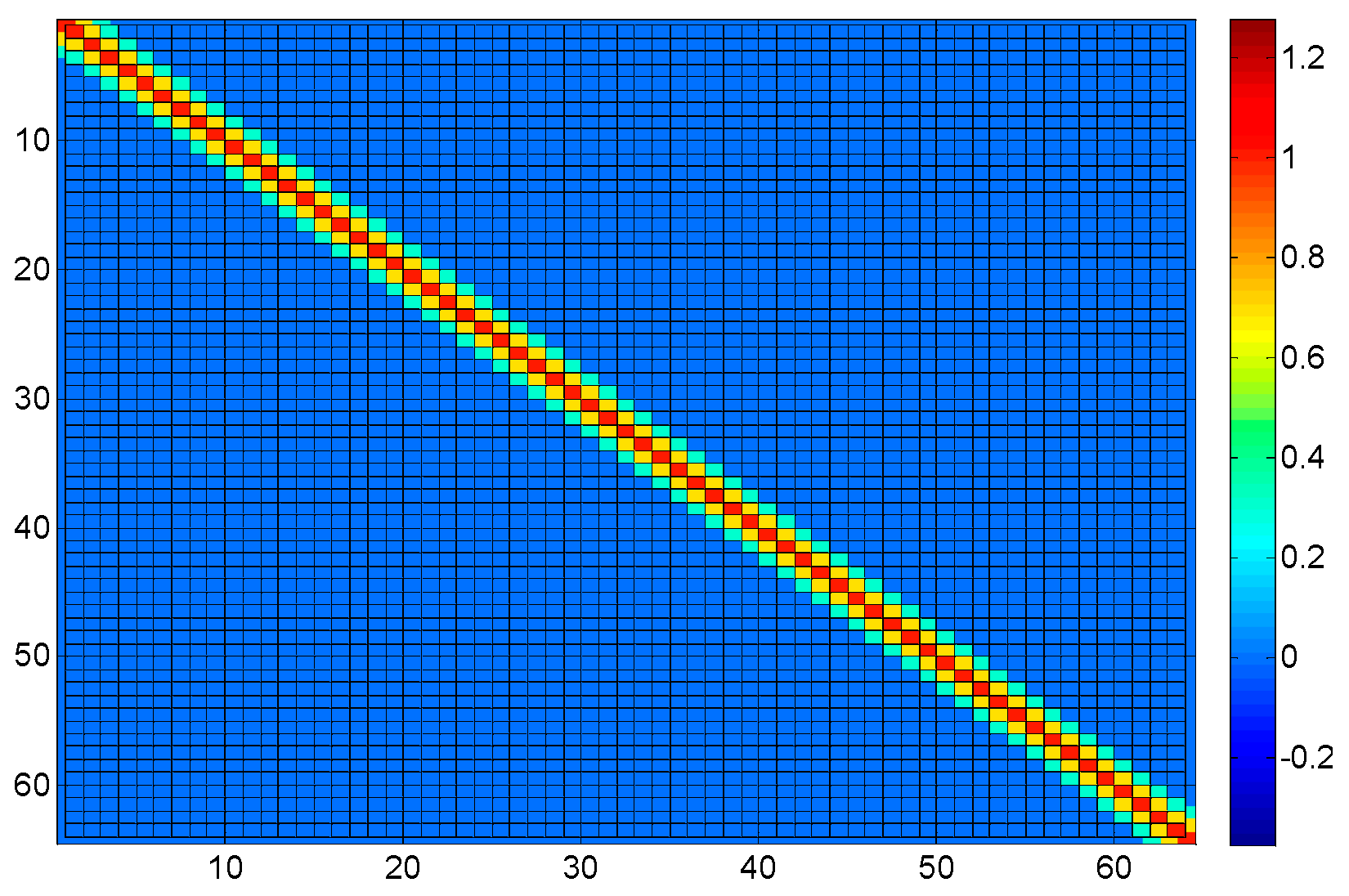
3.2. Identification of Coupling Matrix
3.3. Block and Decomposition Control of Coupling Matrix
3.3.1. Coupling Matrix Blocking
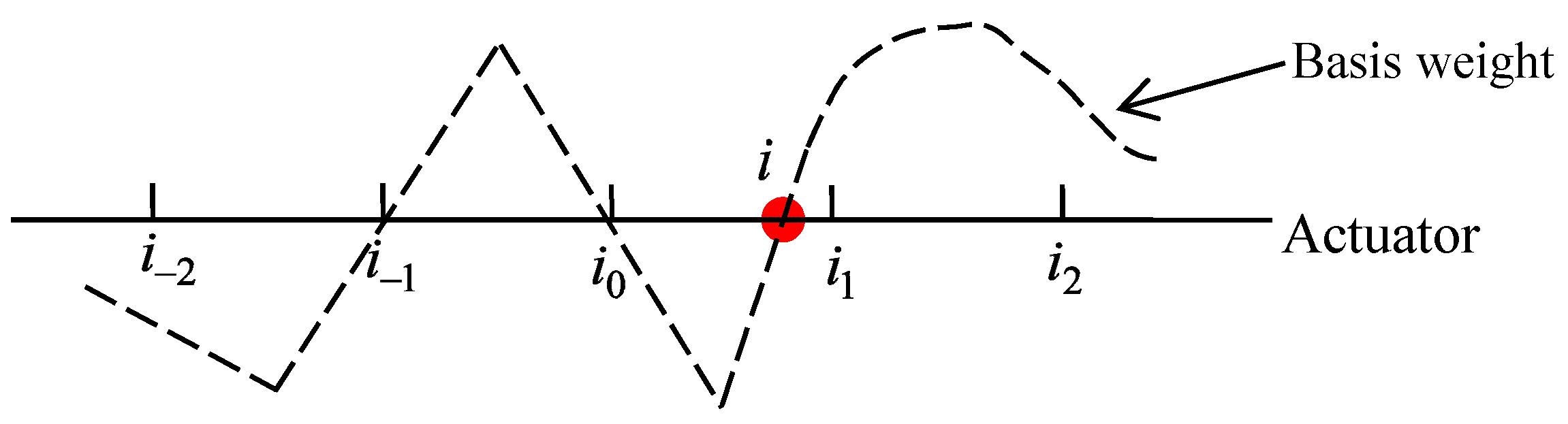
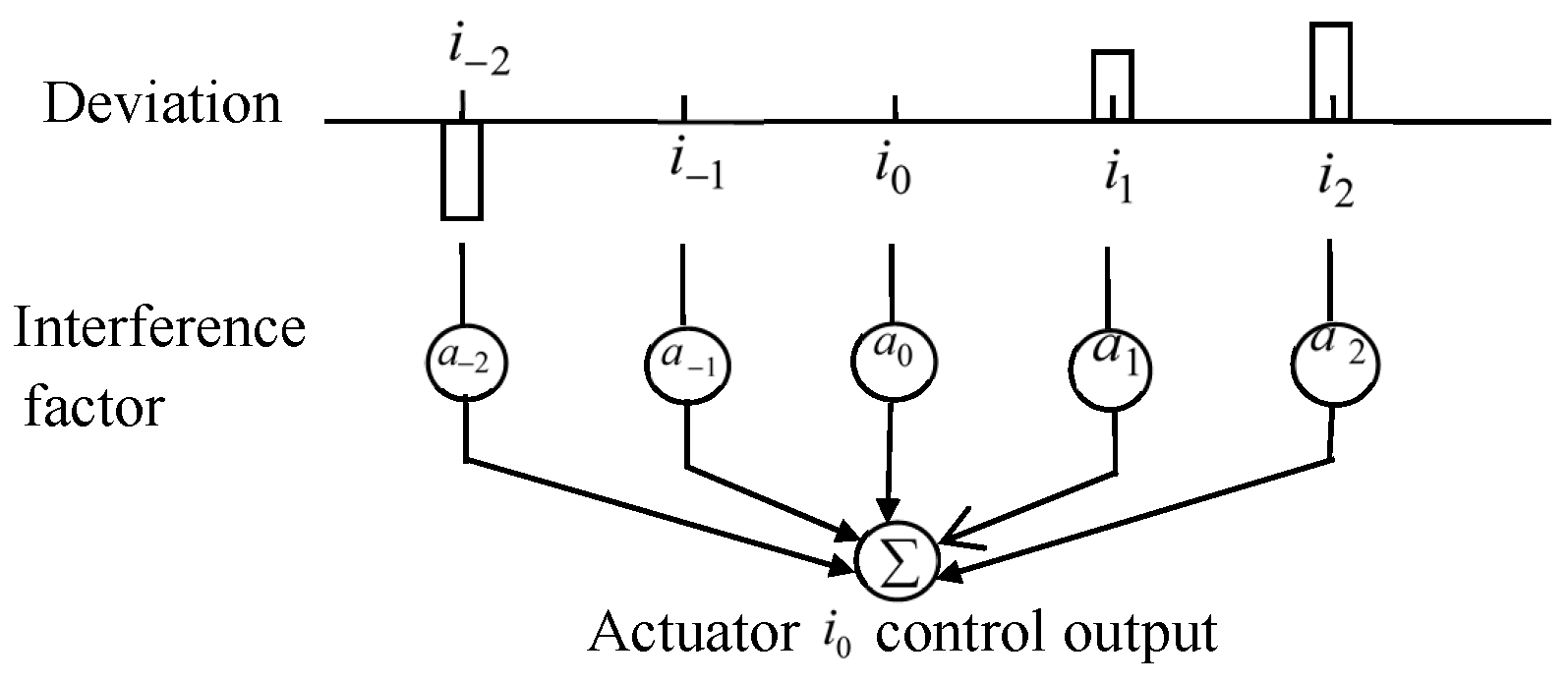
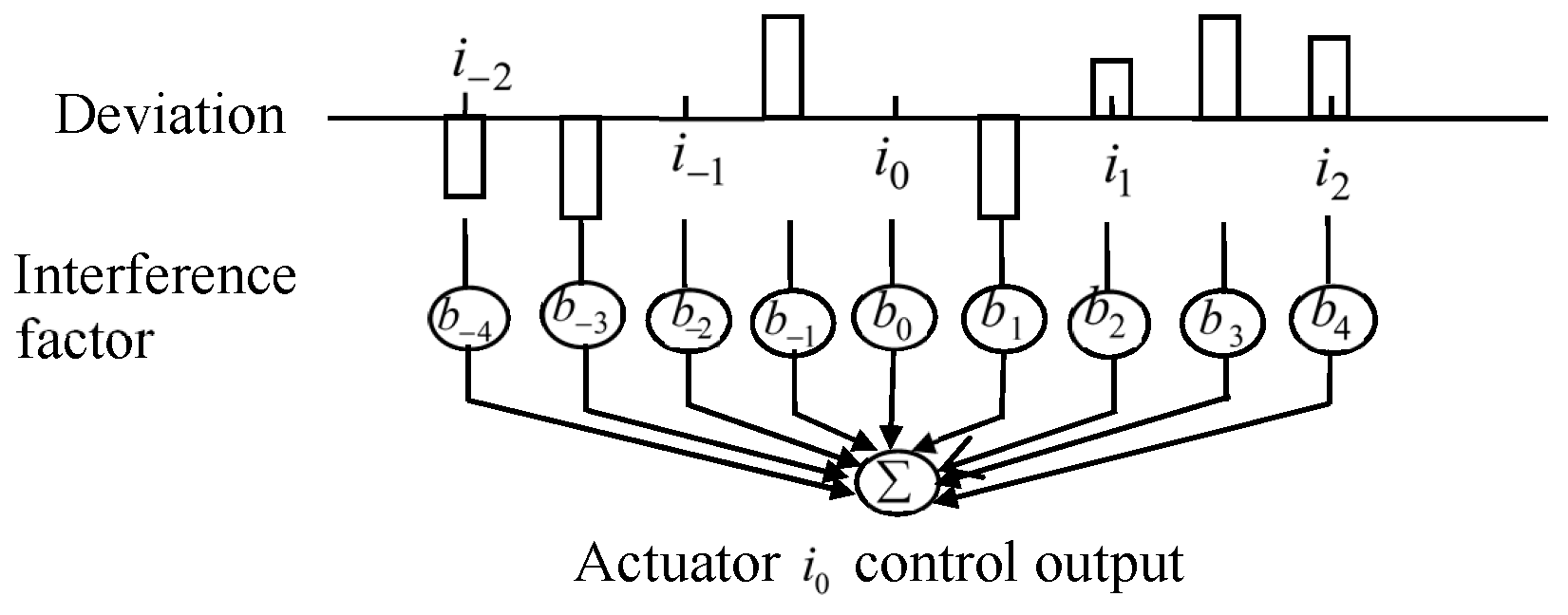
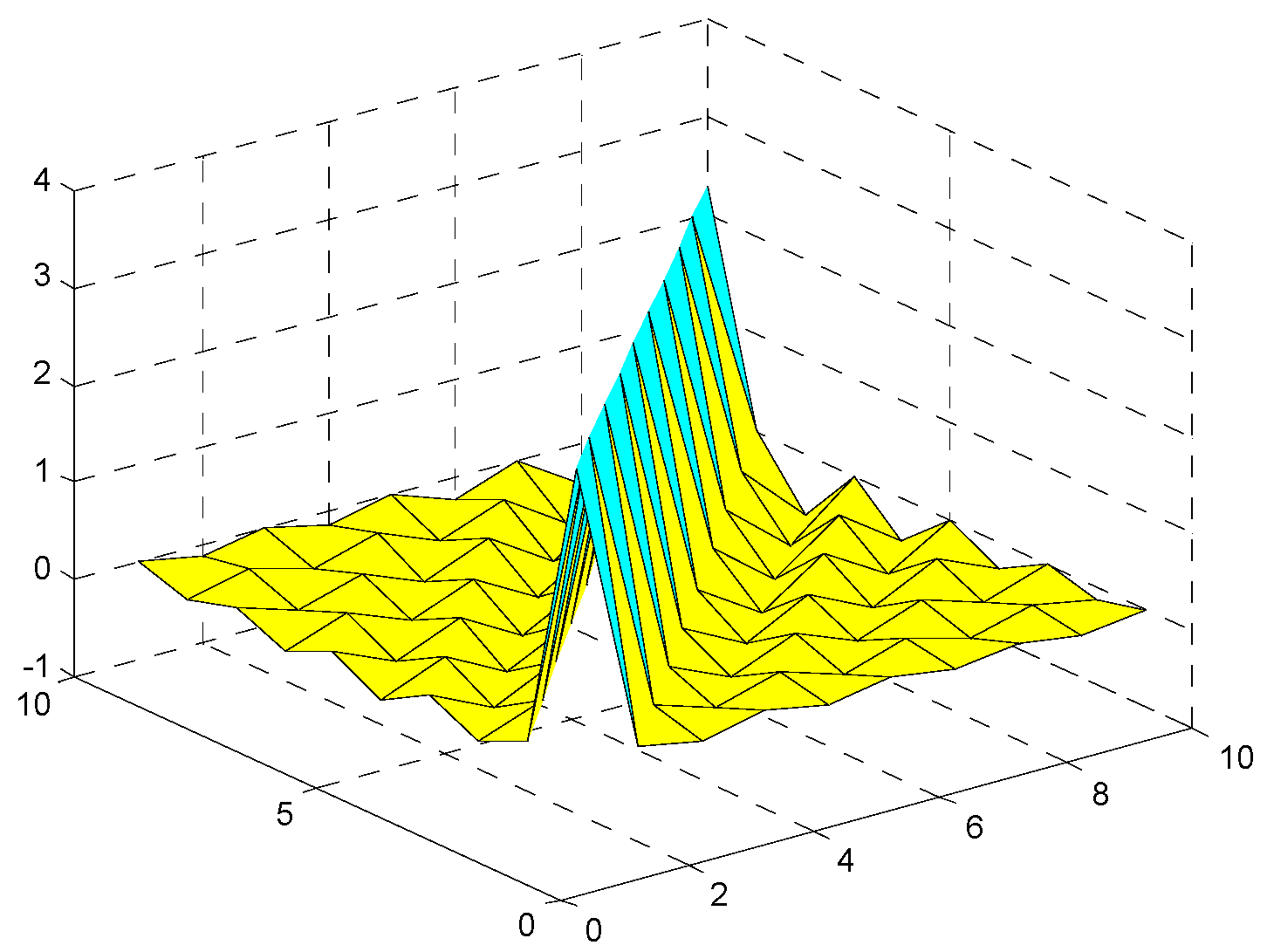
3.3.2. Decomposition Algorithm Control
4. Interpolation Decoupling Strategy for CD Control System
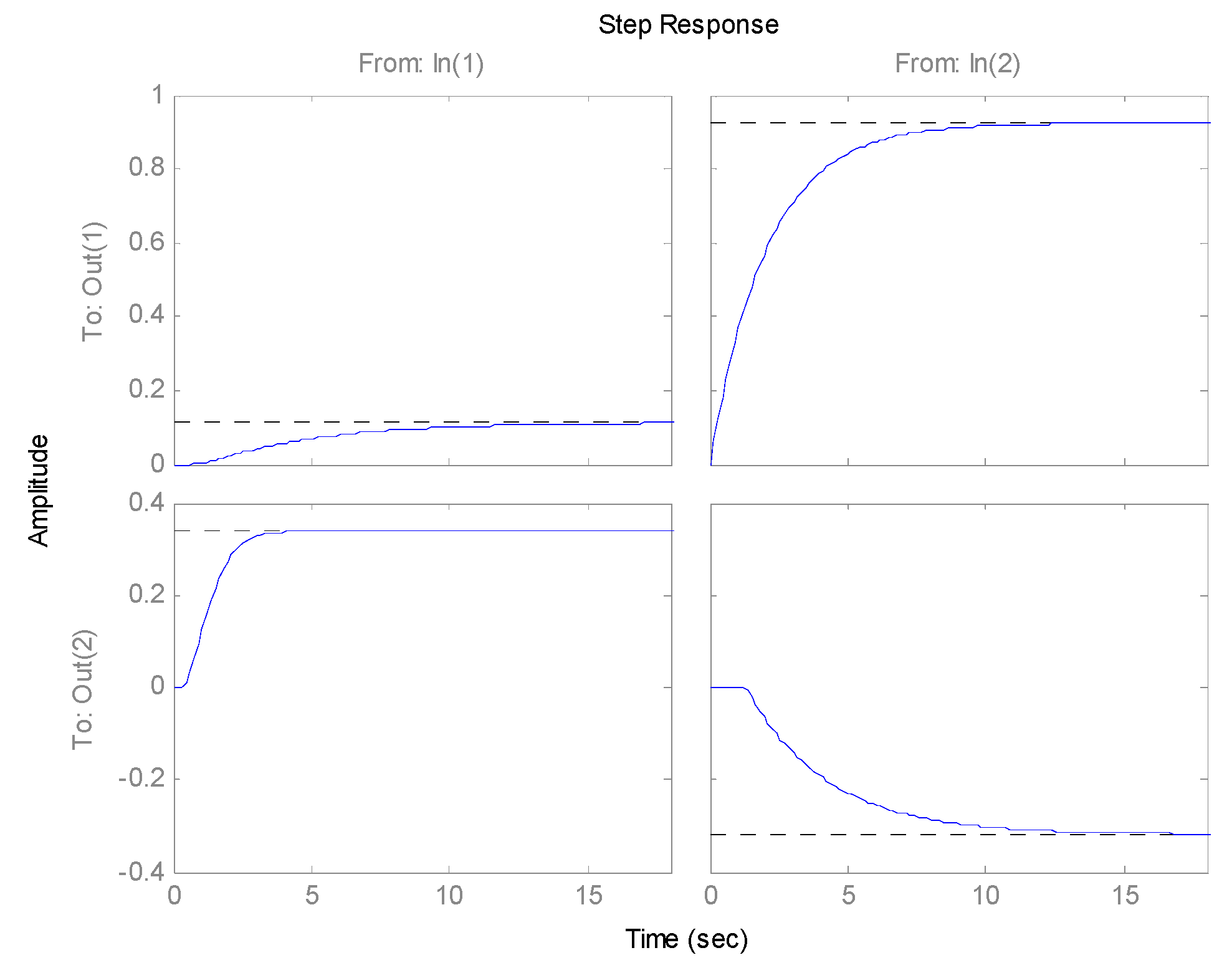
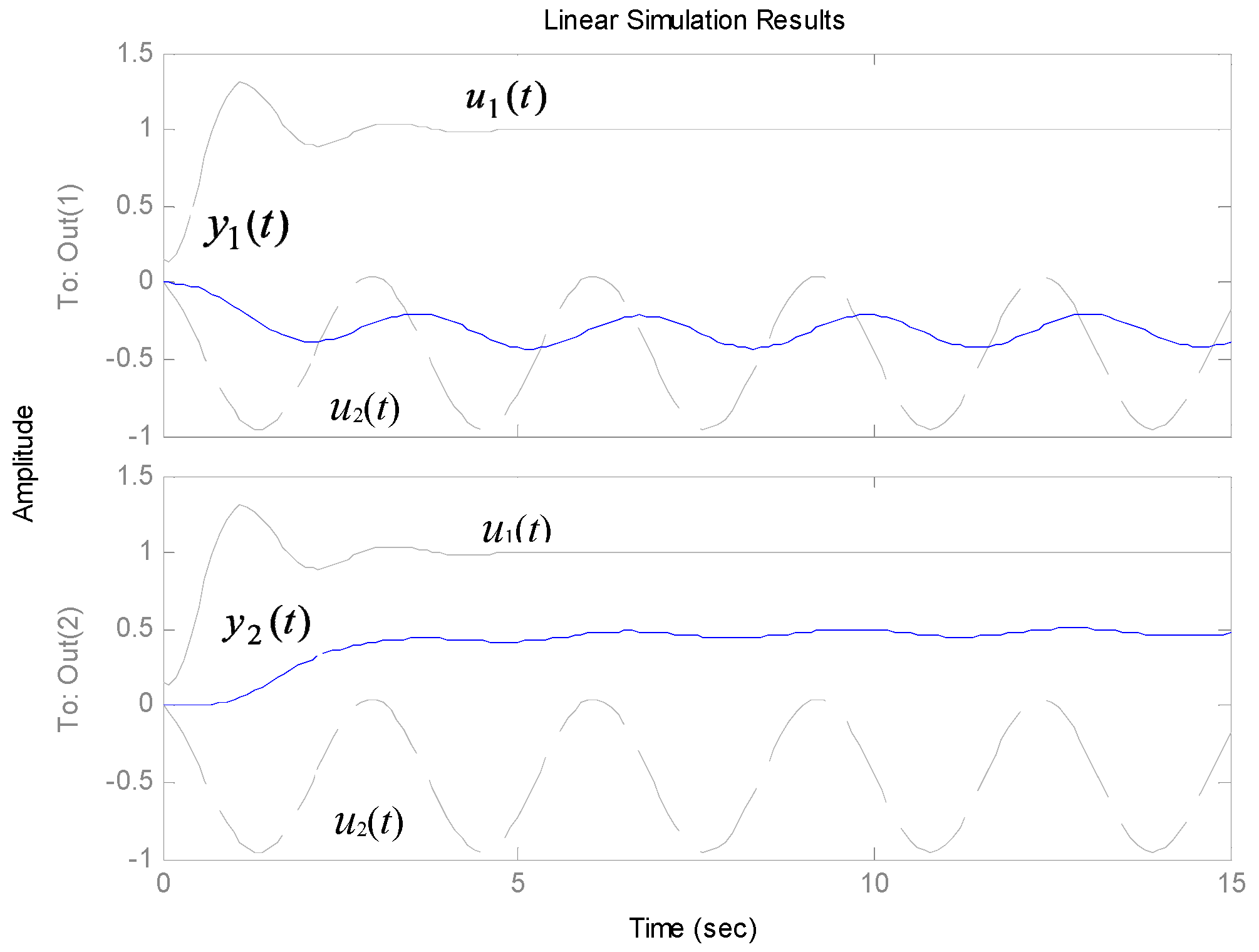
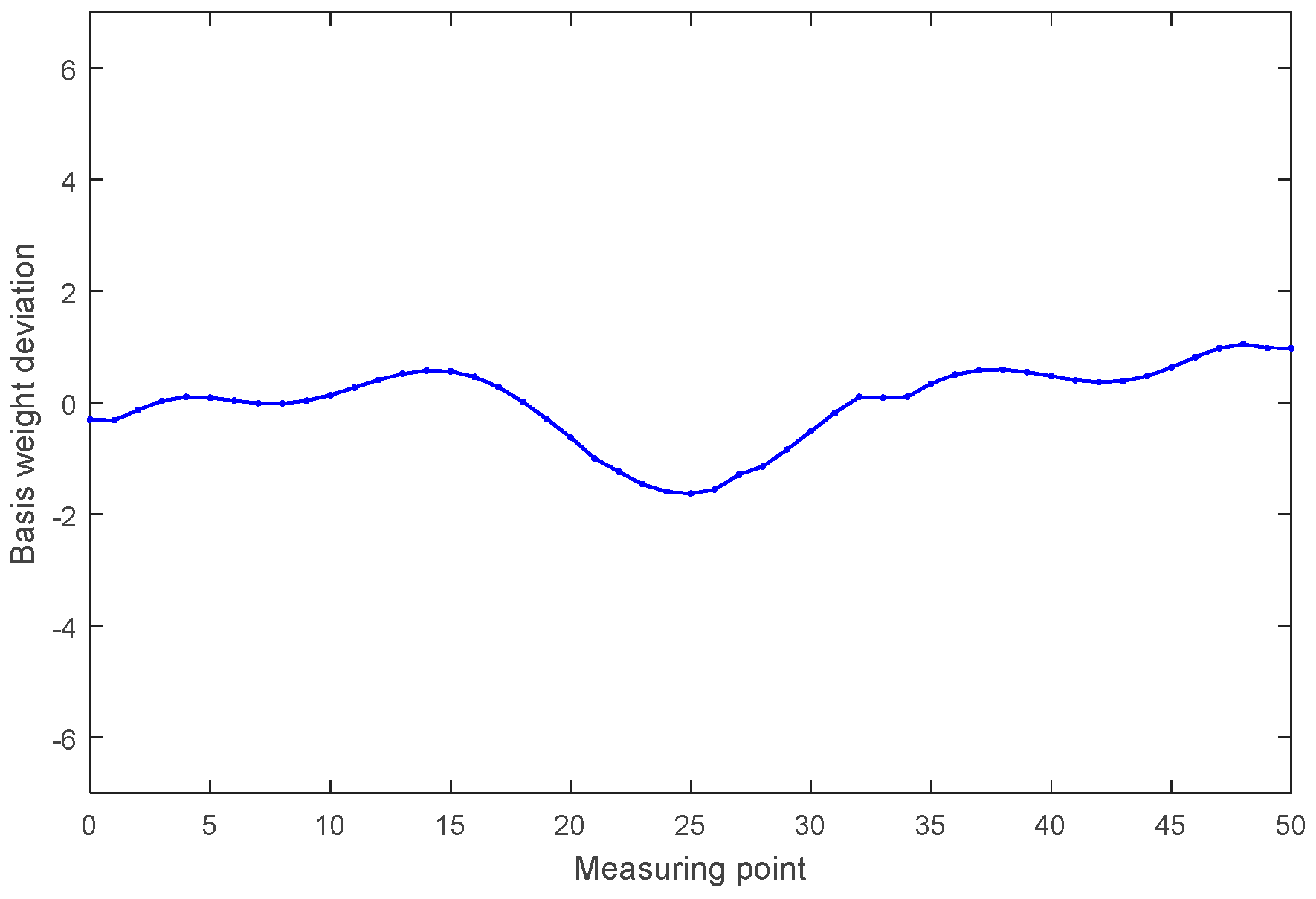
5. Results of Simulation and Application
6. Conclusions
Supplementary Materials
Supplementary File 1Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gorinevsky, M.; Stein, G. Structured Uncertainty Analysis of Robust Stability for Multidimensional Array Systems. IEEE Trans. Autom. Control 2003, 48, 1557–1568. [Google Scholar] [CrossRef]
- Fukumine, H.; Miura, F. Control Parameter Optimization Service for Paper Machine Quality Control Systems, QCS Tune-up Engineering, for Ideal Paper Manufacturing Plant. In Yokogawa Technical Report English Edition; Media Publications: Tokyo, Japan, 2011; Volume 54, pp. 61–64. Available online: https://www.yokogawa.com/th/library/resources/yokogawa-technical-reports/control-parameter-optimization-service-for-paper-machine-quality-control-systems-qcs-tune-up-engineering-for-ideal-paper-manuf/ (accessed on 8 January 2020).
- Stewart, G.E.; Gorinevsky, D.M.; Dumont, G.A. Feedback Controller Design for a Spatially Distributed System: The Paper Machine Problem. IEEE Trans. Control Syst. Technol. 2003, 11, 612–622. [Google Scholar] [CrossRef]
- Gorinevsky, M.; Gheorghe, C. Identification Tool for Cross-directional Processes. IEEE Trans. Control Syst. Technol. 2003, 11, 629–638. [Google Scholar] [CrossRef]
- Gheorghe, C.; Lahouaoula, A.; Chu, D.L. Multivariable CD Control with Adaptive Alignment for a High-production Linerboard Machine. J. Sci. Technol. For. Prod. Process. 2012, 2, 32–42. [Google Scholar]
- Toro, R.; Martínez, C.O.; Logist, F.; Impe, J.V.; Puig, V. Tuning of Predictive Controllers for Drinking Water Networked Systems. In Proceedings of the 18th IFAC World Congress, Milano, Italy, 28 August–2 September 2011. [Google Scholar]
- Ohenoja, M.; Leiviska, K. Multiple Property Cross Direction Control of Paper Machine. Model. Identif. Control 2011, 32, 103–111. [Google Scholar] [CrossRef][Green Version]
- Morales, R.M.; Heath, W.P. The Robustness and Design of Constrained Cross-directional Control via Integral Quadratic Constraints. IEEE Trans. Control Syst. Technol. 2011, 19, 1421–1432. [Google Scholar] [CrossRef]
- Chen, S.C.; Naimimohasses, R.; Zehnpfund, A. Improving Reel-building with Multivariable CD Control. In Proceedings of the Paper Conference and Trade Show: Growing in the Future, New Orleans, LA, USA, 22–25 April 2012. [Google Scholar]
- Amma, M.E.; Dumont, G.A. Identification of Paper Machines Cross-directional Models in Closed-loop. Model. Identif. Control 2013, 3, 245–256. [Google Scholar]
- Featherstone, A.P.; VanAntwerp, J.G.; Braatz, R.D. Cross-Directional Control, 1st ed.; Springer: London, UK, 2000. [Google Scholar]
- Sadighi, A.; Ahmad, A.; Irandoukht, A. Modeling a Pilot FixedBed Hydrocracking Reactor via a Kinetic Base and Neuro-Fuzzy Method. J. Chem. Eng. Jpn. 2010, 43, 174–185. [Google Scholar] [CrossRef]
- Malashenko, A. The Dilution Control Headbox. Pap. Technol. 1997, 12, 42–53. [Google Scholar]
- Hansen, O. MasterJet II—For Super Sheet Formation. Voith Pap. 2008, 25, 24–32. [Google Scholar]
- Jiang, W. Practical Experience of Headbox Rebuilding. China Pulp Pap. 2010, 11, 67–70. [Google Scholar]
- Lin, C. Research and Development of the Key Technology of MC Dilution Hydraulic Headbox. China Pulp Pap. 2010, 29, 56–61. [Google Scholar]
- Shi, X. Observer-based fuzzy adaptive control for multi-input multi-output nonlinear systems with a nonsymmetric control gain matrix and unknown control direction. Fuzzy Sets Syst. 2015, 23, 1–26. [Google Scholar] [CrossRef]
- Dave, P.; Willing, D.A.; Kudva, G.K.; Pekny, J.F.; Doyle, F.J. LP Methods in MPC of Large-Scale Systems: Application to Paper-Machine CD Control. AIChE J. 1997, 43, 1016–1031. [Google Scholar] [CrossRef]
- Jeremy, G.; Andrew, P.; Richard, D. Robust Cross-directional Control of Large Scale Sheet and Film processes. J. Process. Control 2011, 11, 149. [Google Scholar]



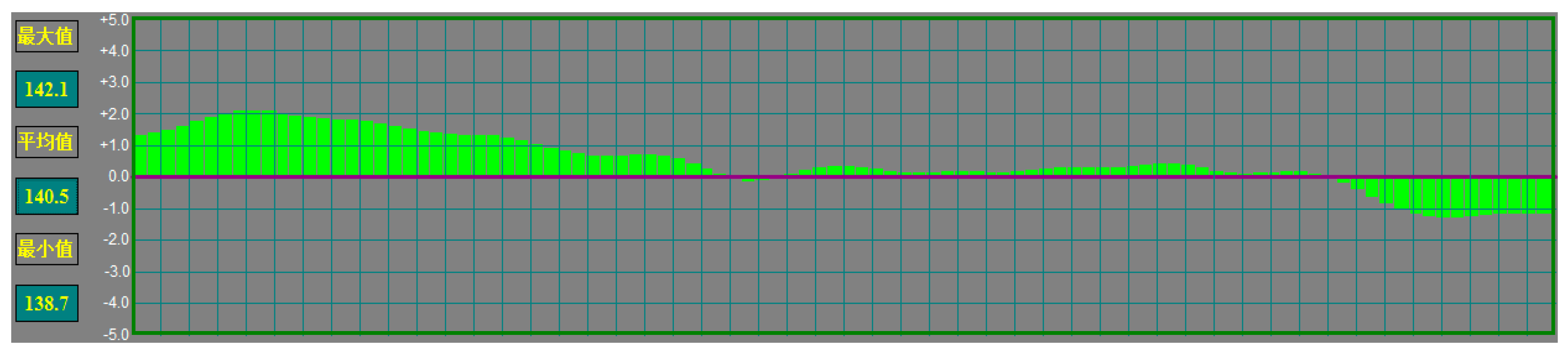
| Time | |||||
|---|---|---|---|---|---|
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shan, W.; Liu, B. Multidimensional Interpolation Decoupling Strategy for CD Basis Weight of Papermaking Process. Symmetry 2020, 12, 149. https://doi.org/10.3390/sym12010149
Shan W, Liu B. Multidimensional Interpolation Decoupling Strategy for CD Basis Weight of Papermaking Process. Symmetry. 2020; 12(1):149. https://doi.org/10.3390/sym12010149
Chicago/Turabian StyleShan, Wenjuan, and Bing Liu. 2020. "Multidimensional Interpolation Decoupling Strategy for CD Basis Weight of Papermaking Process" Symmetry 12, no. 1: 149. https://doi.org/10.3390/sym12010149
APA StyleShan, W., & Liu, B. (2020). Multidimensional Interpolation Decoupling Strategy for CD Basis Weight of Papermaking Process. Symmetry, 12(1), 149. https://doi.org/10.3390/sym12010149





