A Hybrid MCDM Model to Select Optimal Hosts of Variety Shows in the Social Media Era
Abstract
1. Introduction
2. Literature Review
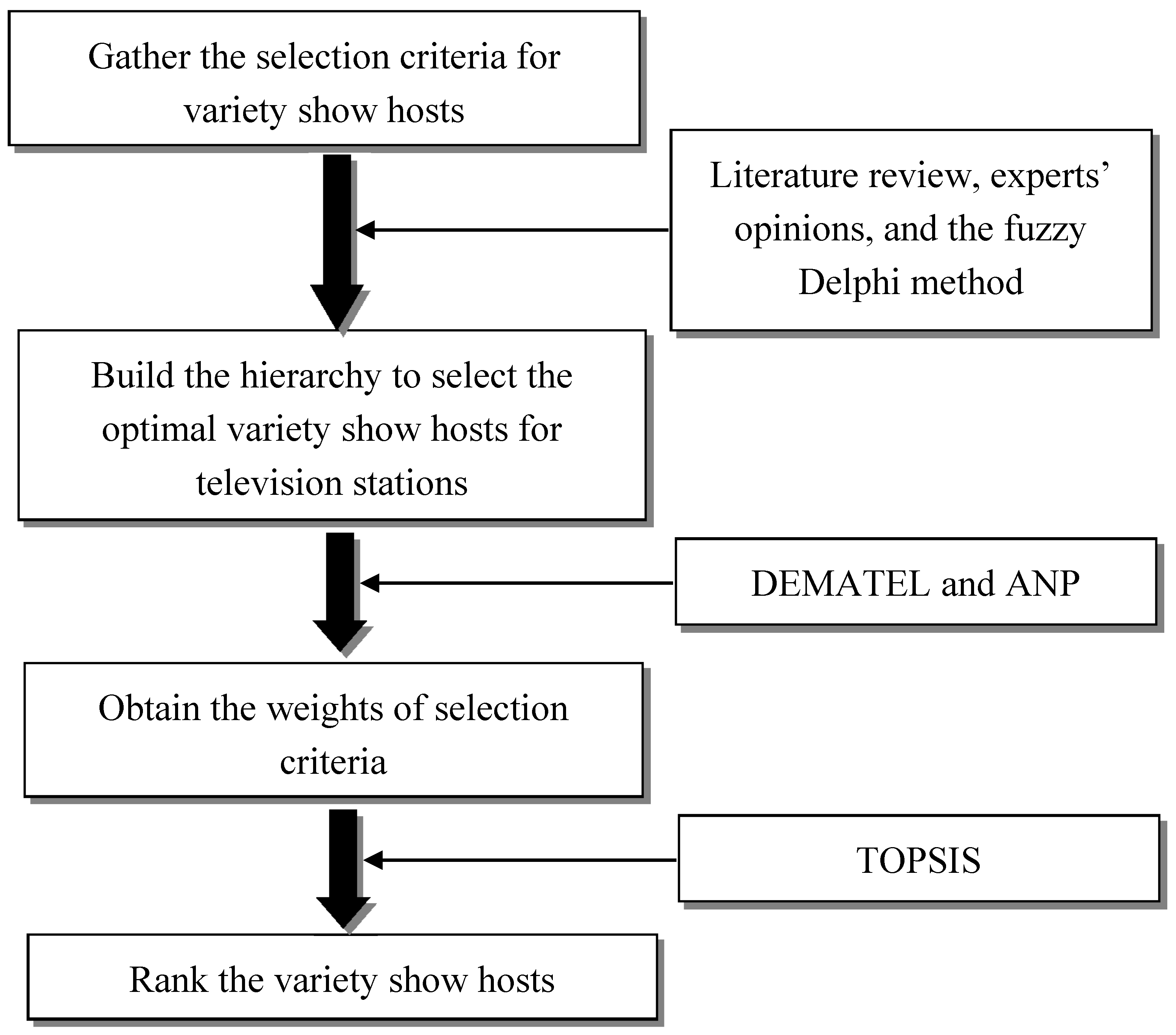
3. Methodology
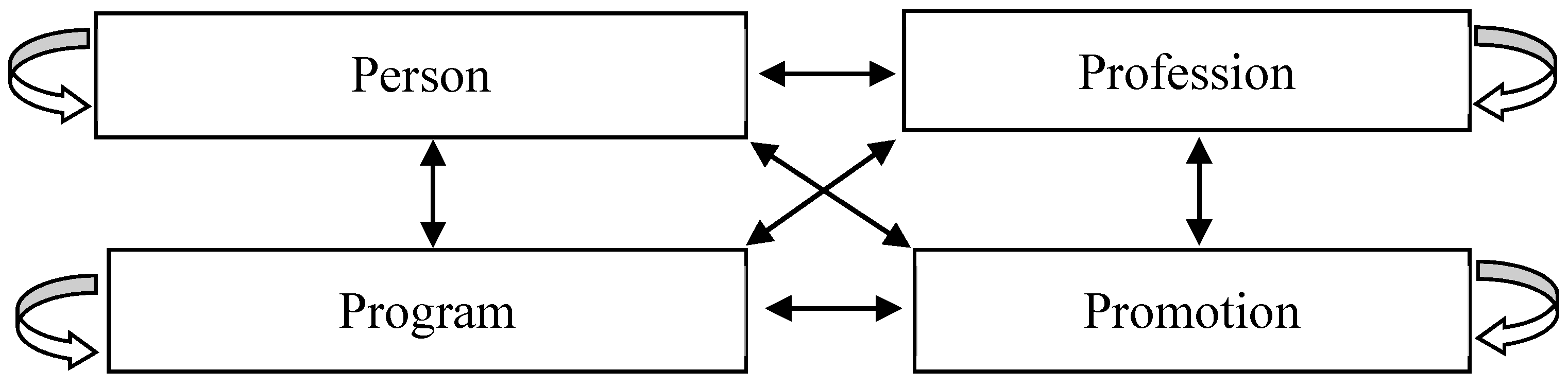
3.1. Conceptual Framework
3.2. Representation of the Selection Model
3.3. Fuzzy Delphi Method
3.4. DEMATEL
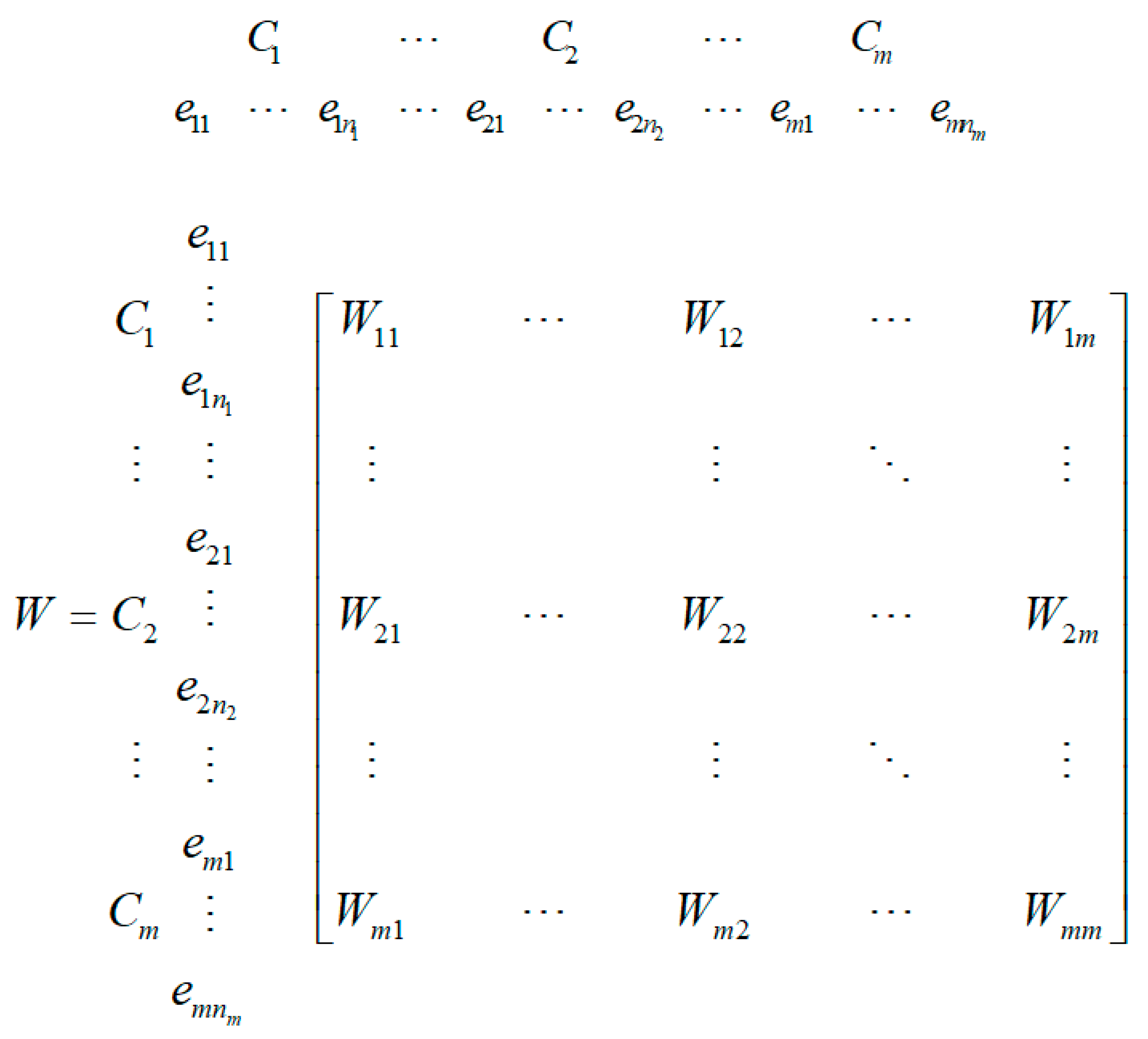
3.5. ANP
3.6. TOPSIS
4. Empirical Study and Results
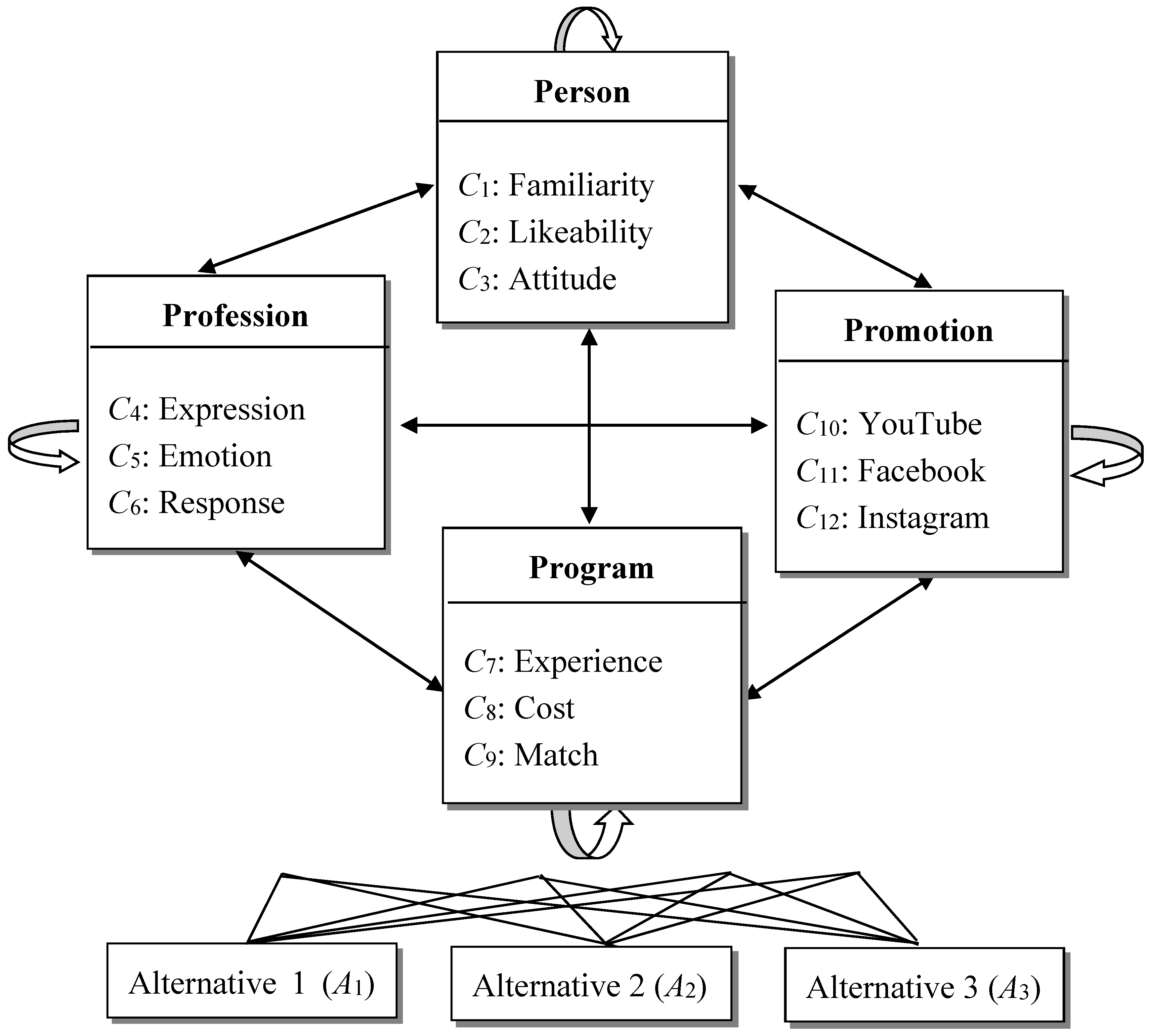
4.1. Construct the Hierarchy
4.2. Complete Pairwise Comparison
4.3. Solve the Supermatrix
4.4. Build a Normalized and a Weighted Evaluation Matrix
4.5. Rank the Alternative
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. The Pairwise Comparison Matrices
| Person | Profession | Program | Promotion | Priority Weights | |
|---|---|---|---|---|---|
| λmax = 4.1092, CR = 0.0368 | |||||
| Person | 1.0000 | 1.5874 | 0.8355 | 1.4736 | 0.2874 |
| Profession | 0.6300 | 1.0000 | 1.4422 | 2.0801 | 0.2850 |
| Program | 1.1968 | 0.6934 | 1.0000 | 1.8171 | 0.2694 |
| Promotion | 0.6786 | 0.4807 | 0.5503 | 1.0000 | 0.1582 |
| Person | Profession | Program | Promotion | Priority Weights | |
|---|---|---|---|---|---|
| λmax = 4.0175, CR = 0.0059 | |||||
| Person | 1.0000 | 0.5754 | 0.5754 | 0.6114 | 0.1631 |
| Profession | 1.7380 | 1.0000 | 1.4422 | 1.1447 | 0.3164 |
| Program | 1.7380 | 0.6934 | 1.0000 | 1.1447 | 0.2635 |
| Promotion | 1.6355 | 0.8736 | 0.8736 | 1.0000 | 0.2570 |
| Person | Profession | Program | Promotion | Priority Weights | |
|---|---|---|---|---|---|
| λmax = 4.0226, CR = 0.0076 | |||||
| Person | 1.0000 | 0.9565 | 1.0455 | 1.1006 | 0.2535 |
| Profession | 1.0455 | 1.0000 | 1.4422 | 1.4422 | 0.3005 |
| Program | 0.9565 | 0.6934 | 1.0000 | 1.4422 | 0.2448 |
| Promotion | 0.9086 | 0.6934 | 0.6934 | 1.0000 | 0.2012 |
| Person | Profession | Program | Promotion | Priority Weights | |
|---|---|---|---|---|---|
| λmax = 4.0359, CR = 0.0121 | |||||
| Person | 1.0000 | 3.8259 | 3.4760 | 3.3019 | 0.5393 |
| Profession | 0.2614 | 1.0000 | 1.4422 | 1.2599 | 0.1739 |
| Program | 0.2877 | 0.6934 | 1.0000 | 1.2599 | 0.1483 |
| Promotion | 0.3029 | 0.7937 | 0.7937 | 1.0000 | 0.1385 |
| Expression | Emotion | Response | Priority Weights | |
|---|---|---|---|---|
| λmax = 3.0136, CR = 0.0103 | ||||
| Expression | 1.0000 | 0.5228 | 0.4055 | 0.1871 |
| Emotion | 1.9129 | 1.0000 | 1.1006 | 0.4022 |
| Response | 2.4662 | 0.9086 | 1.0000 | 0.4107 |
Appendix B. The Unweighted, Weighted, and Limiting Supermatrices
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | C10 | C11 | C12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C1 | 0.2365 | 0.3921 | 0.3921 | 0.5098 | 0.2072 | 0.3869 | 0.2781 | 0.3856 | 0.4808 | 0.2920 | 0.3390 | 0.3143 |
| C2 | 0.4035 | 0.2158 | 0.2158 | 0.2451 | 0.3964 | 0.2262 | 0.2475 | 0.2210 | 0.2696 | 0.3054 | 0.2195 | 0.2059 |
| C3 | 0.3599 | 0.3921 | 0.3921 | 0.2451 | 0.3964 | 0.3869 | 0.4745 | 0.3935 | 0.2496 | 0.4026 | 0.4416 | 0.4798 |
| C4 | 0.1871 | 0.4225 | 0.5294 | 0.5091 | 0.4736 | 0.3014 | 0.3856 | 0.2395 | 0.4600 | 0.2479 | 0.2836 | 0.3143 |
| C5 | 0.4022 | 0.2153 | 0.1840 | 0.2643 | 0.3524 | 0.1727 | 0.2210 | 0.3802 | 0.2211 | 0.2593 | 0.1836 | 0.2059 |
| C6 | 0.4107 | 0.3622 | 0.2866 | 0.2266 | 0.1739 | 0.5259 | 0.3935 | 0.3802 | 0.3189 | 0.4929 | 0.5328 | 0.4798 |
| C7 | 0.1698 | 0.4483 | 0.3316 | 0.5098 | 0.4889 | 0.2438 | 0.3971 | 0.3333 | 0.4193 | 0.2920 | 0.3390 | 0.3143 |
| C8 | 0.4454 | 0.1958 | 0.1282 | 0.2451 | 0.2556 | 0.2525 | 0.2067 | 0.3333 | 0.2351 | 0.3054 | 0.2195 | 0.2059 |
| C9 | 0.3848 | 0.3558 | 0.5403 | 0.2451 | 0.2556 | 0.5037 | 0.3962 | 0.3333 | 0.3456 | 0.4026 | 0.4416 | 0.4798 |
| C10 | 0.4099 | 0.3862 | 0.4587 | 0.4343 | 0.1617 | 0.2940 | 0.2918 | 0.3333 | 0.4457 | 0.3512 | 0.3390 | 0.5098 |
| C11 | 0.2156 | 0.1968 | 0.2524 | 0.2088 | 0.3093 | 0.1719 | 0.1672 | 0.3333 | 0.2142 | 0.3584 | 0.2195 | 0.2451 |
| C12 | 0.3745 | 0.4171 | 0.2889 | 0.3570 | 0.5290 | 0.5341 | 0.5410 | 0.3333 | 0.3401 | 0.2903 | 0.4416 | 0.2451 |
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | C10 | C11 | C12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C1 | 0.0680 | 0.1127 | 0.1127 | 0.0831 | 0.0338 | 0.0631 | 0.0705 | 0.0977 | 0.1219 | 0.1575 | 0.1828 | 0.1695 |
| C2 | 0.1160 | 0.0620 | 0.0620 | 0.0400 | 0.0646 | 0.0369 | 0.0627 | 0.0560 | 0.0683 | 0.1647 | 0.1184 | 0.1110 |
| C3 | 0.1034 | 0.1127 | 0.1127 | 0.0400 | 0.0646 | 0.0631 | 0.1203 | 0.0997 | 0.0633 | 0.2171 | 0.2381 | 0.2587 |
| C4 | 0.0533 | 0.1204 | 0.1509 | 0.1611 | 0.1499 | 0.0954 | 0.1159 | 0.0720 | 0.1382 | 0.0431 | 0.0493 | 0.0547 |
| C5 | 0.1146 | 0.0614 | 0.0524 | 0.0836 | 0.1115 | 0.0547 | 0.0664 | 0.1143 | 0.0665 | 0.0451 | 0.0319 | 0.0358 |
| C6 | 0.1170 | 0.1032 | 0.0817 | 0.0717 | 0.0550 | 0.1664 | 0.1183 | 0.1143 | 0.0959 | 0.0857 | 0.0927 | 0.0834 |
| C7 | 0.0457 | 0.1208 | 0.0893 | 0.1343 | 0.1288 | 0.0642 | 0.0972 | 0.0816 | 0.1026 | 0.0433 | 0.0503 | 0.0466 |
| C8 | 0.1200 | 0.0527 | 0.0345 | 0.0646 | 0.0673 | 0.0665 | 0.0506 | 0.0816 | 0.0576 | 0.0453 | 0.0326 | 0.0305 |
| C9 | 0.1036 | 0.0958 | 0.1455 | 0.0646 | 0.0673 | 0.1327 | 0.0970 | 0.0816 | 0.0846 | 0.0597 | 0.0655 | 0.0712 |
| C10 | 0.0648 | 0.0611 | 0.0726 | 0.1116 | 0.0416 | 0.0755 | 0.0587 | 0.0671 | 0.0897 | 0.0486 | 0.0469 | 0.0706 |
| C11 | 0.0341 | 0.0311 | 0.0399 | 0.0536 | 0.0795 | 0.0442 | 0.0336 | 0.0671 | 0.0431 | 0.0496 | 0.0304 | 0.0339 |
| C12 | 0.0593 | 0.0660 | 0.0457 | 0.0917 | 0.1359 | 0.1373 | 0.1089 | 0.0671 | 0.0684 | 0.0402 | 0.0611 | 0.0339 |
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | C10 | C11 | C12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C1 | 0.1015 | 0.1015 | 0.1015 | 0.1015 | 0.1015 | 0.1015 | 0.1015 | 0.1015 | 0.1015 | 0.1015 | 0.1015 | 0.1015 |
| C2 | 0.0766 | 0.0766 | 0.0766 | 0.0766 | 0.0766 | 0.0766 | 0.0766 | 0.0766 | 0.0766 | 0.0766 | 0.0766 | 0.0766 |
| C3 | 0.1152 | 0.1152 | 0.1152 | 0.1152 | 0.1152 | 0.1152 | 0.1152 | 0.1152 | 0.1152 | 0.1152 | 0.1152 | 0.1152 |
| C4 | 0.1057 | 0.1057 | 0.1057 | 0.1057 | 0.1057 | 0.1057 | 0.1057 | 0.1057 | 0.1057 | 0.1057 | 0.1057 | 0.1057 |
| C5 | 0.0706 | 0.0706 | 0.0706 | 0.0706 | 0.0706 | 0.0706 | 0.0706 | 0.0706 | 0.0706 | 0.0706 | 0.0706 | 0.0706 |
| C6 | 0.0998 | 0.0998 | 0.0998 | 0.0998 | 0.0998 | 0.0998 | 0.0998 | 0.0998 | 0.0998 | 0.0998 | 0.0998 | 0.0998 |
| C7 | 0.0855 | 0.0855 | 0.0855 | 0.0855 | 0.0855 | 0.0855 | 0.0855 | 0.0855 | 0.0855 | 0.0855 | 0.0855 | 0.0855 |
| C8 | 0.0600 | 0.0600 | 0.0600 | 0.0600 | 0.0600 | 0.0600 | 0.0600 | 0.0600 | 0.0600 | 0.0600 | 0.0600 | 0.0600 |
| C9 | 0.0931 | 0.0931 | 0.0931 | 0.0931 | 0.0931 | 0.0931 | 0.0931 | 0.0931 | 0.0931 | 0.0931 | 0.0931 | 0.0931 |
| C10 | 0.0702 | 0.0702 | 0.0702 | 0.0702 | 0.0702 | 0.0702 | 0.0702 | 0.0702 | 0.0702 | 0.0702 | 0.0702 | 0.0702 |
| C11 | 0.0445 | 0.0445 | 0.0445 | 0.0445 | 0.0445 | 0.0445 | 0.0445 | 0.0445 | 0.0445 | 0.0445 | 0.0445 | 0.0445 |
| C12 | 0.0772 | 0.0772 | 0.0772 | 0.0772 | 0.0772 | 0.0772 | 0.0772 | 0.0772 | 0.0772 | 0.0772 | 0.0772 | 0.0772 |
References
- Jia, C.P. On glamour of TV anchors. J. Qinghai Norm. Univ. (Philos. Soc. Sci.) 2011, 33, 150–152. [Google Scholar]
- Aznárez-Mauleón, M. An approach to the host’s discursive style in Spanish “testimony” talk shows. J. Pragmat. 2013, 45, 50–73. [Google Scholar] [CrossRef]
- Wang, D. Research about the hosts of character-type talk show. J. Commun. 2015, 3, 39–44. [Google Scholar]
- Jin, S.V. “Celebrity 2.0 and beyond!” effects of Facebook profile sources on social networking advertising. Comput. Hum. Behav. 2018, 79, 154–168. [Google Scholar] [CrossRef]
- Shepherd, H.; Lane, J. In the mix: Social integration and social media adoption. Soc. Sci. Res. 2019, 82, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Hwang, K.; Zhang, Q. Influence of parasocial relationship between digital celebrities and their followers on followers’ purchase and electronic word-of-mouth intentions, and persuasion knowledge. Comput. Hum. Behav. 2018, 87, 155–173. [Google Scholar] [CrossRef]
- Pérez-Bustamante Ilander, G.O.; Marques, C.S.E.; Jalali, M.S.; Ferreira, F.A.F. The impact of continuous training in small and medium enterprises: Lessons from an industrial case analysis. J. Bus. Econ. Manag. 2016, 17, 234–250. [Google Scholar] [CrossRef]
- Wen, T.C.; Chang, K.H.; Lai, H.H. Improving personnel selection by combining the minimal variance OWA operator and IPA. J. Intell. Fuzzy Syst. 2018, 35, 6229–6239. [Google Scholar] [CrossRef]
- Gonçalves, J.M.; Ferreira, F.A.F.; Ferreira, J.J.M.; Farinha, L.M.C. A multiple criteria group decision-making approach for the assessment of small and medium-sized enterprise competitiveness. Manag. Decis. 2019, 57, 480–500. [Google Scholar] [CrossRef]
- Chang, P.L.; Hsu, C.W. An assessment model for hydrogen fuel cell applications: Fuzzy Delphi approach. Int. J. Soc. Sci. Humanit. 2011, 1, 218–223. [Google Scholar] [CrossRef]
- Chang, P.L.; Hsu, C.W.; Chang, P.C. Fuzzy Delphi method for evaluating hydrogen production technologies. Int. J. Hydrogen Energy 2011, 36, 14172–14179. [Google Scholar] [CrossRef]
- López-Ospina, H.; Quezada, L.E.; Barros-Castro, R.A.; Gonzalez, M.A.; Palominos, P.I. A method for designing strategy maps using DEMATEL and linear programming. Manag. Decis. 2017, 55, 1802–1823. [Google Scholar] [CrossRef]
- Awang, A.; Aizam, N.A.H.; Abdullah, L. An integrated decision-making method based on neutrosophic numbers for investigating factors of coastal erosion. Symmetry 2019, 11, 328. [Google Scholar] [CrossRef]
- Zhang, J. Evaluating regional low-carbon tourism strategies using the fuzzy Delphi- analytic network process approach. J. Clean. Prod. 2017, 141, 409–419. [Google Scholar] [CrossRef]
- Ballı, S.; Korukoğlu, S. Development of a fuzzy decision support framework for complex multi-attribute decision problems: A case study for the selection of skilful basketball players. Expert Syst. 2014, 31, 56–69. [Google Scholar] [CrossRef]
- Dadelo, S.; Turskis, Z.; Zavadskas, E.K.; Dadeliene, R. Multi-criteria assessment and ranking system of sport team formation based on objective-measured values of criteria set. Expert Syst. Appl. 2014, 41, 6106–6113. [Google Scholar] [CrossRef]
- Keršulienė, V.; Turskis, Z. A hybrid linguistic fuzzy multiple criteria group selection of a chief accounting officer. J. Bus. Econ. Manag. 2014, 15, 232–252. [Google Scholar] [CrossRef][Green Version]
- Chang, K.L. The use of a hybrid MCDM model for public relations personnel selection. Informatica 2015, 26, 389–406. [Google Scholar] [CrossRef]
- Chang, K.L.; Liao, S.K.; Chen, Y.C. A hybrid MCDM approach for Taiwanese tour guides selection. J. Mult.-Valued Log. Soft Comput. 2015, 25, 605–621. [Google Scholar]
- Karabasevic, D.; Stanujkic, D.; Urosevic, S.; Maksimovic, M. Selection of candidates in the mining industry based on the application of the SWARA and the MULTIMOORA methods. Acta Montan. Slovaca 2015, 20, 116–124. [Google Scholar]
- Sang, X.; Liu, X.; Qin, J. An analytical solution to fuzzy TOPSIS and its application in personnel selection for knowledge-intensive enterprise. Appl. Soft Comput. 2015, 30, 190–204. [Google Scholar] [CrossRef]
- Asuquo, D.E.; Onuodu, F.E. A fuzzy AHP model for selection of university academic staff. Int. J. Comput. Appl. 2016, 141, 19–26. [Google Scholar]
- Erdem, M.B. A fuzzy analytical hierarchy process application in personnel selection in IT companies: A case study in a spin-off company. Acta Phys. Pol. A 2016, 130, 331–334. [Google Scholar] [CrossRef]
- Karabasevic, D.; Zavadskas, E.K.; Turskis, Z.; Stanujkic, D. The framework for the selection of personnel based on the SWARA and ARAS methods under uncertainties. Informatica 2016, 27, 49–65. [Google Scholar] [CrossRef]
- Kosareva, N.; Zavadskas, E.K.; Krylovas, A.; Dadelo, S. Personnel ranking and selection problem solution by application of KEMIRA method. Int. J. Comput. Commun. Control 2016, 11, 51–66. [Google Scholar] [CrossRef]
- Stanujkic, D.; Karabasevic, D.; Zavadskas, E.K. A new approach for selecting alternatives based on the adapted weighted sum and the SWARA methods: A case of personnel selection. Econ. Comput. Econ. Cybern. Stud. Res. 2017, 51, 39–56. [Google Scholar]
- Urosevic, S.; Karabasevic, D.; Stanujkic, D.; Maksimovic, M. An approach to personnel selection in the tourism industry based on the SWARA and the WASPAS methods. Econ. Comput. Econ. Cybern. Stud. Res. 2017, 51, 75–88. [Google Scholar]
- Deliktas, D.; Üstun, Ö. Multiple criteria decision making approach for industrial engineer selection using fuzzy AHP-fuzzy TOPSIS. Anadolu Univ. J. Sci. Technol. A-Appl. Sci. Eng. 2018, 19, 58–82. [Google Scholar] [CrossRef]
- Ji, P.; Zhang, H.; Wang, J. A projection-based TODIM method under multi-valued neutrosophic environments and its application in personnel selection. Neural Comput. Appl. 2018, 29, 221–234. [Google Scholar] [CrossRef]
- Ding, J.F.; Kuo, J.F.; Tai, W.H. A fuzzy evaluation model of choosing a middle manager for an international shipping service provider. Brodogradnja 2019, 70, 93–107. [Google Scholar] [CrossRef]
- Liao, S.K.; Hsu, H.Y.; Chang, K.L. A novel hybrid MCDM model to select celebrity endorser for airlines. J. Mult.-Valued Log. Soft Comput. 2019, 32, 477–497. [Google Scholar]
- Nabeeh, N.A.; Smarandache, F.; Abdel-Basset, M.; El-Ghareeb, H.A.; Aboelfetouh, A. An integrated neutrosophic-TOPSIS approach and its application to personnel selection: A new trend in brain processing and analysis. IEEE Access 2019, 7, 29734–29744. [Google Scholar] [CrossRef]
- Pehlivan, N.Y.; Ünal, Y.; Kahraman, C. Player selection for a national football team using fuzzy AHP and fuzzy TOPSIS. J. Mult.-Valued Log. Soft Comput. 2019, 32, 369–405. [Google Scholar]
- Yalçın, N.; Pehlivan, N.Y. Application of the fuzzy CODAS method based on fuzzy envelopes for hesitant fuzzy linguistic term sets: A case study on a personnel selection problem. Symmetry 2019, 11, 493. [Google Scholar] [CrossRef]
- Carayannis, E.G.; Ferreira, J.J.M.; Jalali, M.S.; Ferreira, F.A.F. MCDA in knowledge-based economies: Methodological developments and real world applications. Technol. Forecast. Soc. Chang. 2018, 131, 1–3. [Google Scholar] [CrossRef]
- Ferreira, F.A.F.; Marques, C.S.E.; Reis, M.M.; Ferreira, N.C.M.Q.F.; Çipi, A. Evolutionary patterns and development prospects for e-government: A Delphi-based approach to perceptions of the administrative agent. J. Bus. Econ. Manag. 2015, 16, 18–36. [Google Scholar] [CrossRef][Green Version]
- Dalkey, N.; Helmer, O. An experimental application of the Delphi method to the use of experts. Manag. Sci. 1963, 9, 458–467. [Google Scholar] [CrossRef]
- Ferreira, F.A.F.; Santos, S.P. Comparing trade-off adjustments in credit risk analysis of mortgage loans using AHP, Delphi and MACBETH. Int. J. Strateg. Prop. Manag. 2016, 20, 44–63. [Google Scholar] [CrossRef]
- Kuo, Y.F.; Chen, P.C. Constructing performance appraisal indicators for mobility of the service industries using fuzzy Delphi method. Expert Syst. Appl. 2008, 35, 1930–1939. [Google Scholar] [CrossRef]
- Hsu, Y.L.; Lee, C.H.; Kreng, V.B. The application of Fuzzy Delphi Method and Fuzzy AHP in lubricant regenerative technology selection. Expert Syst. Appl. 2010, 37, 419–425. [Google Scholar] [CrossRef]
- Dong, J.; Huo, H.; Liu, D.; Li, R. Evaluating the comprehensive performance of demand response for commercial customers by applying combination weighting techniques and fuzzy VIKOR approach. Sustainability 2017, 9, 1332. [Google Scholar] [CrossRef]
- Murray, T.J.; Pipino, L.L.; van Gigch, J.P. A pilot study of fuzzy set modification of Delphi. Hum. Syst. Manag. 1985, 5, 76–80. [Google Scholar] [CrossRef]
- Ishikawa, A.; Amagasa, M.; Shiga, T.; Tomizawa, G.; Tatsuta, R.; Mieno, H. The max-min Delphi method and fuzzy Delphi method via fuzzy integration. Fuzzy Sets Syst. 1993, 55, 241–253. [Google Scholar] [CrossRef]
- Hsu, T.H.; Yang, T.H. Application of fuzzy analytic hierarchy process in the selection of advertising media. J. Manag. Syst. 2000, 7, 19–40. [Google Scholar]
- Chang, H.Y.; Wu, M.Y.; Sheu, D.F. Perceptions of intellectual capital held by the supervisors of nursing divisions in hospitals in Taiwan. Manag. Decis. 2014, 52, 1101–1115. [Google Scholar] [CrossRef]
- Hwang, K.P.; Lin, C.K.; Hsu, C.H. A joint fuzzy AHP approach in prioritizing urban off-street parking sites. J. Chin. Inst. Transp. 2005, 17, 281–304. [Google Scholar]
- Wu, H.Y. Constructing a strategy map for banking institutions with key performance indicators of the balanced scorecard. Eval. Program Plan. 2012, 35, 303–320. [Google Scholar] [CrossRef]
- Liao, S.K.; Hsu, H.Y.; Chang, K.L. A hybrid multiple criteria decision making model for selecting the location of women’s fitness centers. Math. Probl. Eng. 2018, 2018, 9780565. [Google Scholar] [CrossRef]
- Liao, S.K.; Hsu, H.Y.; Chang, K.L. OTAs selection for hot spring hotels by a hybrid MCDM model. Math. Probl. Eng. 2019, 2019, 4251362. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, Y.; Liu, Y.; Tzeng, G.H. Improving sustainable mobile health care promotion: A novel hybrid MCDM method. Sustainability 2019, 11, 752. [Google Scholar] [CrossRef]
- Si, S.L.; You, X.Y.; Liu, H.C.; Zhang, P. DEMATEL technique: A systematic review of the state-of-the-art literature on methodologies and applications. Math. Probl. Eng. 2018, 2018, 3696457. [Google Scholar] [CrossRef]
- Saaty, T.L. Decision Making with Dependence and Feedback: The Analytic Network Process; RWS Publication: Pittsburgh, PA, USA, 1996. [Google Scholar]
- Sipahi, S.; Timor, M. The analytic hierarchy process and analytic network process: An overview of applications. Manag. Decis. 2010, 48, 775–808. [Google Scholar] [CrossRef]
- Hwang, C.L.; Yoon, K. Multiple Attribute Decision Making, Methods and Applications, Lecture Notes in Economics and Mathematical Systems, 186; Springer: New York, NY, USA, 1981. [Google Scholar]
- Chen, Y.C.; Yang, C.H.; Chang, K.L. Applying fuzzy multi-criteria decision method to the evaluation of the hosts of Taiwan TV-shopping channels. J. Commun. Manag. 2007, 8, 1–22. [Google Scholar]
- Liao, S.K.; Chang, K.L. Select televised sportscasters for Olympic Games by analytic network process. Manag. Decis. 2009, 47, 14–23. [Google Scholar] [CrossRef][Green Version]
- Chang, K.L. Selecting the hosts of Taiwan TV-shopping channels by analytic network process. J. Hum. Resour. Adult Learn. 2007, 3, 103–107. [Google Scholar]
- Ziemba, P. Inter-criteria dependencies-based decision support in the sustainable wind energy management. Energies 2019, 12, 749. [Google Scholar] [CrossRef]
- Ziemba, P.; Wątróbski, J.; Zioło, M.; Karczmarczyk, A. Using the PROSA method in offshore wind farm location problems. Energies 2017, 10, 1755. [Google Scholar] [CrossRef]
| Year | Contributor(s) | Topic | Applied Method(s) |
|---|---|---|---|
| 2014 | Ballı and Korukoğlu [15] | Basketball player | Fuzzy analytic hierarchy process (FAHP) and TOPSIS |
| 2014 | Dadelo et al. [16] | Professional basketball player | Wisdom-of-crowds principles and TOPSIS |
| 2014 | Keršulienė and Turskis [17] | Chief accounting officer | Principles of fusion of fuzzy information, additive ratio assessment with fuzzy numbers (ARAS-F), fuzzy weighted-product model, and analytic hierarchy process (AHP) |
| 2015 | Chang [18] | Public relations personnel | The fuzzy Delphi method, ANP, and TOPSIS |
| 2015 | Chang et al. [19] | Tour guide | The fuzzy Delphi method, ANP, and TOPSIS |
| 2015 | Karabasevic et al. [20] | Mining engineer | Step-wise weight assessment ratio analysis (SWARA) and multi-objective optimization by ratio analysis plus the full multiplicative form (MULTIMOORA) |
| 2015 | Sang et al. [21] | System analyst engineer | Fuzzy TOPSIS (FTOPSIS) based on the Karnik–Mendel (KM) algorithm |
| 2016 | Asuquo and Onuodu [22] | Academic staff | FAHP |
| 2016 | Erdem [23] | Information technology personnel (Junior developer) | FAHP |
| 2016 | Karabasevic et al. [24] | Sales manager | SWARA and additive ratio assessment (ARAS) |
| 2016 | Kosareva et al. [25] | Security guard | KEmeny Median Indicator Rank Accordance (KEMIRA) |
| 2017 | Stanujkic et al. [26] | Promoter | New approach based on adapted weighted sum and SWARA |
| 2017 | Urosevic et al. [27] | Sales manager | SWARA and weighted aggregates sum product assessment (WASPAS) |
| 2018 | Deliktas and Üstun [28] | Industrial engineers | FAHP and FTOPSIS |
| 2018 | Ji et al. [29] | Sales supervisor | Projection-based an acronym in Portuguese of interactive and multi-criteria decision-making (TODIM) |
| 2019 | Ding et al. [30] | Middle manager | Fuzzy MCDM |
| 2019 | Liao et al. [31] | Celebrity endorser | The fuzzy Delphi method, DEMATEL, ANP, and TOPSIS |
| 2019 | Nabeeh et al. [32] | Manager | Neutrosophic AHP and TOPSIS |
| 2019 | Pehlivan et al. [33] | National football team player | FAHP, FTOPSIS, and integrated these two methods |
| 2019 | Yalçın and Pehlivan [34] | Blue-collar personnel | Fuzzy COmbinative Distance-based Assessment (CODAS) method using the fuzzy envelopes of the hesitant fuzzy linguistic term sets (HFLTSs) based on comparative linguistic expressions (CLEs) |
| Criteria | Geometric Mean |
|---|---|
| Expertise | 6.4007 |
| Experience | 7.4466 |
| Education | 6.1803 |
| Appearance | 6.2223 |
| Ability to follow orders | 6.1803 |
| Confidence | 6.1672 |
| Expression | 7.2107 |
| Response | 7.2381 |
| Desire of performance | 5.8800 |
| Living experience | 5.6806 |
| Familiarity | 7.4449 |
| Creativity | 6.2953 |
| Adaptation to company | 5.3741 |
| Teamwork | 6.2518 |
| Interpersonal skill | 6.1682 |
| Adaptation to environment | 6.0776 |
| Attitude | 7.4172 |
| Language | 5.6714 |
| Likeability | 7.4570 |
| Emotion | 7.3461 |
| Cost | 7.4939 |
| Match | 7.9214 |
| YouTube (number of views) | 7.8596 |
| YouTube (number of subscriptions) | 6.9637 |
| Facebook (number of fans) | 7.3322 |
| Facebook (number of posts shared) | 7.0743 |
| 7.6511 |
| Perspective | Criteria | Definition | Contributors |
|---|---|---|---|
| Person | C1: Familiarity | Familiarity to the target audience. | [3,55] |
| C2: Likeability | Likeability to the target audience. | Executive proposed | |
| C3: Attitude | Conscientious toward the work. | [55,56] | |
| Profession | C4: Expression | Expression ability. | [3,55,56,57] |
| C5: Emotion | Emotional steadiness. | Executive proposed | |
| C6: Response | React appropriately to the emergency. | [55,56,57] | |
| Program | C7: Experience | Hosting experience. | [55] |
| C8: Cost | Cost of acquiring the host. | Executive proposed | |
| C9: Match | Match between host and program. | Executive proposed | |
| Promotion | C10: YouTube | Views of the host’s YouTube channel. | Executive proposed |
| C11: Facebook | The number of people in the host’s Facebook fan page. | Executive proposed | |
| C12: Instagram | The number of fans in the host’s Instagram. | Executive proposed |
| Perspectives | Person | Profession | Program | Promotion |
|---|---|---|---|---|
| Person | 0.000 | 4.000 | 3.000 | 3.333 |
| Profession | 4.000 | 0.000 | 3.333 | 3.000 |
| Program | 3.000 | 3.333 | 0.000 | 3.000 |
| Promotion | 4.000 | 3.333 | 3.000 | 0.000 |
| Perspectives | Person | Profession | Program | Promotion |
|---|---|---|---|---|
| Person | 11.4600 | 11.4977 | 10.3333 | 10.3574 |
| Profession | 11.7174 | 11.1985 | 10.3333 | 10.3213 |
| Program | 10.8056 | 10.6011 | 9.3333 | 9.5634 |
| Promotion | 11.7402 | 11.4635 | 10.3333 | 10.1153 |
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | C10 | C11 | C12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A1 | 0.5972 | 0.6466 | 0.6420 | 0.6099 | 0.6191 | 0.6206 | 0.6025 | 0.5774 | 0.6041 | 0.7665 | 0.7786 | 0.7647 |
| A2 | 0.4708 | 0.5084 | 0.5541 | 0.5365 | 0.5408 | 0.5123 | 0.5235 | 0.5774 | 0.5489 | 0.4707 | 0.4438 | 0.4557 |
| A3 | 0.6494 | 0.5687 | 0.5300 | 0.5833 | 0.5694 | 0.5936 | 0.6025 | 0.5774 | 0.5778 | 0.4369 | 0.4438 | 0.4557 |
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | C10 | C11 | C12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A1 | 0.0606 | 0.0496 | 0.0740 | 0.0645 | 0.0437 | 0.0619 | 0.0515 | 0.0346 | 0.0563 | 0.0538 | 0.0347 | 0.0590 |
| A2 | 0.0478 | 0.0390 | 0.0638 | 0.0567 | 0.0382 | 0.0511 | 0.0448 | 0.0346 | 0.0511 | 0.0331 | 0.0198 | 0.0352 |
| A3 | 0.0659 | 0.0436 | 0.0610 | 0.0617 | 0.0402 | 0.0592 | 0.0515 | 0.0346 | 0.0538 | 0.0307 | 0.0198 | 0.0352 |
| Rank | ||||
|---|---|---|---|---|
| A1 | 0.0053 | 0.0453 | 0.8953 | 1 |
| A2 | 0.0452 | 0.0037 | 0.0747 | 3 |
| A3 | 0.0395 | 0.0223 | 0.3607 | 2 |
| Weights From ANP | ANP-TOPSIS | |||
|---|---|---|---|---|
| Min | Max | Range | ||
| C1 | 0.10 | 0.00 | 0.32 | 0.32 |
| C2 | 0.08 | 0.00 | 0.57 | 0.57 |
| C3 | 0.12 | 0.00 | 0.45 | 0.45 |
| C4 | 0.11 | 0.00 | 0.55 | 0.55 |
| C5 | 0.07 | 0.00 | 0.51 | 0.51 |
| C6 | 0.10 | 0.00 | 0.54 | 0.54 |
| C7 | 0.09 | 0.00 | 0.53 | 0.53 |
| C8 | 0.06 | 0.00 | 0.50 | 0.50 |
| C9 | 0.09 | 0.00 | 0.53 | 0.53 |
| C10 | 0.07 | 0.00 | 0.40 | 0.40 |
| C11 | 0.04 | 0.00 | 0.48 | 0.48 |
| C12 | 0.08 | 0.00 | 0.52 | 0.52 |
| Weights From AHP | AHP-TOPSIS | |||
|---|---|---|---|---|
| Min | Max | Range | ||
| C1 | 0.05 | 0.00 | 0.38 | 0.38 |
| C2 | 0.03 | 0.00 | 0.36 | 0.36 |
| C3 | 0.09 | 0.00 | 0.31 | 0.31 |
| C4 | 0.12 | 0.00 | 0.45 | 0.45 |
| C5 | 0.07 | 0.00 | 0.40 | 0.40 |
| C6 | 0.12 | 0.00 | 0.45 | 0.45 |
| C7 | 0.10 | 0.00 | 0.43 | 0.43 |
| C8 | 0.05 | 0.00 | 0.38 | 0.38 |
| C9 | 0.10 | 0.00 | 0.43 | 0.43 |
| C10 | 0.13 | 0.00 | 0.24 | 0.24 |
| C11 | 0.06 | 0.00 | 0.39 | 0.39 |
| C12 | 0.06 | 0.00 | 0.39 | 0.39 |
| Approach | Rank |
|---|---|
| AHP | A1 > A3 > A2 |
| AHP and TOPSIS | A1 > A3 > A2 |
| ANP | A1 > A3 > A2 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, L.-C.; Chang, K.-L.; Liao, S.-K. A Hybrid MCDM Model to Select Optimal Hosts of Variety Shows in the Social Media Era. Symmetry 2020, 12, 125. https://doi.org/10.3390/sym12010125
Wu L-C, Chang K-L, Liao S-K. A Hybrid MCDM Model to Select Optimal Hosts of Variety Shows in the Social Media Era. Symmetry. 2020; 12(1):125. https://doi.org/10.3390/sym12010125
Chicago/Turabian StyleWu, Lee-Chun, Kuei-Lun Chang, and Sen-Kuei Liao. 2020. "A Hybrid MCDM Model to Select Optimal Hosts of Variety Shows in the Social Media Era" Symmetry 12, no. 1: 125. https://doi.org/10.3390/sym12010125
APA StyleWu, L.-C., Chang, K.-L., & Liao, S.-K. (2020). A Hybrid MCDM Model to Select Optimal Hosts of Variety Shows in the Social Media Era. Symmetry, 12(1), 125. https://doi.org/10.3390/sym12010125





