Critical Nodes Identification in Complex Networks
Abstract
:1. Introduction
- (1)
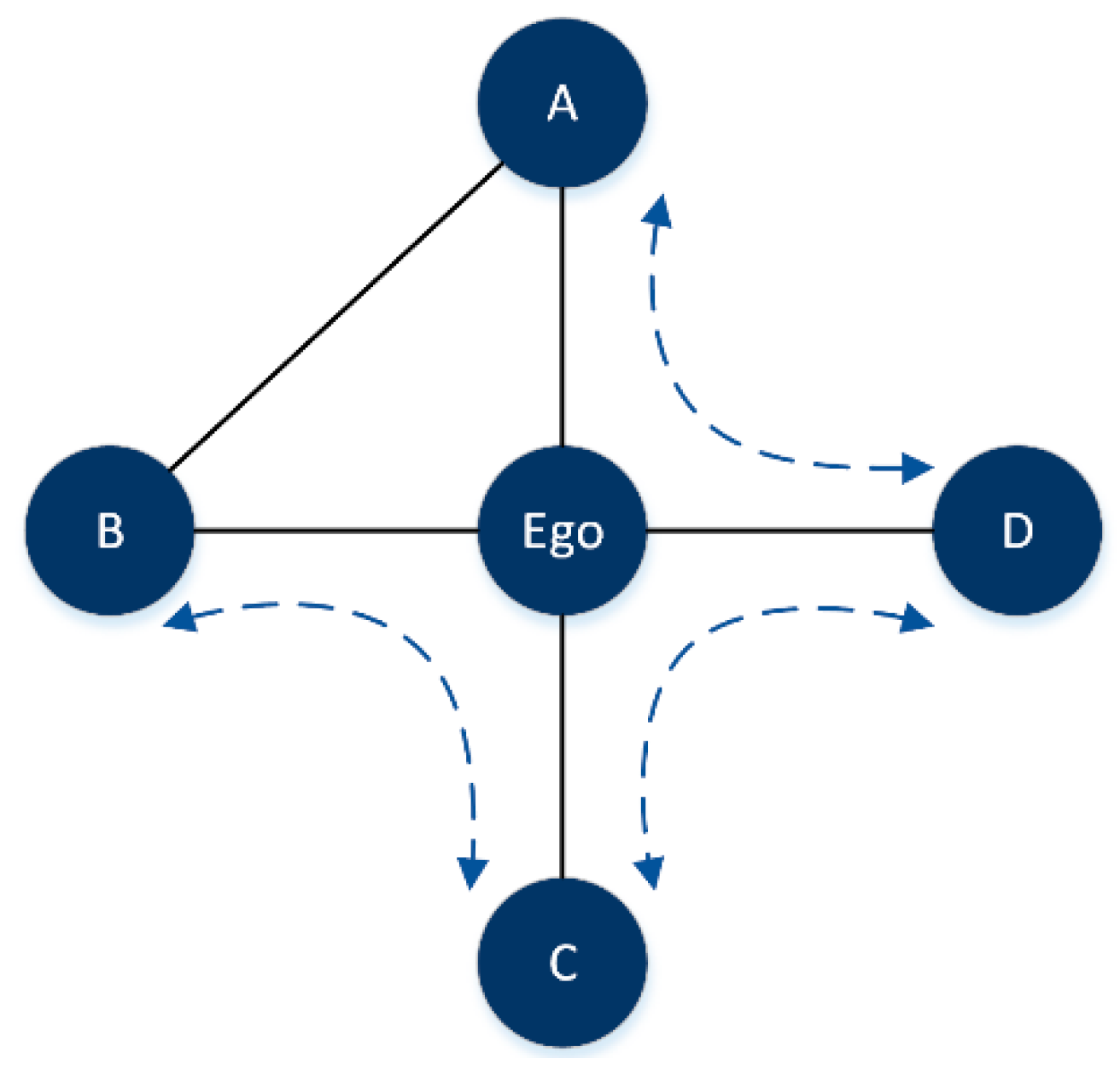
- We draw inspiration from the theory of structural holes [33] and only consider the node’s local neighborhood information to evaluate the importance of nodes. This makes the algorithm more computationally attractive for large-scale networks;
- (2)
- The proposed algorithm can effectively identify the hubs with numerous structural holes, which play important role in bridging different clusters of the network;
- (3)
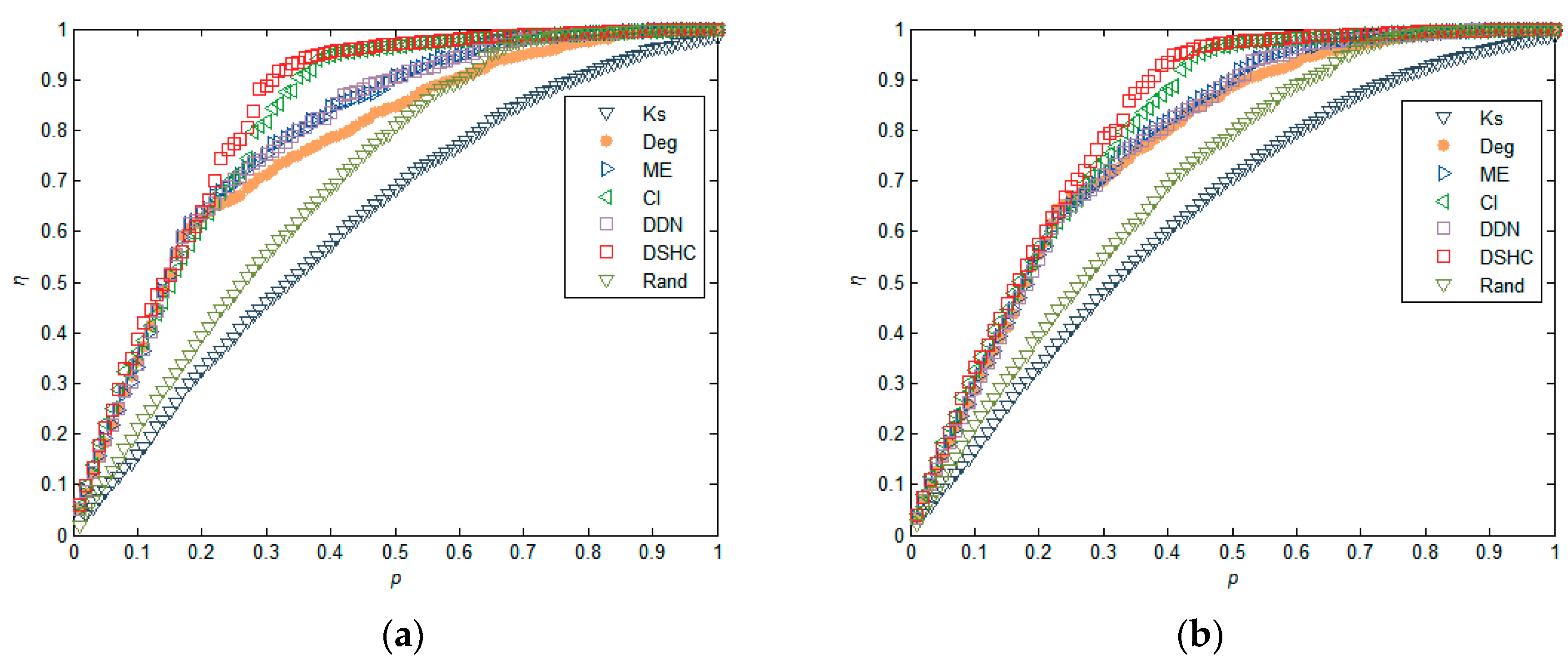
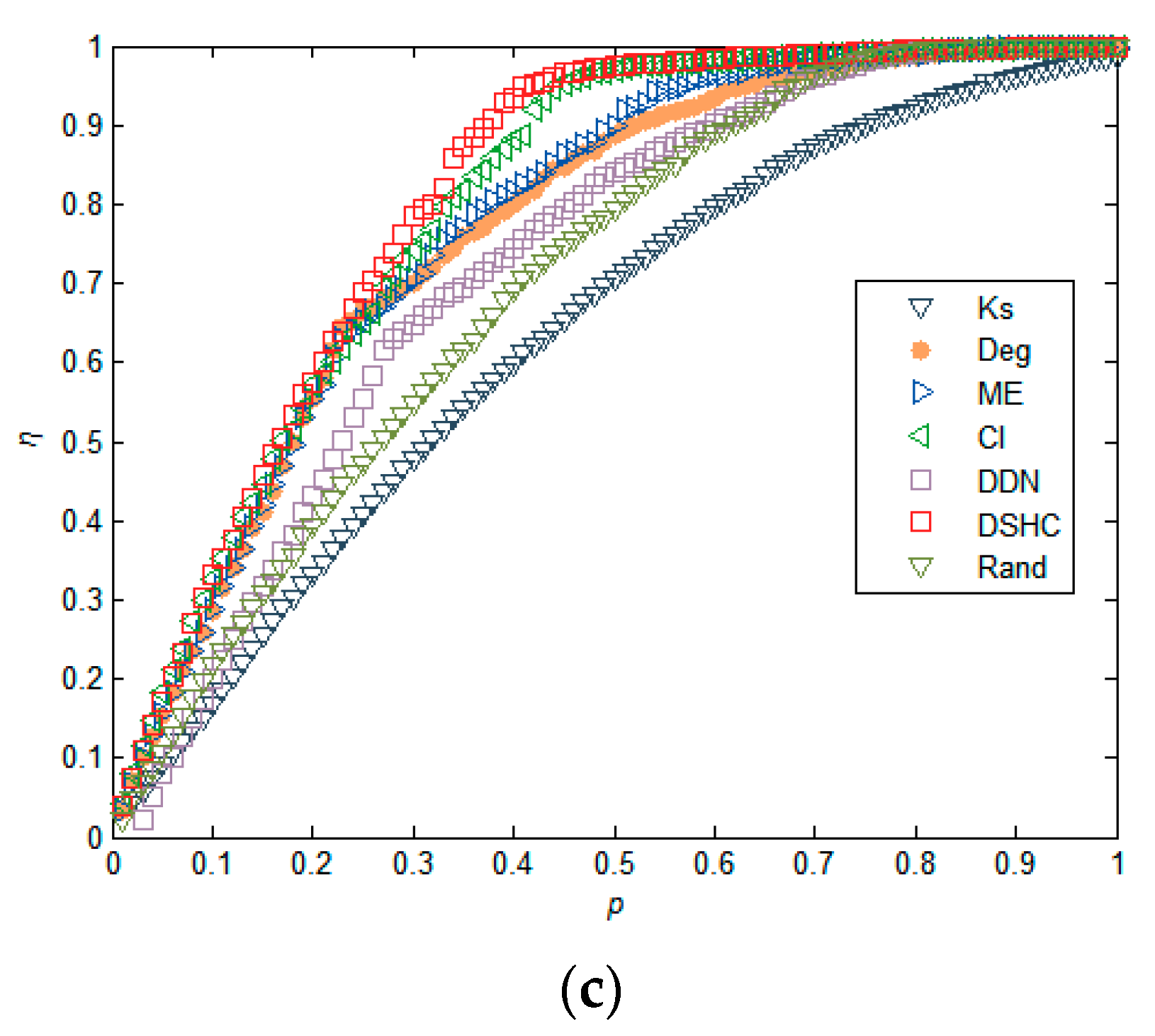
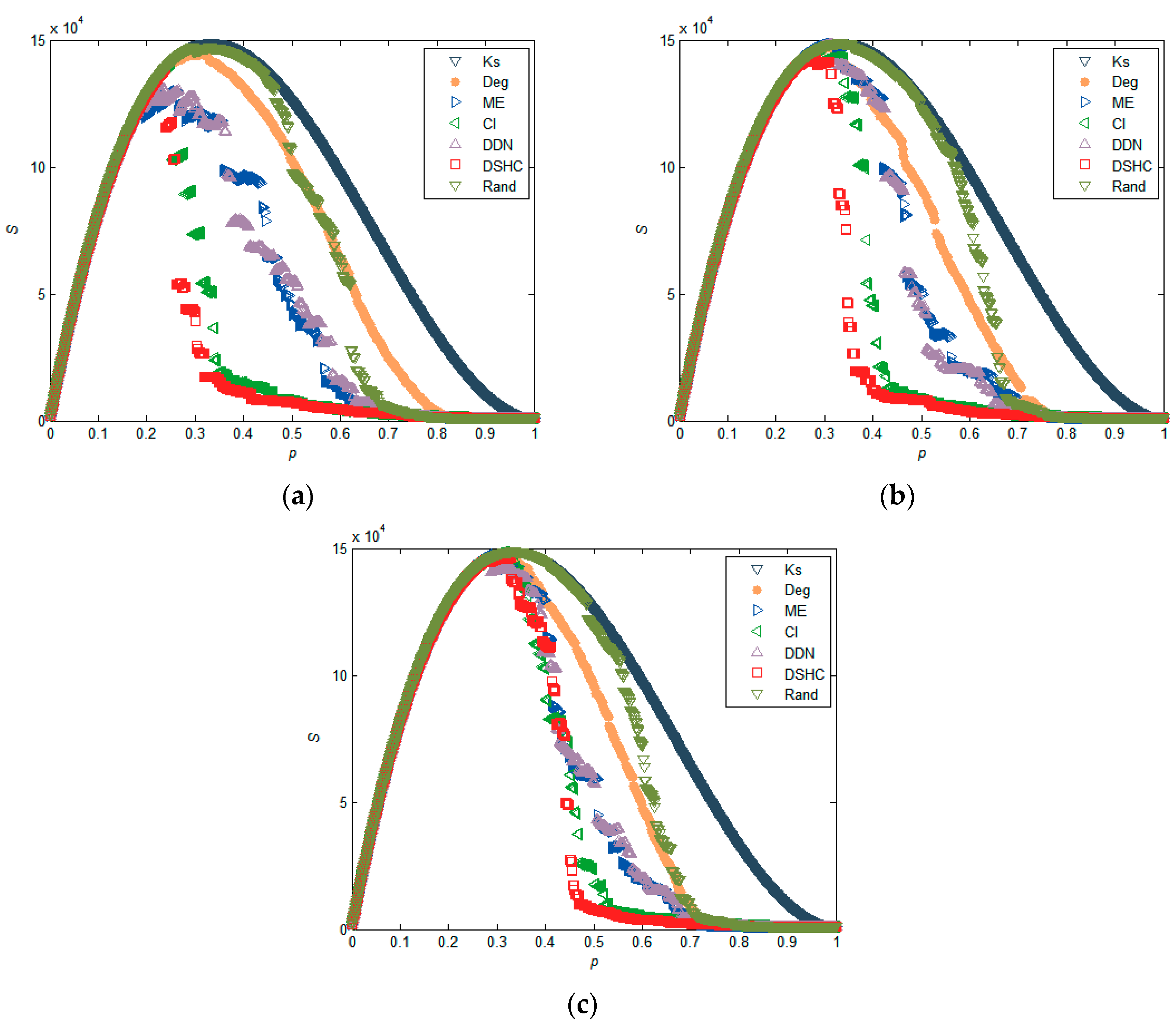
- Empirical analyses on real and synthetic networks demonstrate that the proposed method can outperform Deg, k-shell, ME, CI, DDN [34], and random ranking method (Rand).
2. Materials and Methods
2.1. Measurement of Node Importance Based on Degree and Structural Hole Count
| Algorithm 1 the DSHC Method |
| Input: Network adjacency matrix A(aij), degree of network nodes k, the size of network N |
| Output: The DSHC value of each node |
| 1: for i = 1 to N |
| 2: Si = find (A(aij) =1) // Find the neighbors Si of node i |
| 3: len(Si) = length(Si) // Number of neighbors of node i |
| 4: for j = 1:len(Si) |
| 5: Si_j= find (A(ajk) =1) // Find the neighbors Si_j of neighbor j of node i |
| 6: Δij= |Si_j - intersect(Si, Si_j)| // calculate the number of structural holes formed between node i and j with node i as the intermediary |
| 7: |
| 8: end for |
| 9: DSHCi = sum(DSHCi_j) // according to Equation(1) |
| 10: end for |
| 11: Return DSHC value of each node |
2.2. Benchmark Methods
3. How to Evaluate the Performance
4. Data Description
5. Results and Analysis
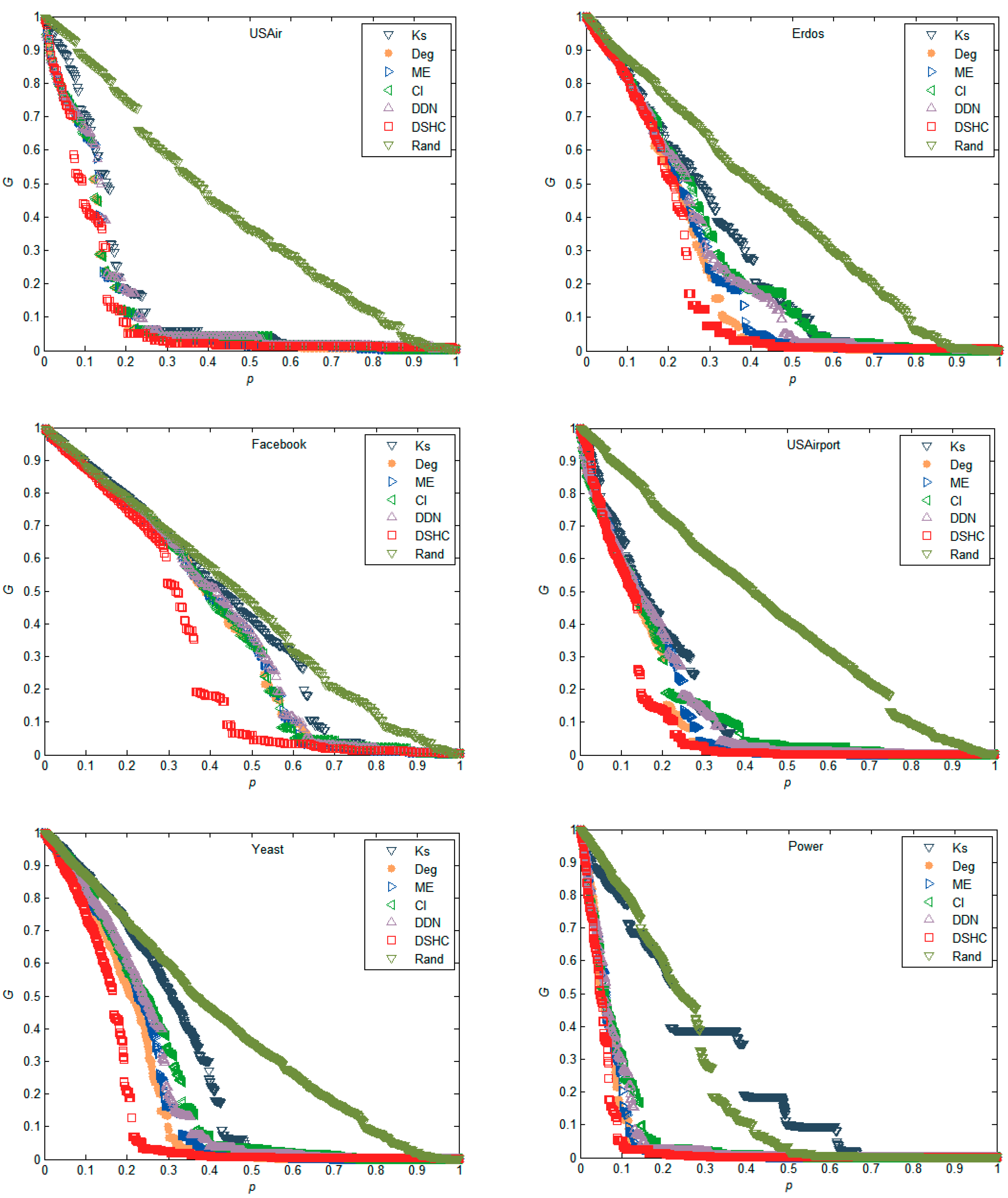
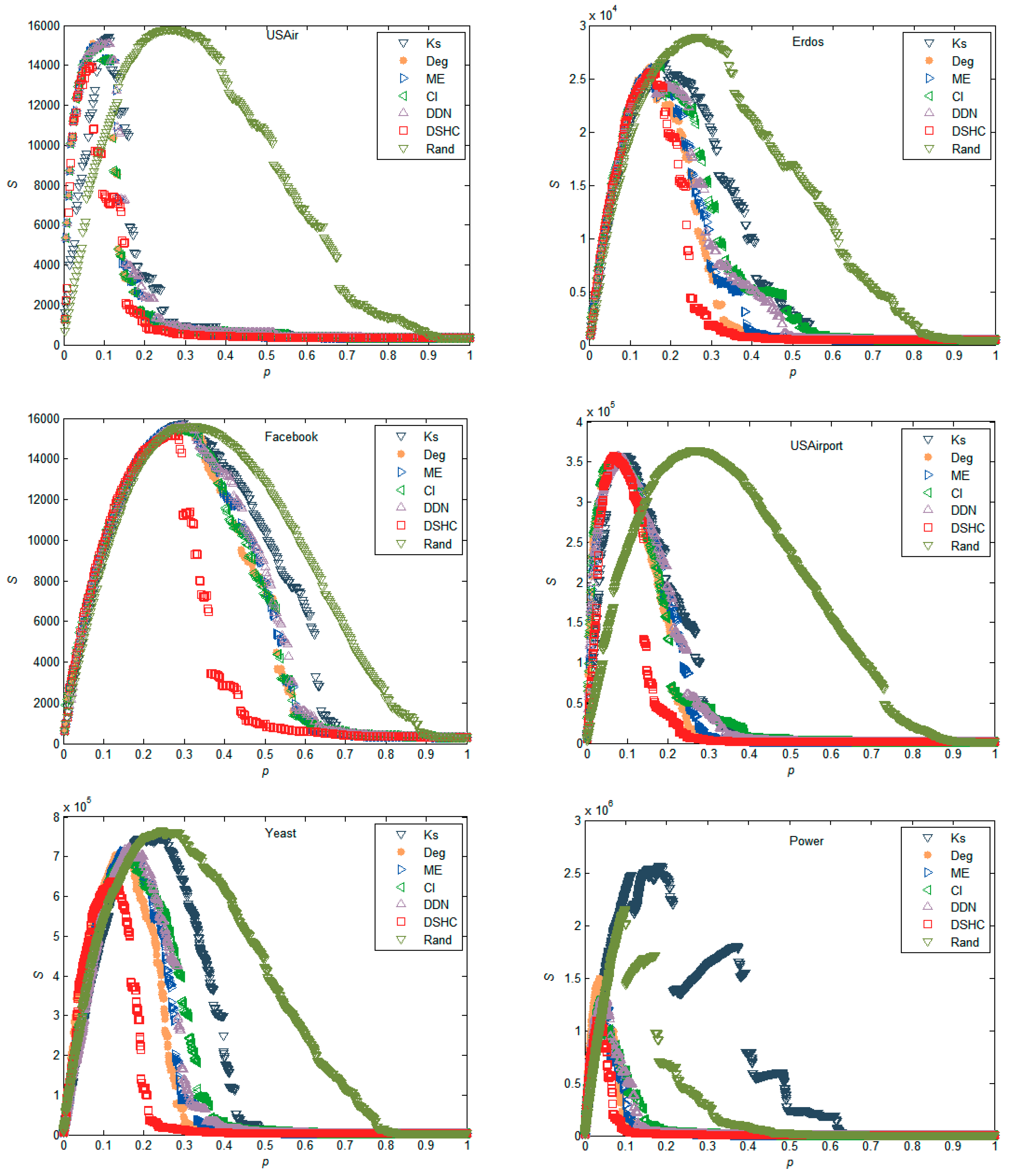
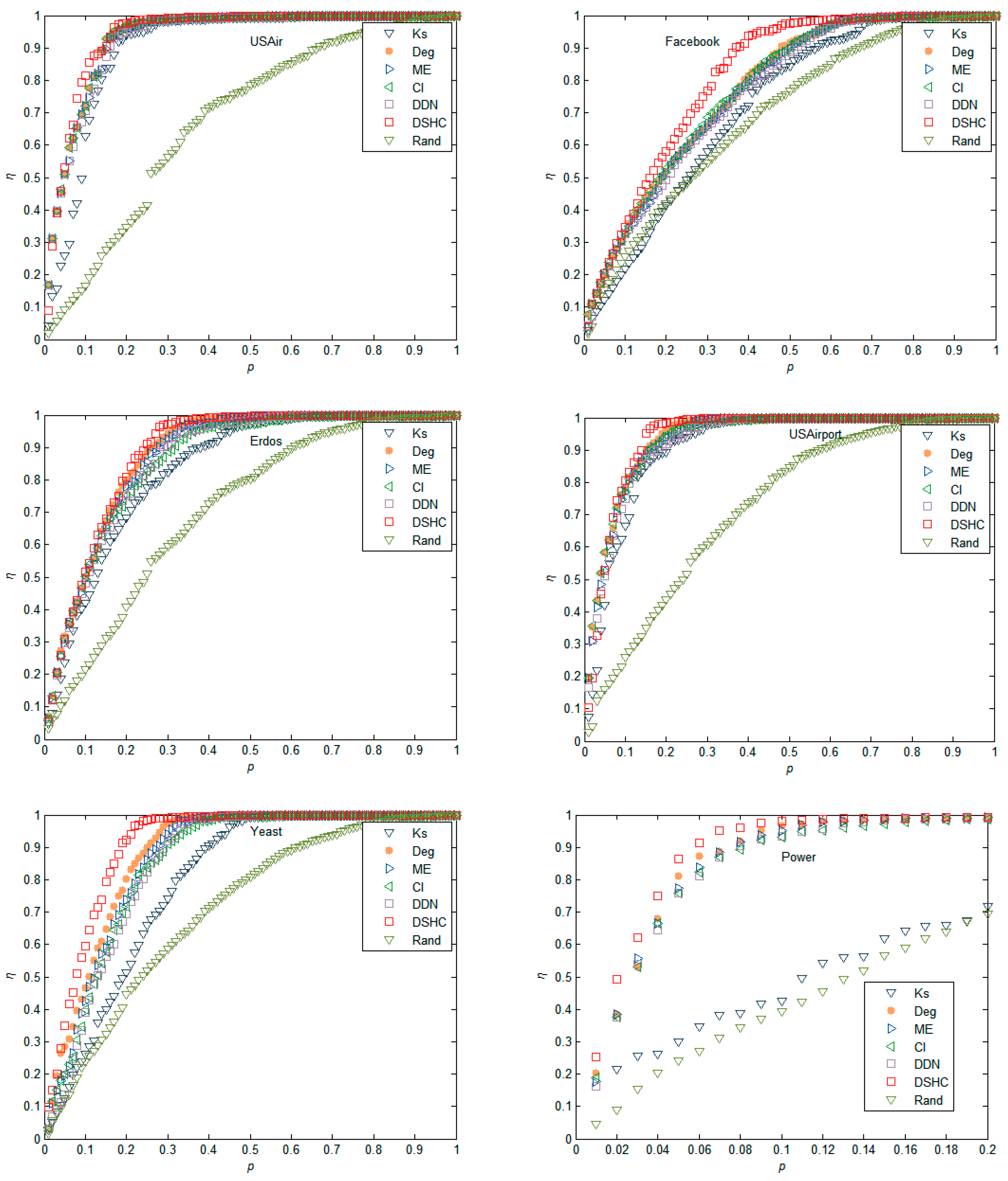
5.1. Experiments in Real Networks
5.2. Experiments in Synthetic Networks
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lü, L.Y.; Chen, D.B.; Ren, X.L.; Zhang, Q.M.; Zhou, T. Vital nodes identification in complex networks. Phys. Rep. 2016, 650, 1–63. [Google Scholar] [CrossRef] [Green Version]
- Albert, R.; Barabási, A.L. Statistical mechanics of complex networks. Rev. Mod. Phys. 2002, 74, 47–97. [Google Scholar] [CrossRef] [Green Version]
- Amini, M.H.; Arasteh, H.; Siano, P. Sustainable smart cities through the lens of complex interdependent infrastructures: Panorama and state-of-the-art. In Sustainable Interdependent Networks II; Springer: Cham, Switzerland, 2019; pp. 45–68. [Google Scholar]
- Liu, J.G.; Ren, Z.M.; Guo, Q.; Wang, B.H. Node importance ranking of complex networks. Acta Phys. Sin. 2013, 62, 178901. [Google Scholar]
- Wang, X.F.; Li, X.; Chen, G.R. Complex Networks Theory and Its Application; Tsinghua University Press: Beijing, China, 2006; pp. 1–100. [Google Scholar]
- Yu, C.H.; Doppler, K.; Ribeiro, C.B.; Tirkkonen, O. Resource sharing optimization for device-to-device communication underlaying cellular networks. IEEE Trans. Wirel. Commun. 2011, 10, 2752–2763. [Google Scholar]
- Liu, H.K.; Zhou, T. Empirical study of Chinese city airline network. Acta Phys. Sin. 2007, 56, 106–111. [Google Scholar]
- Zhao, Y.; Du, W.; Chen, S. Application of complex network theory to Urban transportation network analysis. Urban Transp. China 2009, 7, 57–65. [Google Scholar]
- Cai, K.Q.; Zhang, J.; Du, W.B.; Cao, X.B. Analysis of the Chinese air route network as a complex network. Chin. Phys. B 2012, 21, 028903. [Google Scholar] [CrossRef]
- Watts, D.J.; Dodds, P.S.; Newman, M.E.J. Identity and search in social networks. Science 2012, 296, 1302–1305. [Google Scholar] [CrossRef] [Green Version]
- Fang, X.; Misra, S.; Xue, G.; Yang, D. Smart grid—The new and improved power grid: A survey. IEEE Commun. Surv. Tutor. 2012, 14, 944–980. [Google Scholar] [CrossRef]
- Callaway, D.S.; Newman, M.E.J.; Strogatz, S.H.; Watts, D.J. Network Robustness and Fragility: Percolation on Random Graphs. Phys. Rev. Lett. 2000, 85, 5468. [Google Scholar] [CrossRef] [Green Version]
- Cohen, R.; Erez, K.; ben-Avraham, D.; Havlin, S. Breakdown of the Internet under Intentional Attack. Phys. Rev. Lett. 2001, 86, 3682. [Google Scholar] [CrossRef] [Green Version]
- Hao, Y.H.; Han, J.H.; Lin, Y.; Liu, L. Vulnerability of complex networks under three-level-tree attacks. Physica A 2016, 462, 674–683. [Google Scholar] [CrossRef]
- Ruan, Y.R.; Lao, S.Y.; Wang, J.D.; Bai, L.; Chen, L.D. Node importance measurement based on neighborhood similarity in complex network. Acta Phys. Sin. 2017, 66, 38902. [Google Scholar]
- Ruan, Y.R.; Lao, S.Y.; Xiao, Y.D.; Wang, J.D.; Bai, L. Identifying influence of nodes in complex networks with coreness centrality: Decreasing the impact of densely local connection. Chin. Phys. Lett. 2016, 33, 028901. [Google Scholar]
- Albert, R.; Jeong, H.; Barabási, A.L. Internet: Diameter of the world-wide web. Nature 1999, 401, 130–131. [Google Scholar] [CrossRef] [Green Version]
- Nie, T.Y.; Guo, Z.; Zhao, K.; Lu, Z.M. Using mapping entropy to identify node centrality in complex networks. Physica A 2016, 453, 290–297. [Google Scholar] [CrossRef]
- Morone, F.; Makse, H.A. Influence maximization in complex networks through optimal percolation. Nature 2015, 524, 65–68. [Google Scholar] [CrossRef] [Green Version]
- Chen, D.B.; Lü, L.Y.; Shang, M.S.; Zhang, Y.C.; Zhou, T. Identifying influential nodes in complex networks. Physica A 2012, 391, 1777–1787. [Google Scholar] [CrossRef] [Green Version]
- Bae, J.; Kim, S. Identifying and ranking influential spreaders in complex networks by neighborhood coreness. Physica A 2014, 395, 549–559. [Google Scholar] [CrossRef]
- Lü, L.Y.; Zhou, T.; Zhang, Q.-M.; Stanley, H.E. The h-index of a network node and its relation to degree and coreness. Nat. Commun. 2016, 7, 10168. [Google Scholar] [CrossRef] [Green Version]
- Hage, P.; Harary, F. Eccentricity and centrality in networks. Soc. Netw. 1995, 17, 57–63. [Google Scholar] [CrossRef]
- Stephenson, K.; Zelen, M. Rethinking centrality: Methods and examples. Soc. Netw. 1989, 11, 1–37. [Google Scholar] [CrossRef]
- Katz, L. A new status index derived from sociometric analysis. Psychometrika 1953, 18, 39–43. [Google Scholar] [CrossRef]
- Sabidussi, G. The centrality index of a graph. Psychometrika 1996, 31, 581–603. [Google Scholar] [CrossRef] [PubMed]
- Estrada, E.; Rodriguez-Velazquez, J.A. Subgraph centrality in complex networks. Phys. Rev. E 2005, 71, 056103. [Google Scholar] [CrossRef] [Green Version]
- Brin, S.; Page, L. The anatomy of a large-scale hypertextual web search engine. Web Conf. 1998, 30, 107–117. [Google Scholar] [CrossRef]
- Kleinberg, J.M. Authoritative sources in a hyperlinked environment. J. ACM 1999, 46, 604–632. [Google Scholar] [CrossRef]
- Bonacich, P. Factoring and weighting approaches to status scores and clique identification. J. Math. Sociol. 1972, 2, 113–120. [Google Scholar] [CrossRef]
- Lü, L.Y.; Zhang, Y.C.; Yeung, C.H.; Zhou, T. Leaders in social networks, the delicious case. PLoS ONE 2011, 6, e21202. [Google Scholar] [CrossRef] [Green Version]
- Weng, J.; Lim, E.P.; Jiang, J.; He, Q. Twitterrank: Finding topic-sensitive influential twitterers. In Third ACM International Conference on Web Search and Data Mining; ACM Press: New York, NY, USA, 2010; pp. 261–270. [Google Scholar]
- Burt, R.S. Structural Holes: The Social Structure of Competition; Harvard University Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Wang, J.W.; Rong, L.L.; Guo, T.Z. A new measure method of network node importance based on local characteristics. J. Dalian Univ. Technol. 2010, 50, 822–826. [Google Scholar]
- Kitsak, M.; Gallos, L.K.; Havlin, S.; Liljeros, F.; Muchnik, L.; Eugene Stanley, H.; Makse, H.A. Identification of influential spreaders in complex networks. Nat. Phys. 2010, 6, 888–893. [Google Scholar] [CrossRef] [Green Version]
- Cheng, X.Q.; Ren, F.X.; Shen, H.W.; Zhang, Z.K.; Zhou, T. Bridgeness: A local index on edge significance in maintaining global connectivity. J. Stat. Mech. Theory Exp. 2010, 10, 10011. [Google Scholar] [CrossRef] [Green Version]
- Dereich, S.; Mörters, P. Random networks with sublinear preferential attachment: The giant component. Ann. Probab. 2013, 41, 329–384. [Google Scholar] [CrossRef] [Green Version]
- Vragovi’c, I.; Louis, E.; Díaz-Guilera, A. Efficiency of informational transfer in regular and complex networks. Phys. Rev. E 2005, 71, 36122. [Google Scholar] [CrossRef] [Green Version]
- Latora, V.; Marchiori, M. A measure of centrality based on network efficiency. New J. Phys. 2007, 9, 188. [Google Scholar] [CrossRef]
- Blagus, N.; Šubelj, L.; Bajec, M. Self-similar scaling of density in complex real-world networks. Physica A 2012, 391, 2794–2802. [Google Scholar] [CrossRef] [Green Version]
- Pajek Datasets. Available online: http://vlado.fmf.unilj.si/pub/networks/pajek/data/gphs.htm (accessed on 1 January 2006).
- Batagelj, V.; Mrvar, A. Pajek-program for large network analysis. Connections 1998, 21, 47–57. [Google Scholar]
- Zeng, A.; Liu, W. Enhancing network robustness against malicious attacks. Phys. Rev. E 2012, 85, 66130. [Google Scholar] [CrossRef] [Green Version]
- Sun, X.; Gollnick, V.; Wandelt, S. Robustness analysis metrics for worldwide airport network: A comprehensive study. Chin. J. Aeronaut. 2017, 30, 500–512. [Google Scholar] [CrossRef]
- Von Mering, C.; Krause, R.; Snel, B.; Cornell, M.; Oliver, S.G.; Fields, S.; Bork, P. Comparative assessment of large-scale data sets of protein-protein interactions. Nature 2002, 417, 399–403. [Google Scholar] [CrossRef]
- Guelzim, N.; Bottani, S.; Bourgine, P.; Kepes, F. Topological and causal structure of the yeast transcriptional regulatory network. Nat. Genet. 2002, 31, 60–63. [Google Scholar] [CrossRef]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of small-world networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef] [PubMed]

| Network | N | M | <k> | C | ksmax | L |
|---|---|---|---|---|---|---|
| USAir | 332 | 2126 | 12.807 | 0.625 | 26 | 2.738 |
| 324 | 2218 | 13.69 | 0.466 | 18 | 3.054 | |
| Erdos | 446 | 1417 | 6.33 | 0.296 | 9 | 3.952 |
| USAirport | 1574 | 28,236 | 21.901 | 0.505 | 64 | 3.113 |
| Yeast | 2375 | 11,693 | 9.847 | 0.306 | 40 | 5.094 |
| Power | 4961 | 6964 | 2.669 | 0.080 | 5 | 18.989 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, H.; An, S. Critical Nodes Identification in Complex Networks. Symmetry 2020, 12, 123. https://doi.org/10.3390/sym12010123
Yang H, An S. Critical Nodes Identification in Complex Networks. Symmetry. 2020; 12(1):123. https://doi.org/10.3390/sym12010123
Chicago/Turabian StyleYang, Haihua, and Shi An. 2020. "Critical Nodes Identification in Complex Networks" Symmetry 12, no. 1: 123. https://doi.org/10.3390/sym12010123
APA StyleYang, H., & An, S. (2020). Critical Nodes Identification in Complex Networks. Symmetry, 12(1), 123. https://doi.org/10.3390/sym12010123




