A Novel Linear Antenna Synthesis for Linear Dispersion Codes Based on an Innovative HYBRID Genetic Algorithm
Abstract
:1. Introduction
2. Linear Dispersion Code
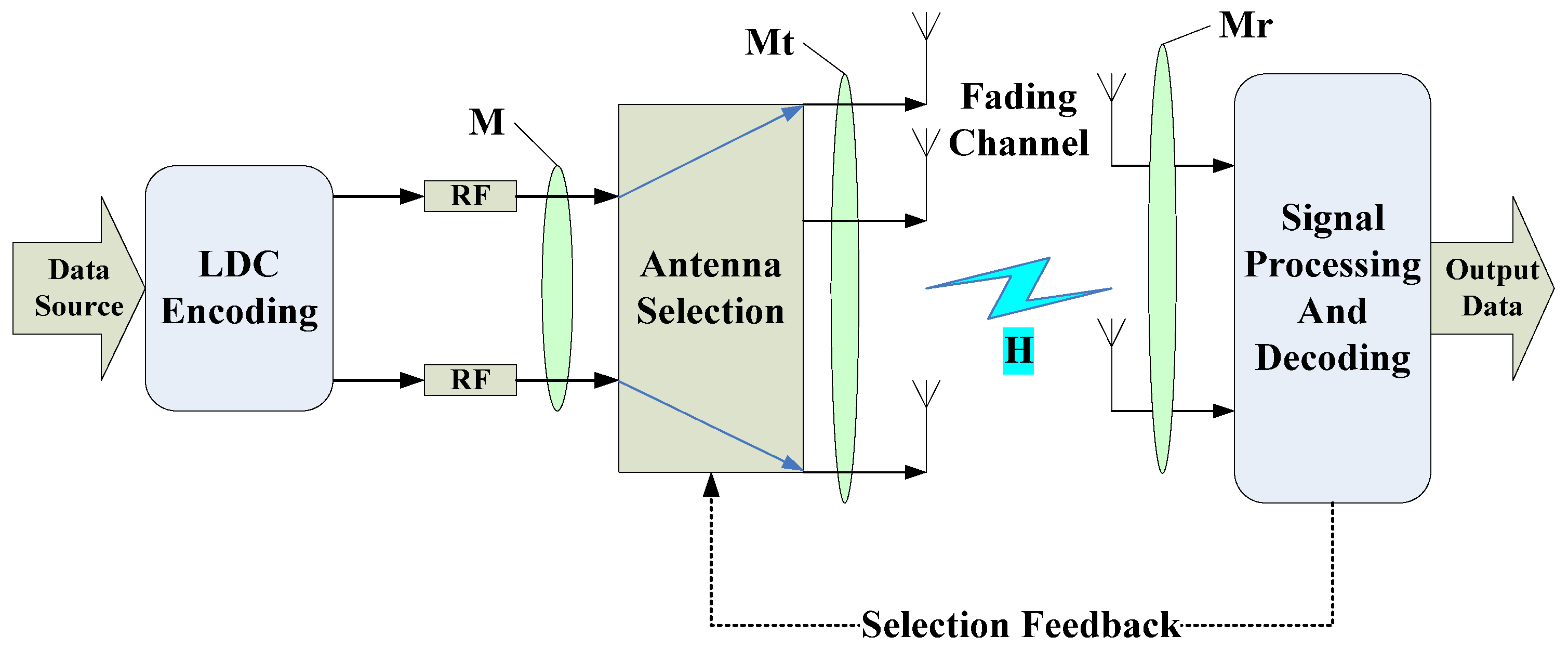
3. System Model
4. Maximum Minimum Posterior SNR Criterion for the LDC-TAS
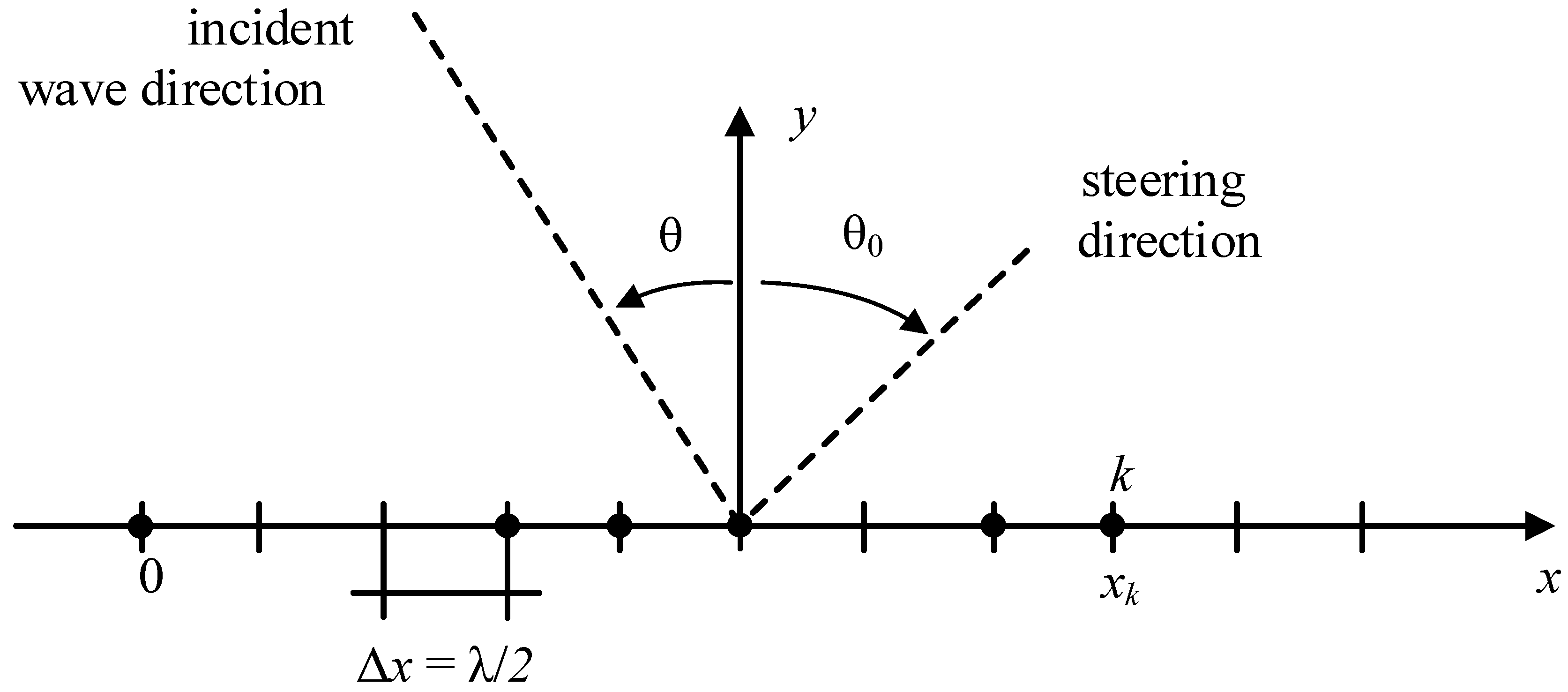
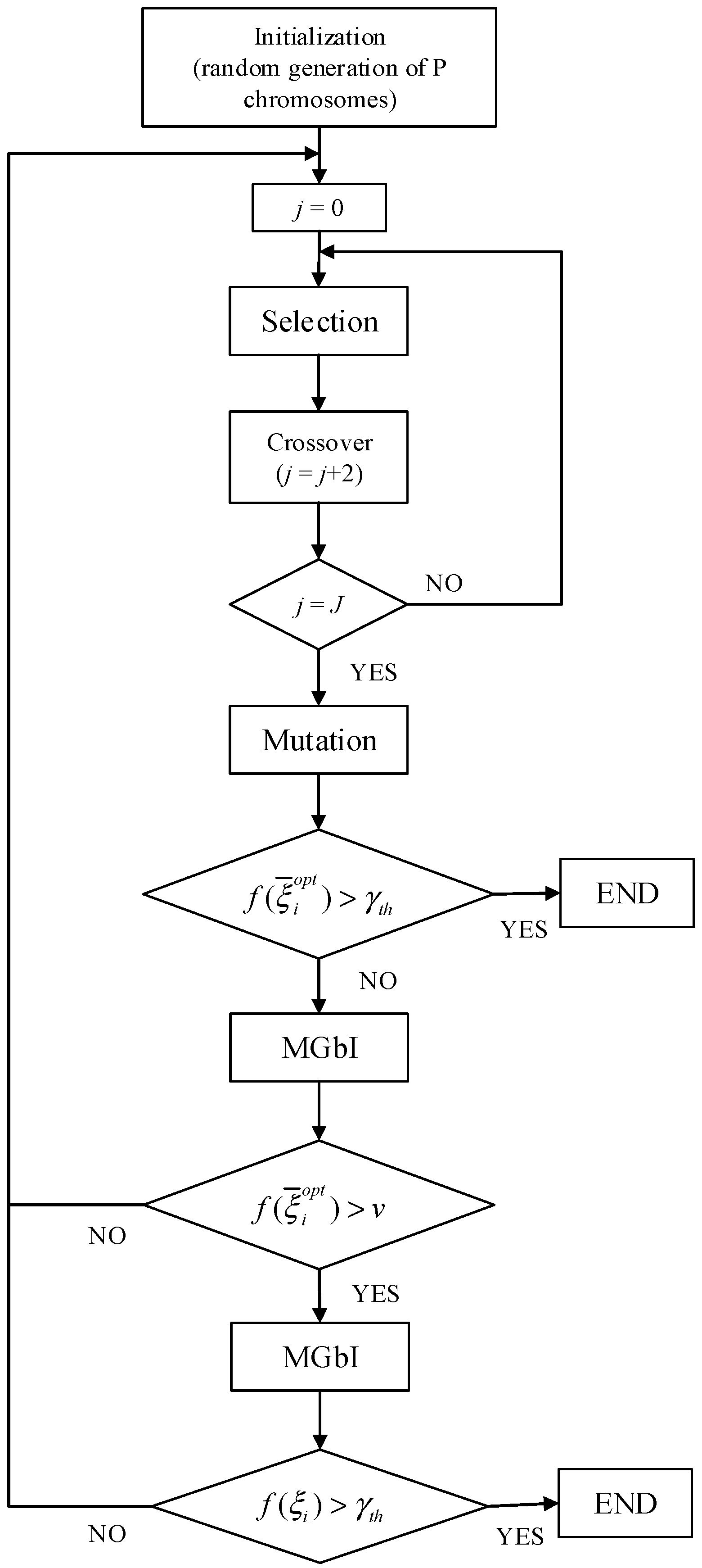
5. Antenna Synthesis Via an Innovative HYBRID Genetic Algorithm
- These SGAs cooperate with the parameters’ coding over computation, not these parameters themselves;
- These SGAs being a multiple-agent hunting process (i.e., a multiple sampling of those hunting spaces);
- These SGAs do not have to make use of those derivatives indeed;
- These SGAs do not apply the deterministic transition schemes, but use some random ones instead.
- The application for a hybrid coding way;
- The non-correlation among the chromosomes’ genes (i.e., the power weights parameters and the genes, which representing the position of those array elements should be optimized synchronously);
- The conception over a prior-knowledge-enhanced operator;
- The design of the scheme for a mind of the adaptive evolution;
- The definition of a hybridization design using the local hunting way.
5.1. The Selection
5.2. The Crossover
5.3. The Mutation
5.4. Elitism
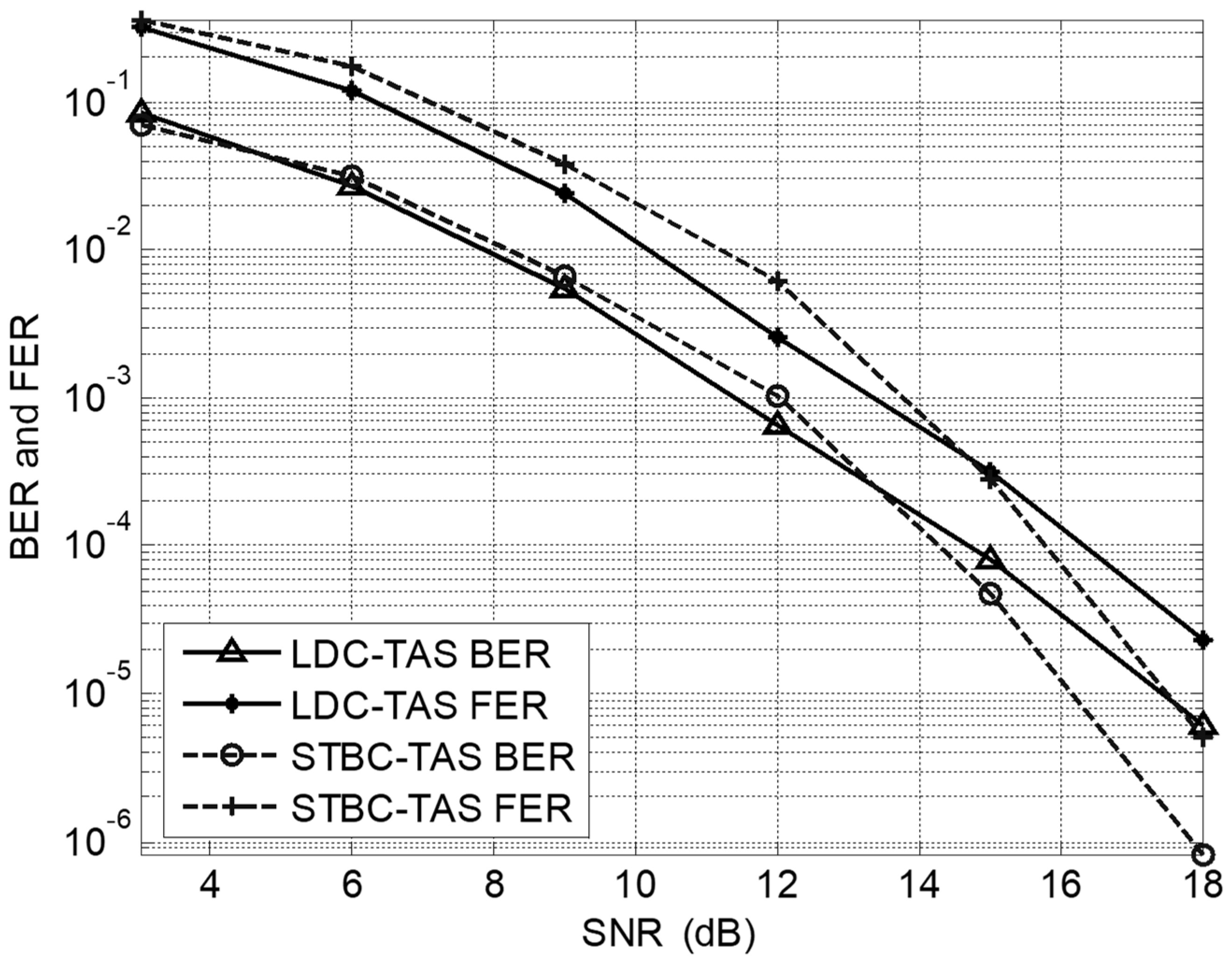
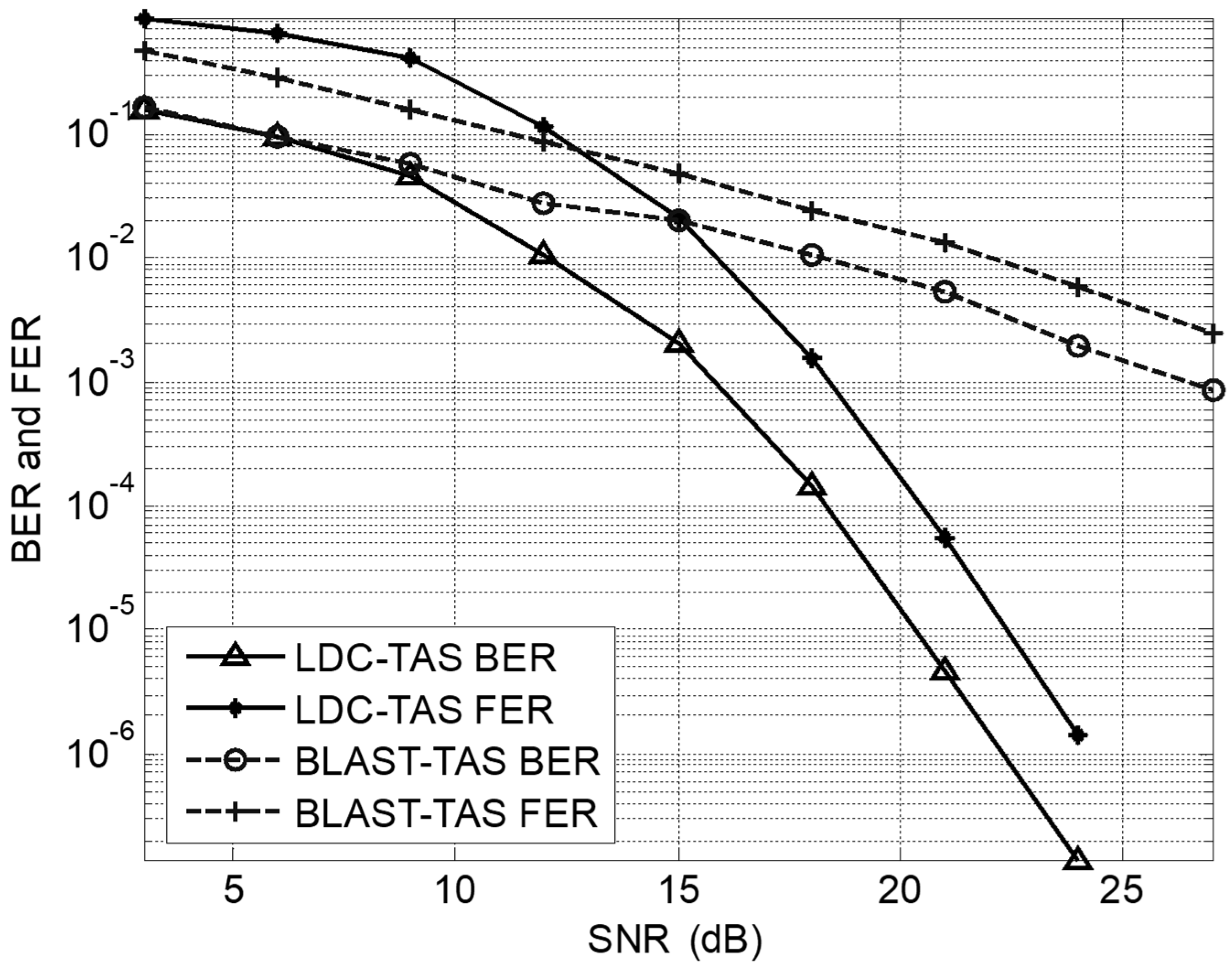
6. Simulation Analyses
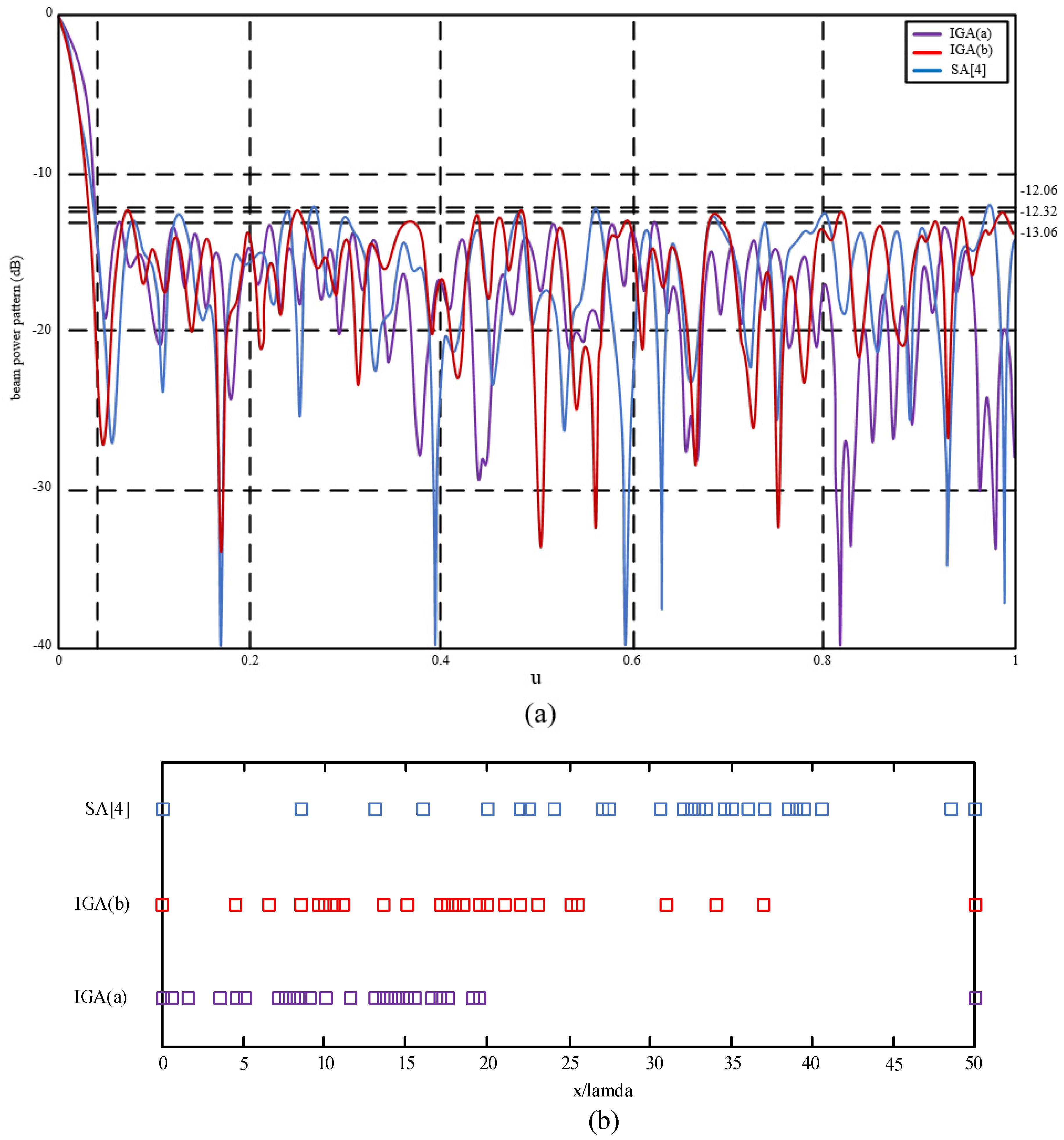
6.1. Result Analyses
6.2. Complexity Analyses
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Santhanam, T.; Padmavathi, M.S. Comparison of K-Means clustering and statistical outliers in reducing medical datasets. In Proceedings of the IEEE International Conference on Science, Engineering and Management Research (ICSEMR), Chennai, India, 27–29 November 2014. [Google Scholar]
- Zhenyu, M.; Jeng-Shyang, P.; Huarong, X. Quasi-Affine, Transformation Evolutionary (QUATRE) algorithm: A cooperative swarm based algorithm for global optimization. Knowl. Based Syst. 2016, 109, 104–121. [Google Scholar]
- Jinpeng, W.; Nianyu, Z.; Yuncui, Z.; Ping, L. Study on downlink performance of multiple access algorithm based on antenna diversity. ICIC Express Lett. 2015, 9, 1221–1225. [Google Scholar]
- Aishwarya, S.; Anto, S. A medical decision support system based on genetic algorithm and least square support vector machine for diabetes disease diagnosis. Int. J. Eng. Sci. Res. Technol. 2014, 3, 4042–4046. [Google Scholar]
- Hassibi, B.; Hochwald, B.M. High-Rate codes that are linear in space and time. IEEE Trans. Inf. Theory 2002, 48, 1804–1824. [Google Scholar] [CrossRef]
- Dorsey, W.M.; Coleman, J.O. Uniform circular array pattern synthesis using second-order cone programming. IET Microw. Antennas Propag. 2015, 9, 723–727. [Google Scholar]
- Weile, D.S.; Michielssen, E. Integer coded Pareto genetic algorithm design of constrained antenna arrays. Electron. Lett. 1996, 32, 1744–1745. [Google Scholar] [CrossRef]
- Trucco, A.; Murino, V. Stochastic optimization of linear sparse arrays. IEEE J. Ocean. Eng. 1999, 24, 291–299. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, S.; Zhang, J. Multi-Hop Maimal Ratio Combining (MHMRC) diversity based on virtual cellular network. J. Jilin Univ. 2011, 41, 533–536. [Google Scholar]
- Chen, K.; He, Z.; Han, C. A modified real GA for the sparse linear array synthesis with multiple constraints. IEEE Trans. Antennas Propag. 2006, 54, 2169–2173. [Google Scholar]
- RaviKumar, G.; Ramachandra, G.A.; Nagamani, K. An efficient feature selection system to integrating SVM with genetic algorithm for large medical datasets. Int. J. Adv. Res. Comput. Sci. Softw. Eng. 2014, 4, 272–277. [Google Scholar]
- Shengbo, E.L.; Renjie, L.; Wang, J.; Xiaosong, H.; Cheng, B.; Keqiang, L. Stabilizing periodic control of automated vehicle platoon with minimized fuel consumption. IEEE Trans. Transp. Electr. 2017, 3, 259–271. [Google Scholar]
- Zou, Q.-F.; Tan, X.-Z.; Liu, M.; Ma, L. Low complexity frequency domain iterative equalization based on minimum mean square error for single carrier systems. Jilin Daxue Xuebao 2015, 45, 2062–2068. [Google Scholar]
- Ghrayeb, A.; Duman, T.M. Performance analysis of MIMO systems with antenna selection over quasi-static fading channels. IEEE Trans. Veh. Technol. 2003, 52, 281–288. [Google Scholar] [CrossRef]
- Chen, J.; Li, J.; Yang, S.; Deng, F. Weighted optimization-based distributed Kalman filter for nonlinear target tracking in collaborative sensor networks. IEEE Trans. Cybern. 2017, 1, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Santhanam, T.; Padmavathi, M.S. Application of K-Means and genetic algorithms for dimension reduction by integrating SVM for diabetes diagnosis. Procedia Comput. Sci. 2015, 8, 76–83. [Google Scholar] [CrossRef]
- Chu, S.-C.; Tsai, P.-W.; Pan, J.-S. Cat swarm optimization. In PRICAI 2006: Trends in Artificial Intelligence; Springer: Berlin, Germany, 2006; pp. 854–858. [Google Scholar]
- Su, S.; Qu, D.; Li, L.; Jiang, T. Invertible subset QC-LDPC codes for PAPR reduction of OFDM signals. IEEE Trans. Broadcast. 2015, 61, 290–298. [Google Scholar]
- Leeper, D.G. Isophoric arrays—Massively thinned phased arrays with well-controlled sidelobes. IEEE Antennas Propag. Mag. 1999, 47, 1825–1835. [Google Scholar] [CrossRef]
- Tiwari, R.; Singh, M.P. Correlation-Based attribute selection using genetic algorithm. Int. J. Comput. Appl. 2010, 4, 28–34. [Google Scholar] [CrossRef]
- Ratnakar, S.; Rajeshwari, K.; Rose, J. Prediction of heart disease using genetic algorithm for selection of optimal reduced set of attributes. Int. J. Adv. Comput. Eng. Netw. 2013, 1, 51–55. [Google Scholar]
- Chai, E.; Shin, K. Low-Overhead control channels in wireless networks. IEEE Trans. Mob. Comput. 2015, 14, 2303–2315. [Google Scholar] [CrossRef]
- Wang, J.; Cao, F.; Zou, N. Multi carrier system joint receiving method based on MAI and ICI. Jilin Daxue Xuebao 2018, 41, 301–305. [Google Scholar]
- Sumit, B.; Praveen, P.; Pillai, G.N. SVM based decision support system for heart disease classification with integer-coded genetic algorithm to select critical features. In Proceedings of the World Congress on Engineering and Computer Science, San Francisco, CA, USA, 22–24 October 2008. [Google Scholar]
- Hu, M.; Li, Y.; Lu, X.; Zhang, H. Tone reservation to minimize nonlinearity impact on OFDM signals. IEEE Transp. Veh. Technol. 2015, 64, 4310–4314. [Google Scholar] [CrossRef]
- Yilmaz, N.; Inan, O.; Uzer, M.S. A new data preparation method based on clustering algorithms for diagnosis systems of heart and diabetes diseases. J. Med. Syst. 2014, 38, 48. [Google Scholar] [CrossRef] [PubMed]
- Guido, R.; Conforti, D. A hybrid genetic approach for solving an integrated multi-objective operating room planning and scheduling problem. Comput. Oper. Res. 2017, 87, 270–282. [Google Scholar] [CrossRef]
- Qiu, X.; Sha, X.-J.; Mei, L. Hybrid carrier CDMA multi-antenna system based on weighted-type fractional fourier transform. Jilin Daxue Xuebao 2013, 43, 218–222. [Google Scholar]
- Guillermo, D.; Rey, P.A.; Wolff, P. Solving the operating room scheduling problem with prioritized lists of patients. ANN Oper. Res. 2016, 258, 395–414. [Google Scholar]
- Yuan, R.; Guangchen, B. Determination of optimal SVM parameters by using genetic algorithm/particle swarm optimization. J. Comput. 2010, 5, 1160–1169. [Google Scholar]
- Patil, B.M.; Joshi, R.C.; Toshniwal, D. Impact of K-Means on the performance of classifiers for labeled data. In International Conference on Contemporary Computing; Springer: Berlin, Germany, 2010; Volume 94, pp. 423–434. [Google Scholar]
- Velmurugan, T. Efficiency of K-Means and K-Medoids algorithms for clustering arbitrary data points. Int. J. Comput. Technol. Appl. 2012, 3, 1758–1764. [Google Scholar]
- Chinneck, J.W. Practical Optimization: A Gentle Introduction. 2014. Available online: http://www.sce.carleton.ca/faculty/chinneck/po/Chapter20.pdf (accessed on 21 December 2018).
- Isa, N.A.M.; Wan Mamat, W.M.F. Clustered-Hybrid multilayer perceptron network for pattern recognition application. Appl. Soft Comput. 2011, 11, 1457–1466. [Google Scholar]
- Anuja Kumari, V.; Chitra, R. Classification of diabetes disease using support vector machine. Int. J. Eng. Res. Appl. 2013, 3, 1797–1801. [Google Scholar]
- Chikh, M.A.; Saidi, M.; Settouti, N. Diagnosis of diabetes diseases using an Artificial Immune Recognition System2 (AIRS2) with fuzzy K-Nearest neighbor. J. Med. Syst. 2012, 36, 2721–2729. [Google Scholar] [CrossRef] [PubMed]
- Abadi, A.; Rajabioun, T.; Ioannou, P. Traffic flow prediction for road transportation networks with limited traffic data. IEEE Trans. Intell. Transp. Syst. 2015, 16, 653–662. [Google Scholar] [CrossRef]
- Lv, Y.; Duan, Y.; Kang, W.; Li, Z.; Wang, F.-Y. Traffic flow prediction with big data: A deep learning approach. IEEE Trans. Intell. Transp. Syst. 2015, 16, 865–873. [Google Scholar] [CrossRef]
- Zhang, L.; Ma, J.; Zhu, C. Theory modeling and application of an adaptive Kalman filter for short-term traffic flow prediction. J. Inf. Comput. Sci. 2012, 9, 5101–5109. [Google Scholar]
- Faruk, D.Á. A hybrid neural network and ARIMA model for water quality time series prediction. Eng. Appl. Artif. Intell. 2010, 23, 586–594. [Google Scholar] [CrossRef]
- Chen, C.-F.; Lai, M.-C.; Yeh, C.-C. Forecasting tourism demand based on empirical mode decomposition and neural network. Knowl. Based Syst. 2012, 26, 281–287. [Google Scholar] [CrossRef]
- Bauza, R.; Gozalvez, J. Traffic congestion detection in large-scale scenarios using vehicle-to-vehicle communications. J. Netw. Comput. Appl. 2013, 36, 1295–1307. [Google Scholar] [CrossRef]
- De Ridder, K.; Kumar, U.; Lauwaet, D.; Van Looy, S.; Lefebvre, W. Kalman filter-based air quality forecast adjustment. In Air Pollution Modeling and Its Application XXII; Springer: Dordrecht, The Netherlands, 2013; pp. 177–181. [Google Scholar]
- Pappula, L.; Ghosh, D. Linear antenna array synthesis using cat swarm optimization. AEU Int. J. Electr. Commun. 2014, 68, 540–549. [Google Scholar] [CrossRef]
- Basak, A.; Pal, S.; Das, S.; Abraham, A.; Snasel, V. A modified invasive weed optimization algorithm for time-modulated linear antenna array synthesis. In Proceedings of the IEEE Congress on Evolutionary Computation, Barcelona, Spain, 18–23 July 2010. [Google Scholar]
- Mahanti, G.K.; Chakraborty, A.; Das, S. Phase-Only and amplitude-phase only synthesis of dual-beam pattern linear antenna arrays using floating-point genetic algorithms. Prog. Electromagn. Res. 2007, 68, 247–259. [Google Scholar] [CrossRef]
- Baskar, S.; Alphones, A.; Suganthan, P.N. Genetic algorithm based design of a reconfigurable antenna array with discrete phase shifter. Microw. Opt. Technol. Lett. 2005, 45, 461–465. [Google Scholar] [CrossRef]
- Mitilineos, S.A.; Mougiakos, K.S.; Thomopoulos, S.C. Design and optimization of ESPAR antennas via impedance measurements and a genetic algorithm (antenna designer’s notebook). IEEE Antennas Propag. Mag. 2009, 51, 118–123. [Google Scholar] [CrossRef]
- Maltsev, A.; Sadri, A.; Pudeyev, A.; Bolotin, I. Highly directional steerable antennas: High-gain antennas supporting user mobility or beam switching for reconfigurable backhauling. IEEE Veh. Technol. Mag. 2016, 11, 32–39. [Google Scholar] [CrossRef]
- Majumdar, B.; Esselle, K.P. Fixed frequency broadside-endfire beam steerable antennas. Electr. Lett. 2016, 21, 1282–1284. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, J.; Zhang, S. Pseudorange measurement method based on AIS signals. Sensors 2017, 5, 22. [Google Scholar] [CrossRef] [PubMed]
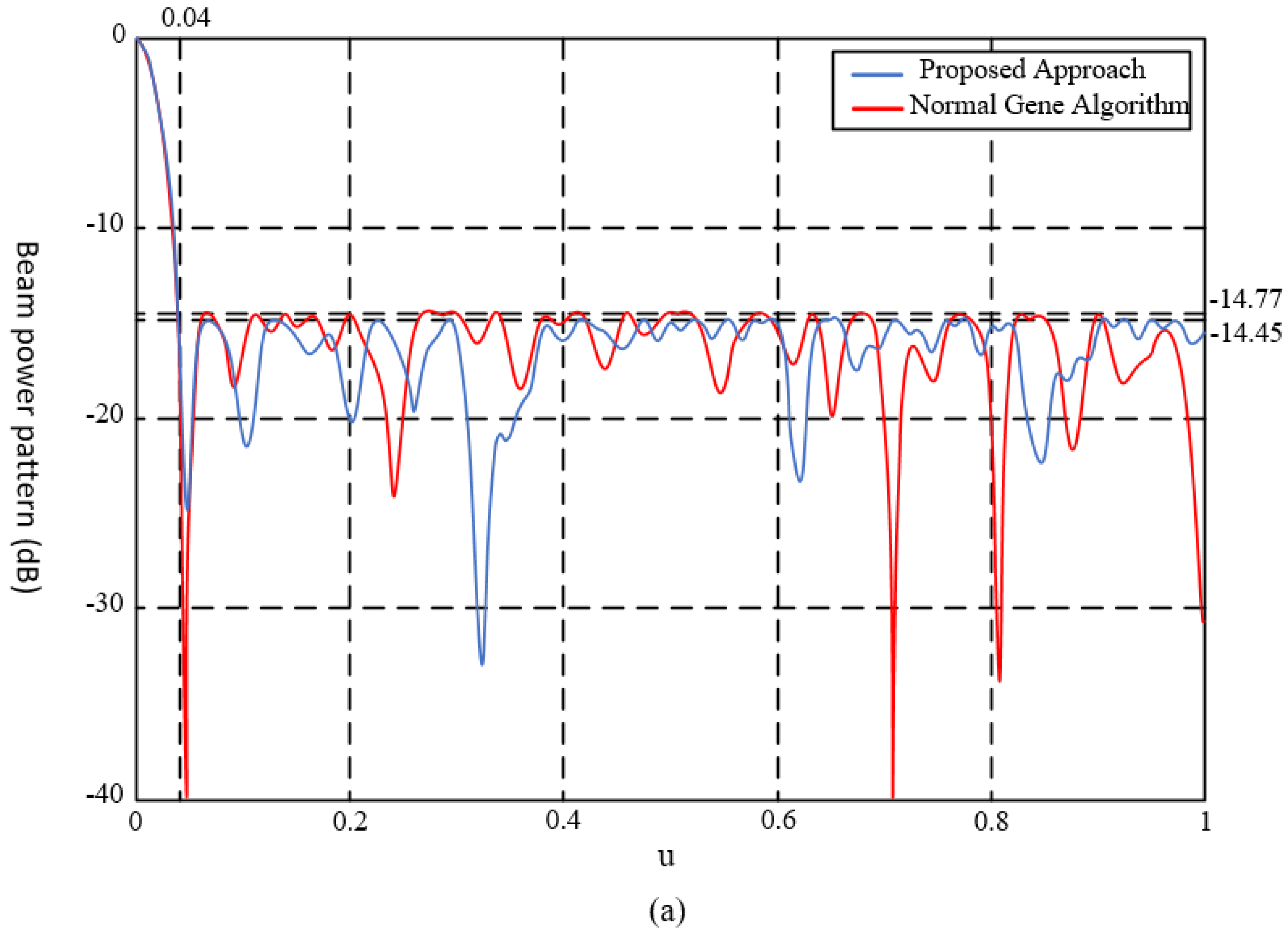
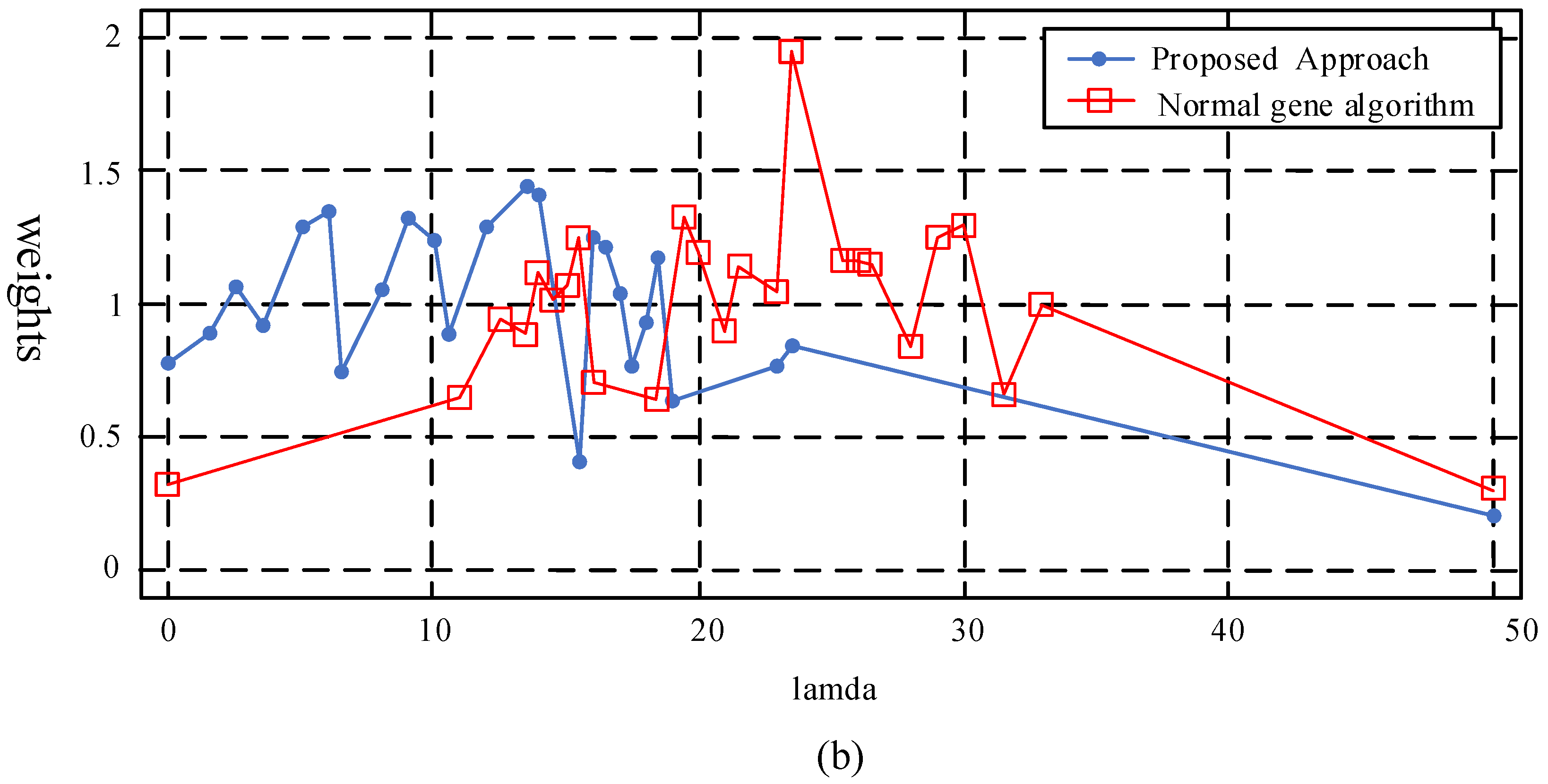
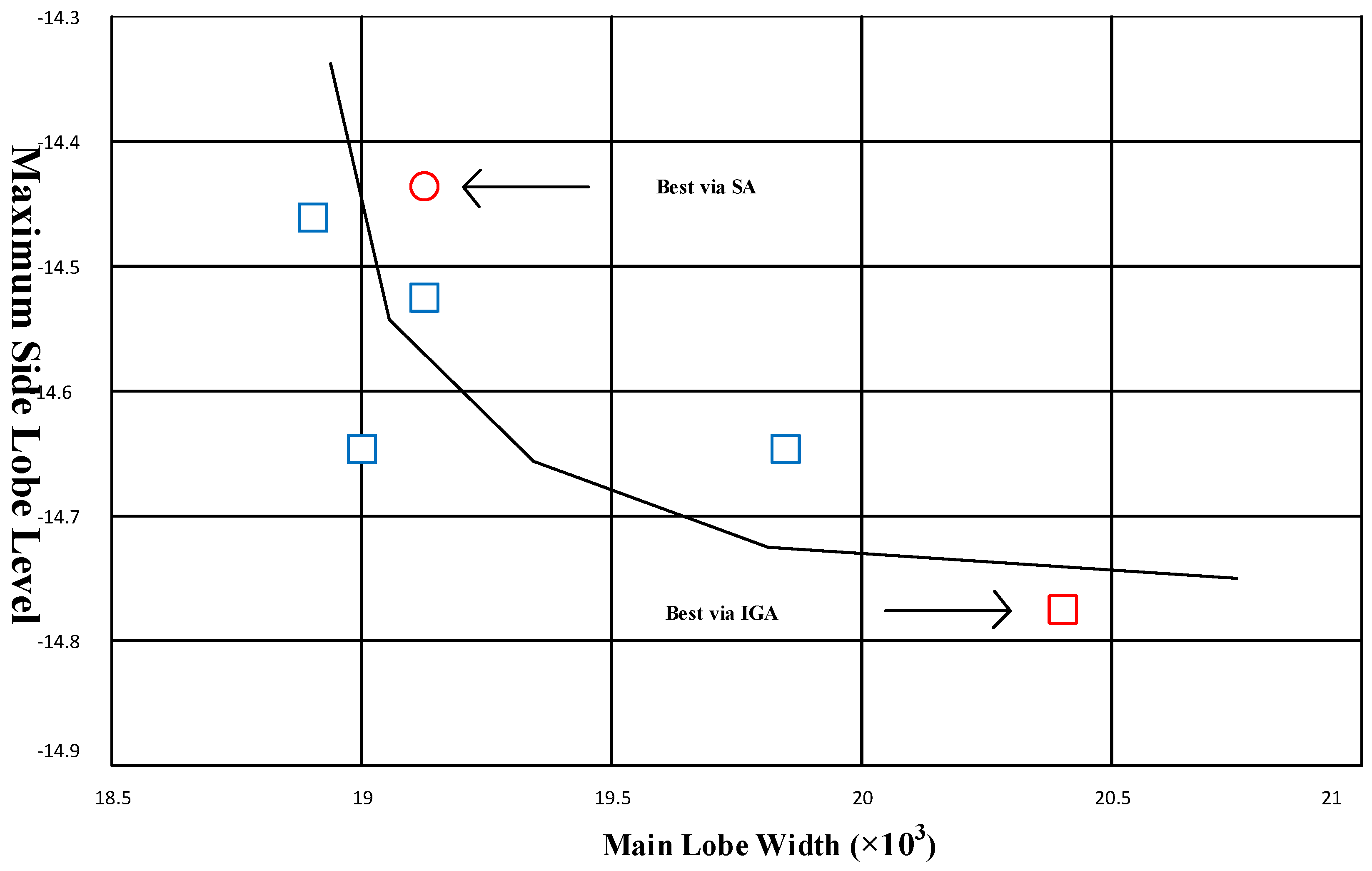
| Region | BP Amplitude Factors |
|---|---|
| 0 < ≤ 0.0418 | 0 dB |
| 0.0419 < ≤ 0.307 | −13.368 dB |
| 0.308 < ≤ 0.446 | −26.876 dB |
| 0.447 < ≤ 0.797 | 13.395 dB |
| 0.798 < ≤ 1 | 0 dB |
| Quantity of the Active Elements (M) | |||
| The Best | The Worst | Average | Std. Dev |
| 149 (73.5%) | 156 (76.5%) | 148.9 (74.8%) | 1.0358 |
| Side-Lobe Peak Value (Φslp; dB) | |||
| The Best | The Worst | Average | Std. Dev |
| −23.19 | −22.61 | −22.91 | 0.2322 |
| Main-Lobe Width (uml) | |||
| The Best | The Worst | Average | Std. Dev |
| 0.0050 | 0.0052 | 0.00508 | ~0 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Ye, Z.; M. Sanders, T.; Li, B.; Zou, N. A Novel Linear Antenna Synthesis for Linear Dispersion Codes Based on an Innovative HYBRID Genetic Algorithm. Symmetry 2019, 11, 1176. https://doi.org/10.3390/sym11091176
Wang J, Ye Z, M. Sanders T, Li B, Zou N. A Novel Linear Antenna Synthesis for Linear Dispersion Codes Based on an Innovative HYBRID Genetic Algorithm. Symmetry. 2019; 11(9):1176. https://doi.org/10.3390/sym11091176
Chicago/Turabian StyleWang, Jinpeng, Zhengpeng Ye, Tarun M. Sanders, Bo Li, and Nianyu Zou. 2019. "A Novel Linear Antenna Synthesis for Linear Dispersion Codes Based on an Innovative HYBRID Genetic Algorithm" Symmetry 11, no. 9: 1176. https://doi.org/10.3390/sym11091176
APA StyleWang, J., Ye, Z., M. Sanders, T., Li, B., & Zou, N. (2019). A Novel Linear Antenna Synthesis for Linear Dispersion Codes Based on an Innovative HYBRID Genetic Algorithm. Symmetry, 11(9), 1176. https://doi.org/10.3390/sym11091176





