On the Effectiveness of Using Elitist Genetic Algorithm in Mutation Testing
Abstract
1. Introduction
- Implementation of GA using the idea of diversification and intensification along with the integration of elitism and mutation-based fitness function. It addresses the problem of costly test suite with fault revealing abilities.
- Comparison of the effectiveness, efficiency and cost of the proposed approach with the state-of-the-art techniques on 14 Java programs on different evaluation metrics.
- Analyzing the impact of other artificial faults on the effectiveness of generated test suite.
2. Methods and Materials
2.1. Terminologies and Illustrations
- (a)
- Software Testing: It is the process of executing a program with the intent of finding the faults [65]. Actual output and expected output of executing a test case are compared and if they differ then it is said that fault is present.
- (b)
- Test Case: A test case is an input to the program with its expected output and is used for testing the functionality of the program [65]. A collection of test cases is called a test suite, e.g., for a single input problem, a test case can be , while for two input problem, .
- (c)
- (d)
- Mutants: The faulty version of a program is known as mutants. A mutant with a single fault is characterized as a single order mutant while those with more than one fault are higher-order mutants.
- (e)
- (f)
- Killing a Mutant: A test (Test Suite) kills a mutant (set of Mutants) if the execution of t can distinguish the behavior of the original program s and mutant program m. It can be expressed as: t kills
- (g)
- Mutation Score: A test t that kills mutants out of M mutants, for t, mutation score (%) is calculated as
- (h)
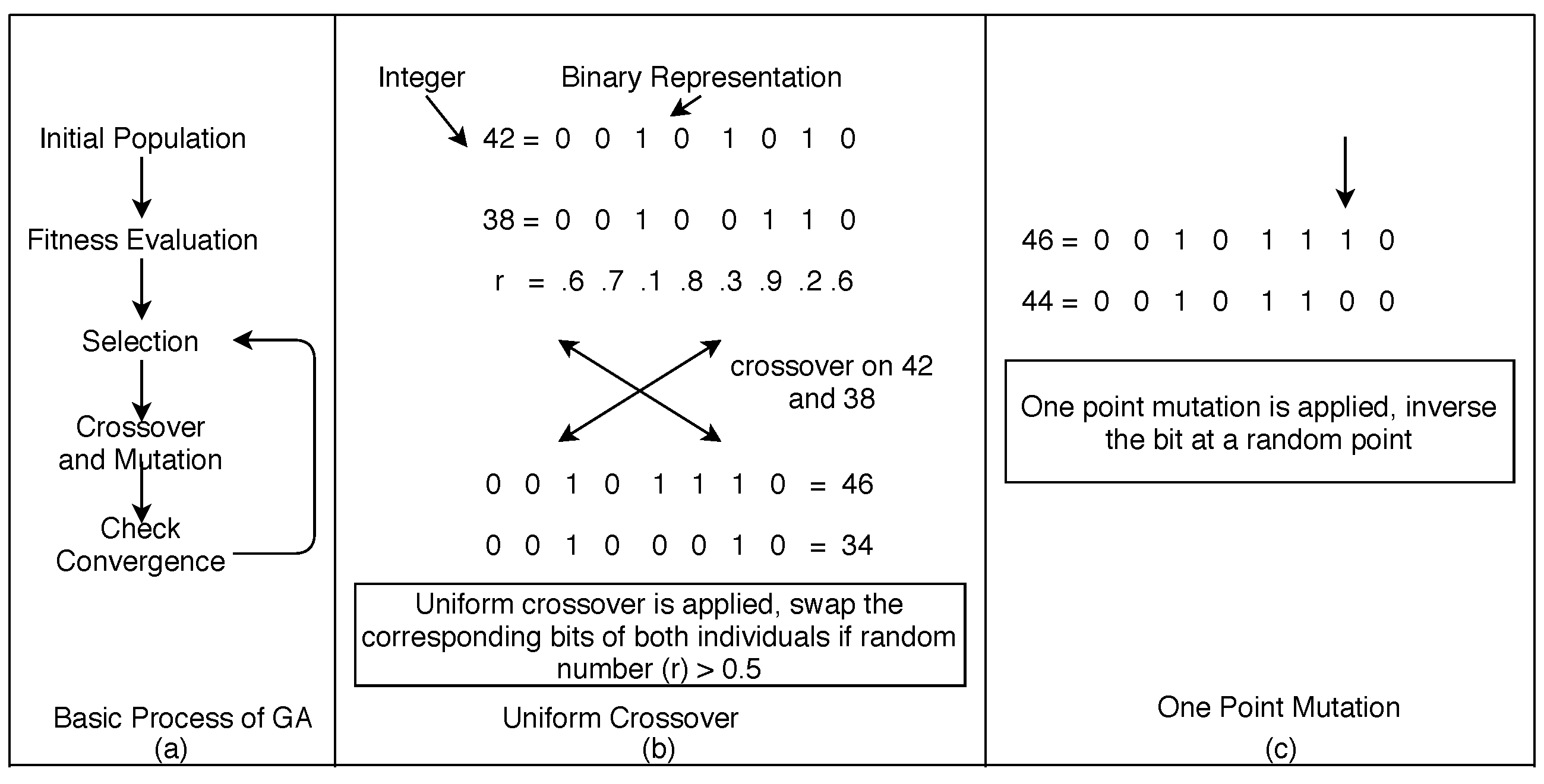
- GA and its Operators: GA is an evolutionary algorithm based on the concept of natural genetics of reproduction [6,7,8]. In an iteration of execution, it starts with the random initial population P, fitness evaluation of P, selection, reproduction (crossover and mutation) and stops re-iterating when an optimal solution is found (Figure 3). Each individual in the population is represented as chromosome (a sequence of genes) and encoded in binary for a binary-encoded GA, which is used in this study. For the evolution of individuals, crossover combines two individuals and produces two new individuals (offspring); on the other hand, mutation flips a bit in the gene of a chromosome [67]. In this work, a population of GA is mapped to the set of test cases, and the chromosome is mapped to the concatenated value of test inputs.
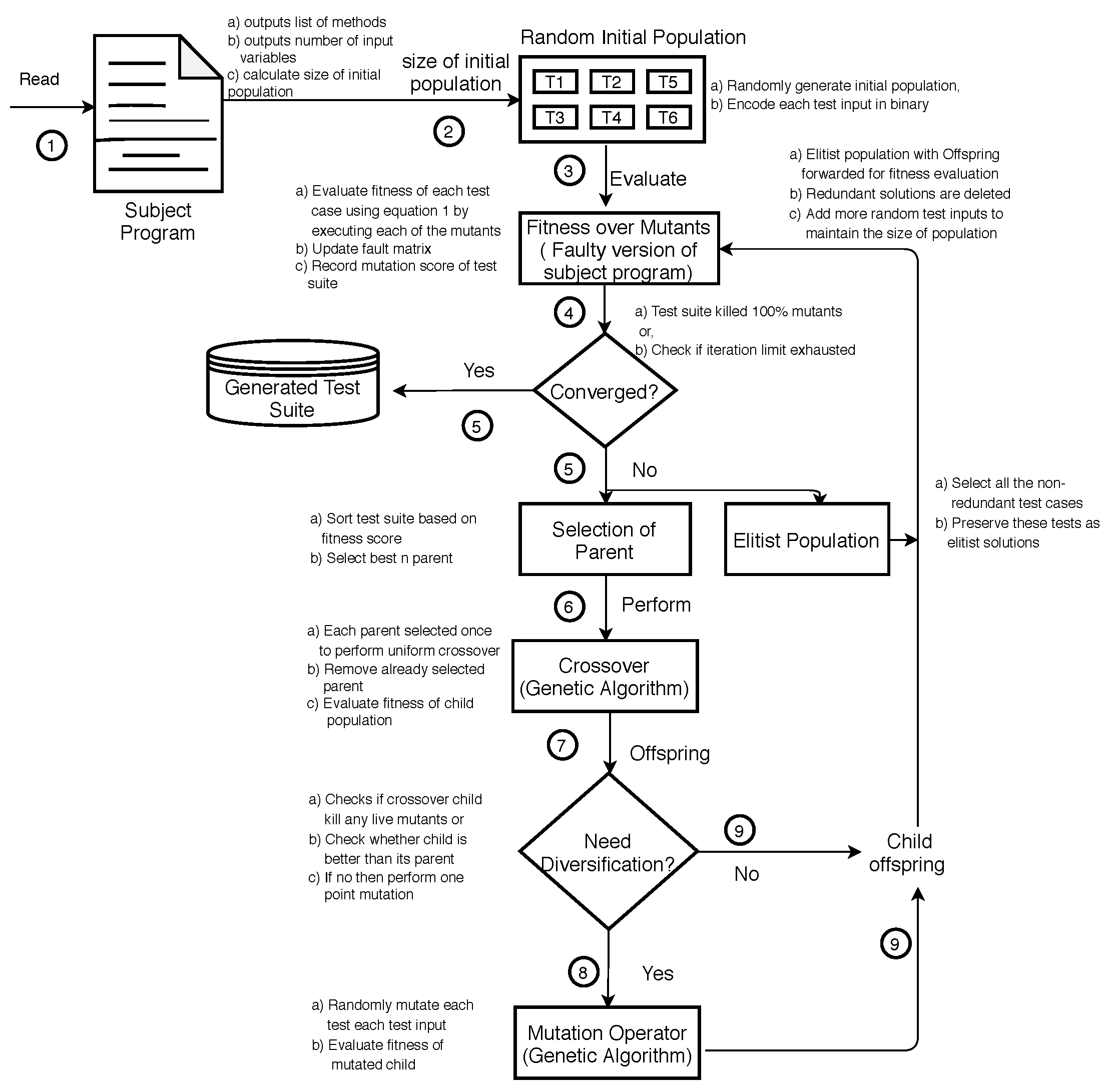
2.2. Description of Proposed Approach
| Algorithm 1: The Proposed Approach tdgen_gamt |
 |
2.2.1. Fitness Evaluation
| Algorithm 2: FitnessEvaluation |
 |
| Algorithm 3: RemoveRedundantTests (T) |
 |
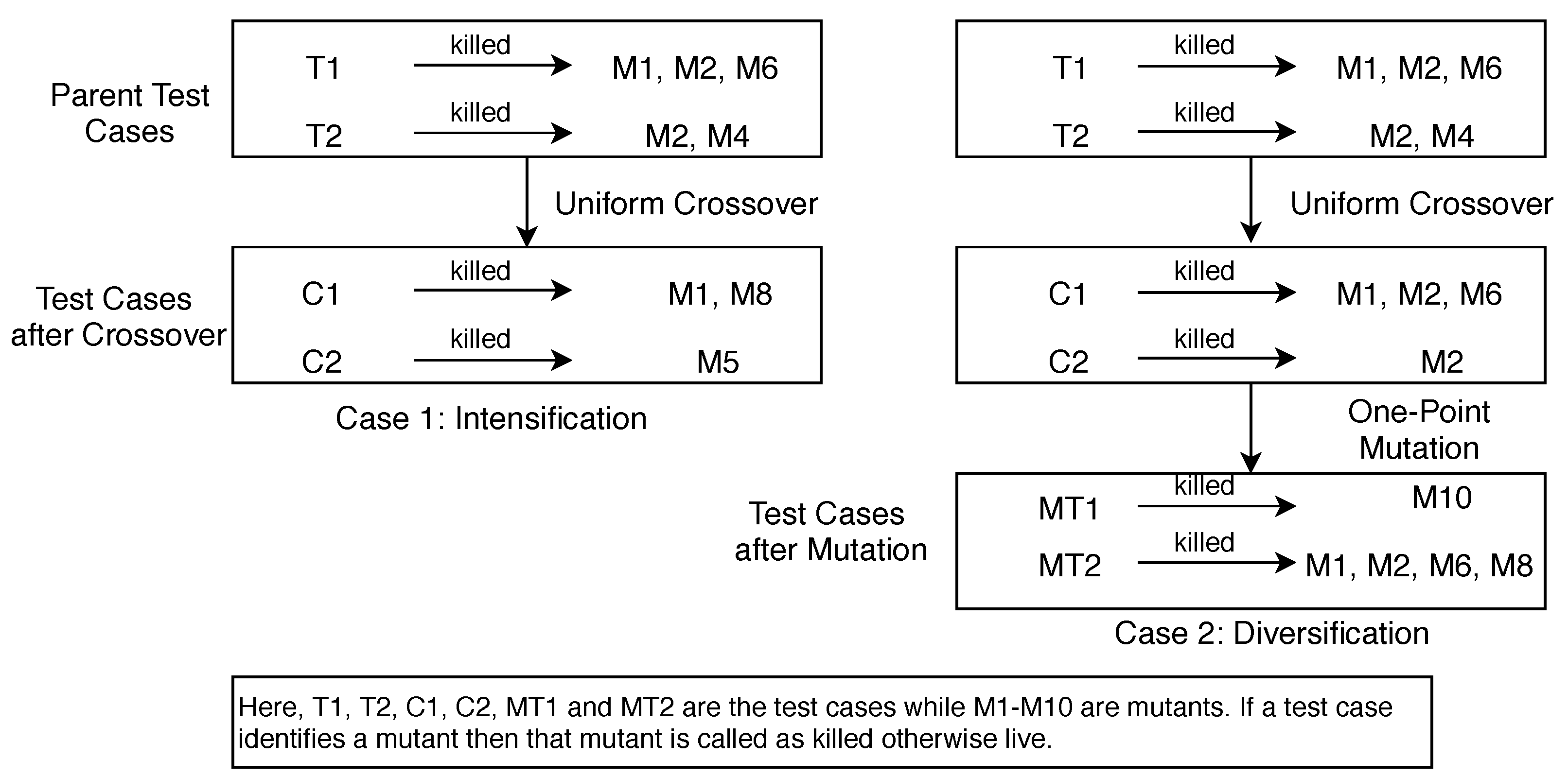
2.2.2. Diversification vs. Intensification for Reproduction
2.2.3. Population Replacement Strategy and Elitism
2.2.4. Convergence
2.3. A Detailed Example
3. Experimental Setup
3.1. Subject Programs under Test
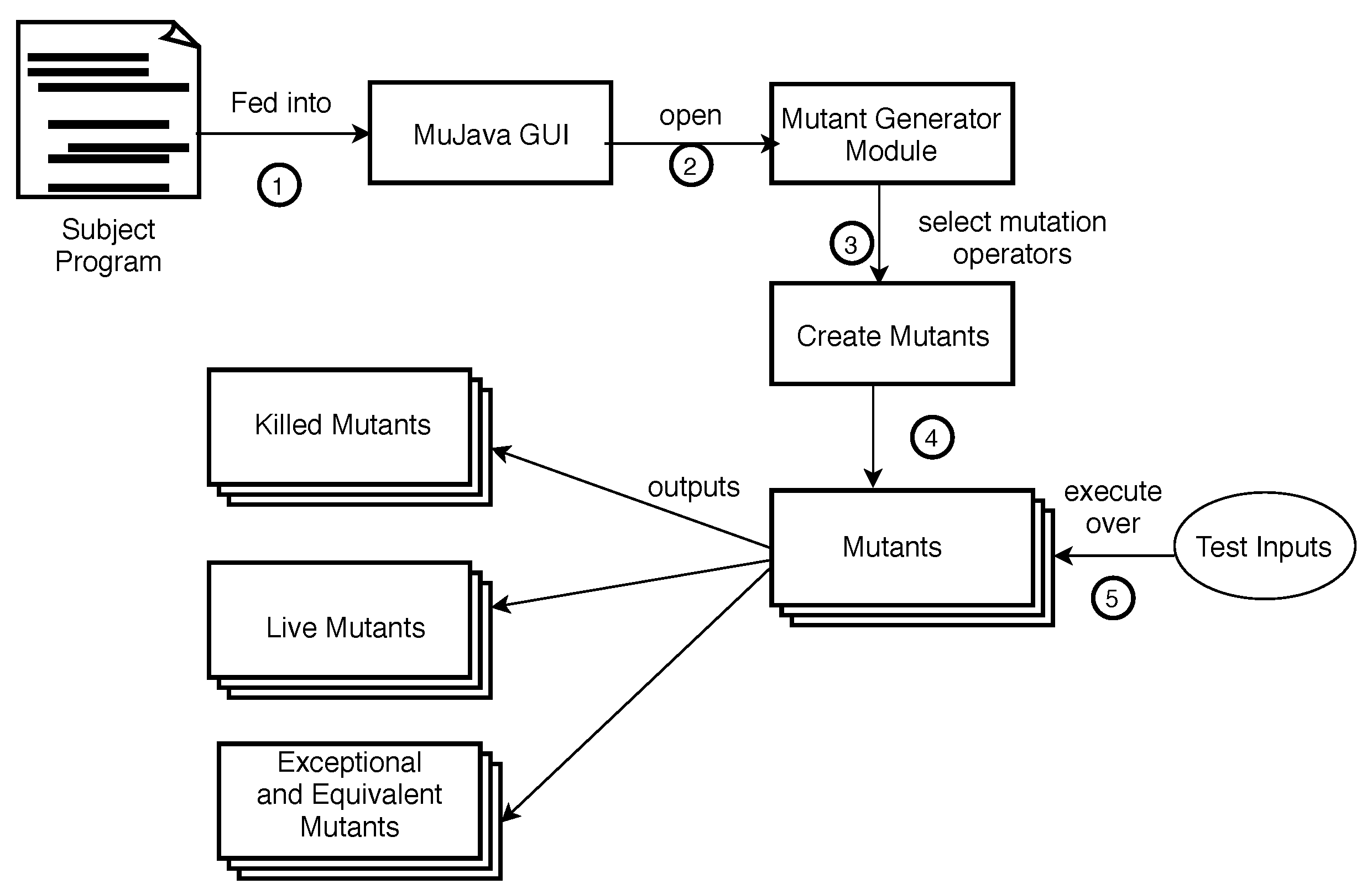
3.2. Mutants Used
3.3. Evaluation Metrics
3.4. Experiments
4. Results and Discussion
4.1. Performance of the Proposed Approach tdgen_gamt
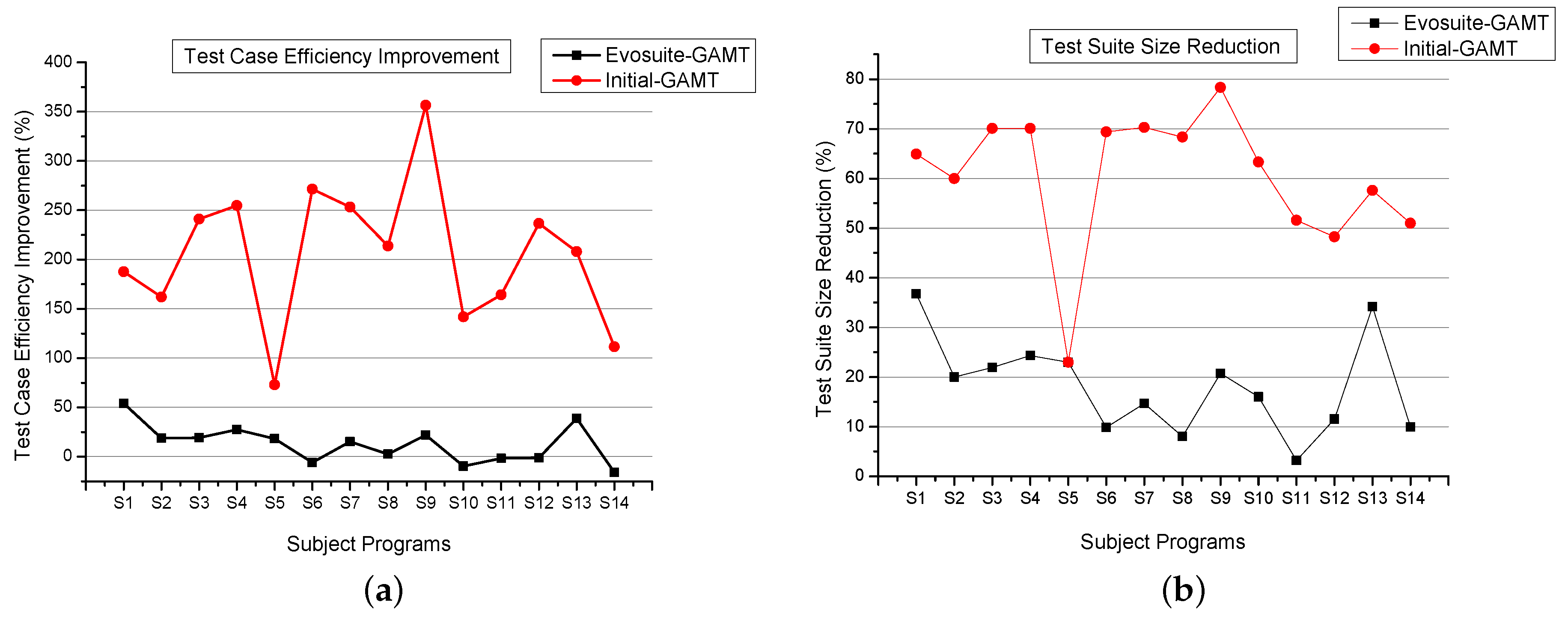
4.2. Effectiveness Comparison with Evosuite and Initial Random Tests
4.3. Efficiency and Cost Comparison with Evosuite and Initial Random Test
4.4. Stability Analysis
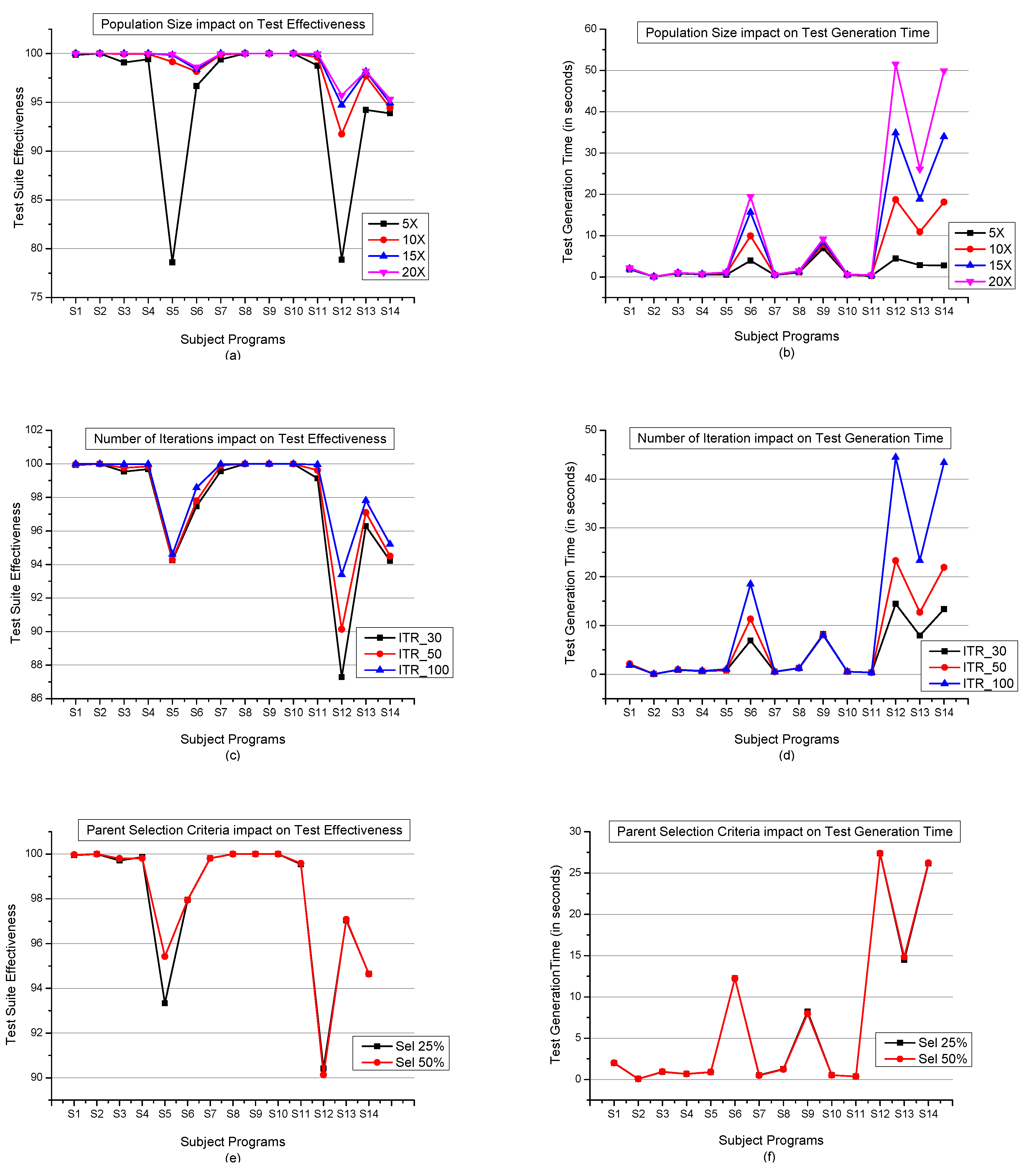
4.5. Selection of Control Parameters
4.6. Limitation of the Proposed Approach
5. Conclusions
- Empirically, the obtained test suite could detect on average 87.83% (tdgen_gamt), 96.35% (Evosuite), and 79.6% (Initial Random tests) executable traditional faults irrespective of test suite size. This anomaly of preponderance can be explained on the account of measuring the effectiveness of the approach by considering the size of the test suite (test case efficiency). The proposed approach detects the maximum number of mutants with fewer and less complex test cases.
- Additionally, we also analyze the detection rate of each fault type from each of the approaches. The results report that tdgen_gamt could perform equally at finding the stubborn mutants. Meanwhile, only 0.3%, 1.1%, and 1.9% SDL-ODL mutants are identified as stubborn by tdgen_gamt, Evosuite, and Initial Random tests, respectively. This indicates tdgen_gamt successfully killed approximately all the mutants and may easily detect stubborn mutants.
- Also the removal of redundant tests raises the efficiency of the approach. In particular, based on the conducted study, our approach tdgen_gamt generates 13%, 205% more efficient and 18%, 60% reduced test suite than Evosuite and Initial Random tests respectively. A set of test cases that is redundant for one set of mutants may not be redundant for another set of mutants.
- During reproduction, crossover operation is performed only once on each parent test case. This choice of reproduction operator also lowers the time complexity of tdgen_gamt.
- The use of elitism helps in fast convergence.
- The suggested fitness function appropriately guides the search process by finding the highly effective and less complex test cases in terms of finding the faults.
- Our approach successfully qualifies the stability test and fails only 5% (on average) in identifying more than 90% mutants.
- Use of low-cost mutation operators (produces 80% fewer mutants than traditional mutants) makes it easily adaptable by others.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Dave, M.; Agrawal, R. Search based techniques and mutation analysis in automatic test case generation: A survey. In Proceedings of the 2015 IEEE International Advance Computing Conference (IACC), Bangalore, India, 12–13 June 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 795–799. [Google Scholar]
- McMinn, P. Search-based software test data generation: A survey: Research articles. Softw. Test. Verif. Reliab. 2004, 14, 105–156. [Google Scholar] [CrossRef]
- McMinn, P. Search-based software testing: Past, present and future. In Proceedings of the 2011 IEEE Fourth International Conference on Software Testing, Verification and Validation Workshops (ICSTW’11), Berlin, Germany, 21–25 March 2011; IEEE Computer Society: Washington, DC, USA, 2011; pp. 153–163. [Google Scholar]
- Sahin, S.; Akay, B. Comparisons of metaheuristic algorithms and fitness functions on software test data generation. Appl. Soft Comput. 2016, 49, 1202–1214. [Google Scholar] [CrossRef]
- Ali, S.; Briand, L.C.; Hemmati, H.; Panesar-Walawege, R.K. A systematic review of the application and empirical investigation of search-based test case generation. IEEE Trans. Softw. Eng. 2010, 36, 742–762. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control and Artificial Intelligence; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Yang, X.-S. Nature-Inspired Optimization Algorithms; Elsevier: Amsterdam, Poland, 2014. [Google Scholar]
- Sivanandan, S.N.; Deepa, S.N. Intorduction to Genetic Algorithms; Springer: Berlin, Germany, 2008. [Google Scholar]
- Fraser, G.; Zeller, A. Mutation-driven generation of unit tests and oracles. IEEE Trans. Softw. Eng. 2012, 38, 278–292. [Google Scholar] [CrossRef]
- Fraser, G.; Arcuri, A. Achieving scalable mutation-based generation of whole test suites. Empir. Soft. Eng. Springer 2015, 20, 783–812. [Google Scholar] [CrossRef]
- Andrews, J.H.; Briand, L.C.; Labiche, Y. Is mutation an appropriate tool for testing experiments? In Proceedings of the 27th International Conference on Software Engineering (ICSE’05). St. Louis, MO, USA, 15–21 May 2005; ACM: Copenhagen, Denmark, 2005; pp. 402–411. [Google Scholar]
- Just, R.; Jalali, D.; Inozemtseva, L.; Ernst, M.D.; Holmes, R.; Fraser, G. Are Mutants a Valid Substitute for Real Faults in Software Testing. In Proceedings of the 22nd ACM SIGSOFT International Symposium on Foundations of Software Engineering (FSE’14), Hong Kong, China, 16–22 November 2014; ACM: Copenhagen, Denmark, 2014; pp. 654–665. [Google Scholar]
- Rad, M.; Akbari, F.; Bakht, A. Implementation of common genetic and bacteriological algorithms in optimizing testing data in mutation testing. In Proceedings of the 2010 International Conference on Computational Intelligence and Software Engineering (CiSE), Wuhan, China, 10–12 December 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 1–6. [Google Scholar]
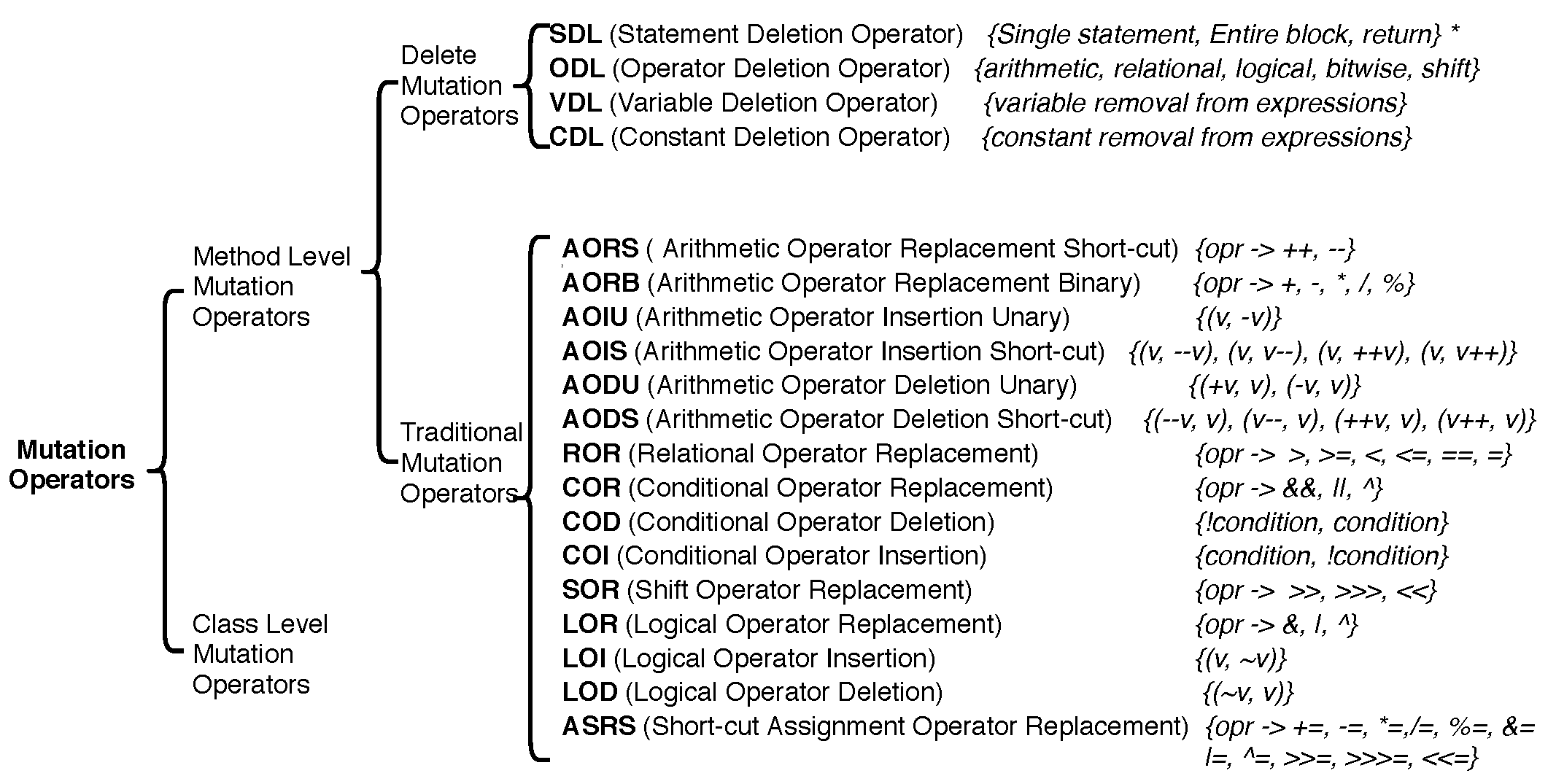
- Ma, Y.S.; Offutt, J. Description of method-level mutation operators for java. Electronics and Telecommunications Research Institute, Korea. 2005. Available online: https://cs.gmu.edu/~offutt/mujava/mutopsMethod.pdf (accessed on 8 September 2019).
- DeMillo, R.A.; Lipton, R.J.; Sayward, F.G. Hints on test data selection: Help for the practicing programmer. Computer 1978, 11, 34–41. [Google Scholar] [CrossRef]
- Hamlet, R.G. Testing programs with the aid of a compiler. IEEE Trans. Softw. Eng. 1977, 3, 279–290. [Google Scholar] [CrossRef]
- Offutt, A.J.; Untch, R.H. Mutation 2000: Uniting the Orthogonal. In Mutation Testing for the New Century, MUTATION 2001 Workshop; Springer: Berlin, Germany, 2001; pp. 34–44. [Google Scholar]
- Jia, Y.; Harman, M. An analysis and survey of the development of mutation testing. IEEE Trans. Softw. Eng. 2011, 37, 649–678. [Google Scholar] [CrossRef]
- Grun, B.J.M.; Schuler, D.; Zeller, A. The Impact of Equivalent Mutants. In Proceedings of the 2009 International Conference on Software Testing, Verification, and Validation Workshops, Denver, CO, USA, 1–4 April 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 192–199. [Google Scholar]
- Just, R.; Schweiggert, F. Higher accuracy and lower run time: Efficient mutation analysis using non-redundant mutation operators. Softw. Test. Verif. Reliab. 2015, 25, 490–507. [Google Scholar] [CrossRef]
- Budd, T.A.; Angluin, D. Two Notions of Correctness and Their Relation to Testing. Acta Inf. Springer 1982, 18, 31–45. [Google Scholar] [CrossRef]
- Offutt, A.J.; Pan, J. Detecting equivalent mutants and the feasible path problem. In Proceedings of the Eleventh Annual Conference on Computer Assurance, Systems Integrity, Software Safety. Process Security(COMPASS’96), Stockholm, Sweden, 17–21 June 1996; IEEE: Piscataway, NJ, USA, 1996; pp. 224–236. [Google Scholar]
- Kintis, M.; Papadakis, M.; Jia, Y.; Malevris, M.; Traon, Y.L.; Harman, M. Detecting Trivial Mutant Equivalences via Compiler Optimisations. IEEE Trans. Softw. Eng. 2018, 44, 308–332. [Google Scholar] [CrossRef]
- Untch, R. Mutation-based Software Testing Using Program Schemata. In Proceedings of the 30th Annual Southeast Regional Conference (ACM-SE’92), Raleigh, NC, USA, 8–10 April 1992; ACM: Copenhagen, Denmark, 1992; pp. 285–291. [Google Scholar]
- Offutt, A.J.; Lee, A.; Rothermel, G.; Untch, R.H.; Zapf, C. An experimental determination of sufficient mutant operators. ACM Trans. Softw. Eng. Methodol. 1996, 5, 99–118. [Google Scholar] [CrossRef]
- Jia, Y.; Harman, M. Constructing Subtle Faults Using Higher Order Mutation Testing. In Proceedings of the 8th International Working Conference on Source Code Analysis and Manipulation (SCAM’08), Beijing, China, 28–29 September 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 249–258. [Google Scholar]
- Mateo, P.R.; Usaola, M.P. Reducing Mutation Costs through uncovered Mutants. Softw. Test. Verif. Reliab. 2015, 25, 464–489. [Google Scholar] [CrossRef]
- Ma, Y.S.; Kim, S. Mutation testing cost reduction by clustering overlapped mutants. J. Syst. Softw. 2016, 115, 18–30. [Google Scholar] [CrossRef]
- Just, R.; Kurtz, B.; Ammann, P. Inferring Mutant Utility from Program Context. In Proceedings of the 26th ACM SIGSOFT International Symposium on Software Testing and Analysis (ISSTA’17), Toronto, ON, Canada, 17–21 July 2017; ACM: Copenhagen, Denmark, 2017; pp. 284–294. [Google Scholar]
- Gopinath, R.; Ahmed, I.; Alipour, M.A.; Jensen, C.; Groce, A. Mutation Reduction Strategies Considered Harmful. IEEE Trans. Reliab. 2017, 66, 854–874. [Google Scholar] [CrossRef]
- Jimenez, M.; Checkam, T.T.; Cordy, M.; Papadakis, M.; Kintis, M.; Traon, Y.L.; Harman, M. Are mutants really natural?: A study on how naturalness helps mutant selection. In Proceedings of the 12th ACM/IEEE International Symposium on Empirical Software Engineering and Measurement (ESEM’18), Oulu, Finland, 11–12 October 2018; ACM: Copenhagen, Denmark, 2018; pp. 1–10. [Google Scholar]
- Papadakis, M.; Checkam, T.T.; Traon, Y.L. Mutant Quality Indicators. In Proceedings of the International Conference on Software Testing, Verification and Validation Workshops (ICSTW), Västerås, Sweden, 9–13 April 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 32–39. [Google Scholar]
- Jimenez, M.; Checkam, T.T.; Cordy, M.; Papadakis, M.; Kintis, M.; Traon, Y.L.; Harman, M. Predicting the fault revelation utility of mutants. In Proceedings of the 40th International Conference on Software Engineering: Companion Proceeedings (ICSE’18), Gothenburg, Sweden, 27 May–3 June 2018; pp. 408–409. [Google Scholar]
- Pizzoleto, A.V.; Ferrari, F.C.; Offutt, J.; Fernandes, L. A systematic literature review of techniques and metrics to reduce the cost of mutation testing. J. Syst. Softw. 2019, 157, 110388. [Google Scholar] [CrossRef]
- Silva, R.A.; de Souza, S.; Do, R.S.; de Souza, P.S.L. A systematic review on search based mutation testing. Inf. Softw. Technol. 2017, 81, 19–35. [Google Scholar] [CrossRef]
- Jatana, N.; Suri, B.; Rani, S. Systematic Literature Review on Search Based Mutation Testing. e-Inf. Softw. Eng. J. 2017, 11, 59–76. [Google Scholar]
- Rodrigues, D.S.; Delamaro, M.E.; Correa, C.G.; Nunes, F.L.S. Using Genetic Algorithms in Test Data Generation: A Critical Systematic Mapping. ACM Comput. Surv. 2018, 51, 41:1–41:23. [Google Scholar] [CrossRef]
- Zhu, Q.; Panichella, A.; Zaidman, A. A Systematic Literature Review on how mutation testing supports quality assurance processes. Softw. Test. Verif. Reliab. 2018, 28, e1675. [Google Scholar] [CrossRef]
- Souza, F.C.; Papadakis, M.; Durelli, V.H.S.; Delamaro, M.E. Test Data Generation Techniques for mutation testing: A systematic mapping. In Proceedings of the 11th Workshop on Experimental Software Engineering Latin Americal Workshop (ESELAW), Pucón, Chile, 23–25 April 2014; Available online: http://pages.cs.aueb.gr/~mpapad/papers/eselaw2014.pdf (accessed on 8 September 2019).
- Baudry, B.; Hanh, V.L.; Jezequel, J.; Traon, Y.L. Building trust into OO components using a genetic analogy. In Proceedings of the 11th International Symposium on Software Reliability Engineering, San Jose, CA, USA, 8–11 October 2000; IEEE: Piscataway, NJ, USA, 2000; pp. 4–14. [Google Scholar]
- Baudry, B.; Hanh, V.L.; Traon, Y.L. Testing-for-trust: The genetic selection model applied to component qualification. In Proceedings of the 33rd International Conference on Technology of Object-Oriented Languages, St. Malo, France, 5–8 June 2000; IEEE: Piscataway, NJ, USA, 2000; pp. 108–119. [Google Scholar]
- Louzada, J.; Camilo-Junior, C.; Vincenzi, A.; Rodrigues, C. An elitist evolutionary algorithm for automatically generating test data. In Proceedings of the 2012 IEEE Congress on Evolutionary Computation (CEC), Brisbane, Australia, 10–15 June 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 1–8. [Google Scholar]
- Subramanian, S.; Natarajan, N. A tool for generation and minimization of test suite by mutant gene algorithm. J. Comput. Sci. 2011, 7, 1581–1589. [Google Scholar] [CrossRef][Green Version]
- Haga, H.; Suehiro, A. Automatic Test Case Generation based on Genetic Algorithm and Mutation Analysis. In Proceedings of the IEEE International Conference on Control System, Computing and Engineering, Penang, Malaysia, 23–25 November 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 119–123. [Google Scholar]
- Rani, S.; Suri, B. Implementing Time-Bounded Automatic Test Data Generation Approach Based on Search Based Mutation Testing. In Progress in Advanced Computing and Intelligent Engineering; Springer: Berlin, Germany, 2018; pp. 113–122. [Google Scholar]
- Molinero, C.; Nunez, M.; Andres, C. Combining Genetic Algorithms and Mutation Testing to Generate Test Sequences. In Proceedings of the International Work-Conference on Artificial Neural Networks, Salamanca, Spain, 9–12 June 2009; Springer: Berlin, Germany, 2009; pp. 343–350. [Google Scholar]
- Nilsson, R.; Offutt, J.; Mellin, J. Test Case Generation for Mutation-based Testing of Timeliness. Electron. Notes Theor. Comput. Sci. 2004, 164, 97–114. [Google Scholar] [CrossRef][Green Version]
- Bottaci, L. A genetic algorithm fitness function for mutation testing. In Proceedings of the International Workshop on Software Engineering, Metaheuristic Innovation Algorithms, Workshop of 23rd International Conference on Software Engineerng, Toronto, ON, Canada, 12–19 May 2001; pp. 3–7. [Google Scholar]
- Masud, M.; Nayak, A.; Zaman, M.; Bansal, N. Strategy for mutation testing using genetic algorithms. In Proceedings of the IEEE CCECE CCGEI, Sankatoon, SK, Canada, 1–4 May 2005; IEEE: Piscataway, NJ, USA, 2005; pp. 1049–1052. [Google Scholar]
- Mishra, K.K.; Tiwari, S.; Kumar, A.; Misra, A.K. An approach for mutation testing using elitist genetic algorithm. In Proceedings of the 3rd IEEE International Conference on Computer Science Information Technology, Chengdu, China, 9–11 July 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 426–429. [Google Scholar]
- Campos, J.; Ge, Y.; Albunian, N.; Fraser, G.; Eler, M.; Arcuri, A. An empirical evaluation of evolutionary algorithms for unit test suite generation. Inf. Softw. Technol. 2018, 104, 207–235. [Google Scholar] [CrossRef]
- Almasi, M.M.; Hemmati, H.; Fraser, G.; Eler, M.; Arcuri, A.; Benefelds, J. An Industrial Evaluation of Unit Test Generation: Finding Real Faults in a Financial Application. In Proceedings of the IEEE/ACM 39th International Conference on Software Engineering: Software Engineering in Practice Track (ICSE-SEIP), Buenos Aires, Argentina, 20–28 May 2017; pp. 263–272. [Google Scholar]
- Shamshiri, S.; Just, R.; Rojas, J.M.; Fraser, G.; McMinn, P.; Arcuri, A. Do Automatically Generated Unit Tests Find Real Faults? An Empirical Study of Effectiveness and Challenges. In Proceedings of the 30th IEEE/ACM International Conference on Automated Software Engineering (ASE), Washington, DC, USA, 9–13 November 2015; pp. 201–211. [Google Scholar]
- Shamshiri, S.; Rojas, J.M.; Gazzola, L.; Fraser, G. Random or Evolutionary Search for Object-Oriented Test Suite Generation? Softw. Test. Verif. Reliab. 2017, 28, 1–29. [Google Scholar] [CrossRef]
- Gay, G. Detecting Real Faults in the Gson Library Through Search-Based Unit Test Generation. In Proceedings of the International Symposium on Search Based Software Engineering (SSBSE), Montpellier, France, 8–9 September 2018; Springer: Berlin, Germany, 2018; pp. 385–391. [Google Scholar]
- Bashir, M.B.; Nadeem, A. A fitness function for evolutionary mutation testing of object-oriented programs. In Proceedings of the 9th International Conference on Emerging Technology, Islamabad, Pakistan, 9–10 December 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1–6. [Google Scholar]
- Bashir, M.B.; Nadeem, A. Improved Genetic Algorithm to Reduce Mutation Testing Cost. IEEE Access 2017, 5, 3657–3674. [Google Scholar] [CrossRef]
- Bashir, M.B.; Nadeem, A. An Experimental Tool for Search-Based Mutation Testing. In Proceedings of the International Conference on Frontiers of Information Technology, Islamabad, Pakistan, 17–19 December 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 30–34. [Google Scholar]
- Bashir, M.B.; Nadeem, A. An Evolutionary Mutation Testing System for Java Programs: eMuJava. In Intelligent Computing, Proceedings of the Intelligent Computing—Proceeding of Computing Conference (CompCom’19), London, UK, 16–17 July 2019; Springer: Berlin, Germany, 2019; Volume 998, pp. 847–865. [Google Scholar]
- Delgado-Pérez, P.; Medina-Bulo, I. Search-based mutant selection for efficient test suite improvement: Evaluation and results. Inf. Softw. Technol. 2018, 104, 130–143. [Google Scholar] [CrossRef]
- Delgado-Pérez, P.; Rose, L.M.; Medina-Bulo, I. Coverage-based quality metric of mutation opertaors for test suite improvement. Softw. Qual. J. 2019, 27, 823–859. [Google Scholar] [CrossRef]
- Delgado-Pérez, P.; Medina-Bulo, I.; Segura, S.; Garcia-Dominguez, A.; Jose, J. GiGAn: Evolutionary mutation testing for C++ object-oriented systems. In Proceedings of the Symposium on Applied Computing, Marrakech, Morocco, 3–7 April 2017; ACM: Copenhagen, Denmark, 2017; pp. 1387–1392. [Google Scholar]
- Ghiduk, A.S.; El-Zoghdy, S.F. CHOMK: Concurrent Higher-Order Mutants Killing Using Genetic Algorithm. Arab. J. Sci. Eng. 2018, 43, 7907–7922. [Google Scholar] [CrossRef]
- Rani, S.; Suri, B. An approach for Test Data Generation based on Genetic Algorithm and Delete Mutation Operators. In Proceedings of the Second International Conference on Advances in Computing and Communication Engineering, Rohtak, Dehradun, India, 1–2 May 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 714–718. [Google Scholar]
- Singh, Y. Software Testing; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Untch, R.H. On reduced neighborhood mutation analysis using a single mutagenic operator. In Proceedings of the 47th Annual Southeast Regional Conference, New York, NY, USA, 19–21 May 2009; ACM: Copenhagen, Denmark, 2009; pp. 71:1–71:4. [Google Scholar]
- Luke, S. Essentials of Metaheuristics, Lulu. 2009. Available online: https://cs.gmu.edu/~sean/book/metaheuristics/Essentials.pdf (accessed on 8 September 2019).
- Chakraborty, U.K.; Janikow, C.Z. An Analysis of Gray versus Binary Encoding in Genetic Search. Inf. Sci. 2003, 156, 253–269. [Google Scholar] [CrossRef]
- Gaffney, G.; Green, D.A.; Pearce, C.E.M. Binary versus real coding for genetic algorithm: A false dichotomy? ANZIAM J. 2009, 51, C347–C359. [Google Scholar] [CrossRef]
- Varshney, S.; Mehrotra, M. Search-Based Test Data Generator for Data-Flow Dependencies Using Dominance Concepts, Branch Distance and Elitism. Arab. J. Sci. Eng. 2016, 41, 853–881. [Google Scholar] [CrossRef]
- Fraser, G.; Wotawa, F. Redundancy Based Test-Suite Reduction. In Proceedings of the 10th International Conference on Fundamental Approaches to Software Engineering, Braga, Portugal, 24 March–1 April 2007; Springer: Berlin, Germany, 2007; pp. 291–305. [Google Scholar]
- Scheibenpflug, A.; Wagner, S. An Analysis of the Intensification and Diversification Behavior of Different Operators for Genetic Algorithms. In Proceedings of the International Conference on Computer Aided Systems Theory, Las Palmas de Gran Canaria, Spain, 10–15 February 2013; Springer: Berlin, Germany, 2013; pp. 364–371. [Google Scholar]
- Wei, W.; Li, C.M.; Zhang, H. A Switching Criterion for Intensification and Diversification in Local Search for SAT. J. Satisf. Boolean Model. Comput. 2008, 4, 219–237. [Google Scholar]
- Yang, X.-S.; Deb, S.; Fong, S. Metaheuristic Algorithms: Optimal Balance of Intensification and Diversification. Appl. Math. Inf. Sci. 2014, 8, 977–983. [Google Scholar] [CrossRef]
- Baluja, S.; Caruana, R. Removing the Genetics from the Standard Genetic Algorithm. In Proceedings of the Twelfth International Conference on International Conference on Machine Learning (ICML’95 P), Tahoe City, CA, USA, 9–12 July 1995; Morgan Kaufmann Publishers: Burlington, MA, USA, 1995; pp. 38–46. [Google Scholar]
- Guan, B.; Zhang, C.; Ning, J. Genetic algorithm with a crossover elitist preservation mechanism for protein–ligand docking. AMB Express 2017, 7, 174. [Google Scholar] [CrossRef] [PubMed]
- Estero-Botaro, A.; Palomo-Lozano, F.; Medina-Bulo, I.; Domínguez-Jiménez, J.J.; García-Domínguez, A. Quality metrics for mutation testing with applications to WS-BPEL compositions. Softw. Test. Verif. Reliab. 2015, 25, 536–571. [Google Scholar] [CrossRef]
- EvoSuite—Automated Generation of JUnit Test Suites for Java Classes. Available online: https://github.com/EvoSuite/evosuite/ (accessed on 8 May 2019).
- Liang, Y.D. Introduction to Java Programming; Pearson Education Inc.: Upper Saddle River, NJ, USA, 2011. [Google Scholar]
- Ammann, P.; Offutt, J. Introduction to Software Testing; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Apache Commons Math. Available online: https://github.com/apache/commons-math (accessed on 8 May 2019).
- Smallest Largest. Available online: https://github.com/VMehta99/SmallestLargest/blob/master/SmallestLargest.java (accessed on 8 August 2018).
- Software-Artifact Infrastructure Repository. Available online: http://sir.unl.edu/portal/index.php (accessed on 8 May 2019).
- Ma, Y.S.; Offutt, J.; Kwon, Y.R. Mujava: An automated class mutation system. Softw. Test. Verif. Reliab. 2005, 15, 97–133. [Google Scholar] [CrossRef]
- Deng, L.; Offutt, J.; Li, N. Empirical evaluation of the statement deletion mutation operator. In Proceedings of the 2013 IEEE Sixth International Conference on Software Testing, Verification and Validation, Luxembourg, 18–20 March 2013; IEEE Computer Society: Washington, DC, USA, 2013; pp. 84–93. [Google Scholar]
- Delamaro, M.E.; Offutt, J.; Ammann, P. Designing deletion mutation operators. In Proceedings of the 2014 IEEE International Conference on Software Testing, Verification, and Validation, Cleveland, OH, USA, 31 March–4 April 2014; IEEE Computer Society: Washington, DC, USA, 2014; pp. 11–20. [Google Scholar]
- Basili, V.R.; Shull, F.; Lanubile, F. Building knowledge through families of experiments. IEEE Trans Softw. Eng. 1999, 25, 456–473. [Google Scholar] [CrossRef]
- Patrick, M.; Jia, Y. KD-ART: Should we intensify or diversify tests to kill mutants? Inf. Softw. Technol. 2017, 81, 36–51. [Google Scholar] [CrossRef][Green Version]
- Gonzalez-Hernandez, L.; Offutt, J.; Potena, P. Using Mutant Stubbornness to Create Minimal and Prioritized Test Sets. In Proceedings of the International Conference on Software Quality, Reliability, and Security, Lisbon, Portugal, 16–20 July 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 446–457. [Google Scholar]


| Authors | Year | Tool Available? | S | M | Approach | P | Fitness Function |
|---|---|---|---|---|---|---|---|
| Baudry [40,41] | 2000 | No | 1 | TM | GA | - | Mutation Score |
| Masud [49] | 2005 | No | - | TM | GA | - | Botacci Fitness function |
| Molinero [46] | 2009 | No | - | - | EGA | 50 | Mutation Score |
| Mishra [50] | 2010 | No | - | TM | EGA | - | Botacci Fitness function |
| Fraser [9] | 2012 | Yes | 10 | TM | GA | 100 | Branch, Mutation Distance & Mutation Impact |
| Fraser [10] | 2015 | Yes | 40 | TM | GA | 100 | Branch, Mutation Distance & Mutation Impact |
| Subramanian [43] | 2011 | No | 21 | TM | GA | - | Mutation Score |
| Haga [44] | 2012 | No | 1 | TM | GA | - | Mutation Score |
| Louzada [42] | 2012 | No | 3 | TM | EGA | - | Mutation Score |
| Bashir [57] | 2017 | Yes | 10 | TM, CM | IGA | 50 | State-Based Fitness Function |
| Ghiduk [63] | 2018 | No | 4 | HOM | GA | 10–20 | Mutation Score |
| Delgado-Perez [60] | 2018 | No | 8 | - | GA | 5% * | Mutation Quality Based Fitness Function |
| This study | - | - | 14 | Delete Mutation Operators | EGA | 10 × I | Test Case Effectiveness and its Complexity in terms of time-steps |
| Initial Population Evaluation | ||||||
|---|---|---|---|---|---|---|
| Initial Population | Mutants Killed | Mutation Score | Fitness | Status | ||
| (24) | 10 | 5 | , , , , | 50 | 50.125 | N |
| (40) | 10 | 3 | , , | 30 | 30.23 | R |
| (59) | 10 | 2 | , | 20 | 20.145 | R |
| (15) | 10 | 2 | , | 20 | 20.52 | R |
| (81) | 10 | 1 | 10 | 10.23 | N | |
| (103) | 10 | 1 | 10 | 10.45 | N | |
| (33) | 10 | 4 | , , , | 40 | 40.245 | N |
| (112) | 10 | 1 | 10 | 10.100 | R | |
| Mutation Coverage for Initial Population: 80%, Live Mutants: , | ||||||
| Begin Iteration 1: Perform Crossover (Intensification) | ||||||
| Selected Cases | Crossover Offspring | Mutants Killed | Mutation Score | Fitness | Status | |
| (24) | (25) | 5 | , , , , | 50 | 50.234 | R |
| (33) | (32) | 1 | 10 | 10.5 | N | |
| At the end of Iteration 1: Non-Redundant Test suite (Crossover and Elitist Test Cases) | ||||||
| Initial Population | Mutants Killed | Mutation Score | Fitness | Status | ||
| (24) | 10 | 5 | , , , , | 50 | 50.125 | N |
| (81) | 10 | 1 | 10 | 10.23 | N | |
| (103) | 10 | 1 | 10 | 10.45 | N | |
| (33) | 10 | 4 | , , , | 40 | 40.245 | N |
| (32) | 10 | 1 | 10 | 10.5 | N | |
| Mutation Coverage for current Population: 90%, Live Mutants: | ||||||
| Begin Iteration 2: Add 3 more test cases to maintain the size of population | ||||||
| Initial Population | Mutants Killed | Mutation Score | Fitness | Status | ||
| (24) | 10 | 5 | , , , , | 50 | 50.125 | N |
| (81) | 10 | 1 | 10 | 10.23 | N | |
| (103) | 10 | 1 | 10 | 10.45 | N | |
| (33) | 10 | 4 | , , , | 40 | 40.245 | N |
| (32) | 10 | 1 | 10 | 10.5 | N | |
| (56) | 10 | 2 | , | 20 | 20.45 | R |
| (78) | 10 | 1 | 10 | 10.20 | R | |
| (87) | 10 | 1 | 10 | 10.30 | R | |
| Perform Crossover (Intensification) | ||||||
| Selected Cases | Crossover Offspring | Mutants Killed | Mutation Score | Fitness | Status | |
| (24) | (40) | 3 | , , | 30 | 30.23 | R |
| (33) | (17) | 2 | , | 20 | 20.55 | R |
| Perform Mutation (Diversification) | ||||||
| Crossover Cases | Mutation Offspring | Mutants Killed | Mutation Score | Fitness | Status | |
| (40) | (44) | 2 | , | 20 | 20.43 | N |
| (17) | (21) | 1 | 10 | 10.8 | R | |
| At the end of Iteration 2: Non-Redundant Test suite (Mutation and Elitist Test Cases) | ||||||
| Initial Population | Mutants Killed | Mutation Score | Fitness | Status | ||
| (24) | 10 | 5 | , , , , | 50 | 50.125 | N |
| (81) | 10 | 1 | 10 | 10.23 | N | |
| (33) | 10 | 4 | , , , | 40 | 40.245 | N |
| (32) | 10 | 1 | 10 | 10.5 | N | |
| (44) | 10 | 2 | , | 20 | 20.43 | N |
| Mutation Coverage for current Population: 100%, No Live Mutants | ||||||
| S | Programs | #Methods | Considered Method | #Inputs | Description |
|---|---|---|---|---|---|
| S1 | Bessj [78] | 3 | bessj | 2 | artificial numeric case study |
| S2 | EvenOdd [4] | 1 | checkEvenOdd | 1 | checks a number if even or odd |
| S3 | GCD* [79] | 1 | gcd | 2 | finds the greatest common divisor |
| S4 | Power [80] | 1 | power | 2 | calculates the power of a number |
| S5 | Primes [81] | 2 | nextPrime | 1 | returns the next prime number |
| S6 | Quadratic [65] | 1 | get_roots | 3 | quadratic equation solver |
| S7 | Remainder [4] | 1 | getRemainder | 2 | returns remainder of two numbers |
| S8 | SmallestLargest [82] | 3 | getMinMax | 5 | finds smallest and largest number |
| S9 | Stats [80] | 1 | computeStats | 6 | returns statistics of given numbers |
| S10 | StudentDivison [65] | 1 | cal_division | 3 | returns the division of a student |
| S11 | TrashAndTakeOut [80] | 2 | trash | 1 | performs some calculations |
| S12 | Trityp [80] | 1 | Triang | 3 | returns the type of triangle |
| S13 | Tritype2 [83] | 1 | Triang | 3 | returns the type of triangle |
| S14 | Triangle [65] | 1 | find_tri_class | 3 | returns the type of triangle |
| S | LOC | ODL% | SDL% | Traditional% |
|---|---|---|---|---|
| S1 | 153 | 100 | 93 | 85 |
| S2 | 19 | 100 | 100 | 91 |
| S3 | 20 | 93 | 80 | 88 |
| S4 | 43 | 100 | 83 | 85 |
| S5 | 54 | 58 | 76 | 55 |
| S6 | 42 | 100 | 100 | 86 |
| S7 | 19 | 100 | 86 | 78 |
| S8 | 62 | 100 | 90 | 90 |
| S9 | 30 | 98 | 85 | 82 |
| S10 | 36 | 86 | 100 | 93 |
| S11 | 37 | 100 | 100 | 77 |
| S12 | 53 | 98 | 97 | 89 |
| S13 | 73 | 100 | 100 | 95 |
| S14 | 44 | 100 | 96 | 95 |
| Total % for S1–S14 | 97% | 92% | 87% |
| S | Equivalent Mutants% | Exceptional Mutants% | ||||
|---|---|---|---|---|---|---|
| ODL | SDL | Traditional | ODL | SDL | Traditional | |
| S1 | 0 | 7 | 11 | 0 | 0 | 4 |
| S2 | 0 | 0 | 4 | 0 | 0 | 4 |
| S3 | 0 | 0 | 3 | 7 | 20 | 9 |
| S4 | 0 | 0 | 5 | 0 | 17 | 10 |
| S5 | 8 | 17 | 16 | 33 | 7 | 29 |
| S6 | 0 | 0 | 10 | 0 | 0 | 4 |
| S7 | 0 | 0 | 9 | 0 | 14 | 13 |
| S8 | 0 | 10 | 9 | 0 | 0 | 1 |
| S9 | 2 | 8 | 5 | 0 | 8 | 12 |
| S10 | 14 | 0 | 5 | 0 | 0 | 2 |
| S11 | 0 | 0 | 14 | 0 | 0 | 9 |
| S12 | 3 | 3 | 10 | 0 | 0 | 1 |
| S13 | 0 | 0 | 4 | 0 | 0 | 2 |
| S14 | 0 | 0 | 4 | 0 | 4 | 1 |
| Total % for S1–S14 | 2% | 5% | 7% | 1% | 3% | 6% |
| Parameters | Description |
|---|---|
| Goal | To investigate how GA with higher mutation coverage perform to automatically generate the low-cost test suite |
| Question | Q1 Is our approach more effective and efficient than Evosuite. How much our approach can improve the Initial Random tests at finding the faults? |
| Q2 Is the approach stable in killing above 90% mutants? | |
| Q3 How different parameters of the approach impacts the performance? | |
| Metric | Mutation Score, Number of Hard Mutants, Test Suite Size, Test Case Efficiency |
| Object of Study | tdgen_gamt, Evosuite and Initial Random tests |
| Purpose | Measure the effectiveness and efficiency of tdgen_gamt and evaluate the improvement in performance over Evosuite and Initial Random tests. To evaluate how much efficient tests are generated. |
| Focus | Generating the low-cost test data, covering the maximum number of faults |
| Perspective | Researcher point of view |
| Context | First Order SDL, ODL and Traditional Method Level Mutants |
| S | Coverage % | TGT* (Seconds) | Iterations | TSS* | Fitness Evaluation |
|---|---|---|---|---|---|
| S1 | 100.00 | 2.1 | 6 | 7 | 92 |
| S2 | 100.00 | 0.1 | 3 | 4 | 24 |
| S3 | 99.91 | 0.8 | 10 | 6 | 168 |
| S4 | 99.90 | 0.7 | 9 | 6 | 146 |
| S5 | 98.62 | 0.7 | 22 | 8 | 105 |
| S6 | 98.00 | 5.5 | 28 | 9 | 633 |
| S7 | 99.60 | 0.7 | 10 | 6 | 166 |
| S8 | 100.00 | 1.2 | 3 | 16 | 107 |
| S9 | 100.00 | 7.9 | 2 | 13 | 117 |
| S10 | 100.00 | 0.5 | 2 | 11 | 60 |
| S11 | 99.06 | 0.4 | 13 | 5 | 99 |
| S12 | 88.11 | 10.2 | 30 | 16 | 532 |
| S13 | 96.85 | 5.8 | 30 | 13 | 574 |
| S14 | 94.24 | 9.3 | 30 | 15 | 513 |
| Average | 98.16% | 3.3 | 14 | 10 | 238 |
| S. No | Mutation Operator |
|---|---|
| 1. | Delete Field |
| 2. | Delete Call |
| 3. | Insert Unary Operator |
| 4. | Replace Arithmetic Operator |
| 5. | Replace Bitwise Operator |
| 6. | Replace Comparison Operator |
| 7. | Replace Constant |
| 8. | Replace Variable |
| S | Coverage Over SDL-ODL Mutants (%) | Coverage Over Traditional Mutants (%) | ||||
|---|---|---|---|---|---|---|
| tdgen_gamt | Evosuite | Initial | tdgen_gamt | Evosuite | Initial | |
| S1 | 100.00 ± 0.000 | 96.33 ± 2.530 | 96.69 ± 0.019 | 95.99 ± 0.005 | 98.53 ± 0.086 | 95.05 ± 0.011 |
| (100.00) | (96.47) | (95.29) | (96.00) | (98.56) | (95.41) | |
| S2 | 100.00 ± 0.000 | 100.00 ± 0.000 | 90.00 ± 0.094 | 90.65 ± 0.007 | 95.35 ± 0.000 | 86.47 ± 0.045 |
| (100.00) | (100.00) | (91.66) | (90.69) | (95.35) | (86.04) | |
| S3 | 99.91 ± 0.006 | 85.91 ± 6.818 | 88.09 ± 0.047 | 92.92 ± 0.018 | 99.88 ± 0.485 | 91.08 ± 0.026 |
| (100.00) | (86.36) | (90.90) | (93.17) | (100.00) | (91.36) | |
| S4 | 99.90 ± 0.007 | 94.40 ± 3.955 | 89.60 ± 0.043 | 96.53 ± 0.007 | 100.00 ± 0.000 | 90.98 ± 0.025 |
| (100.00) | (95.00) | (90.00) | (97.00) | (100.00) | (91.18) | |
| S5 | 98.62 ± 0.020 | 94.14 ± 7.042 | 62.14 ± 0.162 | 88.72 ± 0.023 | 97.46 ± 0.383 | 66.64 ± 0.095 |
| (100.00) | (96.55) | (62.00) | (88.88) | (97.53) | (66.00) | |
| S6 | 98.00 ± 0.009 | 85.85 ± 4.927 | 83.76 ± 0.047 | 83.34 ± 0.057 | 98.10 ± 1.664 | 73.33 ± 0.055 |
| (97.56) | (87.80) | (82.90) | (80.23) | (97.67) | (72.10) | |
| S7 | 99.60 ± 0.016 | 88.67 ± 8.459 | 86.00 ± 0.090 | 98.26 ± 0.009 | 99.83 ± 0.900 | 93.68 ± 0.038 |
| (100.00) | (93.33) | (86.66) | (98.55) | (100.00) | (94.20) | |
| S8 | 100.00 ± 0.000 | 61.09 ± 8.987 | 95.87 ± 0.025 | 92.42 ± 0.007 | 97.98 ± 3.092 | 93.07 ± 0.016 |
| (100.00) | (60.87) | (95.65) | (92.70) | (99.23) | (93.48) | |
| S9 | 100.00 ± 0.000 | 88.69 ± 2.532 | 98.59 ± 0.010 | 95.96 ± 0.006 | 99.23 ± 0.905 | 97.00 ± 0.006 |
| (100.00) | (88.57) | (99.00) | (95.91) | (99.55) | (97.05) | |
| S10 | 100.00 ± 0.000 | 91.62 ± 5.275 | 94.59 ± 0.043 | 69.14 ± 0.046 | 90.98 ± 2.962 | 77.95 ± 0.064 |
| (100.00) | (91.89) | (94.59) | (67.89) | (90.20) | (76.90) | |
| S11 | 99.06 ± 0.022 | 100.00 ± 0.000 | 73.76 ± 0.132 | 86.99 ± 0.039 | 91.30 ± 0.000 | 68.03 ± 0.092 |
| (100.00) | (100.00) | (70.58) | (87.95) | (91.30) | (63.77) | |
| S12 | 88.11 ± 0.049 | 62.82 ± 7.832 | 50.79 ± 0.080 | 79.55 ± 0.052 | 90.93 ± 9.436 | 45.67 ± 0.083 |
| (89.47) | (64.47) | (47.36) | (80.70) | (94.62) | (44.88) | |
| S13 | 96.85 ± 0.018 | 89.53 ± 6.938 | 83.15 ± 0.044 | 90.55 ± 0.022 | 98.94 ± 0.853 | 69.33 ± 0.106 |
| (97.87) | (91.49) | (82.97) | (91.60) | (99.30) | (67.48) | |
| S14 | 94.24 ± 0.010 | 65.10 ± 2.956 | 85.76 ± 0.056 | 68.62 ± 0.091 | 90.38 ± 4.858 | 66.22 ± 0.081 |
| (93.90) | (65.24) | (86.58) | (65.07) | (94.59) | (66.36) | |
| S | SDL-ODL Mutants (%) | Traditional Mutants (%) | ||||
|---|---|---|---|---|---|---|
| tdgen_gamt | Evosuite | Initial | tdgen_gamt | Evosuite | Initial | |
| S1 | 0.0 | 0.0 | 0.0 | 2.6 | 1.4 | 1.4 |
| S2 | 0.0 | 0.0 | 0.0 | 7.0 | 4.7 | 4.7 |
| S3 | 0.0 | 0.0 | 0.0 | 4.3 | 0.0 | 0.0 |
| S4 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 |
| S5 | 0.0 | 0.0 | 0.0 | 4.0 | 2.5 | 2.5 |
| S6 | 0.0 | 0.0 | 2.4 | 0.6 | 0.0 | 1.7 |
| S7 | 0.0 | 0.0 | 0.0 | 1.4 | 0.0 | 0.0 |
| S8 | 0.0 | 0.0 | 0.0 | 3.8 | 0.8 | 0.8 |
| S9 | 0.0 | 1.0 | 0.0 | 2.3 | 0.5 | 0.0 |
| S10 | 0.0 | 0.0 | 0.0 | 2.0 | 2.0 | 0.0 |
| S11 | 0.0 | 0.0 | 0.0 | 1.4 | 8.7 | 1.4 |
| S12 | 1.3 | 1.3 | 9.2 | 3.6 | 3.1 | 5.9 |
| S13 | 0.0 | 0.0 | 2.1 | 0.7 | 0.7 | 2.4 |
| S14 | 1.2 | 6.1 | 3.7 | 2.6 | 5.4 | 4.6 |
| Total (%) | 0.3% | 1.1% | 1.9% | 2.5% | 1.9% | 2.1% |
| S | Test Case Efficiency | Test Suite Size | ||||
|---|---|---|---|---|---|---|
| tdgen_gamt | Evosuite | Initial | tdgen_gamt | Evosuite | Initial | |
| S1 | 13.7 ± 0.24 | 8.9 ± 0.97 | 4.8 ± 0.05 | 7.0 ± 0.14 | 11.1 ± 1.12 | 20.0 ± 0.00 |
| 13.7 | 9.0 | 4.8 | 7.0 | 11.0 | 20.0 | |
| S2 | 22.7 ± 0.18 | 19.1 ± 0.00 | 8.6 ± 0.45 | 4.0 ± 0.00 | 5.0 ± 0.00 | 10.0 ± 0.00 |
| 22.7 | 19.1 | 8.6 | 4.0 | 5.0 | 10.0 | |
| S3 | 15.5 ± 0.47 | 13.1 ± 1.16 | 4.6 ± 0.13 | 6.0 ± 0.14 | 7.7 ± 0.71 | 20.0 ± 0.00 |
| 15.6 | 12.5 | 4.6 | 6.0 | 8.0 | 20.0 | |
| S4 | 16.2 ± 0.36 | 12.7 ± 0.83 | 4.5 ± 0.12 | 6.0 ± 0.14 | 7.9 ± 0.50 | 20.0 ± 0.00 |
| 16.2 | 12.5 | 4.6 | 6.0 | 8.0 | 20.0 | |
| S5 | 11.6 ± 0.72 | 9.7 ± 0.04 | 6.7 ± 0.94 | 7.7 ± 0.61 | 10.0 ± 0.00 | 10.0 ± 0.00 |
| 11.3 | 9.8 | 6.6 | 8.0 | 10.0 | 10.0 | |
| S6 | 9.1 ± 0.24 | 9.6 ± 0.36 | 2.4 ± 0.18 | 9.2 ± 0.39 | 10.2 ± 0.38 | 30.0 ± 0.00 |
| 8.9 | 9.8 | 2.4 | 9.0 | 10.0 | 30.0 | |
| S7 | 16.6 ± 0.73 | 14.4 ± 0.64 | 4.7 ± 0.19 | 5.9 ± 0.24 | 7.0 ± 0.28 | 20.0 ± 0.00 |
| 16.4 | 14.3 | 4.7 | 6.0 | 7.0 | 20.0 | |
| S8 | 5.9 ± 0.22 | 5.7 ± 0.34 | 1.9 ± 0.03 | 15.8 ± 0.63 | 17.2 ± 0.89 | 50.0 ± 0.00 |
| 5.8 | 5.7 | 1.9 | 16.0 | 17.0 | 50.0 | |
| S9 | 7.4 ± 0.04 | 6.1 ± 0.26 | 1.6 ± 0.01 | 13.0 ± 0.00 | 16.4 ± 0.72 | 60.0 ± 0.00 |
| 7.4 | 6.2 | 1.6 | 13.0 | 16.0 | 60.0 | |
| S10 | 6.3 ± 0.41 | 7.0 ± 0.42 | 2.6 ± 0.21 | 11.0 ± 0.00 | 13.1 ± 0.64 | 30.0 ± 0.00 |
| 6.2 | 6.9 | 2.6 | 11.0 | 13.0 | 30.0 | |
| S11 | 18.0 ± 0.96 | 18.3 ± 0.00 | 6.8 ± 0.91 | 4.8 ± 0.37 | 5.0 ± 0.00 | 10.0 ± 0.00 |
| 17.7 | 18.3 | 6.4 | 5.0 | 5.0 | 10.0 | |
| S12 | 5.1 ± 0.22 | 5.2 ± 0.65 | 1.5 ± 0.27 | 15.5 ± 1.01 | 17.5 ± 1.37 | 30.0 ± 0.00 |
| 5.1 | 5.3 | 1.50 | 16.0 | 17.0 | 30.0 | |
| S13 | 7.1 ± 0.11 | 5.2 ± 0.75 | 2.3 ± 0.35 | 12.7 ± 0.50 | 19.3 ± 2.33 | 30.0 ± 0.00 |
| 7.1 | 5.0 | 2.2 | 13.0 | 20.0 | 30.0 | |
| S14 | 4.7 ± 0.62 | 5.6 ± 0.45 | 2.2 ± 0.27 | 14.7 ± 0.46 | 16.3 ± 0.93 | 30.0 ± 0.00 |
| 4.4 | 5.6 | 2.2 | 15.0 | 17.0 | 30.0 | |
| S | |||
|---|---|---|---|
| S1 | 0 | 0 | 0 |
| S2 | 0 | 0 | 0 |
| S3 | 2 | 0 | 0 |
| S4 | 2 | 0 | 0 |
| S5 | 36 | 4 | 0 |
| S6 | 82 | 0 | 0 |
| S7 | 6 | 6 | 0 |
| S8 | 0 | 0 | 0 |
| S9 | 0 | 0 | 0 |
| S10 | 0 | 0 | 0 |
| S11 | 16 | 16 | 0 |
| S12 | 100 | 100 | 64 |
| S13 | 98 | 20 | 0 |
| S14 | 100 | 92 | 0 |
| Parameters | Value |
|---|---|
| Initial Population | 5×Inputs, 10×Inputs, 15×Inputs, 20×Inputs |
| Fitness Function | |
| Parent Selection | Fittest 25%, 50% |
| Crossover | Uniform Crossover |
| Mutation | One-Point Mutation |
| Convergence Criteria | 100% Mutation Score or Iteration Limit |
| Iteration Limit | 30, 50, 100 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rani, S.; Suri, B.; Goyal, R. On the Effectiveness of Using Elitist Genetic Algorithm in Mutation Testing. Symmetry 2019, 11, 1145. https://doi.org/10.3390/sym11091145
Rani S, Suri B, Goyal R. On the Effectiveness of Using Elitist Genetic Algorithm in Mutation Testing. Symmetry. 2019; 11(9):1145. https://doi.org/10.3390/sym11091145
Chicago/Turabian StyleRani, Shweta, Bharti Suri, and Rinkaj Goyal. 2019. "On the Effectiveness of Using Elitist Genetic Algorithm in Mutation Testing" Symmetry 11, no. 9: 1145. https://doi.org/10.3390/sym11091145
APA StyleRani, S., Suri, B., & Goyal, R. (2019). On the Effectiveness of Using Elitist Genetic Algorithm in Mutation Testing. Symmetry, 11(9), 1145. https://doi.org/10.3390/sym11091145





