CSE_E 1.0: An Integrated Automated Theorem Prover for First-Order Logic
Abstract
1. Introduction
2. Overview of the Multi-Clause S-CS Rule in
2.1. Definitions and Some Terminologies
- There does not exist the same variables among (if there exist the same variables, a rename substitution can be applied to make them different);
- For each , a substitution can be applied to ( could be an empty substitution) and the same literals merged after substitution, denoted as ); can be partitioned into two sub-clauses and such that:
- , where and do not share the same literal, can be an empty clause, and cannot be an empty clause; moreover,
- For any , there exists at least one complementary pair among , and is called a separated standard contradiction (S-SC);
- The resulting clause , denoted as (here, “s” means “standard”, ), is called a standard contradiction separation clause (S-CS clause) of .
- , or,
- there exist , where , is a substitution to .
- Standard contradiction: This is a set of sub-clauses of selected literals from each input clause, and there exists at least one complementary pair of literals in it. Binary resolution only eliminates one complementary pair of literals, but the S-CS rule eliminates a standard contradiction.
- S-CS clause: This is the disjunction of the non-selected literals of the input clauses (the selected literals of input clauses are used for building a standard contradiction) and is the generated clause by the S-CS rule.
- Multi-clause deduction: The S-CS rule can handle more than two clauses in each deduction step. As Example 1 illustrates, the S-CS rule handles four input clauses in one deduction step, with three literals eliminated in and , respectively.
- Dynamic deduction: According to Definitions 1 and 2, when the S-CS rule handles multiple clauses, it contains many deduction steps, and the number of clauses involved in different deduction steps might be different. S-CS deduction provides a dynamic deduction process.
- Synergised deduction: In the process of S-CS deduction, the input clauses play a synergised deduction role, i.e., they work together to form a standard contradiction and generate an S-CS clause. As Example 1 illustrates, the S-CS rule handles four input clauses in the deduction step, where in helps to eliminate the literal in and the literal in , and in helps to eliminate the literal in and the literal in .
2.2. Theoretical Analysis of the S-CS Rule
- Ahead deduction: The input clause used in S-CS dynamic deduction can be the newly-generated clause and thus can make up the loss of proof search by binary inference based on saturation to a certain extent.
- Synergised deduction among multiple (two or more) clauses. Different from hyper-resolution and unit-resulting resolution, the S-CS dynamic deduction can make synergised deduction among multiple clauses, so it has a stronger capability of literal elimination. As shown in Example 1, three literals are eliminated in clauses and respectively by the S-CS rule. The bigger the standard contradiction is separated, the stronger the ability of literal elimination.
- In the process of proof search, the S-CS clauses generated by S-CS dynamic deduction are usually difficult to obtain by binary inference under the saturation algorithm with a given strategy. This is because the S-CS clauses usually contain fewer literals, where the separated standard contradiction in each deduction step is not simply composed by multiple (two or more) complementary pairs of literals; it is different from that of binary resolution or the chains of binary resolution method.
- The S-CS clauses usually contain fewer literals. Theory and practice show that under a reasonable control of the heuristic strategy, the S-CS dynamic deduction is guidable and controllable and generates S-CS clauses by separating standard contradictions (the contradiction is a literal set). The S-CS clauses usually have few literals or are unit clauses. Because finding refutation for a problem in first-order logic needs to infer an empty clause, this means that it is getting closer to finding refutation if the generated clauses have a smaller number of literals, and thus, it can potentially improve the deduction efficiency.
- Unit clauses can flexibly participate in S-CS dynamic deduction. According to the definition of the S-CS rule, a separated standard contradiction is still a standard contradiction after adding some unit clauses. At the same time, when a unit clause is participating in the deduction, the literal in the S-CS clause, which is unified complementary to the literal in the unit clause, can be removed and added to the current separated standard contradiction to form a new standard contradiction.
3. Heuristic Strategies in the
- Acceptable deduction: The acceptable deduction means the S-CS deduction step generates an S-CS clause that meets the user-defined requirements (e.g., number of literals, maximum term depth).
- Unacceptable deduction: The unacceptable deduction means the S-CS deduction step generates an S-CS clause that does not meet the user-defined requirements (e.g., number of literals, maximum term depth).
- Deduction distance: This is a measure of the distance of the selected clause to a negated conjecture clause according to the unified complementary relationship between literals.
- Backtracking mechanism: If the S-CS deduction step is an unacceptable deduction, the backtracking mechanism makes the deduction return to the last S-CS deduction step and then reselect a new input clause to participate in S-CS deduction.
- The maximum number of literals in an original clause: The maximum number of literals is recorded and used to guide setting the threshold of the number of literals in S-CS clause.
- The maximum term depth in an original clause: The maximum term depth is recorded and used to guide setting the threshold of the term depth of the S-CS clause and evaluating the substitutions in the process of S-CS dynamic deduction.
- The maximum symbol count in an original literal: The maximum symbol count is recorded and used to guide evaluating the substitutions in the process of S-CS dynamic deduction and the selection of the unit clause.
3.1. Unit Clause Selection Strategy
3.2. Non-Unit Clause Selection Strategy
3.3. Literal Selection Strategy
3.4. S-CS Clause Control Strategy
- Maximum number of literals: The number of literals is an important indicator for clause evaluating, especially for the newly generated clauses by deduction. Control the maximum number of literals in an S-CS clause, and improve the efficiency of the S-CS dynamic deduction. For example, when this threshold value is set to one, the generated S-CS clauses by S-CS dynamic deduction will be all unit clauses. supports two methods to set the threshold of the maximum number of literals in an S-CS clause: one is user-defined by strategy parameter, and the other is automatically set according to the maximum number of literals in different original clause sets when facing different problems.
- Maximum term depth: when a variable in a function symbol is unified in the process of S-CS dynamic deduction, it may increase the depth of the function symbol, which will increase the complexity of subsequent deduction. Control maximum term depth of the S-CS clause, and improve the efficiency of the S-CS dynamic deduction. CSE also supports two methods to set the threshold of the maximum term depth in the S-CS clause: one is user-defined by the strategy parameter, and the other is automatically set according to the maximum term depth in different original clause sets when facing different problems.
4. Multi-Clause S-CS Dynamic Deduction Algorithm in the
- Step 1: According to the strategy parameter, denoted as K, of the number of selected unit clauses, a unit clause set as input clauses is selected by the unit clause selection strategy and added to (a clause set, initially empty). The selected unit clause is denoted as according to the order of the sequence number .
- Step 2: Select an input clause by the non-unit clause selection strategy, and denote it as .
- Step 3: Apply the S-CS rule to the selected clause ; construct a standard contradiction with the input clauses; and get and (m is the serial number of the selected clause). Then, the S-CS clause is generated. If the S-CS clause is an empty clause, go to Step 5. Otherwise, the S-CS clause will be checked based on the control conditions as follows: (1) if the S-CS clause is a tautology or a redundant clause; (2) the number of literals in the S-CS clause exceeds the threshold; (3) the term depth exceeds the threshold. When one of the above three conditions is satisfied, the S-CS deduction is unacceptable. The backtracking algorithm will be performed, and go to Step 2.The backtracking algorithm is used to return to the last deduction step in the process of S-CS dynamic deduction and needs do some clean-up tasks. It mainly includes: (1) clear the substitutions generated in the current deduction step; (2) remove literals in the S-CS clause and the constructed standard contradiction, which was added in the current deduction step; (3) the unacceptable deduction weight of clause increases by one, and the unacceptable deduction weights of literals in clause that were used for standard contradiction construction increase by one; (4) set the sequence number of the proof search in the last deduction step.
- Step 4: If the S-CS clause does not satisfy the three conditions in Step 3, the acceptable deduction weight of the clause increases by one, and the acceptable deduction weights of literals in the clause that were used for standard contradiction construction increases by one. The generated S-CS clause is represented as a lemma and added into the S-CS clause set, with the deduction distance being calculated and the deduction path being recorded. If the exit conditions are satisfied, then go to Step 5. Otherwise, in order to make full use of the clause to achieve a synergised deduction effect, do the following iterative processes: (1) If the clause contains substitution, then record this deduction path to avoid the repetition, clear substitutions of ; reuse ; and go to Step 3. When the number of reused times of the clause exceeds the set threshold, the sequence number j increases by one, and go to Step 2. (2) When the clause does not contain substitution, the sequence number j increases by one, and go to Step 2.
- Step 5: Exit this multi-clause dynamic deduction. The exit conditions include: (1) the S-CS clause is an empty clause, so we can conclude that the original clause set is unsatisfiable; (2) the number of input clauses reaches the set threshold; (3) the runtime reaches the set threshold; (4) the remaining memory reaches the set threshold.
- Step 6: The S-CS clause processing: internal simplification is performed on the generated S-CS clause set; apply forward simplification on the S-CS clause set using the clauses in the clause set; and apply the backward simplification on the clause set using the clauses in the S-CS clause set; then each S-CS clause is added into the clause set.
5. Lemma Filtration in
6. Experimental and Performance Analysis
6.1. Experiment Setup
6.2. Experimental Results and Analysis
6.2.1. Performance of 1.0 on CASC-26 FOF Division Problems
6.2.2. Performance of 1.0 on CASC-J9 FOF Division Problems
7. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Pavlov, V.; Schukin, A.; Cherkasova, T. Exploring Automated Reasoning in First-Order Logic: Tools, Techniques and Application Areas. In Proceedings of the 4th International Conference on Knowledge Engineering and the Semantic Web, St. Petersburg, Russia, 7–9 October 2013; pp. 102–116. [Google Scholar]
- Kovacs, L.; Voronkov, A. Finding Loop Invariants for Programs over Arrays Using a Theorem Prover. In Proceedings of the 12th International Conference on Fundamental Approaches to Software Engineering, York, UK, 22–29 March 2009; pp. 470–485. [Google Scholar]
- Nipkow, T.; Brinkop, H. Amortized Complexity Verified. J. Autom. Reason. 2019, 62, 367–391. [Google Scholar] [CrossRef]
- Sutcliffe, G. The TPTP Problem Library and Associated Infrastructure. From CNF to TH0, TPTP v6.4.0. J. Autom. Reason. 2017, 59, 483–502. [Google Scholar] [CrossRef]
- TSTP Solution Domains. Available online: http://www.tptp.org/cgi-bin/SeeTPTP?Category=Solutions (accessed on 16 May 2019).
- CASC Solution Domains. Available online: http://tptp.org/CASC/ (accessed on 16 May 2019).
- Robinson, J.A. A machine-oriented logic based on the resolution principle. J. ACM 1965, 12, 23–41. [Google Scholar] [CrossRef]
- Bachmair, L.; Ganzinger, H.; Lynch, C.; Snyder, W. Basic paramodulation and superposition. In Proceedings of the 11th International Conference on Automated Deduction, New York, NY, USA, 15–18 June 1992; pp. 462–476. [Google Scholar]
- Loveland, D.W. A linear format for resolution. In Automation of Reasoning 2: Classical Papers on Computational Logic; Siekmann, J.H., Wrightson, G., Eds.; Springer: Berlin/Heidelberg, Germany, 1983; pp. 399–416. [Google Scholar]
- Chang, C.L. The unit proof and the input proof in theorem proving. In Automation of Reasoning 2: Classical Papers on Computational Logic; Siekmann, J.H., Wrightson, G., Eds.; Springer: Berlin/Heidelberg, Germany, 1970; pp. 331–341. [Google Scholar]
- Robinson, J.A. Automatic deduction with hyper-resolution. Int. J. Comput. Math. 1965, 1, 227–234. [Google Scholar]
- Overbeek, R.; Mccharen, J.; Wos, L. Complexity and related enhancements for automated theorem-proving programs. Comput. Math. Appl. 1976, 2, 1–16. [Google Scholar] [CrossRef]
- Slaney, J.; Mccharen, B.W. Conflict resolution: A first-order resolution calculus with decision literals and conflict-driven clause learning. J. Autom. Reason. 2016, 12, 1–24. [Google Scholar]
- Reger, G.; Tishkovsky, D. Cooperating Proof Attempts. In Proceedings of the 25th International Conference on Automated Deduction, Berlin, Germany, 1–7 August 2015; pp. 339–355. [Google Scholar]
- Schulz, S.; Möhrmann, M. Performance of Clause Selection Heuristics for Saturation-Based Theorem Proving. In Proceedings of the 8th International Joint Conference on Automated Reasoning, Coimbra, Portugal, 27 June–2 July 2016; pp. 330–345. [Google Scholar]
- Meng, J.; Paulson, L.C. Lightweight relevance filtering for machine-generated resolution problems. J. Appl. Log. 2009, 7, 41–57. [Google Scholar] [CrossRef]
- Chvalovský, K.; Jakubův, J.; Suda, M.; Urban, J. ENIGMA-NG: Efficient Neural and Gradient-Boosted Inference Guidance for E. In Proceedings of the 27th International Conference on Automated Deduction, Natal, Brazil, 27–30 August 2019; pp. 197–215. [Google Scholar]
- Furbach, U.; Krämer, T.; Schon, C. Names Are Not Just Sound and Smoke: Word Embeddings for Axiom Selection. In Proceedings of the 27th International Conference on Automated Deduction, Natal, Brazil, 27–30 August 2019; pp. 250–268. [Google Scholar]
- Rawson, M.; Reger, G. Old or Heavy? Decaying Gracefully with Age/Weight Shapes. In Proceedings of the 27th International Conference on Automated Deduction, Natal, Brazil, 27–30 August 2019; pp. 462–476. [Google Scholar]
- Piotrowski, B.; Urban, J. ATPboost: Learning Premise Selection in Binary Setting with ATP Feedback. In Proceedings of the 9th International Joint Conference on Automated Reasoning, Oxford, UK, 14–17 July 2018; pp. 566–574. [Google Scholar]
- Xu, Y.; Liu, J.; Chen, S.W.; Zhong, X.M.; He, X.X. Contradiction separation based dynamic multi-clause synergised automated deduction. Inf. Sci. 2018, 462, 93–113. [Google Scholar] [CrossRef]
- Xu, Y.; Chen, S.W.; Liu, J.; Zhong, X.M.; He, X.X. Distinctive features of the contradiction separation based dynamic automated deduction. In Proceedings of the 13th International FLINS Conference, Belfast, UK, 21–24 August 2018; pp. 725–732. [Google Scholar]
- Schulz, S. System description: E 1.8. In Proceedings of the 19th International Conference on Logic for Programming Artificial Intelligence and Reasoning, Stellenbosch, South Africa, 14–19 December 2013; pp. 735–743. [Google Scholar]
- Sutcliffe, G. The 7th IJCAR Automated Theorem Proving System Competition-CASC-J7. AI Commun. 2015, 28, 683–692. [Google Scholar] [CrossRef]
- Sutcliffe, G. The 8th IJCAR Automated Theorem Proving System Competition-CASC-J8. AI Commun. 2016, 29, 607–619. [Google Scholar] [CrossRef]
- Sutcliffe, G. The 9th IJCAR Automated Theorem Proving System Competition-CASC-J9. AI Commun. 2018, 31, 495–507. [Google Scholar] [CrossRef]
- Kaliszyk, C.; Schulz, S.; Urban, J.; Vyskočil, J. System Description: E.T. 0.1. In Proceedings of the 25th International Conference on Automated Deduction, Berlin, Germany, 1–7 August 2015; pp. 389–398. [Google Scholar]
- Kühlwein, D.; Schulz, S.; Urban, J. E-MaLeS 1.1. In Proceedings of the 24th International Conference on Automated Deduction, New York, NY, USA, 9–14 June 2013; pp. 407–413. [Google Scholar]
- Daniel, K.; Urban, J. MaLeS: A Framework for Automatic Tuning of Automated Theorem Provers. J. Autom. Reason. 2013, 55, 91–116. [Google Scholar]
- Denzinger, J.; Kronenburg, M.; SCHULZ, S. DISCOUNT—A distributed and learning equational prover. J. Autom. Reason. 1997, 18, 189–198. [Google Scholar] [CrossRef]
- Mccune, W.; Wos, L. Otter—The CADE-13 competition incarnations. J. Autom. Reason. 1997, 18, 211–220. [Google Scholar] [CrossRef]
- Riazanov, A.; Voronkov, A. The design and implementation of vampire. AI Commun. 2002, 15, 91–110. [Google Scholar]
- Kovács, L.; Voronkov, A. First-order theorem proving and vampire. In Proceedings of the 25th International Conference on Computer Aided Verification, Saint Petersburg, Russia, 13–19 July 2013; pp. 1–35. [Google Scholar]
- BiereIoan, A.; Kovács, D.; Voronkov, A. Experimenting with SAT solvers in Vampire. In Proceedings of the 13th Mexican International Conference on Artificial Intelligence, Tuxtla Gutiérrez, Mexico, 16–22 November 2014; pp. 431–442. [Google Scholar]
- Schulz, S. E—A brainiac theorem prover. AI Commun. 2002, 15, 111–126. [Google Scholar]
- Korovin, K. iProver—An Instantiation-Based Theorem Prover for First-Order Logic (System Description). In Proceedings of the 4th International Joint Conference on Automated Reasoning, Sydney, Australia, 12–15 August 2008; pp. 292–298. [Google Scholar]
- Menouer, T.; Baarir, S. Parallel Satisfiability Solver Based on Hybrid Partitioning Method. In Proceedings of the 25th Euromicro International Conference on Parallel, Distributed and Network-Based Processing, Saint Petersburg, Russia, 6–8 March 2017; pp. 54–60. [Google Scholar]
- Maric, F. Formalization and implementation of modern SAT solvers. J. Autom. Reason. 2009, 43, 81–119. [Google Scholar] [CrossRef]
- Liang, J.H.; Ganesh, V.; Poupart, P.; Czarnecki, K. Learning Rate Based Branching Heuristic for SAT Solvers. In Proceedings of the 19th International Conference on Theory and Applications of Satisfiability Testing, Bordeaux, France, 5–8 July 2016; pp. 123–140. [Google Scholar]
- Moskewicz, M.W.; Madigan, C.F.; Zhao, Y.; Zhang, L.T.; Malik, S. Chaff: Engineering an efficient SAT solver. In Proceedings of the 38th Design Automation Conference, Las Vegas, NV, USA, 18–22 June 2001; pp. 530–535. [Google Scholar]
- Goldberg, E.; Novikov, Y. BerkMin: A Fast and Robust Sat-Solver. In Design, Automation, and Test in Europe; Lauwereins, R., Madsen, J., Eds.; Springer: Dordrecht, The Netherlands, 2008; pp. 465–478. [Google Scholar]
- Wu, G.F.; Chen, Q.S.; Xu, Y.; He, X.X. A Hybrid Learnt Clause Evaluation Algorithm for SAT Problem. Int. J. Comput. Intell. Syst. 2018, 12, 250–258. [Google Scholar] [CrossRef]

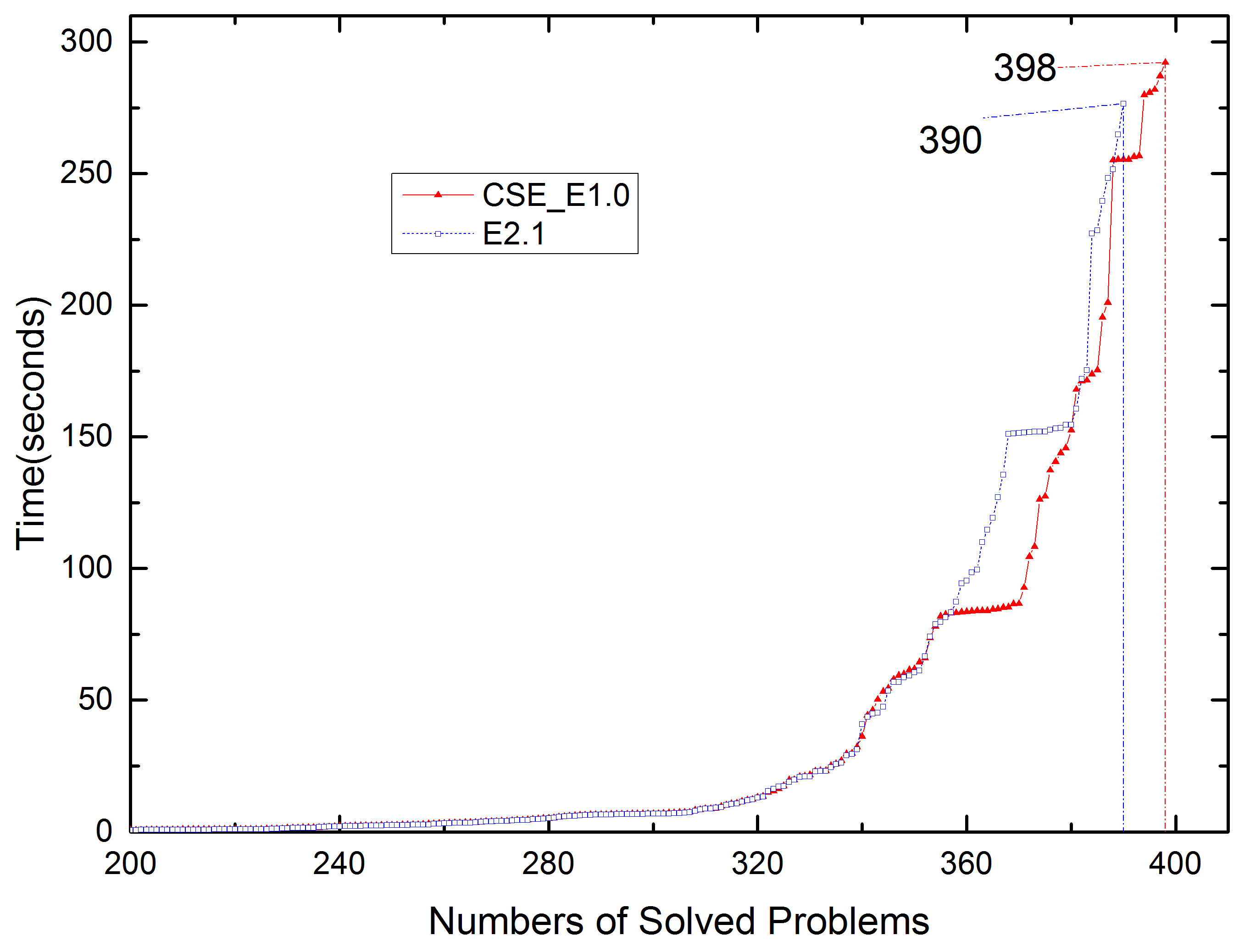
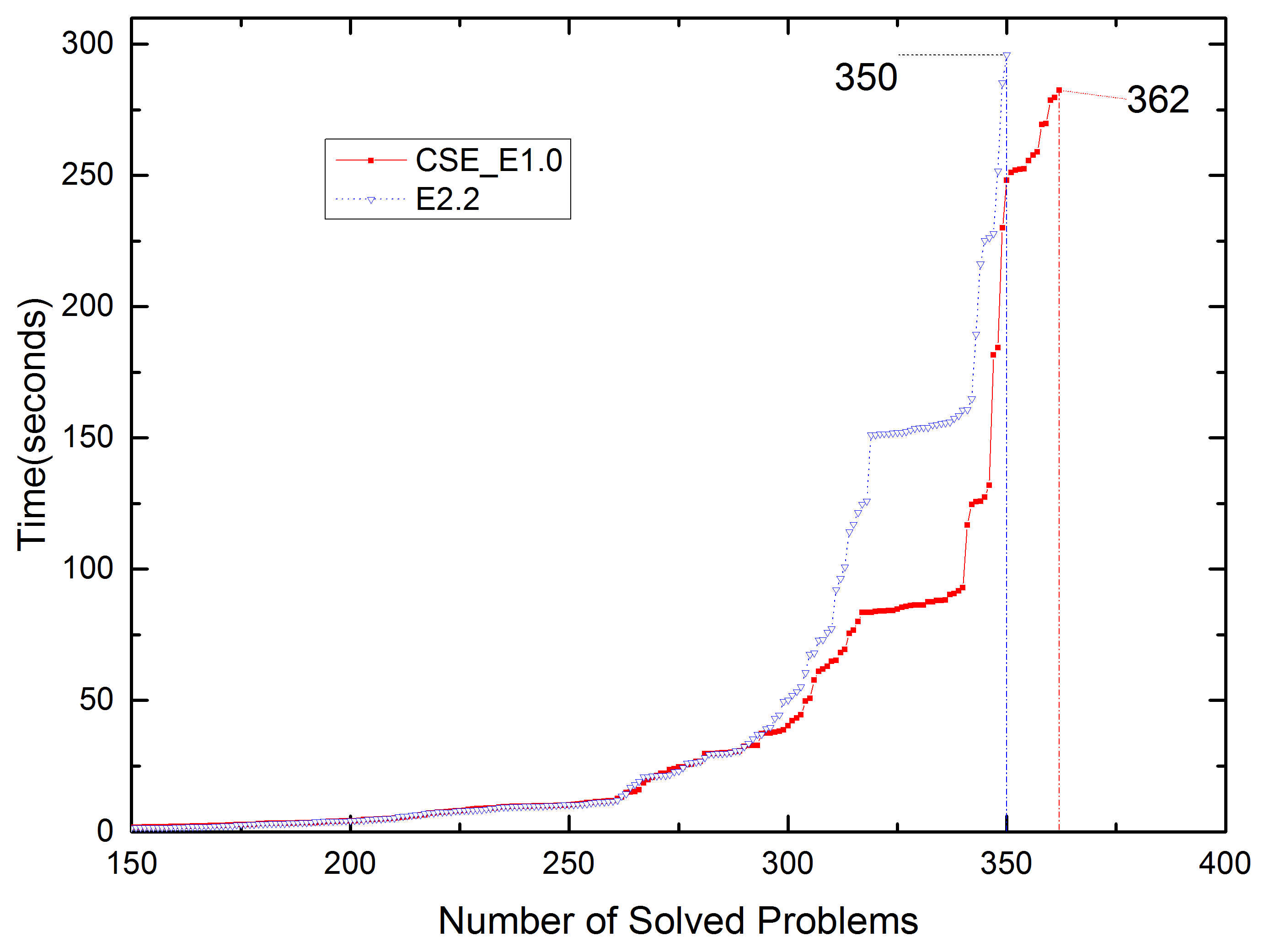
| Problem | Rating | Time (s) | Problem | Rating | Time (s) |
|---|---|---|---|---|---|
| GEO502+1 | 0.59 | 168 | SWB025+1 | 0.72 | 171.2 |
| SWB093+1 | 0.79 | 173.9 | SWB027+1 | 0.79 | 175.4 |
| BOO109+1 | 0.57 | 195.5 | GEO511+1 | 0.9 | 201 |
| GEO495+1 | 0.79 | 255.1 | GEO531+1 | 0.66 | 255.3 |
| GEO532+1 | 0.76 | 255.4 | GEO507+1 | 0.66 | 256.5 |
| SWB081+1 | 0.79 | 256.777 | GEO506+1 | 0.83 | 279.931 |
| AGT011+2 | 0.86 | 280.739 | SWB010+1 | 0.9 | 292.181 |
| Problem | Rating | Time (s) | Problem | Rating | Time (s) |
|---|---|---|---|---|---|
| AGT018+1 | 0.62 | 181.56 | SWB027+1 | 0.79 | 184.4 |
| GEO511+1 | 0.9 | 230.05 | BOO109+1 | 0.57 | 248.16 |
| SWB016+1 | 0.69 | 251.05 | SWB094+1 | 0.79 | 251.95 |
| SWB082+1 | 0.79 | 252.25 | SWW189+1 | 0.9 | 252.46 |
| SWB098+1 | 0.79 | 257.68 | SWV038+1 | 0.28 | 269.39 |
| SCT170+3 | 0.9 | 269.74 | GEO089+1 | 0.62 | 278.67 |
| SCT139+1 | 0.83 | 279.7 | GEO506+1 | 0.83 | 282.36 |
| Problems | Rating | Number of Formulae | Maximal Formula Depth | Number of Variables | Maximal Term Depth | Number of Atoms |
|---|---|---|---|---|---|---|
| GEO506+1 | 0.83 | 143 | 22 | 564 | 3 | 595 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, F.; Xu, Y.; Liu, J.; Chen, S.; Ning, X. CSE_E 1.0: An Integrated Automated Theorem Prover for First-Order Logic. Symmetry 2019, 11, 1142. https://doi.org/10.3390/sym11091142
Cao F, Xu Y, Liu J, Chen S, Ning X. CSE_E 1.0: An Integrated Automated Theorem Prover for First-Order Logic. Symmetry. 2019; 11(9):1142. https://doi.org/10.3390/sym11091142
Chicago/Turabian StyleCao, Feng, Yang Xu, Jun Liu, Shuwei Chen, and Xinran Ning. 2019. "CSE_E 1.0: An Integrated Automated Theorem Prover for First-Order Logic" Symmetry 11, no. 9: 1142. https://doi.org/10.3390/sym11091142
APA StyleCao, F., Xu, Y., Liu, J., Chen, S., & Ning, X. (2019). CSE_E 1.0: An Integrated Automated Theorem Prover for First-Order Logic. Symmetry, 11(9), 1142. https://doi.org/10.3390/sym11091142




