Abstract
On the high-demand bus route where there are commuting passengers, the stops for boarding and alighting passengers are concentrated in a certain section of the route. According to this demand pattern, transit operators need to respond symmetrically. Short-turning services promise benefits for both users and operators because a proportion of vehicles runs within shorter cycles and address a greater demand. The design of short-turning services mainly involves defining running section and frequency. Due to two sections of high and low demand being distinguished under the short-turning service, dealing with each section by vehicle type and selecting an appropriate vehicle type for each section can satisfy passengers demand well, instead of a single vehicle type. Considering the interests of passengers and buses, this paper establishes objective functions to determine the running section of short-turning buses by frequencies and vehicle types. Two optimization models with single and hybrid vehicle type are formulated that can be compared with each other and reflect the differences of method with hybrid vehicle type. Load factor is established as a performance measure to express the degree of utilization of bus resources. A layer-by-layer search method incorporating Monte Carlo simulation is proposed to solve the optimization model. Finally, the optimization approach is tested based on a bus route in Changchun City. Sensitivity analyses are then performed on the passenger demand and travel time.
1. Introduction
Public transit is an important mode of transportation. It can provide transport services for the vast number of passengers and alleviate traffic congestion and reduce emissions, which is conducive to the sustainable development of the city. However, in the transit system, there is a difference for passenger demand at each stop along the bus route. In certain sections, an aggregation of passengers with high passenger demand appears. To address this issue, implementation of a short-turning service that serves a certain section with high demand seems to be a promising operational strategy due to the differentiated service frequency for the stops with high and low demand. Meanwhile, with short-turning service, there are usually two bus fleets: all-stop fleet and short-turning fleet. Short-turning fleet only serves a part of bus route, while all-stop fleet serves every stop to mainly meet the travel demand reset of line. Short-turning services will be beneficial to both passengers and operators [1,2]. The running time of buses can be shortened and passengers at stops within short-turning sections can be treated with a high service frequency.
There is some research on the design problem of operational strategies to deal with the unbalanced distribution of the passengers and improve the efficiency along the corridor. The design of several bus services is explored and studied [3,4,5]. One of them is the limited-stop service: only stops of high demand are served to short the in-vehicle time of passengers and dwell time of buses. The second is short-turning service: some buses are provided to serve shorter cycles with high demand in the both directions. The last is deadheading service: vehicles do not allow boarding of any passengers within a certain section after departure.
With regard to the design of a short-turning service, the problem is to optimize the departure frequency and determine the short-turning section. Jordan and Turnquist [6] set up corresponding departure and service frequencies in different sections for a bus line. Furth [7] and Ceder [8] deemed that the frequency of a bus fleet with short-turning service is proportional to the frequency of vehicles with all-stop line. Site and Filippi [1] maximized the benefits of passenger and bus as an objective function to determine the short-turning stops and the frequency of short-turning line. Cortés et al. [9] introduced deadheading service into a short-turning line for a bus route and output starting and ending stops of bus serving in each direction. Zhang et al. [10] analyzed stop-skipping operation within a short-turning line. Meanwhile, as stochastic processes of bus travel time and reliability of bus operation receive more attention, real-time strategies have appeared for short-turning line [11,12,13,14,15,16]. Zhang et al. [17]) formulated a real-rime short-turning strategy given a passenger arrival distribution, and take a holding action at short-turning stops to improve transit service reliability.
For optimizing vehicle type and bus size, Ferland and Michelon [18] developed a heuristic method to address the bus scheduling problem by extending a single vehicle type to the multiple-vehicle-types problem. Ceder, Lee et al., and Olio et al. [19,20,21] proposed a optimization method considering the association between the characteristics of bus line and its required vehicle type to rationally configure the frequency of bus routes with a main terminal in a given transit timetable. Considering all bus routes sharing a terminal, Zhao et al. [22] optimized vehicle type in different periods to reduce operating costs and the wastage of resources.
These previous studies about the short-turning service usually focus on optimization of frequencies and running operation of buses with a single vehicle type. Meanwhile, based on research for the vehicle type, it can be seen that hybrid vehicle type (i.e., integrated small and large bus types) is an effective alternative to save operators costs and improve the level of bus service. Considering the advantage of hybrid vehicle type and distribution of passenger demand matching, hybrid vehicle type can be used for short-turning service with two bus fleets. Therefore, this paper takes the multiobjective optimization of short-turning service and vehicle type as the research purpose in the hope that bus fleets with suitable vehicle types are obtained to serve high- and low-demand sections along bus route. Following this introduction, Section 2 describes the process of passenger travel and bus operation, and expresses a variety of design models of short-turning service based on performance difference of bus fleets with single and hybrid vehicle types. Section 3 proposes an index denoted as load factor to quantify the effect of hybrid vehicle type. Section 4 constructs a search algorithm according to multiple decision variables in the objective function. Section 5 carries out a numerical case to test validity of the optimization model for short-turning service with hybrid vehicle type, compared with service of single vehicle type. Finally, Section 6 presents the conclusions.
2. Short-Turning Service Design Models for a Bus Route
To describe the design problem of short-turning service with hybrid vehicle type, it is assumed that there are N stops in two directions. According to a departure frequency, buses are dispatched from stop 1 and arrive at terminal stop N/2 in one direction, while in the other direction, stop N/2+1 and stop N are terminal stops in the other direction. Under short-turning service, there are two bus fleets including the short-turning fleet that serves the part of the route with high demand, and the all-stop fleet that serves all stops along the bus route. Buses of short-turning fleet equipped with separate frequency can turn back before they reach the terminal to improve the service level of route with high demand and save the operator costs. In this paper, two vehicle types are implemented for short-turning fleet and all-stop fleet, and it is assumed that the same vehicle type is set for each bus of one fleet. Given an origin–destination (O–D) matrix, the proposed design model is established to determine the short-turning section, frequencies, and optimal vehicle types of the two bus fleets.
2.1. Total Costs of a Bus Route
There are two constituent units in a transit system: passengers and buses. Passengers will spend waiting time at the stop and take an in-vehicle time in the bus to reach their destination, so passengers expect these two times to be minimal and this requires a higher frequency of buses. As for the buses that travel on a bus line, the operator to which the bus belongs expects to reduce operating costs and avoid excessively frequent departures. Considering the benefits to both passenger and operator, the passenger costs and operator costs can constitute optimization objectives.
Based on the travel habit of passengers, passenger costs can be determined by waiting time and in-vehicle time, as follows.
Waiting time cost is that passengers spend time waiting for the arrival of buses at stops. On a normal bus line, where buses serve every stop, the average waiting time is deduced by the frequency of departure (denoted by f), which can be expressed as k/f following Jansson [23]. Parameter k describes arrival distribution of vehicles. If the bus arrival is stochastic (e.g., Poisson distribution) under the influence of signal control or traffic jam, parameter k is set as 1, while with a fixed the interval of bus arrival, parameter k is equal to 0.5.
The expression is contrapuntally applicable for a bus route with a bus fleet, in which there is only one boarding choice for passengers. If there are more bus fleets to choose from (e.g., short-turning line), passengers can take a vehicle of any fleet which will serve their destination. In this circumstance, the waiting time cost of passengers traveling in a co-operation section with multiple bus fleets can be modeled following Zhang et al. (2016), as shown below:
where is the waiting time value per hour-passenger. and are frequencies of buses fleets for normal service and short-turning service. If an O–D pair of passengers is within the co-operation section , their waiting time depends on departure frequencies. If, specially, the origin or destination of an O–D pair is not within the co-operation section (), only one bus fleet is chosen by these passengers and their waiting time is k/fa in order to avoid causing transfer.
In-vehicle time cost of each passenger depend on trip distance and the speed of bus vehicles, so it includes bus running time between stops and the dwell time of buses. Running time and dwell time can be provided with the same value because in-vehicle passengers have the same understanding of the two times. Thus, given an O–D pair (i, j), the in-vehicle time cost of each passenger is formulated as follows:
where is the running time from stop to . is dwell time at stop . is the in-vehicle time value per hour and passenger and just reflects the cost of travel time, which has nothing to do with cost of in-vehicle crowding as the frequency of buses is optimized to meet the passenger demand in this study.
With regards to operator cost, to improve the efficiency of a bus service, it is mainly considered that the costs dependent on running time of vehicles can provide the required departure frequency. Thus, the running time of vehicles within one cycle and the cost per hour should be determined. If the operational cycle time is one hour, operator costs can be expressed by
where is the bus running time value per hour. The first term is operator costs of buses with normal service and second term is the operator costs of buses with the short-turning service.
2.2. Model for Short-Turning Service with Single Vehicle Type
The total costs of transit system for a bus route include the above three costs. In the case of single vehicle type, optimization variables are the serving scheme of short-turning and the frequencies of bus services. Thus, the objective function for this model is formulated as follows:
subject to
where is the passenger demand of an O–D pair (). equals 1 if short-turning vehicles serve the stop i and 0 otherwise. The first term in the above formula presents waiting time cost of two kinds of passenger demand: only choosing all-stop service and choosing both all-stop and short-turning services. It means that if both origin and destination of passengers are serving stops of short-turning vehicles,, passengers can choose short-turning service and their serving frequency is equal to . Correspondingly, the second term expresses in-vehicle time costs with the all-stop fleet and the short-turning fleet. Note that passengers within a short-turning section can take a bus from the all-stop fleet or short-turning fleet, and it is necessary to estimate the demand of these passengers. In this study, we assume that the attraction of each fleet depends on its frequency. The higher the frequency, the more passengers it attracts. Meanwhile, because of the difference between boarding passenger demand between the two fleets, the dwell time of all-stop fleet and short-turning fleet, which are denoted by and , should be calculated separately. This paper defines that is the average boarding time per passenger and is the average alighting time per passenger. Thus, the dwell time is the maximum between boarding time and alighting time, as shown in Formulas (8) and (9). The third term is the running time cost of an all-stop fleet and short-turning fleet. The all-stop fleet serves every stops of bus route () and the short-turning fleet just serves stops within short-turning section (). The constraints (5) and (6) ensure that optimized frequencies of two fleets can provide sufficient in-vehicle space at each stop in order to avoid overcrowding, in which K is the vehicle capacity and , are loads of all-stop fleet and short-turning fleet at stop i, as shown in Formulas (10) and (11).
This objective function can output the short-turning stop , the frequencies of all-stop fleet and short-turning fleet, and the vehicle type, in which there is same vehicle type for all-stop fleet and short-turning fleet. It is the foundation of the research of hybrid vehicle types, and can also be used to compare with the optimization of hybrid vehicle types to test its effectiveness.
2.3. Model for Short Turning Service with Hybrid Vehicle Type
In this study, the strategy of vehicle types is that there are two vehicle types and the all-stop fleet and short-turning fleet are equipped with their own vehicle types. Two vehicle types have differences in capacity, speed, acceleration speed, and bus running time values per hour. Based on the objective function for single vehicle type, the total costs with hybrid vehicle type can be expressed as
subject to
where the difference of objective function between single vehicle type and hybrid vehicle type is reflected in the in-vehicle time cost and running time cost. Due to the various vehicle types, the running time of buses between adjacent stops during the in-vehicle period is divided into the deceleration delay of inbound and outbound, and the travel time after returning to uniform speed. and are speed and acceleration speed of short-turning fleet, while and are speed and acceleration speed of all-stop fleet. The running time of short-turning fleet and all-stop fleet between adjacent stops (denoted by and ) can be expressed as Formulas (17) and (18). The third term includes running time costs of the all-stop fleet and the short-turning fleet with their respective time value (denoted by and ). The constraints (13) and (14) are used to limit the load of vehicles under the capacity of all-stop fleet and short-turning fleet (denoted by and ).
Note that there is a certain gap between the frequency of an all-stop fleet and other fleets from research of operational strategies at the planning level, such as in Cortés et al. (2011). This means that both large and small departure intervals belonging to the two bus fleets appear along the bus route and may cause passengers to concentrate on fleets with small intervals, reducing the load factor of running vehicles. When the two fleets are equipped with the same vehicle type, there will be a slight impact on load factor. However, under the hybrid vehicle type expected to increase the load factor, the gap of frequencies between two fleets can cause a low load factor. Therefore, the constraint (15) is proposed to limit the gap of frequencies between two fleets in which parameter () is an adjustment coefficient and, by adjusting the upper limit of maximum departure interval, to achieve efficient use of in-vehicle space.
3. Performance Measure: Load Factor
In this paper, we analyze operating characteristics of bus fleets for short-turning services and present an optimization method of departure frequency and vehicle type. By considering the concentrated travel of passengers within a short-turning section and adjusting the frequency and vehicle type, sufficient in-vehicle space can be provided for passengers selecting all-stop fleet and short-turning fleet, and the optimization method is expected to save the operator costs. In order to quantify the effect of optimization of departure frequency and vehicle type, we select the load factor as a performance measure besides the above passenger costs and operator costs.
The load factor for bus vehicles is an important operational performance measure for the operators. Low load factor gives rise to the waste of bus resources. This paper divides passenger demand of bus routes into two parts: the boarding demand for an all-stop fleet and the boarding demand for a short-turning fleet. Two vehicle types are set up for passenger demand and, based on matching of bus capacity and passenger demand, the load factor can be increased.
The load factor is related to passenger loads of bus vehicles at stop i, as shown in Formulas (11) and (12). The average value of load factor of both all-stop and short-turning vehicles at every stop is used to show the load factor for a bus route, denoted by F, as shown below:
where and are the load factors of all-stop vehicles and the short-turning vehicle at stop i, respectively, which is a ratio of passenger load of vehicle at stop i to the vehicle capacity.
4. Solution Methods
4.1. A Layer-By-Layer Search Method
The objective function for the design of short turning service with hybrid vehicle type has multiple decision variables, including short-turning stops ( and ), frequencies, and vehicle types of the all-stop fleet and short-turning fleet. Among them, the binary variable is used to describe the operation section of the short-turning fleet in this paper. The following states of correspondence between binary variable and short-turning stops are defined:
where is greater than and the ranges of values of and are and , respectively.
Considering the limit of bus dispatching, there is an exhaustive search for the frequencies ( and ) within a range [0, ] in which is the maximum departure frequency, as shown below:
As regards vehicle types, choosing two vehicle types with a capacity of either 80 or 160 passengers for the all-stop and short-turning fleet, respectively, the optimized scheme can be expressed as
where the first row represents the vehicle type of an all-stop fleet and the second one represents the vehicle type of the short-turning fleet. In order to make it convenient to find the optimal combination of vehicle types, is used to express the above four combinations of vehicle types, in which k = 1, 2, 3, 4.
To solve various decision variables at the same time, a layer-by-layer search algorithm is proposed and programmed in this part. The first layer is to search for short-turning stops ( and ) and the second layer is to search for the frequencies ( and ). Four combinations of vehicle types are selected, in turn, to calculate the total cost in the third layer. Algorithm 1 is as follows:
| Algorithm 1: A layer-by-layer search algorithm |
|
4.2. Solution Simulation Incorporating Monte Carlo Method
As shown in the above search algorithm, calculating the objective function is also a numerical simulation for the progress of passenger travel and bus operation. Although the proposed optimization method is established at the planning level, it is necessary to consider the randomness of the running time of buses. Many studies for the design of bus services take the randomness of travel time into consideration, and the Monte Carlo method is used to deal with the randomness [24] Hence, as a proven and effective method, Monte Carlo is also introduced to deal with the random running time of buses in this paper. In addition, there is a difference between Monte Carlo in this paper and the research mentioned above. Previous studies examine travel time variation of buses with a single vehicle type, in which there is only one speed variable in the simulation sample. However, in this paper, two vehicle types are set up with two corresponding speed variables. The method of calculating the value of the objective function is described as follows.
Step i. Set the counter of simulations nmc and the maximal number of Monte Carlo simulations Nmc ().
Step ii. Generate the speed and based on the mean and variance of two vehicle speed, respectively; perform running time sampling using Formulas (17) and (18).
Step iii. Calculate the total costs using Formula (12). Total costs is replaced by average total costs under nmc samples:
Step iv. Increase the number of simulations by 1. If the number of simulations is exceeding Nmc, then stop and return to Step ii otherwise.
5. Numerical Test
5.1. Experimental Surroundings
The bus route number 6 of Changchun City is selected to test the optimization model for short-turning service with hybrid vehicle type, in which buses run from the southern terminal in Fuqiang Street to northern terminal at Changchun Railway Station with twenty stops over 9.9 km. Passengers travel centrally from uptown (near the southern terminal) to downtown (near northern terminal) during the early peak period. In actual operation, buses serve each stop without short-turning service along the route and with a single vehicle type (capacity of 80 passengers). It takes about 28 minutes between terminals at a speed of 21 km/h and the variance of vehicle speed is 10% of the vehicle speed. The traffic survey was conducted between 7 and 9 a.m. on weekdays. The average passenger demand between stops is shown in Figure 1. We set a uniform destination for waiting passengers at subsequent stops and then the origin–destination trip matrix can be obtained. Meanwhile, we assume that there are no physical barriers in the progress of short-turning operation and buses can drive directly into another direction after serving the short-turning stop.
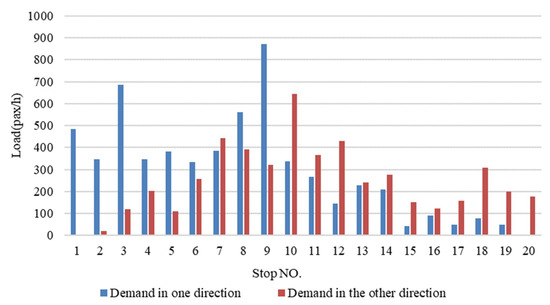
Figure 1.
The average passengers demand in the both direction during the early peak time.
As shown in Section 4, two vehicle types with different passenger capacities are applied in the experiment. The values used for vehicle performance and operating costs of each vehicle type are displayed in Table 1, referring to the practicalities of everyday life. The variances of vehicle speed for small buses and large buses are assumed to be same and 10% of average speed. Vehicles arrive at the stops at random, and parameter k is set as 1. The relevant variables in the objective function are set as , , , and .

Table 1.
Vehicle performance and operating costs of each vehicle type.
The mathematical software MATLAB R2011a is applied to process the proposed solution methods. The parameters in Monte Carlo method are taken as Nmc = 100. In this paper, the average vehicle speed is an important indictor which reflects the performance of different vehicle types. Meanwhile, the average vehicle speed is used to determine the travel time, given distance between stops. In addition, considering dense and non-dense traffic which may occur, previous studies present that travel time between stops follows the normal distribution N. Therefore, in the case of fixed distance between stops, the vehicle speed replaces travel time to express this normal distribution N (, 0.01) that is used to perform speed and running time sampling, in which is average speed. Three are three alternative strategies for the process of testing: (1) single small vehicle type (with capacity of 80 pax), (2) single large vehicle type (with capacity of 160 pax), and (3) hybrid vehicle type (with capacity of 80 and 160 pax). The performances of three different strategies have been evaluated with simulating 10 times, using identical parameters in addition to vehicle performance parameters. Test results are shown in Figure 2. In terms of optimization of total costs, the bus operation with hybrid vehicle type has a more obvious effect than the other two strategies with single vehicle type.
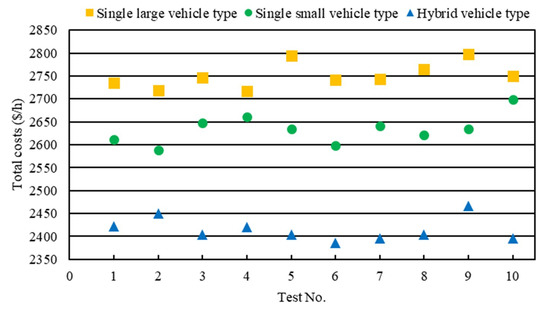
Figure 2.
Test results of three strategies.
5.2. Experimental Results and Analysis
As regards the impact of vehicle type when short-turning service is applied, the average of test results of each strategy is calculated to evaluate effect on total costs, frequencies, and load factor, as shown in Table 2. In the optimization program with hybrid vehicle type, vehicle with capacity of 160 pax is applied to short-turning fleet and vehicle with capacity of 80 pax is chose for all-stop fleet. The optimization results of short-turning stops are relatively consistent. Under strategies with single small and hybrid vehicle type, buses run between stop 1 and 15, while buses with single large vehicle type run between stop 1 and 15. The difference of short-turning stops is caused by the high running time cost of large buses and the short-turning section should be shortened. In terms of costs of passenger and operator, it can be seen that vehicle type with capacity of 80 pax is better suitable for the short-turning service than that of 160 pax under the strategies with single vehicle type. Compared with the two strategies with single vehicle type, the strategy with hybrid vehicle type can significantly reduce the total costs, in which the running time cost of buses dropped to $457.7/h and has decreased markedly. Meanwhile, the load factor under the hybrid vehicle type has the highest value and is 0.78 among the three strategies, which is due to the cooperation between the two vehicle types and allocation of passenger demand within short-turning section. It also helps to reduce running time cost of buses.

Table 2.
Effects of the three strategies.
A further sensitivity analysis on total costs and load factor to passenger demand can be seen in Figure 3. The rate of change of passenger demand r is set, and its range of values is [0.6,1.3]. expresses the current passenger demand. The optimal results of the short-turning service present unsmooth curve that can be decomposed into two parts.

Figure 3.
Total costs and load factor under various passenger demand.
If , the total costs of short-turning service increase from $1318/h to $2124/h. This increasing process has resulted from the increase in travel time of passengers and the input of bus fleet size. Meanwhile, there has been a noticeable increase for the load factor. A high demand level causes an increase in the number of boarding passengers. However, if , although the total costs continued to increase, the load factor increases slowly. Due to the input of bus fleet size, there is a slight influence of increasing passenger demand on the load factor.
In addition, the running time value of large buses is a critical parameter for the optimization of vehicle type in this paper. The sensitivity to running time value of large buses is also discussed, as shown in Figure 4. In order to reflect the impact of changes of running time value of large buses on the frequency, vehicle type of 80 pax is applied to all-stop fleet and vehicle type of 160 pax is applied to short-turning fleet, based on the optimal results of hybrid vehicle type for the bus route. With the increase in running time value of large buses, the total costs increase slowly. It is important that the frequencies of buses with 80 and 160 pax have opposite variation trends. A rational explanation is that the decease in frequency of a short-turning fleet with large buses can reduce the total costs as the running time value of large bus type increases while an increase in the frequency of all-stop fleet with small buses is required to provide sufficient bus capacity to meet passenger demand.

Figure 4.
Total costs and frequencies under various running time values of large buses.
6. Conclusions
In transit systems, the short-turning service has attracted more and more attention from operators and users. This paper develops an optimization model for short-turning service considering hybrid vehicle types to save costs of operators and users and the increased load factor of buses. Based on the concentration of passenger travel demand, small and large vehicle types can be selected pertinently for the two bus fleets. The two vehicle types have different capacities, speeds, acceleration speeds, and bus running time value per hour. Considering those differences between two vehicle types, the operation progress is described, and the objective function for optimization model is established considering benefits of passenger and operator. A layer-by-layer search method is constructed for solving problems. Output schemes include short-turning stops, frequencies, and vehicle types of all-stop fleet and short-turning fleet. From the test, several conclusions can be made that on the basis of short-turning service, optimization of hybrid vehicle type can further reduce the total costs. Meanwhile, it can increase the passenger load of vehicle and make full use of bus resources. Future research may focus on a real-time strategy for determining the appropriate hybrid vehicle type during the period when passenger demand changes, especially during peak and off-peak transition periods.
Author Contributions
Conceptualization, H.Z.; Data curation, S.L.; Formal analysis, S.L.; Funding acquisition, M.M.; Methodology, H.Z.; Writing—review & editing, M.M.
Funding
This research was funded by the Doctoral Research Fund of Shandong Jianzhu University grant number XNBS1819, the National Natural Science Foundation of China grant number 71801153 and 71801149, and the Fifth Batch of Applied Undergraduate Programs in Shanghai Municipal Universities “Automobile Service Engineering Major” Construction (Shanghai Education Commission [2017] NO. 79).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Site, P.D.; Filippi, F. Service optimization for bus corridors with short-turn strategies and variable vehicle size. Transp. Res. Part A Policy Prac. 1998, 32, 19–38. [Google Scholar] [CrossRef]
- Ibarra-Rojas, O.; Delgado, F.; Giesen, R.; Muñoz, J. Planning, operation, and control of bus transport systems: A literature review. Transp. Res. Part B Methodol. 2015, 77, 38–75. [Google Scholar] [CrossRef]
- Furth, P.; Day, F.B. Transit routing and scheduling strategies for heavy demand corridors. Transp. Res. Rec. 1985, 1011, 23–26. [Google Scholar]
- Leiva, C.; Munoz, J.C.; Giesen, R.; Larrain, H. Design of limited-stop services for an urban bus corridor with capacity constraints. Transp. Res. Part B Methodol. 2010, 44, 1186–1201. [Google Scholar] [CrossRef]
- Zhang, H.; Zhao, S.; Liu, H.; Liang, S. Optimising the design of a limited-stop bus service for a branching network. Proc. Inst. Civ. Eng. Munic. Eng. 2017, 170, 230–238. [Google Scholar] [CrossRef]
- Jordan, W.C.; Turnquist, M.A. Zone scheduling of bus routes to improve service reliability. Transp. Sci. 1979, 13, 242–268. [Google Scholar] [CrossRef]
- Furth, P.G. Short turning on transit routes. Transp. Res. Rec. J. Transp. Res. Board 1987, 1108, 42–52. [Google Scholar]
- Ceder, A. Optimal design of transit short-turn trips. Transp. Res. Rec. 1989, 1221, 8–22. [Google Scholar]
- Cortés, C.E.; Jara-Díaz, S.; Tirachini, A. Integrating short turning and deadheading in the optimization of transit services. Transp. Res. Part A Policy Prac. 2011, 45, 419–434. [Google Scholar] [CrossRef]
- Zhang, H.; Zhao, S.; Liu, H.; Liang, S. Design of integrated limited-stop and short-turn services for a bus route. Math. Probl. Eng. 2016, 2016, 1–9. [Google Scholar] [CrossRef]
- Liang, S.; Zhao, S.; Lu, C.; Ma, M. A self-adaptive method to equalize headways: Numerical analysis and comparison. Transp. Res. Part B Methodol. 2016, 87, 33–43. [Google Scholar] [CrossRef]
- Zhao, S.; Lu, C.; Liang, S.; Liu, H. A self-adjusting method to resist bus bunching based on boarding limits. Math. Probl. Eng. 2016, 2016, 1–7. [Google Scholar] [CrossRef]
- Zhang, H.; Zhao, S.; Cao, Y.; Liu, H.; Liang, S. Real-Time integrated limited-stop and short-turning bus control with stochastic travel time. J. Adv. Transp. 2017, 2017, 1–9. [Google Scholar] [CrossRef]
- Wang, Y.; Bie, Y.; Zhang, L. Joint optimization for the locations of time control points and corresponding slack times for a bus route. KSCE J. Civ. Eng. 2018, 23, 411–419. [Google Scholar] [CrossRef]
- Zhang, H.; Zhao, S.; Liu, H.; Liang, S. Design of limited-stop service based on the degree of unbalance of passenger demand. PLoS ONE 2018, 13, e0193855. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Bie, Y.; An, Q. Impacts of winter weather on bus travel time in cold regions: Case study of Harbin, China. J. Transp. Eng. Part A Syst. 2018, 144, 05018001. [Google Scholar] [CrossRef]
- Zhang, H.; Zhao, S.; Liu, H.; Li, J. A dynamic short-turning bus control for uncertain demand. J. Adv. Transp. 2017, 2017, 1–9. [Google Scholar] [CrossRef]
- Ferland, J.A.; Michelon, P. The vehicle scheduling problem with multiple vehicle types. J. Oper. Res. Soc. 1988, 39, 577. [Google Scholar] [CrossRef]
- Ceder, A. Transit vehicle-type scheduling problem. Transp. Res. Rec. 1995, 1995, 34–38. [Google Scholar]
- Lee, K.K.T.; Kuo, S.H.F.; Schonfeld, P.M. Optimal mixed bus fleet for urban operations. Transp. Res. Rec. 1995, 1503, 39–48. [Google Scholar]
- Dell-Olio, L.; Ibeas, A.; Ruisánchez, F. Optimizing bus-size and headway in transit networks. Transportation 2012, 39, 449–464. [Google Scholar] [CrossRef]
- Zhao, S.; Wang, D.; Sun, J.; Liu, H. Optimization model for multi-vehicle-type structure in urban bus systems. Math. Probl. Eng. 2017, 2017, 1–6. [Google Scholar] [CrossRef]
- Jansson, J.O. A simple bus line model for optimization of service frequency and bus size. In: Urban transport. J. Transp. Econ. Policy 2003, 8, 53–80. [Google Scholar]
- Chen, J.; Liu, Z.; Zhu, S.; Wang, W. Design of limited-stop bus service with capacity constraint and stochastic travel time. Transp. Res. Part E Logist. Transp. Rev. 2015, 83, 1–15. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).