Abstract
This paper establishes an optimal generic function model in order to obtain a continuous phase modulated (CPM) signal with a smoother phase modulation function. This is achieved by finding the solution to the symbol signals at different lengths of the CPM function. In the solution process, the unknown amount that needs to be solved is reduced by using the even function symmetry characteristic of the signal to be solved. For each different form of the signal, the time domain form of the CPM function and the corresponding normalized energy spectral density are compared under the influence of the phase modulation signal length and the generic function parameter n. The data transmission rate is improved by introducing inter-symbol interference, and the modulation process is realized using six-way parallel transmission when the CPM function is 6T. The simulation results show that the CPM function obtained by establishing an optimal generic function model has high-quality time-frequency characteristics. The real-time phase trajectory and the high-order derivative are both continuous, and the modulated signal has constant envelope characteristics. The CPM function has a fast rolling-off in the frequency domain and small out-of-band radiation, which greatly improves the characteristics of the frequency band utilization.
1. Introduction
As digital communication technology has advanced, digital modulation and demodulation technologies have also developed rapidly. Continuous phase modulation (CPM) has gained increasing attention as an attractive method of communication modulation, due to having smaller out-of-band radiation, stronger anti-interference ability and higher spectrum utilization than traditional modulation methods [1,2,3]. Conventional minimum shift keying (MSK) signals and other baseband transmission signals usually have phase trajectories that are segment-linear-continuous, while their first-order derivatives or high-order derivatives are not continuous. As a result, there are large side lobes in the frequency domain [4,5]. Therefore, the signal requires a larger frequency band for transmission, resulting in low spectrum utilization. The CPM method can effectively overcome this drawback. Zhanyu Yang et al., normalized the energy spectrum comparison between MSK and quadrature phase shift keying (QPSK) and they indicated that MSK has a fast rolling-off sidelobe spectrum [6]. However, the rate of MSK decline is still slower than the CPM method.
The partial response waveform artificially introduces inter-symbol interference at the symbol sampling time in order to improve the frequency band utilization and accelerate attenuation of the “tail” of the transmitted signal waveform [7,8,9,10]. The interference is then eliminated before the receiver generates the decision waveform to improve the spectral signature. A system that transmits a partial response waveform as a baseband signal is usually called a partial response system [11,12]. A partial response system can not only improve the frequency band utilization, but also has the advantages of large attenuation and fast convergence of the tail of the transmission waveform. For these reasons, it has been widely used in digital baseband transmission systems [13,14]. M.M. Naghsh and M.J. Omidi introduced appropriate per-carrier partial response signaling between successive orthogonal frequency division multiplexing (OFDM) blocks to reduce out-of-band (OOB) radiation [15]. Alan Barbieri et al. considered inter-symbol interference and the spacing between adjacent carriers in a frequency-division multiplexed CPM system and provided an algorithm for optimal spectral efficiency of the system parameters, effectively improving the spectral efficiency of the CPM signal [16]. There are many well known optimization algorithms, including the adaptive algorithms for system identifications and beamforming [17,18,19]. Future research should apply an adaptive algorithm to the optimization of baseband symbol signals.
A continuous phase modulated signal has a low out-of-band energy spread, phase smoothing, and a constant envelope and thus offers a higher frequency spectral efficiency. In this paper, the smoothing effect of the phase change trajectory of a CPM signal is discussed in detail, and modulation is realized using MATLAB. In the solution process, using the even function symmetry characteristic of the signal to be solved, the unknown amount that needs to be solved is reduced. By constructing a generic function model to optimize the partial response CPM signal function, a CPM signal with continuous phase and high-order derivatives is obtained, which further improves the normalized energy spectral characteristics of the CPM signal. The Fourier series coefficients of the symbol signals at different lengths are obtained by simulation, and a phase modulation function with low out-of-band energy radiation is constructed. The corresponding phase modulation function spectral density function is obtained using this phase modulation function. The normalized energy spectral density of the phase modulation function is compared and analyzed for parameter n of the generic function and the length of the CPM signal. In order to prove that the obtained CPM signal has good spectral characteristics, an MSK signal is introduced for comparison purposes. The results show that the obtained CPM signal has faster rolling-off characteristics and less out-of-band radiation. The transient steady-state modulation method, of six-way parallel transmission of phase-modulated signals with inter-symbol interference, improves the transmission efficiency when the baseband signal length is 6T. The obtained CPM signal is verified to have constant envelope characteristics.
2. Establishment of an Optimal Generic Function Model
In order to ensure that the spectral characteristics of the baseband symbol signal satisfy the minimum out-of-band energy radiation requirements, the following generic function criterion is applied when optimizing the signal with a symbol length of 6T [20]:
where is a function that determines the slope of the spectrum rolling-off of the desired signal , and is the energy spectral density function of signal . The length of is 6T and it is assumed that is symmetric about the y-axis over the interval [−3T, 3T]. is taken as the ascending function where the value of n depends on the amount of out-of-band energy radiation to be suppressed. In order to ensure that the generic function integral J converges in the integration, the quadratic falling slope of must be greater than the rising slope of the rising function to ensure the energy spectrum rolling-off speed of the desired signal is defined.
Thus, (1) can be written as follows:
where is the 2n-order derivative of symbol signal .
In this way, the minimum out-of-band energy radiation criterion can be reduced to the problem of solving the baseband symbol function while ensuring that the mathematical universal function J is minimized.
For the sake of brevity, only two additional restrictions are discussed below. The single symbol signal energy constraints and the boundary constraints are used as the Lagrange constraints for numerical solutions of optimal generic function models. Additionally, the optimal symbol length is 6T and [−3T, 3T] is taken as an example for discussion. A generic function that adds a single symbol signal energy limit condition can be expressed as:
where is the Lagrange coefficient and E is the energy of a single symbol signal.
The energy of a single symbol signal can be expressed as:
The desired optimal symbol signal can be expressed as a boundary condition at time and :
where the represents the derivative of at .
The following is a numerical method for solving the optimal generic function using a Fourier complete orthogonal series. Considering that the optimal generic function of the desired function has the symmetry characteristic of the even function, it can be expressed in the following form using a Fourier series:
where the coefficients of the Fourier series are:
Equation (6) can be substituted into Equation (4), but the coefficients of the Fourier series and the Lagrange coefficient are unknown for a specific symbol signal energy E and symbol signal length T in the generic function. If the value of the Fourier series coefficients are found and then substituted into Equation (7), the Fourier series expression of the optimal symbol signal can be obtained. Its accuracy depends on the number of terms of the Fourier series. The more items there are, the closer the numerical solution will be to the analytical solution of .
Thus, H can be written as:
The minimum value of H should satisfy the boundary constraints and the Lagrange equations are as follows:
For convenience, we take T = 1, E = 1, and solve the problem of optimizing the generic function when there are different values for the number of items of the Fourier series.
3. Optimization and Solution of Partial Response CPM Symbol Signal
3.1. Optimization of CPM Signals of Different Lengths
In order to obtain an optimal baseband symbol signal, mathematical models of symbol signals with symbol lengths of 2T and 4T are established based on the optimal generic function model established above for a symbol length of 6T. Firstly, generic expressions of symbol signals of lengths 2T and 4T are obtained. Using the same model building process, the optimization and solution process of the partial response CPM baseband signal for baseband symbol lengths of 2T and 4T are deduced.
Equation (10) is a Fourier series representation of the target baseband symbol signal when the symbol length is 2T and Equation (11) is a Fourier series representation of the target baseband symbol signal when the symbol length is 4T.
The mathematical generic function with additional constraints can then be expressed as follows:
Equation (12) is a generic functional expression of the target baseband symbol signal when the symbol length is 2T and Equation (13) is a generic function expression of the target baseband symbol signal when the symbol length is 4T.
For the specific case of and , only the coefficients and Lagrange constant of the Fourier series are unknown in the mathematical generic function and the solution for signal can be found by solving the coefficients of the Fourier series. The values obtained by MATLAB simulation are substituted into Equations (10) and (11) to obtain the required optimal baseband symbol signal, taking a symbol length of 2T as an example to solve the phase modulation function. After finding the optimal baseband symbol signal function using , the coefficient K is obtained. Thereby obtaining a frequency modulation function . Then, according to , the phase modulation function can be extracted. A generic function model parameter n = 4 is selected here and the frequency modulation functions at different lengths are compared with the phase modulation function when the Fourier series m = 4. An example is shown in Table 1 based on the MATLAB software solution for a spectrogram of the phase modulation function when the Fourier series m = 4 and n = 2, 4 and 6.

Table 1.
Fourier series , when the symbol length is 2T, 4T and 6T, the coefficient values of the Fourier series obtained by taking 2, 4 and 6 respectively, and the corresponding K values.
Based on the values in Table 1, the energy spectral density of the CPM functions are compared in a single plot for m = 4, using the normalized energy spectral density comparison chart of the CPM functions. The different symbol lengths, of n = 2, 4 and 6 are shown in Figure 1, Figure 2 and Figure 3, respectively.
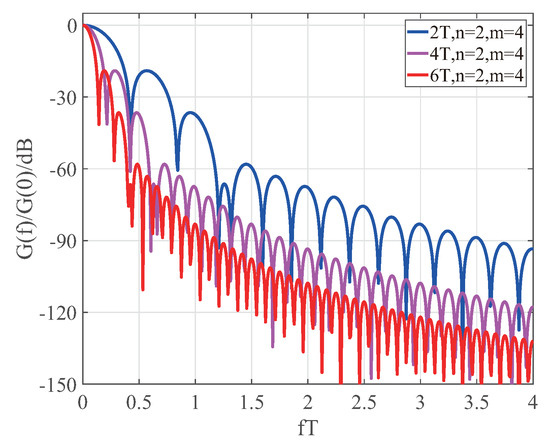
Figure 1.
Comparison of normalized energy spectral densities for different length continuous phase modulated (CPM) functions with n = 2 and m = 4.
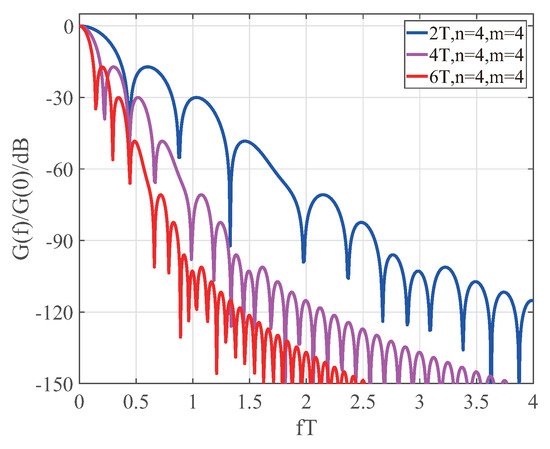
Figure 2.
Comparison of normalized energy spectral densities for different length CPM functions with n = 2 and m = 4.
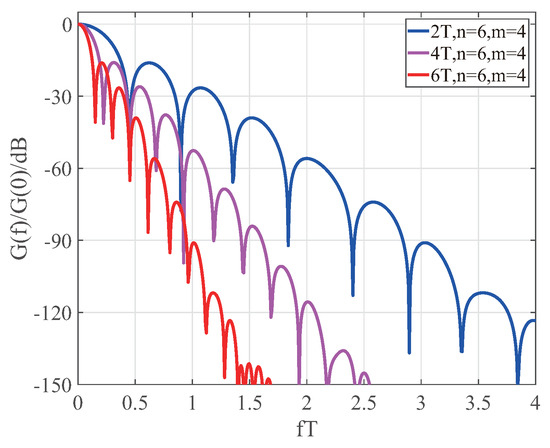
Figure 3.
Comparison of normalized energy spectral densities for different length CPM functions with n = 6 and m = 4.
Based on Figure 1, Figure 2 and Figure 3, the main features of the normalized energy spectral densities of CPM signals for different lengths are analyzed. The properties of a Fourier transform state that when a time domain signal is Fourier transformed into a frequency domain signal, the corresponding frequency domain signal will be narrowed as the time domain signal is broadened [21]. For Figure 1, taking 2fT to 3fT as an example, when the length of the CPM function is 2T, there are approximately four side lobes, and when the length of the CPM function is increased to 4T and 6T, there are approximately eight and 12 side lobes respectively for the same 2fT to 3fT interval, corresponding to a direct multiple of the function length in the time domain. When n = 2, m = 4 and the CPM function length is 6T, the band utilization rate is 2.3 times higher than when the CPM function length is 2T and 1.5 times higher than when the CPM function length is 4T, for a −40 dB bandwidth. When n = 4, m = 4 and the CPM function length is 6T, the band utilization rate is 2.1 times higher than when the CPM function length is 2T and 1.5 times higher than when the CPM function length is 4T, for a −40 dB bandwidth. When n = 6, m = 4 and the CPM function length is 6T, the band utilization rate is 2.9 times higher than when the CPM function length is 2T, and 1.5 times higher than when the CPM function length is 4T, for a −40 dB bandwidth. This analysis shows that increased suppression of interference due to the side lobes is required as the baseband symbol signal grows, but the band utilization can also be improved to some extent in the communication system, since the increased length of the baseband symbol signal also speeds up the decay. Therefore, in a practical communication process, an appropriate solution should be selected depending on the actual requirements.
3.2. The Effect of the N-Value of the Optimal Generic Function Model on the CPM Function
The above discussion investigates the series of changes in the spectral modulation density of the phase modulation function as its length increases, for fixed values of n and m. When the length of the CPM function is constant and the value of m is fixed at 4, the parameter n also has an effect on the spectral density of the phase function in the optimization of the generic function model. To provide a significant contrast with the energy spectrum of the CPM signal obtained by optimizing the generic function model, the energy spectrum of the phase modulation signal of the MSK signal is introduced. For this example, only the time domain diagram of the 6T length CPM function is given, however, other lengths have identical characteristics to 6T. Figure 4 shows the CPM function trajectory for the CPM function length of 6T, and values of n corresponding to 2, 4, and 6 respectively. Figure 5 shows the normalized energy spectrum density when the length of the CPM function is 6T. Figure 6 shows the normalized energy density for the corresponding 2T and 4T CPM functions when n are 2, 4, and 6, respectively.
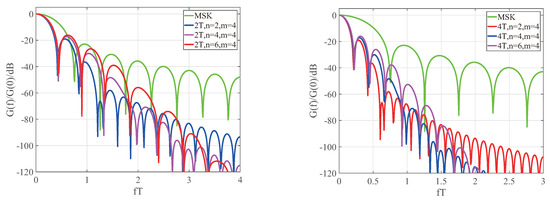
Figure 4.
Minimum shift keying (MSK) energy spectra with CPM function lengths of 2T and 4T and, n = 2, 4 and 6 respectively, and the normalized energy spectral density of the corresponding CPM function.
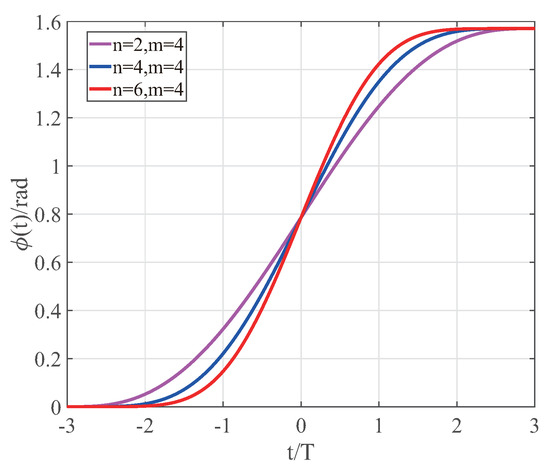
Figure 5.
The CPM function trajectory with a CPM function length of 6T and n values of 2, 4, and 6 respectively.
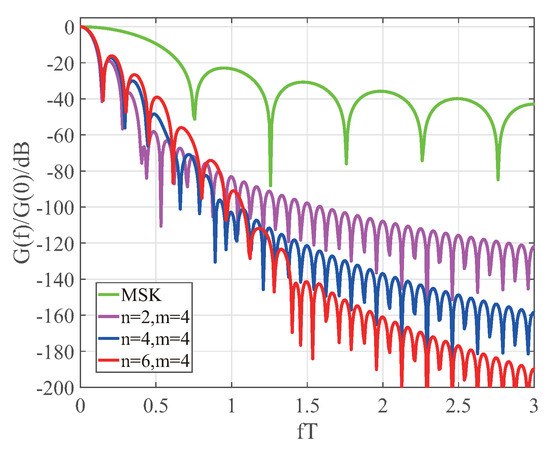
Figure 6.
MSK energy spectrum with CPM function length of 6T and n = 2, 4 and 6 respectively, and the normalized energy spectral density of the corresponding CPM function.
From Figure 5, it can be seen that when the length of the CPM function is constant and the Fourier series is m = 4, as the length of the CPM function increases, the CPM function will become smoother at the boundary. From Figure 5, it can also be seen that for a constant CPM function length, the main lobe is substantially coincident when the value of n increases. This corresponds to their smoothness characteristics at the boundary in the time domain diagram. Another significant feature is that the CPM signal obtained from the optimal generic function decays significantly faster than the MSK signal. For example, from Figure 6, when the length of the CPM signal is 6T, the frequency band utilization of the optimal signal with n = 2 is 7.14 times higher than the MSK signal for a −40 dB bandwidth. For a −60 dB bandwidth, the band utilization of the optimal signal for n = 2 increases to 15.69 times higher than the MSK signal. It shows that the CPM signal has a much higher energy spectrum utilization than the MSK signal i.e. the CPM signal obtained from the optimal generic function has superior spectral characteristics. For CPM function lengths of 2T and 4T and n = 2, 4 and 6, the spectral features discussed above are also applicable.
3.3. Transient and Steady-State Modulation Method for Six-Way Parallel Transmission
The information transmission rate decreases as the length of the extended CPM function increases. To address this issue, inter-symbol interference is introduced [22,23,24]. Taking the 6T CPM function as an example, the CPM function when n = 4 and m = 4 is selected as the transmission signal and is recorded as . We divide the CPM function into two parts, the transient response and the steady state response [25]. The transient response is the component of the CPM function that changes over time. The steady state response is the component of the phase modulation function that is not affected by time and is maintained in a relatively stable state. The steady-state response of the CPM signal of length [−3T, 3T] is the component of the signal with time greater than 3T and this component value is maintained at . The transient response is the component of the signal between [−3T, 3T], which can be seen in Figure 5. The transient steady-state modulation method for six-way parallel transmission of CPM signals introduces inter-symbol interference as follows. Firstly, the baseband symbol signal is serial/parallel converted, the serial symbol is divided into six paths, and the six-way symbol information is stored in six arrays. Each single symbol phase is also divided into a transient and steady state portion in combination with the delay and the single symbol phase function track. The transient portion is obtained from each single symbol phase function, and the steady state portion is accumulated by summing the previous symbol information and multiplying by . The symbol information is combined with the phase function and the six-way parallel time-varying phase trajectories are added to obtain a modulated signal phase trajectory, thereby obtaining a modulated signal. The principle block diagram of the method is shown in Figure 7.
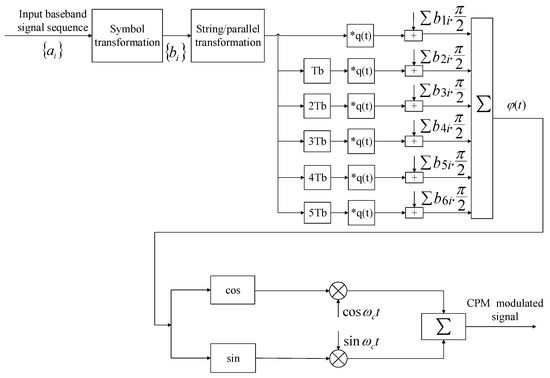
Figure 7.
Schematic diagram of a transient steady-state modulation method for six-way parallel transmission of CPM signals with inter-symbol interference.
The baseband transmission symbol signal is set to {100110 010110 011001 011001 100110 110100}. After serial-to-parallel conversion, six parallel transmission signals are generated. Each channel is delayed by 1T successively in length, and six phase tracks are obtained which each contain six CPM signals. The first baseband symbol signal is {100110}, and the remaining baseband symbol signals are {010110}, {011001}, {011001}, {100110} and {110100}. A corresponding CPM phase trajectory map and phase trajectory are obtained by superimposing the signals with six parallel transmission signals, as shown in Figure 8 where (a)–(f) are the six-way parallel transmission CPM phase trajectories and (g) is the phase trajectory obtained by superimposing the six-way parallel transmission CPM signals.
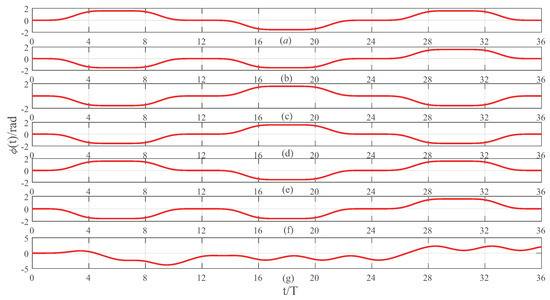
Figure 8.
Six-way parallel CPM transmission signals’ phase trajectory and superimposed phase trajectory.
From Figure 8, it can be clearly observed that (b)–(f) are delayed by 1T-5T with respect to (a). The transmission signal (g) containing inter-symbol interference is obtained by adding (a)–(f) using MATLAB simulation software.
The phase trajectory obtained by superimposing the six-way parallel transmission CPM signals of the first 18T are selected to obtain the CPM signal modulation signal, as shown in Figure 9.
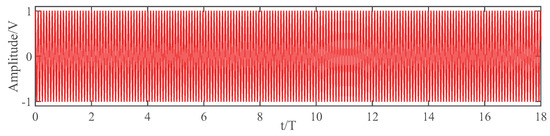
Figure 9.
The phase modulated signal resulting from the superposition of six parallel CPM transmission signals.
It can be seen that the trajectory realized by this method also has the CPM phase characteristic and the modulated signal still maintains a constant envelope.
4. Conclusions
This paper establishes an optimal generic function module for a CPM function by introducing the Fourier series and the complete orthogonal basis. The characteristics of the normalized energy spectral density are analyzed for different contexts using the obtained CPM functions. The band utilization from CPM signals of different lengths with the same parameters are compared. When n = 4, m = 4 and the CPM function length is 6T, the band utilization rate is 2.1 times higher than when the CPM function length is 2T and 1.5 times higher than when the CPM function length is 4T, for a −40 dB bandwidth. When n = 6, m = 4 and the CPM function length is 6T, the band utilization rate is 2.9 times higher than when the CPM function length is 2T, and 1.5 times higher than when the CPM function length is 4T, for a −40 dB bandwidth. The results show that the CPM signal obtained by establishing the generic function model greatly improves the band utilization rate as the CPM function length is increased. Additionally, for the same length of CPM signal and different values of n, the frequency band utilization of the optimal signal with n = 2 is 7.14 times higher than the MSK signal, for a CPM signal length of 6T and a −40 dB bandwidth. For a −60 dB bandwidth, the band utilization of the optimal signal with n = 2 is 15.69 times higher than the MSK signal. The problem of decreasing information transmission rates as the extended CPM function length increases are also discussed in the paper. This problem is solved by introducing inter-symbol interference, which is a temporary steady-state modulation method for six-channel parallel transmission of CPM signals with inter-symbol interference. Using this method, the CPM signal obtained by optimizing the generic function is modulated. The realized trajectory also has a CPM phase characteristic, i.e. the modulated signal still maintains a constant envelope.
References
Author Contributions
J.Q. did the mathematical modeling and the simulations. He also wrote the draft of the paper. M.L. contributed to the revisions and the discussion of the results. B.L., W.X. and S.B.M. put forward the idea and checked the simulation of this paper.
Funding
This research were funded by the Central Universities under Grant HEUCFG201829, the China Postdoctoral Science Foundation (2018M631911) and Heilongjiang Postdoctoral Fund (LBH-Z18055).
Acknowledgments
This research has been supported by the Fundamental Research Funds for the Central Universities under Grant HEUCFG201829, the China Postdoctoral Science Foundation (2018M631911) and Heilongjiang Postdoctoral Fund (LBH-Z18055).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhang, Y.; Li, Q.; Huang, L.; Dai, K.; Song, J. Optimal Design of Cascade LDPC-CPM System Based on Bionic Swarm Optimization Algorithm. IEEE Trans. Broadcast. 2018, 64, 762–770. [Google Scholar] [CrossRef]
- Barbieri, A.; Fertonani, D.; Colavolpe, G. Spectrally-Efficient Continuous Phase Modulations. IEEE Trans. Wireless Commun. 2009, 8, 1564–1572. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, F.; Zhong, Z.; Wang, S. Continuous Phase Modulation Classification via Baum-Welch Algorithm. IEEE Trans. Wireless Commun. 2018, 22, 1390–1393. [Google Scholar] [CrossRef]
- Zhou, J.; Pang, Q.; Xu, D.; Wu, W.; Yang, H. Minimum Frequency Shift Keying. In Principle of Communication; Higher Education Press: Beijing, China, 2015; pp. 185–192. [Google Scholar]
- Fan, C.; Cao, L. Minimum Frequency Shift Keying and Gaussian Minimum Frequency Shift Keying. In Principle of Communication; National Defense Industry Press: Beijing, China, 2015; pp. 231–242. [Google Scholar]
- Yang, Z.; Yu, S.; Chen, L.; Leng, H.; Lan, M.; Qiao, Y.; Gu, W. Constant Envelop Minimum-Shift Keying OFDM Coherent Optical Communication System. J. Lightw. Technol. 2012, 30, 3627–3632. [Google Scholar] [CrossRef]
- Liu, W.; Santhanam, B. Wideband partial response CPM demodulation via multirate frequency transformations and decision feedback equalization. EURASIP J. Wireless Commun. 2018, 2018. [Google Scholar] [CrossRef]
- Li, C.; Mathew, G. Analytical Solution for Optimum Partial-Response Target in Viterbi-Based Receivers. IEEE Trans. Commun. 2006, 54, 1715–1719. [Google Scholar]
- Ishkaev, I.R.; Shevelev, A.E.; Ovsyannikova, A.S.; Zavjalov, S.V.; Volvenko, S.V.; Makarov, S.B. Possibility of Peak-to-Avegare Power Ratio Reduction by Application of Optimal Signal for Transmitter Based on SDR HackRF One. In Proceedings of the 2018 IEEE International Conference on Electrical Engineering and Photonics (EExPolytech), St. Petersburg, Russia, 22–23 October 2018. [Google Scholar]
- Makarov, S.B.; Ovsyannikova, A.S.; Lavrenyuk, I.I.; Zavjalov, S.V.; Volvenko, S.V. Distributions of Probability of Power Values for Random Sequences of Optimal FTN Signals. In Proceedings of the 2018 International Symposium on Consumer Technologies (ISCT), St. Petersburg, Russia, 11–12 May 2018. [Google Scholar]
- Li, J.; Narayanan, K.R.; Georghiades, C.N. An Efficient Algorithm to Compute the Euclidean Distance Spectrum of a General Intersymbol Interference Channel and Its Applications. IEEE Trans. Commun. 2004, 52, 2041–2046. [Google Scholar] [CrossRef]
- Munawar, T.; Saleem, S.; Hassan, S.A.; Zaidi, S.M.H. Estimation of Modulation Index for Partial Response CPM Signal. IEEE Access 2018, 6, 7664–7674. [Google Scholar] [CrossRef]
- Alhussien, H.; Moon, J. The Error-Pattern-Correcting Turbo Equalizer: Spectrum Thinning at High SNRs. IEEE Trans. Inf. Theory 2011, 57, 953–971. [Google Scholar] [CrossRef][Green Version]
- Perrins, E. A Timing False Lock Detector for M-ary Partial-Response CPM. IEEE Trans. Wireless Commun. 2013, 2, 671–674. [Google Scholar] [CrossRef]
- Naghsh, M.M.; Omidi, M.J. Reduction of out of band radiation usingcarrier-by-carrier partial response signallingin orthogonal frequency division multiplexing. IET Commun. 2010, 4, 1433–1442. [Google Scholar] [CrossRef]
- Huang, X.; Li, Y. Simple CPM receivers based on a switched linear modulation model. IEEE Trans. Commun. 2005, 53, 1100–1103. [Google Scholar] [CrossRef]
- Li, Y.; Jiang, Z.; Osman, O.; Han, X.; Yin, J. Mixed Norm Constrained Sparse APA Algorithm for Satellite and Network Echo Channel Estimation. IEEE Access 2018, 6, 65901–65908. [Google Scholar] [CrossRef]
- Shi, W.; Li, Y.; Wang, Y. Noise-free Maximum Correntropy Criterion Algorithm in Non-Gaussian Environment. IEEE Trans. Circuits Syst. Ii Express Briefs 2019, 2019. [Google Scholar] [CrossRef]
- Shi, W.; Li, Y.; Zhao, L.; Liu, X. Controllable Sparse Antenna Array for Adaptive Beamforming. IEEE Access 2019, 7, 6412–6423. [Google Scholar] [CrossRef]
- Xu, Y.; Xue, W.; Shang, W.A. Pan-Function Model for the Utilization of Bandwidth Improvement and PAPR Reduction. Math. Probl. Eng. 2014, 2014. [Google Scholar] [CrossRef]
- Wu, D.; Zhang, Y.; Wang, S.; Guo, B. The Basic Properties of the Fourier Transform. In Signal and Linear System Analysis; Higher Education Press: Beijing, China, 2005; pp. 46–48. [Google Scholar]
- Xue, W.; Guo, L.; Zhang, X.; Ma, W. Inter-code Interference and Symbol Cross-correlation Properties Affect the Signal. J. Harb. Engin. Univ. 2010, 31, 109–114. [Google Scholar]
- Song, S.; Kim, J.; Kim, J. A Passive Equalizer Optimization Method Based on Time-Domain Inter-Symbol Interference Cancellation Technique. IEEE Trans. Electromagn. Compat. 2018, 60, 807–810. [Google Scholar] [CrossRef]
- Chen, M.; Liu, G.; Zhou, H.; Chen, Q.; He, J. Inter-Symbol Differential Detection-Enabled Sampling Frequency Offset Compensation for DDO-OFDM. IEEE Photon. Technol. Lett. 2018, 30, 2095–2098. [Google Scholar] [CrossRef]
- Yang, Y.; Tao, R.; Wang, Y. A New GMSK Orthogonal Modulation Signal Generation Method. Electr. J. 2005, 6, 1095–1098. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).