Abstract
An efficient scheme is proposed in this study to prepare four symmetric hyperentangled cluster states in the polarization degrees of freedom (DOF) and spatial DOF with a two-photon system. This system consists of two nitrogen-vacancy (NV) centers which are coupled to two microtoroidal resonators. The two-photon polarization-spatial hyperentangled cluster states can be generated with our system by virtue of the input and output process. Compared with previous works, our quantum circuit for preparing the hyperentangled cluster states is simple and economic. Moreover, our scheme works deterministically and does not need any extra qubits, making it applicable to existing technologies. Our calculations show that our scheme has high fidelity with current technology, which can help hyperentangled cluster states to play a very useful role in quantum communication networks with long distances and high capacity.
1. Introduction
Hyperentanglement is defined as the simultaneous entanglement in multiple degrees of freedom (DOF) and has been studied extensively in quantum information processing (QIP). In 2005, Ren et al. [1] completed Bell-states analysis using hyper-entanglement, and the generated two-photon wave function uses the Hermite–Gaussian modes. In 2007, Ren et al. [2] prepared the multi-degree and multi-dimensional GHZ state by using the entangled photon pairs. In the same year, Barbieri et al. [3] validated that the polarization Bell states exhibited deterministic and completed discrimination, this letter requires the adoption of standard single photon detectors. In 2008, Barreiro et al. [4] used the hyperentanglement with polarization-orbital-angular momentum, which solved the capacity restriction of the photonic superdense coding, the paper is the first to break the conventional linear-optics threshold. In 2010, Vallone et al. [5] demonstrated the hyperentangled cluster states with six qubits and two photons in three independent DOF. In 2011, a bidirectional and direct quantum communication protocol was proposed by using the hyperentanglement in the spatial DOF and the polarization DOF of the photon pairs; the hyperentanglement can be produced with a beta barium borate crystal [6]. In 2012, Zhao et al. [7] presented a scheme for quantum superdense coding with hyperentanglement, the important device in the scheme is the hyperentangled Bell-state analyzer in both polarization and frequency degrees of freedom. In 2013, Ren and Deng [8] presented the purification protocol of hyperentanglement for the first time in two DOFs. This protocol utilizes the nonlinear optics of a nitrogen-vacancy (NV) center in a diamond embedded in a photonic crystal cavity coupled to a waveguide. In 2014, Hong et al. [9] proposed a safe direct communication protocol by using entanglement swapping as well as hyperentanglement, this protocol provides a high channel capacity because it uses hyperentanglement. In 2015, Perumangatt et al. [10] presented a scheme to generate three-particle hyperentanglement utilizing polarization and orbital momentum of photons; this paper provides a possibility of a new entangled state and its application in a new teleportation method. In the same year, Liu and Zhang [11] presented two schemes to deterministically generate as well as nondestructively analyze the hyperentangled Bell states in polarization DOF and spatial DOF. In 2016, Li et al. [12] used the cross-Kerr nonlinearity to finish the maximally hyperentangled state analysis; the hyperentangled Bell state analysis scheme is for two photons, and the hyperentangled GHZ state analysis scheme is for three photons. In 2017, Deng et al. [13] summarized the development of hyperentanglement and its significant application in QIP. So far, there have been a few reports about the hyperentanglement cluster state by the NV center.
Besides the photon system, people have paid attention to the NV center in diamond, and the NV center is one of the most proper candidates in QIP. The NV center has many excellent advantages, such as having a long decoherence time even at room temperature [14], near unity quantum efficiency [15,16,17,18], fast microwave manipulation as well as narrow-band optical transitions [19]. Because NV centers are isolated from each other, people have worked to combine the NV centers with other systems [20,21,22,23]. In particular, people have made many studies combining NV centers with solid-state cavity quantum electrodynamics (QED) systems [11,24,25,26,27,28,29]. In our system, a scheme for generating deterministically hyperentangled cluster states was proposed. Our system contains two NV centers which are coupled to two microtoroidal resonators (MTR) through a quantized whispering-gallery mode (WGM) cavity QED system. Compared with previous works [11,30,31,32,33], our scheme has many advantages. First, our system does not need the weak cross-Kerr nonlinearity and the homodyne detection, which remarkably weakens the experimental conditions of linear optical elements. Second, compared with the single-sided NV-cavity systems, there are no difficulties in obtaining the phase shift. Third, due to the solid-state quantum system being easily extended, the scheme has very good scalability. Last, according to the calculation, our scheme exhibits a higher fidelity. Experimental realization of the scheme may open up promising future directions for quantum communication with long distance and high capacity of the two DOFs.
2. Model and Hamiltonian
Figure 1a shows the NV center system in the presented schemes. According to [34], the NV center contains a substitutional nitrogen atom together with a neighboring vacancy [11]. Figure 1b displays the NV center regarding its energy-level structure. An NV center exhibits a triplet ground state with 2.87 GHz zero-field splitting between levels (denoted by ) and (denoted by ) owing to the spin-spin interactions [34]. Without being affected by perturbation, e.g., affected by crystal strain or an external magnetic field, one of the six eigenstates of full Hamiltonian is [34] , where and are the orbital states.
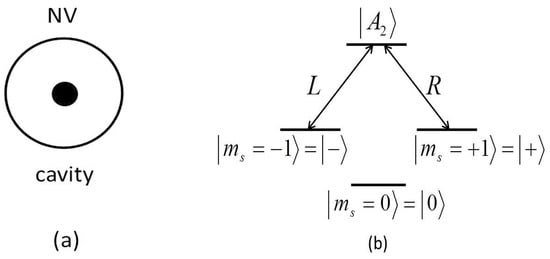
Figure 1.
(a) Schematic diagram of a diamond nitrogen-vacancy (NV) center coupling to a MTR. (b) The possible electron energy-level configuration of an NV center inside an MTR. The transition is driven by a left circularly polarized photon (denoted by ), and is driven by a right circularly polarized photon (denoted by ).
The NV center has a -type three-level structure, and the excited state exhibits equal decaying likelihood to the ground state through the left (L) circularly polarized photon and to through the right (R) circularly polarized photon, respectively. The Heisenberg equations of motion for this system can be given by [35]
where is the annihilation operator exhibited by cavity. and are the lowing operator and inversion operator exhibited by NV center, respectively. , , and are the frequencies of the cavity, photon, and the NV center, respectively. g stands for the coupling efficiency between the cavity and the NV center. is the decay rate of NV center. is the damping rate of cavity. stands for the side leakage efficiency exhibited by cavity. is the input operator of cavity and is the output operator of the cavity.
Being weakly excited, the reflection coefficient of the NV center confined in the cavity can be written as [28,36]
With the NV center not being coupled to cavity, i.e., , the reflection coefficient can be written as
When the cavity is resonant with the NV center and the photon, i.e., , then
Therefore, the below equations display how the input photon changes [28,29]
Under resonant condition , when and ,
3. Generation of Photonic Hyperentangled Cluster States
In this section, we will use the hybrid quantum system to show the generation of polarization-spatial hyperentangled cluster states with two photons, the equation of which in polarization DOF and spatial DOF is shown below.
where and are the Pauli operators. and ( and ) are the right- and left-circular polarization of the photon a (b). and ( and ) stand for distinct spatial modes of the photon a (b). The subscript p denotes the polarization DOF and s denotes the spatial DOF. a and b stand for two photons of hyperentangled cluster states. The below equations express the cluster states in polarization DOF
The below equations express the cluster states in spatial DOF
so there are sixteen hyperentangled cluster states by combining the cluster states in polarization DOF with the cluster states in spatial DOF.
The system of our scheme is shown in Figure 2, which is applied to generating the hyperentangled cluster states with two photons. The SW (switch) in Figure 2 plays an optical switch and the BS (beam splitter) is 50:50. The three can realize the following transformations:
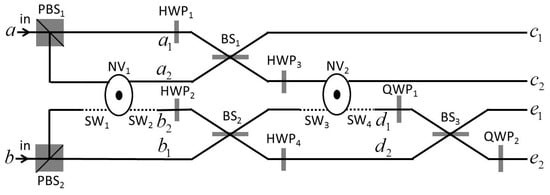
Figure 2.
Schematic diagram showing the two-photon polarization-spatial hyperentangled cluster states. The polarizing beam splitter is used to transmit the right circularly polarized photon and reflect the left circularly polarized photon , respectively. represents the optical switch and represents the beam splitter. The represents the half-wave plate which is used to perform a bit-flip operation on the photon in the polarization degrees of freedom (DOF). represents the quarter-wave plate which is used to realize a Hadamard operation and on the photon in the polarization DOF. and represent different spatial modes.
In the following, we show how to realize the two-photon hyperentangled cluster states by the following six steps.
Step (i): We first prepare the and in superposition state , , and prepare the two photons a and b in the superposition states , . Therefore, the initial state is
Step (ii): Then we send the photons a and b to the system (Figure 2), photons a and b present a time interval, which is shorter than the spin coherence time of photons. The photons a and b first pass through a circular polarizing beam splitter (PBS) successively, then the PBS splits the photon a into two parts, photon a in the state is partially transmitted to the path , and partially reflected to the path . When the photon a passes through and photon b passes through , the initial state involves into
Step (iii): Then the photon a passes through MTR, we apply a SW to the awaiting photon b. When part of the two photons in the state and interacts with the subsequently, the state involves into
Step (iv): The wave packets coming from spatial modes and are then mixed at the first beam splitter , and the wave packets coming from spatial modes and are mixed at the . The half-wave plate (HWP) can be applied to stabilizing the polarization states of the two photons. When photons a and b pass through two and four , the state involves into
Step (v): When photons a and b interact with , they can see entanglement with . The state can be changed into
Here, , .
Step (vi): Then the photon b passes through the quarter-wave plate (, and . The wave packets coming from spatial modes and are mixed at . The QWP is carried out to implement the Hadamard operation on photon b, that is, , . The state can be changed into
From Equation (17), when photons a and b pass through all elements of this system, we can divide the hyperentangled cluster states into two groups, considering the state of () under the measurement of the state (). Table 1 displays the measuring results.

Table 1.
The relation between the outcomes of the two NV centers and four symmetry hyperentangled cluster states.
In Table 1, there are four different hyperentangled cluster states corresponding to various combined states of two NV centers. If we implement a Hadamard operation on the two NV centers, then the states and can be rotated to and [25]. Therefore, the measurement of two NV centers can help us to get the hyperentangled cluster states.
4. Applications
Here, the scheme will exhibit a fidelity of while neglecting the side leakage of cavity. Taking the side leakage of cavity into account, the change of the reflected single photon can be found with Equation (5). We define the fidelity for generating the hyperentangled cluster states as [11]. Here, represents the ultimate state under practical conditions, and represents the ultimate state under ideal conditions. By calculation, we find that the sixteen hyperentangled cluster states have the same parity conditions. Then, we can plot the fidelity of the sixteen hyperentangled cluster states in Figure 3.
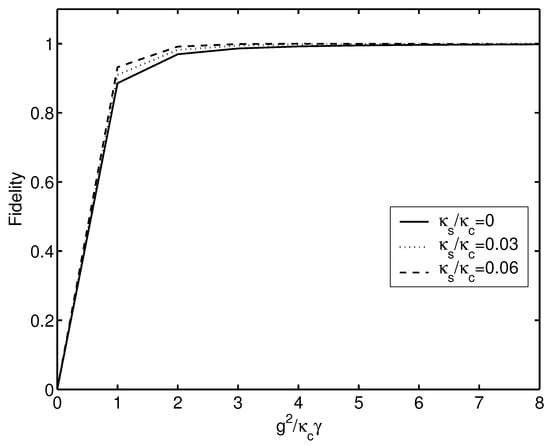
Figure 3.
The fidelities of the sixteen hyperentangled cluster states vs the parameter for the different leakage rates , , and , respectively.
From Figure 3, we can see that when the parameter is 2.25, the fidelities for the sixteen hyperentangled cluster states are (), (), and (). With the parameter over 4, the fidelity will exceed for the three leakage rates. That is to say, the higher fidelities are decided by higher ratio of the NV-cavity coupling strength and decay rates exhibited by NV center, damping the rate of cavity. In practical experiments, we consider the realistic parameters, e.g., GHz [37], GHz [38], GHz [38], then we have . The fidelities of our scheme can be larger than . Moreover, the manipulation of the NV centers to realize the quantum information procession task has been reported [39], which provides the possibility for our scheme. Therefore, our scheme is feasible in experiments.
5. Conclusions
To sum up, a scheme is proposed in the study to deterministically generate hyperentangled cluster states in the polarization DOF and spatial DOF. Compared with previous works [5,31,40], our scheme is very simple and very easy to implement in experiments. Under current experimental conditions, the scheme presents a high fidelity of over 99% and a stronger experimental feasibility. Once utilized, this hybrid system is applicable for constructing a diamond-based quantum network for quantum communication over long distances and with high capacity, such as quantum cryptography, quantum teleportation, as well as quantum superdense coding.
Author Contributions
L.T. gave the basic idea of the manuscript, Y.Z. wrote the main manuscript text, L.Z., F.Z. and S.X. contributed to the discussion and introduction, K.S. implemented the modification of this paper in order to improve its quality. All authors read and approved the final manuscript.
Funding
This work was supported by National Natural Science Foundation of China under Grant (No. 11574081, 11374096 and 11074072).
Acknowledgments
This work was supported by Natural Science Foundation of Hunan Province (No.2017JJ2214) and Science Research Foundation of Education Department of Hunan Province (No. 17C1264).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ren, X.F.; Guo, G.P.; Li, J.; Guo, G.C. Entanglement of the Hermite–Gaussian modes states of photons. Phys. Lett. A 2005, 341, 81–86. [Google Scholar] [CrossRef][Green Version]
- Guo, G.P.; Ren, X.F.; Huang, Y.F.; Li, C.F.; Ou, Z.Y.; Guo, G.C. Observation of two-photon coherence in plasmon-assisted transmission. Phys. Lett. A 2007, 361, 218–222. [Google Scholar] [CrossRef]
- Barbieri, M.; Vallone, G.; Mataloni, P.; Martini, F.D. Complete and deterministic discrimination of polarization Bell states assisted by momentum entanglement. Phys. Rev. A 2007, 75, 042317. [Google Scholar] [CrossRef]
- Barreiro, J.T.; Wei, T.C.; Kwiat, P.G. Beating the channel capacity limit for linear photonic superdense coding. Nat. Phys. 2008, 4, 282. [Google Scholar] [CrossRef]
- Vallone, G.; Donati, G.; Ceccarelli, R.; Mataloni, P. Six-qubit two-photon hyperentangled cluster states: Characterization and application to quantum computation. Phys. Rev. A 2010, 81, 052301. [Google Scholar] [CrossRef]
- Bin, G.; Yu-Gai, H.; Xia, F.; Chen, Y.L. Bidirectional quantum secure direct communication network protocol with hyperentanglement. Commun. Theor. Phys. 2011, 56, 659. [Google Scholar]
- Zhao, R.T.; Guo, Q.; Chen, L.; Wang, H.F.; Zhang, S. Quantum superdense coding based on hyperentanglement. Chin. Phys. B 2012, 21, 080303. [Google Scholar] [CrossRef]
- Ren, B.C.; Deng, F.G. Hyperentanglement purification and concentration assisted by diamond NV centers inside photonic crystal cavities. Laser. Phys. Lett. 2013, 10, 115201. [Google Scholar] [CrossRef]
- Hong, C.H.; Heo, J.; Lim, J.I.; Hyung, J.Y. Quantum secure direct communication network with hyperentanglement. Chin. Phys. B 2014, 23, 090309. [Google Scholar] [CrossRef]
- Perumangatt, C.; Rahim, A.A.; Salla, G.R.; Paul, G.; Singh, R.P. Three-particle hyper-entanglement: Teleportation and quantum key distribution. Quantum Inf. Process. 2015, 14, 3813–3826. [Google Scholar] [CrossRef][Green Version]
- Liu, Q.; Zhang, M. Generation and complete nondestructive analysis of hyperentanglement assisted by nitrogen-vacancy centers in resonators. Phys. Rev. A 2015, 91, 062321. [Google Scholar] [CrossRef]
- Li, X.H.; Ghose, S. Self-assisted complete maximally hyperentangled state analysis via the cross-Kerr nonlinearity. Phys. Rev. A 2016, 93, 022302. [Google Scholar] [CrossRef]
- Deng, F.G.; Ren, B.C.; Li, X.H. Quantum hyperentanglement and its applications in quantum information processing. Sci. Bull. 2017, 62, 46–68. [Google Scholar] [CrossRef]
- Jelezko, F.; Gaebel, T.; Popa, I.; Gruber, A.; Wrachtrup, J. Observation of coherent oscillations in a single electron spin. Phys. Rev. Lett. 2004, 92, 076401. [Google Scholar] [CrossRef] [PubMed]
- Yuan, T.; Zhou, F.; Chen, S.; Xiang, S.; Song, K.; Zhao, Y. Multipurpose Quantum Simulator Based on a Hybrid Solid-State Quantum Device. Symmetry 2019, 11, 467. [Google Scholar] [CrossRef]
- Zhao, Y.; Chen, X.; Shi, Z.; Zhou, F.; Xiang, S.; Song, K. Implementation of one-way quantum computing with a hybrid solid-state quantum system. Chin. J. Electron. 2017, 26, 27–34. [Google Scholar] [CrossRef]
- Chen, S.; Xiang, S.; Song, K.; Zhao, Y. Influence from cavity decay on entanglement evolution of three superconducting charge qubits coupled to a cavity. Chin. J. Electron. 2014, 23, 157–162. [Google Scholar]
- Zhao, Y.; Fang, X.M.; Zhou, F.; Song, K.H. Preparation of N-qubit GHZ state with a hybrid quantum system based on nitrogen-vacancy centers. Chin. Phys. Lett. 2013, 30, 050304. [Google Scholar] [CrossRef]
- Kennedy, T.A.; Colton, J.S.; Butler, J.E.; Linares, R.C.; Doering, P.J. Long coherence times at 300 K for nitrogen-vacancy center spins in diamond grown by chemical vapor deposition. Appl. Phys. Lett. 2013, 83, 4190–4192. [Google Scholar] [CrossRef]
- Zhou, F.; Zhao, Y.; Zhou, W.; Tang, D.S. Temperature-Dependent Raman Scattering of Large Size Hexagonal Bi2Se3 Single-Crystal Nanoplates. Appl. Sci. 2018, 8, 1794. [Google Scholar] [CrossRef]
- Zhou, F.; Zhao, Y.; Zhou, W.; Tang, D.S. Temperature dependent Raman of BiTe nanotubes. AIP Adv. 2018, 8, 125330. [Google Scholar] [CrossRef]
- Zhao, Y.F.X.M.; Zhou, F.; Song, K.H. Scheme for realizing quantum-information storage and retrieval from quantum memory based on nitrogen-vacancy centers. Phys. Rev. A 2012, 86, 052325. [Google Scholar] [CrossRef]
- Zhao, Y.; Mi, X.W.; Xiang, S.; Zhou, F.; Song, K. Entanglement Dynamics of Three Superconducting Charge Qubits Coupled to a Cavity. Commun. Theor. Phys. 2011, 55, 775. [Google Scholar] [CrossRef]
- Twamley, J.; Barrett, S.D. Superconducting cavity bus for single nitrogen-vacancy defect centers in diamond. Phys. Rev. B 2010, 81, 241202. [Google Scholar] [CrossRef]
- Marcos, D.; Wubs, M.; Taylor, J.M.; Lukin, M.D.; Sϕrensen, A.S. Coupling nitrogen-vacancy centers in diamond to superconducting flux qubits. Phys. Rev. Lett. 2010, 105, 210501. [Google Scholar] [CrossRef] [PubMed]
- Yang, W.L.; Yin, Z.Q.; Xu, Z.Y.; Feng, M.; Oh, C.H. Quantum dynamics and quantum state transfer between separated nitrogen-vacancy centers embedded in photonic crystal cavities. Phys. Rev. A 2011, 84, 043849. [Google Scholar] [CrossRef]
- Yang, W.L.; Xu, Z.Y.; Feng, M.; Du, J.F. Entanglement of separate nitrogen-vacancy centers coupled to a whispering-gallery mode cavity. New J. Phys. 2010, 12, 113039. [Google Scholar] [CrossRef]
- Chen, Q.; Yang, W.; Feng, M.; Du, J.F. Entangling separate nitrogen-vacancy centers in a scalable fashion via coupling to microtoroidal resonators. Phys. Rev. A 2011, 83, 054305. [Google Scholar] [CrossRef]
- Wei, H.R.; Deng, F.G. Compact quantum gates on electron-spin qubits assisted by diamond nitrogen-vacancy centers inside cavities. Phys. Rev. A 2013, 88, 042323. [Google Scholar] [CrossRef]
- Vallone, G.; Ceccarelli, R.; Martini, D.F.; Mataloni, P. Hyperentanglement of two photons in three degrees of freedom. Phys. Rev. A 2009, 79, 030301. [Google Scholar] [CrossRef]
- Yan, X.; Yu, Y.F.; Zhang, Z.M. Generation of hyperentangled four-photon cluster state via cross-Kerr nonlinearity. Chin. Phys. B 2014, 23, 060306. [Google Scholar] [CrossRef]
- Wei, H.R.; Deng, F.G.; Long, G.L. Hyper-parallel Toffoli gate on three-photon system with two degrees of freedom assisted by single-sided optical microcavities. Opt. Express 2016, 24, 18619–18630. [Google Scholar] [CrossRef] [PubMed]
- Ciampini, M.A.; Orieux, A.; Paesani, S.; Ramponi, R.; Osellame, R.; Mataloni, P. Path-polarization hyperentangled and cluster states of photons on a chip. Light Sci. Appl. 2016, 5, e16064. [Google Scholar] [CrossRef] [PubMed]
- Togan, E.; Chu, Y.; Trifonov, A.S. Quantum entanglement between an optical photon and a solid-state spin qubit. Nature 2010, 466, 730. [Google Scholar] [CrossRef] [PubMed]
- Walls, D.F.; Milburn, G.J.; Garrison, J.C. Quantum Optics. Phys. Today 1995, 48, 55–56. [Google Scholar] [CrossRef]
- An, J.H.; Feng, M.; Oh, C.H. Quantum-information processing with a single photon by an input-output process with respect to low-Q cavities. Phys. Rev. A 2009, 79, 032303. [Google Scholar] [CrossRef]
- Park, Y.S.; Cook, A.K.; Wang, H. Cavity QED with diamond nanocrystals and silica microspheres. Nano Lett. 2006, 6, 2075–2079. [Google Scholar] [CrossRef] [PubMed]
- Barclay, P.E.; Fu, K.M.C.; Santori, C.; Faraon, A.; Beausoleil, R.G. Hybrid nanocavity resonant enhancement of color center emission in diamond. Phys. Rev. X 2011, 1, 011007. [Google Scholar] [CrossRef]
- Neumann, P.; Kolesov, R.; Naydenov, B.; Steiner, M.; Jacques, V.; Balasubramanian, G.; Markham, M.L.; Twitchen, D.J. Quantum register based on coupled electron spins in a room-temperature solid. Nat. Phys. 2010, 6, 249. [Google Scholar] [CrossRef]
- Ji, Y.Q.; Jin, Z.; Zhu, A.D.; Wang, H.F.; Zhang, S. Complete hyperentangled state analysis and generation of multi-particle entanglement based on charge detection. Chin. Phys. B 2014, 23, 050306. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).