Effects of Salt Stress on the Leaf Shape and Scaling of Pyrus betulifolia Bunge

Abstract

Leaf shape can reflect the survival and development of plants in different environments. In particular, leaf area, showing a scaling relationship with other leaf-shape indices, has been used to evaluate the extent of salt stress on plants. Based on the scaling relationships between leaf area and other leaf-shape indices in experiments at different levels of salt stress, we could examine which leaf-shape indices are also related to salt stress. In the present study, we explored the effects of different salt concentration treatments on leaf dry mass per unit area (LMA), the quotient of leaf perimeter and leaf area (QPA), the quotient of leaf width and length (QWL), the areal quotient (AQ) of left and right sides of a leaf and the standardized index (SI) for bilateral symmetry. We treated Pyrus betulifolia Bunge under NaCl salt solution of 2‰, 4‰ and 6‰, respectively, with fresh water with no salt as the control. The reduced major axis (RMA) was used to fit a linear relationship of the log-transformed data between any leaf trait measures and leaf area. We found that leaf fresh weight and dry weight decrease with salt concentration increasing, whereas the exponents of leaf dry weight versus leaf area exhibit an increasing trend, which implies that the leaves expanding in higher salt environments are prone to have a higher cost of dry mass investment to increase per unit leaf area than those in lower salt environments. Salt concentration has a significant influence on leaf shape especially QWL, and QWL under 6‰ concentration treatment is significantly greater than the other treatments. However, there is no a single increasing or decreasing trend for the extent of leaf bilateral symmetry with salt concentration increasing. In addition, we found that the scaling exponents of QPA versus leaf area for four treatments have no significant difference. It indicates that the scaling relationship of leaf perimeter versus leaf area did not change with salt concentration increasing. The present study suggests that salt stress can change leaf functional traits especially the scaling relationship of leaf dry weight versus leaf area and QWL, however, it does not significantly affect the scaling relationships between leaf morphological measures (including QPA and the extent of leaf bilateral symmetry) and leaf area.

1. Introduction

Land salinization has been a global environmental issue, especially in more than 100 countries located in the arid, semi-arid and coastal areas [1,2]. The global area of salinized soil is around 1 billion hectares, accounting for 25% of the world’s land area [3]. It has been estimated that land salinization could lead to a 50% loss of arable land by 2050 [4]. Crop yields from salt and other related abiotic stress can drop by half [5,6]. Due to the vast territory, complex geology and terrain, as well as the interaction between the Eurasian continental climate and the Pacific monsoon, soil salinization is relatively pronounced in China [7], with its 33% of cultivated land area about 9.9 × 10⁷ hectares characterized as saline-alkali [8]. Intensifying human activities in the country will further accelerate soil salinization at an annual rate of increase by millions of hectares. This trend will inevitably suppress land productivity and agriculture sustainability, posing adverse effects on the environment and the socioeconomic system. It is of great ecological and social values to develop approaches to alleviate soil salinity at a massive scale.

To date, there are two main methods to develop and utilize saline-alkali land: (i) directly change salt content and related chemical properties in the soil, and (ii) use genetic engineering and plant cultivation to improve salt tolerance in plants [9]. The first method normally adopts the strategy of washing salt by drainage or irrigation to reduce the salt content. It has high demand for fresh water, which is scarce in most saline-alkali land distributed mainly in arid or semi-arid areas, and thus cannot be widely implemented. Washing salt would also take away soil nutrients, causing it to become barren. The second method is to screen salt-tolerant genotypes and salt-tolerant plants. It can potentially improve saline-alkali soil by absorbing soil salt and increasing soil organic matter and nutrients. It could be quickly expanded to a large extent and add additional economic value from plants producing industrial raw materials such as gum, resin, pulp and feed. Consequently, it has been favored over the first method in addressing the regional issue of land salinization.

The response of plants to salt stress is complex, in the form of plant physiology, morphology and metabolism. Different plant varieties [10,11] in different growth periods [12,13] have different salt-tolerance mechanisms and abilities. Energy consumption for plants under long-term salt stress can be greater than energy production, reducing energy supply and leaf area (wilting and reduction in leaf number). Salt stress can also reduce photosynthetic rate and nutrient supply, slowing down organic matter accumulation in roots, stems and leaves, thus inhibiting plant growth [14]. Enzyme activities related to plant physiology and metabolism can also be affected by salt stress, leading to failed life cycles and ultimately plant death [15]. The most notable effect of salt damage on plants is on the morphology and phenotypic characteristics of plants. Leaf is an important organ for plants to maintain normal growth and life cycles [16] through photosynthesis and transpiration [17,18]. Leaf condition can be indicative of plant health status. Under salt stress, leaves will exhibit corresponding responses. As leaf-shape indices can reflect the growth and development of leaves; they can be used to evaluate plant performance in different environments [19], including under salt stress. In particular, leaf area has been used as an important index to assess salt damage in plants [20] as demonstrated using common beans (Phaseolus vulgaris L. cv. Derakhshan) [21].

Leaf shape can be captured by a rich array of indices [22,23,24], and few studies have explored the possibility of using other leaf-shape indices to detect salt impact [25,26]. By analyzing the relationship between other leaf-shape indices and leaf area, we can quantify different facets of salt stress in plants. Here, we chose leaf dry mass per unit area (LMA), the quotient of leaf perimeter and leaf area (QPA), the quotient of leaf width and length (QWL), the areal quotient (AQ) of left side and right side of a leaf and standardized index (SI) for bilateral symmetry to detect salt damage. In particular, the scaling relationship between leaf area and dry weight [27] can be represented by LMA [21]. LMA is related to leaf thickness, shape and area, and reflects the ability of light interception and self-protection under strong light. LMA follows an increasing function of leaf area [28,29]. The proportional model proposed by Montgomery [30] provides a non-damage approach to measure leaf area by the product of leaf width and length [31,32] and can be used to compare leaf shape under different conditions [33]. Leaf bilateral symmetry (AQ and SI), which refers to the comparison of the leaf area along the left and right sides of the main vein, is also an important characteristic of leaf shape, resulted from light heterogeneity [34]. In addition, we included QPA to explore the relationship between leaf shape and salt tolerance, as little research has been done on the relationship between leaf perimeter and leaf area and the potential cross-effect of leaf perimeter on leaf symmetry and leaf area [35].

Pyrus betulifolia Bunge is a wild species of the genus Pyrus L. of Rosaceae family. As a variety of Oriental pear (Asian pear) [36], it is native to East Asia and mainly distributed in China, Korean peninsula and Japan [37]. It has good grafting affinity with the Oriental pear and Western pear, and is an important parent of dwarf rootstock and resistance breeding [38,39]. It is the main grafting stock of pear varieties in northern China. The characteristics of the rootstock can affect the absorption of mineral nutrients, tree shape, tree yield and fruit quality. Using P. betulifolia as grafted rootstock can significantly improve the salt tolerance of Pyrus [40,41], with the grafted pear varieties possessing abilities for wind, cold, drought and salt-alkali resistance, as well as a well-developed root system, fast growth and strong adaptability. It is an important resistance resource of Pyrus germplasm [42].

2. Experimental Process and Data Analysis

2.1. Experimental Materials

We selected 24 healthy biennial P. betulifolia seedlings with similar height and ground diameter from the field in Baima Town of Jiangsu Province (31°36′45″ N, 119°12′43″ E) on 26 March 2018, and transplanted each into plastic flower pots with a diameter of 30 cm and a height of 30 cm. The soil matrix was composed of nutrient soil: vermiculite: perlite = 1:1:1 volume ratio. The seedlings were maintained in the Teaching and Learning Base of Nanjing Forestry University (31°36′45″ N, 119°09′16″ E) in Baima Town. The seedlings were kept for six months to ensure root restoration, during which we unified regular and quantitative watering, daily maintenance and management, as well as pest control, to ensure the healthy growth of seedlings.

We chose to carry out the experiment in early autumn of 2018 to avoid the potential effect of summer high temperature in Nanjing. All dates included in this paper refer to the same year. On 10 September, seedlings with similar growth were selected for salt stress treatment. NaCl was used to prepare 2‰, 4‰, 6‰ salt solution (NaCl mass as a percentage of soil dry weight) and 0‰ solution as control. Six seedlings were treated with each salt concentration. Every other day, 200 mL 2‰ salt solution was added to the pot (a tray was placed at the bottom of each pot; any solution in the tray was poured back into the pot). When the treatment reached the required salt concentration, the same amount of water was added to ensure the consistency of the experiment. For seven days, all plant pots reached the specified salt concentration. This not only prevents plants from dying immediately after being suddenly exposed to a high concentration solution, but also prevents the solution from flowing out from the bottom of the pot. The 35-day salt treatment experiment started on 16 September, and 200 mL of water was used every three days to irrigate the soil to ensure that there was no drying.

All intact and undamaged leaves from experimental plants (with a mean of 40–50 leaves per plant) were picked at 9 a.m. on 20 October and placed in self-sealing bags (28 cm × 20 cm). In other words, the healthy leaves of all experimental plants were used to reduce the potential influence caused by the sampling positions of leaves. The leaves (at least 200 leaves per salt concentration) treated with the same salt concentration were placed in the same self-sealing bags. All leaves were placed in the incubator with ice bags to avoid water loss. Then, the petiole was reduced to the same length with scissors, and the leaf was wiped and weighed quickly with an electronic balance (Type: ML 204; Mettler Toledo Company, Greifensee, Switzerland; measurement accuracy is 0.0001 g).

2.2. Leaf Image Acquisition and Leaf Edge Extraction

Leaf was scanned by a scanner (Type: Aficio MP 7502; Ricoh, Tokyo, Japan), and all image pixels were set to 600 dpi. The extraction of plane coordinates of leaf edge was obtained by using the Matlab program compiled by Shi et al. [43,44]. The leaves were then placed in kraft paper envelopes (16.5 cm × 22.5 cm) and dried in ovens (Type: XMTD-8222; Jinghong Experimental Equipment Co., Ltd., Shanghai, China). The leaves were first dried at 105 °C for 2 h, then dried at 80 °C for 48 h until the weight of the leaves was constant. The leaves were taken out and cooled to room temperature (25 °C). The dry weight of the leaves was measured by the electronic balance.

2.3. Data Acquisition of Leaf-Shape Indices

The leaf-shape indices including leaf area, LMA, leaf perimeter, leaf width, leaf length, AQ and SI were obtained by R script developed in references [44,45] based on R statistical software (version 3.2.2) [46].

2.4. Data Analysis

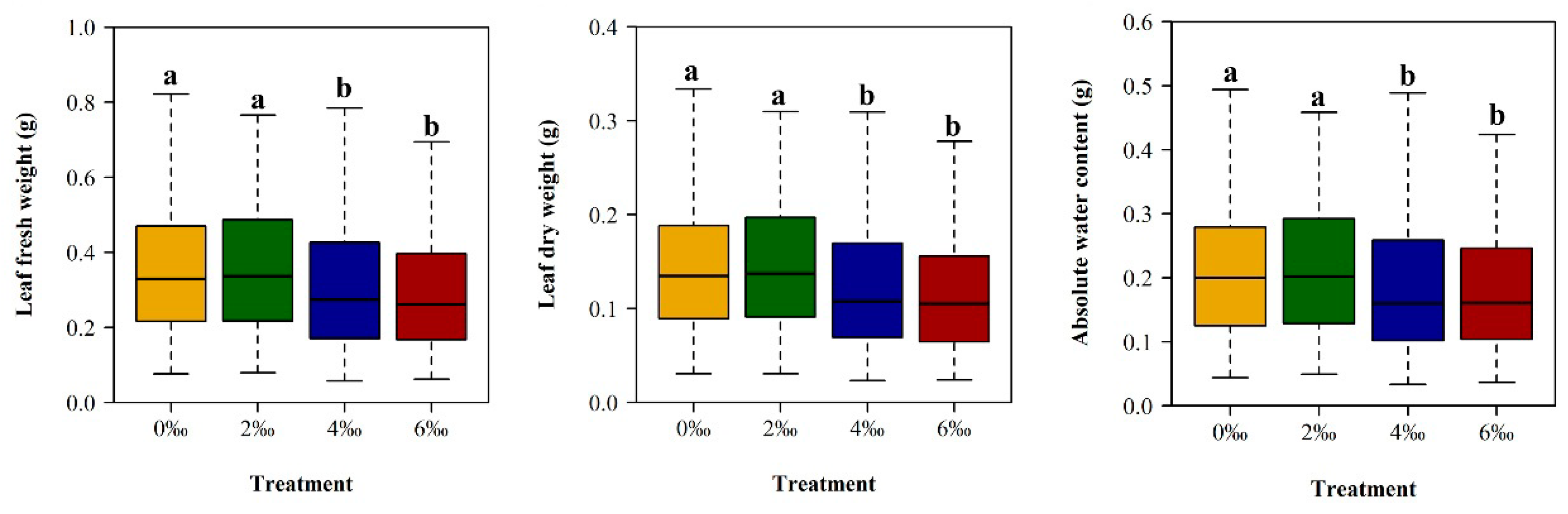
2.4.1. Leaf Water Content

We calculated the absolute water content (W_a) as:

$$W_a=W_F-W_D$$

(1)

where W_F is leaf fresh weight; W_D is leaf dry weight.

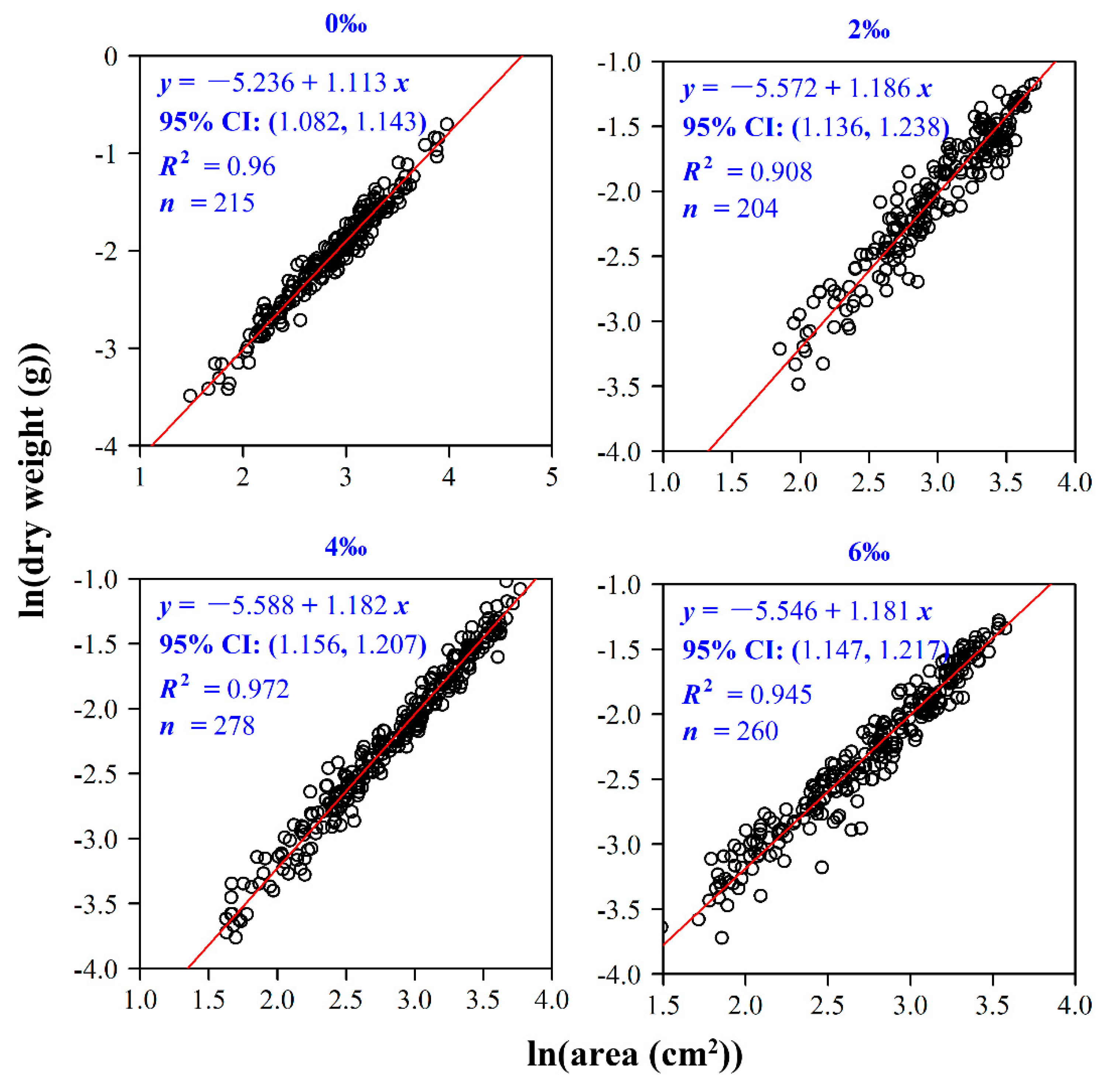
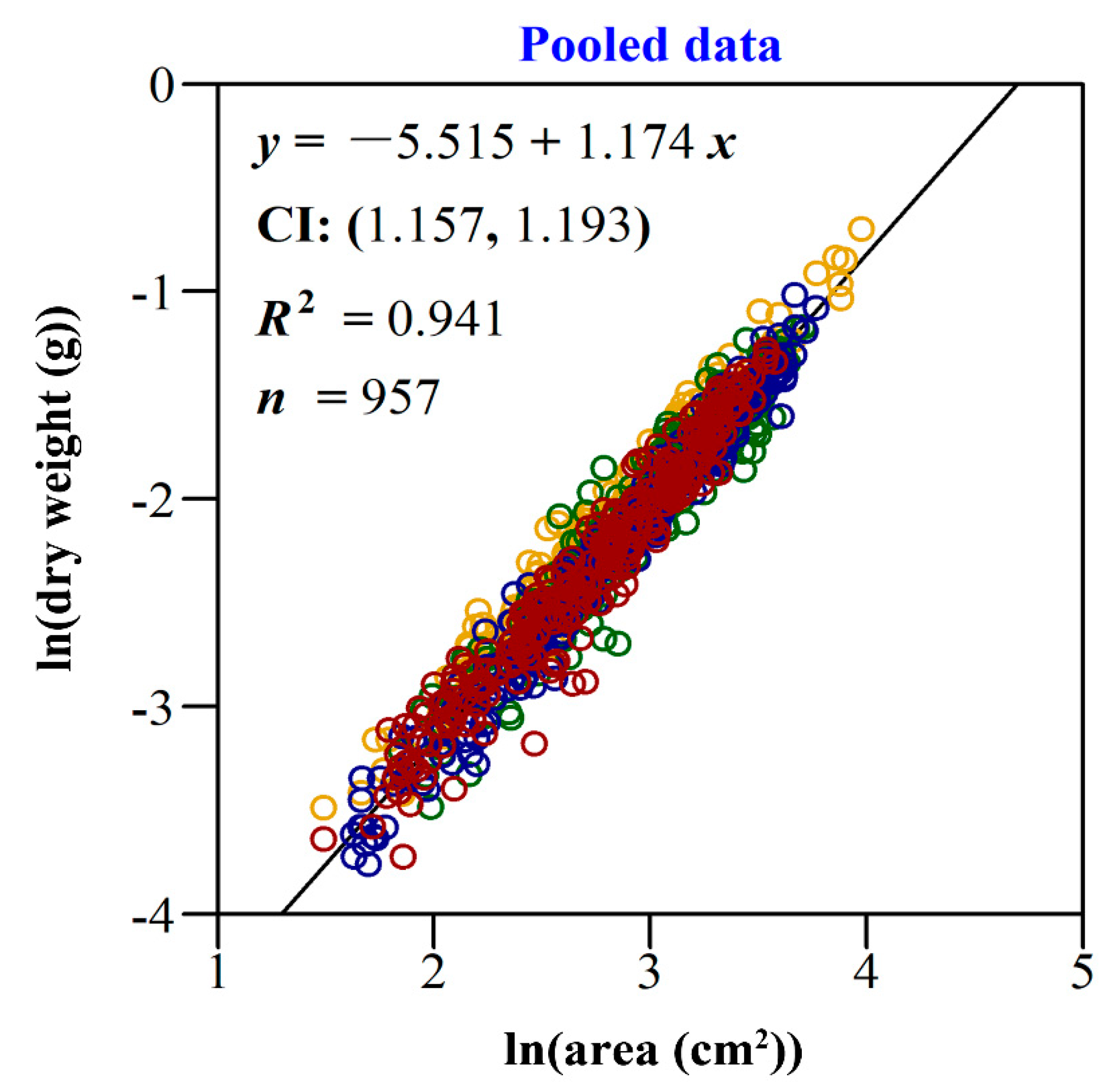
2.4.2. The Relationship between Leaf Area and Dry Weight

The power function formulas and logarithmic linearization of the power function for leaf area (A, cm²) and dry weight (W_D, g) [28,29] are described as follows:

$$W_D=a{A}^b\iff ln\left(W_D\right)=ln\left(a\right)+bln\left(A\right)$$

(2)

where a and b are the constants to be estimated.

2.4.3. The Relationship between Leaf Area and LMA

LMA is the quotient of dry weight and leaf area:

$$\mathrm{LMA}=\frac{W_D}{A}$$

(3)

The following formula can be deduced from Equations (2) and (3), and logarithmic linearization of the power function:

$$\mathrm{LMA}=a{A}^{b-1}\iff ln\left(\mathrm{LMA}\right)=ln\left(a\right)+\left(b-1\right)ln\left(A\right)$$

(4)

$$\Rightarrow y=\alpha +\left(b-1\right)x$$

(5)

where x = ln(A), y = ln(LAM), α = ln(a).

2.4.4. The Relationship between Leaf Area and QPA

We define QPA as the quotient of leaf perimeter (P, cm) and leaf area:

$$\mathrm{QPA}=\frac{P}{A}$$

(6)

There is a proportional relationship between leaf area and perimeter as follows:

$$P=\beta A^{\theta }$$

(7)

where β and θ are both constants to be fitted.

From Equations (6) and (7), the relationship between leaf area and QPA can be obtained, and the power function is logarithmically linearized to obtain the following formula:

$$\mathrm{QPA}=\beta A^{\theta -1}\iff \ln \left(\mathrm{QPA}\right)=\ln \left(\beta \right)+\left(\theta -1\right)\ln \left(A\right)$$

(8)

$$\Rightarrow y=c+\left(\theta -1\right)x$$

(9)

where x = ln(A), y = ln(QPA), c = ln(β).

2.4.5. The Relationship between Leaf Area and QWL

There is a proportional relationship between leaf area and product of leaf width (w, cm) and length (l, cm) [31,32]:

$$A=k\left(w\times l\right)$$

(10)

where k is a constant to be fitted.

If the quotient of leaf width and length is a constant (λ), that is:

$$\lambda =\frac{w}{l}$$

(11)

From Formulas (10) and (11), we can deduce the following formulae:

$$A=k\lambda l^2\mathrm{or}A=\frac{k{w}^2}{\lambda }$$

(12)

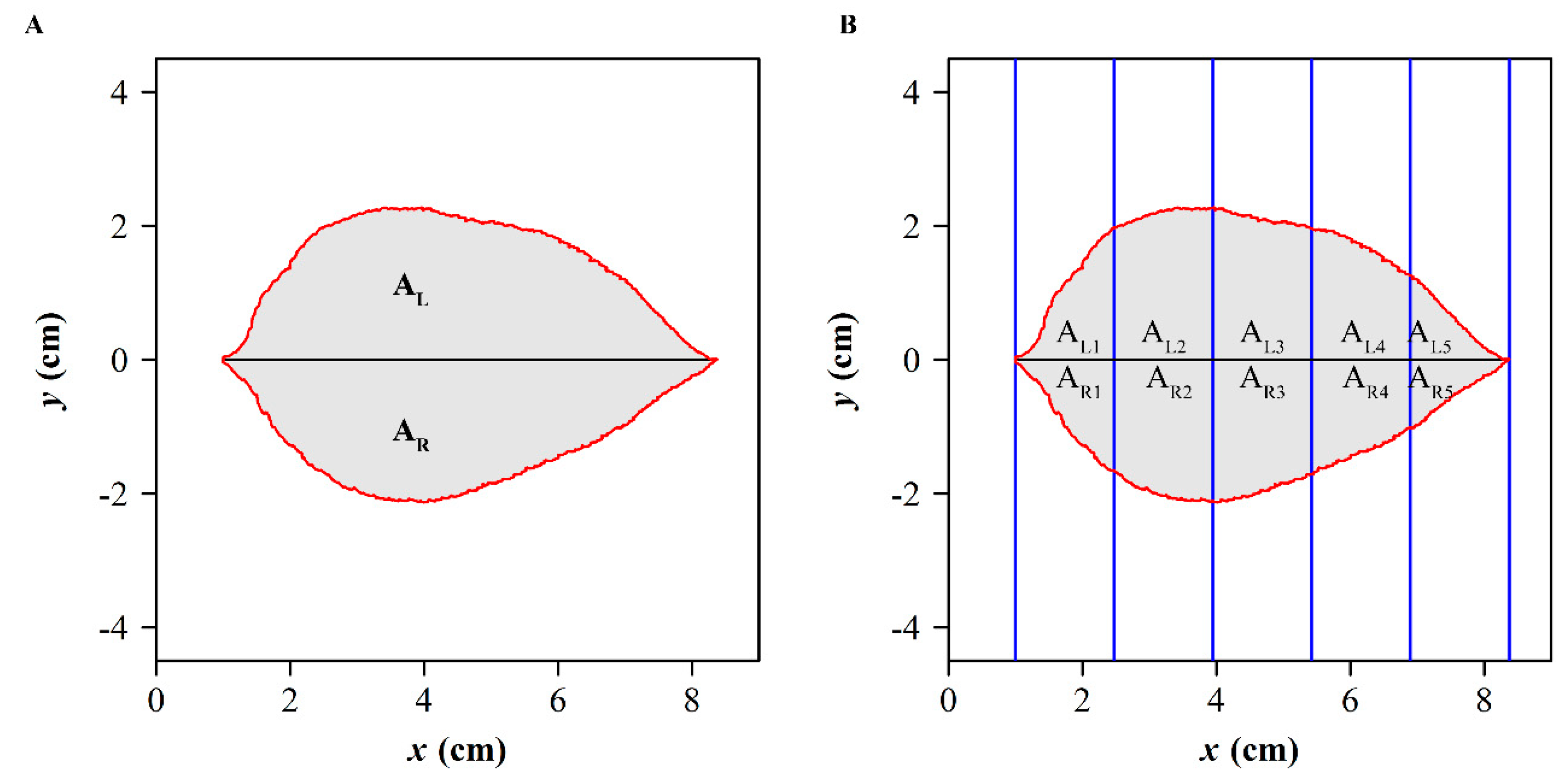
2.4.6. The Areal Quotient of the Left Side and Right Side

A leaf can be divided into left side and right side by the symmetrical axis along the central main vein (Figure 1A). The leaf symmetry extent can be expressed by the areal quotient of the left side (A_L, cm²) and right side (A_R, cm²), namely AQ:

$$\mathrm{AQ}=\frac{A_L}{A_R}$$

(13)

2.4.7. Standardized Index for Bilateral Symmetry

We used strips of the same width to cut the line segment through leaf apex and base vertically (Figure 1B), and used A_Li and A_Ri to represent the area of the strips on the leaf left and right sides. SI can be expressed as the following Formula [47]:

$$\mathrm{SI}=\frac{1}{n}{\displaystyle \sum }_{i=0}^n\frac{\left|A_{Li}-A_{Ri}\right|}{A_{Li}+A_{Ri}}$$

(14)

where n denotes the number of strips.

3. Results

After five weeks of salt stress, we can clearly detect phenotypic differences between leaves of P. betulifolia treated with different salt concentrations (Figure 2).

It can be seen from Figure 3 that leaf fresh weight, leaf dry weight and absolute water content of P. betulifolia showed the same trend under different salt treatments. The three indices were significantly higher under the control and 2‰ salt concentration treatment than those under the two other higher concentration treatments.

Among the four treatments, the estimates of the slope obtained from fitting the data of leaf dry weight and area data for different treatments are different, ranging from 1.113 (0‰) to 1.186 (2‰), and all slope estimates are greater than 1.0. All coefficients of determination (i.e., R² values) are high, ranging from 0.908 to 0.972 (Figure 4). At the same time, we aggregated all leave data. The slope estimates of leave area and dry weight are still greater than 1.0 (Figure 5), between the minimum (1.113) and maximum (1.186) of a single treatment (Figure 4).

We detected significant differences both in leaf area and LMA among different salt treatments (Figure 6), with the overall trends (except the 2‰ salt concentration treatment whose median was slightly greater than that of the control group) gradually decreasing with the increase of salt concentration (

Table 1. Effects of different salt treatments on leaf area and LMA of P. betulifolia.

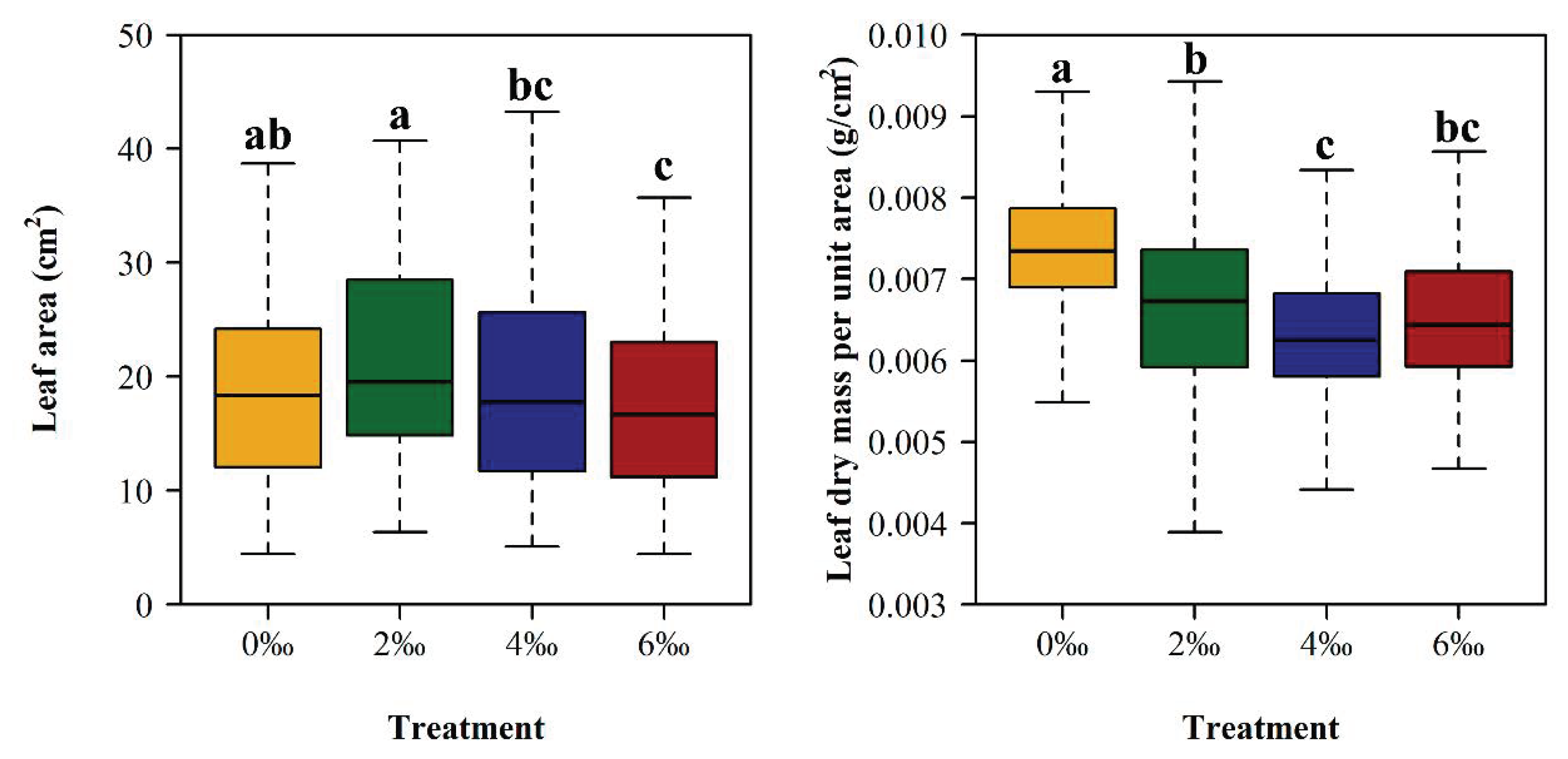
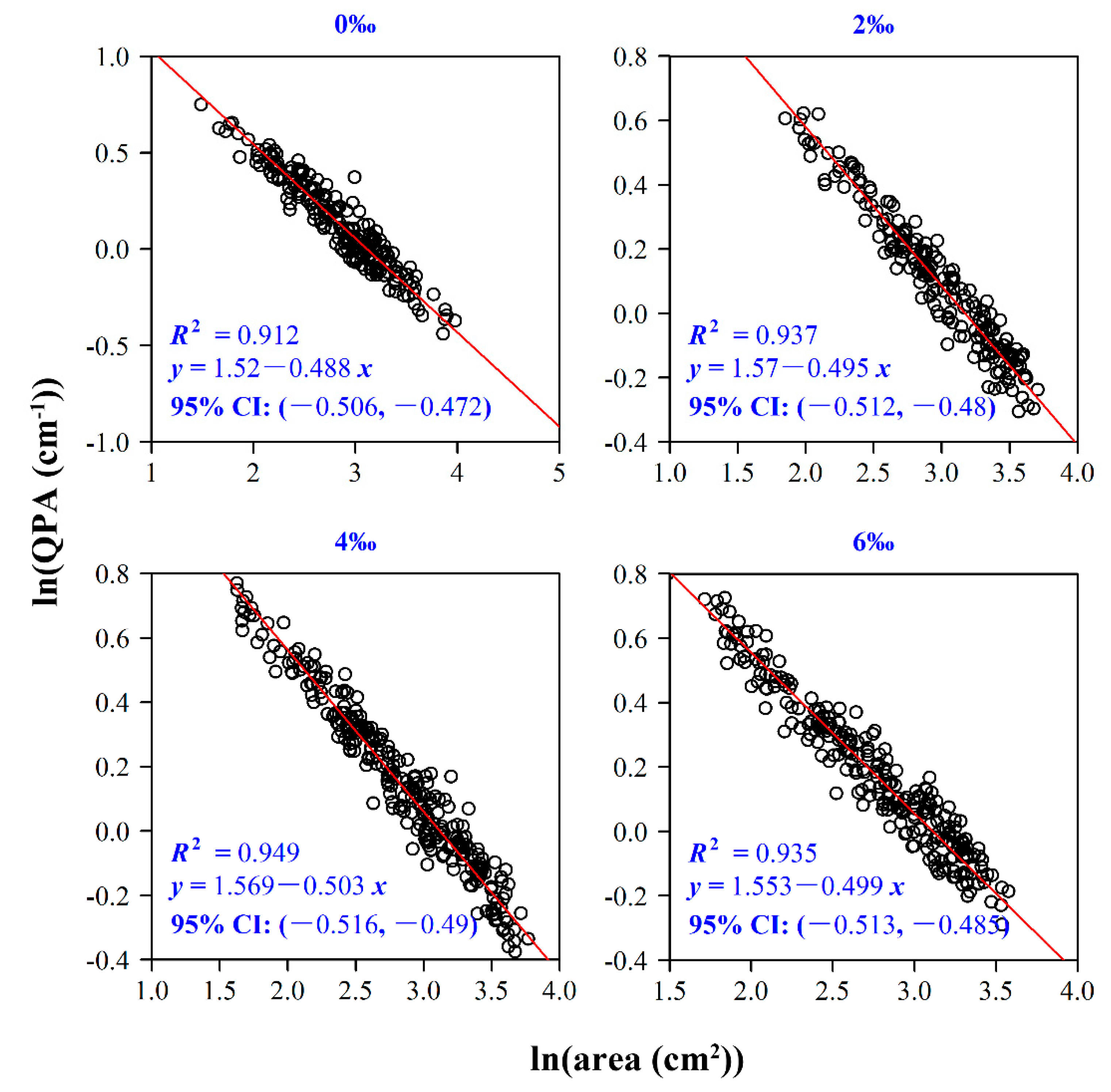
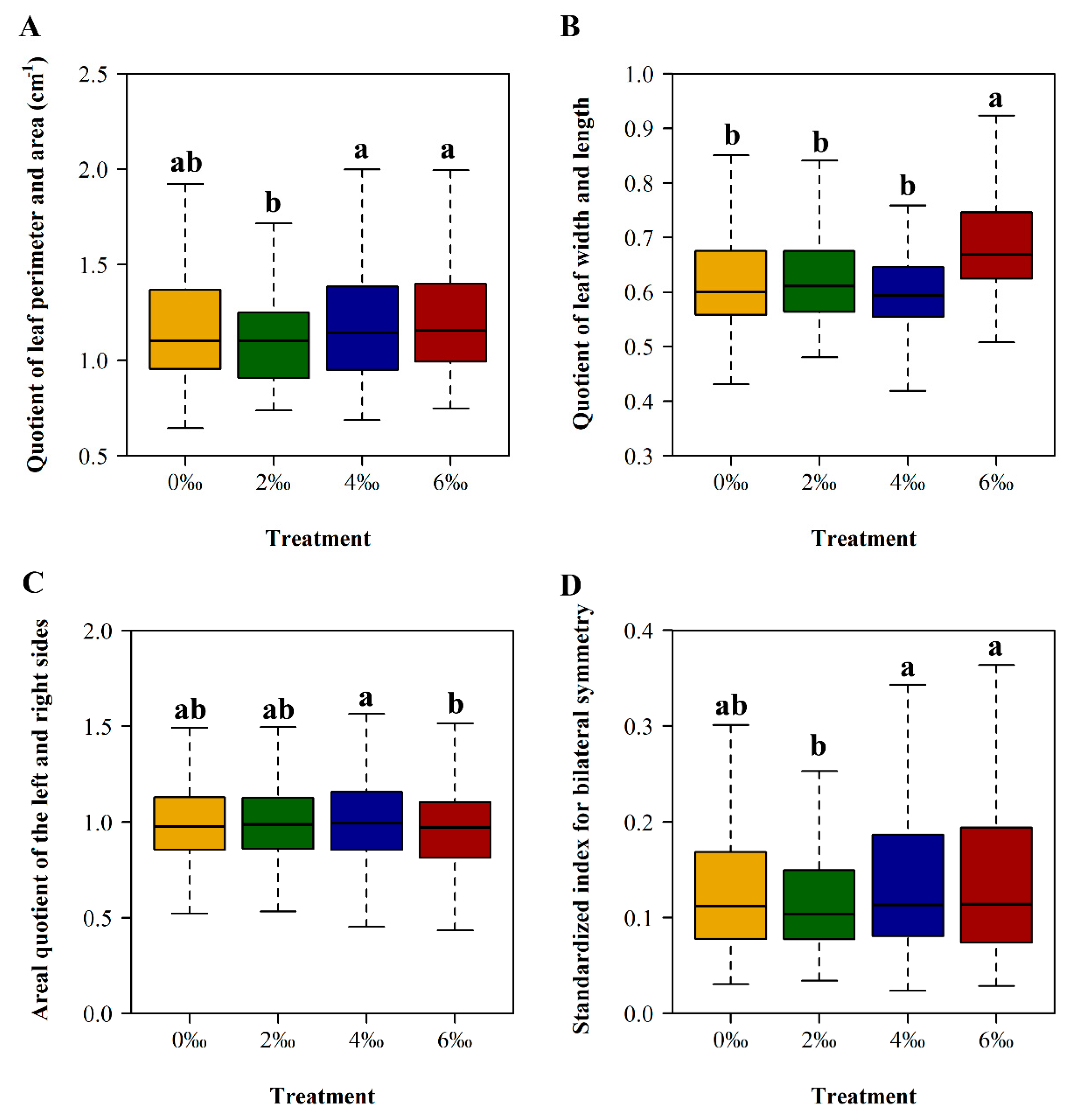
Treatment	A (cm2)	LMA (g/cm2)
0‰	19.36 ± 9.14 ab	0.0074 ± 0.0009 a
2‰	21.43 ± 8.55 a	0.0067 ± 0.0011 b
4‰	19.03 ± 9.02 bc	0.0063 ± 0.0009 c
6‰	17.26 ± 7.39 c	0.0065 ± 0.0008 bc

Notes: a, b and c are used to show the significance of difference between means of any two treatments. In each column of Table 1, the same letters represent a non-significant difference, whereas different letters represent a significant difference at p < 0.05.

).

There is a negative correlation between leaf area and QPA (Figure 7). The correlation coefficients of leaf area and QPA are all negative, and all corresponding P values are smaller than 0.01 (

Table 2. Correlation coefficients between QPA (and QWL) and leaf area (A) of P. betulifolia. P below represents the significance of any correlation coefficient.

Treatment	QPA-A	P	QWL-A	P
0‰	−0.8739	<0.01	−0.0204	0.7664
2‰	−0.9168	<0.01	−0.1022	0.1459
4‰	−0.9094	<0.01	−0.0001	0.9984
6‰	−0.9081	<0.01	−0.1808	<0.01

). Therefore, there is a strong negative correlation between leaf area and QPA. There are significant differences in QPA of leaves treated with different salt concentrations (Figure 8A). QPA increased gradually with the increase of salt concentration.

There is a significant proportional relationship between width and length (

Table 3. Estimates of the coefficient of proportionality between leaf length and width, standard deviations (SD), and coefficients of determination (R²) for four salt treatments of P. betulifolia.

Treatment	Estimate	SD	R2
0‰	0.6048	0.0059	0.9799
2‰	0.6167	0.0062	0.9801
4‰	0.6002	0.0053	0.9792
6‰	0.6707	0.0052	0.9845

). The quotient of leaf width and length varied with salt concentration, ranging from 0.6002 to 0.6707, with the coefficients of determination from 0.9792 to 0.9845. Although QWL treated with 6‰ salt treatment is significantly higher than other low salt concentrations (Figure 8B) and the correlation coefficients between QWL and leaf area are all negative (Table 2), there are no significant differences.

There are significant differences in AQ among the four salt concentrations (Figure 8C). The AQ value treated with 4‰ salt concentration is the highest (

Table 4. Effects of different salt treatments on leaf AQ and SI of P. betulifolia.

Treatment	AQ	SI
0‰	1.0101 ± 0.2506 ab	0.1337 ± 0.0783 ab
2‰	1.0202 ± 0.2676 ab	0.1265 ± 0.0740 b
4‰	1.0789 ± 0.4167 a	0.1517 ± 0.1075 a
6‰	0.9785 ± 0.2986 b	0.1510 ± 0.1079 a

Notes: a and b are used to show the significance of difference between means of any two treatments. In each column of Table 1, the same letters represent a non-significant difference, whereas different letters represent a significant difference at p < 0.05.

), but there is no obvious rule. The correlation coefficients between AQ and leaf area of four salt concentrations are positive and negative (ranging from −0.2669 to 0.0169), indicating a weak correlation (

Table 5. Correlation coefficients between AQ and SI and leaf area (A) of P. betulifolia. P below represents the significance of any correlation coefficient.

Treatment Code	AQ-A	P	SI-A	P
0‰	0.0169	0.8054	−0.1449	<0.05
2‰	−0.0791	0.2607	−0.2468	<0.01
4‰	−0.2669	<0.01	−0.4138	<0.01
6‰	0.1075	0.0837	−0.4400	<0.01

).

There are significant differences in SI among the four salt concentrations (Figure 8D). The SI value treated with 6‰ salt concentration is the highest (Table 4). The correlation coefficients between leaf area and SI of four salt concentrations range from −0.4400 to −0.1449 (all p < 0.05), indicating a strong negative relationship (Table 5).

4. Discussion

As an important index of leaf shape, leaf area is positively correlated with leaf dry weight, but its increase usually does not keep pace with that of leaf dry weight [28,29]. The determination coefficients under all treatments were greater than 0.9 (Figure 4 and Figure 5), indicating that the scaling relationship between leaf mass and leaf area under different salt treatments are all strong. The leaf area of 2‰ salt concentration treatment was only slightly higher than that of the control (Table 1), potentially due to the stimulation from low concentration of salt in soil. Such low concentration of salt can be decomposed by plants to provide some inorganic ions as nutrients, promoting to some extent the plant growth [48]. This may only be a short-term effect, as long-term exposure to even low concentrations of salt in the environment can produce an inhibitory effect. In particular, when a plant is under salt stress, salt solution in the root system has a low water potential and cannot supply water to the leaves. The leaves suffer due to the lack of water and excessive concentration of ions, resulting in partial ion and nutrient loss. Due to the key role of water during leaf photosynthesis [15], plant growth and development will slow down from salt stress, resulting in a decrease in the development rate of leaf area expansion [49,50]. Specifically, salt damage can shorten the elongation zone and/or period of the leaves, reducing the growth rate of leaves and the rate of local blade expansion [51]. That is, the reduction of leaf area reduction is the adaptation of plants to salt stress. It is beneficial to reduce water transpiration and nutrient supply demand, and leading to the destruction of the energy distribution of leaf supply growth.

There is a negative correlation between leaf area and QPA (Figure 7). The high coefficient of determination indicates a strong relationship between the two. QPA values have no significant difference among three salt treatments (Figure 8A), and QPA under 2‰ salt concentration is lower than those under two higher salt concentration treatments (Table 2). It again indicates that 2‰ salt concentration could have produced a short-term proliferating effect on leaf growth.

Leaves treated with same salt concentration had a similar width-length quotient (i.e., λ in λ = w/l could be expressed as a constant), although the quotient differed significantly between treatments of different salt concentrations. As the determination coefficients from linear regression of width and length was high, ranging from 0.979 to 0.985 (Table 3), it supports a proportional relationship between leaf width and length. Since the formula of leaf area versus the width and length is known (Equation (10)), we can expect a linear relationship between leaf area and the square of leaf width or the square of leaf length: that is, A = kλl² or A = (kw²)/λ, which is independent of the quotient of leaf width and length. Therefore, QWL could not reflect the salt tolerance of plants.

As plants are often engaging in intense light/space competition with neighboring plants in a community [52,53], trees will change their tree structure by expanding horizontally and vertically the branch and crown for basic survival and growth [54]. Such competition will also affect the leaf-shape indices and the bilateral symmetry of leaves [55]. When one part of the leaf is occluded and the other part illuminated by light, the nutrient supply in the leaf will become asymmetric, which can be reflected by the leaf shape and its bilateral symmetry. A leaf in a relatively regular and sufficient space normally has strong bilateral symmetry [31]. Plants need to have different intensities of light to maintain basic metabolism and production in diverse environments. The light utilization efficiency of P. betulifolia leaves, as expected, differed among different salinity conditions, which in turn affects the bilateral symmetry of leaf (depicted by the areal quotient of the left and right side of a leaf, AQ, and the standardized index for bilateral symmetry, SI). Little regularity was found between AQ and salt concentration (Figure 8C, Table 4), and between AQ and leaf area (Table 5). AQ thus cannot be used as a leaf index to evaluate plant salt tolerance. When the leaf shape is approximately a parallelogram, AQ approaches 0, equivalent to complete symmetry. This was the reason why we also introduced SI to test whether leaf symmetry can be indicative of salt damage. According to Equation (14), the quotient of absolute value of the difference between the left and right side area of each strip to total area of each strip was superimposed to avoid the situation that the areas of the left and right side were similar but with different shapes. From Table 5, we can see that the correlation coefficient between SI and leaf area was all negative (p < 0.05), and SI increased gradually with the increase of salt concentration (Figure 8D). However, the SI of leaves treated with 2‰ salt concentration was slightly lower than that of control, exhibiting a similar pattern of leaf area and QPA, mainly due to the short-term stimulation of low salt concentration on plant growth.

5. Conclusions

We found that there are significant differences in leaf biomass (both for leaf fresh weight and dry weight) among the control group and two higher salt concentration treatments (i.e., 4‰ and 6‰) whereas there is no significant difference in leaf biomass between the control group and the 2‰ salt concentration treatment. The estimates of the scaling exponent of leaf dry weight versus leaf area for two higher salt concentration treatments are slightly greater than that of the control group because the 95% CIs for the former two treatments do not overlap with that of the control group. However, the estimated scaling exponent of leaf dry weight versus leaf area for the lower salt concentration treatment (i.e., 2‰ salt concentration) has no significant difference with that of the control group. This means that to increase per unit leaf area for two higher salt concentration treatments will require more leaf dry mass input than the control group and the 2‰ salt concentration treatment. Thus, a high salt concentration is more likely to result in small leaves to reduce the cost of dry mass investment for enlarging leaf area (i.e., diminishing returns [29]). However, a higher concentration appears not to largely change the leaf shape of P. betulifolia. Despite a weak positive correlation between leaf area and the quotient of leaf width and length (QWL) under 6‰ salt concentration treatment, QWL did not show a significant correction with leaf area for the remaining treatments including the control group. However, we demonstrated that leaf width is proportional to leaf length, which implies that leaf area can be approximately proportional to the square of leaf length according to the Montgomery equation assuming that leaf area is proportional to the product of leaf length and width. In addition, we found that there is a significant scaling relationship between the quotient of leaf perimeter and area (QPA) and area, and the estimated scaling exponents of QPA versus area for four treatments were approximately equal to −1/2, which indicates that leaf perimeter is actually proportional to leaf area to the power 1/2. With regard to leaf bilateral symmetry measure, the areal quotient (AQ) of the left and right sides has been demonstrated to have no correlation or a weak correlation with leaf area for different treatments, but the standardized index (SI) for leaf bilateral symmetry was found to be strongly related to leaf area in this study, which suggests that to use AQ as a leaf bilateral symmetry measure indicator is better than SI for this plant. We then found that there are no significant differences in AQ among the control group and the 2‰ and 4‰ salt concentration treatments. However, the 6‰ salt concentration treatment has a significant difference in leaf bilateral symmetry with another three salt concentration treatments. Furthermore, it also has a significant difference in QWL with the others. This means that the 6‰ salt concentration treatment has actually led to a change in leaf shape of P. betulifolia. However, we did not measure the influence of the salt concentrations higher than 6‰ on leaf traits of this tree species, which deserves a further investigation.