DFT Calculations of the Structural, Mechanical, and Electronic Properties of TiV Alloy Under High Pressure
Abstract
1. Introduction
2. Methodology
3. Results and Discussion
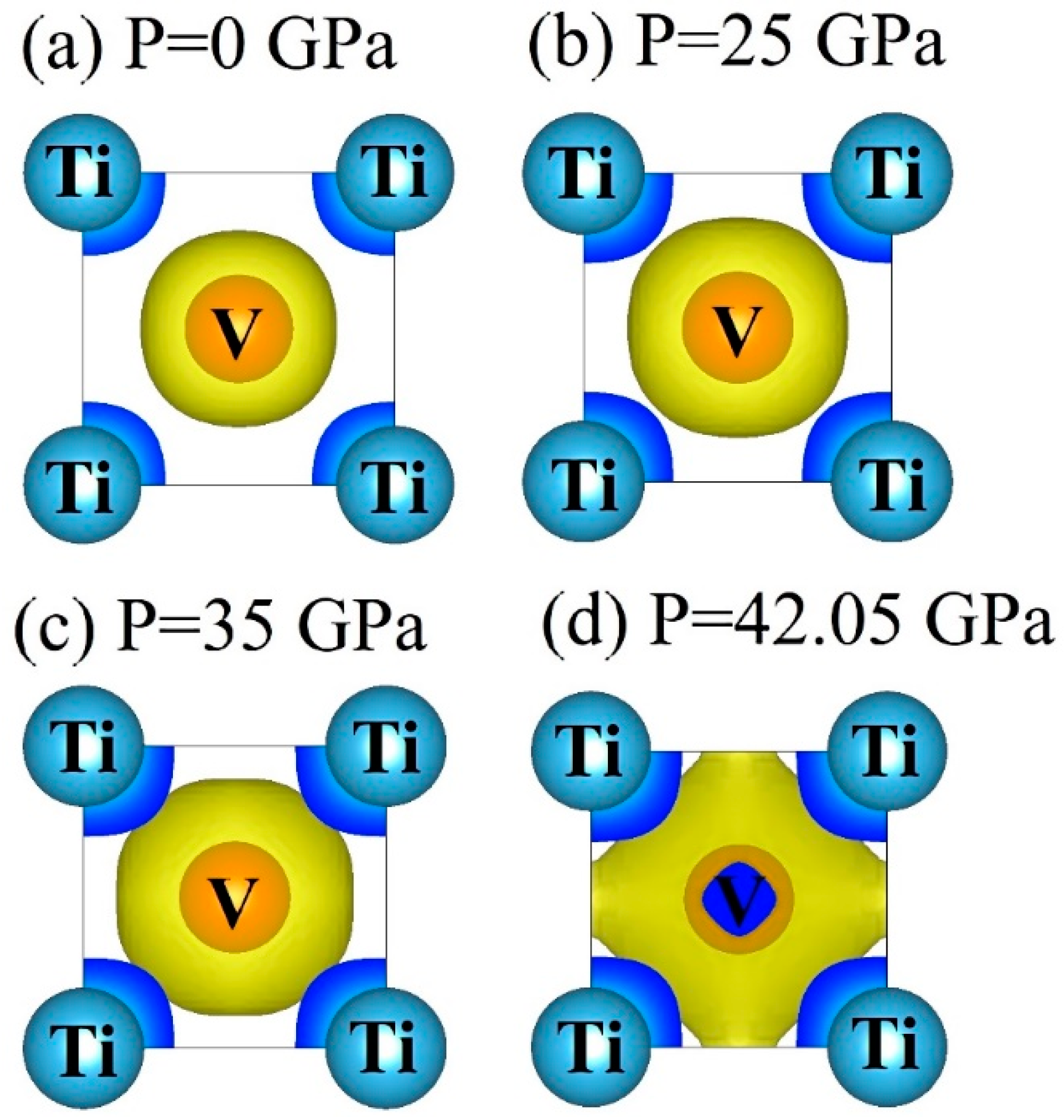
3.1. Structural Properties and Stability
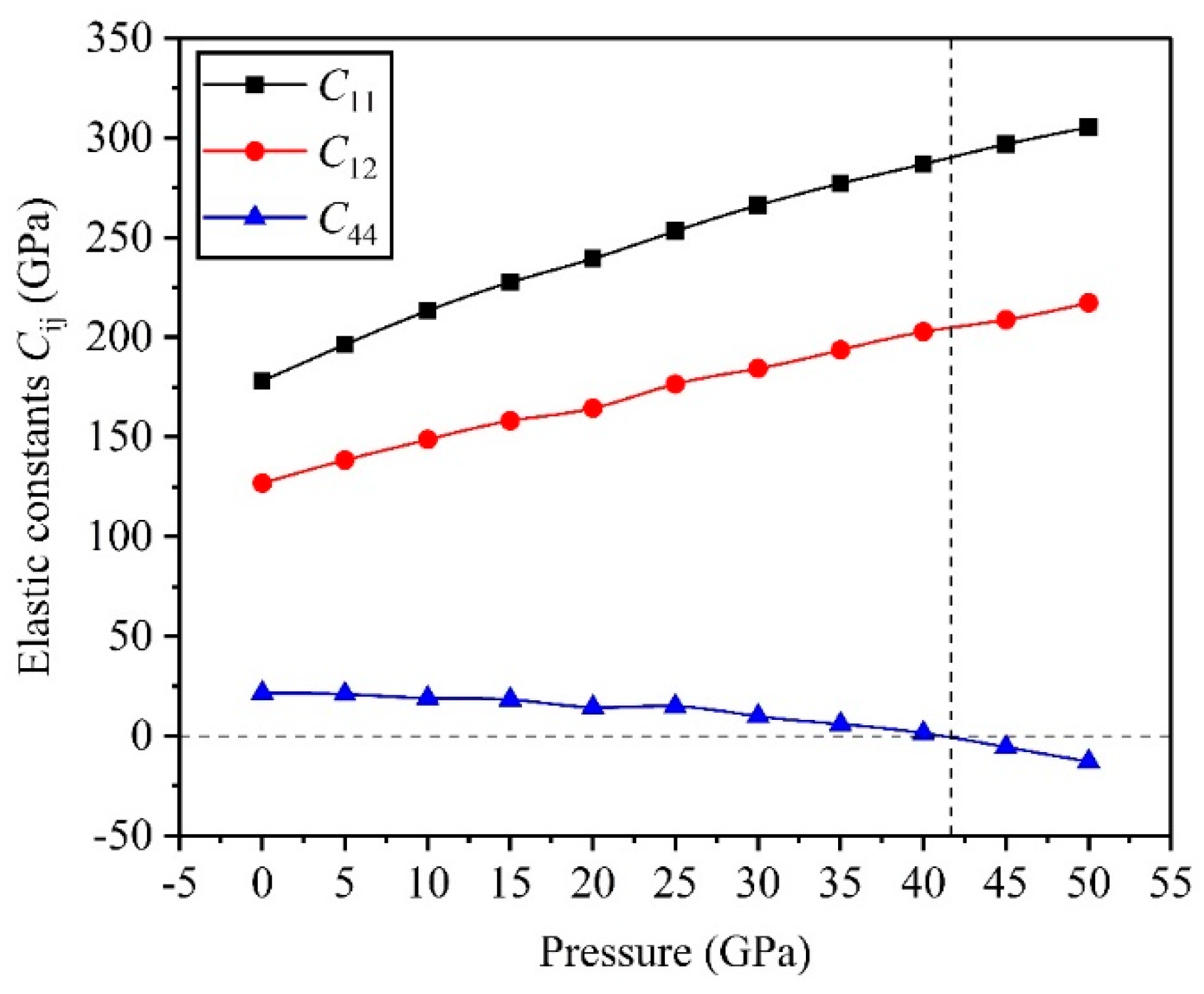
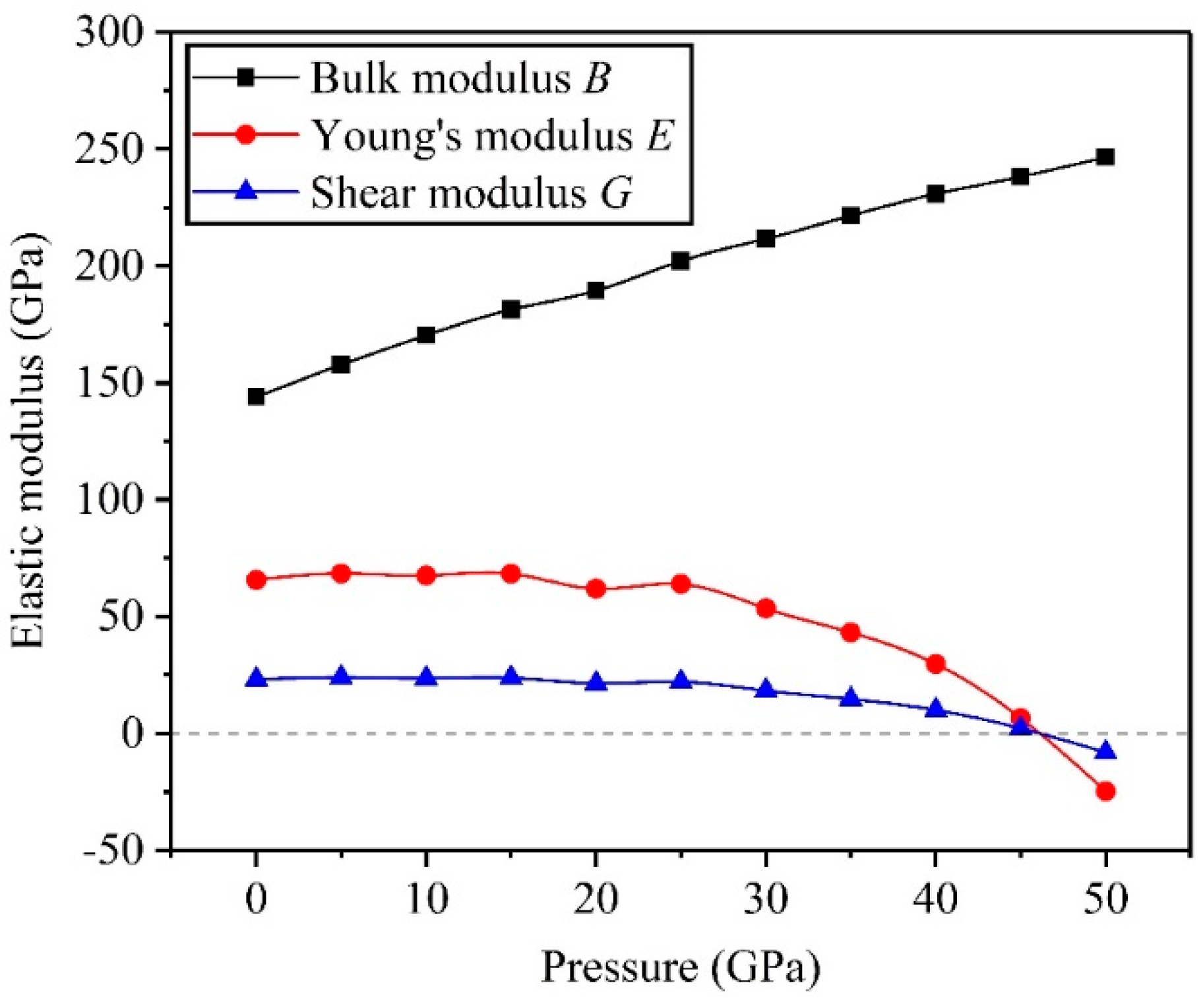
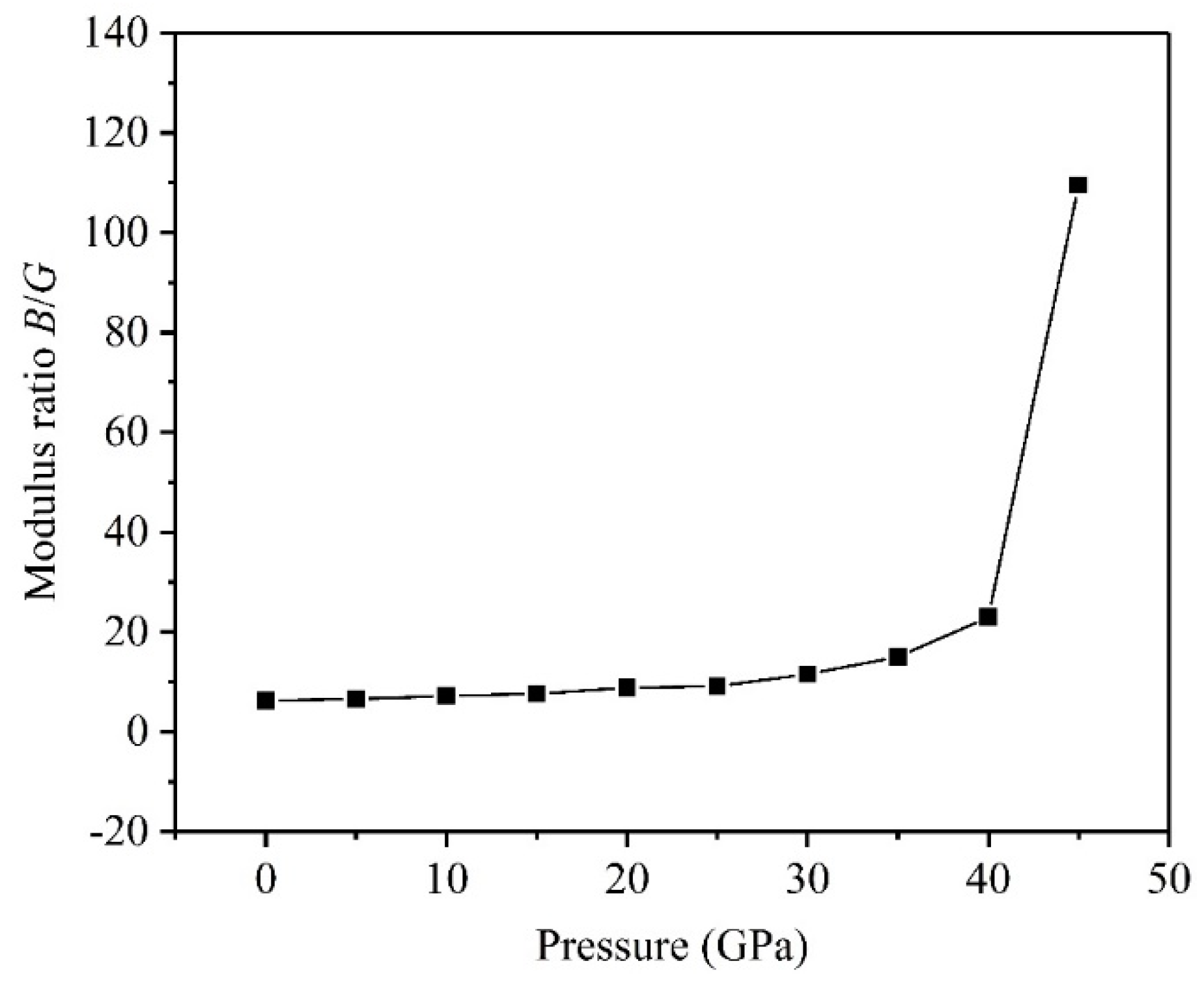
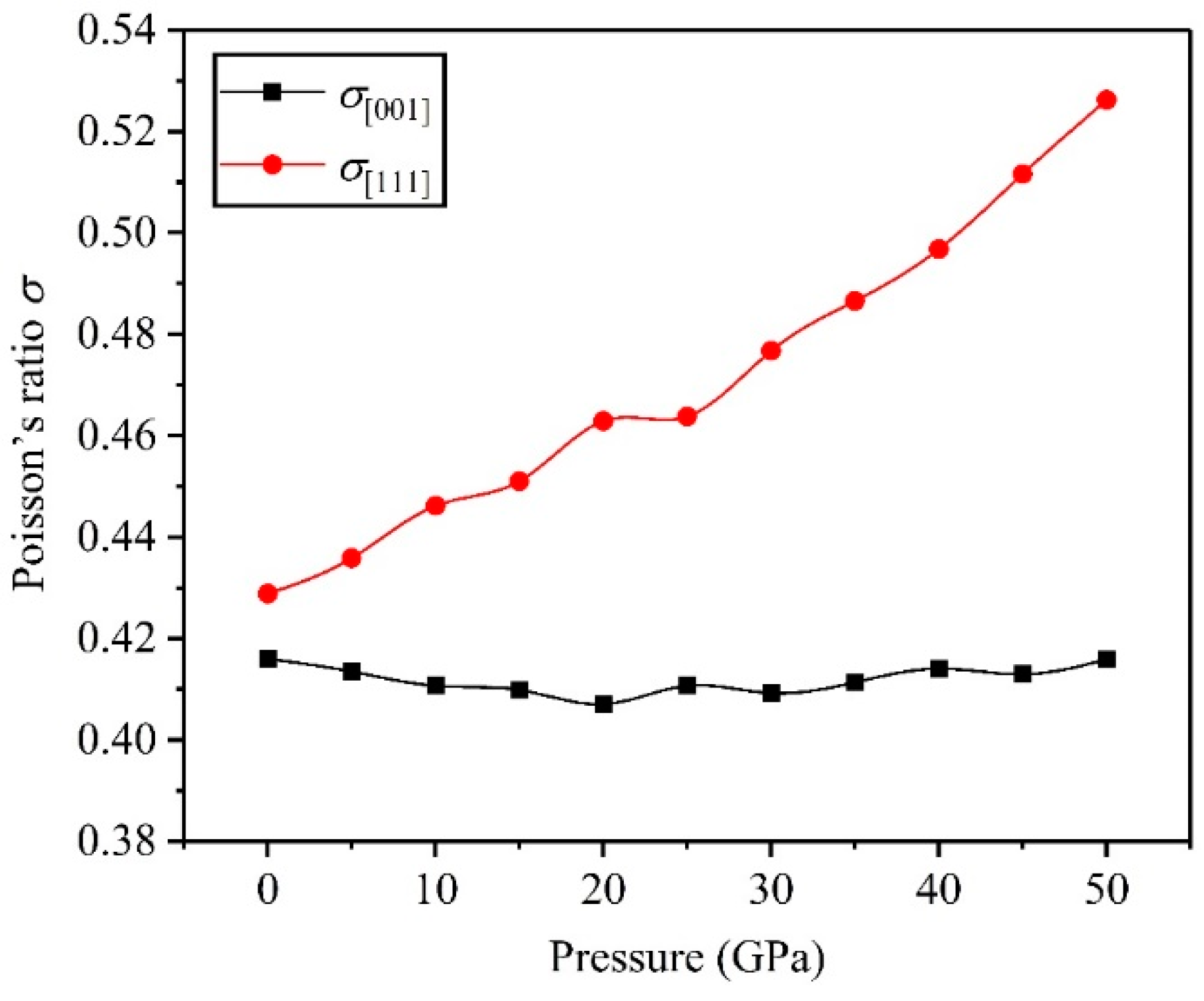
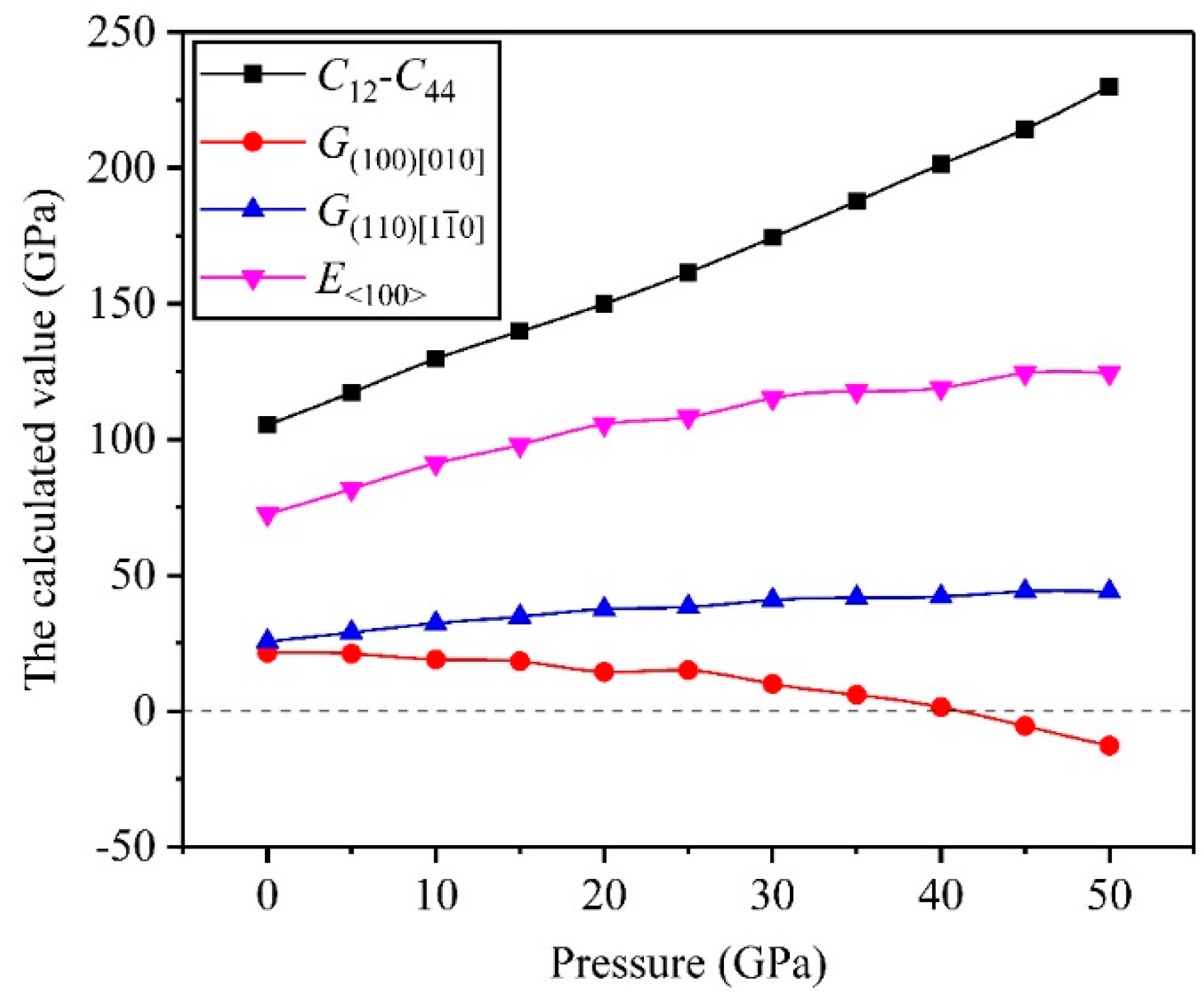
3.2. Mechanical Properties
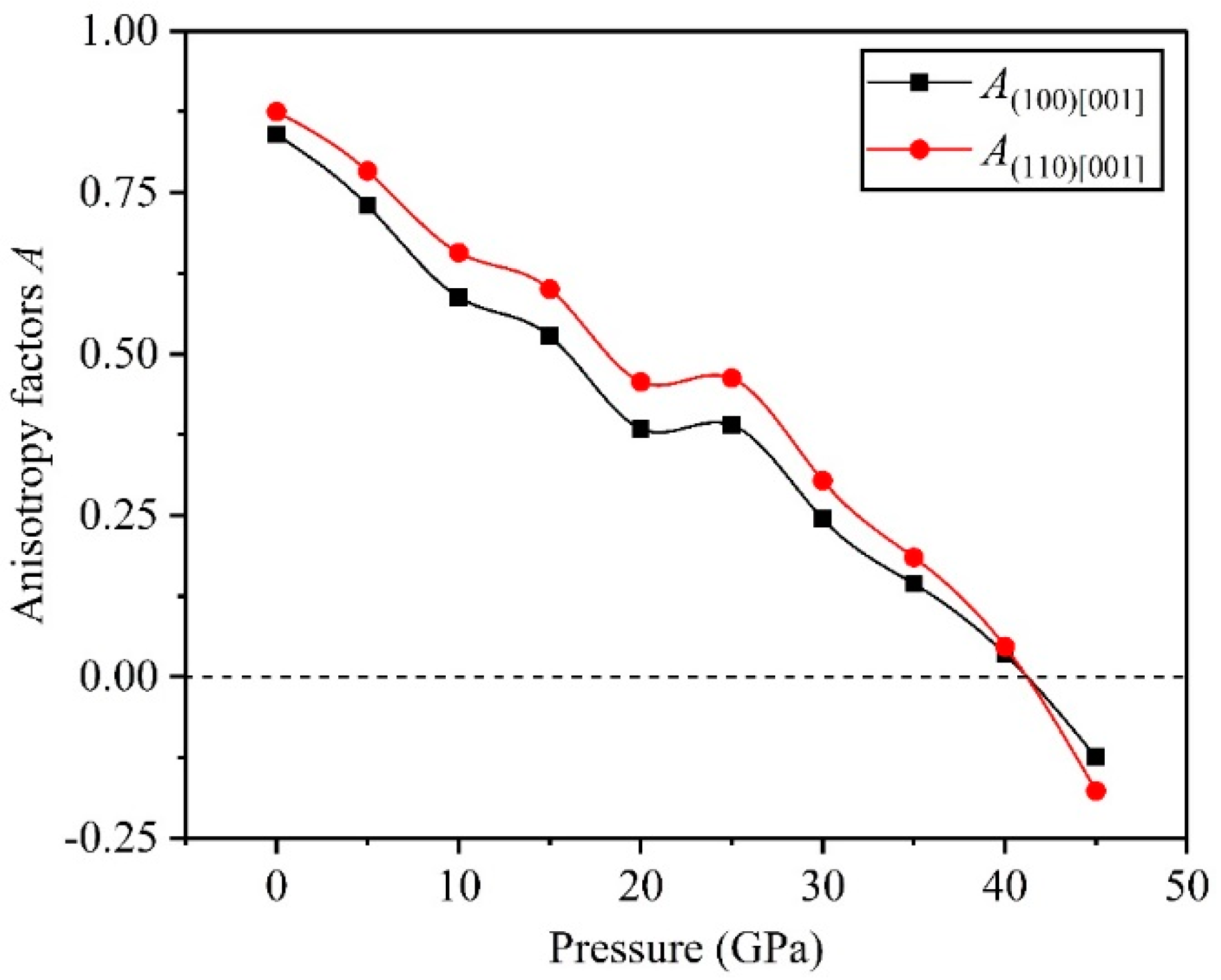
3.3. Anisotropy
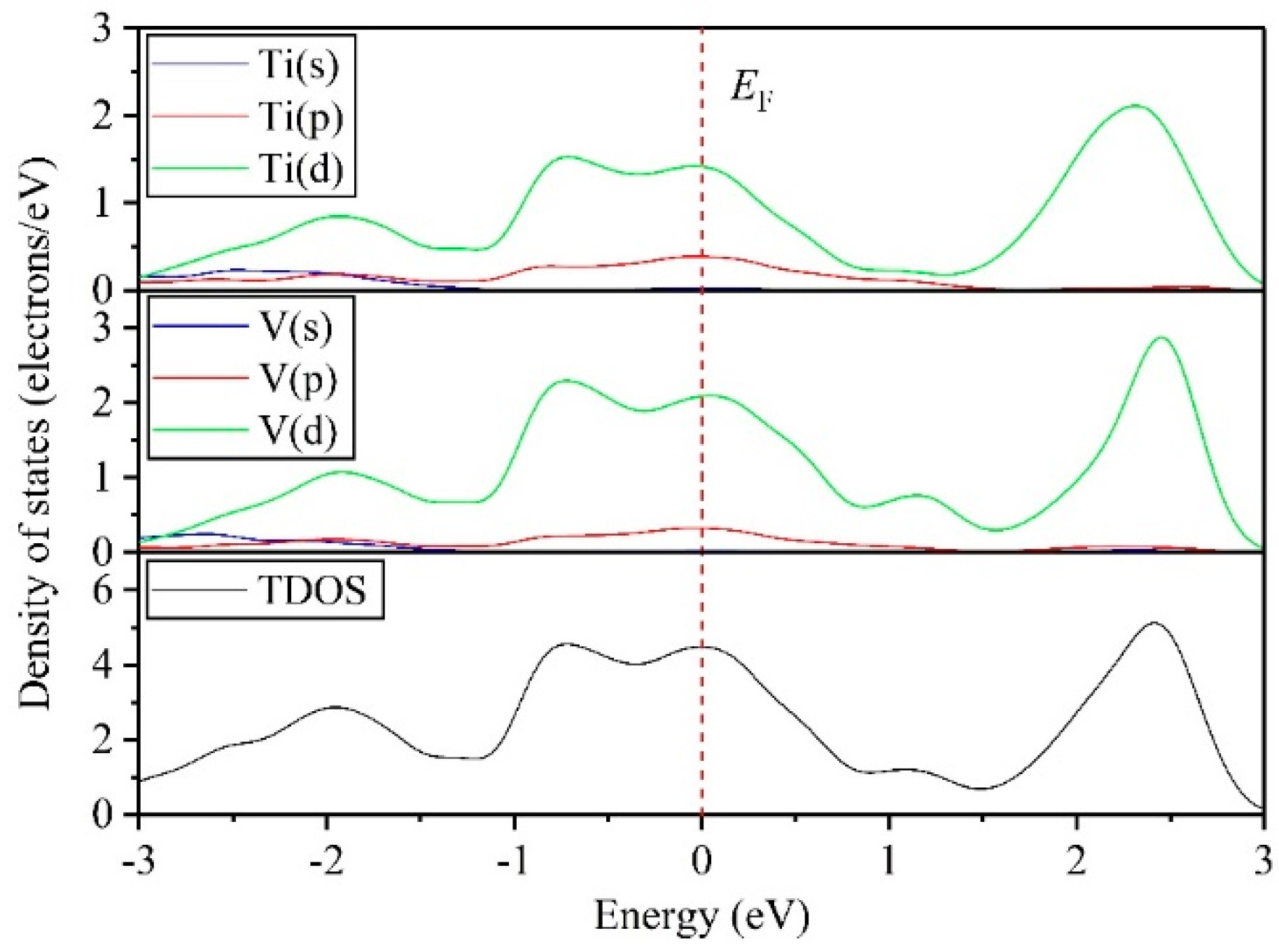
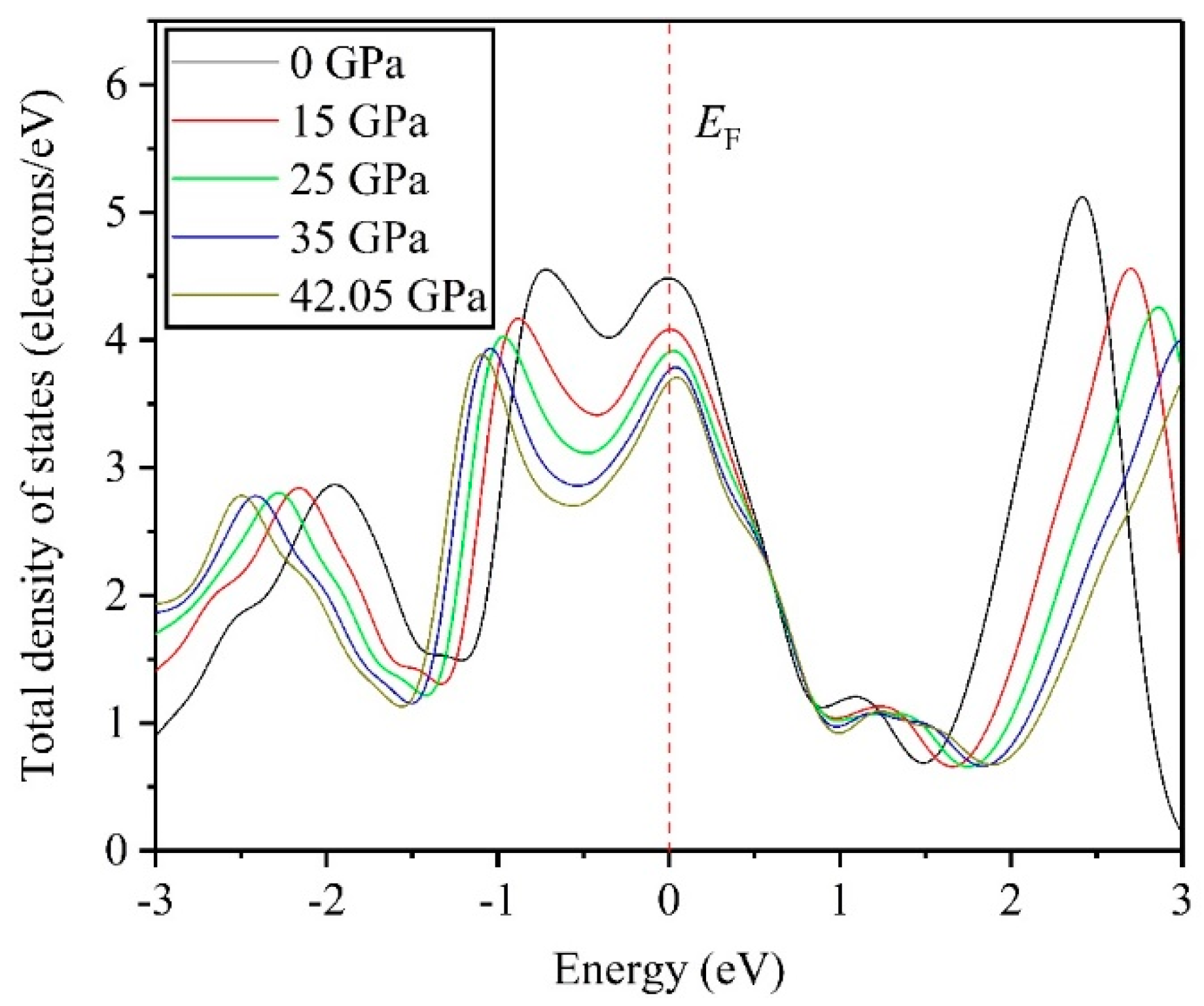
3.4. Electronic Properties
4. Conclusions
- (1)
- The critical pressure of the structural phase transition for the TiV alloy is 42.05 GPa, and the symmetric crystal structure of the TiV alloy produces structural phase transition when the applied pressure exceeds 42.05 GPa.
- (2)
- The high pressure can improve resistance to volume change, but the biggest resistances to elastic and shear deformation occur under for the TiV alloy.
- (3)
- The results of Pugh’s ratio suggest that the TiV alloy is essentially characterized by excellent ductility, and high pressure can enhance the ductility of the TiV alloy.
- (4)
- The direction has stronger resistance to shear deformation than the direction, and high pressure improves resistance to elastic deformation in the direction. Cauchy pressure reveals that the atomic bonding of the TiV alloy is mainly the metallic bond, and high pressure leads to strong atomic bonding.
- (5)
- DOS results indicate that the TiV alloy presents metallicity, and high pressure disrupts the structural stability of the TiV alloy, thereby inducing structural phase transition.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bibienne, T.; Tousignant, M.; Bobet, J.L.; Huot, J. Synthesis and hydrogen sorption properties of TiV(2−x)Mnx BCC alloys. J. Alloy. Compd. 2015, 624, 247–250. [Google Scholar] [CrossRef]
- Massicot, B.; Latroche, M.; Joubert, J.M. Hydrogenation properties of Fe–Ti–V bcc alloys. J. Alloy. Compd. 2011, 509, 372–379. [Google Scholar] [CrossRef]
- Huot, J.; Ravnsbæk, D.B.; Zhang, J.; Cuevas, F.; Latroche, M.; Jensen, T.R. Mechanochemical synthesis of hydrogen storage materials. Prog. Mater. Sci. 2013, 58, 30–75. [Google Scholar] [CrossRef]
- Yu, X.B.; Yang, Z.X.; Feng, S.L.; Wu, Z.; Xu, N.X. Influence of Fe addition on hydrogen storage characteristics of Ti–V-based alloy. Int. J. Hydrog. Energy 2006, 31, 1176–1181. [Google Scholar] [CrossRef]
- Iba, H.; Akiba, E. Hydrogen absorption and modulated structure in Ti–V–Mn alloys. J. Alloy. Compd. 1997, 253, 21–24. [Google Scholar] [CrossRef]
- Yu, X.B.; Wu, Z.; Xia, B.J.; Huang, T.Z.; Chen, J.Z.; Wang, Z.S.; Xu, N.X. Hydrogen storage in Ti–V-based body-centered-cubic phase alloys. J. Mater. Res. 2003, 18, 2533–2536. [Google Scholar] [CrossRef]
- Nomura, K.; Akiba, E. H2 Absorbing-desorbing characterization of the Ti-V-Fe alloy system. J. Alloy. Compd. 1995, 231, 513–517. [Google Scholar] [CrossRef]
- Seo, C.Y.; Kim, J.H.; Lee, P.S.; Lee, J.Y. Hydrogen storage properties of vanadium-based b.c.c. solid solution metal hydrides. J. Alloy. Compd. 2003, 348, 252–257. [Google Scholar] [CrossRef]
- Pan, H.G.; Li, R.; Gao, M.X.; Liu, Y.F.; Wang, Q.D. Effects of Cr on the structural and electrochemical properties of TiV-based two-phase hydrogen storage alloys. J. Alloy. Compd. 2005, 404, 669–674. [Google Scholar] [CrossRef]
- Balcerzak, M. Structure and hydrogen storage properties of mechanically alloyed Ti-V alloys. Int. J. Hydrog. Energy 2017, 42, 23698–23707. [Google Scholar] [CrossRef]
- Dou, T.; Wu, Z.; Mao, J.F.; Xu, N.X. Application of commercial ferrovanadium to reduce cost of Ti–V-based BCC phase hydrogen storage alloys. Mater. Sci. Eng. A 2008, 476, 34–38. [Google Scholar] [CrossRef]
- Milman, V.; Winkler, B.; White, J.A.; Pickard, C.J.; Payne, M.C.; Akhmatskaya, E.V.; Nobes, R.H. Electronic Structure, Properties, and Phase Stability of Inorganic Crystals: A Pseudopotential Plane-Wave Study. Int. J. Quantum Chem 2000, 77, 895–910. [Google Scholar] [CrossRef]
- Segall, M.D.; Lindan, P.J.D.; Probert, M.J.; Pickard, C.J.; Hasnip, P.J.; Clark, S.J.; Payne, M.C. First-Principles Simulation: Ideas, Illustrations and the CASTEP Code. J. Phys. Condens. Matter 2002, 14, 2717–2744. [Google Scholar] [CrossRef]
- Clark, S.J.; Segall, M.D.; Pickard, C.J.; Hasnip, P.J.; Probert, M.I.J.; Refson, K.; Payne, M.C. First principles methods using CASTEP. Z. Krist. Cryst. Mater. 2005, 220, 567–570. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Vanderbilt, D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys. Rev. B 1990, 41, 7892–7895. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Fischer, T.H.; Almlof, J. General methods for geometry and wave function optimization. J. Phys. Chem. 1992, 96, 9768–9774. [Google Scholar] [CrossRef]
- Birch, F. Finite Elastic Strain of Cubic Crystals. Phys. Rev. 1947, 71, 809–824. [Google Scholar] [CrossRef]
- Aurelio, G.; Guillermet, A.F.; Cuello, G.J.; Campo, J. Metastable phases in the Ti-V system: Part I. Neutron diffraction study and assessment of structural properties. Metall. Mater. Trans. A 2002, 33, 1307–1317. [Google Scholar] [CrossRef]
- Ming, L.C.; Manghnani, M.H.; Katahara, K.W. Phase transformations in the Ti-V system under high pressure up to 25 GPa. Acta Metall. 1981, 29, 479–485. [Google Scholar] [CrossRef]
- Basak, S.; Shashikala, K.; Sengupta, P.; Kulshreshtha, S.K. Hydrogen absorption properties of Ti–V–Fe alloys: Effect of Cr substitution. Int. J. Hydrog. Energy 2007, 32, 4973–4977. [Google Scholar] [CrossRef]
- Hagi, T.; Sato, Y.; Yasuda, M.; Tanaka, K. Structure and phase diagram of the Ti-V-H system at room temperature. Trans. Jpn. Inst. Met. 1987, 28, 198–204. [Google Scholar] [CrossRef]
- Stern, A.; Kaplan, N.; Shaltiel, D. Superconducting transition temperatures of the system V1−xTixHy. Solid State Commun. 1981, 38, 445–450. [Google Scholar] [CrossRef]
- Ikehata, H.; Nagasako, N.; Furuta, T.; Fukumoto, A.; Miwa, K.; Saito, T. First-principles calculations for development of low elastic modulus Ti alloys. Phys. Rev. B 2004, 70, 174113. [Google Scholar] [CrossRef]
- Wang, J.H.; Yip, S.; Phillpot, S.R.; Wolf, D. Crystal instabilities at finite strain. Phys. Rev. Lett. 1993, 71, 4182–4185. [Google Scholar] [CrossRef]
- Patil, S.K.R.; Khare, S.V.; Tuttle, B.R.; Bording, J.K.; Kodambaka, S. Mechanical stability of possible structures of PtN investigated using first-principles calculations. Phys. Rev. B 2006, 73, 104118. [Google Scholar] [CrossRef]
- Pugh, S.F. XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Philos. Mag. 1954, 45, 823–843. [Google Scholar] [CrossRef]
- Cao, Y.; Zhu, J.C.; Nong, Z.S.; Yang, X.W.; Liu, Y.; Lai, Z.H. First-principles studies of the structural, elastic, electronic and thermal properties of Ni3Nb. Comput. Mater. Sci. 2013, 77, 208–213. [Google Scholar] [CrossRef]
- Iotova, D.; Kioussis, N.; Lim, S.P. Electronic structure and elastic properties of the Ni3X (X=Mn, Al, Ga, Si, Ge) intermetallics. Phys. Rev. B 1996, 54, 14413–14422. [Google Scholar] [CrossRef]
- Hill, R. The elastic behaviour of a crystalline aggregate. Proc. Phys. Soc. Sect A 1952, 65, 349–354. [Google Scholar] [CrossRef]
- Mattesini, M.; Ahuja, R.; Johansson, B. Cubic Hf3N4 and Zr3N4: A class of hard materials. Phys. Rev. B 2003, 68, 184108. [Google Scholar] [CrossRef]
- Fu, H.Z.; Li, D.H.; Peng, F.; Gao, T.; Cheng, X.L. Ab initio calculations of elastic constants and thermodynamic properties of NiAl under high pressures. Comput. Mater. Sci. 2008, 44, 774–778. [Google Scholar] [CrossRef]
- Yoo, M.H. On the theory of anomalous yield behavior of Ni3Al—Effect of elastic anisotropy. Scr. Metall. 1986, 20, 915–920. [Google Scholar] [CrossRef]
- Lau, K.; Mccurdy, A.K. Elastic anisotropy factors for orthorhombic, tetragonal, and hexagonal crystals. Phys. Rev. B 1998, 58, 8980–8984. [Google Scholar] [CrossRef]
- Fu, H.Z.; Li, X.F.; Liu, W.F.; Ma, Y.M.; Gao, T.; Hong, X.H. Electronic and dynamical properties of NiAl studied from first principles. Intermetallics 2011, 19, 1959–1967. [Google Scholar] [CrossRef]
- Reed, R.P.; Clark, A.F. American Society of Metals; Metals Park: Geauga County, OH, USA, 1983. [Google Scholar]
- Friák, M.; Šob, M.; Vitek, V. Ab initio calculation of tensile strength in iron. Philos. Mag. 2003, 83, 3529–3537. [Google Scholar] [CrossRef]
- Fu, H.Z.; Peng, W.M.; Gao, T. Structural and elastic properties of ZrC under high pressure. Mater. Chem. Phys. 2009, 115, 789–794. [Google Scholar] [CrossRef]
- Pettifor, D.G. Theoretical predictions of structure and related properties of intermetallics. Mater. Sci. Technol. 1992, 8, 345–349. [Google Scholar] [CrossRef]
- Johnson, R.A. Analytic nearest-neighbor model for fcc metals. Phys. Rev. B 1988, 37, 3924–3931. [Google Scholar] [CrossRef]
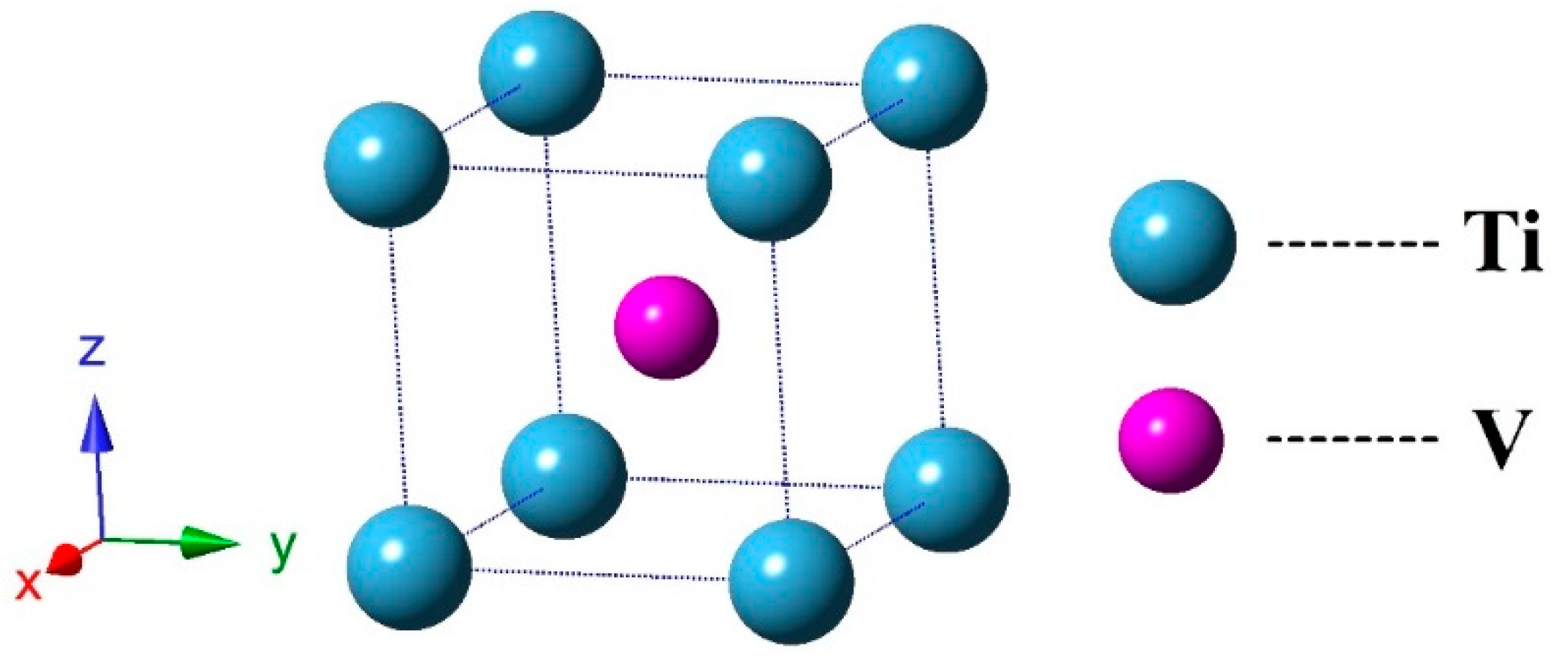
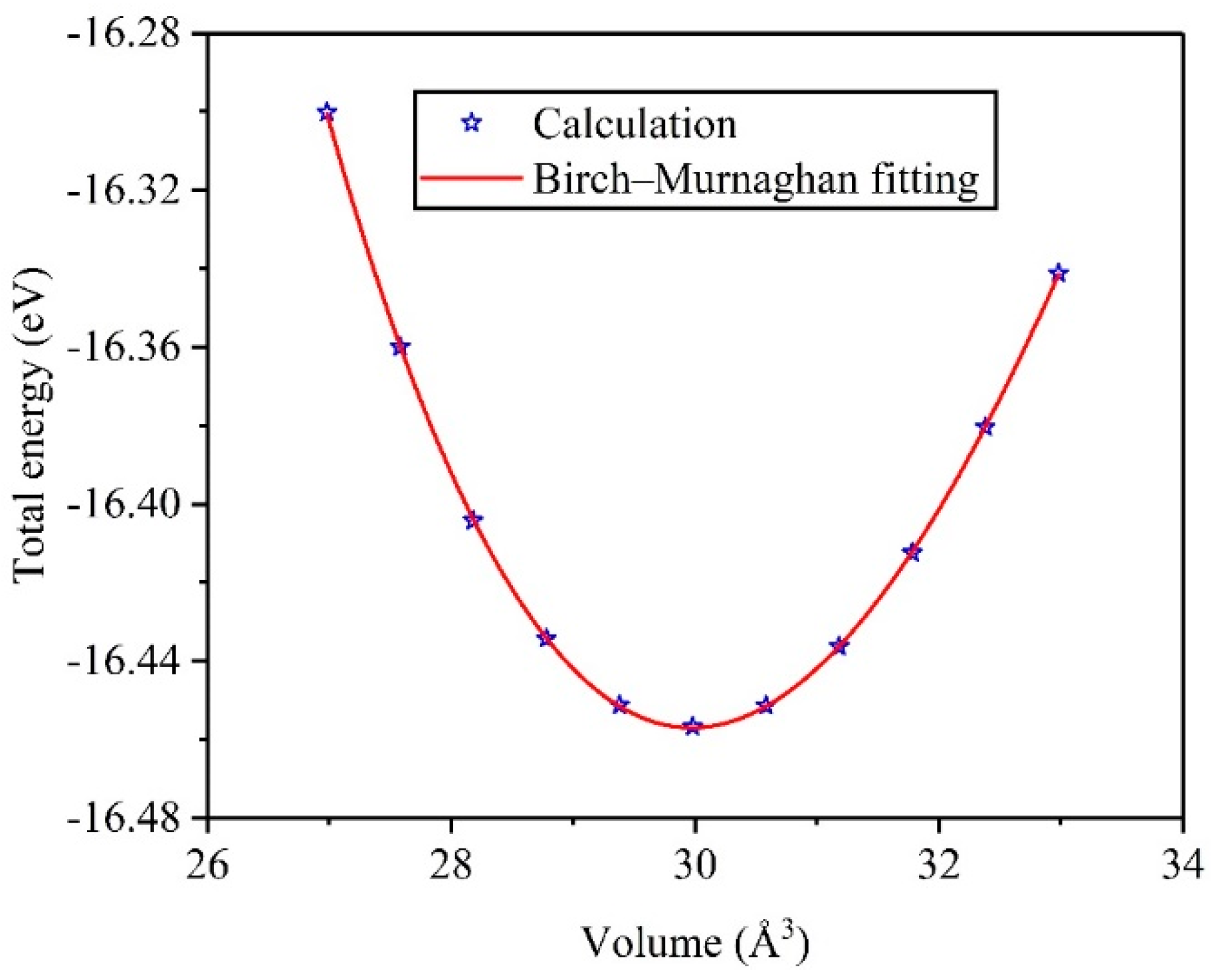

| TiV Alloy | This Work | Others |
|---|---|---|
| Lattice constant (Å) | 3.107 | 3.156 [10], 3.163 [20], 3.165 [21] 3.120 [22], 3.159 [23], 3.140 [24] 3.280 [25] |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, F.; Liu, Y. DFT Calculations of the Structural, Mechanical, and Electronic Properties of TiV Alloy Under High Pressure. Symmetry 2019, 11, 972. https://doi.org/10.3390/sym11080972
Yu F, Liu Y. DFT Calculations of the Structural, Mechanical, and Electronic Properties of TiV Alloy Under High Pressure. Symmetry. 2019; 11(8):972. https://doi.org/10.3390/sym11080972
Chicago/Turabian StyleYu, Fang, and Yu Liu. 2019. "DFT Calculations of the Structural, Mechanical, and Electronic Properties of TiV Alloy Under High Pressure" Symmetry 11, no. 8: 972. https://doi.org/10.3390/sym11080972
APA StyleYu, F., & Liu, Y. (2019). DFT Calculations of the Structural, Mechanical, and Electronic Properties of TiV Alloy Under High Pressure. Symmetry, 11(8), 972. https://doi.org/10.3390/sym11080972





