Design and Experiment of Symmetrical Shape Deployable Arc Profiling Mechanism Based on Composite Multi-Cam Structure
Abstract
:1. Introduction
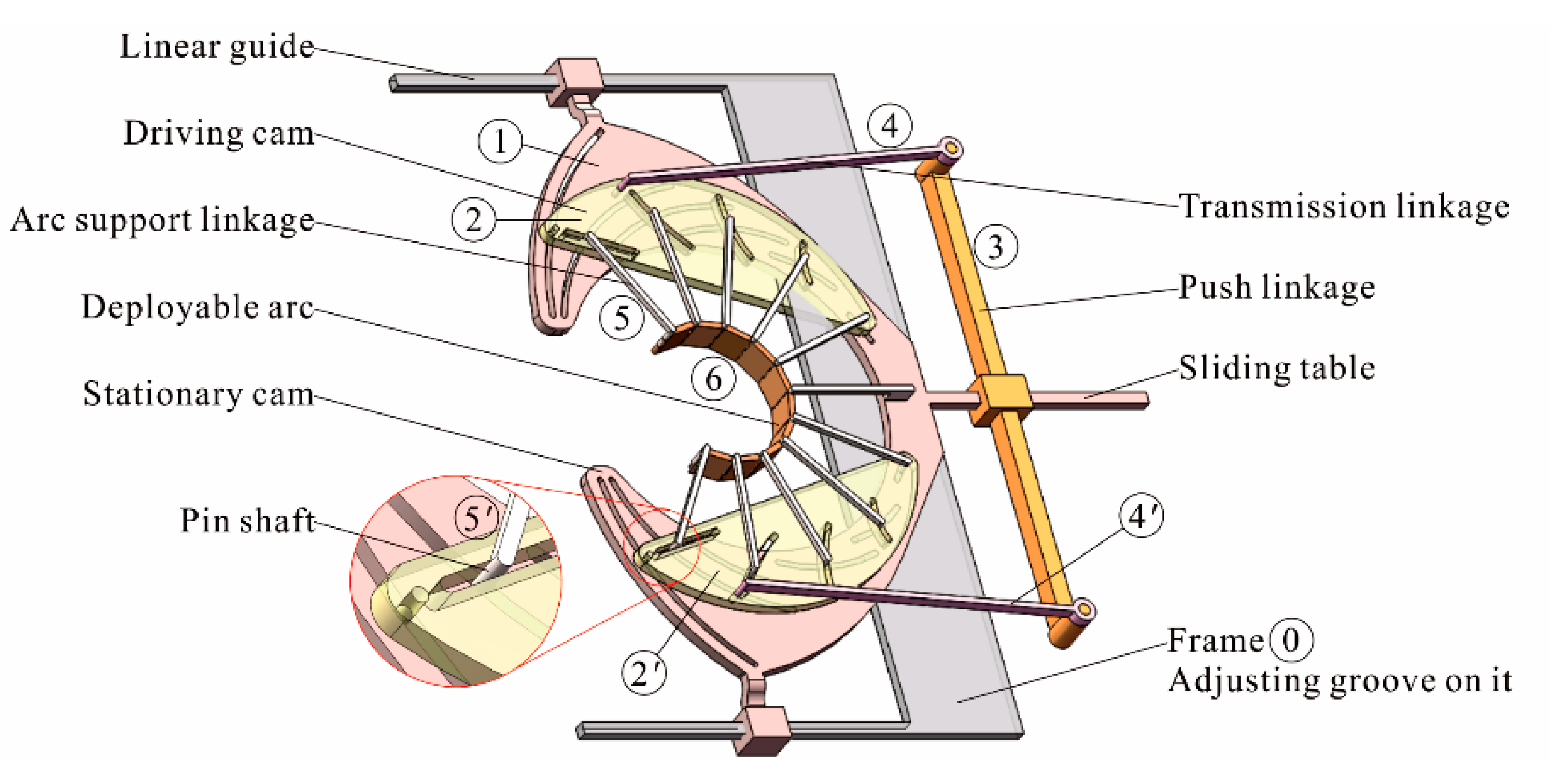
2. Description of Deployable Arc Profiling Mechanism
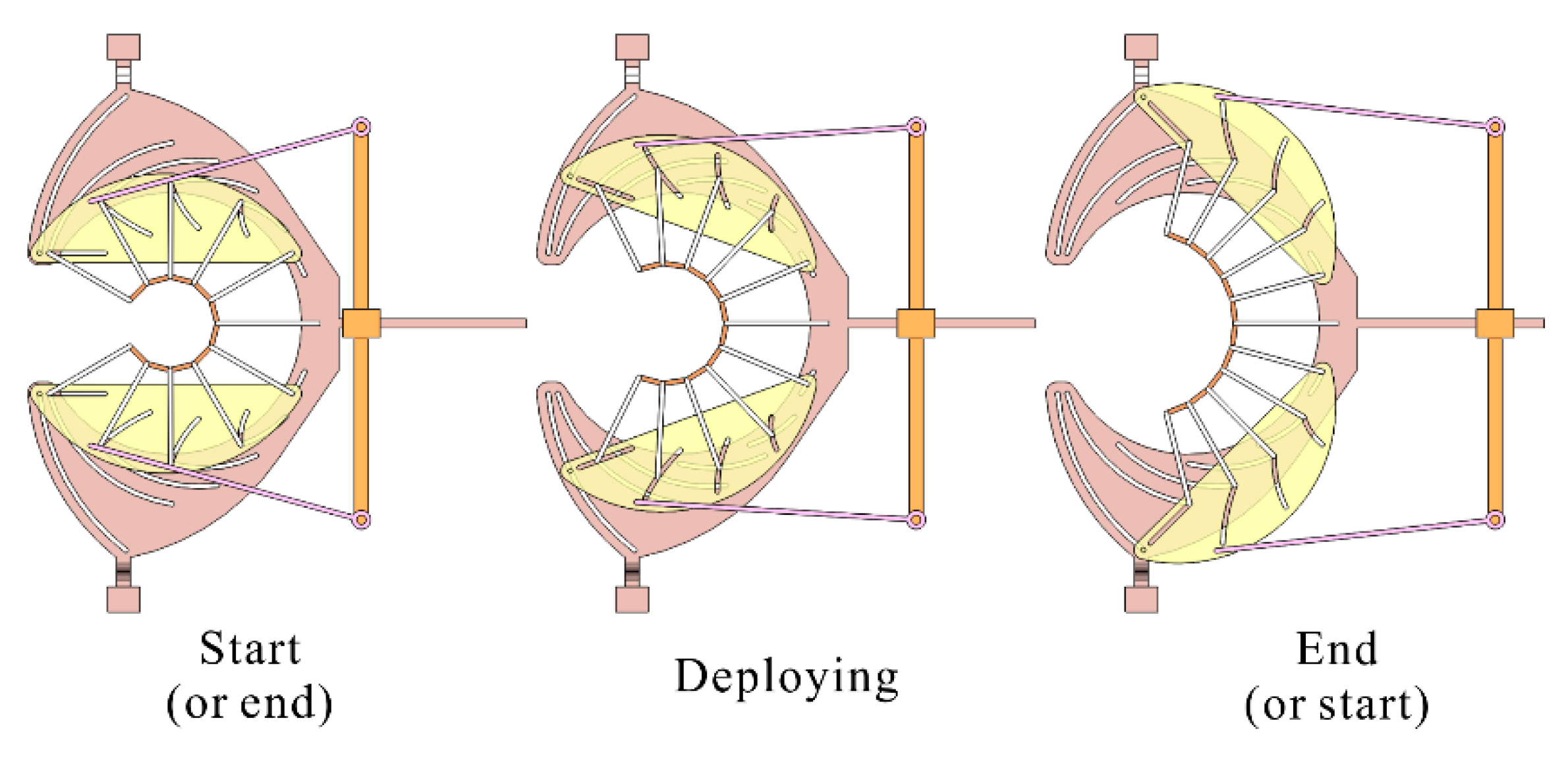
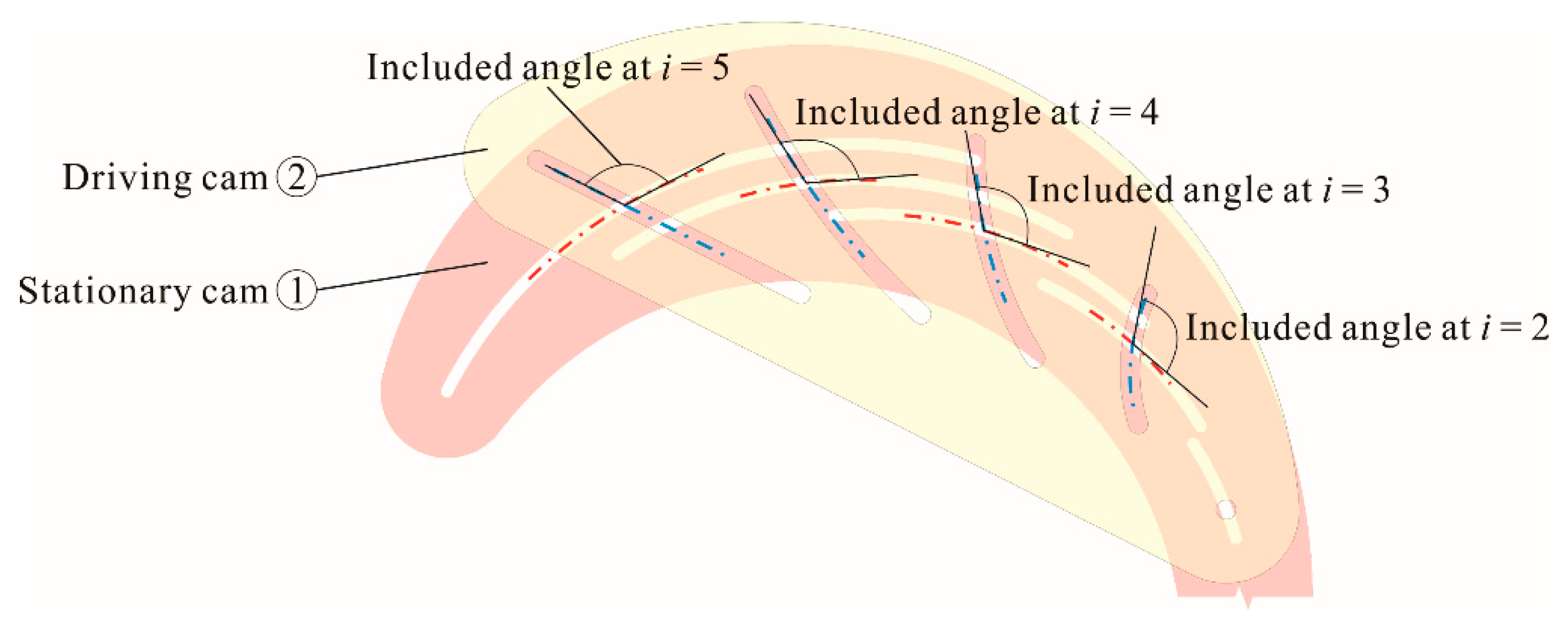
2.1. Structure of Mechanism
2.2. Design Principle of Mechanism
3. Parameter Design of Deployable Arc Profiling Mechanism
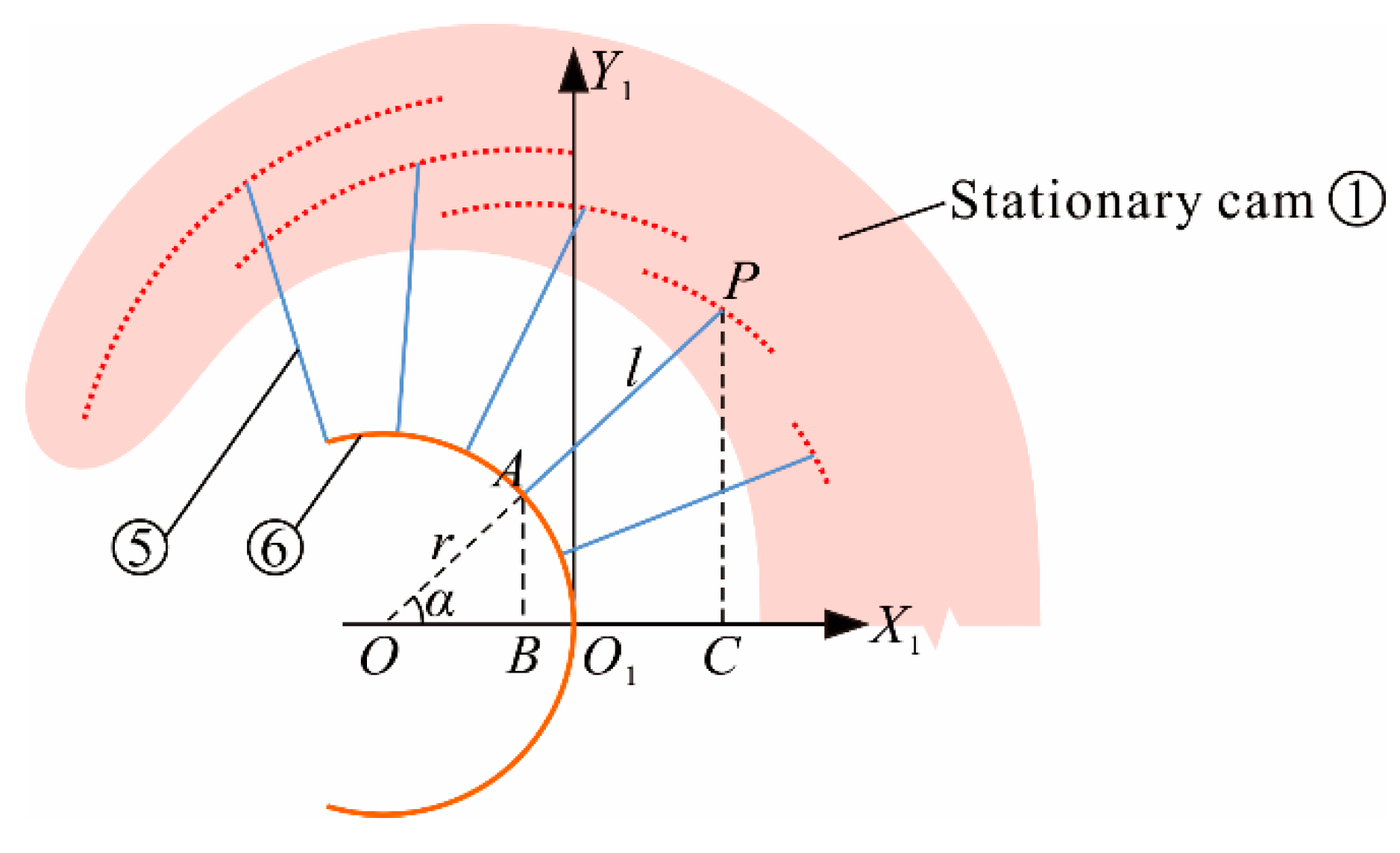
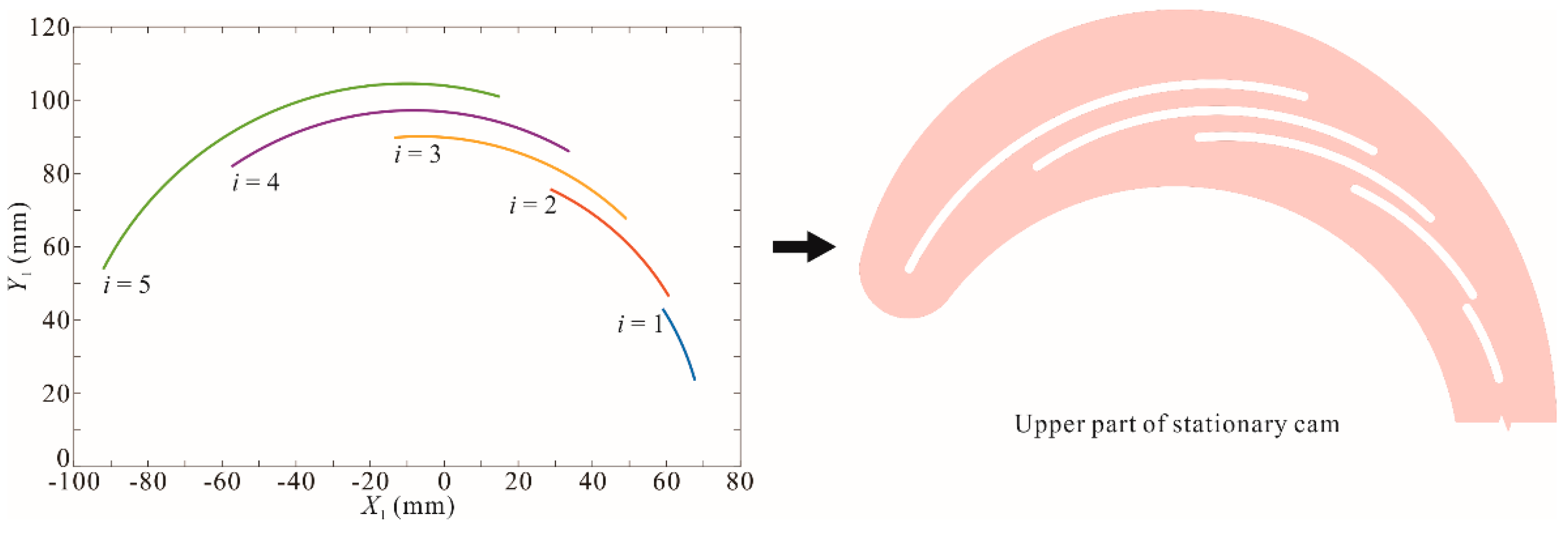
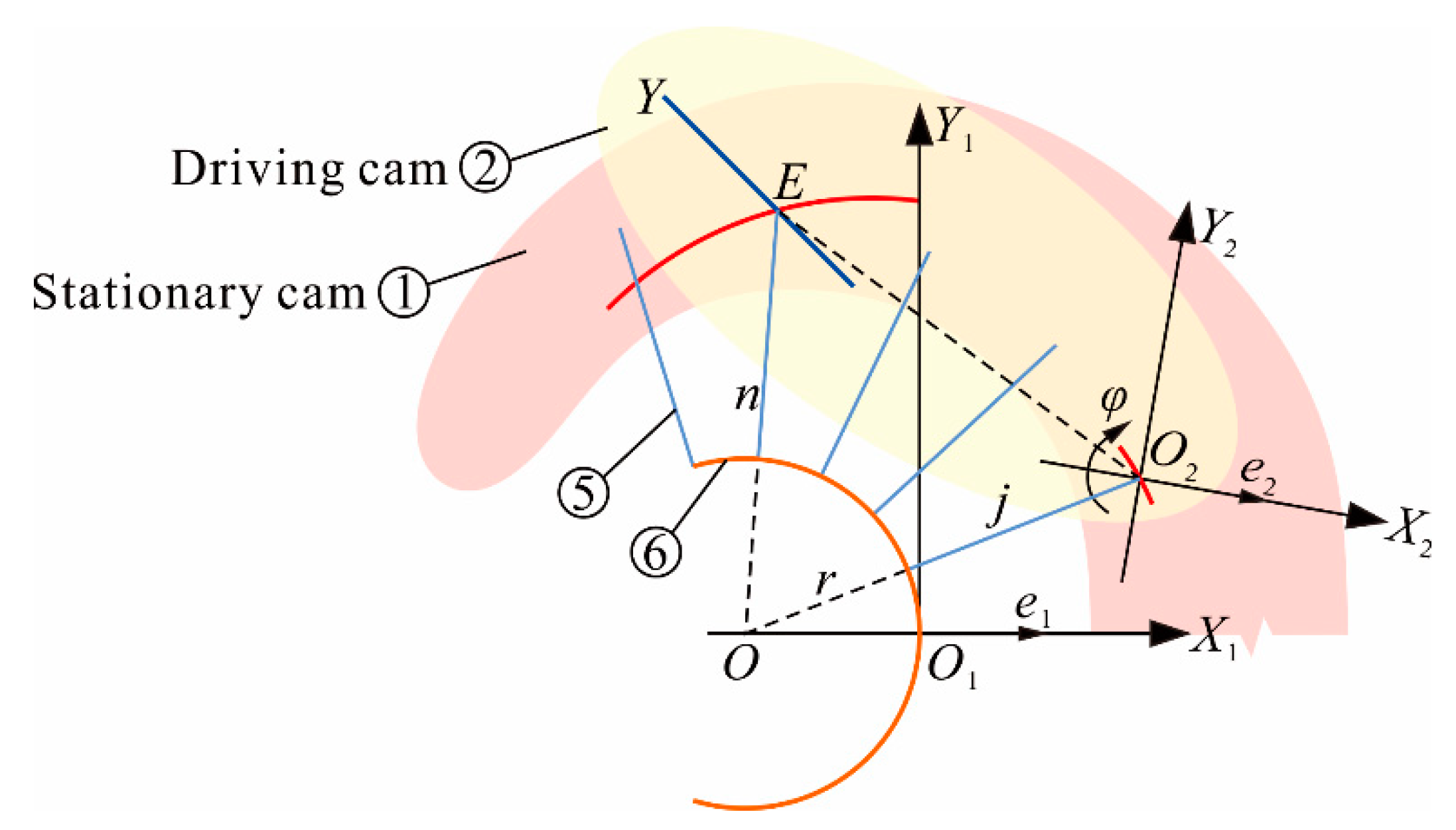
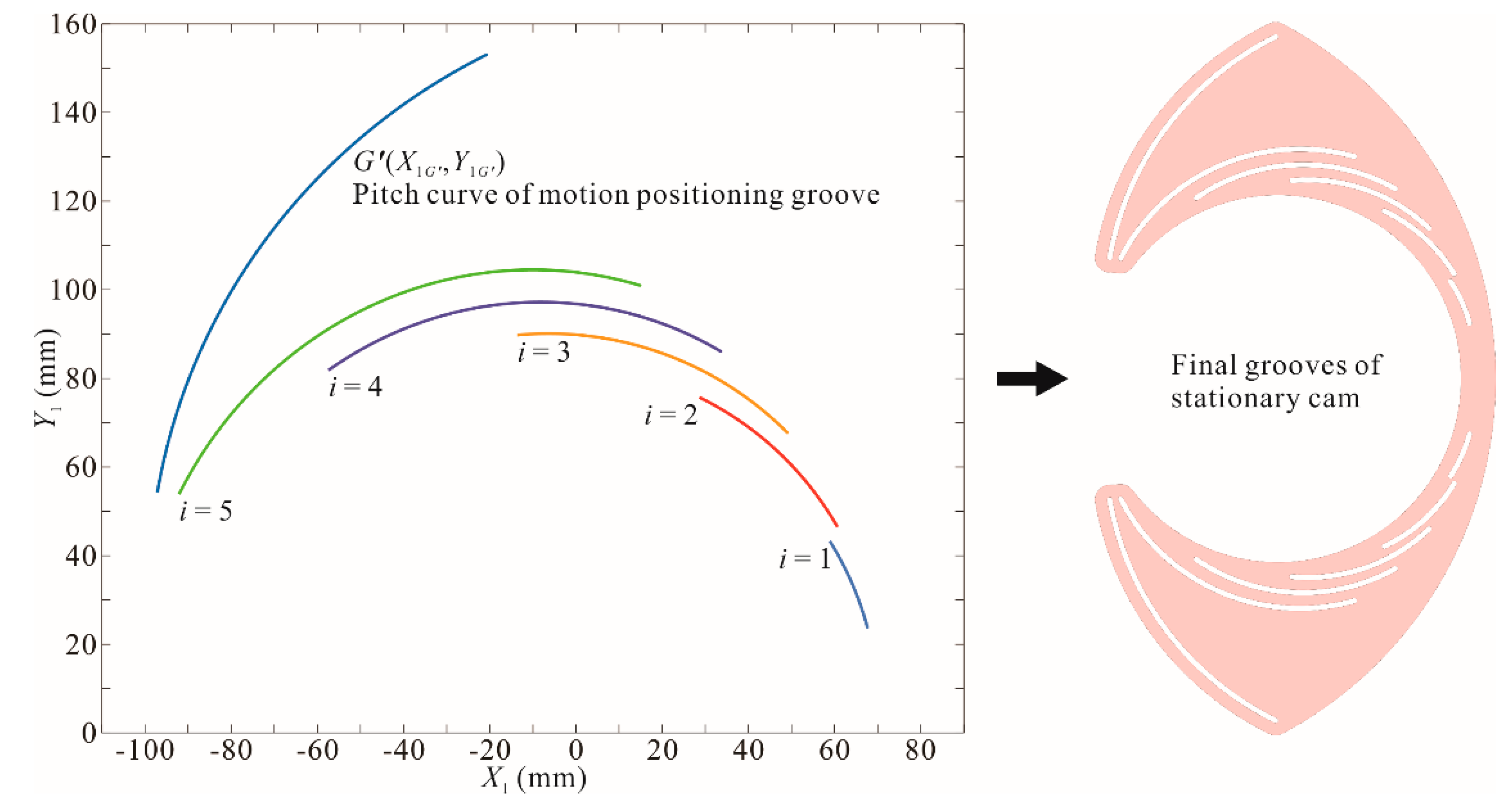
3.1. Pitch Curve of Stationary Cam Groove
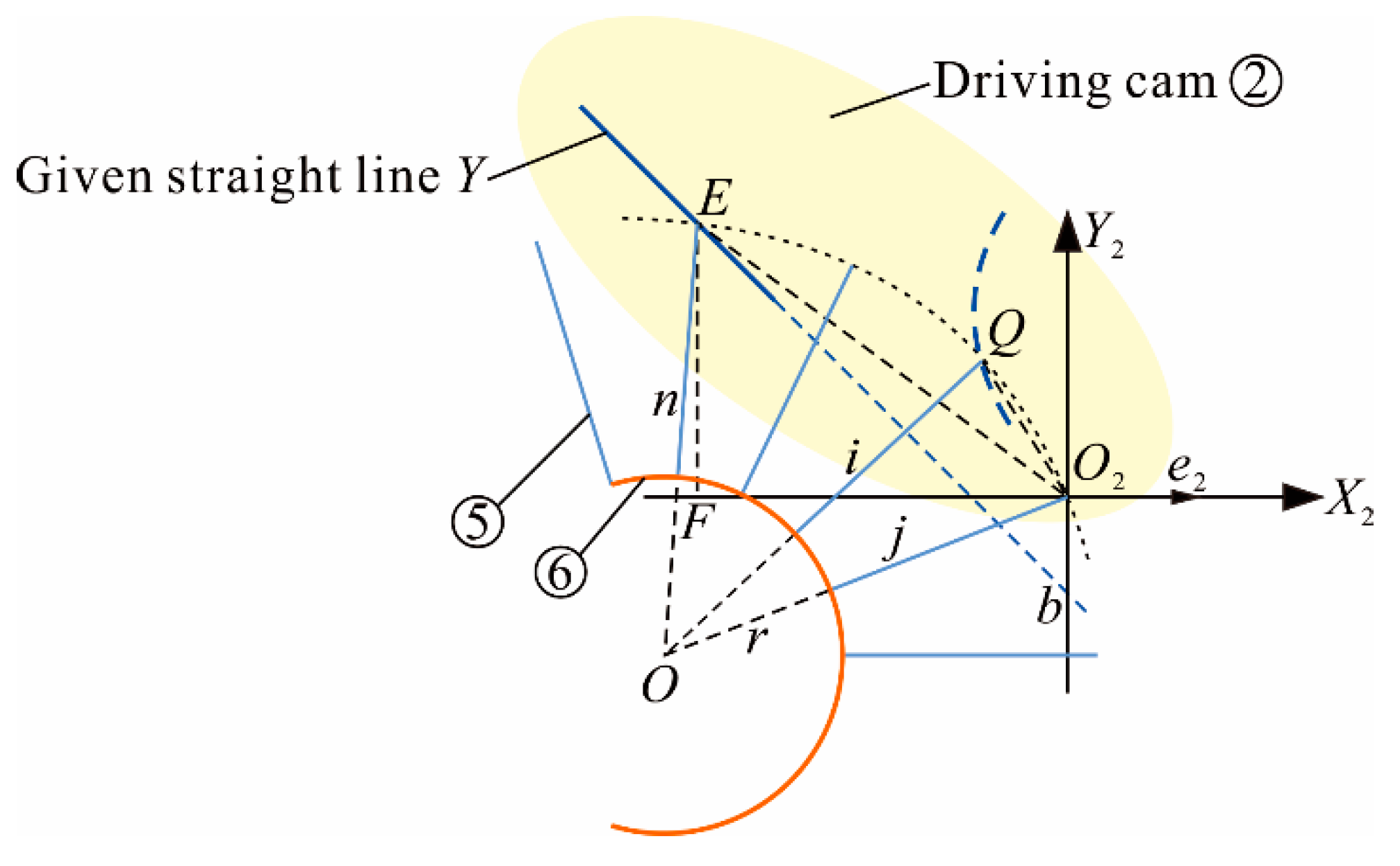
3.2. Parameter Design of Driving Cam
- Pitch curve design of driving cam grooves, which can drive the support linkages to carry out regular movement.
- Driving motion equation design.
- Motion positioning groove design, which enables driving cam to be driven according to the resulted motion parameters.
3.2.1. Pitch Curve of Driving Cam Grooves
3.2.2. Driving Motion Equation
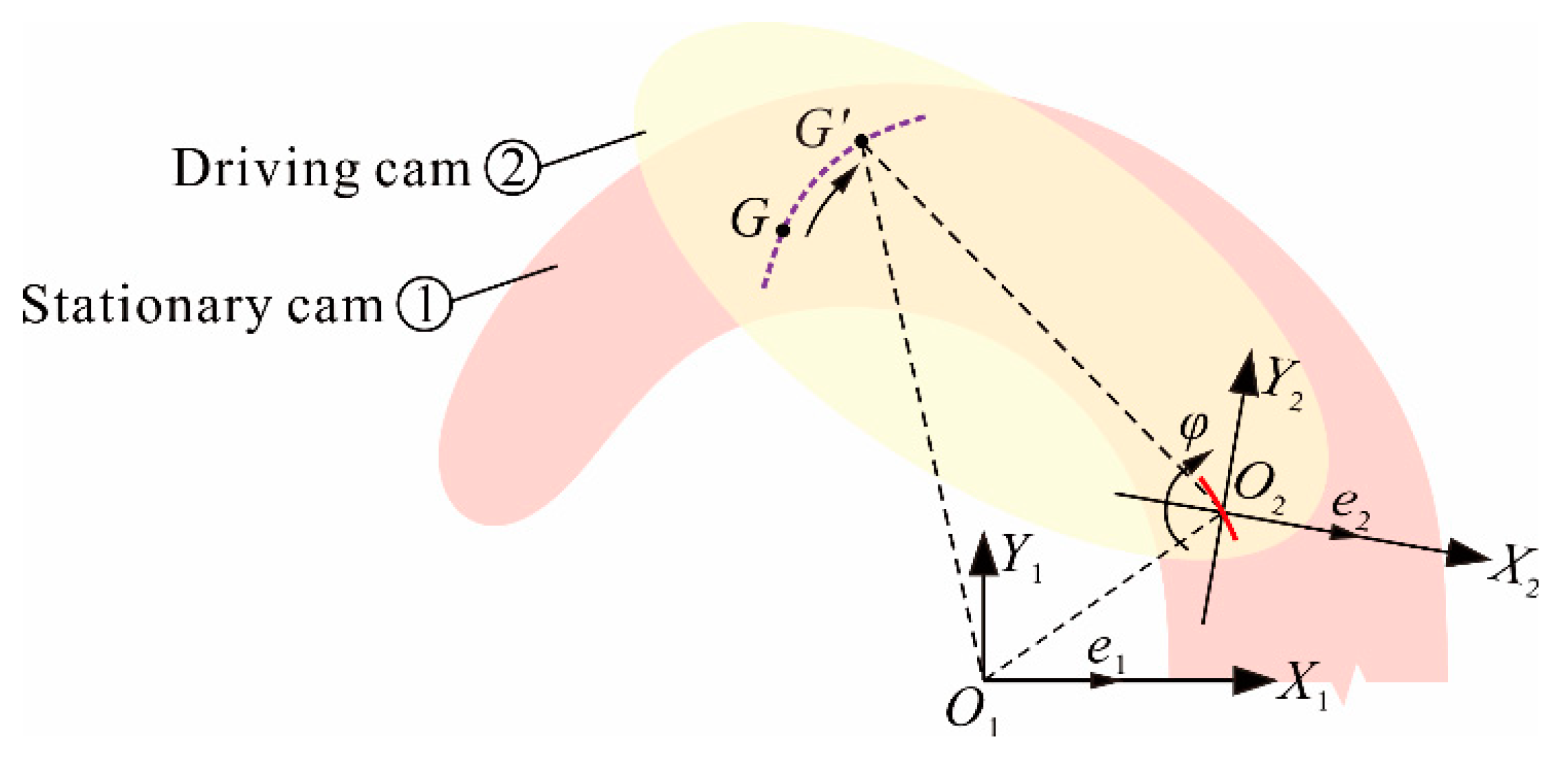
3.2.3. Motion Positioning Groove
3.3. Pitch Curve of Adjusting Groove
3.4. Driving Parameter of Deployable Arc Profiling Mechanism
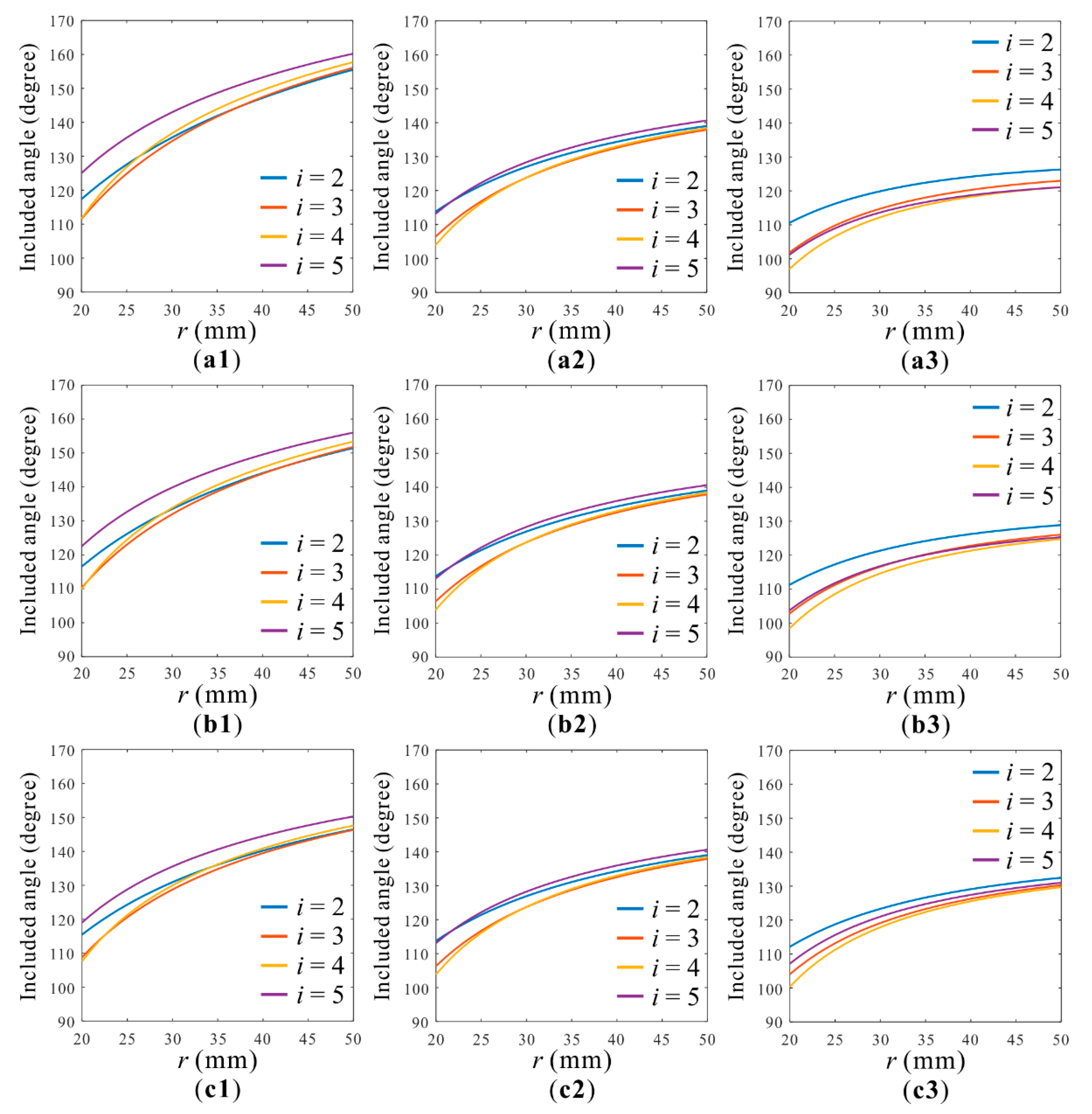
4. Analysis and Experiment
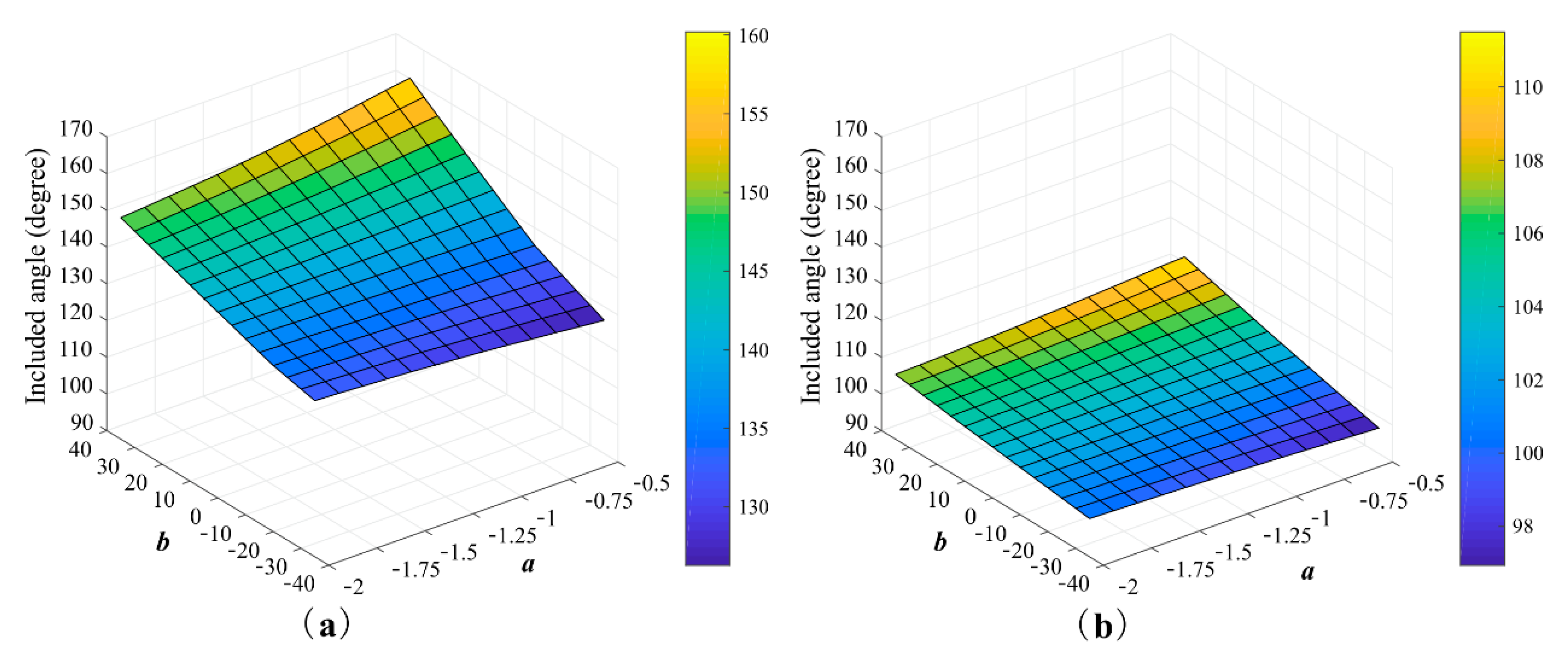
4.1. Impact of Parameters a and b
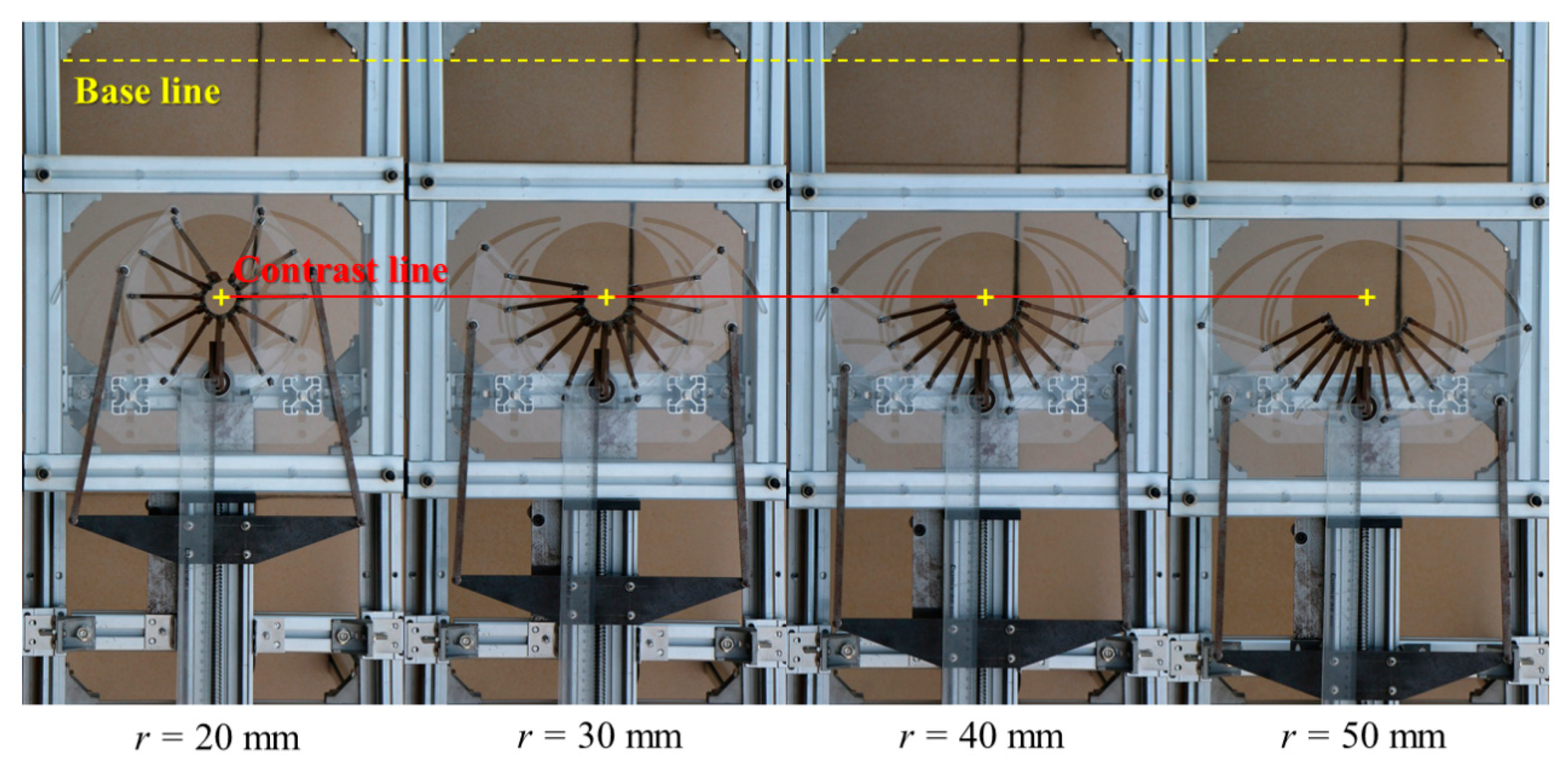
4.2. Prototype Verification
5. Conclusions
6. Patent
Author Contributions
Funding
Conflicts of Interest
References
- Abbas, A.T. A general algorithm for profiling and dressing grinding wheels when using a grinding spindle on a CNC lathe. Int. J. Prod. Res. 2004, 42, 3995–4008. [Google Scholar] [CrossRef]
- Dudas, I.; Bodzas, S.; Dudas, I.S.; Mandy, Z. Development of spiroid worm gear drive having arched profile in axial section and a new technology of spiroid worm manufacturing with lathe center displacement. Int. J. Adv. Manuf. Technol. 2015, 79, 1881–1892. [Google Scholar] [CrossRef]
- Wang, P.J.; Wu, Y.; Qi, J.F.; Chen, J.H.; Xiang, H. The development of special CNC system for profiling lathe based on digital capture measurement. Appl. Mech. Mater. 2013, 423, 2780. [Google Scholar] [CrossRef]
- Liu, Z.Q.; Qiu, H.; Li, X.; Yang, S.L. Review of large spacecraft deployable membrane antenna structures. Chin. J. Mech. Eng. 2017, 30, 1447–1459. [Google Scholar] [CrossRef]
- Dai, L.; Guan, F.L. Shape–sizing nested optimization of deployable structures using SQP. J. Cent. South Univ. 2014, 21, 2915–2920. [Google Scholar] [CrossRef]
- Freeland, R.E.; Bilyeu, G.D.; Veal, G.R.; Steiner, M.D.; Carson, D.E. Large inflatable deployable antenna flight experiment results. Acta Astronaut. 1997, 41, 267–277. [Google Scholar] [CrossRef]
- Hodges, R.E.; Chahat, N.; Hoppe, D.J.; Vacchione, J.D. A deployable high–gain antenna bound for mars developing a new folded–panel reflect array for the first CubeSat mission to mars. IEEE Antennas Propag. Mag. 2017, 59, 39–49. [Google Scholar] [CrossRef]
- Chahat, N.; Sauder, J.; Hodges, R.E.; Thomson, M.; Rahmat–Samii, Y. The deep–space network telecommunication CubeSat antenna using the deployable Ka–band mesh reflector antenna. IEEE Antennas Propag. Mag. 2017, 59, 31–38. [Google Scholar] [CrossRef]
- Ding, X.L.; Yang, Y.; Dai, J.S. Design and kinematic analysis of a novel prism deployable mechanism. Mech. Mach. Theory. 2013, 63, 35–49. [Google Scholar] [CrossRef]
- Zeng, W.; Gao, F.; Jiang, H.; Huang, C.; Liu, J.X.; Li, H.F. Design and analysis of a compliant variable–diameter mechanism used in variable–diameter wheels for lunar rover. Mech. Mach. Theory. 2018, 125, 240–258. [Google Scholar] [CrossRef]
- Feng, C.M.; Liu, T.S. A graph–theory approach to designing deployable mechanism of reflector antenna. Acta Astronaut. 2013, 87, 40–47. [Google Scholar] [CrossRef]
- Feng, C.M.; Liu, T.S. A bionic approach to mathematical modeling the fold geometry of deployable reflector antennas on satellites. Acta Astronaut. 2014, 103, 36–44. [Google Scholar] [CrossRef]
- Cao, W.A.; Yang, D.H.; Ding, H.F. Topological structural design of umbrella–shaped deployable mechanisms based on new spatial closed–loop linkage units. J. Mech. Des. 2018, 140, 062302. [Google Scholar] [CrossRef]
- Huang, H.L.; Li, B.; Zhang, T.S.; Zhang, Z.; Qi, X.Z.; Hu, Y. Design of large single–mobility surface–deployable mechanism using irregularly shaped triangular prismoid modules. J. Mech. Des. 2019, 141, 012301. [Google Scholar] [CrossRef]
- Figliolini, G.; Angeles, J. Synthesis of conjugate Geneva mechanisms with curved slots. Mech. Mach. Theory. 2002, 37, 1043–1061. [Google Scholar] [CrossRef]
- Lee, J.J.; Cho, C.C. Improving kinematic and structural performance of Geneva mechanisms using the optimal control method. Proc. Inst. Mech. Eng. Part C-J. Eng. Mech. Eng. Sci. 2002, 216, 761–774. [Google Scholar] [CrossRef]
- Lee, J.J.; Huang, K.F. Geometry analysis and optimal design of Geneva mechanisms with curved slots. Proc. Inst. Mech. Eng. Part C-J. Eng. Mech. Eng. Sci. 2004, 218, 449–459. [Google Scholar] [CrossRef]
- Lee, J.J.; Jan, B.H. Design of Geneva mechanisms with curved slots for non–undercutting manufacturing. Mech. Mach. Theory. 2009, 44, 1192–1200. [Google Scholar] [CrossRef]
- Ion, S.; Victor, M.; Liviu, C. On the Synthesis of Self Centering Grippers. In Proceedings of the NATO Advanced Study Institute Symposium on “Computational Methods in Mechanisms”, Varna, Bulgaria, 16 June 1997; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1997. [Google Scholar]
- Ion, S.; Ion, I. Mathematical models of grippers. In Proceedings of the 10th WSEAS International Conference on Mathematical and Computational Methods in Science and Engineering, Corfu, Greece, October 26 2008; WSEAS Press: Stevens Point, WI, USA, 2008. [Google Scholar]
- Ion, S.; Cătalin, I. Optimum design of self centering grippers. U.P.B. Sci. Bull. Series D. 2011, 73, 43–52. [Google Scholar]
- Chen, J.H.; Lin, Z.; Wu, Y.J. Design of cylindrical cam with oscillating follower based on 3D expansion of planar profile model. Chin. J. Mech. Eng. 2009, 22, 665–670. [Google Scholar] [CrossRef]
- Soong, R.C. A new cam–geared mechanism for exact path generation. J. Adv. Mech. Des. Syst. Manuf. 2015, 9, 15–00144. [Google Scholar] [CrossRef]
- Soong, R.C. A cam–geared mechanism for rigid body guidance. Trans. Can. Soc. Mech. Eng. 2017, 41, 143–157. [Google Scholar] [CrossRef]
- Todd, G.N.; Robert, J.L.; Spencer, P.M.; Larry, L.H. Curved–folding–inspired deployable compliant rolling–contact element (D–CORE). Mech. Mach. Theory. 2016, 96, 225–238. [Google Scholar] [CrossRef]
- Zhou, C.J.; Hu, B.; Chen, S.Y.; Ma, L. Design and analysis of high–speed cam mechanism using Fourier series. Mech. Mach. Theory. 2016, 104, 118–129. [Google Scholar] [CrossRef]
- Li, M.; Wang, R.X.; Zhao, Z.H. Passive nonlinear actuators for deploying mesh antennas. Acta Astronaut. 2018, 152, 254–261. [Google Scholar] [CrossRef]
- Li, J.L.; Yan, S.Z.; Guo, F.; Guo, P.F. Effects of damping, friction, gravity, and flexibility on the dynamic performance of a deployable mechanism with clearance. Proc. Inst. Mech. Eng. Part C-J. Eng. Mech. Eng. Sci. 2013, 227, 1791–1803. [Google Scholar] [CrossRef]
- Sanmiguel, R.E.; Hidalgo, M.M. Cam mechanisms based on a double roller translating follower of negative radius. Mech. Mach. Theory. 2016, 95, 93–101. [Google Scholar] [CrossRef]
- Ye, H.L.; Zhang, Y.; Yang, Q.S.; Xiao, Y.N.; Ramana, V.G.; Christopher, C.F. Optimal design of a three tape–spring hinge deployable space structure using an experimentally validated physics–based model. Struct. Multidiscip. Optim. 2017, 56, 973–989. [Google Scholar] [CrossRef]





| Parameter | Value |
|---|---|
| Range of variation of radius r (mm) | 20~50 |
| Arc length of segment arc c (mm) | 10.5 |
| Length of arc support linkage l (mm) | 70 |
| Total number n of arc support linkages in upper part of mechanism | 5 |
| Length of push linkage s (mm) | 150 |
| Length of transmission linkage t (mm) | 265 |
| Given straight line | Y = −X/2 − 35 |
| Coordinate of motion positioning point G | (−160, 43) |
| Coordinate of connecting point U | (−87, 79) |
| Test Arc Radius r (mm) | Corresponding Parameter d (mm) | Measured Arc Radius r (mm) | Radius Deviation (mm) | Accuracy (%) |
|---|---|---|---|---|
| 20 | 213.7 | 19.285 | 0.715 | 96.425 |
| 25 | 244.2 | 24.300 | 0.700 | 97.200 |
| 30 | 269.0 | 29.290 | 0.710 | 97.633 |
| 35 | 288.8 | 34.285 | 0.715 | 97.957 |
| 40 | 304.8 | 39.295 | 0.705 | 98.238 |
| 45 | 317.8 | 44.290 | 0.710 | 98.422 |
| 50 | 328.6 | 49.290 | 0.710 | 98.580 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Z.; Yang, Z.; Duan, J.; Jin, M.; Mo, J.; Zhao, L.; Guo, J.; Yao, H. Design and Experiment of Symmetrical Shape Deployable Arc Profiling Mechanism Based on Composite Multi-Cam Structure. Symmetry 2019, 11, 958. https://doi.org/10.3390/sym11080958
Xu Z, Yang Z, Duan J, Jin M, Mo J, Zhao L, Guo J, Yao H. Design and Experiment of Symmetrical Shape Deployable Arc Profiling Mechanism Based on Composite Multi-Cam Structure. Symmetry. 2019; 11(8):958. https://doi.org/10.3390/sym11080958
Chicago/Turabian StyleXu, Zeyu, Zhou Yang, Jieli Duan, Mohui Jin, Jiasi Mo, Lei Zhao, Jie Guo, and Huanli Yao. 2019. "Design and Experiment of Symmetrical Shape Deployable Arc Profiling Mechanism Based on Composite Multi-Cam Structure" Symmetry 11, no. 8: 958. https://doi.org/10.3390/sym11080958
APA StyleXu, Z., Yang, Z., Duan, J., Jin, M., Mo, J., Zhao, L., Guo, J., & Yao, H. (2019). Design and Experiment of Symmetrical Shape Deployable Arc Profiling Mechanism Based on Composite Multi-Cam Structure. Symmetry, 11(8), 958. https://doi.org/10.3390/sym11080958







