Symmetry Analysis of an Interest Rate Derivatives PDE Model in Financial Mathematics
Abstract
1. Introduction
2. Governing Equation and Symmetry Analysis
3. Exact Invariant Solutions of Equation (5)
3.1. New Solutions via Group Point Transformations
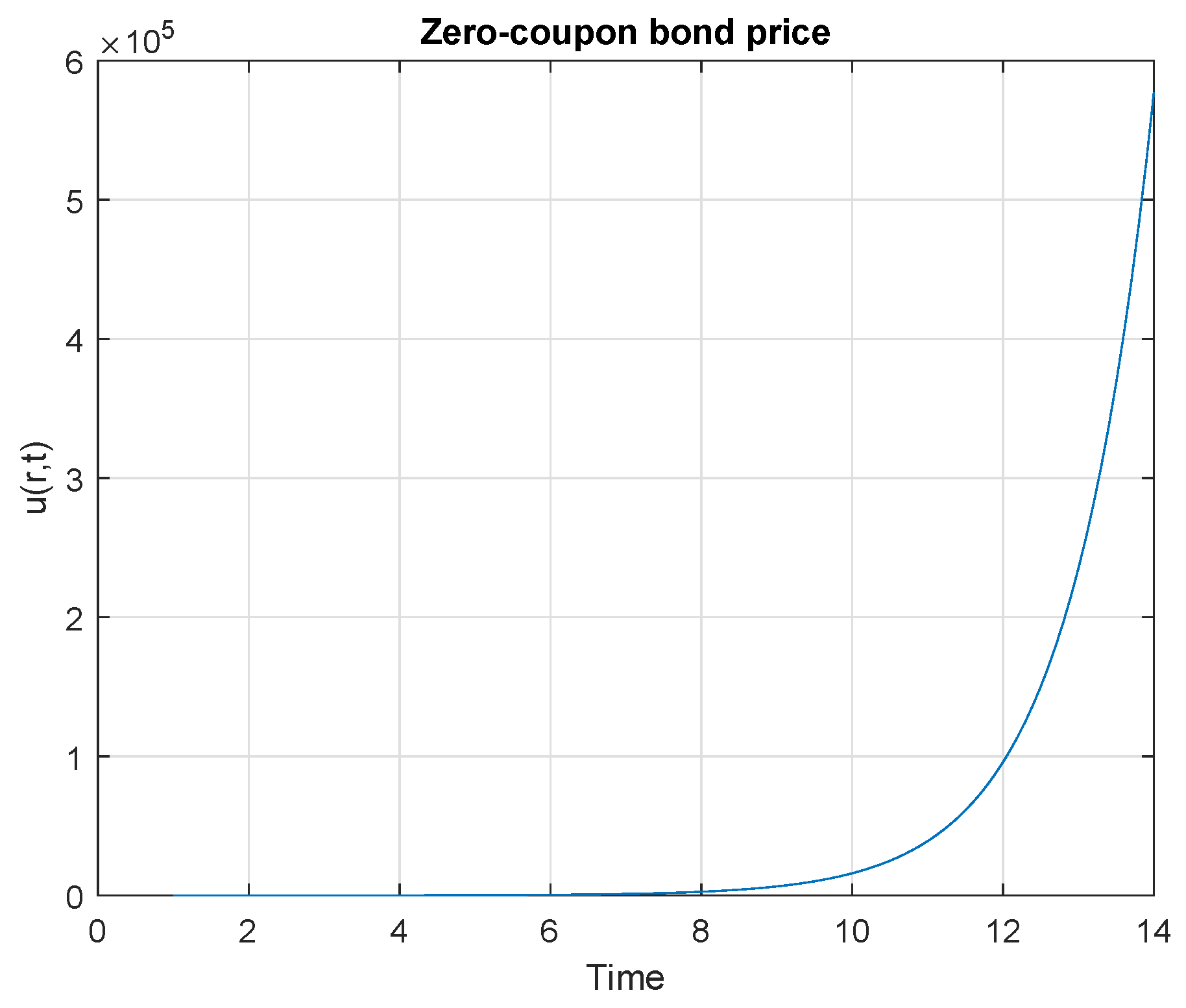
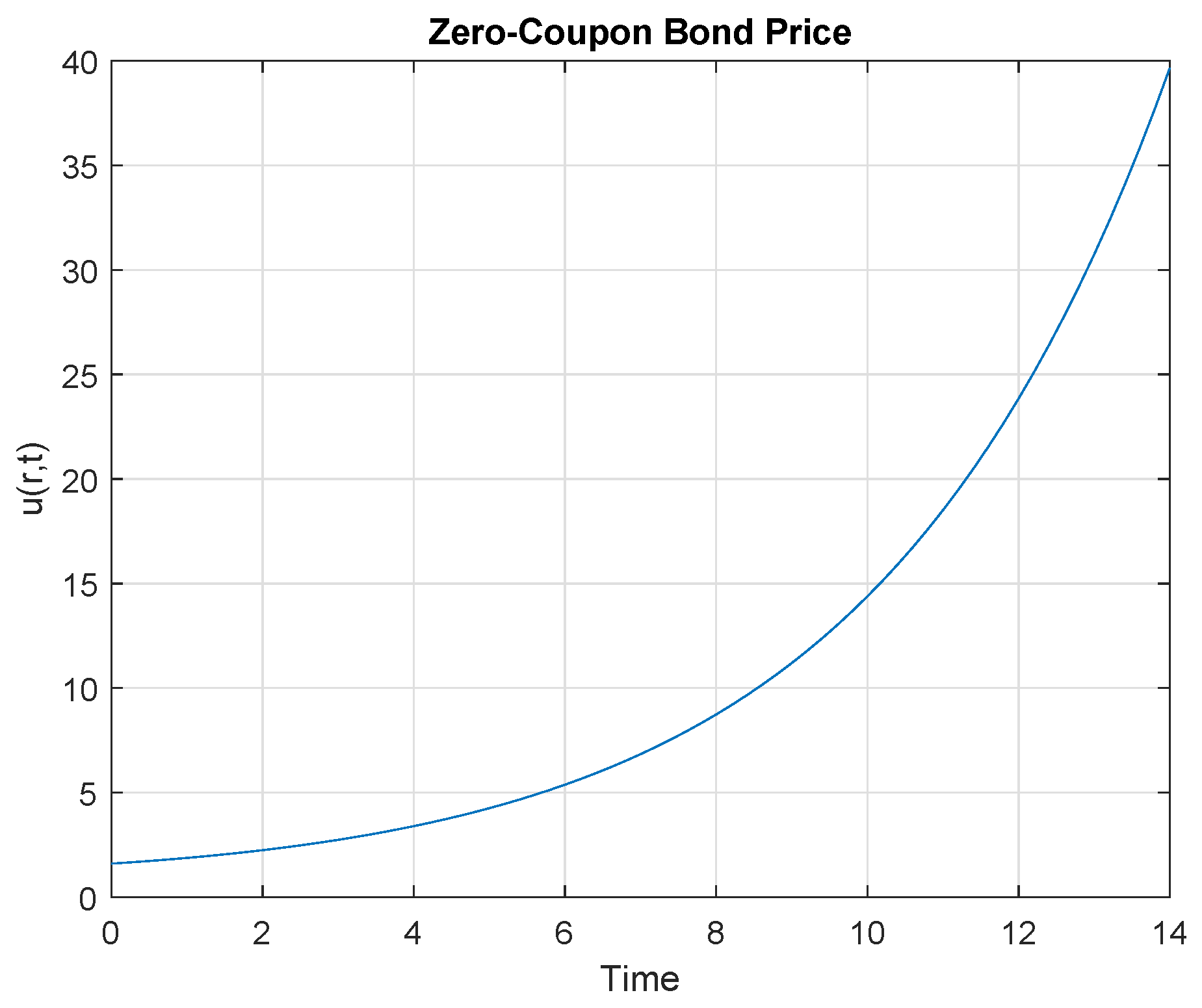
4. Results Discussion
- interest rate (risk-free) r = 0.90,
- volatility ,
- parameter ,
- parameter ,
- constant 1 ,
- constant 2 ,
- time to expiration T = 14 years.
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Vasicek, O. An equilibrium characterization of the term structure. J. Financ. Econ. 1973, 5, 177–188. [Google Scholar] [CrossRef]
- Cox, J.C.; Ingersoll, J.E.; Ross, S.A. An intertemporal general equilibrium model of asset prices. Econometrica 1985, 53, 363–384. [Google Scholar] [CrossRef]
- Wilmott, P.; Dewynne, J.; Howison, S. Option Pricing: Mathematical Models and Computation; Oxford Financial Press: Oxford, UK, 1994. [Google Scholar]
- Black, F.; Scholes, M. The Pricing of Options and Corporate Liabilities. J. Political Econ. 1973, 81, 637–654. [Google Scholar] [CrossRef]
- Merton, R.C. Theory of rational option pricing. Bel. J. Econ. Man. Sci. 1973, 4, 141–183. [Google Scholar] [CrossRef]
- Gazizov, R.K.; Ibragimov, N.H. Lie symmetry analysis of differential equations in finance. Nonlinear Dyn. 1998, 17, 387–407. [Google Scholar] [CrossRef]
- Goard, J. New solutions to the bond-pricing equation via Lie’s classical method. Math. Comput. Model. 2000, 32, 299–313. [Google Scholar] [CrossRef]
- Pooe, C.A.; Mohomed, F.M.; Soh, C.W. Fundamental solutions for zero-coupon bond pricing models. Nonlinear Dyn. 2004, 36, 69–76. [Google Scholar] [CrossRef]
- Sinkala, W.; Leach, P.G.L.; O’ Hara, J.G. Zero-coupon bond prices in the Vasicek and CIR models: Their computation as group-invariant solutions. Math. Methods Appl. Sci. 2008, 31, 665–678. [Google Scholar] [CrossRef]
- Khalique, C.M.; Motsepa, T. Lie symmetries, group-invariant solutions and conservation laws of the Vasicek pricing equation of mathematical finance. Phys. A Stat. Mech. Appl. 2018, 505, 871–879. [Google Scholar] [CrossRef]
- Luo, S.; Yan, J.; Zhang, Q. A functional transformation approach to interest rate modelling. In Stochastic Processes, Finance and Control: A Festschrift in Honor of Robert J Elliott; World Scientific: Hackensack, NJ, USA, 2012; pp. 303–315. [Google Scholar]
- Dimas, S.; Soubelis, D.T. SYM: A new symmetry—Finding package for Mathematica. In Proceedings of the 10th International Conference in Modern Group Analysis, Larnaca, Cyprus, 24–31 October 2004; Ibragimov, N.H., Sophocleous, C., Damianou, P.A., Eds.; University of Cyprus Press: Nicosia, Cyprus, 2005; pp. 64–70. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions; Dover Publication, INC: New York, NY, USA, 1972. [Google Scholar]
- Chern, I.L.; Financial Mathematics. Department of Mathematics, National Taiwan University and University of Hong Kong. Available online: http://www.math.ntu.edu.tw/~chern/notes/finance.pdf (accessed on 14 December 2017).
- Bodie, Z.; Kane, A.; Marcus, A. Investments, 5th ed.; McGraw-Hill Education: New York, NY, USA, 2003. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaibe, B.C.; O’Hara, J.G. Symmetry Analysis of an Interest Rate Derivatives PDE Model in Financial Mathematics. Symmetry 2019, 11, 1056. https://doi.org/10.3390/sym11081056
Kaibe BC, O’Hara JG. Symmetry Analysis of an Interest Rate Derivatives PDE Model in Financial Mathematics. Symmetry. 2019; 11(8):1056. https://doi.org/10.3390/sym11081056
Chicago/Turabian StyleKaibe, Bosiu C., and John G. O’Hara. 2019. "Symmetry Analysis of an Interest Rate Derivatives PDE Model in Financial Mathematics" Symmetry 11, no. 8: 1056. https://doi.org/10.3390/sym11081056
APA StyleKaibe, B. C., & O’Hara, J. G. (2019). Symmetry Analysis of an Interest Rate Derivatives PDE Model in Financial Mathematics. Symmetry, 11(8), 1056. https://doi.org/10.3390/sym11081056




