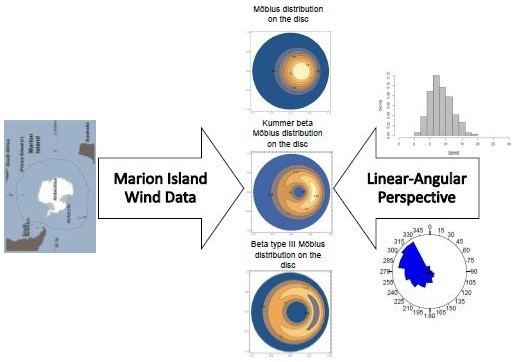
From Symmetry to Asymmetry on the Disc Manifold: Modeling of Marion Island Data
Abstract
1. Introduction
- A new class of distributions on the disc for the joint modeling of a linear and angular variable is introduced. This class includes as a special case the Möbius distribution on the disc. The class can assume a parametric or semi-parametric model based on the choice of the practitioner.
- In the semi-parametric model, a general class is introduced. For this model, we propose a computational algorithm which simplifies to a univariate kernel density function in order to obtain the parameter estimates.
- The proposed class of distributions includes an embedded correlation structure present in the model to account for any relation between the linear and angular variables. This is addresses a shortcoming in the joint modeling of linear and angular variables. The embedded correlation structure reduces any assumption of the univariate models for the linear and angular variables.
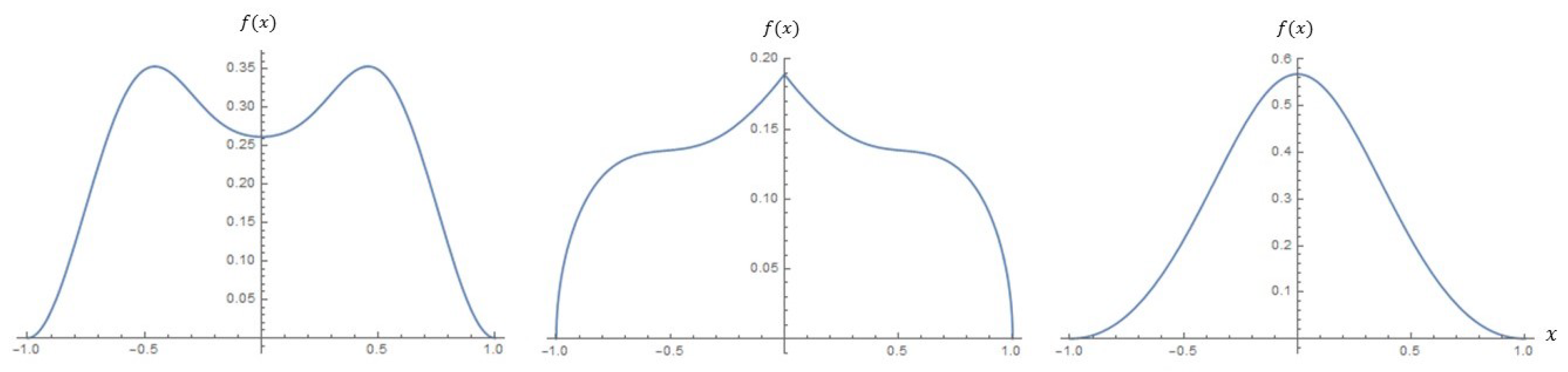
- The need for flexible models on a disc is addressed by introducing a class of distributions that can account for bimodality and skewness present in the data. An advantage of the proposed model is that it extends the shape characteristics of the model on the unit disc proposed by Jones [3] to account for more flexibility.
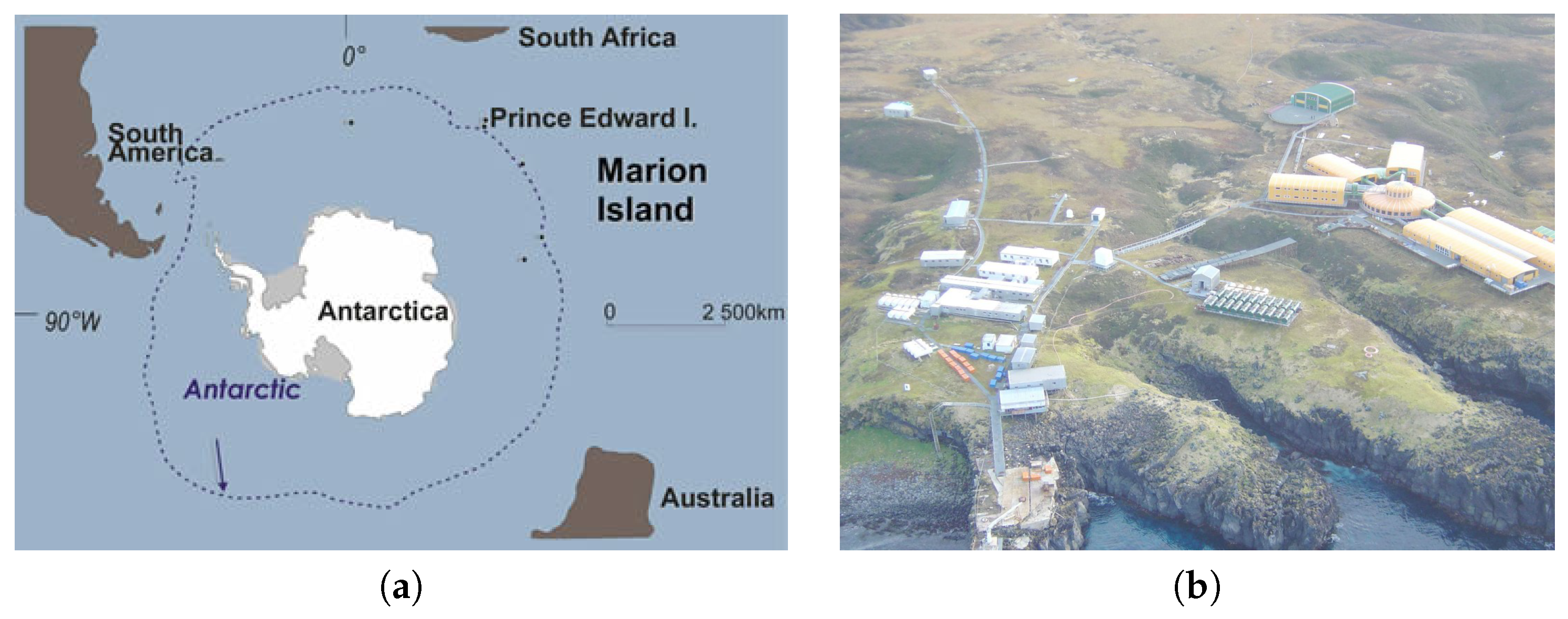
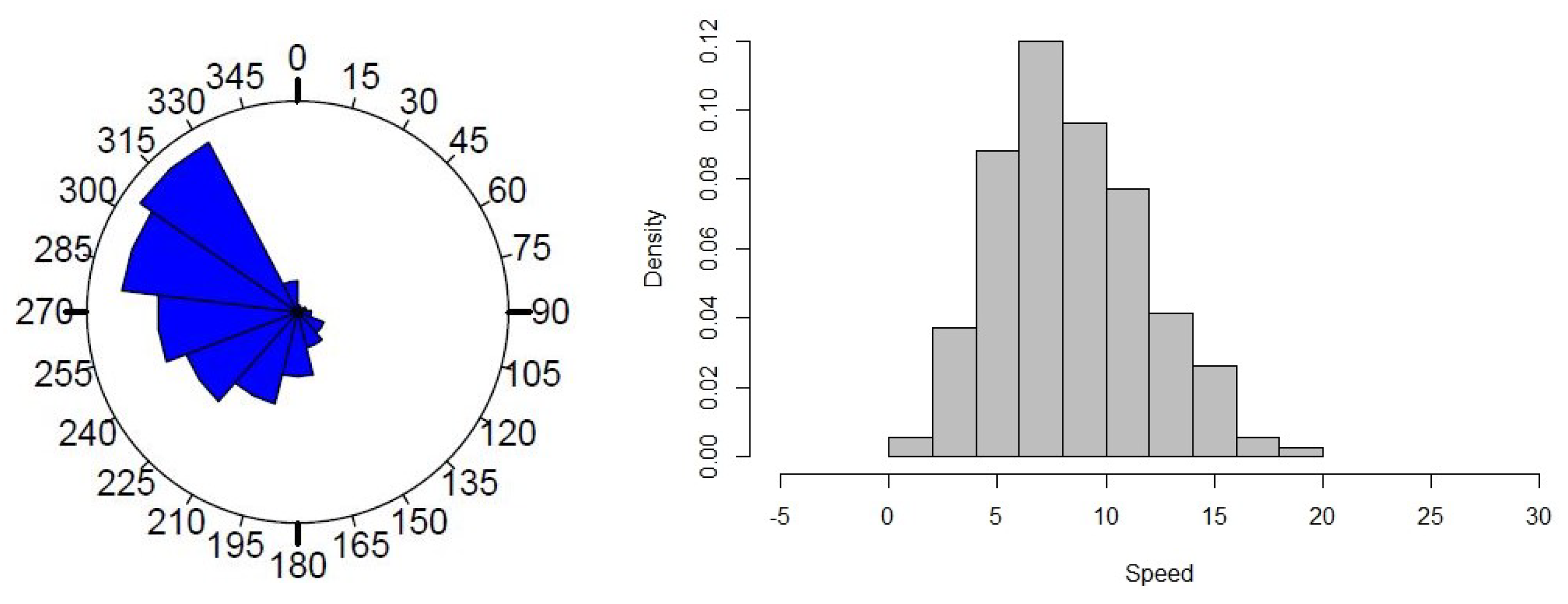
- The modeling of the wind speed and wind direction data at Marion Island was jointly analyzed for the first time in this study.
2. Background
3. Construction Methodology
3.1. Möbius Transformation
3.2. Cartesian Coordinate Configuration of the General Class
3.3. A New Möbius Distribution Class on the Disc
3.4. Maximum Likelihood Estimation
| Algorithm 1 ML estimation algorithm |
|
4. Special Cases
4.1. Möbius Distribution on the Disc
Maximum Likelihood Estimation
4.2. Kummer Beta Möbius Distribution on the Disc
Maximum Likelihood Estimation
4.3. Beta Type III Möbius Distribution on the Disc
Maximum Likelihood Estimation
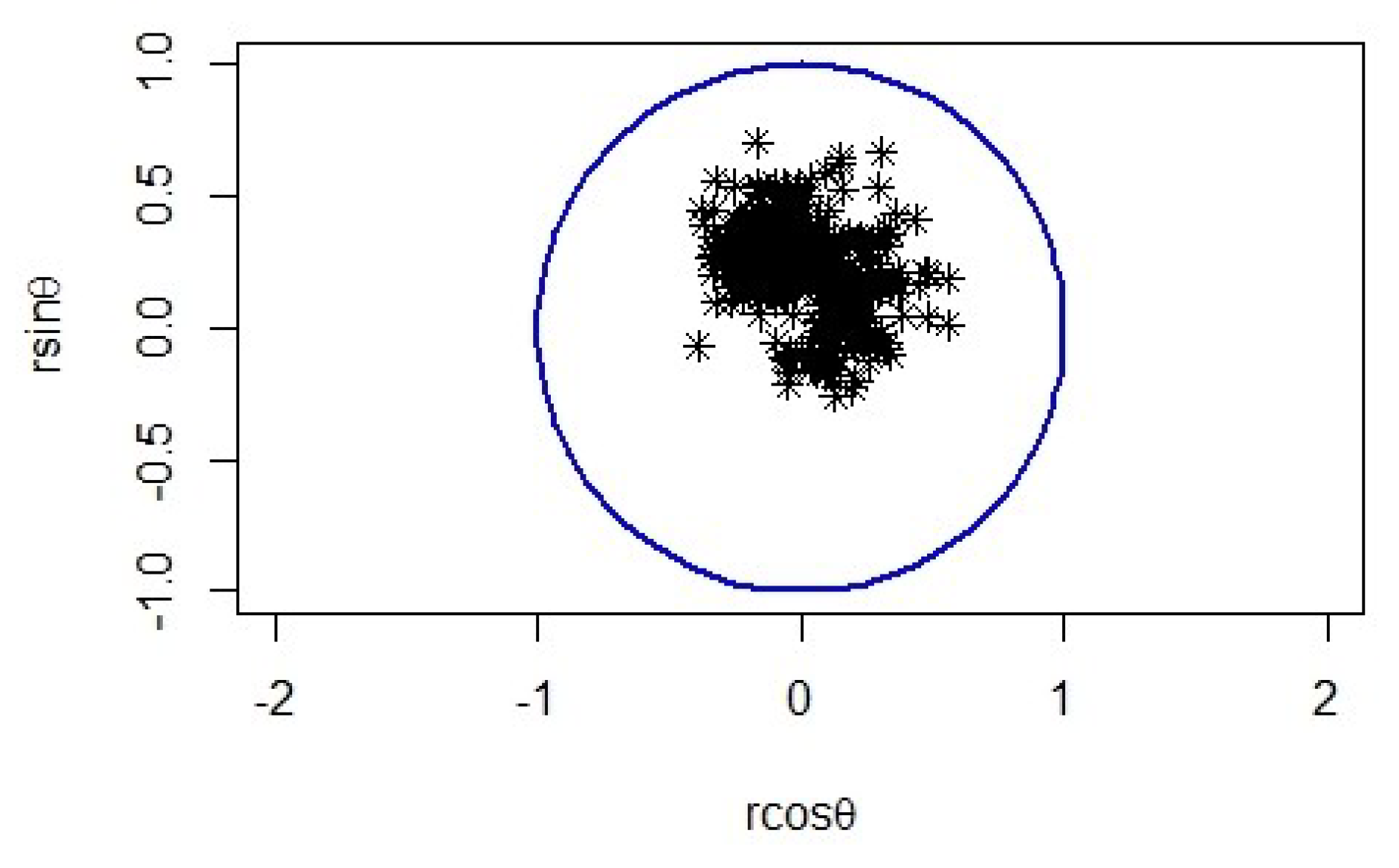
5. Illustrative Example: Marion Island Data
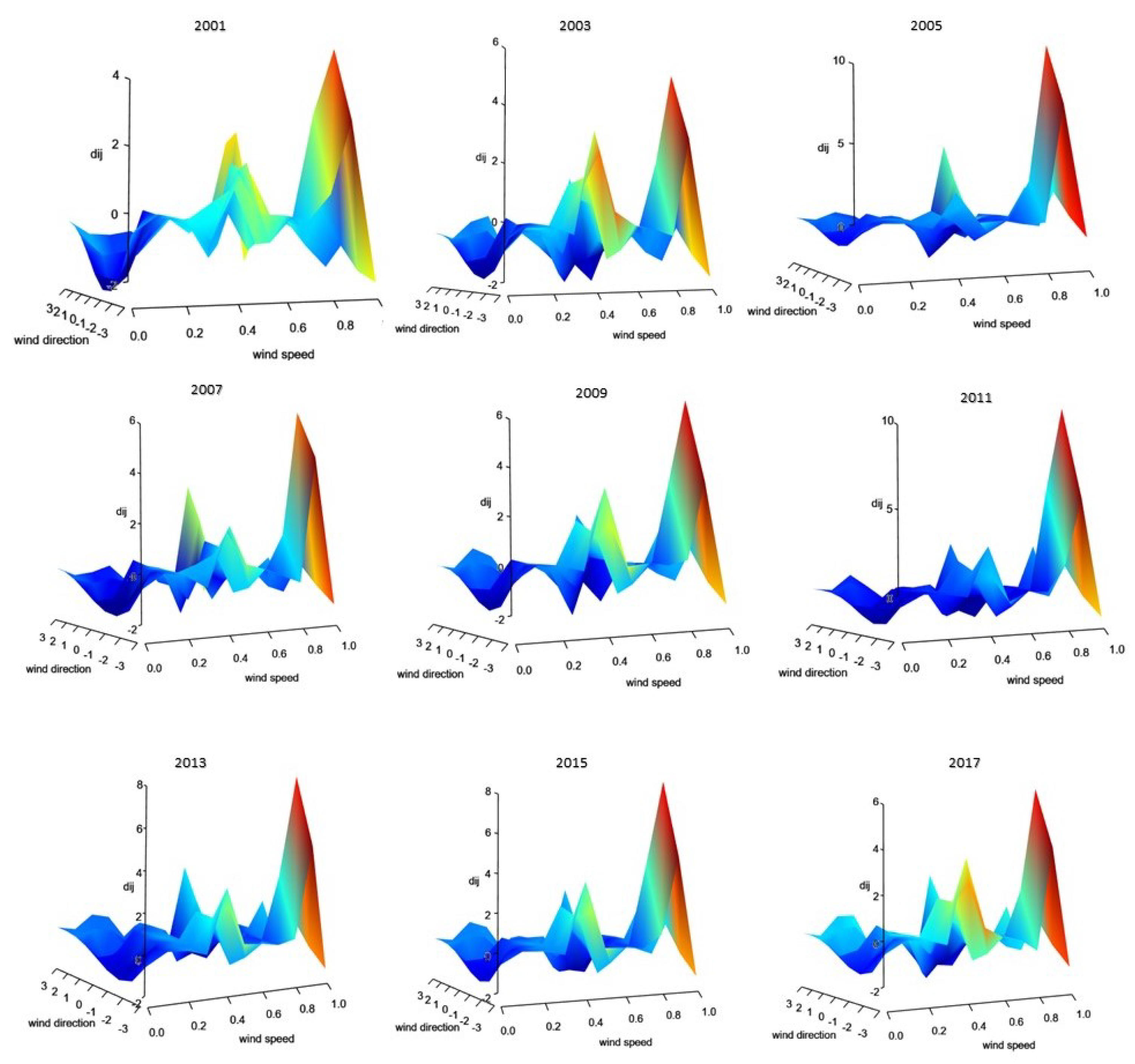
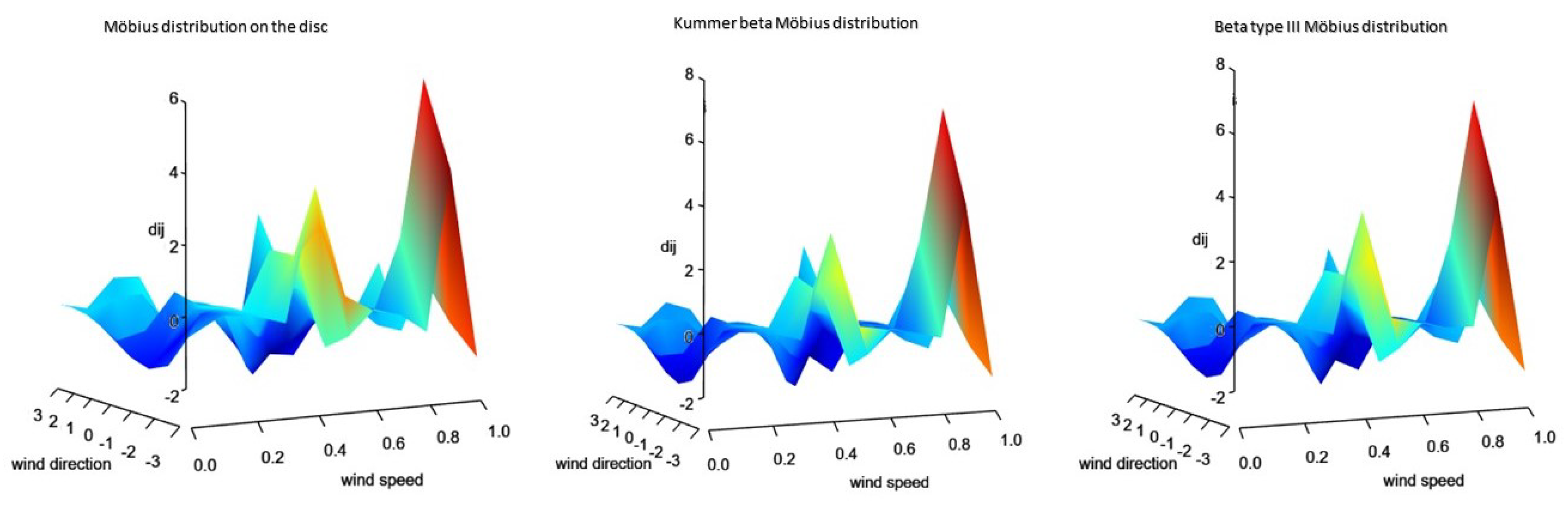
- The general Möbius distribution (Equation (4)) performs fairly well most of the time and has the advantage of no distributional assumptions. However, it is worth noting that the selection of the bandwidth plays an important role in the directional analysis.
- The Möbius distribution on the disc (Equation (9)) outperforms when there is unimodal behavior inherent in the data. This can be seen for the years 2003, 2005, 2007, 2013, 2015 and 2017.
- The Beta type III Möbius distribution in Equation (19) outperforms when there is bimodal behavior inherent in the data. This can be seen for the years 2001, 2009 and 2011. It is also worth noting that the Beta type III Möbius distribution has the ability to model unimodality as well as bimodality. Hence, the performance of this model fairs well against the Möbius distribution on the disc.
- It is interesting to note that the parameters introduced by the Möbius transformation, a and , have the same estimated values for the three parametric models. This highlights the influence of the Möbius transformation to the generator models.
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Möbius Distribution on This Disc
Appendix A.2. Kummer Beta Möbius Distribution
Appendix A.3. Beta Type III Möbius Distribution
References
- Soukissian, T.H.; Karathanasi, F.E. On the selection of bivariate parametric models for wind data. Appl. Energy 2017, 188, 280–304. [Google Scholar] [CrossRef]
- Jones, M.C. Marginal replacement in multivariate densities, with application to skewing spherically symmetric distributions. J. Multivar. Anal. 2002, 81, 85–99. [Google Scholar] [CrossRef][Green Version]
- Jones, M.C. The Möbius distribution on the disc. Ann. Inst. Stat. Math. 2004, 56, 733–742. [Google Scholar] [CrossRef]
- Uesu, K.; Shimizu, K.; SenGupta, A. A possibly asymmetric multivariate generalization of the Möbius distribution for directional data. J. Multivar. Anal. 2015, 134, 146–162. [Google Scholar] [CrossRef]
- Abe, T.; Ley, C. A tractable, parsimonious and flexible model for cylindrical data, with applications. Econom. Stat. 2017, 4, 91–104. [Google Scholar] [CrossRef]
- Fernández-Durán, J.J. Models for circular–linear and circular–circular data constructed from circular distributions based on nonnegative trigonometric sums. Biometrics 2007, 63, 579–585. [Google Scholar] [CrossRef] [PubMed]
- Johnson, R.A.; Wehrly, T. Measures and models for angular correlation and angular-linear correlation. J. R. Stat. Soc. Ser. B Methodol. 1977, 39, 222–229. [Google Scholar] [CrossRef]
- Mardia, K.V.; Jupp, P.E. Directional Statistics; John Wiley & Sons: Chichester, UK, 2009; Volume 494. [Google Scholar]
- Ley, C.; Verdebout, T. Modern Directional Statistics; Chapman and Hall/CRC: New York, NY, USA, 2017. [Google Scholar]
- Pewsey, A.; Neuhäuser, M.; Ruxton, G.D. Circular Statistics in R; Oxford University Press: Oxford, UK, 2013. [Google Scholar]
- Basile, S.; Burlon, R.; Morales, F. Joint probability distributions for wind speed and direction. A case study in Sicily. In Proceedings of the 2015 International Conference on Renewable Energy Research and Applications (ICRERA), Palermo, Italy, 22–25 November 2015; pp. 1591–1596. [Google Scholar]
- Carta, J.A.; Ramirez, P.; Bueno, C. A joint probability density function of wind speed and direction for wind energy analysis. Energy Convers. Manag. 2008, 49, 1309–1320. [Google Scholar] [CrossRef]
- Han, Q.; Hao, Z.; Hu, T.; Chu, F. Non-parametric models for joint probabilistic distributions of wind speed and direction data. Renew. Energy 2018, 126, 1032–1042. [Google Scholar] [CrossRef]
- Zhang, J.; Chowdhury, S.; Messac, A.; Castillo, L. A multivariate and multimodal wind distribution model. Renew. Energy 2013, 51, 436–447. [Google Scholar] [CrossRef]
- Zhang, L.; Li, Q.; Guo, Y.; Yang, Z.; Zhang, L. An investigation of wind direction and speed in a featured wind farm using joint probability distribution methods. Sustainability 2018, 10, 4338. [Google Scholar] [CrossRef]
- Sanusi, N.; Zaharim, A.; Mat, S.; Sopian, K. Comparison of Univariate and Bivariate Parametric Model for Wind Energy Analysis. J. Adv. Res. Fluid Mech. Therm. Sci. 2018, 49, 1–10. [Google Scholar]
- Truswell, J.F. Marion Island, South Indian Ocean. Nature 1965, 205, 64. [Google Scholar] [CrossRef]
- Chown, S.; Froneman, P.W. (Eds.) The Prince Edward Islands: Land-Sea Interactions in a Changing Ecosystem; African Sun Media: Stellenbosch/Bloemfontein, South Africa, 2008. [Google Scholar]
- Schulze, B.R. The climate of Marion Island. In Marion and Prince Edward Island, Report on the South African Biological and Geological Expedition 1965–1966; Van Zinderen Bakke, E.M., Sr., Winterbotton, J.M., Dyer, R.A., Eds.; A.A. Balkema: Cape Town, South Africa, 1971; pp. 16–31. [Google Scholar]
- Le Roux, P.C. Azorella selago (Apiaceae) as a Model for Examining Climate Change Effects in the Sub-Antarctic. Ph.D. Thesis, Stellenbosch University, Stellenbosch, South Africa, 2004. [Google Scholar]
- Rouault, M.; Mélice, J.L.; Reason, C.J.; Lutjeharms, J.R. Climate variability at Marion Island, southern ocean, since 1960. J. Geophys. Res. Oceans 2005. [Google Scholar] [CrossRef]
- Rudin, W. Real and Complex Analysis, 3rd ed.; McGraw-Hill: New York, NY, USA, 1987; pp. 249–250. [Google Scholar]
- Krantz, S.G. Handbook of Complex Analysis; Birkhäuser: Basel, Switzerland, 1999. [Google Scholar]
- Kato, S.; Jones, M.C. A family of distributions on the circle with links to, and applications arising from, Möbius transformation. J. Am. Stat. Assoc. 2010, 105, 249–262. [Google Scholar] [CrossRef]
- Minh, D.L.; Farnum, N.R. Using bilinear transformations to induce probability distributions. Commun. Stat. Theory Methods 2003, 32, 1–9. [Google Scholar] [CrossRef]
- Johnson, M.E. Multivariate Statistical Simulation; Wiley: New York, NY, USA, 1987. [Google Scholar]
- Nagar, D.K.; Gupta, A.K. Matrix-variate Kummer-beta distribution. J. Aust. Math. Soc. 2002, 73, 11–26. [Google Scholar] [CrossRef]
- Cardeno, L.; Nagar, D.K.; Sánchez, L.E. Beta type 3 distribution and its multivariate generalization. Tamsui Oxf. J. Math. Sci. 2005, 21, 225–242. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables; Courier Corporation: Mineola, NY, USA, 1965; Volume 55. [Google Scholar]
- Mathisen, J.; Bitner-Gregersen, E. Joint distributions for significant wave height and wave zero-up-crossing period. Appl. Ocean Res. 1990, 12, 93–103. [Google Scholar] [CrossRef]


| Year | |||||||
|---|---|---|---|---|---|---|---|
| 2001 | 0.59 | −1.38 | 0.40 | 0.89 | 1.14 | −1.60 | −3.38 |
| 2003 | 0.58 | −1.43 | 0.41 | 0.90 | 1.18 | −1.67 | −3.02 |
| 2005 | 0.58 | −1.52 | 0.41 | 0.91 | 1.21 | −1.70 | −2.84 |
| 2007 | 0.48 | 1.48 | 0.52 | 1.02 | 2.20 | −0.84 | −1.59 |
| 2009 | 0.57 | −1.56 | 0.43 | 0.93 | 1.35 | −1.55 | −2.41 |
| 2011 | 0.57 | 1.56 | 0.43 | 0.93 | 1.33 | −1.58 | −2.45 |
| 2013 | 0.56 | 1.53 | 0.44 | 0.94 | 1.39 | −1.56 | −2.24 |
| 2015 | 0.56 | 1.52 | 0.43 | 0.93 | 1.36 | −1.58 | −2.32 |
| 2017 | 0.53 | 1.45 | 0.47 | 0.97 | 1.71 | −1.11 | −2.04 |
| Estimates | Performance | |||||||
|---|---|---|---|---|---|---|---|---|
| Model | Log-Likelihood | AIC | BIC | |||||
| Year 2001 | ||||||||
| General Möbius distribution (h = 0.0109) | 0.3 | 1.88 | - | - | - | −295.68 | 595.37 | 602.85 |
| Möbius distribution on disc | 0.17 | 1.95 | 9.46 | - | - | −293.38 | 592.75 | 603.97 |
| Kummer beta | 0.16 | 1.97 | 2.66 | 1.42 | 12.52 | −286.85 | 583.71 | 602.41 |
| Beta type III | 0.15 | 1.93 | 6.89 | 1.40 | - | −286.87 | 581.74 | 596.69 |
| Year 2003 | ||||||||
| General Möbius distribution (h = 0.0088) | 0.4 | 1.88 | - | - | - | −281.06 | 566.11 | 573.91 |
| Möbius distribution on disc | 0.21 | 1.74 | 11.55 | - | - | −276.29 | 558.57 | 570.27 |
| Kummer beta | 0.21 | 1.76 | 11.86 | 1.15 | 1.86 | −274.16 | 558.31 | 577.81 |
| Beta type III | 0.21 | 1.78 | 7.41 | 1.24 | - | −275.01 | 558.01 | 573.61 |
| Year 2005 | ||||||||
| General Möbius distribution (h = 0.0096) | 0.3 | 1.26 | - | - | - | −277.18 | 558.36 | 566.08 |
| Möbius distribution on disc | 0.20 | 1.28 | 11.39 | - | - | −271.14 | 548.27 | 559.85 |
| Kummer beta | 0.20 | 1.27 | 9.13 | 1.03 | 3.25 | −271.39 | 552.77 | 572.06 |
| Beta type III | 0.20 | 1.28 | 6.45 | 1.04 | - | −272.18 | 552.36 | 567.79 |
| Year 2007 | ||||||||
| General Möbius distribution (h = 0.0107) | 0.2 | 1.26 | - | - | - | −354.05 | 712.10 | 719.89 |
| Möbius distribution on disc | 0.18 | 1.59 | 9.33 | - | - | −349.50 | 705.01 | 716.70 |
| Kummer beta | 0.18 | 1.60 | 1.18 | 1.17 | 11.69 | −346.84 | 703.68 | 723.17 |
| Beta type III | 0.17 | 1.61 | 6.22 | 1.23 | - | −347.00 | 702.01 | 717.59 |
| Year 2009 | ||||||||
| General Möbius distribution (h = 0.0079) | 0.3 | 1.26 | - | - | - | −282.38 | 568.77 | 576.57 |
| Möbius distribution on disc | 0.19 | 1.59 | 11.91 | - | - | −280.42 | 566.83 | 578.53 |
| Kummer beta | 0.19 | 1.61 | 7.69 | 1.34 | 9.16 | −274.04 | 558.08 | 577.58 |
| Beta type III | 0.20 | 1.62 | 8.67 | 1.38 | - | −274.31 | 556.63 | 572.23 |
| Year 2011 | ||||||||
| General Möbius distribution (h = 0.0078) | 0.2 | 1.88 | - | - | - | −277.24 | 558.48 | 566.27 |
| Möbius distribution on disc | 0.18 | 1.51 | 13.54 | - | - | −275.09 | 556.19 | 567.88 |
| Kummer beta | 0.18 | 1.47 | 14.84 | 1.24 | 1.88 | −270.37 | 550.74 | 570.22 |
| Beta type III | 0.18 | 1.48 | 9.36 | 1.29 | - | −270.53 | 549.06 | 564.65 |
| Year 2013 | ||||||||
| General Möbius distribution (h = 0.0089) | 0.3 | 1.88 | - | - | - | −258.28 | 520.56 | 528.32 |
| Möbius distribution on disc | 0.19 | 1.56 | 12.55 | - | - | −251.43 | 508.86 | 520.51 |
| Kummer beta | 0.19 | 1.55 | 10.22 | 1.19 | 4.99 | −249.76 | 509.52 | 528.92 |
| Beta type III | 0.20 | 1.56 | 8.27 | 1.25 | - | −250.50 | 509.00 | 524.52 |
| Year 2015 | ||||||||
| General Möbius distribution (h = 0.0073) | 0.2 | 1.88 | - | - | - | −261.57 | 527.15 | 534.95 |
| Möbius distribution on disc | 0.19 | 1.59 | 13.79 | - | - | −253.29 | 512.58 | 524.27 |
| Kummer beta | 0.19 | 1.54 | 13.28 | 1.04 | 0.61 | −253.79 | 517.57 | 537.06 |
| Beta type III | 0.19 | 1.56 | 8.15 | 1.12 | - | −253.77 | 515.55 | 531.14 |
| Year 2017 | ||||||||
| General Möbius distribution (h = 0.00818) | 0.2 | 1.26 | - | - | - | −261.99 | 527.98 | 535.77 |
| Möbius distribution on disc | 0.22 | 1.59 | 12.14 | - | - | −258.51 | 523.01 | 534.69 |
| Kummer beta | 0.21 | 1.57 | 11.59 | 1.15 | 2.44 | −257.25 | 524.50 | 543.97 |
| Beta type III | 0.21 | 1.61 | 7.56 | 1.15 | - | −257.91 | 523.82 | 539.39 |
| Year | Best Fit Model | Range | Median |
|---|---|---|---|
| 2001 | Beta type III Möbius (19) | (−2.651791; 5.920593) | −0.1554433 |
| 2003 | Möbius distribution on the disc (9) | (−2.312973; 6.288503) | −0.147436 |
| 2005 | Möbius distribution on the disc (9) | (−3.453434; 12.743586) | −0.1662767 |
| 2007 | Möbius distribution on the disc (9) | (−2.610813; 7.522888) | −0.3437355 |
| 2009 | Beta type III Möbius (19) | (−3.000686; 7.984593) | −0.05206841 |
| 2011 | Beta type III Möbius (19) | (−2.482695; 12.845301) | −0.08473761 |
| 2013 | Möbius distribution on the disc (9) | (−2.404983; 9.312558) | −0.05009261 |
| 2015 | Möbius distribution on the disc (9) | (−2.516891; 9.782227) | −0.03193083 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bekker, A.; Nagar, P.; Arashi, M.; Rautenbach, H. From Symmetry to Asymmetry on the Disc Manifold: Modeling of Marion Island Data. Symmetry 2019, 11, 1030. https://doi.org/10.3390/sym11081030
Bekker A, Nagar P, Arashi M, Rautenbach H. From Symmetry to Asymmetry on the Disc Manifold: Modeling of Marion Island Data. Symmetry. 2019; 11(8):1030. https://doi.org/10.3390/sym11081030
Chicago/Turabian StyleBekker, Andriette, Priyanka Nagar, Mohammad Arashi, and Hannes Rautenbach. 2019. "From Symmetry to Asymmetry on the Disc Manifold: Modeling of Marion Island Data" Symmetry 11, no. 8: 1030. https://doi.org/10.3390/sym11081030
APA StyleBekker, A., Nagar, P., Arashi, M., & Rautenbach, H. (2019). From Symmetry to Asymmetry on the Disc Manifold: Modeling of Marion Island Data. Symmetry, 11(8), 1030. https://doi.org/10.3390/sym11081030