Modeling the Performance Indicators of Financial Assets with Neutrosophic Fuzzy Numbers

Abstract

This research sets the basis for modeling the performance indicators of financial assets using triangular neutrosophic fuzzy numbers. This type of number allows for the modeling of financial assets performance indicators by taking into consideration all the possible scenarios of their achievement. The key performance indicators (KPIs) modeled with the help of triangular fuzzy neutrosophic numbers are the return on financial assets, the financial assets risk, and the covariance between financial assets. Thus far, the return on financial assets has been studied using statistical indicators, like the arithmetic and geometric mean, or using the financial risk indicators with the help of the squared deviations from the mean and covariance. These indicators are well known as the basis of portfolio theory. This paper opens the perspective of modeling these three mentioned statistical indicators using triangular neutrosophic fuzzy numbers due to the major advantages they have. The first advantage of the neutrosophic approach is that it includes three possible symmetric scenarios of the KPIs achievement, namely the scenario of certainty, the scenario of non-realization, and the scenario of indecision, in which it cannot be appreciated whether the performance indicators are or are not achieved. The second big advantage is its data series clustering, representing the financial performance indicators by which these scenarios can be delimitated by means of neutrosophic fuzzy numbers in very good, good or weak performance indicators. This clustering is realized by means of the linguistic criteria and measuring the belonging degree to a class of indicators using fuzzy membership functions. The third major advantage is the selection of risk mitigation analysis scenarios and the formation of financial assets’ optimal portfolios.

1. Introduction

Financial markets specialists have shown a particular interest for financial assets lately, both due to returns they generate for investors and also because they can predict the future evolution of financial performance [1]. Researchers in financial markets, starting with Markowittz [2], developed the modern theory of financial asset portfolios, focusing on the financial assets return ($R_a$) and on the financial assets risk (${\sigma }_a^2$). An extremely important issue in the modern theory of financial assets portfolios is the risk diversification; in the famous words of Markowitz: “Don’t put all your eggs in one basket.” These studies, regarding the risk of diversification, have led to the foundation of Markowitz’s efficient frontier, demonstrating that the financial assets portfolio risk is much lower than the individual risk of each financial assets’ category [2].

In order to evaluate financial asset returns, the literature has enabled two categories of models. The first model is known as market return model, and it is based on the financial asset market price at two moments of time ($t_1$) and ($t_0$). The market-based return calculation is as follows:

$$R_a=\frac{P_1-P_0+D_1}{P_0}$$

where $P_1$ represents the market price at time ($t_1$), $P_0$ represents the market price at time ($t_0$), and $D_1$ represents the dividend at time ($t_1$).

The second model for evaluating returns on financial assets is based on the market portfolio (M), as well as on the return on the risk-free financial asset ($R_f$) as a result of applying the Capital Assets Price Model (CAPM). The financial assets return is, in this case:

$$R_a=R_f+\beta (R_M-R_f),$$

where $R_M$ is the portfolio return, and β is the volatility coefficient of the financial asset, which is determined by a relation of the form:

$$\beta =\raisebox{1ex}{${\sigma }_{aM}$}\!\left/ \!\raisebox{-1ex}{${\sigma }_M^2$}\right.,$$

where ${\sigma }_{aM}$ is the covariance between the asset and the portfolio and ${\sigma }_M^2$ represents the portfolio risk. If the financial asset return is considered to be fairly measured using the CAPM model, then two situations are encountered in regard to the investors’ decision to trade the financial asset on the capital market. In the first situation, if $R_a<R_a(CAPM),$ then $R_a$ has to decrease by increasing $P_0$—as such, investors will buy financial assets. In the second situation, if $R_a<R_a(CAPM),$ then $R_a$ should increase by subtracting $P_0$—as such, the investors will sell the financial assets.

In order to assess financial asset risk, the following statistical indicators are used: The squared deviations from the mean, given by the formula:

$${\sigma }_a^2=\frac{1}{N-1}{\displaystyle \sum }_{i=1}^N{(R_{ai}-\overline{R})}^2$$

and the variance:

$${\sigma }_a=\sqrt{\frac{1}{N-1}{\displaystyle \sum }_{i=1}^N{(R_{ai}-\overline{R})}^2}$$

to express the deviation of the financial asset over a period of time from the average return value. The higher the value of the deviation is, the higher the risk assumed by the investors will be. Otherwise, the lower the deviation value is, the lower the risk.

Regardless of the model used to evaluate financial asset return, there is a certain degree of probability that characterizes the achievement of financial asset return. Similarly, also the risk assumed by investors can be manifested with different intensities (this risk may take maximum or minimum values, and there is also an area where the risk intensity is uncertain). This degree of uncertainty for the obtaining of the financial asset return, noted as ($D_u(R_a)),$ can be grouped into three main categories:

• The first category: A high degree of obtaining financial asset returns, denoted by $\mu (D_u(\sigma a,Ra)),$ which is the value of the financial asset return that can be achieved with a high probability, approximated by a professional judgment of around 50%. For each financial asset, this degree has specific values.
• The second category: A low degree of obtaining financial asset returns, denoted by $\vartheta (D_u(\sigma a, Ra))$. Here, there is no prospect of achieving the financial asset return. The causes that lead to these situations are various: The risk assumed by investors is appropriate to the value of the realizable asset’s return, the expected return should record high values above the market level, or the dynamics of the exchange rate market is not known. The degree of probability for this situation approximated by professional judgement is 30%, and it is specific to each financial asset.
• The third category: The degree for obtaining the financial asset return is uncertain, denoted by $\lambda (D_u(\sigma a,R_a)),$ corresponding to the situation in which the realization or non-realization of the return is uncertain or not appreciated. This area of uncertainty is approximated at 20%, and it is also specific to each category of financial assets.

The introduction of these criteria for assessing financial asset return allows for the analysis of these performance indicators in line with the real needs of investors. They can thus select portfolios of financial assets for which the likelihood of achieving profitability is known. Additionally, by introducing these specific notions, the basis for the use of neutrosophic fuzzy numbers is created in the field of modeling financial decision-making to form financial assets portfolios.

The aim of this paper is to properly model the indicators from portfolio theory using triangular neutrosophic fuzzy numbers (considering the major advantages they provide) while solving the problems that arise in the classical approach—these being several limitations which might appear in the case of the financial assets’ performance indicators use.

2. State of the Art

Neutrosophic fuzzy numbers represent a quite new research area that has captured the attention of researchers worldwide since 2013. Querying the WoS (Web of Science) database for the keywords “neutrosophic fuzzy numbers,” the search results indicated 184 ISI Web of Science articles. Analyzing by publication year, it can be observed that, since the appearance of this research topic, interest has increased exponentially each and every year, starting from two ISI articles published in 2013 to seven ISI articles in both 2014 and 2015, 18 in 2016, 41 in 2017, and 77 in 2018. Researchers from all over the world have started to use this niche of fuzzy intelligence, but the majority of these studies have come from China, India, USA, Turkey and Pakistan.

Most of these articles are included in the following categories: Computer science and artificial intelligence (47%), multidisciplinary sciences (20%), information systems (10%), automation control systems (7%), management (2%), economics (1%), and business (0.5%). The first articles published in 2013 targeted color image segmentation with applicability in image processing, pattern recognition and computer vision [3] and the topic of neutrosophic fuzzy classifications [4]. The advantage of using the neutrosophic set was shown by Ali and Smarandache [5] in their paper, where they studied the complexity of this topic and revealed that neutrosophic fuzzy numbers can handle imprecise, indeterminate, inconsistent, and incomplete information.

The most cited articles that have used neutrosophic fuzzy numbers as a research methodology to target the decision-making problem. Pramanik et al. [6] used an extension of the interval neutrosophic set, namely the interval bipolar neutrosophic set, in order to develop a multi-attribute decision-making strategy. Ye [7] introduced the concept of simplified neutrosophic sets in order to solve a multicriteria decision-making problem. Zhang et al. [8] also proposed an interval neutrosophic set to address a multicriteria decision-making problem. The paper published by Liu and Teng [9] presented a new method based on a single-valued neutrosophic normalized weighted Bonferroni mean that demonstrated its effectiveness for solving decision-making problems. Peng et al. [10] developed a new outranking approach for multi-criteria decision-making problems. This method was developed in a simplified neutrosophic environment where the truth-membership degree, indeterminacy-membership degree, and falsity-membership degree were subsets in [0,1].

None of the studies indexed in WoS have targeted portfolio theory or the finance domain. Even if there have been a lot of studies that have focused on solving multi-criteria decision-making problems, none of them have addressed this portfolio theory or the finance domain. There are only five articles that have approached the economic area of research. The first of them is the study proposed by Bausys et al. [11], in which the complex proportional assessment method (COPRAS) was used in the context of single value neutrosophic sets in order to select the location of a liquefied natural gas terminal. In the same year, Bausys and Zavadskas [12] published another article in which was created an extension of the Vlse Kriterijumska Optimizacija Kompromisno Resenje (VIKOR) method for the solution of multicriteria decision-making problems. The applicability and efficiency of neutrosophic fuzzy numbers were studied by Nabadan et al. [13]. The authors compared neutrosophic fuzzy numbers to other fuzzy methods used in the decision-making field, and their results showed higher values of efficiency for this new approach. The fourth article in economic domain targeted the tourism area [14] by creating a decision support model for satisfactory restaurants using social information. The model used neutrosophic fuzzy numbers to sign online ratings, and it used the Bonferroni mean to consider interdependence among criteria. Tian et al. [15] used a life cycle assessment technique to develop an innovative multi-criteria group decision-making approach that incorporates aggregation operators and the Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS)-based QUALIFLEX method. This study managed to offer a solution for green product design selection problems using neutrosophic linguistic information. As for the performance indicators used in financial analysis, a series of recent papers have addressed optimal portfolio selection, corporate entrepreneurship, indicators selection or portfolio optimization [16,17,18,19,20,21,22].

Thus, our study has an innovative approach, as it introduces in the literature the modeling of the financial performance indicators with the help of neutrosophic fuzzy numbers with the portfolio theory. The financial performance indicators modeled using neutrosophic fuzzy numbers refer to: The financial return of assets (neutrosophic return), financial risk (neutrosophic risk), and financial covariance (neutrosophic covariance).

This research paper solves the identified problem that consist of the limitations of the classical approach for the financial assets’ performance indicators. Performance indicators of financial assets are modeled using classical statistical indicators, namely arithmetic mean, geometric mean, squared deviation from the mean, and variance. These indicators show a series of limitations, including the following:

• Not taking into account possible scenarios for achieving performance indicators of financial assets; as such, investor cannot assess the chance of achieving them.
• Not allowing data series stratification to delimit the values of the financial performance indicators—the very good, good and low values—so that the investor can select the scenarios best suited to his/her investment profile.
• Not allowing the selection of performance indicators scenarios that characterize financial assets for analyzing financial risk mitigation or building optimal portfolios of financial assets.

These limitations in financial assets’ performance indicators make them subject to some degree of rigidity in substantiating decisions and also affect their capacity to respond properly to information needed by capital market investors.

In order to solve these shortcomings, the proposed solution introduces the modeling of financial assets performance indicators using triangular neutrosophic fuzzy numbers due to the numerous advantages they present, namely:

• Allow for the consideration of all possible achievement scenarios for the financial assets’ performance indicators like the scenario of certainty, the scenario of non-realization, and the scenario of indecision—these scenarios derive from the neutrosophic components such as truth, indeterminacy and falsehood, which are symmetric in form, as the truth is opposite to false, with respect to the indeterminacy [23].
• Allow for financial performance indicators’ data series stratification or clustering. The delimitation of these data series was done using linguistic criteria with assigned values such as: very good, good and weak.
• Allow for the selection of analysis scenarios to mitigate financial risk or to form optimal portfolios of financial assets, both of which could lead to a better substantiation of financial asset decisions.

The methodology used in this paper is aimed at combining portfolio theory with the fuzzy intelligence and neutrosophic numbers in order to enable the decision-making process for investors. The proposed model allows for the modeling of financial assets performance indicators by taking into consideration all possible scenarios of their achievement. Additionally, the model clusters the data series, representing the financial performance indicators, by delimitating these scenarios by means of neutrosophic fuzzy numbers in very good, good or weak performance indicators. This clustering is realized with the help of the linguistic criteria which belong to degrees of a class of indicators using fuzzy membership functions. This methodology offers the possibility to form financial assets’ optimal portfolios that are characterized by low risk and high return.

The effective neutrosophic fuzzy modeling is presented in the following paragraphs of the paper.

3. Establishment of Neutrosophic Numbers for the Financial Assets Risk and Return

Financial asset return and risk are manifested by varying intensities, depending on the particularities of the assets that form a portfolio. These intensities may take high, low, or even uncertain values. Neutrosophic fuzzy numbers are formed and defined separately for each of the two indicators mentioned above [24,25].

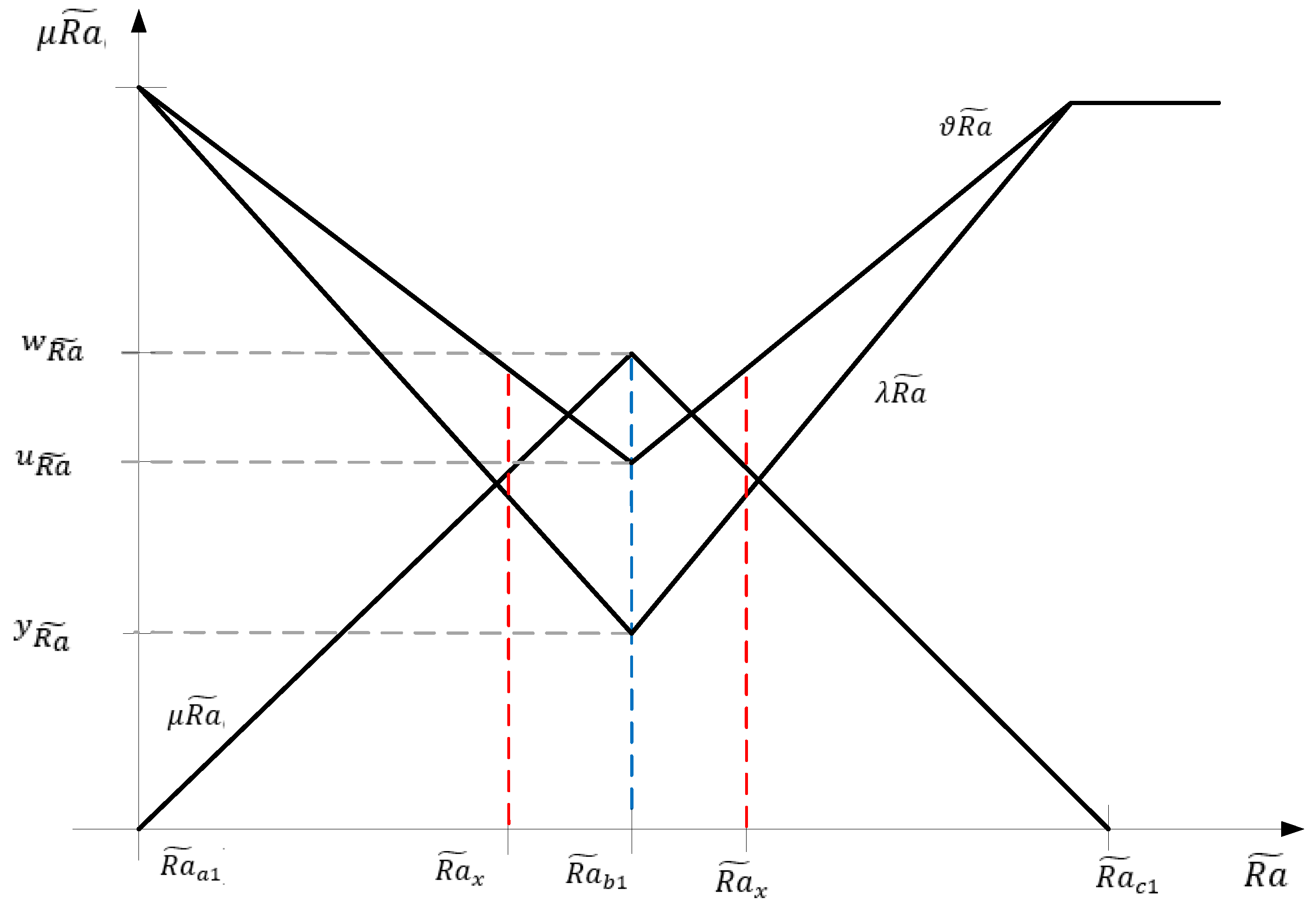
Definition 1.

Let the financial asset return on the financial market be$(R_a),$and let F$\left[0,1\right]$be the rules set for all fuzzy triangular numbers. The fuzzy number$(\widetilde{Ra})$is considered the triangular neutrosophic fuzzy number of the financial assets return:

$$\widetilde{Ra}=\left\{\langle \widetilde{r_a},{\mu }_{\widetilde{Ra}},{\vartheta }_{\widetilde{Ra}}, {\lambda }_{\widetilde{Ra}}\rangle /r_a\in R_a\right\},$$

where${\mu }_{\widetilde{Ra}}:R_a\to \left[0,1\right]$;${\vartheta }_{\widetilde{Ra}}:R_a\to \left[0,1\right]$and${\lambda }_{\widetilde{Ra}}:R_a\to \left[0,1\right]$, for which the membership functions are defined according to the relations depicted in Figure 1.

The truth membership, which is the membership function for the financial assets return with the highest degree of realization $(\mu {\widetilde{Ra}}_{(x)}),$ is the following:

$$\mu {\widetilde{Ra}}_{(x)}=\{\begin{array}{c}\frac{w_{\widetilde{Ra}}({\widetilde{Ra}}_x-{\widetilde{Ra}}_{a1})}{{\widetilde{Ra}}_{b1}-{\widetilde{Ra}}_{a1}} for {\widetilde{Ra}}_{a1}\le {\widetilde{Ra}}_x\le {\widetilde{Ra}}_{b1}\\ w_{\widetilde{Ra}} for {\widetilde{Ra}}_x={\widetilde{Ra}}_{b1}\\ \frac{w_{\widetilde{Ra}}({\widetilde{Ra}}_{c1}-{\widetilde{Ra}}_x)}{{\widetilde{Ra}}_{c1}-{\widetilde{Ra}}_{b1}} for {\widetilde{Ra}}_{b1}\le {\widetilde{Ra}}_x\le {\widetilde{Ra}}_{c1}\\ 0 for others values out of range \left[{\widetilde{Ra}}_{c1};{\widetilde{Ra}}_{a1}\right]\end{array}$$

(1)

The indeterminacy membership, which is the membership function for the financial assets return with the medium degree of realization $(\vartheta {\widetilde{Ra}}_{(x)})$, is the following:

$$\vartheta {\widetilde{Ra}}_{(x)}=\{\begin{array}{c}\frac{u_{\widetilde{Ra}}({\widetilde{Ra}}_x-{\widetilde{Ra}}_{a1})+{\widetilde{Ra}}_{b1}-{\widetilde{Ra}}_x}{{\check{Ra}}_{b1}-{\check{Ra}}_{a1}} for {\widetilde{Ra}}_{a1}\le {\widetilde{Ra}}_x\le {\widetilde{Ra}}_{b1} \\ u_{Ra} for R{a}_x=R{a}_{b1}\\ \frac{u_{\widetilde{Ra}}({\widetilde{Ra}}_{c1}-{\widetilde{Ra}}_x)+{\widetilde{Ra}}_x-{\widetilde{Ra}}_{b1}}{{\widetilde{Ra}}_{c1}-{\widetilde{Ra}}_{b1}} for {\widetilde{Ra}}_{b1}\le {\widetilde{Ra}}_x\le {\widetilde{Ra}}_{c1}\\ 0 for others values out of range \left[{\widetilde{Ra}}_{c1};{\widetilde{Ra}}_{a1}\right]\end{array}$$

(2)

The falsity membership, which is the membership function for the financial assets return with low degree of realization $(\lambda {\widetilde{Ra}}_{(x)})$, is the following:

$$\lambda {\widetilde{Ra}}_{(x)}=\{\begin{array}{c}\frac{y_{\widetilde{R_a}}({\widetilde{Ra}}_x-{\widetilde{Ra}}_{a1})+{\widetilde{Ra}}_{b1}-{\widetilde{Ra}}_x}{{\widetilde{Ra}}_{b1}-{\widetilde{Ra}}_{a1}} for {\widetilde{Ra}}_{a1}\le {\widetilde{Ra}}_x\le {\widetilde{Ra}}_{b1}\\ {\lambda }_{\widetilde{R_a}} for {\widetilde{Ra}}_x={\widetilde{Ra}}_{b1}\\ \frac{y_{\widetilde{Ra}}({\widetilde{Ra}}_{c1}-{\widetilde{Ra}}_x)+{\widetilde{Ra}}_x-{\widetilde{Ra}}_{b1}}{{\widetilde{Ra}}_{c1}-{\widetilde{Ra}}_{b1}} for {\widetilde{Ra}}_{b1}\le {\widetilde{Ra}}_x\le {\widetilde{Ra}}_{c1}\\ 0 for others values out of range \left[{\widetilde{Ra}}_{c1};{\widetilde{Ra}}_{a1}\right]\end{array}$$

(3)

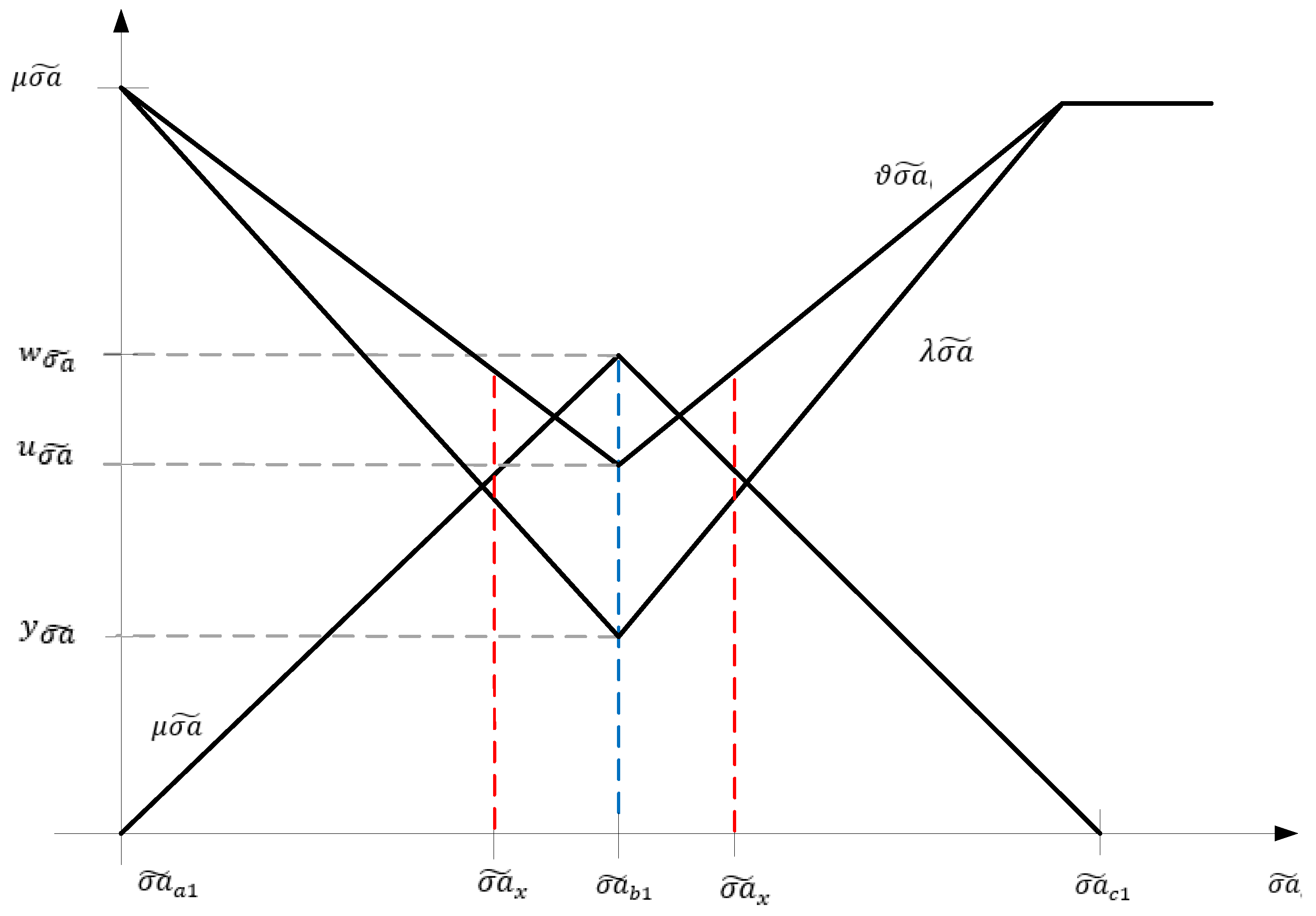
Definition 2.

Let the financial asset risk on the financial market be$({\sigma }_a),$and let F$\left[0,1\right]$be the rules set for all triangular fuzzy numbers. The fuzzy number$(\widetilde{{\sigma }_a})$is considered the triangular neutrosophic fuzzy number of the financial assets risk:

$$\widetilde{{\sigma }_a}=\left\{\langle \widetilde{{\sigma }_a},{\mu }_{\widetilde{{\sigma }_a}},{\vartheta }_{\widetilde{{\sigma }_a}}, {\lambda }_{\widetilde{{\sigma }_a}}\rangle /\widetilde{{\sigma }_a}\in {\sigma }_A\right\},$$

where${\mu }_{\widetilde{{\sigma }_a}}:{\sigma }_A\to \left[0,1\right]$;${\vartheta }_{\widetilde{{\sigma }_a}}:{\sigma }_A\to \left[0,1\right]$and${\lambda }_{\widetilde{{\sigma }_a}}:{\sigma }_A\to \left[0,1\right]$, for which the membership functions are defined according to the relations depicted in Figure 2.

The truth membership, which is the membership function for the financial assets risk with the highest degree of realization $(\mu {\widetilde{\sigma a}}_{(x)}),$ is the following:

$$\mu {\widetilde{\sigma a}}_{(x)}=\{\begin{array}{c}\frac{w_{\widetilde{{\sigma }_a}}({\widetilde{\sigma a}}_x-{\widetilde{\sigma a}}_{a1})}{{\widetilde{\sigma a}}_{b1}-{\widetilde{\sigma a}}_{a1}} for {\widetilde{\sigma a}}_{a1}\le {\widetilde{\sigma a}}_x\le {\widetilde{\sigma a}}_{b1}\\ w_{\widetilde{{\sigma }_a}} for {\widetilde{\sigma a}}_x={\widetilde{\sigma a}}_{b1}\\ \frac{w_{\widetilde{{\sigma }_a}}({\widetilde{\sigma a}}_{c1}-{\widetilde{\sigma a}}_x)}{{\widetilde{\sigma a}}_{c1}-{\widetilde{\sigma a}}_{b1}} for {\widetilde{\sigma a}}_{b1}\le {\widetilde{\sigma a}}_x\le {\widetilde{\sigma a}}_{c1}\\ 0 for others values out of range \left[{\widetilde{\sigma a}}_{c1};{\widetilde{\sigma a}}_{a1}\right]\end{array}$$

(4)

The indeterminacy membership, which is the membership function for the financial assets risk with the medium degree of realization $(\vartheta {\widetilde{\sigma a}}_{(x)}),$ is the following:

$$\vartheta {\widetilde{\sigma a}}_{(x)}=\{\begin{array}{c} \\ \frac{u_{\widetilde{\sigma a}}({\widetilde{\sigma a}}_x-{\widetilde{\sigma a}}_{a1})+{\widetilde{\sigma a}}_{b1}-{\widetilde{\sigma a}}_x}{{\widetilde{\sigma a}}_{b1}-{\widetilde{\sigma a}}_{a1}} for {\widetilde{\sigma a}}_{a1}\le {\widetilde{\sigma a}}_x\le {\widetilde{\sigma a}}_{b1}\\ u_{\widetilde{\sigma a}} for {\widetilde{\sigma a}}_x={\widetilde{\sigma a}}_{b1}\\ \frac{u_{\widetilde{\sigma a}}({\widetilde{\sigma a}}_{c1}-{\widetilde{\sigma a}}_x)+{\widetilde{\sigma a}}_x-{\widetilde{\sigma a}}_{b1}}{{\widetilde{\sigma a}}_{c1}-{\widetilde{\sigma a}}_{b1}} for {\widetilde{\sigma a}}_{b1}\le {\widetilde{\sigma a}}_x\le {\widetilde{\sigma a}}_{c1}\\ 0 for others values out of range \left[{\widetilde{\sigma a}}_{c1};{\widetilde{\sigma a}}_{a1}\right]\end{array}$$

(5)

The falsity membership, which is the membership function for the financial assets risk with low degree of realization $\lambda {\widetilde{\sigma a}}_{(x)},$ is the following:

$$\lambda {\widetilde{\sigma a}}_{(x)}=\{\begin{array}{c}\frac{y_{\widetilde{{\sigma }_a}}({\widetilde{\sigma a}}_x-{\widetilde{\sigma a}}_{a1})+{\widetilde{\sigma a}}_{b1}-{\widetilde{\sigma a}}_x}{{\widetilde{\sigma a}}_{b1}-{\widetilde{\sigma a}}_{a1}} for {\widetilde{\sigma a}}_{a1}\le {\widetilde{\sigma a}}_x\le {\widetilde{\sigma a}}_{b1}\\ {\lambda }_{\widetilde{{\sigma }_a}} for {\widetilde{\sigma a}}_x={\widetilde{\sigma a}}_{b1}\\ \frac{y_{\widetilde{\sigma a}}({\widetilde{\sigma a}}_{c1}-{\widetilde{\sigma a}}_x)+{\widetilde{\sigma a}}_x-{\widetilde{\sigma a}}_{b1}}{{\widetilde{\sigma a}}_{c1}-{\widetilde{\sigma a}}_{b1}} for {\widetilde{\sigma a}}_{b1}\le {\widetilde{\sigma a}}_x\le {\widetilde{\sigma a}}_{c1}\\ 0 for \left[{\widetilde{\sigma a}}_{c1};{\widetilde{\sigma a}}_{a1}\right]\end{array}$$

(6)

The two neutrosophic numbers that characterize the return and the risk of a financial asset are as follows:

$${\widetilde{Ra}}_i=\langle ({\widetilde{Ra}}_{ai},{\widetilde{Ra}}_{bi},{\widetilde{Ra}}_{ci});w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle ,\mathrm{for}i=\overline{1,n}$$

(7)

$${\widetilde{\sigma a}}_i=\langle ({\widetilde{\sigma a}}_{ai},{\widetilde{\sigma a}}_{bi},{\widetilde{\sigma a}}_{ci});w\widetilde{\sigma a},u\widetilde{\sigma a},y\widetilde{\sigma a}\rangle ,\mathrm{for}i=\overline{1,n}$$

(8)

Definition 3.

Two specific neutrosophic numbers are considered for the two financial assets that define the financial asset return:

$${\widetilde{Ra}}_1=\langle ({\widetilde{Ra}}_{a1},{\widetilde{Ra}}_{b1},{\widetilde{Ra}}_{c1});w\widetilde{R{a}_1},u{\widetilde{Ra}}_1,y{\widetilde{Ra}}_1\rangle$$

for the first financial asset$(A_1)$;

$${\widetilde{Ra}}_2=\langle ({\widetilde{Ra}}_{a2},{\widetilde{Ra}}_{b2},{\widetilde{Ra}}_{c2});w{\widetilde{Ra}}_2,u{\widetilde{Ra}}_2,y{\widetilde{Ra}}_2\rangle$$

for the second financial asset$(A_2)$and the parameter$\gamma \ne 0$,$\gamma \in R$.

The following arithmetical operations are valid:

• Addition:

  $$\begin{gathered} {\widetilde{Ra}}_1+{\widetilde{Ra}}_2=\langle ({\widetilde{Ra}}_{a1}+{\widetilde{Ra}}_{a2},{\widetilde{Ra}}_{b1}+{\widetilde{Ra}}_{b2},{\widetilde{Ra}}_{c1} \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+{\widetilde{Ra}}_{c2})w\widetilde{R{a}_1}\wedge w{\widetilde{Ra}}_2,u{\widetilde{Ra}}_1\vee u{\widetilde{Ra}}_2,y{\widetilde{Ra}}_1\vee y{\widetilde{Ra}}_2\rangle \end{gathered}$$

  (9)
• Subtraction:

  $$\begin{gathered} {\widetilde{Ra}}_1-{\widetilde{Ra}}_2=\langle ({\widetilde{Ra}}_{a1}-{\widetilde{Ra}}_{a2},{\widetilde{Ra}}_{b1}-{\widetilde{Ra}}_{b2},{\widetilde{Ra}}_{c1} \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-{\widetilde{Ra}}_{c2})w\widetilde{R{a}_1}\wedge w{\widetilde{Ra}}_2,u{\widetilde{Ra}}_1\vee u{\widetilde{Ra}}_2,y{\widetilde{Ra}}_1\vee y{\widetilde{Ra}}_2\rangle \end{gathered}$$

  (10)
• Multiplication:
  • for ${\widetilde{Ra}}_{c1}>0$ and ${\widetilde{Ra}}_{c2}>0$;

    $$\begin{array}{c}{\widetilde{Ra}}_1\times {\widetilde{Ra}}_2\hfill \\ =\langle ({\widetilde{Ra}}_{a1}X{\widetilde{Ra}}_{a2},{\widetilde{Ra}}_{b1}X{\widetilde{Ra}}_{b2},{\widetilde{Ra}}_{c1}X{\widetilde{Ra}}_{c2})w\widetilde{R{a}_1}\wedge w{\widetilde{Ra}}_2,u{\widetilde{Ra}}_1\vee u{\widetilde{Ra}}_2,y{\widetilde{Ra}}_1\vee y{\widetilde{Ra}}_2\rangle \hfill \end{array}$$

    (11)
  • for ${\widetilde{Ra}}_{c1}<0$ and ${\widetilde{Ra}}_{c2}>0$;

    $$\begin{array}{c}{\widetilde{Ra}}_1\times {\widetilde{Ra}}_2\hfill \\ =\langle ({\widetilde{Ra}}_{a1}X{\widetilde{Ra}}_{c2},{\widetilde{Ra}}_{b1}X{\widetilde{Ra}}_{b2},{\widetilde{Ra}}_{c1}X{\widetilde{Ra}}_{a2});w\widetilde{R{a}_1}\wedge w{\widetilde{Ra}}_2,u{\widetilde{Ra}}_1\vee u{\widetilde{Ra}}_2,y{\widetilde{Ra}}_1\vee y{\widetilde{Ra}}_2\rangle \hfill \end{array}$$

    (12)
  • for ${\widetilde{Ra}}_{c1}<0$ and ${\widetilde{Ra}}_{c2}<0$;

    $$\begin{gathered} {\widetilde{Ra}}_1\times {\widetilde{Ra}}_2=\langle ({\widetilde{Ra}}_{c1}\times {\widetilde{Ra}}_{c2},{\widetilde{Ra}}_{b1}\times {\widetilde{Ra}}_{b2},{\widetilde{Ra}}_{a1} \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\times {\widetilde{Ra}}_{a2});w\widetilde{R{a}_1}\wedge w{\widetilde{Ra}}_2,u{\widetilde{Ra}}_1\vee u{\widetilde{Ra}}_2,y{\widetilde{Ra}}_1\vee y{\widetilde{Ra}}_2\rangle \end{gathered}$$

    (13)
• Division:
  • for ${\widetilde{Ra}}_{c1}>0$ and ${\widetilde{Ra}}_{c2}>0$;

    $$\begin{gathered} {\widetilde{Ra}}_1/{\widetilde{Ra}}_2=\langle ({\widetilde{Ra}}_{a1}/{\widetilde{Ra}}_{c2},{\widetilde{Ra}}_{b1}/{\widetilde{Ra}}_{b2},{\widetilde{Ra}}_{c1} \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}/{\widetilde{Ra}}_{a2});w\widetilde{R{a}_1}\wedge w{\widetilde{Ra}}_2,u{\widetilde{Ra}}_1\vee u{\widetilde{Ra}}_2,y{\widetilde{Ra}}_1\vee y{\widetilde{Ra}}_2\rangle \end{gathered}$$

    (14)
  • for ${\widetilde{Ra}}_{c1}<0$ and ${\widetilde{Ra}}_{c2}>0$;

    $$\begin{gathered} {\widetilde{Ra}}_1/{\widetilde{Ra}}_2=\langle ({\widetilde{Ra}}_{c1}/{\widetilde{Ra}}_{c2},{\widetilde{Ra}}_{b1}/{\widetilde{Ra}}_{b2},{\widetilde{Ra}}_{a1} \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}/{\widetilde{Ra}}_{a2});w\widetilde{R{a}_1}\wedge w{\widetilde{Ra}}_2,u{\widetilde{Ra}}_1\vee u{\widetilde{Ra}}_2,y{\widetilde{Ra}}_1\vee y{\widetilde{Ra}}_2\rangle \end{gathered}$$

    (15)
  • for ${\widetilde{Ra}}_{c1}<0$ and ${\widetilde{Ra}}_{c2}<0$;

    $$\begin{gathered} {\widetilde{Ra}}_1/{\widetilde{Ra}}_2=\langle ({\widetilde{Ra}}_{c1}/{\widetilde{Ra}}_{a2},{\widetilde{Ra}}_{b1}/{\widetilde{Ra}}_{b2},{\widetilde{Ra}}_{a1} \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}/{\widetilde{Ra}}_{c2});w\widetilde{R{a}_1}\wedge w{\widetilde{Ra}}_2,u{\widetilde{Ra}}_1\vee u{\widetilde{Ra}}_2,y{\widetilde{Ra}}_1\vee y{\widetilde{Ra}}_2\rangle \end{gathered}$$

    (16)
• Scalar multiplication:
  • for $\gamma >0$;

    $$\gamma \times {\widetilde{Ra}}_1=\langle (\gamma \times {\widetilde{Ra}}_{a1},\gamma \times {\widetilde{Ra}}_{b1},\gamma \times {\widetilde{Ra}}_{c1});w\widetilde{R{a}_1},u{\widetilde{Ra}}_1,y{\widetilde{Ra}}_1\rangle$$

    (17)
  • for $\gamma <0$;

    $$\gamma \times {\widetilde{Ra}}_1=\langle (\gamma \times {\widetilde{Ra}}_{c1},\gamma \times {\widetilde{Ra}}_{b1},\gamma \times {\widetilde{Ra}}_{a1});w\widetilde{R{a}_1},u{\widetilde{Ra}}_1,y{\widetilde{Ra}}_1\rangle$$

    (18)
• The inverse of a neutrosophic number:

  $${\widetilde{Ra}}_1{}^{-1}=\langle (1/{\widetilde{Ra}}_{c1},1/{\widetilde{Ra}}_{b1},1/{\widetilde{Ra}}_{a1});w\widetilde{R{a}_1},u{\widetilde{Ra}}_1,y{\widetilde{Ra}}_1\rangle$$

  (19)

It is important to notice that the arithmetic operations with the neutrosophic numbers defined for the financial asset return ${\widetilde{Ra}}_i=\langle ({\widetilde{Ra}}_{ai},{\widetilde{Ra}}_{bi},{\widetilde{Ra}}_{ci});w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle$ are the same as the specific arithmetic operations for the financial asset risk: ${\widetilde{\sigma a}}_i=\langle ({\widetilde{\sigma a}}_{ai},{\widetilde{\sigma a}}_{bi},{\widetilde{\sigma a}}_{ci});w\widetilde{\sigma a},u\widetilde{\sigma a},y\widetilde{\sigma a}\rangle$ for any $i=\overline{1,n}$.

Definition 4.

Let the neutrosophic number defined for the financial asset return be of the following form:

$${\widetilde{Ra}}_i=\langle ({\widetilde{Ra}}_{ai},{\widetilde{Ra}}_{bi},{\widetilde{Ra}}_{ci});w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle$$

for any$i=\overline{1,n}$. To assure the comparability of the neutrosophic fuzzy numbers, a score function is introduced [4,5]:

$$S_{a1}=\frac{1}{8}\left[{\widetilde{Ra}}_{a1}+{\widetilde{Ra}}_{b1}+{\widetilde{Ra}}_{c1}\right]+(2+w\widetilde{R{a}_1}-u{\widetilde{Ra}}_1-y{\widetilde{Ra}}_1)$$

(20)

This is an accuracy function of the form:

$$A_{a1}=\frac{1}{8}\left[{\widetilde{Ra}}_{a1}+{\widetilde{Ra}}_{b1}+{\widetilde{Ra}}_{c1}\right]-(2+w\widetilde{R{a}_1}-u{\widetilde{Ra}}_1-y{\widetilde{Ra}}_1)$$

(21)

Definition 5.

There are two neutrosophic numbers that define the financial asset return:

$${\widetilde{Ra}}_1=\langle ({\widetilde{Ra}}_{a1},{\widetilde{Ra}}_{b1},{\widetilde{Ra}}_{c1});w\widetilde{R{a}_1},u{\widetilde{Ra}}_1,y{\widetilde{Ra}}_1\rangle$$

for the first asset$(A_1)$and

$${\widetilde{Ra}}_2=\langle ({\widetilde{Ra}}_{a2},{\widetilde{Ra}}_{b2},{\widetilde{Ra}}_{c2});w{\widetilde{Ra}}_2,u{\widetilde{Ra}}_2,y{\widetilde{Ra}}_2\rangle$$

for the second asset$(A_2)$. As such:

• If$S({\widetilde{Ra}}_1)<S({\widetilde{Ra}}_2),$then${\widetilde{Ra}}_1$, and it is noted that${\widetilde{Ra}}_1<{\widetilde{Ra}}_2$;
• If$S({\widetilde{Ra}}_1)>S({\widetilde{Ra}}_2),$then${\widetilde{Ra}}_1$is higher than${\widetilde{Ra}}_2$, and it is noted that${\widetilde{Ra}}_1>{\widetilde{Ra}}_2$;
• If$S({\widetilde{Ra}}_1)=S({\widetilde{Ra}}_2)$are distinguished two cases:
  • If$A({\widetilde{Ra}}_1)<A({\widetilde{Ra}}_2)$, then${\widetilde{Ra}}_1$is smaller than${\widetilde{Ra}}_2,$and it is noted that${\widetilde{Ra}}_1<{\widetilde{Ra}}_2$;
  • If$A({\widetilde{Ra}}_1)=A({\widetilde{Ra}}_2),$then the neutrosophic numbers are equal, and it is noted that${\widetilde{Ra}}_1={\widetilde{Ra}}_2;$

4. Modeling the Financial Assets Return Using the Neutrosophic Fuzzy Numbers

The financial assets return, as mentioned above, is the most relevant performance indicator, because it provides information on the earnings that investors can obtain over a limited period of time as a result of asset ownership. In literature, the model for determining the financial assets return is based on: The capital gain $\frac{P_1-P_0}{P_0} ,$ formed by the stock price differences at time ($t_1$) and ($t_0$), as well as on the return on invested capital, represented by the ratio between the dividend at time ($t_1$) and the price at time ($t_0$). $\frac{D_1}{P_0}$, illustrates a remuneration form for the invested capital. The market model that evaluates the financial asset return thus becomes $Ra=\frac{P_1-P_0+D_1}{P_0}$, where the gains are the exchange rate differences and the dividend. For each financial asset ($A_i$), there are different return values over a time horizon [0, t] at different time moments of the form:

$$Ra:\left(\begin{array}{ccccccccc}{t}_0& t_1& t_2& t_3& \dots & t_{k-1}& t_k& \dots & t_n\\ R{a}_0& R{a}_1& R{a}_2& R{a}_3& \dots & R{a}_{k-1}& R{a}_k& \dots & R{a}_n\end{array}\right) t=\overline{1,n}$$

(22)

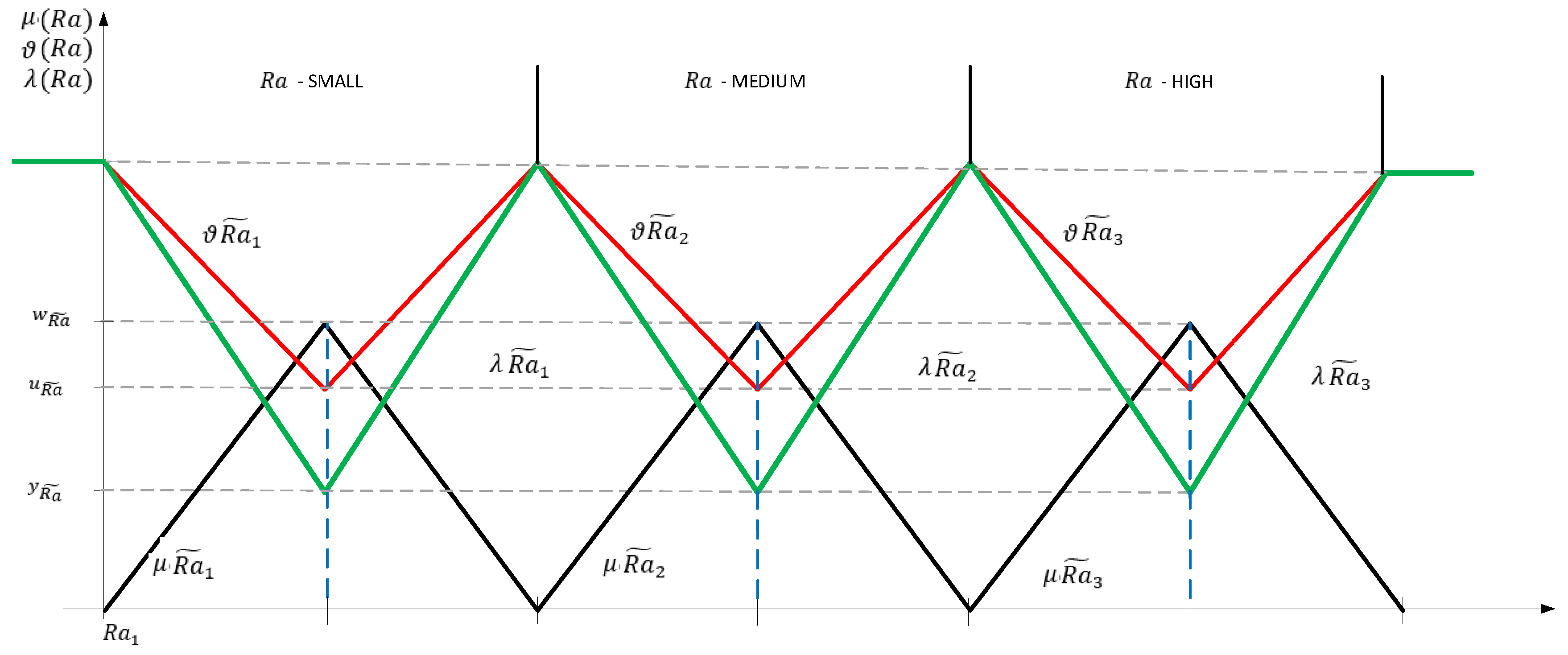
The formed data series is modeled using neutrosophic fuzzy numbers due to the many advantages they have: The possibility of stratification for the financial asset; clustering the return values according to linguistic criteria such as high, medium or small financial asset return; the possibility of selection the return category desired by the investor in order to maximize his profit; or analyzing the financial asset return by means of probability grades. The neutrosophic fuzzy numbers built for the financial asset return, on the above data series, are presented in Figure 3.

The financial assets return is thus characterized by three neutrosophic numbers:

$$\begin{gathered} {\widetilde{Ra}}_1=\langle ({\widetilde{Ra}}_{a1},{\widetilde{Ra}}_{b1},{\widetilde{Ra}}_{c1});w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle \mathrm{for}\widetilde{Ra}\in \left[{\widetilde{Ra}}_{a1},{\widetilde{Ra}}_{c1}\right] \\ {\widetilde{Ra}}_2=\langle ({\widetilde{Ra}}_{a2},{\widetilde{Ra}}_{b2},{\widetilde{Ra}}_{c2});w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle \mathrm{for}\widetilde{Ra}\in \left[{\widetilde{Ra}}_{a2},{\widetilde{Ra}}_{c2}\right] \\ {\widetilde{Ra}}_3=\langle ({\widetilde{Ra}}_{a3},{\widetilde{Ra}}_{b3},{\widetilde{Ra}}_{c3});w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle \mathrm{for}\widetilde{Ra}\in \left[{\widetilde{Ra}}_{a3},{\widetilde{Ra}}_{c3}\right] \end{gathered}$$

(23)

Definition 6.

The following conditions lead to a function called a weighting function f: [0,1] → R:

(a) 

It is monotone increasing ∀x, y ∈ R and x ≤ y results that f(x) ≤ f(y).

(b) 

Checks the normality condition:${{\displaystyle \int }}_0^{1}f(\alpha )d\alpha =1$

The weighting function is used in the calculation of the neutrosophic fuzzy numbers main indicators—the arithmetic mean and the squared deviation from the mean and the covariance. The most frequently used weighting function is $f(\alpha )=2\alpha ,$ which meets the conditions imposed above, namely:

(a)

It is monotone increasing $\forall {\alpha }_1,{\alpha }_2\in R$ with ${\alpha }_1\le {\alpha }_2$ results that $f({\alpha }_1)\le f({\alpha }_2)$. From this condition, it follows that $2{\alpha }_1\le 2{\alpha }_2,$ and, as such, the ${\alpha }_1\le {\alpha }_2$ is a condition fulfilled.

(b)

Checks the normality ${{\displaystyle \int }}_0^{1}f(\alpha )d\alpha ={{\displaystyle \int }}_0^{1}2\alpha d\alpha =2\frac{{\alpha }^2}{2}{│}_0^1=1$.

The required conditions are fulfilled, and, thus, the function f(α) = 2α is a weighting function for calculating the specific indicators of the triangular neutrosophic fuzzy numbers. The weighting function f(α) = 2α is part of a weighting class of the form: $f(\alpha )=(n+1){\alpha }^n$ with $n\in N$. This class of functions is used to determine the main statistical indicators of fuzzy numbers.

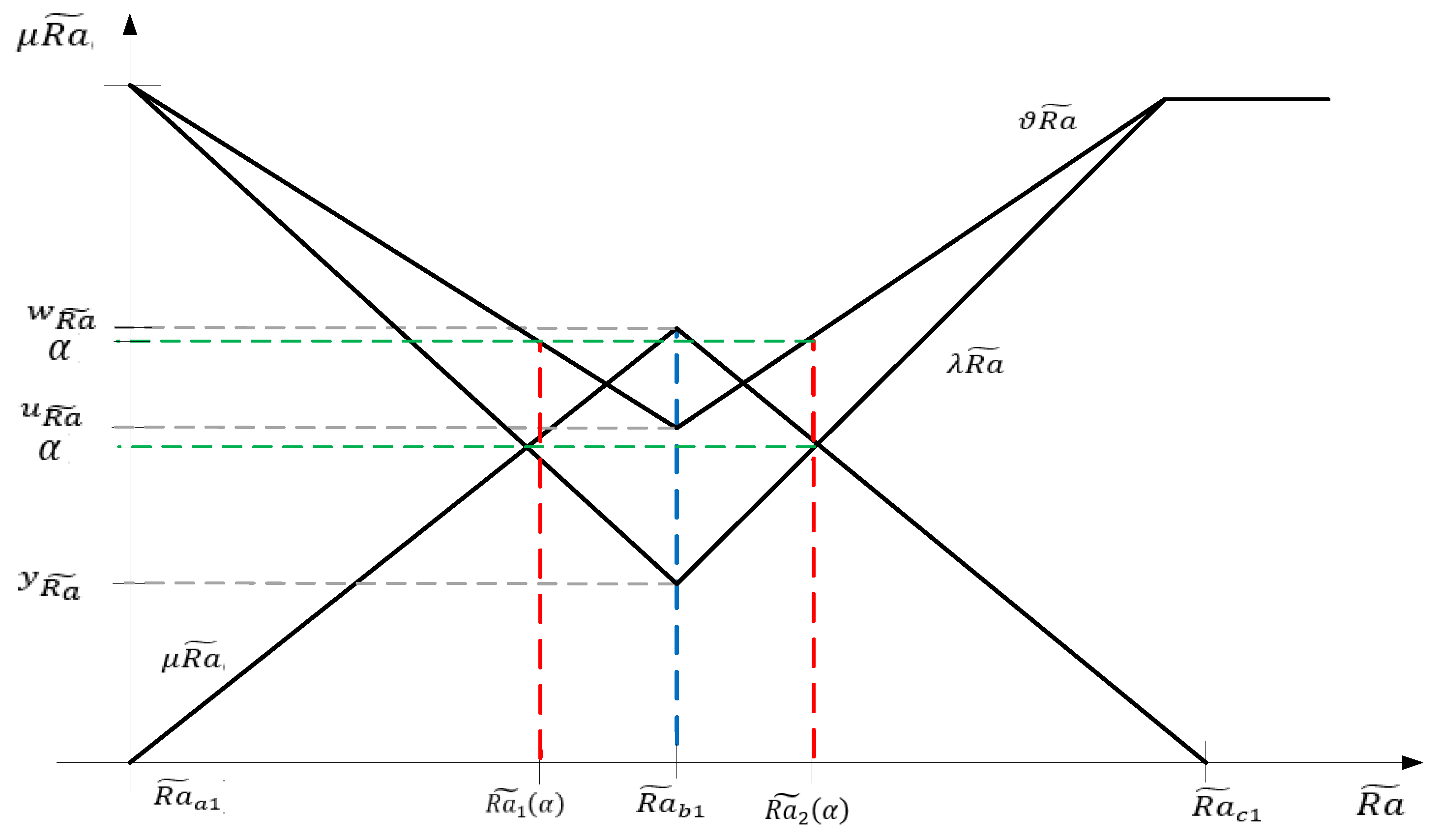
Definition 7.

This is considered the triangular neutrosophic fuzzy number that defines the financial asset return of the form:

$${\widetilde{Ra}}_i=\langle ({\widetilde{Ra}}_{ai},{\widetilde{Ra}}_{bi},{\widetilde{Ra}}_{ci});w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle ,\mathrm{for}\mathrm{every}i=\overline{1,n}.$$

It is considered that the set${\left[\widetilde{R_a}\right]}^{\alpha }=\left[\widetilde{R{a}_1}(\alpha );\widetilde{R{a}_2}(\alpha )\right]$for every$\alpha \in R$is the level set of the triangular neutrosophic fuzzy numbers, where:

$$\widetilde{R{a}_1}(\alpha )=\langle ({\widetilde{Ra}}_{b1}-{\widetilde{Ra}}_{a1})\alpha +{\widetilde{Ra}}_{a1};w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle$$

and$\widetilde{R{a}_2}(\alpha )=\langle {\widetilde{Ra}}_{c1}-({\widetilde{Ra}}_{c1}-{\widetilde{Ra}}_{b1})\alpha ;w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle$. See Figure 4.

Definition 8.

The medium value of a neutrosophic fuzzy number,${\widetilde{Ra}}_i=\langle ({\widetilde{Ra}}_{ai},{\widetilde{Ra}}_{bi},{\widetilde{Ra}}_{ci});w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle$, is given by:

$$E_f({\widetilde{Ra}}_i)=\frac{1}{2}{{\displaystyle \int }}_0^1\langle (\widetilde{R{a}_1}(\alpha )+\widetilde{R{a}_2}(\alpha ));w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle f(\alpha )d\alpha$$

(24)

When the weighting function is$f(\alpha )=2\alpha$, the medium value of the neutrosophic fuzzy number will be:$E_f({\widetilde{Ra}}_i)={{\displaystyle \int }}_0^1\langle (\widetilde{R{a}_1}(\alpha )+\widetilde{R{a}_2}(\alpha ));w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle \alpha d\alpha$.

Proposition 1.

The medium value of a triangular neutrosophic fuzzy number of the form,${\widetilde{Ra}}_i=\langle ({\widetilde{Ra}}_{ai},{\widetilde{Ra}}_{bi},{\widetilde{Ra}}_{ci});w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle ,$is given by the relationship:

$$E_f({\widetilde{Ra}}_i)=\langle (\frac{1}{6}({\widetilde{Ra}}_{a1}+{\widetilde{Ra}}_{c1})+\frac{2}{3}{\widetilde{Ra}}_{b1});w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle$$

(25)

Demonstration 1.

According to Definition 8, the medium value of the neutrosophic fuzzy number is calculated with the relation:

$$E_f({\widetilde{Ra}}_i)=\frac{1}{2}{{\displaystyle \int }}_0^1\langle (\widetilde{R{a}_1}(\alpha )+\widetilde{R{a}_2}(\alpha ));w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle f(\alpha )d\alpha$$

Which is computed as:

$$\begin{array}{c}\langle (\widetilde{R{a}_1}(\alpha )+\widetilde{R{a}_2}(\alpha ));w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle \hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} =\langle ({\widetilde{Ra}}_{b1}-{\widetilde{Ra}}_{a1})\alpha +{\widetilde{Ra}}_{a1}+{\widetilde{Ra}}_{c1}-({\widetilde{Ra}}_{c1}-{\widetilde{Ra}}_{b1})\alpha ;w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle \hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} =\langle ({\widetilde{Ra}}_{b1}\alpha -{\widetilde{Ra}}_{a1}\alpha +{\widetilde{Ra}}_{a1}+{\widetilde{Ra}}_{c1}-{\widetilde{Ra}}_{c1}\alpha +{\widetilde{Ra}}_{b1}\alpha );w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle \hfill \end{array}$$

$$\begin{gathered} \langle (\widetilde{R{a}_1}(\alpha )+\widetilde{R{a}_2}(\alpha ));w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=\langle ({\widetilde{Ra}}_{a1}(1-\alpha )+2{\widetilde{Ra}}_{b1}\alpha +{\widetilde{Ra}}_{c1}(1-\alpha ));w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle \end{gathered}$$

The formula above can be rewritten as follows:

$$\begin{gathered} \langle (\widetilde{R{a}_1}(\alpha )+\widetilde{R{a}_2}(\alpha ));w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=\langle ((1-\alpha )({\widetilde{Ra}}_{a1}+{\widetilde{Ra}}_{c1})+2{\widetilde{Ra}}_{b1}\alpha );w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle \end{gathered}$$

The medium value of a triangular neutrosophic fuzzy number becomes:

$$\begin{gathered} E_f({\widetilde{Ra}}_i)=\frac{1}{2}{{\displaystyle \int }}_0^1\langle (\widetilde{R{a}_1}(\alpha )+\widetilde{R{a}_2}(\alpha ));w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle f(\alpha )d\alpha \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=\frac{1}{2}{{\displaystyle \int }}_0^1[\langle ((1-\alpha )({\widetilde{Ra}}_{a1}+{\widetilde{Ra}}_{c1})+2{\widetilde{Ra}}_{b1}\alpha );w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle ]2\alpha d\alpha \end{gathered}$$

$$\begin{gathered} \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{E}_f({\widetilde{Ra}}_i)=\langle ({\widetilde{Ra}}_{a1}+{\widetilde{Ra}}_{c1});w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle {{\displaystyle \int }}_0^1(\alpha -{\alpha }^2)d\alpha \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+2\langle {\widetilde{Ra}}_{b1};w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle {{\displaystyle \int }}_0^1{\alpha }^{2}d\alpha \end{gathered}$$

$$\begin{gathered} =\langle ({\widetilde{Ra}}_{a1}+{\widetilde{Ra}}_{c1});w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle \frac{{\alpha }^2}{2}{│}_0^1-\langle ({\widetilde{Ra}}_{a1}+{\widetilde{Ra}}_{c1});w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle \frac{{\alpha }^3}{3}{│}_0^1+ \\ 2\langle {\widetilde{Ra}}_{b1};w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle \frac{{\alpha }^3}{3}{│}_0^1; \end{gathered}$$

$$E_f({\widetilde{Ra}}_i)=\frac{1}{6}\langle ({\widetilde{Ra}}_{a1}+{\widetilde{Ra}}_{c1});w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle +\frac{2}{3}\langle {\widetilde{Ra}}_{b1};w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle ;$$

$$E_f({\widetilde{Ra}}_i)=\langle (\frac{1}{6}({\widetilde{Ra}}_{a1}+{\widetilde{Ra}}_{c1})+\frac{2}{3}{\widetilde{Ra}}_{b1});w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle$$

Example 1.

There are three financial assets$(A_1,A_2,A_3),$to which three specific triangular neutrosophic fuzzy numbers are attached for the financial assets return:

$${\widetilde{Ra}}_1=\langle (0.2 0.3 0.5);0.5, 0.2, 0.3\rangle \mathrm{for}\widetilde{Ra}\in \left[0,2;0,5\right];$$

$${\widetilde{Ra}}_2=\langle (0.1 0.2 0.3);0.6, 0.3, 0.2\rangle \mathrm{for}\widetilde{Ra}\in \left[0,1;0,3\right];$$

$${\widetilde{Ra}}_2=\langle (0.3 0.4 0.6);0.4, 0.3, 0.3\rangle \mathrm{for}\widetilde{Ra}\in \left[0,3;0,6\right];$$

In order to determine the average return on financial assets resulting from the model using the neutrosophic fuzzy numbers, was applied the result obtained from Proposition 1, which stipulates that:

$$E_f({\widetilde{Ra}}_i)=\langle (\frac{1}{6}({\widetilde{Ra}}_{a1}+{\widetilde{Ra}}_{c1})+\frac{2}{3}{\widetilde{Ra}}_{b1});w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle$$

Thus, it is obtained:

$$E_f({\widetilde{Ra}}_1)=\langle (\frac{1}{6}(0.2+0.5)+\frac{2}{3}\times 0.3);0.5, 0.2, 0.3\rangle$$

$$E_f({\widetilde{Ra}}_1)=\langle (\frac{1}{6}0.7+\frac{2}{3}0.3);0.5, 0.2, 0.3\rangle$$

$$E_f({\widetilde{Ra}}_1)=\langle 0.316;0.5, 0.2, 0.3\rangle ;$$

$$E_f({\widetilde{Ra}}_2)=\langle (\frac{1}{6}(0.1+0.3)+\frac{2}{3}\times 0.2);0.6, 0.3, 0.2\rangle$$

$$E_f({\widetilde{Ra}}_2)=\langle (\frac{1}{6}0.4+\frac{2}{3}0.2);0.6, 0.3, 0.2\rangle$$

$$E_f({\widetilde{Ra}}_2)=\langle 0.199;0.5, 0.2, 0.3\rangle ;$$

$$E_f({\widetilde{Ra}}_3)=\langle (\frac{1}{6}(0.3+0.6)+\frac{2}{3}\times 0.4);0.4, 0.3, 0.3\rangle$$

$$E_f({\widetilde{Ra}}_3)=\langle (\frac{1}{6}0.9+\frac{2}{3}0.4);0.4, 0.3, 0.3\rangle$$

$$E_f({\widetilde{Ra}}_3)=\langle 0.416;0.4, 0.3, 0.3\rangle ;$$

In conclusion, it can be argued that the financial assets return modeled by neutrosophic fuzzy numbers ensures the determination of the average value of the asset’s return at the same time as establishing the degrees of truth, falsity, and indeterminacy in the process of obtaining the profitability expected by the investors.

5. Modelling the Financial Assets Risk Using the Neutrosophic Fuzzy Numbers

As mentioned above, the risk of financial assets is represented by the squared deviation from the mean (${\sigma }_a^2$) which means the return on financial assets deviation from the average recorded value. Thus, the financial risk will be higher when the deviation of the financial return from the average is higher. Contrary to this, the risk exposure will be low.

Definition 9.

The financial asset risk modeled by the neutrosophic fuzzy number${\widetilde{\sigma a}}_i=\langle ({\widetilde{\sigma a}}_{ai},{\widetilde{\sigma a}}_{bi},{\widetilde{\sigma a}}_{ci});w\widetilde{\sigma a},u\widetilde{\sigma a},y\widetilde{\sigma a}\rangle$is given by the neutrosophic fuzzy number variance, determined by the formula:

$$\begin{gathered} \widetilde{{\mathsf{\sigma }}_{\mathrm{f}}{\mathrm{a}}_{\mathrm{i}}}=\frac{1}{2}{{\displaystyle \int }}_0^1[\langle {({\widetilde{\mathrm{Ra}}}_1(\mathsf{\alpha })-{\mathrm{E}}_{\mathrm{f}}({\widetilde{\mathrm{Ra}}}_{\mathrm{i}}))}^2;\mathrm{w}\widetilde{\mathrm{Ra}},\mathrm{u}\widetilde{\mathrm{Ra}},\mathrm{y}\widetilde{\mathrm{Ra}}\rangle \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+{\langle ({\widetilde{\mathrm{Ra}}}_2(\mathsf{\alpha })-{\mathrm{E}}_{\mathrm{f}}({\widetilde{\mathrm{Ra}}}_{\mathrm{i}}))}^2;\mathrm{w}\widetilde{\mathrm{Ra}},\mathrm{u}\widetilde{\mathrm{Ra}},\mathrm{y}\widetilde{\mathrm{Ra}}\rangle ]\mathrm{f}(\mathsf{\alpha })\mathrm{d}\mathsf{\alpha } \end{gathered}$$

(26)

If the weighting function is$f(\alpha )=2\alpha ,$then the neutrosophic fuzzy number variance is of the form:

$$\begin{gathered} \widetilde{{\mathsf{\sigma }}_{\mathrm{f}}{\mathrm{a}}_{\mathrm{i}}}={{\displaystyle \int }}_0^1[\langle {\left({\widetilde{\mathrm{Ra}}}_1(\mathsf{\alpha })-{\mathrm{E}}_{\mathrm{f}}({\widetilde{\mathrm{Ra}}}_{\mathrm{i}})\right)}^2;\mathrm{w}\widetilde{\mathrm{Ra}},\mathrm{u}\widetilde{\mathrm{Ra}},\mathrm{y}\widetilde{\mathrm{Ra}}\rangle \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+{\langle \left({\widetilde{\mathrm{Ra}}}_2(\mathsf{\alpha })-{\mathrm{E}}_{\mathrm{f}}({\widetilde{\mathrm{Ra}}}_{\mathrm{i}})\right)}^2;\mathrm{w}\widetilde{\mathrm{Ra}},\mathrm{u}\widetilde{\mathrm{Ra}},\mathrm{y}\widetilde{\mathrm{Ra}}\rangle ]\mathsf{\alpha }\mathrm{d}\mathsf{\alpha } \end{gathered}$$

(27)

Proposition 2.

The financial asset variance modeled by the neutrosophic fuzzy number can be determined by the formula:

$$\begin{gathered} \widetilde{{\mathsf{\sigma }}_{\mathrm{f}}{\mathrm{a}}_{\mathrm{i}}}=\frac{1}{2}{{\displaystyle \int }}_0^1\langle \left({\widetilde{\mathrm{Ra}}}_1^2(\mathsf{\alpha })+{\widetilde{\mathrm{Ra}}}_2^2(\mathsf{\alpha })\right);\mathrm{w}\widetilde{\mathrm{Ra}},\mathrm{u}\widetilde{\mathrm{Ra}},\mathrm{y}\widetilde{\mathrm{Ra}}\rangle \mathrm{f}(\mathsf{\alpha })\mathrm{d}\mathsf{\alpha } \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-\frac{1}{2}\langle {\mathrm{E}}_{\mathrm{f}}^2({\widetilde{\mathrm{Ra}}}_{\mathrm{i}});\mathrm{w}\widetilde{\mathrm{Ra}},\mathrm{u}\widetilde{\mathrm{Ra}},\mathrm{y}\widetilde{\mathrm{Ra}}\rangle {{\displaystyle \int }}_0^1\mathrm{f}(\mathsf{\alpha })\mathrm{d}\mathsf{\alpha } \end{gathered}$$

(28)

Demonstration 2.

It is known that:

$$\begin{gathered} \widetilde{{\sigma }_f{a}_i}=\frac{1}{2}{{\displaystyle \int }}_0^1[\langle {({\widetilde{\mathrm{Ra}}}_1(\mathsf{\alpha })-{\mathrm{E}}_{\mathrm{f}}({\widetilde{\mathrm{Ra}}}_{\mathrm{i}}))}^2;\mathrm{w}\widetilde{\mathrm{Ra}},\mathrm{u}\widetilde{\mathrm{Ra}},\mathrm{y}\widetilde{\mathrm{Ra}}\rangle \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\frac{1}{2}{\langle \left({\widetilde{\mathrm{Ra}}}_2(\mathsf{\alpha })-{\mathrm{E}}_{\mathrm{f}}({\widetilde{\mathrm{Ra}}}_{\mathrm{i}})\right)}^2;\mathrm{w}\widetilde{\mathrm{Ra}},\mathrm{u}\widetilde{\mathrm{Ra}},\mathrm{y}\widetilde{\mathrm{Ra}}\rangle ]\mathrm{f}(\mathsf{\alpha })\mathrm{d}\alpha \end{gathered}$$

From the relation illustrated above is obtained that:

$$\begin{gathered} \widetilde{{\sigma }_f{a}_i}=\frac{1}{2}{{\displaystyle \int }}_0^1[\langle ({\widetilde{Ra}}_1^2(\alpha )-2{\widetilde{Ra}}_1(\alpha )E_f({\widetilde{Ra}}_i)+E_f^2({\widetilde{Ra}}_i));w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\langle \left({\widetilde{Ra}}_2^2(\alpha )-2{\widetilde{Ra}}_2(\alpha )E_f({\widetilde{Ra}}_i)+E_f^2({\widetilde{Ra}}_i)\right);w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle ]f(\alpha )d\alpha \end{gathered}$$

$$\begin{gathered} \widetilde{{\sigma }_f{a}_i}=\frac{1}{2}{{\displaystyle \int }}_0^1\langle \left({\widetilde{Ra}}_1^2(\alpha )+{\widetilde{Ra}}_2^2(\alpha )\right);w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle f(\alpha )d\alpha \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-2E_f({\widetilde{Ra}}_i){{\displaystyle \int }}_0^1\langle \left(\frac{{\widetilde{Ra}}_1(\alpha )+{\widetilde{Ra}}_2(\alpha )}{2}\right);w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle f(\alpha )d\alpha \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+2\frac{1}{2}\langle E_f^2({\widetilde{Ra}}_i);w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle {{\displaystyle \int }}_0^{1}f(\alpha )d\alpha \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=\frac{1}{2}{{\displaystyle \int }}_0^1\langle ({\widetilde{Ra}}_1^2(\alpha )+{\widetilde{Ra}}_2^2(\alpha ));w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle f(\alpha )d\alpha \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-2\langle \left(E_f({\widetilde{Ra}}_i)E_f({\widetilde{Ra}}_i)\right);w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle {{\displaystyle \int }}_0^{1}f(\alpha )d\alpha \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+2\frac{1}{2}\langle \left(E_f^2({\widetilde{Ra}}_i)\right);w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle {{\displaystyle \int }}_0^{1}f(\alpha )d\alpha \end{gathered}$$

$$\begin{gathered} \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\widetilde{{\sigma }_f{a}_i}=\frac{1}{2}{{\displaystyle \int }}_0^1\langle \left({\widetilde{Ra}}_1^2(\alpha )+{\widetilde{Ra}}_2^2(\alpha )\right);w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle f(\alpha )d\alpha - \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}2\langle \left(E_f^2({\widetilde{Ra}}_i)\right);w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle {{\displaystyle \int }}_0^{1}f(\alpha )d\alpha +\langle \left(E_f^2({\widetilde{Ra}}_i)\right);w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle {{\displaystyle \int }}_0^{1}f(\alpha )d\alpha ; \end{gathered}$$

$$\begin{gathered} \widetilde{{\sigma }_f{a}_i}=\frac{1}{2}{{\displaystyle \int }}_0^1\langle \left({\widetilde{Ra}}_1^2(\alpha )+{\widetilde{Ra}}_2^2(\alpha )\right);w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle f(\alpha )d\alpha \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-\frac{1}{2}\langle (E_f^2({\widetilde{Ra}}_i));w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle {{\displaystyle \int }}_0^{1}f(\alpha )d\alpha \end{gathered}$$

Proposition 3.

The neutrosophic fuzzy number variance of the form${\widetilde{\sigma a}}_i=\langle ({\widetilde{\sigma a}}_{ai},{\widetilde{\sigma a}}_{bi},{\widetilde{\sigma a}}_{ci});w\widetilde{\sigma a},u\widetilde{\sigma a},y\widetilde{\sigma a}\rangle$is given by:

$$\begin{gathered} \widetilde{{\sigma }_f{a}_i}=\langle \frac{1}{4}\left[{({\widetilde{Ra}}_{b1}-{\widetilde{Ra}}_{a1})}^2+{({\widetilde{Ra}}_{c1}-{\widetilde{Ra}}_{b1})}^2\right];w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\frac{2}{3}\langle \left[{\widetilde{Ra}}_{a1}({\widetilde{Ra}}_{b1}-{\widetilde{Ra}}_{a1})-{\widetilde{Ra}}_{c1}({\widetilde{Ra}}_{c1}-{\widetilde{Ra}}_{b1})\right];w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle \\ \hspace{1em}\hspace{1em}+\langle \frac{1}{2}({\widetilde{Ra}}_{a1}^2+{\widetilde{Ra}}_{c1}^2);w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle \\ -\langle \frac{1}{2}{E}_f^2({\widetilde{Ra}}_i);w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle \end{gathered}$$

(29)

Demonstration 3.

From Proposition Number 2, it is known the computing relationship for the neutrosophic fuzzy number variance leads to:

$$\begin{gathered} \widetilde{{\sigma }_f{a}_i}=\frac{1}{2}{{\displaystyle \int }}_0^1\langle \left({\widetilde{Ra}}_1^2(\alpha )+{\widetilde{Ra}}_2^2(\alpha )\right);w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle f(\alpha )d\alpha \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-\frac{1}{2}\langle E_f^2({\widetilde{Ra}}_i);w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle {{\displaystyle \int }}_0^{1}f(\alpha )d\alpha \end{gathered}$$

From Definition 7, it is also known the fact that the triangular fuzzy number level sets are of the form:

$$\widetilde{R{a}_1}(\alpha )=\langle ({\widetilde{Ra}}_{b1}-{\widetilde{Ra}}_{a1})\alpha +{\widetilde{Ra}}_{a1};w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle$$

$$\widetilde{R{a}_2}(\alpha )=\langle {\widetilde{Ra}}_{c1}-({\widetilde{Ra}}_{c1}-{\widetilde{Ra}}_{b1})\alpha ;w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle$$

After computing, the following expression is obtained:

$$\begin{gathered} \langle \left({\widetilde{\mathrm{Ra}}}_1^2(\mathsf{\alpha })+{\widetilde{\mathrm{Ra}}}_2^2(\mathsf{\alpha })\right);\mathrm{w}\widetilde{\mathrm{Ra}},\mathrm{u}\widetilde{\mathrm{Ra}},\mathrm{y}\widetilde{\mathrm{Ra}}\rangle \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}={\left[({\widetilde{\mathrm{Ra}}}_{\mathrm{b}1}-{\widetilde{\mathrm{Ra}}}_{\mathrm{a}1})\mathsf{\alpha }+{\widetilde{\mathrm{Ra}}}_{\mathrm{a}1};\mathrm{w}\widetilde{\mathrm{Ra}},\mathrm{u}\widetilde{\mathrm{Ra}},\mathrm{y}\widetilde{\mathrm{Ra}}\right]}^2 \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+{\left[{\widetilde{\mathrm{Ra}}}_{\mathrm{c}1}-({\widetilde{\mathrm{Ra}}}_{\mathrm{c}1}-{\widetilde{\mathrm{Ra}}}_{\mathrm{b}1})\mathsf{\alpha };\mathrm{w}\widetilde{\mathrm{Ra}},\mathrm{u}\widetilde{\mathrm{Ra}},\mathrm{y}\widetilde{\mathrm{Ra}}\right]}^2 \end{gathered}$$

$$\begin{gathered} \langle \left({\widetilde{\mathrm{Ra}}}_1^2(\mathsf{\alpha })+{\widetilde{\mathrm{Ra}}}_2^2(\mathsf{\alpha })\right);\mathrm{w}\widetilde{\mathrm{Ra}},\mathrm{u}\widetilde{\mathrm{Ra}},\mathrm{y}\widetilde{\mathrm{Ra}}\rangle = \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}={\langle ({\widetilde{\mathrm{Ra}}}_{\mathrm{b}1}-{\widetilde{\mathrm{Ra}}}_{\mathrm{a}1})}^2{\mathsf{\alpha }}^2+{\widetilde{\mathrm{Ra}}}_{\mathrm{a}1}^2+2{\widetilde{\mathrm{Ra}}}_{\mathrm{a}1}({\widetilde{\mathrm{Ra}}}_{\mathrm{b}1}-{\widetilde{\mathrm{Ra}}}_{\mathrm{a}1})\mathsf{\alpha };\mathrm{w}\widetilde{\mathrm{Ra}},\mathrm{u}\widetilde{\mathrm{Ra}},\mathrm{y}\widetilde{\mathrm{Ra}}\rangle \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+{\langle ({\widetilde{\mathrm{Ra}}}_{\mathrm{c}1}-{\widetilde{\mathrm{Ra}}}_{\mathrm{b}1})}^2{\mathsf{\alpha }}^2+{\widetilde{\mathrm{Ra}}}_{\mathrm{c}1}^2-2{\widetilde{\mathrm{Ra}}}_{\mathrm{c}1}({\widetilde{\mathrm{Ra}}}_{\mathrm{c}1}-{\widetilde{\mathrm{Ra}}}_{\mathrm{b}1})\mathsf{\alpha };\mathrm{w}\widetilde{\mathrm{Ra}},\mathrm{u}\widetilde{\mathrm{Ra}},\mathrm{y}\widetilde{\mathrm{Ra}}\rangle \end{gathered}$$

$$\begin{gathered} \langle \left({\widetilde{\mathrm{Ra}}}_1^2(\mathsf{\alpha })+{\widetilde{\mathrm{Ra}}}_2^2(\mathsf{\alpha })\right);\mathrm{w}\widetilde{\mathrm{Ra}},\mathrm{u}\widetilde{\mathrm{Ra}},\mathrm{y}\widetilde{\mathrm{Ra}}= \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=\langle {\mathsf{\alpha }}^2\left[{({\widetilde{\mathrm{Ra}}}_{\mathrm{b}1}-{\widetilde{\mathrm{Ra}}}_{\mathrm{a}1})}^2+{({\widetilde{\mathrm{Ra}}}_{\mathrm{c}1}-{\widetilde{\mathrm{Ra}}}_{\mathrm{b}1})}^2\right] \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\mathsf{\alpha }\left[2{\widetilde{\mathrm{Ra}}}_{\mathrm{a}1}({\widetilde{\mathrm{Ra}}}_{\mathrm{b}1}-{\widetilde{\mathrm{Ra}}}_{\mathrm{a}1})-2{\widetilde{\mathrm{Ra}}}_{\mathrm{c}1}({\widetilde{\mathrm{Ra}}}_{\mathrm{c}1}-{\widetilde{\mathrm{Ra}}}_{\mathrm{b}1})\right] \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+{\widetilde{\mathrm{Ra}}}_{\mathrm{a}1}^2+{\widetilde{\mathrm{Ra}}}_{\mathrm{c}1}^2;\mathrm{w}\widetilde{\mathrm{Ra}},\mathrm{u}\widetilde{\mathrm{Ra}},\mathrm{y}\widetilde{\mathrm{Ra}}\rangle \end{gathered}$$

The above expression can be written as:

$$\begin{gathered} \langle \left({\widetilde{Ra}}_1^2(\alpha )+{\widetilde{Ra}}_2^2(\alpha )\right);w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=\langle {\alpha }^2\left[{({\widetilde{Ra}}_{b1}-{\widetilde{Ra}}_{a1})}^2+{({\widetilde{Ra}}_{c1}-{\widetilde{Ra}}_{b1})}^2\right] \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+2\alpha \left[{\widetilde{Ra}}_{a1}({\widetilde{Ra}}_{b1}-{\widetilde{Ra}}_{a1})-{\widetilde{Ra}}_{c1}({\widetilde{Ra}}_{c1}-{\widetilde{Ra}}_{b1})\right] \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+{\widetilde{Ra}}_{a1}^2+{\widetilde{Ra}}_{c1}^2;w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle \end{gathered}$$

By replacing the values for the level set in the variance expression, we get:

$$\begin{array}{c}\widetilde{{\sigma }_f{a}_i}=\frac{1}{2}{{\displaystyle \int }}_0^1\langle \left({\widetilde{Ra}}_1^2(\alpha )+{\widetilde{Ra}}_2^2(\alpha )\right);w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle f(\alpha )d\alpha \hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-\frac{1}{2}\langle E_f^2({\widetilde{Ra}}_i);w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle {{\displaystyle \int }}_0^{1}f(\alpha )d\alpha \hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=\frac{1}{2}{{\displaystyle \int }}_0^1\langle {\alpha }^2\left[{({\widetilde{Ra}}_{b1}-{\widetilde{Ra}}_{a1})}^2+{({\widetilde{Ra}}_{c1}-{\widetilde{Ra}}_{b1})}^2\right];w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle 2\alpha d\alpha \hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\frac{1}{2}{{\displaystyle \int }}_0^1\langle 2\alpha [{\widetilde{Ra}}_{a1}({\widetilde{Ra}}_{b1}-{\widetilde{Ra}}_{a1})-{\widetilde{Ra}}_{c1}({\widetilde{Ra}}_{c1}-{\widetilde{Ra}}_{b1})];w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle 2\alpha d\alpha \hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\frac{1}{2}{{\displaystyle \int }}_0^1\langle {\widetilde{Ra}}_{a1}^2+{\widetilde{Ra}}_{c1}^2;w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle 2\alpha d\alpha \hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-\frac{1}{2}\langle E_f^2({\widetilde{Ra}}_i);w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle {{\displaystyle \int }}_0^{1}2\alpha d\alpha \hfill \end{array}$$

$$\begin{gathered} \widetilde{{\sigma }_f{a}_i}=\langle {({\widetilde{Ra}}_{b1}-{\widetilde{Ra}}_{a1})}^2+{({\widetilde{Ra}}_{c1}-{\widetilde{Ra}}_{b1})}^2;w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle \frac{{\alpha }^4}{4}{│}_0^1 \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+2\langle \left[{\widetilde{Ra}}_{a1}({\widetilde{Ra}}_{b1}-{\widetilde{Ra}}_{a1})-{\widetilde{Ra}}_{c1}({\widetilde{Ra}}_{c1}-{\widetilde{Ra}}_{b1})\right];w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle \frac{{\alpha }^3}{3}{│}_0^1 \\ \hspace{1em}\hspace{1em}+\langle ({\widetilde{Ra}}_{a1}^2+{\widetilde{Ra}}_{c1}^2);w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle \frac{{\alpha }^2}{2}{│}_0^1 \\ -\langle E_f^2({\widetilde{Ra}}_i);w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle \frac{{\alpha }^2}{2}{│}_0^1 \end{gathered}$$

After making the calculations, we get:

$$\begin{gathered} \widetilde{{\mathsf{\sigma }}_{\mathrm{f}}{\mathrm{a}}_{\mathrm{i}}}=\langle \frac{1}{4}\left[{({\widetilde{\mathrm{Ra}}}_{\mathrm{b}1}-{\widetilde{\mathrm{Ra}}}_{\mathrm{a}1})}^2+{({\widetilde{\mathrm{Ra}}}_{\mathrm{c}1}-{\widetilde{\mathrm{Ra}}}_{\mathrm{b}1})}^2\right];\mathrm{w}\widetilde{\mathrm{Ra}},\mathrm{u}\widetilde{\mathrm{Ra}},\mathrm{y}\widetilde{\mathrm{Ra}}\rangle \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\langle \frac{2}{3}\left[{\widetilde{\mathrm{Ra}}}_{\mathrm{a}1}({\widetilde{\mathrm{Ra}}}_{\mathrm{b}1}-{\widetilde{\mathrm{Ra}}}_{\mathrm{a}1})-{\widetilde{\mathrm{Ra}}}_{\mathrm{c}1}({\widetilde{\mathrm{Ra}}}_{\mathrm{c}1}-{\widetilde{\mathrm{Ra}}}_{\mathrm{b}1})\right];\mathrm{w}\widetilde{\mathrm{Ra}},\mathrm{u}\widetilde{\mathrm{Ra}},\mathrm{y}\widetilde{\mathrm{Ra}}\rangle \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\langle \frac{1}{2}({\widetilde{\mathrm{Ra}}}_{\mathrm{a}1}^2+{\widetilde{\mathrm{Ra}}}_{\mathrm{c}1}^2);\mathrm{w}\widetilde{\mathrm{Ra}},\mathrm{u}\widetilde{\mathrm{Ra}},\mathrm{y}\widetilde{\mathrm{Ra}}\rangle -\langle \frac{1}{2}{\mathrm{E}}_{\mathrm{f}}^2({\widetilde{\mathrm{Ra}}}_{\mathrm{i}});\mathrm{w}\widetilde{\mathrm{Ra}},\mathrm{u}\widetilde{\mathrm{Ra}},\mathrm{y}\widetilde{\mathrm{Ra}}\rangle \end{gathered}$$

Example 2.

There are three financial assets ($A_1,A_2,A_3$) to which are attached three triangular neutrosophic fuzzy numbers for the financial assets return:

$${\widetilde{Ra}}_1=\langle (0.2 0.3 0.5);0.5, 0.2, 0.3\rangle \mathrm{for}\widetilde{Ra}\in \left[0.2;0.5\right]$$

$${\widetilde{Ra}}_2=\langle (0.1 0.2 0.3);0.6, 0.3, 0.2\rangle \mathrm{for}\widetilde{Ra}\in \left[0.1;0.3\right]$$

$${\widetilde{Ra}}_2=\langle (0.3 0.4 0.6);0.4, 0.3, 0.3\rangle \mathrm{for}\widetilde{Ra}\in \left[0.3;0.6\right]$$

These triangular neutrosophic fuzzy numbers are known as the neutrosophic numbers. Using the form computed in the previous example, we get:

$$E_f({\widetilde{Ra}}_1)=\langle 0.316;0.5, 0.2, 0.3\rangle$$

$$E_f({\widetilde{Ra}}_2)=\langle 0.199;0.5, 0.2, 0.3\rangle$$

$$E_f({\widetilde{Ra}}_3)=\langle 0.416;0.4, 0.3, 0.3\rangle$$

In order to determine the financial assets variance modeled by neutrosophic numbers, the following relation is used, according to Proposition 3:

$$\begin{gathered} \widetilde{{\mathsf{\sigma }}_{\mathrm{f}}{\mathrm{a}}_{\mathrm{i}}}=\langle \frac{1}{4}\left[{({\widetilde{\mathrm{Ra}}}_{\mathrm{b}1}-{\widetilde{\mathrm{Ra}}}_{\mathrm{a}1})}^2+{({\widetilde{\mathrm{Ra}}}_{\mathrm{c}1}-{\widetilde{\mathrm{Ra}}}_{\mathrm{b}1})}^2\right];\mathrm{w}\widetilde{\mathrm{Ra}},\mathrm{u}\widetilde{\mathrm{Ra}},\mathrm{y}\widetilde{\mathrm{Ra}}\rangle \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\langle \frac{2}{3}\left[{\widetilde{\mathrm{Ra}}}_{\mathrm{a}1}({\widetilde{\mathrm{Ra}}}_{\mathrm{b}1}-{\widetilde{\mathrm{Ra}}}_{\mathrm{a}1})-{\widetilde{\mathrm{Ra}}}_{\mathrm{c}1}({\widetilde{\mathrm{Ra}}}_{\mathrm{c}1}-{\widetilde{\mathrm{Ra}}}_{\mathrm{b}1})\right];\mathrm{w}\widetilde{\mathrm{Ra}},\mathrm{u}\widetilde{\mathrm{Ra}},\mathrm{y}\widetilde{\mathrm{Ra}}\rangle \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\langle \frac{1}{2}({\widetilde{\mathrm{Ra}}}_{\mathrm{a}1}^2+{\widetilde{\mathrm{Ra}}}_{\mathrm{c}1}^2);\mathrm{w}\widetilde{\mathrm{Ra}},\mathrm{u}\widetilde{\mathrm{Ra}},\mathrm{y}\widetilde{\mathrm{Ra}}\rangle -\langle \frac{1}{2}{\mathrm{E}}_{\mathrm{f}}^2({\widetilde{\mathrm{Ra}}}_{\mathrm{i}});\mathrm{w}\widetilde{\mathrm{Ra}},\mathrm{u}\widetilde{\mathrm{Ra}},\mathrm{y}\widetilde{\mathrm{Ra}}\rangle \end{gathered}$$

By replacing the data in the above expression, this is obtained:

$$\begin{gathered} \widetilde{{\mathsf{\sigma }}_{\mathrm{f}}}{\mathrm{a}}_1=\langle \frac{1}{4}\left[{(0.3-0.2)}^2+{(0.5-0.3)}^2\right];0.5,0.2,0.3\rangle \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\langle \frac{2}{3}(0.2(0.3-0.2)-0.5(0.5-0.2));0.5,0.2,0.3\rangle \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\langle \frac{1}{2}({0.2}^2+{0.5}^2);0.5,0.2,0.3\rangle -\langle \frac{1}{2}{(0.316)}^2;0.5,0.2,0.3\rangle \end{gathered}$$

$$\begin{gathered} \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\widetilde{{\mathsf{\sigma }}_{\mathrm{f}}}{\mathrm{a}}_1=\langle \frac{1}{4}(0.01+0.04);0.5,0.2,0.3\rangle +\langle \frac{2}{3}(0.02-0.15);0.5,0.2,0.3\rangle + \\ \langle \frac{1}{2}0.29;0.5,0.2,0.3\rangle -\langle \frac{1}{2}0,099;0.5,0.2,0.3\rangle ; \end{gathered}$$

$$\widetilde{{\mathsf{\sigma }}_{\mathrm{f}}}{\mathrm{a}}_1=\langle (0.0125-0.086+0,145-0.049;0.5,0.2,0.3)\rangle ;$$

$$\widetilde{{\mathsf{\sigma }}_{\mathrm{f}}}{\mathrm{a}}_1=\langle 0.0225;0.5,0.2,0.3\rangle$$

$$\begin{gathered} \widetilde{{\sigma }_f}{a}_2=\langle \frac{1}{4}\left[{(0.2-0.1)}^2+{(0.3-0.2)}^2\right];0.6, 0.3, 0.2\rangle \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\langle \frac{2}{3}(0.1(0.2-0.1)-0.3(0.3-0.1));0.6, 0.3, 0.2\rangle \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\langle \frac{1}{2}({0.1}^2+{0.3}^2);0.6, 0.3, 0.2\rangle -\langle \frac{1}{2}{(0,199)}^2;0.6, 0.3, 0.2\rangle \end{gathered}$$

$$\begin{array}{c}\widetilde{{\sigma }_f}{a}_2=\langle \frac{1}{4}(0.01+0.01);0.6, 0.3, 0.2\rangle +\langle \frac{2}{3}(0.01-0.03);0.6, 0.3, 0.2\rangle +\hfill \\ \langle \frac{1}{2}0.10;0.6, 0.3, 0.2\rangle -\langle \frac{1}{2}0,039;0.6, 0.3, 0.2\rangle ;\hfill \end{array}$$

$$\begin{array}{c}\widetilde{{\sigma }_f}{a}_2=\langle (0.005-0.013+0,05-0.0195;0.6, 0.3, 0.2)\rangle ;\hfill \end{array}$$

$$\widetilde{{\sigma }_f}{a}_2=\langle 0.0180;0.6, 0.3, 0.2\rangle$$

$$\begin{gathered} \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\widetilde{{\mathsf{\sigma }}_{\mathrm{f}}}{\mathrm{a}}_3=\langle \frac{1}{4}\left[{(0.4-0.3)}^2+{(0.6-0.4)}^2\right];0.4,0.3,0.3\rangle +\langle \frac{2}{3}(0.3(0.4-0.3)-0.6(0.6 \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-0.4));0.4,0.3,0.3\rangle +\langle \frac{1}{2}({0.3}^2+{0.6}^2);0.4,0.3,0.3\rangle -\langle \frac{1}{2}{(0,416)}^2;0.4,0.3,0.3\rangle ; \end{gathered}$$

$$\begin{gathered} \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\widetilde{{\mathsf{\sigma }}_{\mathrm{f}}}{\mathrm{a}}_3=\langle \frac{1}{4}(0.01+0.04);0.4,0.3,0.3\rangle +\langle \frac{2}{3}(0.03-0,12);0.4,0.3,0.3\rangle + \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\langle \frac{1}{2}0.45;0.4,0.3,0.3\rangle -\langle \frac{1}{2}0.173;0.4,0.3,0.3\rangle ; \end{gathered}$$

$$\widetilde{{\mathsf{\sigma }}_{\mathrm{f}}}{\mathrm{a}}_3=\langle (0.0125-0.059+0,225-0.086;0.4,0.3,0.3)\rangle$$

$$\widetilde{{\mathsf{\sigma }}_{\mathrm{f}}}{\mathrm{a}}_3=\langle 0.0925;0.4,0.3,0.3\rangle$$

In conclusion we can state that the triangular neutrosophic fuzzy number variance depends on the values of ${\widetilde{Ra}}_{a1};{\widetilde{Ra}}_{b1};{\widetilde{Ra}}_{c1},$ all of which are part of its level sets and are also on the average value of the return of the financial asset $E_f^2({\widetilde{Ra}}_i)$.

6. Determination of Covariance Using the Triangular Neutrosophic Fuzzy Numbers

The covariance between two triangular neutrosophic fuzzy numbers that model the return of two financial assets defines the intensity of the links between two fuzzy numbers and the way they mutually influence their profitability. There may be three possible situations:

• If the return of two financial assets increases, ${\widetilde{Ra}}_1>0$ and ${\widetilde{Ra}}_2>0,$ both financial assets show a positive growth trend. As such, we can say that the return on financial assets is positively correlated.
• If the return of two financial assets registers different growth trends, ${\widetilde{Ra}}_1>0$ and ${\widetilde{Ra}}_2<0$, or ${\widetilde{Ra}}_1<0$ and ${\widetilde{Ra}}_2>0$, we can say that the return on financial assets isn’t correlated.
• If the return of two financial assets shows negative growth trends, ${\widetilde{Ra}}_1<0$ and ${\widetilde{Ra}}_2<0,$ both returns on financial assets decrease. As such, we can say they are negatively correlated.

Definition 10.

There are two triangular neutrosophic fuzzy numbers that define the return of two financial assets:

$${\widetilde{Ra}}_1=\langle ({\widetilde{Ra}}_{a1},{\widetilde{Ra}}_{b1},{\widetilde{Ra}}_{c1});w{\widetilde{Ra}}_1,u{\widetilde{Ra}}_1,y{\widetilde{Ra}}_1\rangle ,$$

and

$${\widetilde{Ra}}_2=\langle ({\widetilde{Ra}}_{a2},{\widetilde{Ra}}_{b2},{\widetilde{Ra}}_{c2});w{\widetilde{Ra}}_1,u{\widetilde{Ra}}_1,y{\widetilde{Ra}}_1\rangle .$$

In addition, their level sets, of the form:

$${\left[\widetilde{R_a}\right]}^{\alpha }=\left[\widetilde{R{a}_1}(\alpha );\widetilde{R{a}_2}(\alpha )\right]$$

for every $\alpha \in \left[0,1\right]$ where:

• For the neutrosophic level set, ${\left[\widetilde{R_{a1}}\right]}^{\alpha }$ will have:

  $$\widetilde{R{a}_{11}}(\alpha )=\langle ({\widetilde{Ra}}_{b11}-{\widetilde{Ra}}_{a11})\alpha +{\widetilde{Ra}}_{a11};w{\widetilde{Ra}}_1,u{\widetilde{Ra}}_1,y{\widetilde{Ra}}_1\rangle$$

  (30)

  $$\widetilde{R{a}_{12}}(\alpha )=\langle {\widetilde{Ra}}_{c11}-({\widetilde{Ra}}_{c11}-{\widetilde{Ra}}_{b11})\alpha ;w{\widetilde{Ra}}_1,u{\widetilde{Ra}}_1,y{\widetilde{Ra}}_1\rangle$$

  (31)
• For the neutrosophic level set, ${\left[\widetilde{R_{a2}}\right]}^{\alpha }$ will have:

  $$\widetilde{R{a}_{21}}(\alpha )=\langle ({\widetilde{Ra}}_{b21}-{\widetilde{Ra}}_{a21})\alpha +{\widetilde{Ra}}_{a21};w{\widetilde{Ra}}_2,u{\widetilde{Ra}}_2,y{\widetilde{Ra}}_2\rangle$$

  (32)

  $$\widetilde{R{a}_{22}}(\alpha )=\langle {\widetilde{Ra}}_{c21}-({\widetilde{Ra}}_{c21}-{\widetilde{Ra}}_{b21})\alpha ;w{\widetilde{Ra}}_2,u{\widetilde{Ra}}_2,y{\widetilde{Ra}}_2\rangle$$

  (33)

The covariance between two triangular neutrosophic fuzzy numbers ${\widetilde{Ra}}_1$ and ${\widetilde{Ra}}_2$ can be given by the following relationship:

$$\begin{array}{cc}\hfill cov({\widetilde{Ra}}_1,{\widetilde{Ra}}_2)& =\frac{1}{2}{{\displaystyle \int }}_0^1[\langle (\widetilde{R{a}_{11}}(\alpha )-E_f({\widetilde{Ra}}_1))(\widetilde{R{a}_{21}}(\alpha )\hfill \\ & -E_f({\widetilde{Ra}}_2));w\widetilde{R{a}_1}\wedge w{\widetilde{Ra}}_2,u{\widetilde{Ra}}_1\vee u{\widetilde{Ra}}_2,y{\widetilde{Ra}}_1\vee y{\widetilde{Ra}}_2\rangle \hfill \\ & +\langle (\widetilde{R{a}_{12}}(\alpha )-E_f({\widetilde{Ra}}_1))(\widetilde{R{a}_{22}}(\alpha )\hfill \\ & -E_f({\widetilde{Ra}}_2));w\widetilde{R{a}_1}\wedge w{\widetilde{Ra}}_2,u{\widetilde{Ra}}_1\vee u{\widetilde{Ra}}_2,y{\widetilde{Ra}}_1\vee y{\widetilde{Ra}}_2\rangle ]f(\alpha )d\alpha \hfill \end{array}$$

(34)

If the weighting function is f(α) = 2α, then the covariance between the two neutrosophic fuzzy numbers will be written as follows:

$$\begin{array}{cc}\hfill cov({\widetilde{Ra}}_1,{\widetilde{Ra}}_2)& ={{\displaystyle \int }}_0^1[\langle (\widetilde{R{a}_{11}}(\alpha )-E_f({\widetilde{Ra}}_1))(\widetilde{R{a}_{21}}(\alpha )\hfill \\ & -E_f({\widetilde{Ra}}_2));w\widetilde{R{a}_1}\wedge w{\widetilde{Ra}}_2,u{\widetilde{Ra}}_1\vee u{\widetilde{Ra}}_2,y{\widetilde{Ra}}_1\vee y{\widetilde{Ra}}_2\rangle \hfill \\ & +\langle (\widetilde{R{a}_{12}}(\alpha )-E_f({\widetilde{Ra}}_1))(\widetilde{R{a}_{22}}(\alpha )\hfill \\ & -E_f({\widetilde{Ra}}_2));w\widetilde{R{a}_1}\wedge w{\widetilde{Ra}}_2,u{\widetilde{Ra}}_1\vee u{\widetilde{Ra}}_2,y{\widetilde{Ra}}_1\vee y{\widetilde{Ra}}_2\rangle ]\alpha d\alpha \hfill \end{array}$$

(35)

Proposition 4.

The covariance between two triangular neutrosophic fuzzy numbers can be determined by the following relationship:

$$\begin{array}{c}cov({\widetilde{Ra}}_1,{\widetilde{Ra}}_2)\hfill \\ =\frac{1}{2}{{\displaystyle \int }}_0^1\langle (\widetilde{R{a}_{11}}(\alpha )\widetilde{R{a}_{21}}(\alpha )\hfill \\ +\widetilde{R{a}_{12}}(\alpha )\widetilde{R{a}_{22}}(\alpha ));w\widetilde{R{a}_1}\wedge w{\widetilde{Ra}}_2,u{\widetilde{Ra}}_1\vee u{\widetilde{Ra}}_2,y{\widetilde{Ra}}_1\vee y{\widetilde{Ra}}_2\rangle f(\alpha )d\alpha \hfill \\ +{{\displaystyle \int }}_0^1\langle (E_f({\widetilde{Ra}}_1)E_f({\widetilde{Ra}}_2))w\widetilde{R{a}_1}\wedge w{\widetilde{Ra}}_2,u{\widetilde{Ra}}_1\vee u{\widetilde{Ra}}_2,y{\widetilde{Ra}}_1\vee y{\widetilde{Ra}}_2;\rangle f(\alpha )d\alpha \hfill \end{array}$$

(36)

Demonstration 4.

$$\begin{array}{cc}\hfill cov({\widetilde{Ra}}_1,{\widetilde{Ra}}_2)& =\frac{1}{2}{{\displaystyle \int }}_0^1\widetilde{R{a}_{11}}(\alpha )\widetilde{R{a}_{21}}(\alpha )-(\widetilde{R{a}_{11}}(\alpha )+\widetilde{R{a}_{12}}(\alpha ))E_f({\widetilde{Ra}}_2)-(\widetilde{R{a}_{21}}\hfill \\ & +\widetilde{R{a}_{22}}(\alpha ))E_f({\widetilde{Ra}}_1)+\widetilde{R{a}_{12}}(\alpha )\widetilde{R{a}_{22}}(\alpha )\hfill \\ & +2E_f({\widetilde{Ra}}_1)E_f({\widetilde{Ra}}_2);w\widetilde{R{a}_1}\wedge w{\widetilde{Ra}}_2,u{\widetilde{Ra}}_1\vee u{\widetilde{Ra}}_2,y{\widetilde{Ra}}_1\vee y{\widetilde{Ra}}_{2}f(\alpha )d\alpha \hfill \end{array}$$

$$\begin{gathered} \langle \left(\widetilde{R{a}_{11}}(\alpha )+\widetilde{R{a}_{12}}(\alpha )\right)E_f({\widetilde{Ra}}_2);w{\widetilde{Ra}}_1,u{\widetilde{Ra}}_1,y{\widetilde{Ra}}_1\rangle =\langle ({\widetilde{Ra}}_{b11}-{\widetilde{Ra}}_{a11})\alpha + \\ {\widetilde{Ra}}_{a11};w{\widetilde{Ra}}_1,u{\widetilde{Ra}}_1,y{\widetilde{Ra}}_1\rangle + \end{gathered}$$

$$\begin{gathered} + \langle {\widetilde{Ra}}_{c11}-({\widetilde{Ra}}_{c11}-{\widetilde{Ra}}_{b11})\alpha ;w{\widetilde{Ra}}_1,u{\widetilde{Ra}}_1,y{\widetilde{Ra}}_1\rangle \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=\langle ((1-\alpha ){\widetilde{Ra}}_{a11}+(1-\alpha ){\widetilde{Ra}}_{c11});w{\widetilde{Ra}}_1,u{\widetilde{Ra}}_1,y{\widetilde{Ra}}_1\rangle \end{gathered}$$

$$\begin{gathered} \langle \left(\widetilde{R{a}_{21}}+\widetilde{R{a}_{22}}(\alpha )\right)E_f({\widetilde{Ra}}_1);w{\widetilde{Ra}}_2,u{\widetilde{Ra}}_2,y{\widetilde{Ra}}_2\rangle =\langle ({\widetilde{Ra}}_{b21}-{\widetilde{Ra}}_{a21})\alpha + \\ {\widetilde{Ra}}_{a21};w{\widetilde{Ra}}_2,u{\widetilde{Ra}}_2,y{\widetilde{Ra}}_2\rangle ; \end{gathered}$$

$$\begin{gathered} +\langle {\widetilde{Ra}}_{c21}-({\widetilde{Ra}}_{c21}-{\widetilde{Ra}}_{b21})\alpha ;w{\widetilde{Ra}}_2,u{\widetilde{Ra}}_2,y{\widetilde{Ra}}_2\rangle =\langle \left((1-\alpha ){\widetilde{Ra}}_{a21}+(1- \\ \alpha ){\widetilde{Ra}}_{c21}\right);w{\widetilde{Ra}}_2,u{\widetilde{Ra}}_2,y{\widetilde{Ra}}_2\rangle \end{gathered}$$

$$\begin{gathered} \langle (\widetilde{R{a}_{11}}(\alpha )+\widetilde{R{a}_{12}}(\alpha ))E_f({\widetilde{Ra}}_2);w{\widetilde{Ra}}_1,u{\widetilde{Ra}}_1,y{\widetilde{Ra}}_1 \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-(\widetilde{R{a}_{21}}+\widetilde{R{a}_{22}}(\alpha ))E_f({\widetilde{Ra}}_1);w{\widetilde{Ra}}_2,u{\widetilde{Ra}}_2,y{\widetilde{Ra}}_2\rangle \\ =[((1-\alpha ){\widetilde{Ra}}_{a11} \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+(1-\alpha ){\widetilde{Ra}}_{c11});w\widetilde{R{a}_1}\wedge w{\widetilde{Ra}}_2,u{\widetilde{Ra}}_1\vee u{\widetilde{Ra}}_2,y{\widetilde{Ra}}_1\vee y{\widetilde{Ra}}_2]E_f({\widetilde{Ra}}_2) \\ -[((1-\alpha ){\widetilde{Ra}}_{a21} \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+(1-\alpha ){\widetilde{Ra}}_{c21});w\widetilde{R{a}_1}\wedge w{\widetilde{Ra}}_2,u{\widetilde{Ra}}_1\vee u{\widetilde{Ra}}_2,y{\widetilde{Ra}}_1\vee y{\widetilde{Ra}}_2]E_f({\widetilde{Ra}}_1) \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=\langle 0;w\widetilde{R{a}_1}\wedge w{\widetilde{Ra}}_2,u{\widetilde{Ra}}_1\vee u{\widetilde{Ra}}_2,y{\widetilde{Ra}}_1\vee y{\widetilde{Ra}}_2\rangle \end{gathered}$$

The expression for covariance between two triangular neutrosophic fuzzy numbers can be written under these conditions as:

$$\begin{array}{c}cov({\widetilde{Ra}}_1,{\widetilde{Ra}}_2)=\frac{1}{2}{{\displaystyle \int }}_0^1\langle (\widetilde{R{a}_{11}}(\alpha )\widetilde{R{a}_{21}}(\alpha )\hfill \\ +\widetilde{R{a}_{12}}(\alpha )\widetilde{R{a}_{22}}(\alpha ));w\widetilde{R{a}_1}\wedge w{\widetilde{Ra}}_2,u{\widetilde{Ra}}_1\vee u{\widetilde{Ra}}_2,y{\widetilde{Ra}}_1\vee y{\widetilde{Ra}}_2\rangle f(\alpha )d\alpha \hfill \\ +{{\displaystyle \int }}_0^1\langle (E_f({\widetilde{Ra}}_1)E_f({\widetilde{Ra}}_2))w\widetilde{R{a}_1}\wedge w{\widetilde{Ra}}_2,u{\widetilde{Ra}}_1\vee u{\widetilde{Ra}}_2,y{\widetilde{Ra}}_1\vee y{\widetilde{Ra}}_2;\rangle f(\alpha )d\alpha \hfill \end{array}$$

Proposition 5.

The covariance between two triangular neutrosophic fuzzy numbers can be determined as:

$$\begin{array}{cc}\hfill cov({\widetilde{Ra}}_1,{\widetilde{Ra}}_2)& =\langle (\frac{1}{4}[({\widetilde{Ra}}_{b11}-{\widetilde{Ra}}_{a11})({\widetilde{Ra}}_{b21}-{\widetilde{Ra}}_{a21})\hfill \\ & +({\widetilde{Ra}}_{c11}-{\widetilde{Ra}}_{b11})({\widetilde{Ra}}_{c21}-{\widetilde{Ra}}_{b21})]\hfill \\ & +\frac{1}{3}\left\{\right[{\widetilde{Ra}}_{a21}({\widetilde{Ra}}_{b11}-{\widetilde{Ra}}_{a11})+{\widetilde{Ra}}_{a11}({\widetilde{Ra}}_{b21}-{\widetilde{Ra}}_{a21})]\hfill \\ & -\left[{\widetilde{Ra}}_{c11}({\widetilde{Ra}}_{c21}-{\widetilde{Ra}}_{b21})+{\widetilde{Ra}}_{c21}({\widetilde{Ra}}_{c11}-{\widetilde{Ra}}_{b11})\right]\}\hfill \\ & +\frac{1}{2}({\widetilde{Ra}}_{a11}{\widetilde{Ra}}_{a21}+{\widetilde{Ra}}_{c11}{\widetilde{Ra}}_{c21})\hfill \\ & +\frac{1}{2}{E}_f({\widetilde{Ra}}_1)E_f({\widetilde{Ra}}_2));w\widetilde{R{a}_1}\wedge w{\widetilde{Ra}}_2,u{\widetilde{Ra}}_1\vee u{\widetilde{Ra}}_2,y{\widetilde{Ra}}_1\vee y{\widetilde{Ra}}_2\rangle \hfill \end{array}$$

Demonstration 5.

It is known from Proposition. 4 that the covariance can be determined using the relationship:

$$\begin{array}{cc}\hfill cov({\widetilde{Ra}}_1,{\widetilde{Ra}}_2)& =\frac{1}{2}{{\displaystyle \int }}_0^1\langle (\widetilde{R{a}_{11}}(\alpha )\widetilde{R{a}_{21}}(\alpha )\hfill \\ & +\widetilde{R{a}_{12}}(\alpha )\widetilde{R{a}_{22}}(\alpha ));w\widetilde{R{a}_1}\wedge w{\widetilde{Ra}}_2,u{\widetilde{Ra}}_1\vee u{\widetilde{Ra}}_2,y{\widetilde{Ra}}_1\vee y{\widetilde{Ra}}_2\rangle f(\alpha )d\alpha \hfill \\ & +{{\displaystyle \int }}_0^1\langle (E_f({\widetilde{Ra}}_1)E_f({\widetilde{Ra}}_2))w\widetilde{R{a}_1}\wedge w{\widetilde{Ra}}_2,u{\widetilde{Ra}}_1\vee u{\widetilde{Ra}}_2,y{\widetilde{Ra}}_1\vee y{\widetilde{Ra}}_2;\rangle f(\alpha )d\alpha \hfill \end{array}$$

At the same time, we know the expressions for the level sets as follows:

• For the neutrosophic number’s level set, ${\left[\widetilde{R_{a1}}\right]}^{\alpha }$ will have:

  $$\widetilde{R{a}_{11}}(\alpha )=\langle ({\widetilde{Ra}}_{b11}-{\widetilde{Ra}}_{a11})\alpha +{\widetilde{Ra}}_{a11};w{\widetilde{Ra}}_1,u{\widetilde{Ra}}_1,y{\widetilde{Ra}}_1\rangle$$

  $$\widetilde{R{a}_{12}}(\alpha )=\langle {\widetilde{Ra}}_{c11}-({\widetilde{Ra}}_{c11}-{\widetilde{Ra}}_{b11})\alpha ;w{\widetilde{Ra}}_1,u{\widetilde{Ra}}_1,y{\widetilde{Ra}}_1\rangle$$
• For the neutrosophic number’s level set, ${\left[\widetilde{R_{a2}}\right]}^{\alpha }$ will have:

  $$\widetilde{R{a}_{21}}(\alpha )=\langle ({\widetilde{Ra}}_{b21}-{\widetilde{Ra}}_{a21})\alpha +{\widetilde{Ra}}_{a21};w{\widetilde{Ra}}_2,u{\widetilde{Ra}}_2,y{\widetilde{Ra}}_2\rangle$$

  $$\widetilde{R{a}_{22}}(\alpha )=\langle {\widetilde{Ra}}_{c21}-({\widetilde{Ra}}_{c21}-{\widetilde{Ra}}_{b21})\alpha ;w{\widetilde{Ra}}_2,u{\widetilde{Ra}}_2,y{\widetilde{Ra}}_2\rangle$$

From Proposition 1, we know that the average values of the neutrosophic triangular fuzzy numbers by which the financial assets return is modeled:

$$E_f({\widetilde{Ra}}_1)=\langle \left(\frac{1}{6}({\widetilde{Ra}}_{a11}+{\widetilde{Ra}}_{c11})+\frac{2}{3}{\widetilde{Ra}}_{b11}\right);w{\widetilde{Ra}}_1,u{\widetilde{Ra}}_1,y{\widetilde{Ra}}_1\rangle$$

$$E_f({\widetilde{Ra}}_2)=\langle \left(\frac{1}{6}({\widetilde{Ra}}_{a21}+{\widetilde{Ra}}_{c21})+\frac{2}{3}{\widetilde{Ra}}_{b21}\right);w{\widetilde{Ra}}_2,u{\widetilde{Ra}}_2,y{\widetilde{Ra}}_2\rangle$$

By replacing in the covariance expression, we obtain:

$$\begin{array}{cc}\hfill cov({\widetilde{Ra}}_1,{\widetilde{Ra}}_2)& =\frac{1}{2}{{\displaystyle \int }}_0^1\langle (\widetilde{R{a}_{11}}(\alpha )\widetilde{R{a}_{21}}(\alpha )\hfill \\ & +\widetilde{R{a}_{12}}(\alpha )\widetilde{R{a}_{22}}(\alpha ));w\widetilde{R{a}_1}\wedge w{\widetilde{Ra}}_2,u{\widetilde{Ra}}_1\vee u{\widetilde{Ra}}_2,y{\widetilde{Ra}}_1\vee y{\widetilde{Ra}}_2\rangle f(\alpha )d\alpha \hfill \\ & +{{\displaystyle \int }}_0^1\langle \left(E_f({\widetilde{Ra}}_1)E_f({\widetilde{Ra}}_2)\right)w\widetilde{R{a}_1}\wedge w{\widetilde{Ra}}_2,u{\widetilde{Ra}}_1\vee u{\widetilde{Ra}}_2,y{\widetilde{Ra}}_1\vee y{\widetilde{Ra}}_2;\rangle f(\alpha )d\alpha \hfill \end{array}$$

$$\begin{array}{cc}\hfill cov({\widetilde{Ra}}_1,{\widetilde{Ra}}_2)& =\frac{1}{2}{{\displaystyle \int }}_0^1\langle ({\widetilde{Ra}}_{b11}-{\widetilde{Ra}}_{a11})\alpha +{\widetilde{Ra}}_{a11};w{\widetilde{Ra}}_1,u{\widetilde{Ra}}_1,y{\widetilde{Ra}}_1\rangle \langle ({\widetilde{Ra}}_{b21}-{\widetilde{Ra}}_{a21})\alpha \hfill \\ & +{\widetilde{Ra}}_{a21};w{\widetilde{Ra}}_2,u{\widetilde{Ra}}_2,y{\widetilde{Ra}}_2\rangle +\langle {\widetilde{Ra}}_{c11}-({\widetilde{Ra}}_{c11}-{\widetilde{Ra}}_{b11})\alpha ;w{\widetilde{Ra}}_1,u{\widetilde{Ra}}_1,y{\widetilde{Ra}}_1\rangle \langle {\widetilde{Ra}}_{c21}\hfill \\ & -({\widetilde{Ra}}_{c21}-{\widetilde{Ra}}_{b21})\alpha ;w{\widetilde{Ra}}_2,u{\widetilde{Ra}}_2,y{\widetilde{Ra}}_2\rangle f(\alpha )d\alpha \hfill \\ & +{{\displaystyle \int }}_0^1\langle \left(E_f({\widetilde{Ra}}_1)E_f({\widetilde{Ra}}_2)\right)w\widetilde{R{a}_1}\wedge w{\widetilde{Ra}}_2,u{\widetilde{Ra}}_1\vee u{\widetilde{Ra}}_2,y{\widetilde{Ra}}_1\vee y{\widetilde{Ra}}_2;\rangle f(\alpha )d\alpha \hfill \end{array}$$

$$\begin{array}{cc}\hfill cov({\widetilde{Ra}}_1,{\widetilde{Ra}}_2)& =\frac{1}{2}{{\displaystyle \int }}_0^1\langle (({\widetilde{Ra}}_{b11}-{\widetilde{Ra}}_{a11})({\widetilde{Ra}}_{b21}-{\widetilde{Ra}}_{a21}){\alpha }^2\hfill \\ & +\left[{\widetilde{Ra}}_{a21}({\widetilde{Ra}}_{b11}-{\widetilde{Ra}}_{a11})+{\widetilde{Ra}}_{a11}({\widetilde{Ra}}_{b21}-{\widetilde{Ra}}_{a21})\right]\alpha +{\widetilde{Ra}}_{a11}{\widetilde{Ra}}_{a21}\hfill \\ & +{\alpha }^2({\widetilde{Ra}}_{c11}-{\widetilde{Ra}}_{b11})({\widetilde{Ra}}_{c21}-\alpha [{\widetilde{Ra}}_{c11}({\widetilde{Ra}}_{c21}-{\widetilde{Ra}}_{b21})+{\widetilde{Ra}}_{c21}({\widetilde{Ra}}_{c11}-{\widetilde{Ra}}_{b11})]\hfill \\ & +{\widetilde{Ra}}_{c11}{\widetilde{Ra}}_{c21};w\widetilde{R{a}_1}\wedge w{\widetilde{Ra}}_2,u{\widetilde{Ra}}_1\vee u{\widetilde{Ra}}_2,y{\widetilde{Ra}}_1\vee y{\widetilde{Ra}}_2\rangle f(\alpha )d\alpha \hfill \\ & +{{\displaystyle \int }}_0^1\langle \left(E_f({\widetilde{Ra}}_1)E_f({\widetilde{Ra}}_2)\right);w\widetilde{R{a}_1}\wedge w{\widetilde{Ra}}_2,u{\widetilde{Ra}}_1\vee u{\widetilde{Ra}}_2,y{\widetilde{Ra}}_1\vee y{\widetilde{Ra}}_2;\rangle f(\alpha )d\alpha \hfill \end{array}$$

$$\begin{array}{cc}\hfill cov({\widetilde{Ra}}_1,{\widetilde{Ra}}_2)& =\langle ({\widetilde{Ra}}_{b11}-{\widetilde{Ra}}_{a11})({\widetilde{Ra}}_{b21}-{\widetilde{Ra}}_{a21})\frac{{\alpha }^4}{4}{│}_0^1\hfill \\ & +[{\widetilde{Ra}}_{a21}({\widetilde{Ra}}_{b11}-{\widetilde{Ra}}_{a11})\hfill \\ & ++{\widetilde{Ra}}_{a11}({\widetilde{Ra}}_{b21}-{\widetilde{Ra}}_{a21})]\frac{{\alpha }^3}{3}{│}_0^1+{\widetilde{Ra}}_{a11}{\widetilde{Ra}}_{a21}\frac{{\alpha }^3}{2}{│}_0^1\hfill \\ & +({\widetilde{Ra}}_{c11}-{\widetilde{Ra}}_{b11})({\widetilde{Ra}}_{c21}-{\widetilde{Ra}}_{b21})\frac{{\alpha }^4}{4}{│}_0^1\hfill \\ & -\left[{\widetilde{Ra}}_{c11}({\widetilde{Ra}}_{c21}-{\widetilde{Ra}}_{b21})+{\widetilde{Ra}}_{c21}({\widetilde{Ra}}_{c11}-{\widetilde{Ra}}_{b11})\right]\frac{{\alpha }^3}{3}{│}_0^1\hfill \\ & +{\widetilde{Ra}}_{c11}{\widetilde{Ra}}_{c21}\frac{{\alpha }^3}{2}{│}_0^1;w\widetilde{R{a}_1}\wedge w{\widetilde{Ra}}_2,u{\widetilde{Ra}}_1\vee u{\widetilde{Ra}}_2,y{\widetilde{Ra}}_1\vee y{\widetilde{Ra}}_2\rangle \hfill \\ & +E_f({\widetilde{Ra}}_1)E_f({\widetilde{Ra}}_2)\frac{{\alpha }^3}{2}{│}_0^1;w\widetilde{R{a}_1}\wedge w{\widetilde{Ra}}_2,u{\widetilde{Ra}}_1\vee u{\widetilde{Ra}}_2,y{\widetilde{Ra}}_1\vee y{\widetilde{Ra}}_2\rangle \hfill \end{array}$$

The above equation can be written as:

$$\begin{array}{cc}\hfill cov({\widetilde{Ra}}_1,{\widetilde{Ra}}_2)& =\langle \frac{1}{4}[({\widetilde{Ra}}_{b11}-{\widetilde{Ra}}_{a11})({\widetilde{Ra}}_{b21}-{\widetilde{Ra}}_{a21})\hfill \\ & +({\widetilde{Ra}}_{c11}-{\widetilde{Ra}}_{b11})({\widetilde{Ra}}_{c21}-{\widetilde{Ra}}_{b21})]\hfill \\ & +\frac{1}{3}\{\left[{\widetilde{Ra}}_{a21}({\widetilde{Ra}}_{b11}-{\widetilde{Ra}}_{a11})+{\widetilde{Ra}}_{a11}({\widetilde{Ra}}_{b21}-{\widetilde{Ra}}_{a21})\right]\hfill \\ & -\left[{\widetilde{Ra}}_{c11}({\widetilde{Ra}}_{c21}-{\widetilde{Ra}}_{b21})+{\widetilde{Ra}}_{c21}({\widetilde{Ra}}_{c11}-{\widetilde{Ra}}_{b11})\right]\}\hfill \\ & +\frac{1}{2}({\widetilde{Ra}}_{a11}{\widetilde{Ra}}_{a21}+{\widetilde{Ra}}_{c11}{\widetilde{Ra}}_{c21})\hfill \\ & +\frac{1}{2}{E}_f({\widetilde{Ra}}_1)E_f({\widetilde{Ra}}_2));w\widetilde{R{a}_1}\wedge w{\widetilde{Ra}}_2,u{\widetilde{Ra}}_1\vee u{\widetilde{Ra}}_2,y{\widetilde{Ra}}_1\vee y{\widetilde{Ra}}_2\rangle \hfill \end{array}$$

In conclusion, for the triangular neutrosophic fuzzy numbers, the expressions for the following statistical indicators were obtained:

(a)

The financial asset return:

$$E_f({\widetilde{Ra}}_i)=\langle \left(\frac{1}{6}({\widetilde{Ra}}_{a1}+{\widetilde{Ra}}_{c1})+\frac{2}{3}{\widetilde{Ra}}_{b1}\right);w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle$$

(b)

The variance, or the financial asset’s risk:

$$\begin{gathered} \widetilde{{\sigma }_f{a}_i}=\langle \left(\frac{1}{4}\left[{({\widetilde{Ra}}_{b1}-{\widetilde{Ra}}_{a1})}^2+{({\widetilde{Ra}}_{c1}-{\widetilde{Ra}}_{b1})}^2\right] \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\frac{2}{3}\left[{\widetilde{Ra}}_{a1}({\widetilde{Ra}}_{b1}-{\widetilde{Ra}}_{a1})-{\widetilde{Ra}}_{c1}({\widetilde{Ra}}_{c1}-{\widetilde{Ra}}_{b1})\right] \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\frac{1}{2}({\widetilde{Ra}}_{a1}^2+{\widetilde{Ra}}_{c1}^2)-\frac{1}{2}{E}_f^2({\widetilde{Ra}}_i)\right);w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle \end{gathered}$$

(c)

The covariance between two financial assets modeled with triangular neutrosophic fuzzy numbers:

$$\begin{array}{cc}\hfill cov({\widetilde{Ra}}_1,{\widetilde{Ra}}_2)& =\langle \left(\frac{1}{4}\right[({\widetilde{Ra}}_{b11}-{\widetilde{Ra}}_{a11})({\widetilde{Ra}}_{b21}-{\widetilde{Ra}}_{a21})\hfill \\ & +({\widetilde{Ra}}_{c11}-{\widetilde{Ra}}_{b11})({\widetilde{Ra}}_{c21}-{\widetilde{Ra}}_{b21})]\hfill \\ & +\frac{1}{3}\left\{\right[{\widetilde{Ra}}_{a21}({\widetilde{Ra}}_{b11}-{\widetilde{Ra}}_{a11})+{\widetilde{Ra}}_{a11}({\widetilde{Ra}}_{b21}-{\widetilde{Ra}}_{a21})]\hfill \\ & -\left[{\widetilde{Ra}}_{c11}({\widetilde{Ra}}_{c21}-{\widetilde{Ra}}_{b21})+{\widetilde{Ra}}_{c21}({\widetilde{Ra}}_{c11}-{\widetilde{Ra}}_{b11})\right]\}\hfill \\ & +\frac{1}{2}({\widetilde{Ra}}_{a11}{\widetilde{Ra}}_{a21}+{\widetilde{Ra}}_{c11}{\widetilde{Ra}}_{c21})\hfill \\ & +\frac{1}{2}{E}_f({\widetilde{Ra}}_1)E_f({\widetilde{Ra}}_2));w\widetilde{R{a}_1}\wedge w{\widetilde{Ra}}_2,u{\widetilde{Ra}}_1\vee u{\widetilde{Ra}}_2,y{\widetilde{Ra}}_1\vee y{\widetilde{Ra}}_2\rangle \hfill \end{array}$$

Example 3.

There are two financial assets,$(A_1,A_2),$to which two triangular neutrosophic fuzzy numbers are attached:

$${\widetilde{Ra}}_1=\langle (0.2 0.3 0.5);0.5, 0.2, 0.3\rangle \mathrm{for}\widetilde{Ra}\in \left[0,2;0,5\right]$$

$${\widetilde{Ra}}_2=\langle (0.1 0.2 0.3);0.6, 0.3, 0.2\rangle \mathrm{for}\widetilde{Ra}\in \left[0,1;0,3\right]$$

In order to determine the covariance between two financial assets to determine the $cov({\widetilde{Ra}}_1,{\widetilde{Ra}}_2)$ and the variance–covariance matrix, the following formula can be used:

$$\begin{array}{cc}\hfill cov({\widetilde{Ra}}_1,{\widetilde{Ra}}_2)& =\langle \left(\frac{1}{4}\right[({\widetilde{Ra}}_{b11}-{\widetilde{Ra}}_{a11})({\widetilde{Ra}}_{b21}-{\widetilde{Ra}}_{a21})\hfill \\ & +({\widetilde{Ra}}_{c11}-{\widetilde{Ra}}_{b11})({\widetilde{Ra}}_{c21}-{\widetilde{Ra}}_{b21})]\hfill \\ & +\frac{1}{3}\left\{[{\widetilde{Ra}}_{a21}({\widetilde{Ra}}_{b11}-{\widetilde{Ra}}_{a11})+{\widetilde{Ra}}_{a11}({\widetilde{Ra}}_{b21}-{\widetilde{Ra}}_{a21})\right]\hfill \\ & -[{\widetilde{Ra}}_{c11}({\widetilde{Ra}}_{c21}-{\widetilde{Ra}}_{b21})+{\widetilde{Ra}}_{c21}({\widetilde{Ra}}_{c11}-{\widetilde{Ra}}_{b11})\left]\right\}\hfill \\ & +\frac{1}{2}({\widetilde{Ra}}_{a11}{\widetilde{Ra}}_{a21}+{\widetilde{Ra}}_{c11}{\widetilde{Ra}}_{c21})\hfill \\ & +\frac{1}{2}{E}_f({\widetilde{Ra}}_1)E_f({\widetilde{Ra}}_2));w\widetilde{R{a}_1}\wedge w{\widetilde{Ra}}_2,u{\widetilde{Ra}}_1\vee u{\widetilde{Ra}}_2,y{\widetilde{Ra}}_1\vee y{\widetilde{Ra}}_2\rangle \hfill \end{array}$$

By replacing in the formula, we can obtain:

$$\begin{array}{cc}\hfill cov({\widetilde{Ra}}_1,{\widetilde{Ra}}_2)& =\langle \frac{1}{4}\left[(0.3-0.2)(0.2-0.1)+(0.5-0.3)(0.3-0.2)\right]\hfill \\ & +\frac{1}{3}\left[0.1(0.3-0.2)+0.2(0.2-0.1)\right]\hfill \\ & -\left[0.5(0.3-0.2)+0.3(0.5-0.3)\right]\hfill \\ & +\frac{1}{2}(0.2\ast 0.1+0.5\ast 0.3)+\frac{1}{2}0,316\ast 0,199;0.5\wedge 0.6, 0.2\vee 0.3,0.3\vee 0.2\rangle \hfill \end{array}$$

$$\begin{array}{cc}\hfill cov({\widetilde{Ra}}_1,{\widetilde{Ra}}_2)& =\langle \frac{1}{4}\left[0.01+0.02\right]+\frac{1}{3}\left[0.01+0.02\right]-\left[0.05+0.06\right]+\frac{1}{2}(0.02+0.15)\hfill \\ & +\frac{1}{2}0.062;0.6, 0.2, 0.2\rangle \hfill \end{array}$$

$$cov({\widetilde{Ra}}_1,{\widetilde{Ra}}_2)=\langle 0.0075-0.053+0.085+0.031;0.6, 0.2, 0.2\rangle$$

$$cov({\widetilde{Ra}}_1,{\widetilde{Ra}}_2)=\langle 0.0705;0.6, 0.2, 0.2\rangle$$

The variance–covariance matrix is then:

$$\mathsf{\Omega }=\left(\begin{array}{cc}\langle 0.0225;0.5, 0.2, 0.3\rangle & \langle 0.0705;0.6, 0.2, 0.2\rangle \\ \langle 0.0705;0.6, 0.2, 0.2\rangle & \langle 0.0180;0.6, 0.3, 0.2\rangle \end{array}\right)$$

Modeling the performance indicators leads to the following results:

• The financial asset return:

  $$E_f({\widetilde{Ra}}_i)=\langle \left(\frac{1}{6}({\widetilde{Ra}}_{a1}+{\widetilde{Ra}}_{c1})+\frac{2}{3}{\widetilde{Ra}}_{b1}\right);w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle$$
• The variance of the financial asset risk:

  $$\begin{gathered} \widetilde{{\sigma }_f{a}_i}=\langle (\frac{1}{4}\left[{({\widetilde{Ra}}_{b1}-{\widetilde{Ra}}_{a1})}^2+{({\widetilde{Ra}}_{c1}-{\widetilde{Ra}}_{b1})}^2\right] \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\frac{2}{3}\left[{\widetilde{Ra}}_{a1}({\widetilde{Ra}}_{b1}-{\widetilde{Ra}}_{a1})-{\widetilde{Ra}}_{c1}({\widetilde{Ra}}_{c1}-{\widetilde{Ra}}_{b1})\right]+\frac{1}{2}({\widetilde{Ra}}_{a1}^2+{\widetilde{Ra}}_{c1}^2) \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-\frac{1}{2}{E}_f^2({\widetilde{Ra}}_i));w\widetilde{Ra},u\widetilde{Ra},y\widetilde{Ra}\rangle \end{gathered}$$
• The covariance between two financial assets modelled with the triangular neutrosophic fuzzy numbers:

  $$\begin{array}{cc}\hfill cov({\widetilde{Ra}}_1,{\widetilde{Ra}}_2)& =\langle \left(\frac{1}{4}\right[({\widetilde{Ra}}_{b11}-{\widetilde{Ra}}_{a11})({\widetilde{Ra}}_{b21}-{\widetilde{Ra}}_{a21})\hfill \\ & +({\widetilde{Ra}}_{c11}-{\widetilde{Ra}}_{b11})({\widetilde{Ra}}_{c21}-{\widetilde{Ra}}_{b21})]\hfill \\ & +\frac{1}{3}\left\{\right[{\widetilde{Ra}}_{a21}({\widetilde{Ra}}_{b11}-{\widetilde{Ra}}_{a11})+{\widetilde{Ra}}_{a11}({\widetilde{Ra}}_{b21}-{\widetilde{Ra}}_{a21})]\hfill \\ & -[{\widetilde{Ra}}_{c11}({\widetilde{Ra}}_{c21}-{\widetilde{Ra}}_{b21})+{\widetilde{Ra}}_{c21}({\widetilde{Ra}}_{c11}-{\widetilde{Ra}}_{b11})]\}\hfill \\ & +\frac{1}{2}({\widetilde{Ra}}_{a11}{\widetilde{Ra}}_{a21}+{\widetilde{Ra}}_{c11}{\widetilde{Ra}}_{c21})\hfill \\ & +\frac{1}{2}{E}_f({\widetilde{Ra}}_1)E_f({\widetilde{Ra}}_2));w\widetilde{R{a}_1}\wedge w{\widetilde{Ra}}_2,u{\widetilde{Ra}}_1\vee u{\widetilde{Ra}}_2,y{\widetilde{Ra}}_1\vee y{\widetilde{Ra}}_2\rangle \hfill \end{array}$$

Conclusion: The covariance of two financial assets determined according to the above formula shows that there is a weak link between the two financial assets modeled by triangular neutrosophic fuzzy numbers $cov({\widetilde{Ra}}_1,{\widetilde{Ra}}_2)=\langle 0.0705;0.6, 0.2, 0.2\rangle .$ The covariance is positive, resulting in the fact that the financial returns of the two assets increase and register a favorable trend.

7. Conclusions

The performance indicators of the financial assets are represented by the return on financial assets, the financial assets risk, and the covariance between them, the latter of which, as mentioned above, indicates the intensity of the links between the return on financial assets. Modeling these three performance indicators of the financial assets has been achieved with the help of triangular neutrosophic fuzzy numbers, which presents a number of advantages:

• The neutrosophic approach of these three financial assets performance indicators must take all the possible scenarios for their achievement into account—these are the scenario of certainty, the scenario of non-realization, and the scenario of indecision (in which it cannot be appreciated whether the performance indicators are or are not achieved). All three scenarios have attached performance, non-execution, or uncertainty ratios according to the investor’s professional judgment.
• The possibility of stratification or the clustering of the financial asset return values according to linguistic criteria such as very good, good or weak performance indicators. This method of stratification can be also applied in the calculation/determination of financial risk. Stratification/clustering takes place with the help of triangular neutrosophic fuzzy numbers.
• The possibility of selecting the desired return/risk group in order to maximize the investor earnings, analyzing the profitability of the financial asset by means of probability grades or other purposes desired by investors, etc.

The results obtained by modeling with triangular neutrosophic fuzzy numbers: The financial assets return, the financial risk, and the covariance between two financial assets were tested on three practical examples in order to confirm their applicability. For future research, two aspects for modelling with the help of neutrosophic fuzzy intelligence are being considered: The mitigation of portfolio risk and optimal portfolios.