Abstract
In the integrated services digital broadcasting-terrestrial (ISDB-T) system, the combination of digital terrestrial transmission and MPEG-4 advanced video coding (MPEG-4 AVC) has offered ways to provide a variety of digital high-definition television (HDTV) programs. Using band segmented transmission orthogonal frequency division multiplexing (BST-OFDM), the delivery of innovative video-on-demand and HDTV services is supported. To take full advantage of the attractive benefits of BST-OFDM, it is important to estimate integer frequency offset (IFO) without a priori knowledge on the segment type that is transmitted over transmission and the multiplexing configuration control (TMCC) signal. To address this issue, an efficient IFO detection method is proposed for the ISDB-T system employing BST-OFDM. To enable IFO detection independent of the segment type, information-bearing TMCC signals that are asymmetrically distributed in the frequency domain are used as pilot symbols. Numerical analysis is performed to present the relationship between error probability and design parameter. We show via the numerical results that the multiple transmitted TMCC information is efficiently used for blind estimation of the IFO, achieving robust estimation in the presence of the fractional frequency offset.
1. Introduction
Orthogonal frequency division multiplexing (OFDM) is a leading multicarrier modulation scheme with the capability to combat multipath fading distortions and support high data rates. Due to its appealing features, OFDM has been considered as the standard multiplexing technique for many international digital television terrestrial broadcasting (DTTB) systems, such as the advanced television standards committee (ATSC), digital television/terrestrial multimedia broadcasting (DTMB), digital video broadcasting-terrestrial-second generation (DVB-T2), and integrated services digital broadcasting-terrestrial (ISDB-T) [1,2,3,4]. The ISDB-T system is designed to support reliable reception and commonality for high-definition television (HDTV) services using MPEG-4 advanced video coding (MPEG-4 AVC) over terrestrial networks [5]. One special feature in the ISDB-T system is the combination of band segmented transmission (BST) and OFDM, which is known as BST-OFDM. Using different modulation and coding schemes (MCS) in one or more OFDM segments forms the basis of hierarchical transmission [4,5,6]. With the use of the segmented structure and hierarchical partition, different modulation modes, such as coherent and differential modulation, can be applied to different OFDM segments. More specifically, ISDB-T is based on the transmission of MPEG-4 compressed video data containers, which can be used to transmit a flexible mixture of compressed video, audio, and other data services.
Despite its many excellent benefits, OFDM has some principal problems that need to be overcome. One of the major disadvantages of OFDM is its vulnerability for frequency misalignment, which can be introduced by the Doppler shift and oscillator instabilities [7]. To fully utilize the appealing features of OFDM, it is crucial for the receiver to reliably perform time and frequency synchronization, which usually includes estimation of symbol timing offset (STO), carrier frequency offset (CFO), and sampling frequency offset (SFO). In OFDM, the STO can result in inter-symbol interference (ISI) and a rotated phase, of which value is proportional to the subcarrier index. On the other hand, the CFO can be split into integer and fractional offsets, each influencing the system in a different way. If not correctly detected and removed, the fractional CFO (FFO) gives rise to the imperfection of the orthogonality among the subcarriers, leading to the inter-carrier interference (ICI), while the integer CFO (IFO) produces a cyclic shifting of all subcarriers in the frequency domain [8]. To address this issue, a lot of estimation methods have been studied for the estimation of the FFO and the IFO [9,10,11,12,13,14,15,16,17,18].
1.1. Synchronization in OFDM
The synchronization procedure in the OFDM system generally involves three steps. During the first step of the procedure, the receiver exploits the redundant information to find the FFO and initial STO [9,10,11], which is performed in the time domain. In continuous transmission mode, such as terrestrial broadcasting systems, the cyclic prefix can be used for these synchronization tasks. On the other hand, dedicated training symbols are inserted at the beginning of the OFDM frame in the case of burst-mode OFDM systems, which are used for time and frequency synchronization. After FFO compensation and cyclic prefix removal, the frequency domain samples are obtained via fast Fourier transform (FFT) processing. Once the first step is completed, the IFO is estimated together with residual STO, which can usually be done in the frequency domain [12,13,14,15,16,17,18]. After frequency synchronization, there are residual CFO and SFO errors that continuously rotate the phase of the OFDM symbol. During the tracking phase, the residual CFO and SFO are typically estimated based on a set of dedicated pilots, which are estimated and compensated periodically because of its time-accumulative nature [19,20,21]. Since data demodulation can be correctly performed only after successful compensation of the IFO, the IFO represents an important task in the overall synchronization procedure. Hence, we focus on the estimation of the IFO in this paper.
The IFO estimation can be classified into two main categories—namely, blind estimation and pilot-aided estimation. The blind estimation method relies on the utilization of any inherent structural information in the OFDM symbol, which is preferred due to its bandwidth efficiency. In [12,13,14,15], the blind approaches were proposed utilizing the combination of data subcarriers and null subcarriers (NSCs) present at the edges of the OFDM spectrum. The main disadvantage of such a blind estimation strategy is that it requires an exhaustive search for IFO estimates. Unlike the blind approach, a pilot-aided IFO estimation can be accomplished using periodically transmitted pilot information [14,15,16,17]. Maximum likelihood (ML) estimation has been successfully used to estimate the IFO [15], based on the observation of pilot information. The ML estimator achieves accurate CFO estimation at the sacrifice of spectral efficiency and computational load. The work in [17] proposes a new pilot structure together with its pilot-specific estimation algorithm. Another strategy for data-aided IFO detection has been recently presented, exploiting the spatial redundancy introduced by the use of space-frequency block codes [18]. Despite showing good detection capability, these estimation schemes developed in [17,18] are incompatible with legacy ISDB-T devices.
1.2. Contribution
In ISDB-T, the scattered pilot (SP) and continuous pilot (CP) are specified to help the receiver accomplish frequency and channel estimation. Meanwhile, the auxiliary channel (AC) and the transmission and multiplexing configuration controls (TMCC) play the role of an additional channel that can function as a control signal needed for demodulation, which can be used for synchronization purposes. Since the number of explicit CPs differs depending on the modulation mode adopted in the ISDB-T segment, which is available after TMCC information and perfectly decoded, a direct application of the conventional IFO estimation algorithm to the ISDB-T system can result in some performance loss. To perform a reliable estimation independent of the TMCC decoding process, the conventional IFO estimation schemes have to be modified to take the information-conveying TMCC signal into account, which is common, regardless of the segment type.
To account for this problem, an efficient IFO estimation method using the information-bearing TMCC signal is proposed in the ISDB-T system. Since the TMCC signal is transmitted in the same format, independent of the modulation mode, the redundancy present in the multiple transmitted TMCC information enables the estimation of the IFO in a blind manner. To assess the feasibility of the proposed detection method, the probability of erroneous estimation is numerically derived, including the effect of the FFO. It is shown from simulation results that the proposed IFO estimator achieves robust estimation with low processing complexity in the presence of the FFO, where the conventional approaches show unsatisfactory performance.
The remainder of this paper is structured as follows. A signal model used in this paper is described in Section 2. In Section 3, the existing IFO detection methods are briefly addressed when applied to the ISDB-T system. Section 4 presents an efficient IFO estimation method utilizing the TMCC information as a pilot symbol, and its detection accuracy is numerically discussed in terms of the probability of erroneous estimations. In Section 5, simulation results are provided to verify the reliable operation of the proposed IFO estimator, followed by concluding remarks in Section 6.
2. System Description
Let us consider an OFDM system which uses N-point FFT and non-zero subcarriers. In the frequency domain, NSCs are zero-padded. The frequency-domain signal is transformed by an N-point inverse FFT (IFFT) unit to create the time-domain signal, and a guard interval (GI) with a length of samples is copied at the front of the OFDM symbol to remove both the ISI and ICI. Then, the n-th sample of the l-th OFDM symbol can be written by
where is the symbol at subcarrier k with transmitted power . Correspondingly, the effective duration of each OFDM symbol is equal to , where T is the sampling period satisfying the Nyquist rate and . At the transmitter, the equivalent baseband signal takes the expression
where for , and elsewhere.
The radio signal is transmitted through a multipath fading channel corrupted by additive white Gaussian noise (AWGN). Due to the mismatch between the receiver and transmitter oscillators, the local oscillator’s frequency is different from the received carrier frequency , so that the frequency offset remains after down conversion. Since the performance of IFO estimators is only marginally influenced by the STO [15,16,17], we restrict our attention to the detection of the IFO, considering the situation where the STO has been perfectly known at the receiver. Meanwhile, let us assume that the FFO has been estimated irrespective of the existence of the IFO so that there will remain a small FFO. As such, the time-domain signal at the receiving side is written by
where ⊗ is the linear convolution, denotes the channel impulse response (CIR), and denotes a complex zero-mean AWGN process. Considering perfect knowledge of the STO, the time-domain signal sampled at the time instant is given by [16,17]
where , is the normalized frequency offset by subcarrier spacing , is the equivalent discrete-time CIR, and is a complex zero-mean AWGN having variance . According to the amount of the frequency offset between the receiver and transmitter oscillators, the frequency offset can be divided into an integer part and a fractional part , leading to . After extracting the GI samples and taking the FFT operation at the receiver, the frequency-domain signal at subcarrier k over the l-th symbol duration appears as
where is the power leakage due to the FFO, is the FFT of with variance , is the contribution to ICI with variance , and is the FFT of with variance . For small values of FFO, and the variance of ICI can be easily obtained as [19].
In the ISDB-T system, a flexible and high-efficiency video/audio coding system, such as MPEG-4 advanced video coding (MPEG-4 AVC) is adopted. As a result, many types of broadcasting services, such as HDTV, HDTV/SDTV, and multi-channel SDTV are supported by ISDB-T. For this purpose, the entire bandwidth is evenly split into 13 segments, such that each segment can support different services using different MCS. The bandwidth of ISDB-T is classified into two types: wideband ISDB-T composed of 13 segments, and narrowband ISDB-T using one, or up to three segments. The broadband ISDB-T is used to simultaneously provide a range of services, such as HDTV and other high-speed multimedia services. Figure 1 shows the ISDB-T service examples and transmission signals. Some kinds of pilot and control symbols, such as SP, CP, AC, and TMCC, are specified to enable reliable synchronization between the transmitter and receiver, whose configuration varies according to the ISDB-T segment format. The CP is mainly utilized to perform time and frequency synchronization [20,21], whereas the SP is provided only in coherent modulated segments for the purposes of channel estimation [22,23]. The AC2 is present only in differential modulated segments. On the other hand, the TMCC signal is used to carry some sort of basic transmission information, like hierarchical configuration and OFDM-segment transmission parameters. The multiple uses of the TMCC signal can also be explored for receiver synchronization. Since the TMCC is the information-bearing signal, the existing pilot-aided IFO estimation schemes are not applied directly to ISDB-T when the TMCC information is used as a pilot symbol.
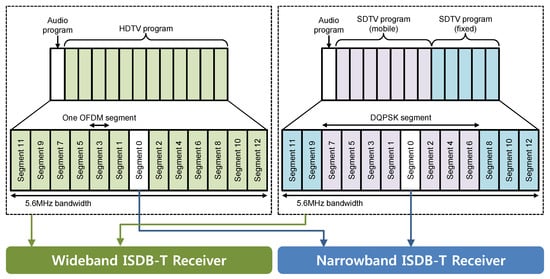
Figure 1.
Configuration of ISDB-T transmission.
3. Conventional Detection Schemes
In OFDM, the IFO is generally detected exploiting redundant information present in the OFDM symbol [12,13,14,15], which is called blind estimation. Meanwhile, the IFO estimation method can be developed by performing pilot-based correlation in the frequency domain [15,16,17]. The former has the problem of high computational load when compared to the latter. Although the blind estimation strategy is too computationally intensive, it can be considered as a possible candidate because the number of explicit pilot symbols is limited, and some sort of pilot configuration is available only after TMCC decoding in the ISDB-T system.
3.1. Conventional Scheme A
In [12], the blind IFO estimation scheme was proposed using the power difference between data and null subcarriers. In this approach, the power-based objective metric is given by
where m is the trial value for offset-matching, is the set of non-zero data subcarrier indices including members, is the set of NSC indices including members, and is the magnitude operation. The IFO can be estimated by
where M is the maximum allowable range of , which is determined by the stability between the oscillators at the transmitting and receiving ends. The performance of such a blind method depends on the ratio between the number of data subcarriers, , and the number of null subcarriers, .
3.2. Conventional Scheme B
Here, another blind detection method is presented employing a data-based objective function between two consecutive QPSK symbols [15]:
where , denotes the conjugate product from two consecutive observations, and and are the real and imaginary components of the enclosed complex number, respectively. Considering that the QPSK modulation is used for date subcarriers and the signal-to-noise ratio (SNR) is high, the data-based objective metric is approximated as
The IFO can be estimated identically to (7) with replaced by . Despite achieving good performance, this scheme can only be applied to QPSK modulation, and its computational complexity is high, proportional to the number of used subcarriers.
3.3. Conventional Scheme C
Contrary to the blind estimation method, a pilot-aided IFO estimation scheme uses periodic pilot symbols, as developed in [15]. By using CPs, the basic concept can be straightforwardly extended to the ISDB-T configuration. The CP-based objective metric can be represented by
where is the set of CP subcarrier indices having members, and is assumed to be a symbol available to the receiver. In such a case, the pilot-assisted IFO detection scheme is expressed in an identical fashion to (7) with replaced by .
Since the number of CP subcarriers is insufficient in the ISDB-T system, the TMCC subcarrier can be an alternative, which is non-symmetrically distributed in the frequency domain. Because of the information-bearing feature of the TMCC signal, however, the IFO estimation schemes, which depend on the explicit pilot symbol like CP, cannot be directly applied when the TMCC signal is used as a pilot symbol. Hence, some changes to the existing pilot-assisted estimation method are necessary for reliable IFO estimation.
4. Proposed Detection Scheme
In this section, a reduced-complexity IFO detection method that depends on the inherent property of the TMCC information is proposed in the digital terrestrial television broadcasting system using BST-OFDM. As a performance measure, we analytically derive the probability of erroneous estimation of the proposed IFO estimator.
4.1. Algorithm Description
Since the TMCC signal is information-bearing, its content is available after TMCC decoding and the pilot-compensated signal is not obtained in the presence of the IFO, as performed in (10). On the other hand, the common TMCC information is present in fixed subcarrier positions regardless of modulation mode, which is transmitted by ways of differential binary phase-shift keying (DBPSK) modulation. Using this property of the continuous-type TMCC signal, the correlation from two received OFDM symbols is in the form:
where is the contribution to combined ICI given by
and is the contribution to the combined AWGN, equal to
As can be seen from (11), the residual FFO affects the objective metric in two ways—one is to rotate the phases of all sub-carriers by the same amount, and the other is to cause the ICI.
Using the differential relation between two consecutive symbols, the TMCC-based objective metric can be defined as
where is the set of TMCC subcarrier indices having members, and the condition informs us that a true IFO exists at the m-th shift, or rather, . In this case, recognizing that for , the phase-rotated TMCC-based objective metric takes the form
where and denotes the differential relation from two consecutive TMCC symbols. For notational brevity, the phase rotation term was omitted in the first quantity on the right-hand side (RHS) in (15), since its effect is removed by taking the absolute value in the proposed approach. Note that is statistically equivalent to . Under the assumption of a relatively large , (15) can be safely approximated as
From the central limit theorem, (16) can be modeled as a Gaussian random variable having mean and variance , where is the variance of , and is the variance of , if , is an unknown random signal whose mean is zero. In this hypothesis, is expressed as
which can be assumed to be a zero-mean Gaussian random variable with variance , where is the variance of the first term on the RHS of (17).
Since the DBPSK-modulated TMCC signal is common to all TMCC subcarriers, for at a true trial ; that is, is constant regardless of TMCC subcarrier indices. Therefore, the estimated IFO is obtained by taking the absolute value of (14)
where the use of instead of does not affect the detection performance because the effect of is removed by taking the absolute value.
4.2. Probability of Erroneous Estimation
In order to measure how well the estimator performs, the probability of erroneous estimation is derived in the AWGN channel. From (16), the probability density function (PDF) of under hypothesis , or equivalently when , can be given by
where , , and stands for the modified Bessel function of the first kind and zero order. Under hypothesis (), it can be seen from (17) that has the Rayleigh distribution
where . For equally likely IFOs, the probability of a correct estimation is expressed as
Using the binomial expansion, (22) can be further derived as
where the integral has a closed-form solution [24]. After some mathematical manipulations, a closed-form expression for the probability of correct estimation can be obtained as
5. Simulation Results
In this section, the performance of the IFO estimation schemes is evaluated in the ISDB-T system, with transmission parameters given in Table 1. The carrier center frequency was set to MHz, and the sampling time was [4]. Let us consider the six-path Typical Urban (TU) and Hilly Terrain (HT) channels with a maximum excess delay of and , respectively [25]. The SNR is defined by the ratio of the received average signal power to the noise power, including the NSCs. To make a parallel between (10) and (14), we consider the situation where the CP-based objective metric (10) uses the same number of explicit pilot symbols as the TMCC, that is, , although the number of usable CPs is small when compared to that of TMCC subcarriers. In order to apply (10) to the ISDBT system, it is thus assumed that the TMCC information has been perfectly decoded. In the following, the effectiveness of the IFO estimation schemes is evaluated in terms of the probability of erroneous estimation and the computational complexity resulted from the estimation of the IFO.

Table 1.
Main system parameters.
5.1. Performance Evaluation
Figure 2 presents the probability of erroneous estimation of the proposed IFO estimation scheme in the AWGN channel, considering the presence of residual FFO. A good match between analytical curves (lines) and simulated curves (symbols) is observed, regardless of the ISDB-T mode and residual FFO. In the case of the 2k mode, there is a slight gap between the theoretical and simulated curves for the high SNR region due to inaccuracy of the approximation used in (16), which tends to be more accurate as increases. As expected, the performance of the IFO estimation scheme improves as the FFT size N increases, because the number of TMCC subcarriers is exactly proportional to the ISDB-T mode, as shown in Table 1. In particular, to cope with a limited number of TMCC subcarriers in 2k mode, the averaging strategy can be an appealing solution at the sacrifice of the processing delay, since the TMCC signal is continuously transmitted. In addition, the increase of uncertainty region for the IFO leads to the loss of detection accuracy, which becomes more prominent for a smaller number of TMCC subcarriers.
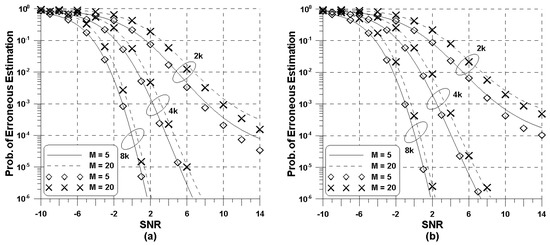
Figure 2.
Performance of the proposed IFO estimation scheme for the AWGN channel: (a) , (b) .
Figure 3 shows the probability of an erroneous estimation of the proposed and conventional IFO estimators in the flat fading channel with the IFO range being fixed to , taking into consideration different transmission modes. It can be seen that the performance of the pilot-aided IFO detection scheme (10) can be better than that of the proposed detection scheme (14) in the absence of residual FFO if the same number of pilot symbols as the TMCC is used in (10). The performance gap between both IFO estimators (10) and (14) is reduced to less than 1dB as the number of pilots increases. When the residual FFO is present, however, it follows that this gap between both methods is further diminished, and eventually, the performance trend becomes reversed as the SNR increases. This is mainly because the performance of (14) is affected by the ICI only, whereas the performance of (10) is dependent on both the ICI and phase rotation caused by . When , the probability of erroneous detection of the blind estimation schemes (6) and (9) approaches zero when the SNR tends to infinity, whereas the probability of erroneous detection of the other schemes suffers from error floors. Due to the limited number of TMCC subcarriers in 2k mode, the blind estimation scheme (9) outperforms the proposed estimation scheme, whereas this phenomenon is reversed as grows in 4k mode. This can be explained by recalling that the performance of the blind detection is constant to the ISDB-T mode.
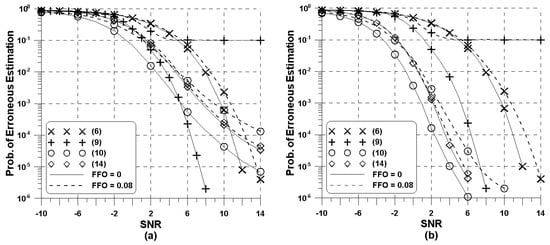
Figure 3.
Performance of the conventional and proposed IFO estimation schemes for the flat fading channel: (a) 2k mode, (b) 4k mode.
Figure 4 depicts the probability of erroneous estimation of the proposed and conventional IFO estimators in the TU channel, under the same simulation scenarios of Figure 3. Immediately, one can see that the trend of the curves is similar to that in Figure 3. Regardless of the ISDB-T mode, it is observed that the detection capability of the conventional IFO estimation methods (6) and (9) do not change. The reason for this is that its performance depends on the ratio of the number of data and null subcarriers. It is evident from Table 1 that this ratio is almost the same for all ISDB-T modes. More interestingly, the increased frequency selectivity gives rise to the performance degradation for all IFO estimators, when compared to the case of the flat fading channel. This phenomenon is more pronounced in the case of the blind estimation schemes (6) and (9). Due to its high vulnerability to frequency selectivity and residual FFO, there are some limitations to applying the conventional schemes (6) and (9) to the ISDB-T system.
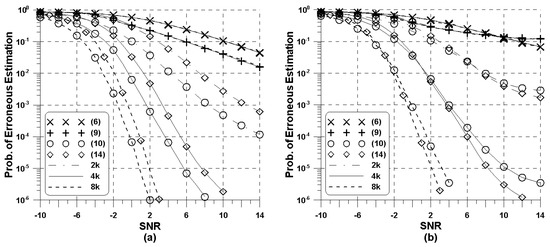
Figure 4.
Performance of the conventional and proposed IFO estimation schemes for the TU channel: (a) , (b) .
In Figure 5, the probability of erroneous estimation of the IFO estimation methods for the ISDB-T 4k mode is illustrated as a function of when dB is fixed. Here, we adopted the TU and HT channels. From the presented results, the conventional detection schemes (6) and (9) fail to properly estimate the IFO in the presence of the FFO. On the other hand, it can be found that the proposed IFO detection scheme is not significantly affected by the amount of the FFO, whereas the detection accuracy of the conventional estimation method (10) severely deteriorates at or higher. This observation indicates that the presence of residual FFO is not a crucial issue for the proposed IFO detection. Therefore, the proposed detection strategy can alleviate the need for sophisticated FFO estimation techniques.
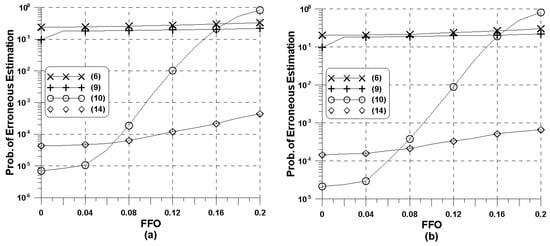
Figure 5.
Performance of the conventional and proposed IFO estimation schemes versus when : (a) TU channel, (b) HT channel.
5.2. Complexity Comparison
Finally, we compare the processing complexity of the IFO detectors. For a fair complexity comparison, the mathematical operations were converted to the number of real floating point operations (flops). In doing so, we counted one complex addition as two real flops, whereas one complex multiplication is equivalent to six real flops [26]. It can be readily seen that the flops of the algorithms (6), (9), (10) and (14) are , , , and , respectively. Considering the number of IFO hypotheses in (7) and (18), the total number of flops is times. It is worth mentioning that the complexity of the proposed detection method (14) is about 2/5 times that of the conventional scheme (10), if is applied in (10) and (14).
When , the computational load of the proposed blind IFO estimator is reduced by about 60% compared to that of the pilot-aided IFO estimator (10), while up to 99% complexity reduction over the blind IFO estimation scheme (9) is obtained. It is concluded that the use of the TMCC signal ensures significant savings of mathematical operations, achieving a good estimation performance in the presence of typical values of residual FFO.
6. Conclusions
In the ISDB-T system, the hierarchical configuration differs from which modulation mode is used in OFDM segment. For reliable frequency synchronization, it is crucial to accomplish IFO estimation without a priori knowledge on the segment format. To address this requirement, we presented an effective IFO detection method independent of the transmitted modulation mode in the ISDB-T system. For this purpose, the redundantly transmitted TMCC signal was used for IFO detection. Because of the information-bearing feature of the TMCC signal, the existing IFO detection strategy cannot be directly used for the ISDB-T system. The proposed approach, using the TMCC signal as the pilot symbol, was found to facilitate a modulation-mode, independent IFO detection. Like the pilot-aided method, the performance of the blind method was greatly influenced by the phase rotation due to the existence of residual FFO, whereas the detection accuracy of the proposed scheme was insensitive to residual FFO. The performance was assessed in terms of theoretical probability of erroneous estimation. The simulation results have shown that such a design relieves computational load and provides good detection performance in the presence of residual FFO and frequency selective channel distortion. It has also been found that the ISDB-T system contains rich structural information, enabling it to effectively detect the IFO.
Author Contributions
Y.-A.J. designed the detection scheme and carried out computer simulations. Y.-H.Y. performed numerical analysis of the detection method and verified simulated results.
Funding
This research was supported by Basic Science Research Program through the National Research Foundation of Korea(NRF) funded by the Ministry of Education(NRF-2018R1D1A1B07048819).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Document A/322. ATSC Standard: Physical Layer Protocol. Available online: https://www.atsc.org/ (accessed on 16 July 2018).
- GB20600-2006. Framing Structure, Channel Coding and Modulation for Digital Television Terrestrial Broadcasting System. Available online: https://www.gbstandards.org/ (accessed on 16 July 2018).
- ETSI EN 302 755 V.1.4.1. Digital video broadcasting (DVB). Frame Structure Channel Coding and Modulation for a Second Generation Digital Terrestrial Television Broadcasting System (DVB-T2); Association à but Non Lucratif: Grasse, France, 2015. [Google Scholar]
- ARIB Standard STD-B31 Ver.2.2. Transmission System for Digital Terrestrial Television Broadcasting. Available online: https://www.arib.or.jp/ (accessed on 16 July 2018).
- El-Hajjar, M.; Hanzo, L. A survey of digital television broadcast transmission techniques. IEEE Commun. Surv. Tutor. 2013, 15, 1924–1941. [Google Scholar] [CrossRef]
- Sotelo, R.; Joskowicz, J.; Rondan, N. An integrated broadcast-broadband system that merges ISDB-T with HbbTV 2.0. IEEE Trans. Broadcast. 2018, 64, 709–720. [Google Scholar] [CrossRef]
- Yuan, J.; Torlak, M. Joint CFO and SFO estimator for OFDM receiver using common reference frequency. IEEE Trans. Broadcast. 2016, 62, 141–149. [Google Scholar] [CrossRef]
- Ai, B.; Ge, J.-H.; Wang, Y.; Yang, S.-Y.; Liu, P. Decimal frequency offset estimation in COFDM wireless communications. IEEE Trans. Broadcast. 2004, 50, 154–158. [Google Scholar] [CrossRef]
- Cvetkovic, Z.; Tarokh, V.; Yoon, S. On frequency offset estimation for OFDM. IEEE Trans. Wirel. Commun. 2013, 12, 1062–1072. [Google Scholar] [CrossRef]
- Lmai, S.; Bourre, A.; Laot, C.; Houcke, S. An efficient blind estimation of carrier frequency offset in OFDM systems. IEEE Trans. Veh. Technol. 2014, 63, 1945–1950. [Google Scholar] [CrossRef]
- Zhou, M.; Feng, Z.; Liu, Y.; Huang, X. An efficient algorithm and hardware architecture for maximum-likelihood based carrier frequency offset estimation in MIMO systems. IEEE Access 2018, 6, 50105–50116. [Google Scholar] [CrossRef]
- Huang, D.; Letaief, K.B. Carrier frequency offset estimation for OFDM systems using null sub-carriers. IEEE Trans. Commun. 2006, 54, 813–823. [Google Scholar] [CrossRef]
- Zhu, J.; Lee, W. Carrier frequency offset estimation for OFDM systems with null subcarriers. IEEE Trans. Veh. Technol. 2006, 55, 1677–1690. [Google Scholar] [CrossRef]
- Zhan, Q.; Minn, H. New integer normalized carrier frequency offset estimators. IEEE Trans. Signal Process. 2015, 63, 3697–3710. [Google Scholar] [CrossRef]
- Toumpakaris, D.; Lee, J.W.; Lou, H.-L. Estimation of integer carrier frequency offset in OFDM systems based on the maximum likelihood principle. IEEE Trans. Broadcast. 2009, 55, 95–108. [Google Scholar] [CrossRef]
- Pham, T.H.; Fahmy, S.A.; McLoughlin, I.V. Efficient integer frequency offset estimation architecture for enhanced OFDM synchronization. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2016, 24, 1412–1420. [Google Scholar] [CrossRef]
- Li, D.; Li, Y.; Zhang, H.; Cimini, L.; Fang, Y. Integer frequency offset estimation for OFDM systems with residual timing offset over frequency selective fading channels. IEEE Trans. Veh. Technol. 2012, 61, 2848–2853. [Google Scholar] [CrossRef]
- Marey, M. Integer CFO estimation algorithm for SFBC-OFDM systems. IEEE Commun. Lett. 2018, 22, 1632–1635. [Google Scholar] [CrossRef]
- Murin, Y.; Dabora, R. Low complexity estimation of carrier and sampling frequency offsets in burst-mode OFDM systems. Wirel. Commun. Mob. Comput. 2016, 16, 1018–1034. [Google Scholar] [CrossRef]
- Dantas, C.; Castro, D.; Panazio, C. On enhancing the pilot-aided sampling clock offset estimation of mobile OFDM systems. J. Commun. Inf. Syst. 2016, 31, 108–117. [Google Scholar] [CrossRef]
- Jung, Y.A.; You, Y.H. Effective blind frequency offset estimation scheme for BST-OFDM based HDTV broadcast systems. Symmetry 2018, 10, 379. [Google Scholar] [CrossRef]
- Paderna, R.; Thang, D.Q.; Hou, Y.; Higashino, T.; Okada, M. Low-complexity compressed sensing-based channel estimation with virtual oversampling for digital terrestrial television broadcasting. IEEE Trans. Broadcast. 2017, 63, 82–91. [Google Scholar] [CrossRef]
- Ferdian, R.; Hou, Y.; Okada, M. A low-complexity hardware implementation of compressed sensing-based channel estimation for ISDB-T system. IEEE Trans. Broadcast. 2017, 63, 92–102. [Google Scholar] [CrossRef]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series, and Products; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Failli, M. Digital Land Mobile Radio Communications-COST 207; Final Report; Commission of the European Community: Brussels, Belgium, 1989. [Google Scholar]
- Golub, G.H.; Vanloan, C.F. Matrix Computations; The Johns Hopkins University Press: Baltimore, MA, USA, 1996. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).