Segmentation of Articular Cartilage and Early Osteoarthritis based on the Fuzzy Soft Thresholding Approach Driven by Modified Evolutionary ABC Optimization and Local Statistical Aggregation
Abstract
1. Introduction
2. Recent Methods of Cartilage Segmentation
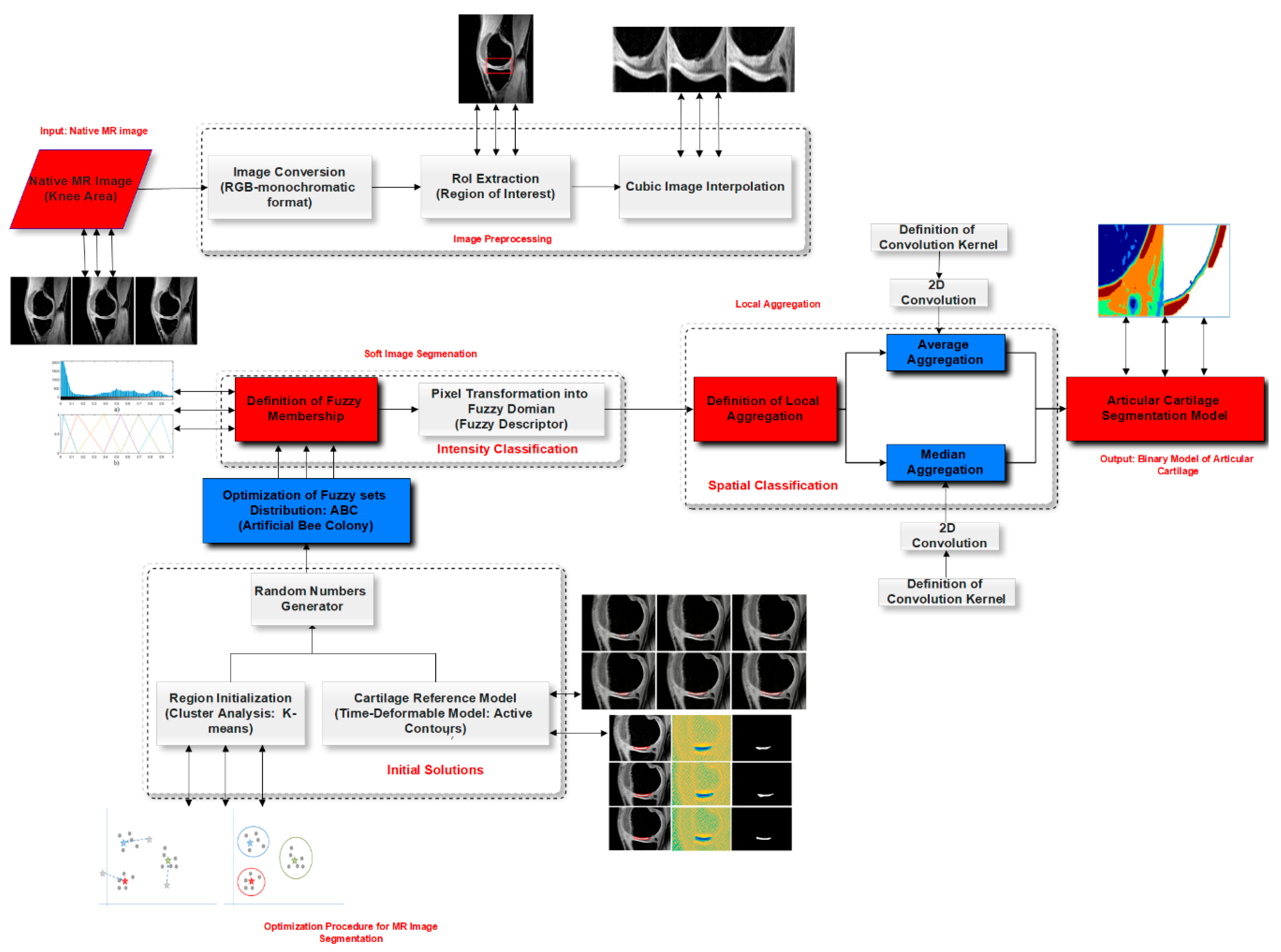
3. Materials and Methods
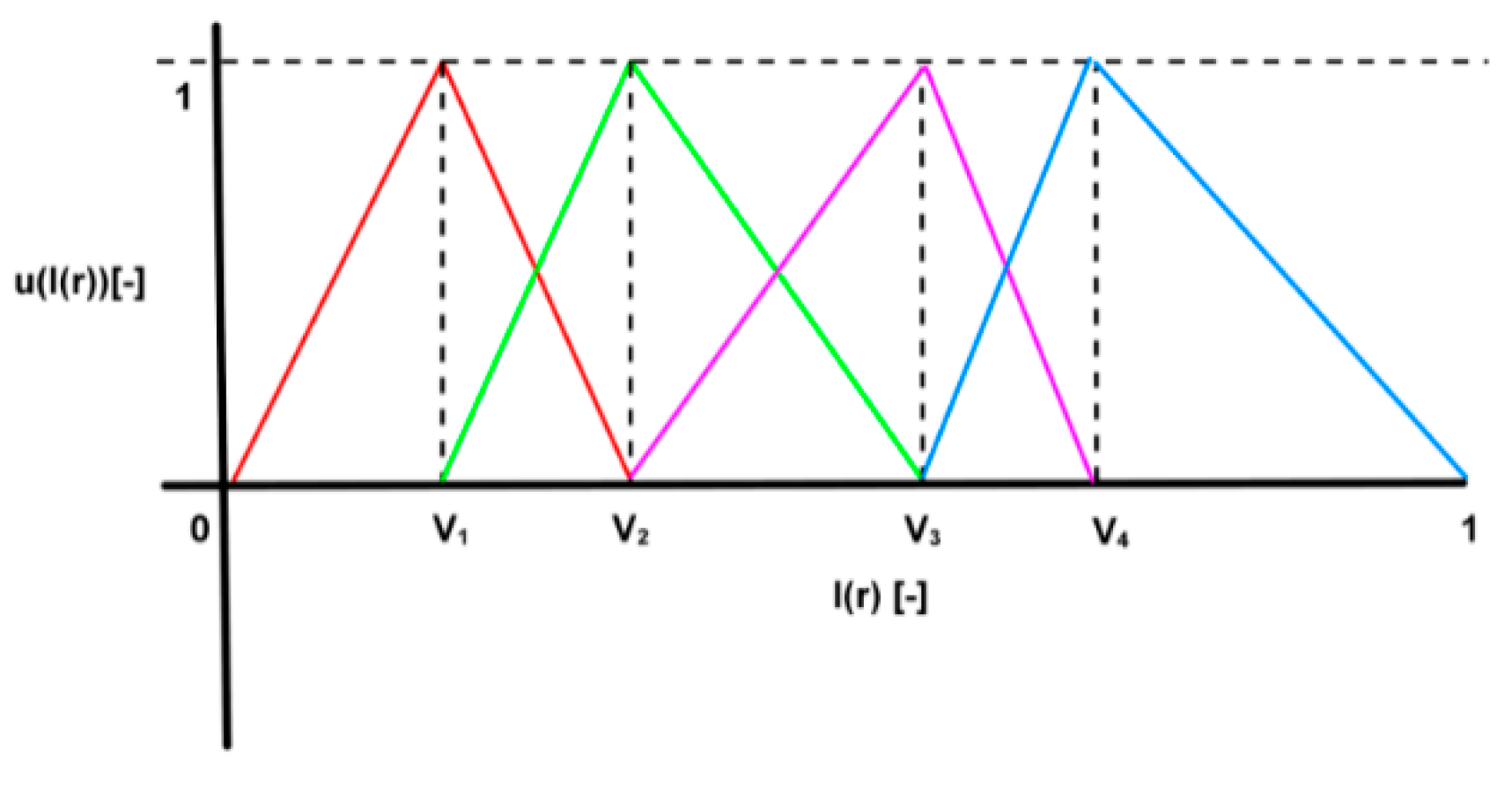
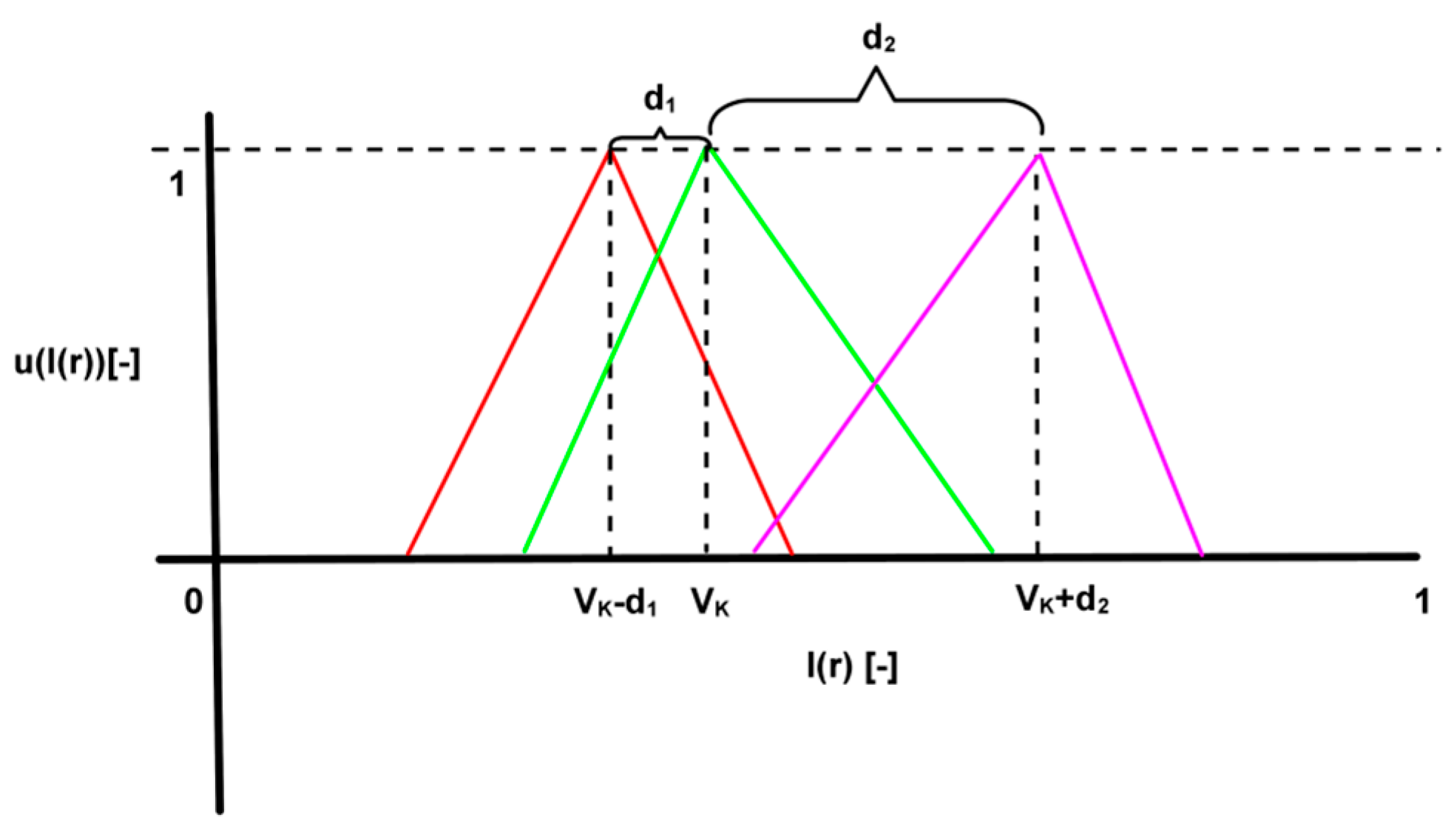
3.1. Soft Segmentation of Intensity Spectrum
- Complete division: , so that .
- Consistency: if , then .
- Normality: .
- Intersection between adjacent fuzzy sets: .
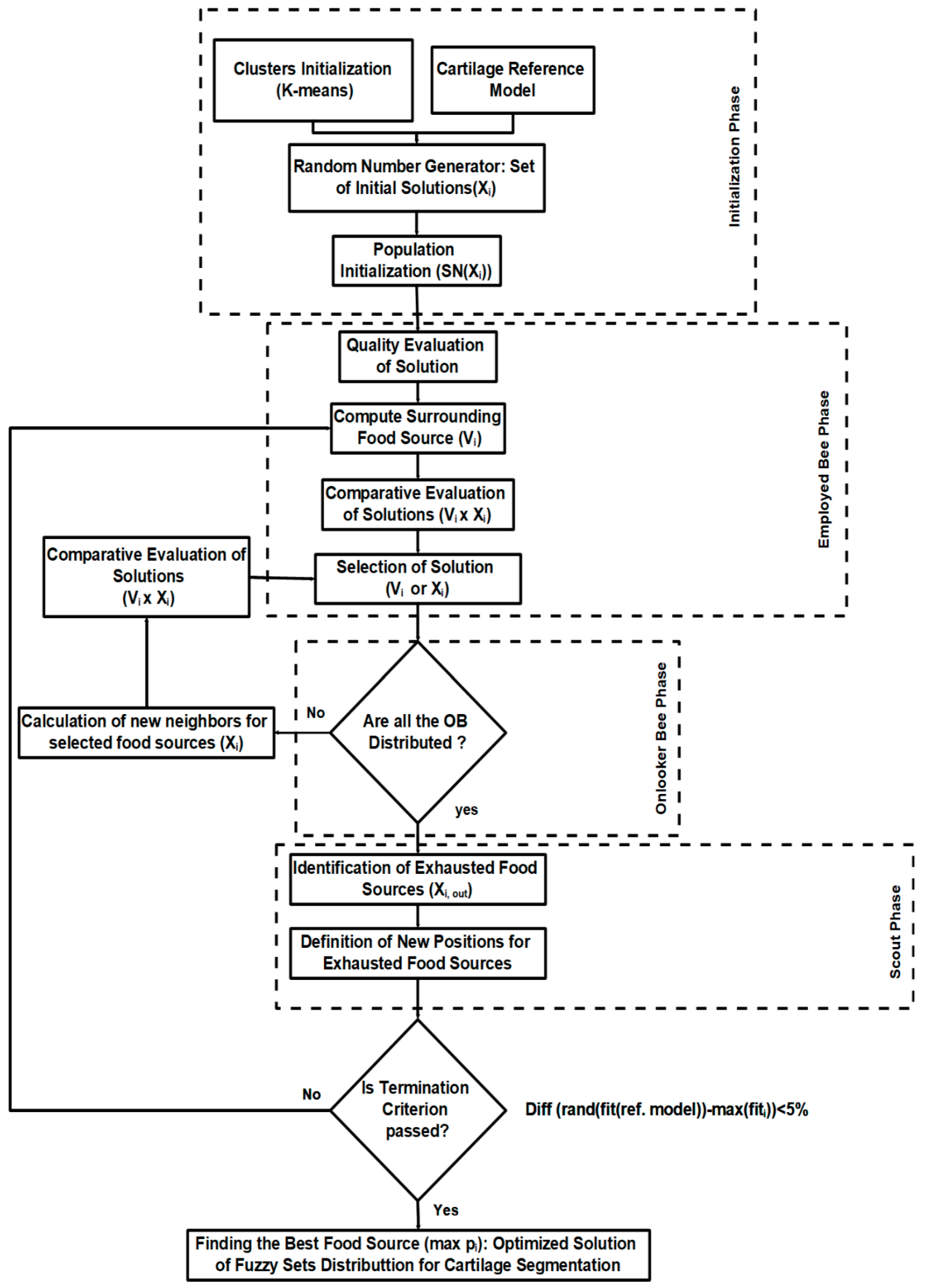
3.2. Process of Centroids Extraction
3.3. Modified ABC Algorithm
3.4. Features Extraction Based on Fitness Function
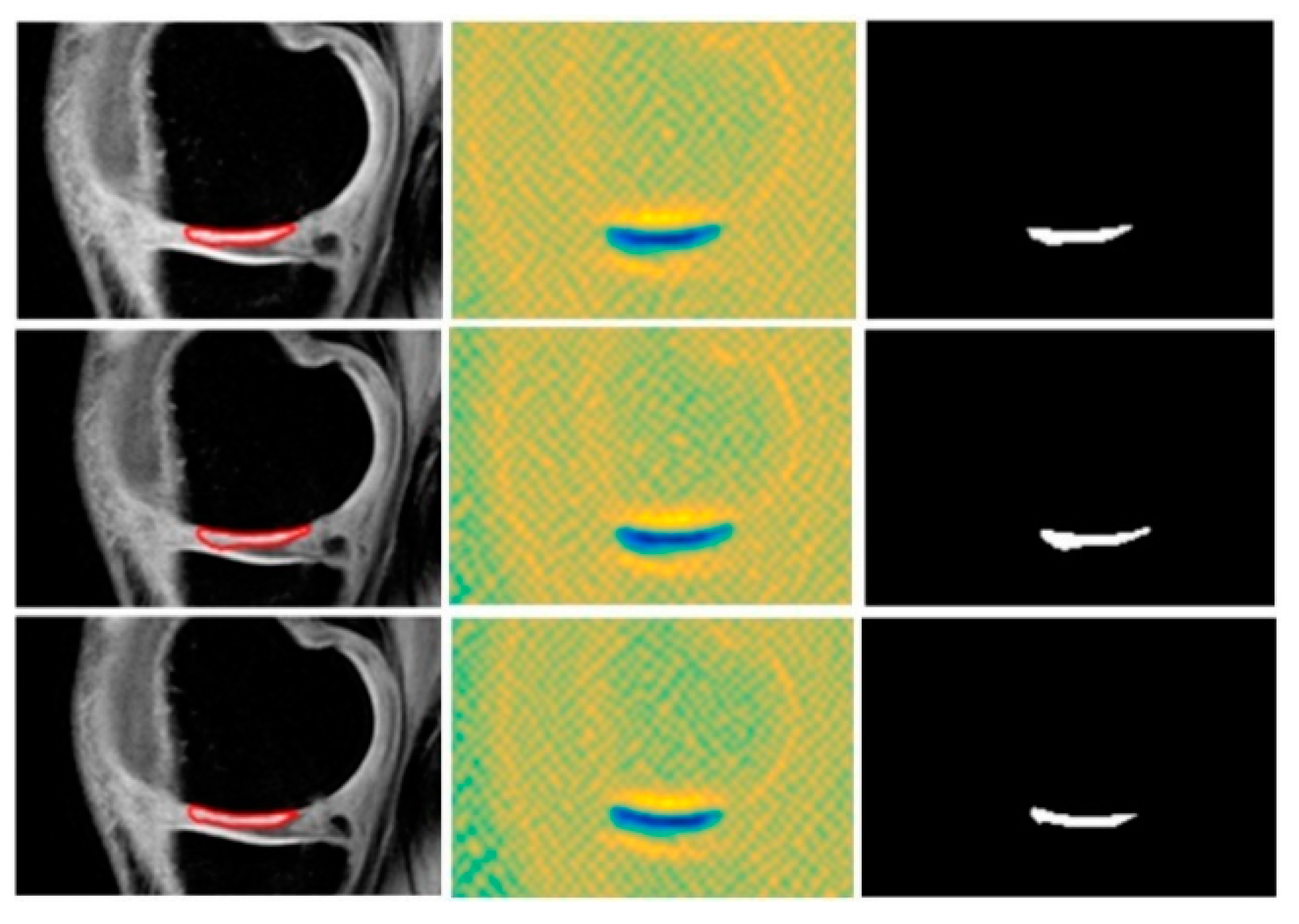
3.5. Local Statistical Aggregation
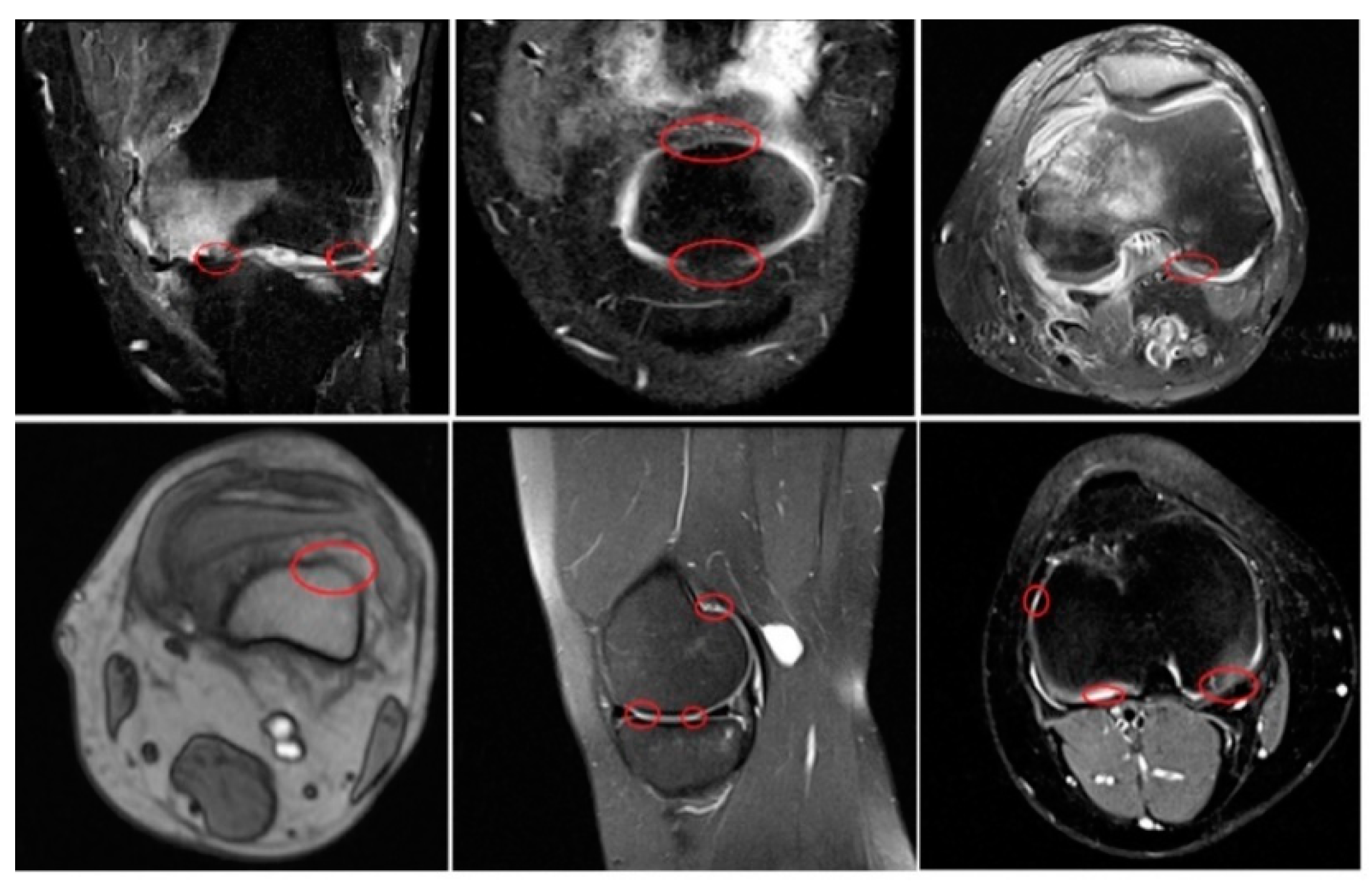
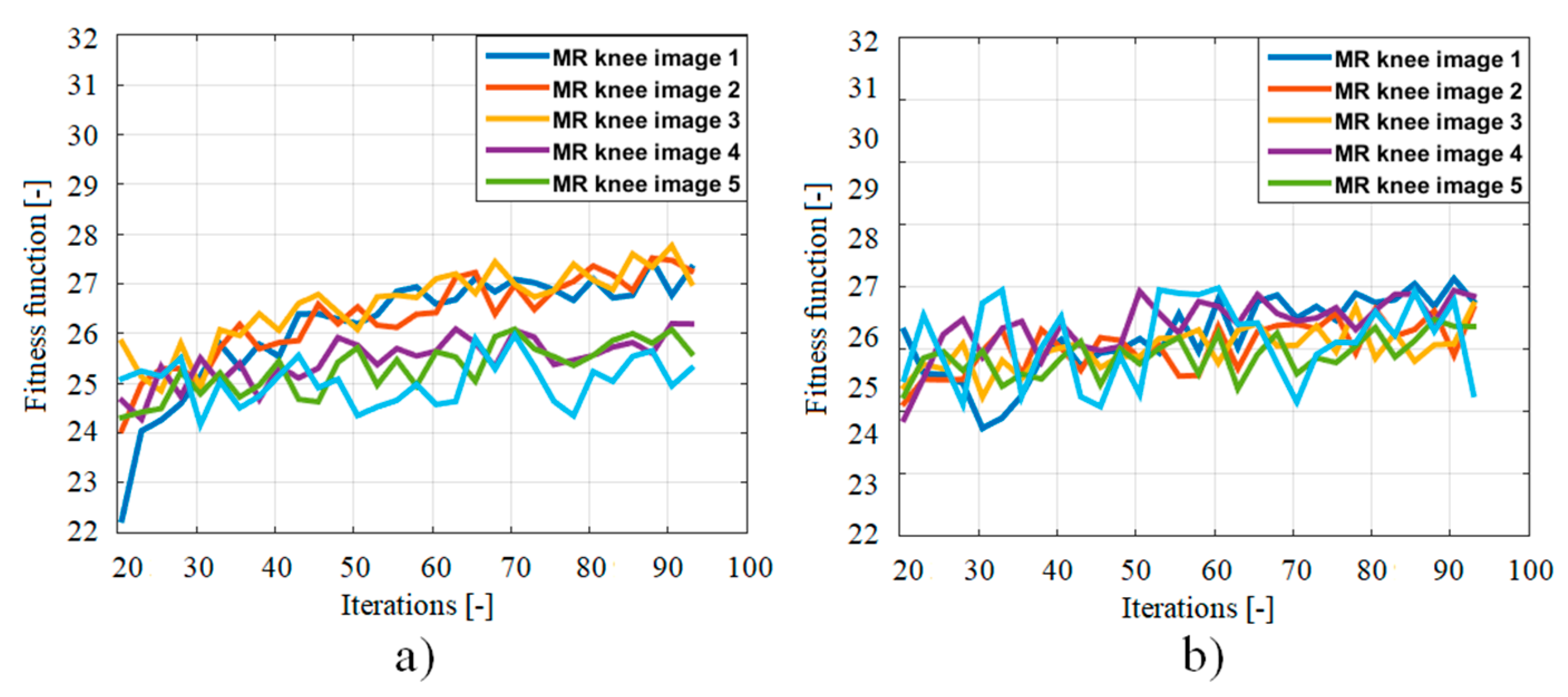
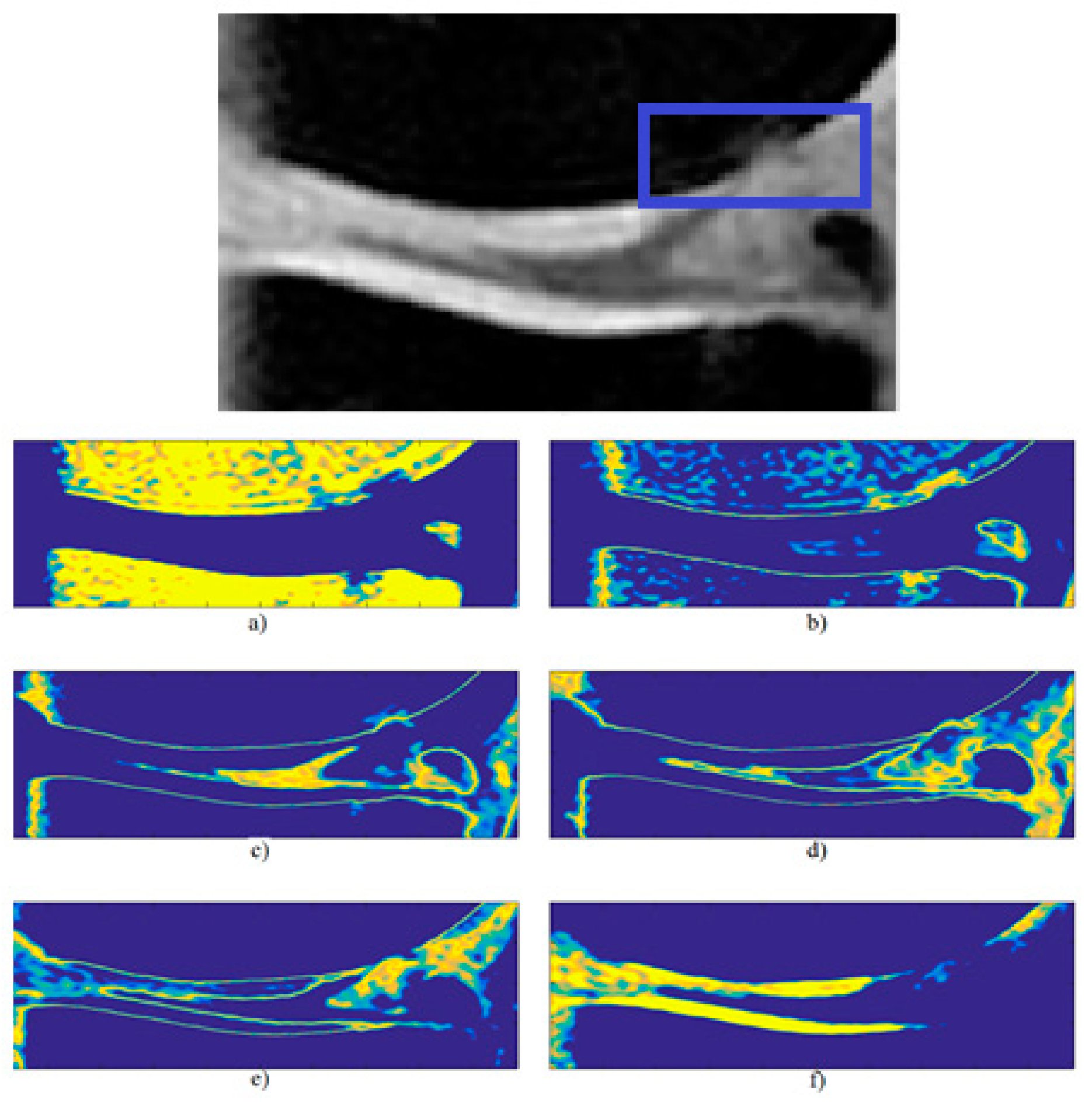
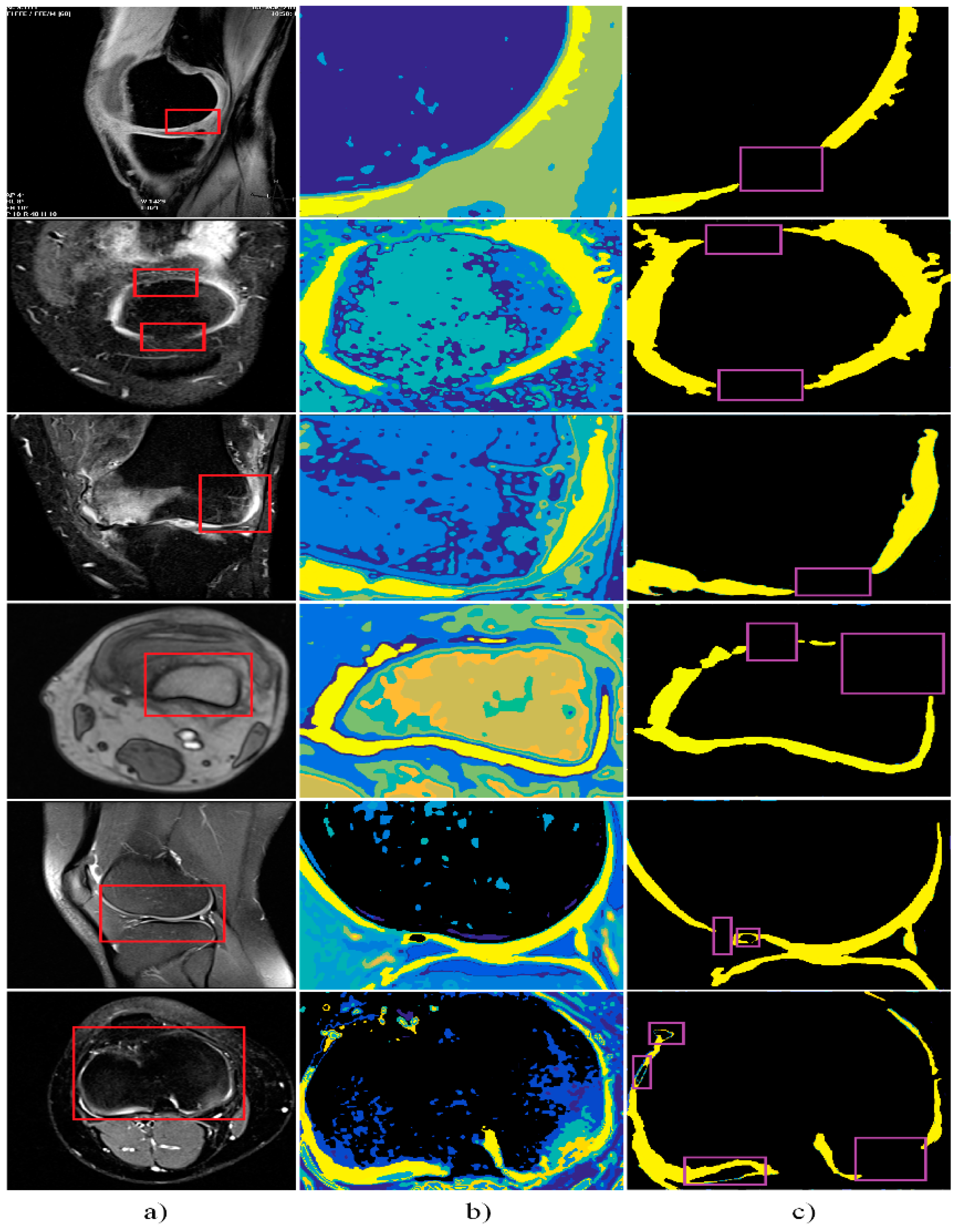
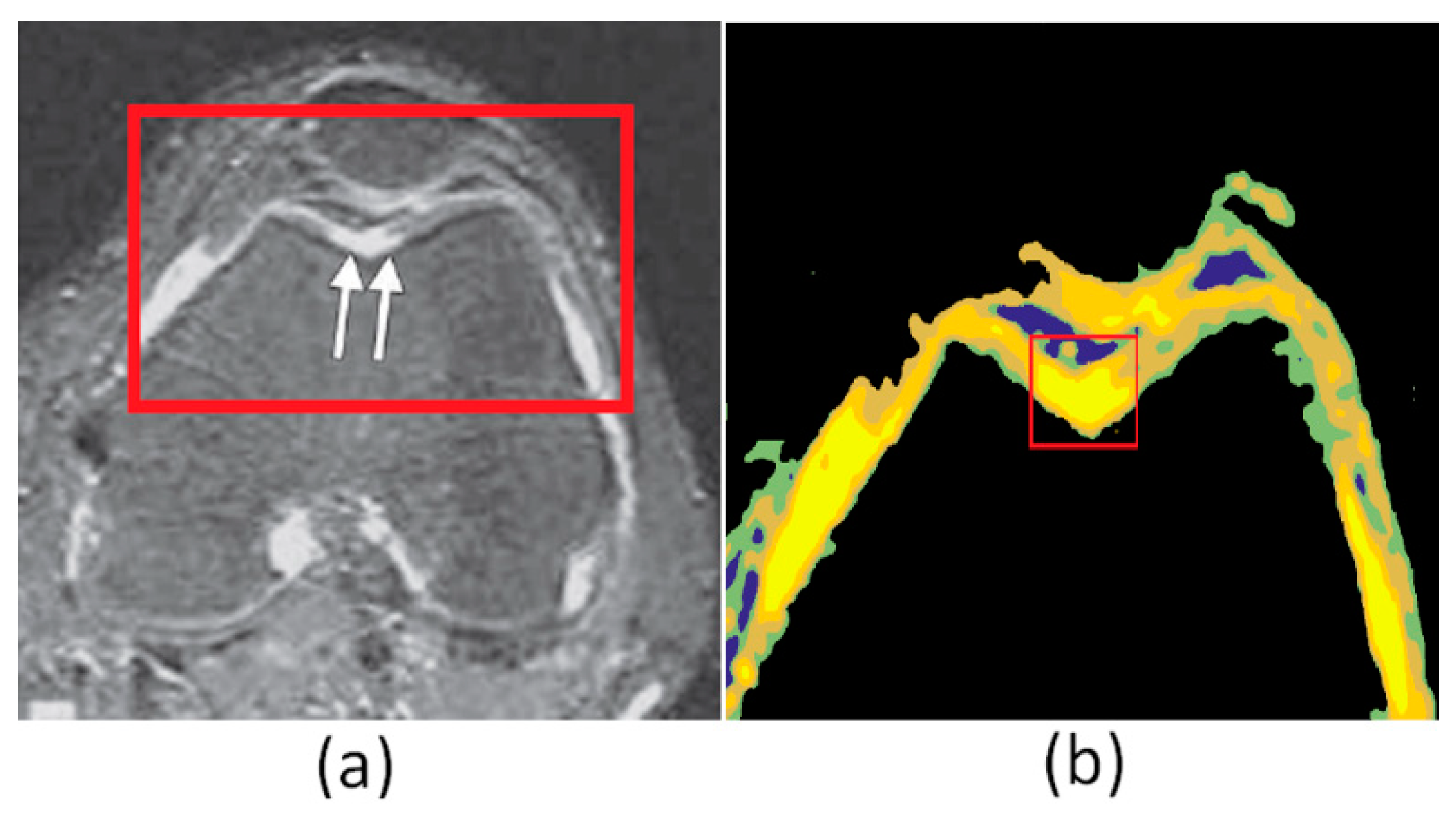
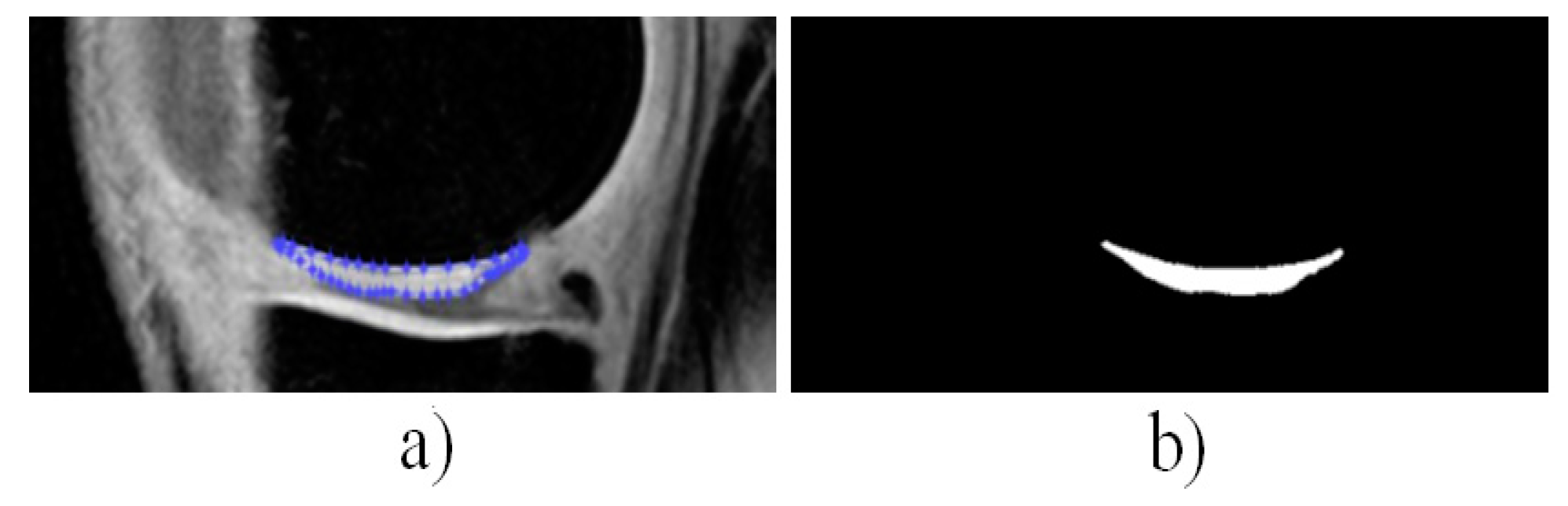
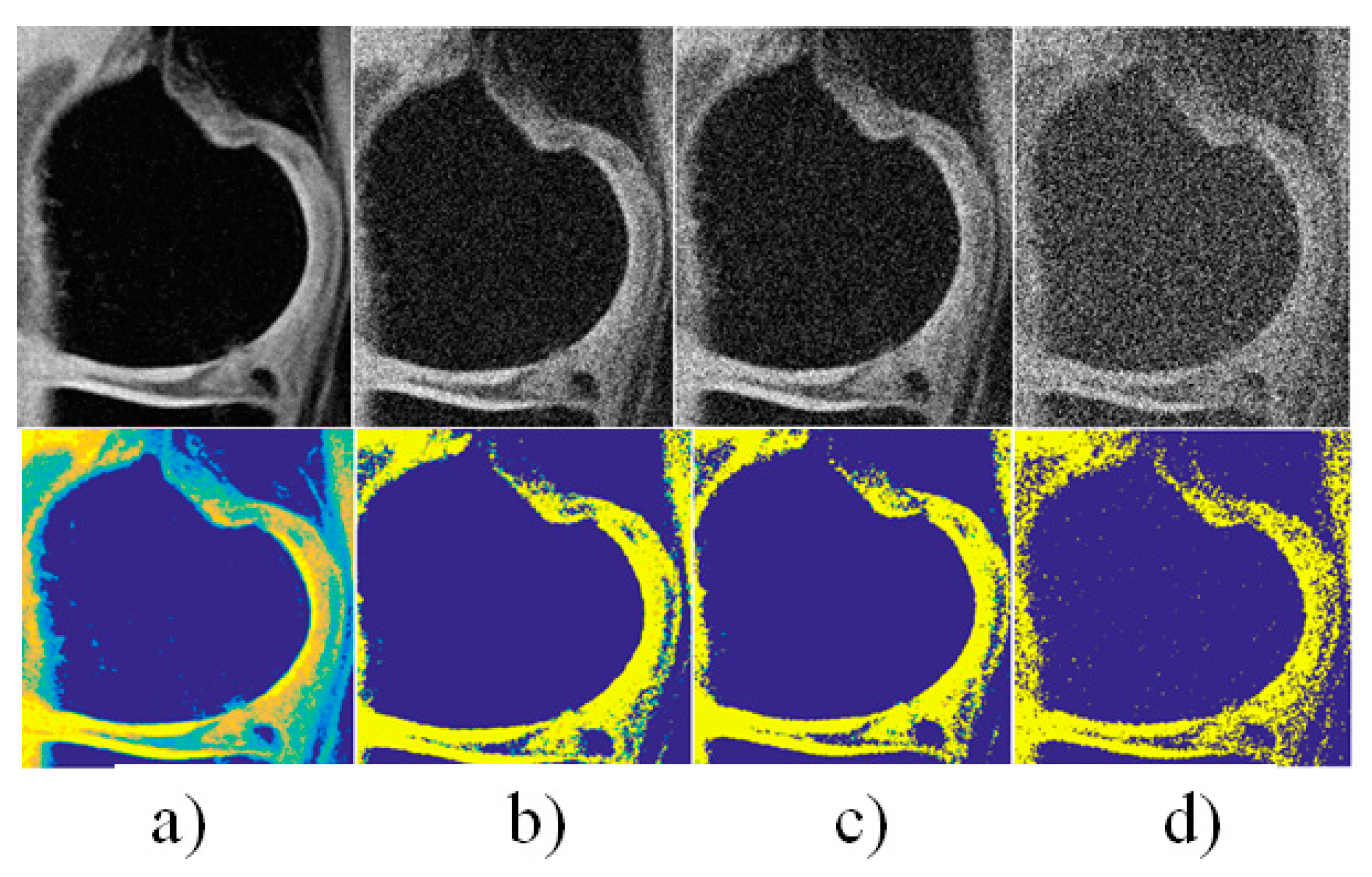
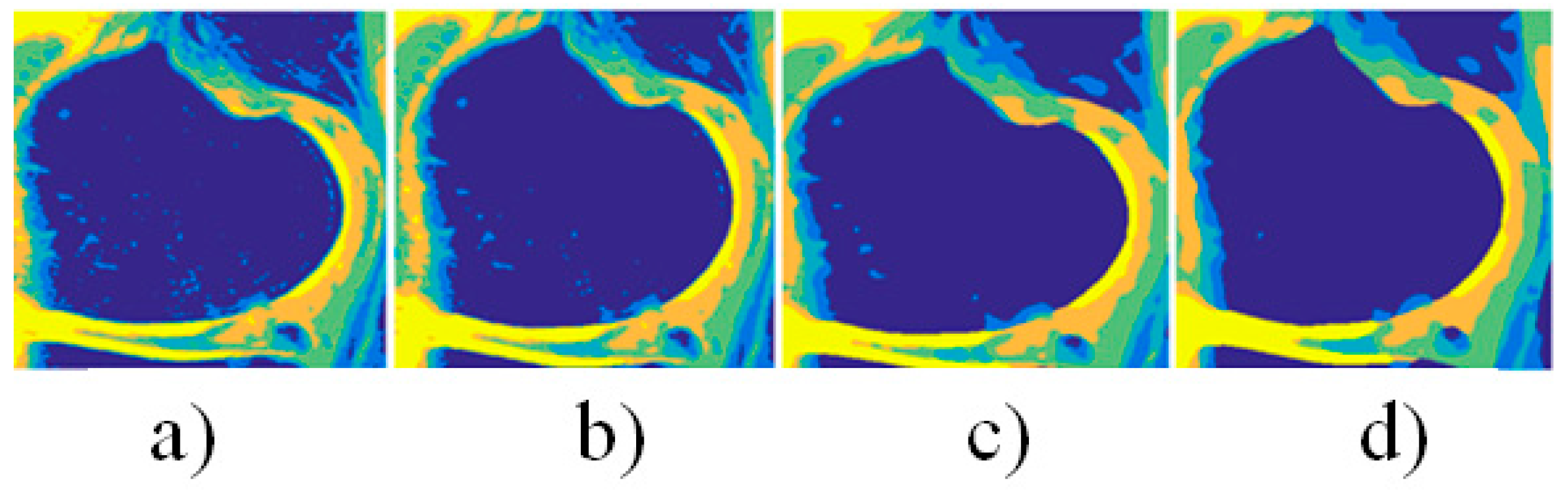
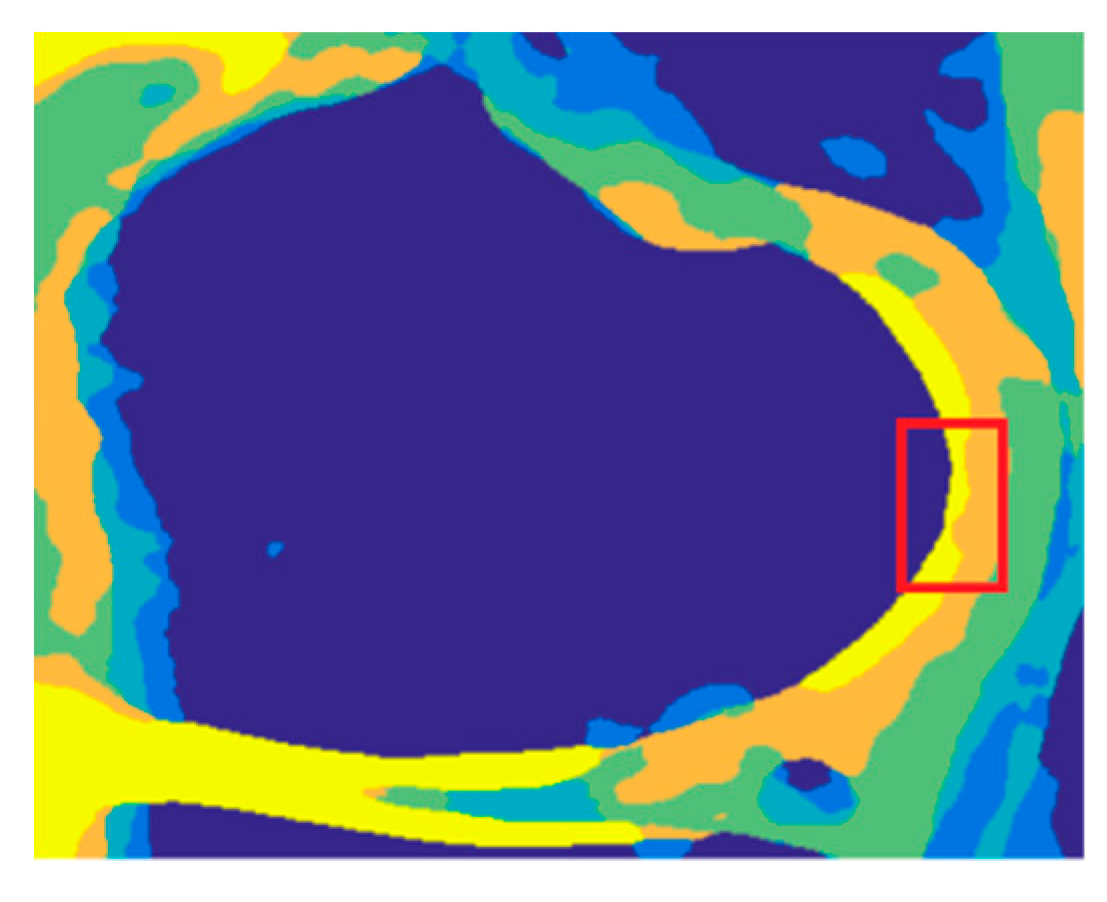
4. Results
5. Quantitative Comparison and Segmentation Performance
- Otsu thresholding (Otsu-N): Hard thresholding segmentation utilizing image partitioning into N regions.
- Fuzzy C means (FCM): Represents clustering. An algorithm generates clusters into c parts, attempts to find centroids of natural clusters in the data. For this task, a minimization of the inner clustering variance based on error function is used.
- Iterative thresholding (ITS): The initial thresholding is iteratively adjusted based on the local information and the resulting threshold is less sensitive against the noise.
- Maximal Spatial Probability (MASP): It is a segmentation, considering the spatial information. A probability of pixel’s belonging to respective class, in a frame of spatial restrictions, is defined as spatial probability.
6. Discussion
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Hayashi, D.; Roemer, F.W.; Jarraya, M.; Guermazi, A. Imaging of osteoarthritis. In Geriatric Imaging; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar] [CrossRef]
- Felson, D.T.; Niu, J.; Gross, K.D.; Englund, M.; Sharma, L.; Cooke, T.D.V.; Guermazi, A.; Roemer, F.W.; Segal, N.; Nevitt, M.C. Valgus malalignment is a risk factor for lateral knee osteoarthritis incidence and progression: Findings from the multicenter osteoarthritis study and the osteoarthritis initiative. Arthritis Rheum. 2013, 65, 355–362. [Google Scholar] [CrossRef] [PubMed]
- Link, T.M. MR imaging in osteoarthritis: Hardware, coils, and sequences. Radiol. Clin. 2009, 474, 617–632. [Google Scholar] [CrossRef] [PubMed]
- Guermazi, A.; Hayashi, D.; Roemer, F.W.; Felson, D.T. Osteoarthritis: A review of strengths and weaknesses of different imaging options. Rheum. Dis. Clin. 2013, 39, 567–591. [Google Scholar] [CrossRef] [PubMed]
- Park, H.J.; Kim, S.S.; Lee, S.Y.; Park, N.H.; Park, J.Y.; Choi, Y.J.; Jeon, H.J. A practical MRI grading system for osteoarthritis of the knee: Association with Kellgren-Lawrence radiographic scores. Eur. J. Radiol. 2013, 82, 112–117. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Pedoia, V.; Kumar, D.; Rivoire, J.; Wyatt, C.; Lansdown, D.; Amano, K.; Okazaki, N.; Savic, D.; Koff, M.F.; et al. Cartilage T 1ρ and T 2 relaxation times: Longitudinal reproducibility and variations using different coils, MR systems and sites. Osteoarthr. Cartil. 2015, 23, 2214–2223. [Google Scholar] [CrossRef] [PubMed]
- Shelbourne, K.D.; Urch, S.E.; Gray, T.; Freeman, H. Loss of normal knee motion after anterior cruciate ligament reconstruction is associated with radiographic arthritic changes after surgery. Am. J. Sports Med. 2012, 40, 108–113. [Google Scholar] [CrossRef] [PubMed]
- Hunter, D.J.; Arden, N.; Conaghan, P.G.; Eckstein, F.; Gold, G.; Grainger, A.; Zhang, W. Definition of osteoarthritis on MRI: Results of a Delphi exercise. Osteoarthr. Cartil. 2011, 19, 863–969. [Google Scholar] [CrossRef]
- Sheehy, L.; Culham, E.; McLean, L.; Niu, J.; Lynch, J.; Segal, N.A.; Cooke, T.D.V. Validity and sensitivity to change of three scales for the radiographic assessment of knee osteoarthritis using images from the Multicenter Osteoarthritis Study (MOST). Osteoarthr. Cartil. 2015, 23, 1491–1498. [Google Scholar] [CrossRef] [PubMed]
- Stefanik, J.J.; Guermazi, A.; Zhu, Y.; Zumwalt, A.C.; Gross, K.D.; Clancy, M.; Felson, D.T. Quadriceps weakness, patella alta, and structural features of patellofemoral osteoarthritis. Arthr. Care Res. 2011, 63, 1391–1397. [Google Scholar] [CrossRef] [PubMed]
- Braun, H.J.; Gold, G.E. Diagnosis of osteoarthritis: Imaging. Bone 2012, 51, 278–288. [Google Scholar] [CrossRef]
- Boesen, M.; Ellegaard, K.; Henriksen, M.; Gudbergsen, H.; Hansen, P.; Bliddal, H.; Riis, R.G. Osteoarthritis year in review 2016: Imaging. Osteoarthr. Cartil. 2017, 25, 216–226. [Google Scholar] [CrossRef] [PubMed]
- Wenham, C.Y.J.; Grainger, A.J.; Conaghan, P.G. The role of imaging modalities in the diagnosis, differential diagnosis and clinical assessment of peripheral joint osteoarthritis. Osteoarthr. Cartil. 2014, 22, 1692–1702. [Google Scholar] [CrossRef] [PubMed]
- Trattnig, S.; Winalski, C.S.; Marlovits, S.; Jurvelin, J.S.; Welsch, G.H.; Potter, H.G. Magnetic resonance imaging of cartilage repair: A review. Cartilage 2011, 2, 5–26. [Google Scholar] [CrossRef] [PubMed]
- Kijowski, R.; Blankenbaker, D.G.; Munoz del Rio, A.; Baer, G.S.; Graf, B.K. Evaluation of the Articular Cartilage of the Knee Joint: Value of adding a T2 mapping sequence to a routine mr imaging protocol. Radiology 2013, 267, 503–513. [Google Scholar] [CrossRef] [PubMed]
- Guermazi, A.; Roemer, F.W.; Alizai, H.; Winalski, C.S.; Welsch, G.; Brittberg, M.; Trattnig, S. State of the art: MR imaging after knee cartilage repair surgery. Radiology 2015, 277, 23–43. [Google Scholar] [CrossRef]
- Ho-Fung, V.M.; Jaramillo, D. Cartilage imaging in children. Current indications, magnetic resonance imaging techniques, and imaging findings. Radiol. Clin. N. Am. 2013. [Google Scholar] [CrossRef]
- Jungmann, P.M.; Baum, T.; Bauer, J.S.; Karampinos, D.C.; Erdle, B.; Link, T.M.; Welsch, G.H. Cartilage repair surgery: Outcome evaluation by using noninvasive cartilage biomarkers based on quantitative mri techniques? BioMed Res. Int. 2014. [Google Scholar] [CrossRef]
- Suppanee, R.; Yazdifar, M.; Chizari, M.; Esat, I.; Bardakos, N.V.; Field, R.E. Simulating osteoarthritis: The effect of the changing thickness of articular cartilage on the kinematics and pathological bone-to-bone contact in a hip joint with femoroacetabular impingement. Eur. Orthop. Traumatol. 2014, 5, 65–73. [Google Scholar] [CrossRef]
- Wu, Y.; Krishnan, S.; Rangayyan, R.M. Computer-aided diagnosis of knee-joint disorders via vibroarthrographic signal analysis: A review. Crit. Rev. TM Biomed. Eng. 2012, 38. [Google Scholar] [CrossRef]
- Eckstein, F.; Glaser, C. Measuring cartilage morphology with quantitative magnetic resonance imaging. Semin. Musculoskelet. Radiol. 2004. [Google Scholar] [CrossRef]
- Lee, K.Y.; Dunn, T.C.; Steinbach, L.S.; Ozhinsky, E.; Ries, M.D.; Majumdar, S. Computer-aided quantification of focal cartilage lesions of osteoarthritic knee using MRI. Magn. Reson. Imaging 2004, 22, 1105–1115. [Google Scholar] [CrossRef] [PubMed]
- Dam, E.B.; Folkesson, J.; Pettersen, P.C.; Christiansen, C. Semi-automatic knee cartilage segmentation. Prog. Biomed. Opt. Imaging—Proc. SPIE 2006, 6144, 614441. [Google Scholar]
- Görres, J.; Brehler, M.; Franke, J.; Vetter, S.Y.; Grützner, P.A.; Meinzer, H.-P.; Wolf, I. Articular surface segmentation using active shape models for intraoperative implant assessment. Int. J. Comput. Assist. Radiol. Surg. 2016, 11, 1661–1672. [Google Scholar] [CrossRef] [PubMed]
- Tabrizi, P.R.; Zoroofi, R.A.; Yokota, F.; Nishii, T.; Sato, Y. Shape-based acetabular cartilage segmentation: Application to CT and MRI datasets. Int. J. Comput. Assist. Radiol. Surg. 2016, 11, 1247–1265. [Google Scholar] [CrossRef] [PubMed]
- Tabrizi, P.R.; Zoroofi, R.A.; Yokota, F.; Tamura, S.; Nishii, T.; Sato, Y. Acetabular cartilage segmentation in CT arthrography based on a bone-normalized probabilistic atlas. Int. J. Comput. Assist. Radiol. Surg. 2015, 10, 433–446. [Google Scholar] [CrossRef] [PubMed]
- Fripp, J.; Crozier, S.; Warfield, S.K.; Ourselin, S. Automatic segmentation and quantitative analysis of the articular cartilages from magnetic resonance images of the knee. IEEE Trans. Med. Imaging 2010, 29, 55–64. [Google Scholar] [CrossRef] [PubMed]
- Kumarv, A.; Jayanthy, A.K. Classification of MRI images in 2D coronal view and measurement of articular cartilage thickness for early detection of knee osteoarthritis. In Proceedings of the 2016 IEEE International Conference on Recent Trends in Electronics, Information and Communication Technology (RTEICT 2016), Bangalore, India, 20–21 May 2016; pp. 1907–1911. [Google Scholar]
- Kubicek, J.; Penhaker, M.; Augustynek, M.; Bryjova, I.; Cerny, M. Segmentation of Knee Cartilage: A Comprehensive Review. J. Med. Imaging Health Inform. 2018, 8, 401–418. [Google Scholar] [CrossRef]
- Gougoutas, A.J.; Wheaton, A.J.; Borthakur, A.; Shapiro, E.M.; Kneeland, J.B.; Udupa, J.K.; Reddy, R. Cartilage volume quantification via Live Wire segmentation. Acad. Radiol. 2004, 11, 1389–1395. [Google Scholar] [CrossRef]
- Mikulka, J.; Gescheidtova, E.; Bartusek, K. Modern edge-based and region-based segmentation methods. In Proceedings of the TSP 2009—32nd International Conference on Telecommunications and Signal Processing, Dunakiliti, Hungary, 26 August 2009; pp. 89–91. [Google Scholar]
- Kubicek, J.; Vicianova, V.; Penhaker, M.; Augustynek, M. Time deformable segmentation model based on the active contour driven by Gaussian energy distribution: Extraction and modeling of early articular cartilage pathological interuptions. Front. Artif. Intell. Appl. 2017, 297, 242–255. [Google Scholar]
- Aja-Fernández, S.; Curiale, A.H.; Vegas-Sánchez-Ferrero, G. A local fuzzy thresholding methodology for multiregion image segmentation. Knowl.-Based Syst. 2015, 83, 1–12. [Google Scholar] [CrossRef]
- Ma, M.; Liang, J.; Guo, M.; Fan, Y.; Yin, Y. SAR image segmentation based on artificial bee colony algorithm. Appl. Soft Comput. J. 2011, 11, 5205–5214. [Google Scholar] [CrossRef]
- Horng, M.H. Multilevel thresholding selection based on the artificial bee colony algorithm for image segmentation. Expert Syst. Appl. 2011, 38, 13785–13791. [Google Scholar] [CrossRef]
- Sağ, T.; Çunkaş, M. Color image segmentation based on multiobjective artificial bee colony optimization. Appl. Soft Comput. J. 2015, 34, 389–401. [Google Scholar] [CrossRef]
- Osuna-Enciso, V.; Cuevas, E.; Sossa, H. A comparison of nature inspired algorithms for multi-threshold image segmentation. Expert Syst. Appl. 2013, 40, 1213–1219. [Google Scholar] [CrossRef]
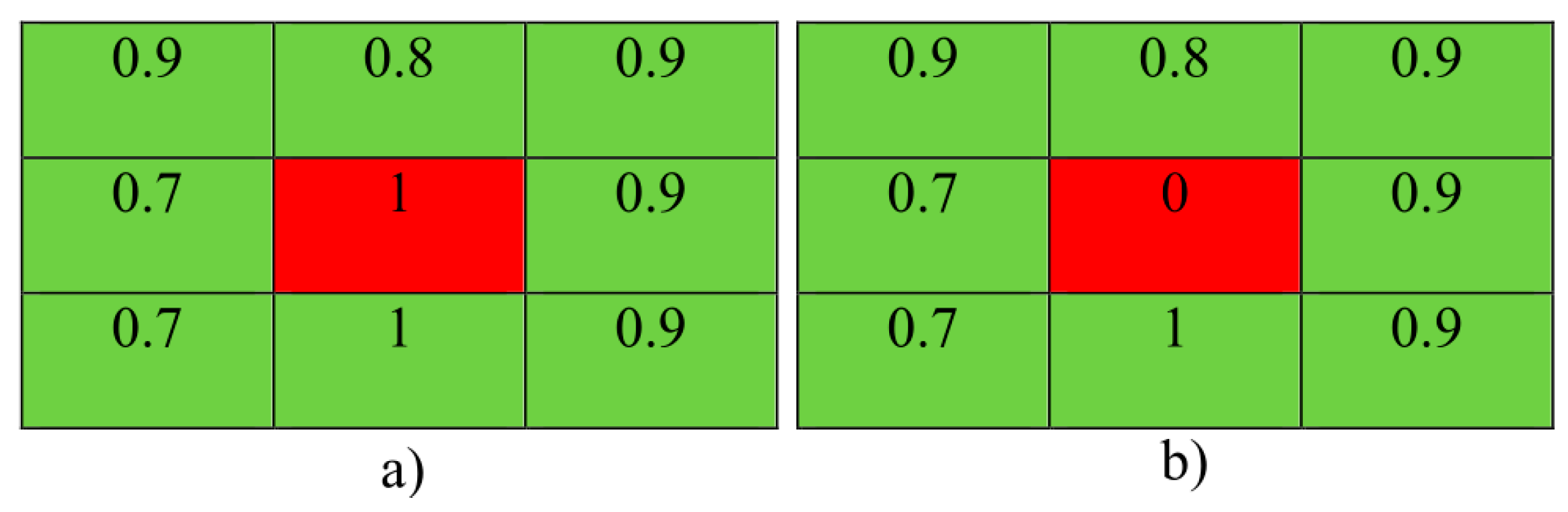
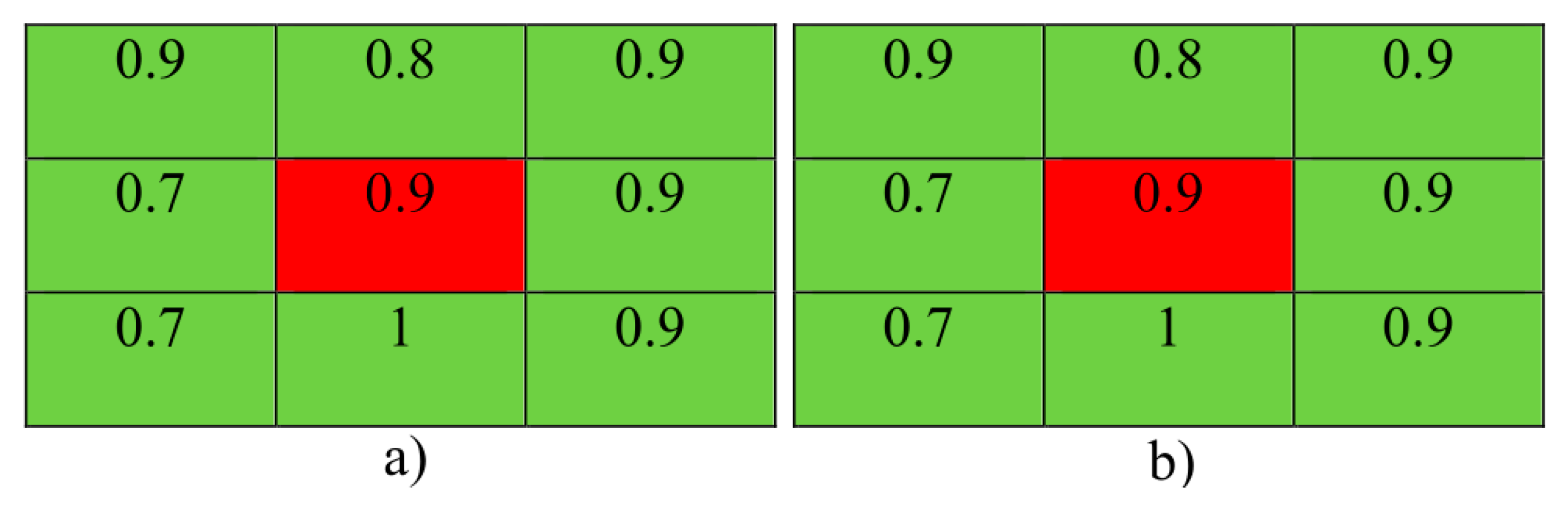
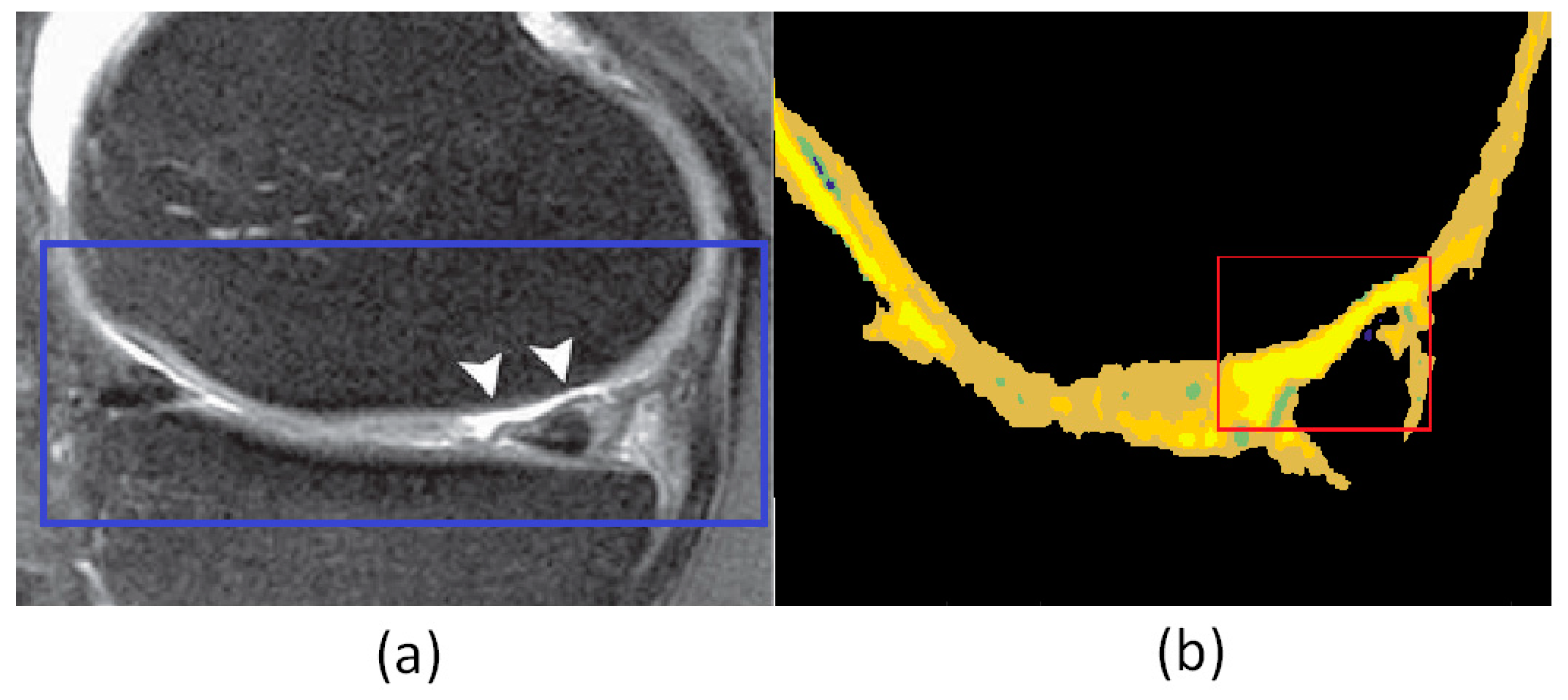
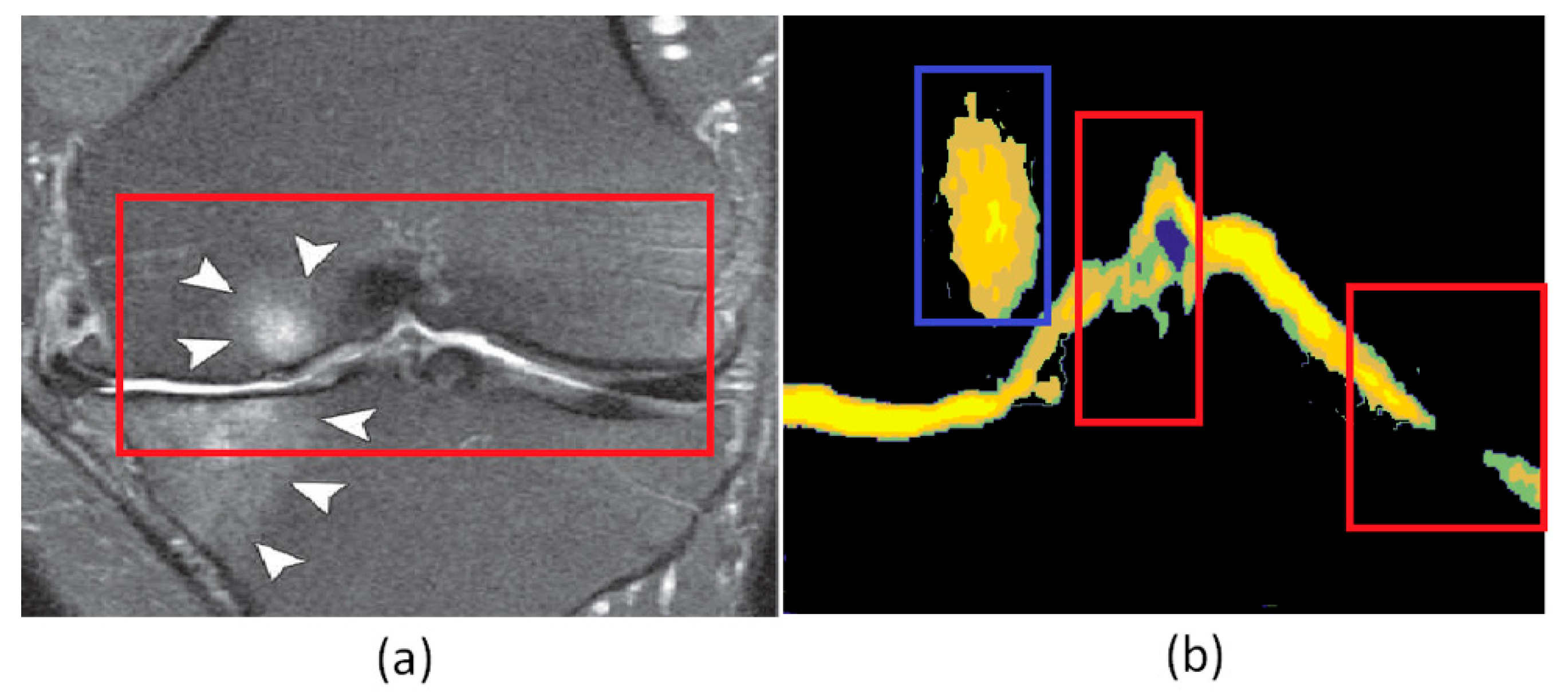
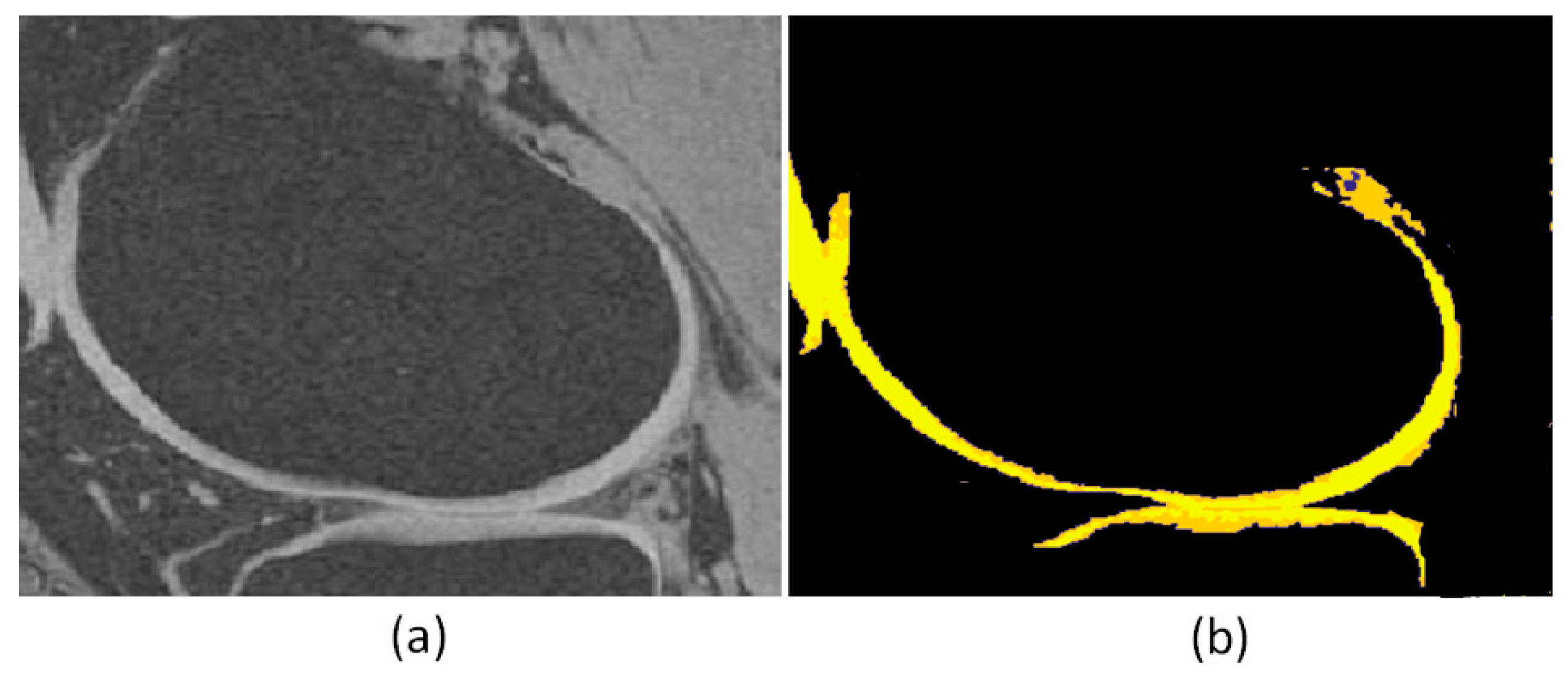
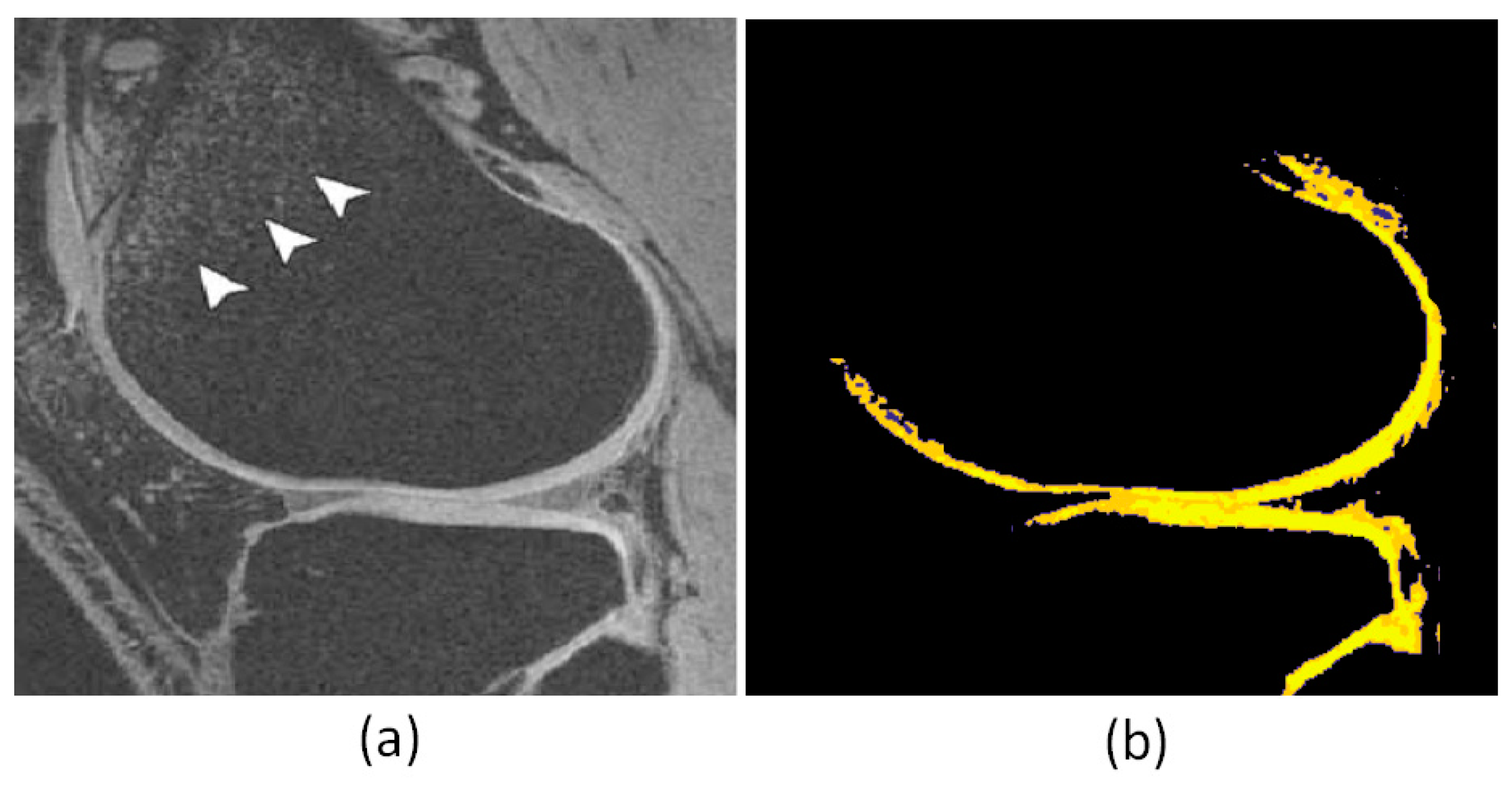



| Interval median estimation | |
| Gastwirth median estimation | 〈209.12; 211.95〉 |
| Testing Image | Number of Classes | |||||
|---|---|---|---|---|---|---|
| 1 | 6 | 21.43 | 21.11 | 21.43 | 21.41 | 0.11 |
| 2 | 6 | 22.65 | 22.14 | 22.33 | 22.29 | 0.14 |
| 3 | 6 | 22.44 | 21.99 | 22.12 | 22.11 | 0.12 |
| 4 | 6 | 22.12 | 21.44 | 21.99 | 21.97 | 0.11 |
| 5 | 6 | 21.99 | 21.54 | 21.68 | 21.72 | 0.21 |
| Testing Image [px] | Image Order | Number of Classes | Time Complexity [s] |
|---|---|---|---|
| (800 × 800) | 1 | 6 | 8.92 |
| 2 | 6 | 10.54 | |
| 3 | 6 | 10.12 | |
| (300 × 300) | 1 | 6 | 9.91 |
| 2 | 6 | 9.11 | |
| 3 | 6 | 8.59 | |
| (150 × 150) | 1 | 6 | 5.45 |
| 2 | 6 | 5.22 | |
| 3 | 6 | 6.12 |
| MedAg | AvAg | FCM | Otsu-N | ITS | MASP | ||
|---|---|---|---|---|---|---|---|
| RI | Nat. | 0.791 | 0.728 | 0.723 | 0.723 | 0.739 | 0.698 |
| Gauss. | 0.697 | 0.669 | 0.601 | 0.683 | 0.681 | 0.667 | |
| Mult. | 0.681 | 0.697 | 0.665 | 0.654 | 0.612 | 0.571 | |
| VI | Nat. | 2.956 | 2.611 | 2.979 | 2.675 | 2.922 | 3.459 |
| Gauss. | 3.122 | 3.788 | 3.312 | 3.367 | 3.122 | 3.998 | |
| Mult. | 3.233 | 3.811 | 3.711 | 3.568 | 3.679 | 3.799 | |
| Nat. | 0.366 | 0.343 | 0.354 | 0.343 | 0.371 | 0.219 | |
| Gauss. | 0.298 | 0.322 | 0.291 | 0.262 | 0.312 | 0.242 | |
| Mult. | 0.345 | 0.289 | 0.271 | 0.233 | 0.327 | 0.236 | |
| Nat. | 0.498 | 0.448 | 0.455 | 0.411 | 0.467 | 0.341 | |
| Gauss. | 0.499 | 0.295 | 0.353 | 0.412 | 0.399 | 0.277 | |
| Mult. | 0.391 | 0.365 | 0.343 | 0.367 | 0.389 | 0.311 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kubicek, J.; Penhaker, M.; Augustynek, M.; Cerny, M.; Oczka, D. Segmentation of Articular Cartilage and Early Osteoarthritis based on the Fuzzy Soft Thresholding Approach Driven by Modified Evolutionary ABC Optimization and Local Statistical Aggregation. Symmetry 2019, 11, 861. https://doi.org/10.3390/sym11070861
Kubicek J, Penhaker M, Augustynek M, Cerny M, Oczka D. Segmentation of Articular Cartilage and Early Osteoarthritis based on the Fuzzy Soft Thresholding Approach Driven by Modified Evolutionary ABC Optimization and Local Statistical Aggregation. Symmetry. 2019; 11(7):861. https://doi.org/10.3390/sym11070861
Chicago/Turabian StyleKubicek, Jan, Marek Penhaker, Martin Augustynek, Martin Cerny, and David Oczka. 2019. "Segmentation of Articular Cartilage and Early Osteoarthritis based on the Fuzzy Soft Thresholding Approach Driven by Modified Evolutionary ABC Optimization and Local Statistical Aggregation" Symmetry 11, no. 7: 861. https://doi.org/10.3390/sym11070861
APA StyleKubicek, J., Penhaker, M., Augustynek, M., Cerny, M., & Oczka, D. (2019). Segmentation of Articular Cartilage and Early Osteoarthritis based on the Fuzzy Soft Thresholding Approach Driven by Modified Evolutionary ABC Optimization and Local Statistical Aggregation. Symmetry, 11(7), 861. https://doi.org/10.3390/sym11070861





