Total Weak Roman Domination in Graphs

Abstract

Given a graph $G=(V,E)$, a function $f:V\to \{0,1,2,\cdots \}$ is said to be a total dominating function if ${\sum }_{u\in N\left(v\right)}f\left(u\right)>0$ for every $v\in V$, where $N\left(v\right)$ denotes the open neighbourhood of v. Let $V_i=\{x\in V:f\left(x\right)=i\}$. We say that a function $f:V\to \{0,1,2\}$ is a total weak Roman dominating function if f is a total dominating function and for every vertex $v\in V_0$ there exists $u\in N\left(v\right)\cap (V_1\cup V_2)$ such that the function $f^{\prime }$, defined by $f^{\prime }\left(v\right)=1$, $f^{\prime }\left(u\right)=f\left(u\right)-1$ and $f^{\prime }\left(x\right)=f\left(x\right)$ whenever $x\in V\backslash \{u,v\}$, is a total dominating function as well. The weight of a function f is defined to be $w\left(f\right)={\sum }_{v\in V}f\left(v\right).$ In this article, we introduce the study of the total weak Roman domination number of a graph G, denoted by ${\gamma }_{tr}\left(G\right)$, which is defined to be the minimum weight among all total weak Roman dominating functions on G. We show the close relationship that exists between this novel parameter and other domination parameters of a graph. Furthermore, we obtain general bounds on ${\gamma }_{tr}\left(G\right)$ and, for some particular families of graphs, we obtain closed formulae. Finally, we show that the problem of computing the total weak Roman domination number of a graph is NP-hard.

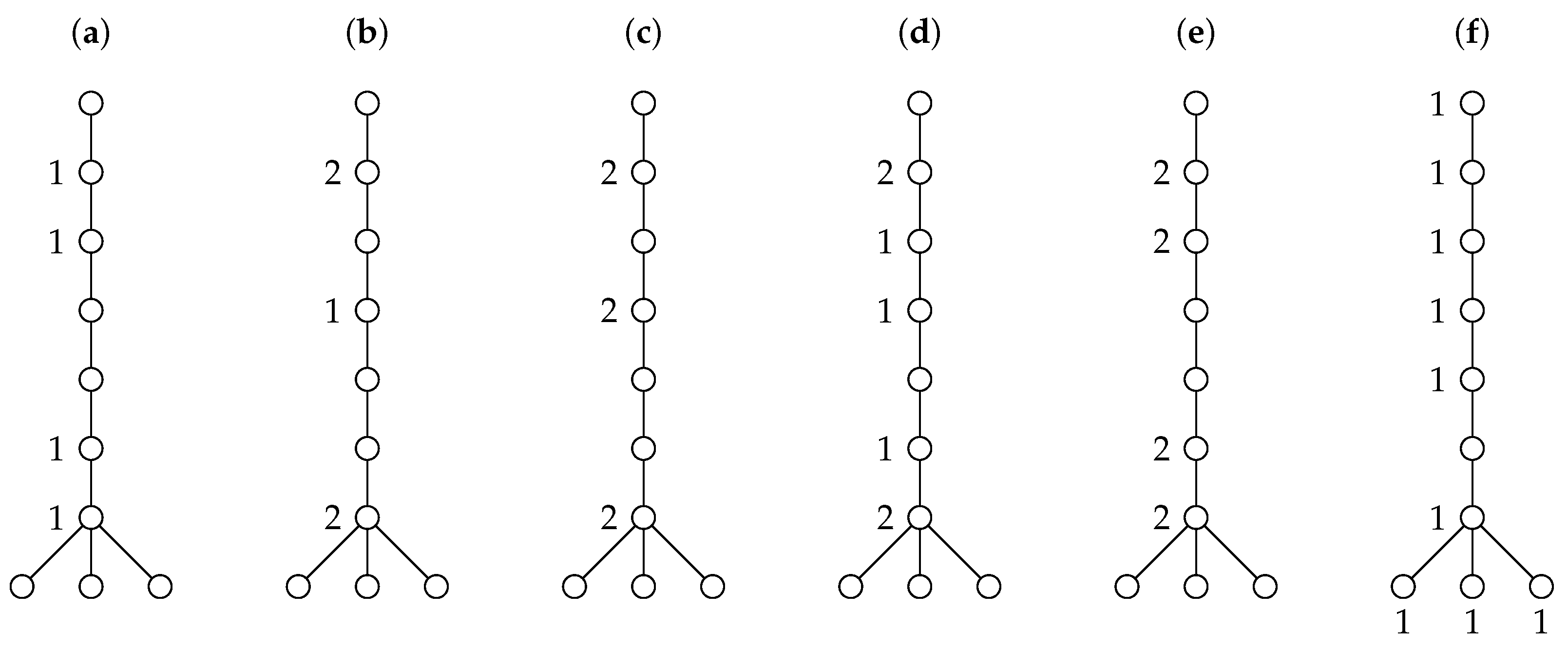
1. Introduction

The theory of domination in (finite) graphs can be developed using functions $f:V\left(G\right)\to A$, where $V\left(G\right)$ is the vertex set of a graph G and A is a set of nonegative numbers. With this approach, the different types of domination are obtained by imposing certain restrictions on f. To begin with, let us consider the two simplest cases: f is said to be a dominating function if for every vertex v such that $f\left(v\right)=0$, there exists a vertex u, adjacent to v, such that $f\left(u\right)>0$; furthermore, f is said to be a total dominating function (TDF) if for every vertex v, there exists a vertex u, adjacent to v, such that $f\left(u\right)>0$. Analogously, a set $X\subseteq V\left(G\right)$ is a (total) dominating set if there exists a (total) dominating function f such that $f\left(x\right)>0$ if and only if $x\in X$. The (total) domination number of G, denoted by (${\gamma }_t\left(G\right)$) $\gamma \left(G\right)$, is the minimum cardinality among all (total) dominating sets. These two parameters have been extensively studied. While the use of functions is not necessary to reach the concept of (total) domination number, later we will see that this idea helps us to easily introduce other more elaborate concepts.

From now on, we restrict ourselves to the case of functions $f:V\left(G\right)\to \{0,1,2\}$, which are related to the following approach to protection of a graph described by Cockayne et al. [1]. Suppose that one or more entities are stationed at some of the vertices of a simple graph G and that an entity at a vertex can deal with a problem at any vertex in its closed neighbourhood. In this context, an entity could consist of a robot, an observer, a guard, a legion, and so on. Consider a function $f:V\left(G\right)\to \{0,1,2\}$ where $f\left(v\right)$ denotes the number of entities stationed at v, and let $V_i=\{v\in V\left(G\right):f\left(v\right)=i\}$ for every $i\in \{0,1,2\}$. We will identify the function f with the partition of $V\left(G\right)$ induced by f and write $f(V_0,V_1,V_2).$ The weight of f is defined to be $\omega \left(f\right)=f\left(V\left(G\right)\right)={\sum }_{v\in V\left(G\right)}f\left(v\right)={\sum }_{i}i\left|V_i\right|$. Informally, we say that G is protected under the function f if there exists at least one entity available to handle a problem at any vertex. We now define some particular subclasses of protected graphs considered in [1] and introduce a new one. The functions in each subclass protect the graph according to a certain strategy.

A Roman dominating function (RDF) is a function $f(V_0,V_1,V_2)$ such that for every vertex $v\in V_0$ there exists a vertex $u\in V_2$ which is adjacent to v. The Roman domination number, denoted by ${\gamma }_R\left(G\right)$, is the minimum weight among all RDFs on G. This concept of protection has historical motivation [2] and was formally proposed by Cockayne et al. in [3]. A Roman dominating function with minimum weight ${\gamma }_{{}_R}\left(G\right)$ on G is called a ${\gamma }_{{}_R}\left(G\right)$-function. A similar agreement will be assumed when referring to optimal functions (and sets) associated to other parameters used in the article.

A total Roman dominating function (TRDF) on a graph G is a RDF on G with the additional condition of being a TDF. The total Roman domination number of G, denoted by ${\gamma }_{{}_{tR}}\left(G\right)$, was defined by Liu and Chang [4] as the minimum weight among all TRDFs on G. For recent results on total Roman domination in graphs we cite [5].

The remaining domination parameters considered in this paper are directly related to the following idea of protection of a vertex. A vertex $v\in V_0$ is said to be (totally) protected under $f(V_0,V_1,V_2)$ if there exists a vertex $u\in V_1\cup V_2$, adjacent to v, such that the function $f^{\prime }$, defined by $f^{\prime }\left(v\right)=1$, $f^{\prime }\left(u\right)=f\left(u\right)-1$ and $f^{\prime }\left(x\right)=f\left(x\right)$ whenever $x\in V\left(G\right)\backslash \{u,v\}$, is a (total) dominating function. In such a case, if it is necessary to emphasize the role of u, then we will say that v is (totally) protected by u under f.

A weak Roman dominating function (WRDF) is a function $f(V_0,V_1,V_2)$ such that every vertex in $V_0$ is protected under f. The weak Roman domination number, denoted by ${\gamma }_r\left(G\right)$, is the minimum weight among all WRDFs on G. This concept of protection was introduced by Henning and Hedetniemi [6] and studied further in [7,8,9].

A secure dominating function is a WRDF function $f(V_0,V_1,V_2)$ in which $V_2=\varnothing$. In this case, it is convenient to define this concept of protection by the properties of $V_1$. Obviously $f(V_0,V_1,\varnothing )$ is a secure dominating function if and only if $V_1$ is a dominating set and for every $v\in V_0$ there exists $u\in V_1$ which is adjacent to v and $(V_1\backslash \left\{u\right\})\cup \left\{v\right\}$ is a dominating set as well. In such a case, $V_1$ is said to be a secure dominating set. The secure domination number, denoted by ${\gamma }_s\left(G\right)$, is the minimum cardinality among all secure dominating sets. This concept of protection was introduced by Cockayne et al. in [1], and studied further in [7,8,10,11,12,13].

A set $X\subseteq V\left(G\right)$ is said to be a secure total dominating set of G if it is a total dominating set and for every vertex $v\notin X$ there exists $u\in X$ which is adjacent to v and $(X\backslash \{u\left\}\right)\cup \left\{v\right\}$ is a total dominating set as well. The secure total domination number, denoted by ${\gamma }_{st}\left(G\right)$, is the minimum cardinality among all secure total dominating sets. This concept of protection was introduced by Benecke et al. in [14].

In this article we introduce the study of total weak Roman domination in graphs. We define a total weak Roman dominating function (TWRDF) to be a TDF $f(V_0,V_1,V_2)$ such that every vertex in $V_0$ is totally protected under f. The total weak Roman domination number, denoted by ${\gamma }_{tr}\left(G\right)$, is the minimum weight among all TWRDFs on G. In particular, we can define a secure total dominating function (STDF) to be a TWRDF $f(V_0,V_1,V_2)$ in which $V_2=\varnothing$. Obviously $f(V_0,V_1,\varnothing )$ is a STDF if and only if $V_1$ is a secure total dominating set.

Figure 1 shows a graph G satisfying ${\gamma }_t\left(G\right)<{\gamma }_R\left(G\right)<{\gamma }_{tr}\left(G\right)<{\gamma }_{tR}\left(G\right)$ and ${\gamma }_r\left(G\right)<{\gamma }_R\left(G\right)<{\gamma }_{tr}\left(G\right)<{\gamma }_{st}\left(G\right)$.

The remainder of this paper is structured as follows. Section 2 will briefly cover some notation and terminology which have not been stated yet. Section 3 introduces basic results which show the close relationship that exists between the total weak Roman domination number and other domination parameters. In Section 4 we obtain general bounds and discuss the extreme cases, while in Section 5 we restrict ourselves to the case of rooted product graphs. Finally, we show that the problem of finding the total weak Roman domination number of a graph is NP-hard.

2. Notation

Throughout the paper, we will use the following notation. We consider finite, undirected, and simple graphs G with vertex set $V\left(G\right)$ and edge set $E\left(G\right)$. Given a vertex v of G, $N\left(v\right)$ will denote the open neighbourhood of v in G, while the closed neighbourhood will be denoted by $N\left[v\right]$. We say that a vertex $v\in V\left(G\right)$ is universal if $N\left[v\right]=V\left(G\right)$.

We denote the minimum degree of G by $\delta \left(G\right)={min}_{v\in V\left(G\right)}\left\{\right|N\left(v\right)\left|\right\}$ and the maximum degree by $\Delta \left(G\right)={max}_{v\in V\left(G\right)}\left\{\right|N\left(v\right)\left|\right\}$. For a set $S\subseteq V\left(G\right)$, its open neighbourhood is the set $N\left(S\right)={\cup }_{v\in S}N\left(v\right)$, and its closed neighbourhood is the set $N\left[S\right]=N\left(S\right)\cup S$.

The graph obtained from G by removing all the vertices in $S\subseteq V\left(G\right)$ and all the edges incident with a vertex in S will be denoted by $G-S$. Analogously, the graph obtained from G by removing all the edges in $U\subseteq E\left(G\right)$ will be denoted by $G-U$. If H is a graph, then we say that G is H-free if G does not contain a copy of H as an induced subgraph.

Given a set $S\subseteq V\left(G\right)$ and a vertex $v\in S$, the external private neighbourhood of v with respect to S is defined to be $epn(v,S)=\{u\in V(G)\backslash S:N(u)\cap S=\{v\left\}\right\}$.

The set of leaves, support vertices and strong support vertices of a graph G, will be denoted by $L\left(G\right)$, $S\left(G\right)$ and $S_s\left(G\right)$, respectively.

We will use the notation $N_n$, $K_n$, $K_{1,n-1}$, $P_n$, $C_n$, and $K_{r,n-r}$ for empty graphs, complete graphs, star graphs, path graphs, cycle graphs and complete bipartite graphs of order n, respectively. A subdivided star graph, denoted by $K_{1,(n-1)/2}^{*}$, is a graph of order n (odd) obtained from a star graph $K_{1,(n-1)/2}$ by subdividing every edge exactly once.

Let G and H be two graphs, respectively. The corona product $G\odot H$ is defined as the graph obtained from G and H by taking one copy of G and $\left|V\right(G\left)\right|$ copies of H and joining by an edge each vertex from the ith-copy of H with the ith-vertex of G.

From now on, definitions will be introduced whenever a concept is needed.

3. General Results

We begin with two inequality chains relating several domination parameters.

Proposition 1.

The following inequalities hold for any graph G with no isolated vertex.

(i)

$\gamma \left(G\right)\le {\gamma }_r\left(G\right)\le {\gamma }_{tr}\left(G\right)\le {\gamma }_{tR}\left(G\right)\le 2{\gamma }_t\left(G\right)$.

(ii)

${\gamma }_t\left(G\right)\le {\gamma }_{tr}\left(G\right)\le {\gamma }_{st}\left(G\right)$.

Proof. 

It was shown in [5] that ${\gamma }_{tR}\left(G\right)\le 2{\gamma }_t\left(G\right)$, and in [6] that $\gamma \left(G\right)\le {\gamma }_r\left(G\right)$. To conclude the proof of (i), we only need to observe that any TWRDF is a WRDF, which implies that ${\gamma }_r\left(G\right)\le {\gamma }_{tr}\left(G\right)$, and any TRDF is a TWRDF, which implies that ${\gamma }_{tr}\left(G\right)\le {\gamma }_{tR}\left(G\right)$.

Now, to prove (ii), we only need to observe that any TWRDF is a TDF, which implies that ${\gamma }_t\left(G\right)\le {\gamma }_{tr}\left(G\right)$, and any STDF is a TWRDF, which implies that ${\gamma }_{tr}\left(G\right)\le {\gamma }_{st}\left(G\right)$. □

From Proposition 1 we immediately derive the following problem.

Problem 1.

In each of the following cases, characterize the graphs satisfying the equality.

(i)

${\gamma }_{tr}\left(G\right)={\gamma }_t\left(G\right)$.

(ii)

${\gamma }_{tr}\left(G\right)={\gamma }_r\left(G\right)$.

(iii)

${\gamma }_{tr}\left(G\right)={\gamma }_{st}\left(G\right)$.

(iv)

${\gamma }_{tr}\left(G\right)={\gamma }_{tR}\left(G\right)$.

The solution of Problem 1 (i) can be found in Theorem 20. While we will give some examples of graphs satisfying the remaining equalities, these problems remain open.

Theorem 1.

Let G be a graph. The following statements are equivalent.

(a)

${\gamma }_{tr}\left(G\right)={\gamma }_r\left(G\right)$.

(b)

There exists a ${\gamma }_r\left(G\right)$-function $f(V_0,V_1,V_2)$ such that $V_1=\varnothing$ and $V_2$ is a total dominating set.

(c)

${\gamma }_r\left(G\right)=2{\gamma }_t\left(G\right)$.

Proof. 

Suppose that ${\gamma }_{tr}\left(G\right)={\gamma }_r\left(G\right)$ and let $f(V_0,V_1,V_2)$ be a ${\gamma }_{tr}\left(G\right)$-function. Notice that f is a ${\gamma }_r\left(G\right)$-function and $V_1\cup V_2$ is a total dominating set. Now, suppose that there exists $u\in V_1$. Since every vertex in $V_0$ has at least one neighbour in $V_2$ or at least two neighbours in $V_1$, we can conclude that the function g, defined by $g\left(u\right)=0$ and $g\left(x\right)=f\left(x\right)$ whenever $x\in V\left(G\right)\backslash \left\{u\right\}$, is a WRDF of weight $\omega \left(g\right)=\omega \left(f\right)-1={\gamma }_r\left(G\right)-1$, which is a contradiction. Thus, $V_1=\varnothing$ and consequently $V_2$ is a total dominating set.

Now, if there exists a ${\gamma }_r\left(G\right)$-function $f(V_0,V_1,V_2)$ such that $V_1=\varnothing$ and $V_2$ is a total dominating set, then $2{\gamma }_t\left(G\right)\le 2\left|V_2\right|={\gamma }_r\left(G\right)$, and Proposition 1 (i) leads to ${\gamma }_r\left(G\right)=2{\gamma }_t\left(G\right)$.

Finally, if ${\gamma }_r\left(G\right)=2{\gamma }_t\left(G\right)$, then for any ${\gamma }_t\left(G\right)$-set A, there exists a ${\gamma }_r\left(G\right)$-function $f^{\prime }(V_0^{\prime },V_1^{\prime },V_2^{\prime })$ such that $V_1^{\prime }=\varnothing$ and $V_2^{\prime }=A$, which is a TWRDF. Hence, ${\gamma }_{tr}\left(G\right)\le \omega \left(f^{\prime }\right)={\gamma }_r\left(G\right)$ and Proposition 1 (i) leads to ${\gamma }_{tr}\left(G\right)={\gamma }_r\left(G\right)$. □

From the theorem above and Proposition 1 we deduce the following result.

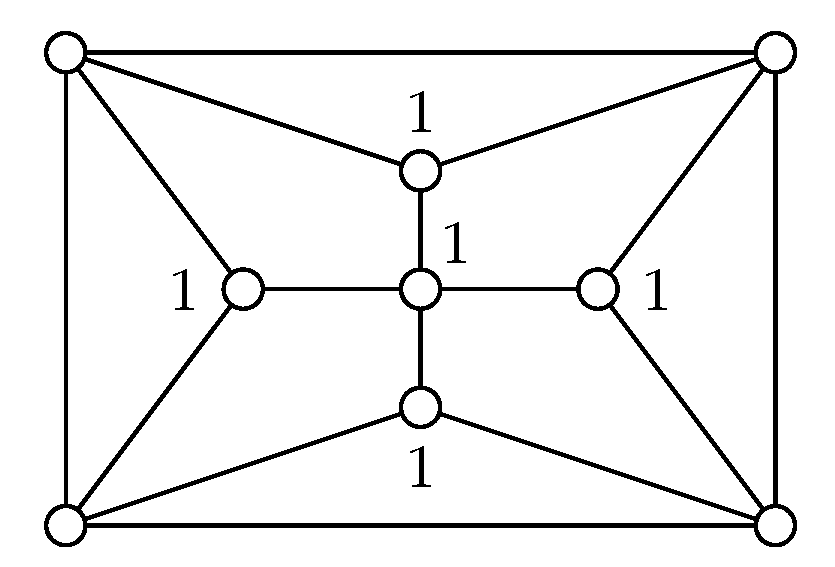
Theorem 2.

For any graph G with no isolated vertex,

$${\gamma }_{tr}\left(G\right)\ge \gamma \left(G\right)+1.$$

The bound above is tight. For instance, if G is a graph having two universal vertices, then ${\gamma }_{tr}\left(G\right)=\gamma \left(G\right)+1=2.$ Another example is shown in Figure 2.

Theorem 3.

The following statements are equivalent.

(i)

${\gamma }_{tr}\left(G\right)=\gamma \left(G\right)+1$.

(ii)

${\gamma }_{st}\left(G\right)=\gamma \left(G\right)+1$.

Proof. 

First, suppose that (i) holds. Let $f(V_0,V_1,V_2)$ be a ${\gamma }_{tr}\left(G\right)$-function. Since $V_1\cup V_2$ is a total dominating set, $|V_1|+2|V_2|={\gamma }_{tr}\left(G\right)=\gamma \left(G\right)+1\le {\gamma }_t\left(G\right)+1\le |V_1|+|V_2|+1$. Thus, $|V_2|\le 1$. Suppose that $V_2=\left\{u\right\}$ and let $v\in N\left(u\right)\cap V_1$. Notice that in this case $V_1\cup V_2$ is a $\gamma \left(G\right)$-set. Now, since v does not have external private neighbours with respect to $V_1\cup V_2$, we have that $(V_1\cup V_2)\backslash \left\{v\right\}$ is a dominating set, which is a contradiction. Hence, $V_2=\varnothing$ and so f is a ${\gamma }_{st}\left(G\right)$-function. Therefore, ${\gamma }_{st}\left(G\right)=\omega \left(f\right)=\gamma \left(G\right)+1$ and (ii) follows.

Conversely, if (ii) holds, then by Proposition 1 and Theorem 2 we have that $\gamma \left(G\right)+1={\gamma }_{st}\left(G\right)\ge {\gamma }_{tr}\left(G\right)\ge \gamma \left(G\right)+1$. Therefore, ${\gamma }_{tr}\left(G\right)=\gamma \left(G\right)+1$ and (i) follows. □

We continue our analysis by showing another family of graphs satisfying that ${\gamma }_{tr}\left(G\right)={\gamma }_{st}\left(G\right)$, where $K_{1,3}+e$ is the graph obtained by adding an edge to $K_{1,3}$.

Theorem 4.

For any $\{K_{1,3},K_{1,3}+e\}$-free graph G with no isolated vertex,

$${\gamma }_{tr}\left(G\right)={\gamma }_{st}\left(G\right).$$

Proof. 

Let $f(V_0,V_1,V_2)$ be a ${\gamma }_{tr}\left(G\right)$-function such that $|V_2|$ is minimum. We suppose that ${\gamma }_{tr}\left(G\right)<{\gamma }_{st}\left(G\right)$. In such a case, $V_2\ne \varnothing$ and we fix a vertex $v\in V_2$. Notice that there exist $y\in N\left(v\right)\cap V_0$ and $z\in N\left(v\right)\cap (V_1\cup V_2)$. We consider the function $f^{\prime }(V_0^{\prime },V_1^{\prime },V_2^{\prime })$ defined by $f^{\prime }\left(v\right)=1$, $f^{\prime }\left(y\right)=1$ and $f^{\prime }\left(x\right)=f\left(x\right)$ whenever $x\in V\left(G\right)\backslash \{v,y\}$. We claim that $f^{\prime }$ is a TWRDF on G. First, we observe that, by construction, $f^{\prime }$ is a TDF on G. Now, let $w\in V_0^{\prime }\subseteq V_0$ and consider the following two cases.

Case 1.

w is not adjacent to v. Since f is a TWRDF on G, w is totally protected under f and, since $w\notin N\left(v\right)$, w is also totally protected under $f^{\prime }$.

Case 2.

w is adjacent to v. Notice that $w\ne y$. In order to show that w is totally protected under $f^{\prime }$, we define $f^{{}^{″}}(V_0^{{}^{″}},V_1^{{}^{″}},V_2^{{}^{″}})$ by $f^{{}^{″}}\left(v\right)=0$, $f^{{}^{″}}\left(w\right)=1$ and $f^{{}^{″}}\left(x\right)=f^{\prime }\left(x\right)$ whenever $x\in V\left(G\right)\backslash \{v,w\}$. Clearly, every vertex $x\in V\left(G\right)\backslash N\left(v\right)$ is adjacent to some vertex in $V_1^{{}^{″}}\cup V_2^{{}^{″}}$. Now, we fix $u\in N\left(v\right)$ and let D be the set of vertices formed by v, u and two vertices in $\{w,y,z\}\backslash \left\{u\right\}$. As G is a $\{K_{1,3},K_{1,3}+e\}$-free graph, it follows that at least one vertex in $D\backslash \left\{v\right\}$ is adjacent to the another two vertices in D. Since $w,y,z\in V_1^{{}^{″}}\cup V_2^{{}^{″}}$, we have that $u\in N(V_1^{{}^{″}}\cup V_2^{{}^{″}})$ and so $f^{{}^{″}}$ is a TDF on G, as desired.

Thus $f^{\prime }$ is a TWRDF on G with $\omega \left(f^{\prime }\right)=\omega \left(f\right)$ and $|V_2^{\prime }|<|V_2|$, which is a contradiction. Consequently, we conclude that ${\gamma }_{tr}\left(G\right)={\gamma }_{st}\left(G\right)$. □

We would emphasize that the equality ${\gamma }_{tr}\left(G\right)={\gamma }_{st}\left(G\right)$ is not restrictive to $\{K_{1,3},K_{1,3}+e\}$-free graphs. To see this, we can take $G\cong C_3\square P_3$ (see Figure 4).

As a direct consequence of the result above we have that any graph G obtained as the disjoin union of paths and/or cycles satisfies that ${\gamma }_{tr}\left(G\right)={\gamma }_{st}\left(G\right)$.

Corollary 1.

For any graph G with no isolated vertex and maximum degree $\Delta \left(G\right)\le 2$,

$${\gamma }_{tr}\left(G\right)={\gamma }_{st}\left(G\right).$$

From Corollary 1 and the values of ${\gamma }_{st}\left(P_n\right)$ and ${\gamma }_{st}\left(C_n\right)$ obtained in [14], we derive the following result.

Remark 1.

For any path $P_n$ and any cycle $C_n$ [14],

(i)

${\gamma }_{tr}\left(P_n\right)={\gamma }_{st}\left(P_n\right)=⌈\frac{5(n-2)}{7}⌉+2.$

(ii)

${\gamma }_{tr}\left(C_n\right)={\gamma }_{st}\left(C_n\right)=⌈\frac{5n}{7}⌉$.

Our next result will become a useful tool to study the total weak Roman domination number.

Proposition 2.

If H is a spanning subgraph (with no isolated vertex) of a graph G, then

$${\gamma }_{tr}\left(G\right)\le {\gamma }_{tr}\left(H\right).$$

Proof. 

Let $E^{-}=\{e_1,\cdots ,e_k\}$ be the set of all edges of G not belonging to the edge set of H. Let $H_0=G$ and, for every $i\in \{1,\cdots ,k\}$, let $X_i=\{e_1,\cdots ,e_i\}$ and $H_i=G-X_i$. Since any TWRDF on $H_i$ is a TWRDF on $H_{i-1}$, we can conclude that ${\gamma }_{tr}\left(H_{i-1}\right)\le {\gamma }_{tr}\left(H_i\right)$. Hence, ${\gamma }_{tr}\left(G\right)={\gamma }_{tr}\left(H_0\right)\le {\gamma }_{tr}\left(H_1\right)\le \cdots \le {\gamma }_{tr}\left(H_k\right)={\gamma }_{tr}\left(H\right)$. □

From Remark 1 and Proposition 2 we obtain the following result.

Corollary 2.

Let G be a graph of order n.

• If G is a Hamiltonian graph, then ${\gamma }_{tr}\left(G\right)\le ⌈\frac{5n}{7}⌉.$
• If G has a Hamiltonian path, then ${\gamma }_{tr}\left(G\right)\le ⌈\frac{5(n-2)}{7}⌉+2.$

The bounds above are tight, as they are achieved for $C_n$ and $P_n$, respectively.

A 2-packing of a graph G is a set $X\subseteq V\left(G\right)$ such that $N\left[u\right]\cap N\left[v\right]=\varnothing$ for every pair of different vertices $u,v\in X$. The 2-packing number $\rho \left(G\right)$ is defined as the maximum cardinality among all 2-packings of G. It is well known that for any graph G, $\gamma \left(G\right)\ge \rho \left(G\right)$ (see for instance [15]). Furthermore, Meir and Moon [16] showed in 1975 that $\gamma \left(T\right)=\rho \left(T\right)$ for every tree T.

Theorem 5.

For any graph G with no isolated vertex,

$${\gamma }_{tr}\left(G\right)\ge 2\rho \left(G\right).$$

Furthermore, for any tree T,

$${\gamma }_{tr}\left(T\right)\ge 2\gamma \left(T\right).$$

Proof. 

Let f be a ${\gamma }_{tr}\left(G\right)$-function and S a $\rho \left(G\right)$-set. Since $f\left(N\right[v\left]\right)\ge 2$ for every vertex $v\in V\left(G\right)$, and $N\left[x\right]\cap N\left[y\right]=\varnothing$ for every pair of different vertices $x,y\in S$,

$${\gamma }_{tr}\left(G\right)\ge \sum _{v\in S}f\left(N\left[v\right]\right)\ge 2\left|S\right|=2\rho \left(G\right).$$

Therefore, the result follows. □

To show that the bound above is tight we can consider the case of corona graphs (see Theorem 30).

Theorem 6.

For any graph G with no isolated vertex,

$${\gamma }_{tr}\left(G\right)\le {\gamma }_t\left(G\right)+\gamma \left(G\right).$$

Proof. 

Let D be a ${\gamma }_t\left(G\right)$-set and S a $\gamma \left(G\right)$-set. We define the function $f(V_0,V_1,V_2)$ on G, where $V_2=D\cap S$ and $V_1=(D\cup S)\backslash V_2$. We claim that f is a TWRDF on G. First, notice that f is a TDF on G. Now, let $v\in V_0$. If v has a neighbour in $V_2$, then v is totally protected under f. If v has no neighbour in $V_2$, then v has a neighbour $x\in D\backslash V_2$ and a neighbour $y\in S\backslash V_2$. Consider the function $f^{\prime }$ defined by $f^{\prime }\left(v\right)=1$, $f^{\prime }\left(y\right)=0$, and $f^{\prime }\left(x\right)=f\left(x\right)$ whenever $x\in V\left(G\right)\backslash \{v,y\}$. Since D is a total dominating set of G, $f^{\prime }$ is a TDF on G. Hence, f is a TWRDF on G of weight $\omega \left(f\right)=2|V_2|+|V_1|=|D|+|S|={\gamma }_t\left(G\right)+\gamma \left(G\right)$. Therefore, the result follows. □

Notice that for any graph G of order n, minimum degree $\delta \left(G\right)\ge 1$ and maximum degree $\Delta \left(G\right)\ge n-2$, we have that ${\gamma }_t\left(G\right)=2$. Therefore, Theorem 6 leads to the following result.

Corollary 3.

For any graph G of order n, minimum degree $\delta \left(G\right)\ge 1$ and maximum degree $\Delta \left(G\right)\ge n-2$,

$${\gamma }_{tr}\left(G\right)\le 4.$$

It is not difficult to check that the bound above is achieved for any graph G constructed by joining with an edge the vertex of a trivial graph $N_1$ and a leaf of a star graph $K_{1,n-2}$, where $n\ge 4$.

If a graph G has diameter two, then for any vertex $v\in V\left(G\right)$ the open neighbourhood $N\left(v\right)$ is a dominating set and the closed neighbourhood $N\left[v\right]$ is a total dominating set. Hence, the following result is derived from Theorem 6.

Corollary 4.

If G is a graph of diameter two and minimum degree $\delta \left(G\right)$, then

$${\gamma }_{tr}\left(G\right)\le 2\delta \left(G\right)+1.$$

The bound above is tight. For instance, it is achieved for any star graph $K_{1,n-1}$ with $n\ge 3$.

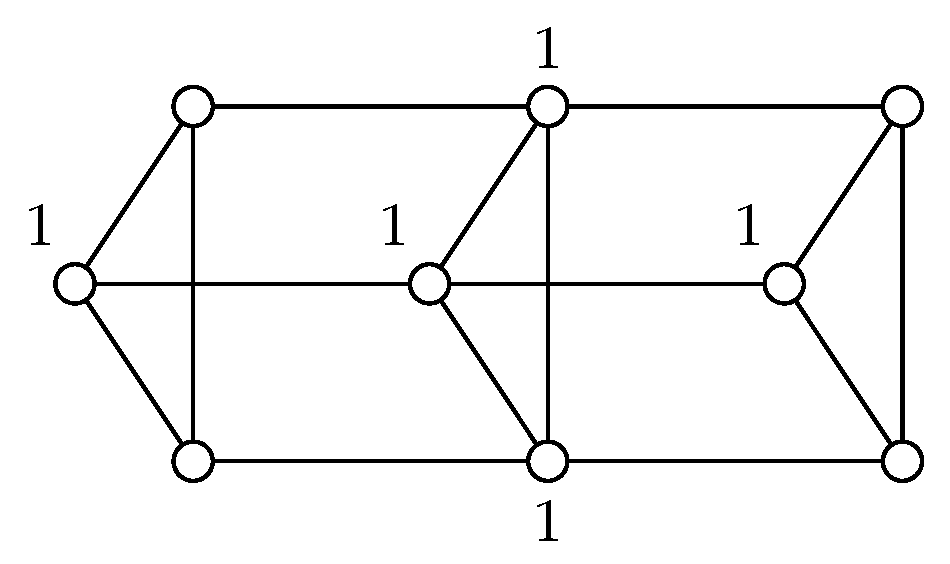
As shown in [17], if G is a planar graph of diameter two, then ${\gamma }_t\left(G\right)\le 3$, and $\gamma \left(G\right)\le 2$ or G is the graph shown in Figure 3. Hence, from these inequalities and Theorem 6 we derive the following tight bound.

Theorem 7.

If G is a planar graph of diameter two, then ${\gamma }_{tr}\left(G\right)\le 5$.

We already know that ${\gamma }_{tr}\left(G\right)\le 2{\gamma }_t\left(G\right)$ (Proposition 1 (i)). Hence, as a direct consequence of this inequality and Theorems 1 and 6 we deduce the following result.

Theorem 8.

Let G be a graph. If ${\gamma }_{tr}\left(G\right)={\gamma }_r\left(G\right)$, then ${\gamma }_t\left(G\right)=\gamma \left(G\right)$.

In general, ${\gamma }_t\left(G\right)=\gamma \left(G\right)$ does not imply that ${\gamma }_{tr}\left(G\right)={\gamma }_r\left(G\right)$. For instance, see the graph shown in Figure 4.

Theorem 9 

([5]). If G is a graph with no isolated vertex, then ${\gamma }_{tR}\left(G\right)\le 3\gamma \left(G\right)$. Furthermore, if ${\gamma }_{tR}\left(G\right)=3\gamma \left(G\right)$, then every $\gamma \left(G\right)$-set is a 2-packing of G.

The following result is a direct consequence of combining Proposition 1 (i) and Theorems 6 and 9.

Theorem 10.

For any graph G with no isolated vertex,

$${\gamma }_{tr}\left(G\right)\le 3\gamma \left(G\right).$$

Furthermore, if ${\gamma }_{tr}\left(G\right)=3\gamma \left(G\right)$ then ${\gamma }_t\left(G\right)=2\gamma \left(G\right)$ and every $\gamma \left(G\right)$-set is a 2-packing of G.

Notice that the inequality ${\gamma }_{tr}\left(G\right)\le 3\gamma \left(G\right)$ can be also deduced from the following result.

Theorem 11.

For any graph G with no isolated vertex,

$${\gamma }_{tr}\left(G\right)\le {\gamma }_r\left(G\right)+\gamma \left(G\right).$$

Proof. 

Let $f(V_0,V_1,V_2)$ be a ${\gamma }_r\left(G\right)$-function such that $|V_2|$ is maximum among all ${\gamma }_r\left(G\right)$-functions and let S be a $\gamma \left(G\right)$-set. Now, we consider the function $f^{\prime }(V_0^{\prime },V_1^{\prime },V_2^{\prime })$ defined as follows.

(a)

For every $x\in V_2\cap S$, choose a vertex $u\in (V_0\cap N\left(x\right))\backslash S$ if it exists, and label it as $f^{\prime }\left(u\right)=1$.

(b)

For every $x\in V_1\cap S$, choose a vertex $u\in epn(x,V_1\cup V_2)\backslash S$ if it exists, otherwise choose a vertex $u\in (V_0\cap N\left(x\right))\backslash S$ (if exists) and label it as $f^{\prime }\left(u\right)=1$.

(c)

For every vertex $x\in V_0\cap S$, $f^{\prime }\left(x\right)=1$.

(d)

For any other vertex u not previously labelled, $f^{\prime }\left(u\right)=f\left(u\right)$.

We claim that $f^{\prime }$ is a TWRDF on G. Firstly, observe that $f^{\prime }$ is a TDF on G. Let $v\in V_0^{\prime }\subseteq V_0$. If there exists a vertex $u\in N\left(v\right)\cap V_2\subseteq V_2^{\prime }$, then v is totally protected under $f^{\prime }$. Now, suppose that $N\left(v\right)\cap V_2=\varnothing$ and let $u\in N\left(v\right)\cap V_1\subseteq V_1^{\prime }$ such that v is protected by u under f. In order to show that v is totally protected under $f^{\prime }$, we consider the function $f^{″}(V_0^{″},V_1^{″},V_2^{″})$ defined by $f^{″}\left(v\right)=1$, $f^{″}\left(u\right)=0$ and $f^{″}\left(x\right)=f^{\prime }\left(x\right)$ whenever $x\in V\left(G\right)\backslash \{v,u\}$. We only need to show that $f^{″}$ is a TDF on G. By definition of $f^{″}$, every vertex in $V\left(G\right)\backslash N\left(u\right)$ is adjacent to some vertex in $V_1^{″}\cup V_2^{″}$. Hence, we differentiate the following cases for any $w\in N\left(u\right)$.

Case 1.

$w\in (V_1\cup V_2)\backslash \left\{u\right\}$. If w has degree one, then $f\left(w\right)=f\left(u\right)=1$ and we can construct a ${\gamma }_r\left(G\right)$-function where the number of vertices with label two is greater than $|V_2|$, which is a contradiction. Hence, $N\left(w\right)\cap (V_1\cup V_2)\backslash \left\{u\right\}\ne \varnothing$ or $N\left(w\right)\cap V_0\ne \varnothing$. In the first case, we conclude that w is adjacent to some vertex in $(V_1\cup V_2)\backslash \left\{u\right\}\subseteq V_1^{″}\cup V_2^{″}$. If this case does not occur, then by (b) and (c) in the definition of $f^{\prime }$, there exists $y\in N\left(w\right)\cap V_0$ satisfying that $y\in V_1^{\prime }\backslash \left\{u\right\}\subseteq V_1^{″}$.

Case 2.

$w\in V_0$. If $w\notin epn(u,V_1\cup V_2)$ then it is adjacent to some vertex in $(V_1\cup V_2)\backslash \left\{u\right\}\subseteq V_1^{″}\cup V_2^{″}$. From now on, suppose that $w\in epn(u,V_1\cup V_2)$. If $v\ne w$, then w must be adjacent to $v\in V_1^{″}$, as v is protected by u under f. Now, if $v=w$ and $u\notin S$, then w is adjacent to some vertex in $S\subseteq V_1^{″}\cup V_2^{″}$. Finally, if $v=w$ and $u\in S$, then by (b) in the definition of $f^{\prime }$ we have that $f^{\prime }\left(v\right)=1$, which is a contradiction.

From the two cases above we can conclude that $f^{″}$ is a TDF on G, as required. Therefore, $f^{\prime }$ is a TWRDF and, as a consequence, ${\gamma }_{tr}\left(G\right)\le \omega \left(f^{\prime }\right)\le {\gamma }_r\left(G\right)+\gamma \left(G\right)$. □

Corollary 5.

For any graph G with no isolated vertex,

$${\gamma }_{tr}\left(G\right)\le 2{\gamma }_r\left(G\right).$$

Furthermore, if ${\gamma }_r\left(G\right)>\gamma \left(G\right)$, then ${\gamma }_{tr}\left(G\right)\le 2{\gamma }_r\left(G\right)-1$.

In order to derive another consequence of Theorem 11 we need to state the following result.

Theorem 12 

([12]). For any connected graph $G\ncong C_5$ of order n and minimum degree $\delta \left(G\right)\ge 2$,

$${\displaystyle {\gamma }_s\left(G\right)\le ⌊\frac{n}{2}⌋.}$$

Since ${\gamma }_r\left(G\right)\le {\gamma }_s\left(G\right)$, from Theorems 11 and 12 we immediately have the next theorem.

Theorem 13.

For any connected graph G of order n and minimum degree $\delta \left(G\right)\ge 2$,

$${\displaystyle {\gamma }_{tr}\left(G\right)\le ⌊\frac{n}{2}⌋+\gamma \left(G\right).}$$

The bound above is tight. It is achieved for the graph $C_5$.

Theorem 14.

Let G be a graph with no isolated vertex. For any ${\gamma }_r\left(G\right)$-function $f(V_0,V_1,V_2)$,

$${\gamma }_{tr}\left(G\right)\le 2{\gamma }_r\left(G\right)-\left|V_2\right|.$$

Proof. 

Let $g(V_0,V_1,V_2)$ be a ${\gamma }_r\left(G\right)$-function such that $|V_2|$ is maximum, and consider the function $g^{\prime }(V_0^{\prime },V_1^{\prime },V_2^{\prime })$ defined on G as follows.

(a)

For every $x\in V_2$, choose a vertex $u\in V_0\cap N\left(x\right)$ and label it as $g^{\prime }\left(u\right)=1$.

(b)

For every $x\in V_1$, choose a vertex $u\in epn(x,V_1\cup V_2)$ if it exists, otherwise choose a vertex $u\in V_0\cap N\left(x\right)$ (if exists) and label it as $g^{\prime }\left(u\right)=1$.

(c)

For any other vertex u not previously labelled, $g^{\prime }\left(u\right)=g\left(u\right)$.

We claim that $g^{\prime }$ is a TWRDF on G. Firstly, observe that $g^{\prime }$ is a TDF on G. Let $v\in V_0^{\prime }\subseteq V_0$. If there exists a vertex $u\in N\left(v\right)\cap V_2$, then v is totally protected under $g^{\prime }$. Now, suppose that $N\left(v\right)\cap V_2=\varnothing$ and let $u\in N\left(v\right)\cap V_1$ such that v is protected by u under f. In order to show that v is totally protected under $g^{\prime }$, we consider the function $g^{*}(V_0^{*},V_1^{*},V_2^{*})$ defined by $g^{*}\left(v\right)=1$, $g^{*}\left(u\right)=0$ and $g^{*}\left(x\right)=g^{\prime }\left(x\right)$ if $x\in V\left(G\right)\backslash \{v,u\}$. We only need to show that $g^{*}$ is a TDF on G.

By definition of $g^{*}$, every vertex in $V\left(G\right)\backslash N\left(u\right)$ is adjacent to some vertex in $V_1^{*}\cup V_2^{*}$. Hence, we differentiate the following two cases for any $w\in N\left(u\right)$.

Case 1.

$w\in (V_1\cup V_2)\backslash \left\{u\right\}$. If w has degree one, then we can construct a ${\gamma }_r\left(G\right)$-function where the number of vertices with label two is greater than $|V_2|$, which is a contradiction. Hence, $N\left(w\right)\cap (V_1\cup V_2)\backslash \left\{u\right\}\ne \varnothing$ or $N\left(w\right)\cap V_0\ne \varnothing$. In the first case, we conclude that w is adjacent to some vertex in $(V_1\cup V_2)\backslash \left\{u\right\}\subseteq V_1^{*}\cup V_2^{*}$. If this case does not occur, then by definition of $g^{\prime }$ there exists $y\in N\left(w\right)\cap V_0$ satisfying that $y\in V_1^{\prime }\backslash \left\{u\right\}\subseteq V_1^{*}$.

Case 2.

$w\in V_0$. If $w\notin epn(u,V_1\cup V_2)$ then it is adjacent to some vertex in $(V_1\cup V_2)\backslash \left\{u\right\}\subseteq V_1^{*}\cup V_2^{*}$. From now on, we suppose that $w\in epn(u,V_1\cup V_2)$. If $w\ne v$, then w must be adjacent to $v\in V_1^{*}$, as v is protected by u under f. Now, if $w=v$, then by (b) in the definition of $g^{\prime }$ and the fact that v is protected by u under f we have that there exists $y\in V_1^{\prime }\cap epn(u,V_1\cup V_2)\cap N\left(v\right)$.

From the two cases above we can conclude that, $g^{*}$ is a TDF on G. Thus, $g^{\prime }$ is a TWRDF and, as a consequence, ${\gamma }_{tr}\left(G\right)\le \omega \left(g^{\prime }\right)=|V_1^{\prime }|+2|V_2^{\prime }|\le |V_1|+2|V_2|+|V_1|+|V_2|=2{\gamma }_r\left(G\right)-\left|V_2\right|$. Finally, since $|V_2|$ is maximum among all ${\gamma }_{tr}\left(G\right)$-functions, the result follows. □

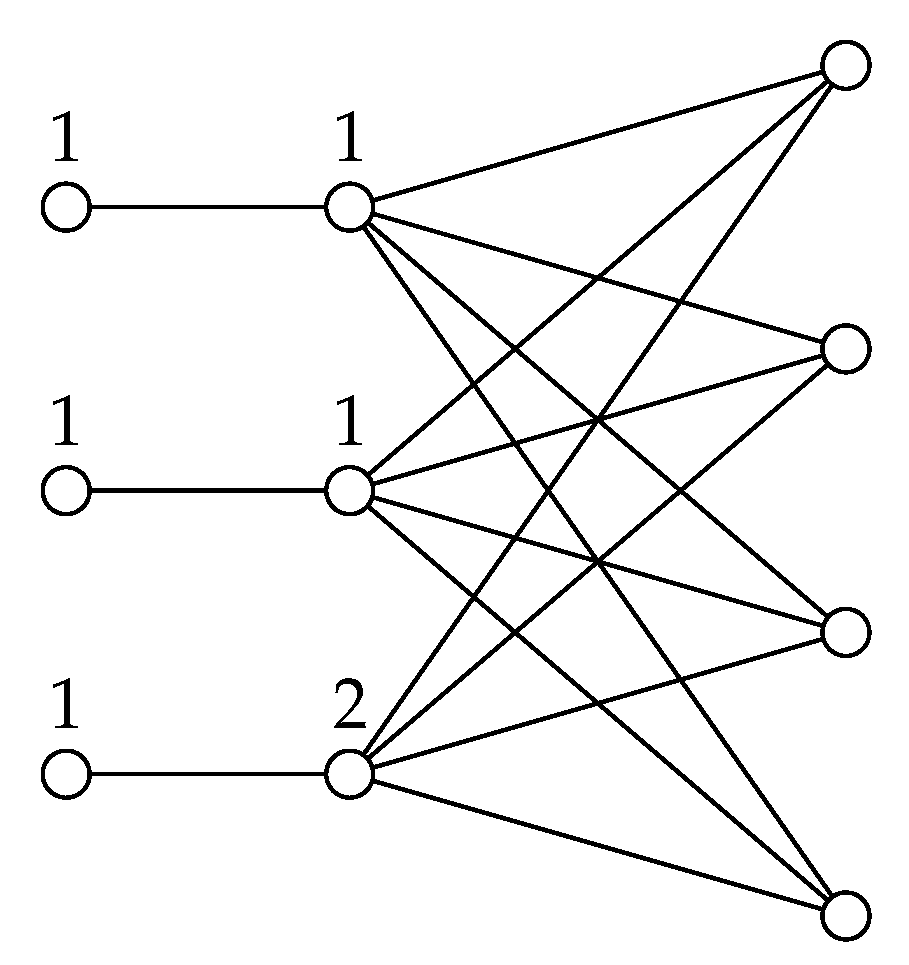
We now proceed to construct a family of graphs $G_{p,q}$ with ${\gamma }_r\left(G_{p,q}\right)=p+1$ and ${\gamma }_{tr}\left(G_{p,q}\right)=2p+1$, where $q\ge p\ge 2$ are integers. The graph $G_{p,q}$ is constructed from the complete bipartite graph $K_{p,q}$ and the empty graph $N_p$ by adding p new edges which form a matching between the vertices of $N_p$ and the vertices of degree q in $K_{p,q}$. Notice that there exists a ${\gamma }_r\left(G_{p,q}\right)$-function $g(V_0,V_1,V_2)$ with $|V_2|=1$. Therefore, ${\gamma }_{tr}\left(G_{p,q}\right)=2p+1=2(p+1)-1=2{\gamma }_r\left(G_{p,q}\right)-1=2{\gamma }_r\left(G_{p,q}\right)-\left|V_2\right|$.

Figure 5 shows the graph $G_{3,4}$ and a ${\gamma }_{tr}\left(G_{3,4}\right)$-function $g(V_0,V_1,V_2)$, obtained by using the construction of the proof of Theorem 14. One can check that ${\gamma }_{tr}\left(G_{3,4}\right)=7$, ${\gamma }_r\left(G_{3,4}\right)=4$ and $|V_2|=1$, concluding that ${\gamma }_{tr}\left(G_{3,4}\right)=2{\gamma }_r\left(G_{3,4}\right)-\left|V_2\right|$.

If ${\gamma }_r\left(G\right)<{\gamma }_s\left(G\right)$, then there exists a ${\gamma }_r\left(G\right)$-function $f(V_0,V_1,V_2)$ such that $V_2\ne \varnothing$. Therefore, the following result is a direct consequence of Theorem 14.

Corollary 6.

Let G be a graph with no isolated vertex. If ${\gamma }_r\left(G\right)<{\gamma }_s\left(G\right)$, then

$${\gamma }_{tr}\left(G\right)\le 2{\gamma }_r\left(G\right)-1.$$

We continue with a result that provides a new relationship between the total weak Roman domination number and the Roman domination number. To this end, we need to state the following known result.

Theorem 15 

([5]). If G is a graph of order n with no isolated vertex, then ${\gamma }_{tR}\left(G\right)\le 2{\gamma }_R\left(G\right)-1$. Furthermore, ${\gamma }_{tR}\left(G\right)=2{\gamma }_R\left(G\right)-1$ if and only if $\Delta \left(G\right)=n-1$.

Theorem 16.

For any graph G of order n with no isolated vertex,

$${\gamma }_{tr}\left(G\right)\le 2{\gamma }_R\left(G\right)-1.$$

Furthermore, ${\gamma }_{tr}\left(G\right)=2{\gamma }_R\left(G\right)-1$ if and only if ${\gamma }_{tr}\left(G\right)=3$ and $\Delta \left(G\right)=n-1$.

Proof. 

By Proposition 1 (i) and Theorem 15, the inequality holds. Furthermore, if ${\gamma }_{tr}\left(G\right)=2{\gamma }_R\left(G\right)-1$ then, again by Proposition 1 and Theorem 15, ${\gamma }_{tR}\left(G\right)=2{\gamma }_R\left(G\right)-1$ and this implies that $\Delta \left(G\right)=n-1$. Thus, ${\gamma }_R\left(G\right)=2$, and so ${\gamma }_{tr}\left(G\right)=3$. Conversely, if ${\gamma }_{tr}\left(G\right)=3$ and $\Delta \left(G\right)=n-1$, then ${\gamma }_R\left(G\right)=2$ and ${\gamma }_{tr}\left(G\right)=2{\gamma }_R\left(G\right)-1$. □

4. General Bounds

Our next two results provide bounds in terms of the order, the minimum degree and the maximum degree of G.

Theorem 17.

For any graph G of order n with $\delta \left(G\right)\ge 1$,

$$⌈\frac{2n}{\Delta \left(G\right)+1}⌉\le {\gamma }_{tr}\left(G\right)\le n-\delta \left(G\right)+1.$$

Proof. 

Let $f(V_0,V_1,V_2)$ be a ${\gamma }_{tr}\left(G\right)$-function and let $V_0^2=\{x\in V_0:N\left(x\right)\cap V_2\ne \varnothing \}$ and $V_0^1=V_0\backslash V_0^2$. Since every vertex in $V_2$ can have at most $\Delta \left(G\right)-1$ neighbours in $V_0^2$, we obtain that $|V_0^2|\le (\Delta \left(G\right)-1)|V_2|$. Furthermore, since every vertex in $V_0^1$ has at least two neighbours in $V_1$ and every vertex in $V_1$ has at most $\Delta \left(G\right)-1$ neighbours in $V_0^1$, we deduce that $2|V_0^1|\le (\Delta \left(G\right)-1)|V_1|$. Hence,

$$\begin{array}{cc}\hfill n& =|V_0^1|+|V_0^2|+|V_1|+|V_2|\hfill \\ & \le (\Delta \left(G\right)-1)|V_1|/2+(\Delta \left(G\right)-1)|V_2|+|V_1|+|V_2|=(\Delta \left(G\right)+1)|V_1|/2+\Delta \left(G\right)|V_2|\hfill \\ & \le (\Delta \left(G\right)+1)|V_1|/2+\Delta \left(G\right)|V_2|+|V_2|\hfill \\ & \le (\Delta \left(G\right)+1)\left(\right|V_1|/2+|V_2\left|\right)=(\Delta \left(G\right)+1){\gamma }_{tr}\left(G\right)/2.\hfill \end{array}$$

Therefore, ${\gamma }_{tr}\left(G\right)\ge ⌈\frac{2n}{\Delta \left(G\right)+1}⌉$.

The upper bound follows for $\delta \left(G\right)=1$, so we assume that $\delta \left(G\right)\ge 2$. Let $v\in V\left(G\right)$ be a vertex of degree $\delta \left(G\right)$ and $u\in N\left(v\right)$. It is readily seen that the function g, defined by $g\left(x\right)=0$ for every $x\in N\left(v\right)\backslash \left\{u\right\}$ and $g\left(x\right)=1$ otherwise, is a TWRDF on G. Therefore, ${\gamma }_{tr}\left(G\right)\le \omega \left(g\right)=n-\delta \left(G\right)+1$. □

The bounds above are tight. For instance, they are achieved for any complete nontrivial graph and for the cycles $C_n$ with $n\le 5$. Furthermore, the wheel graph $K_1+C_4$ achieves the upper bound and any corona graph $K_2\odot H$ achieves the lower bound, where $\left|V\right(H\left)\right|\ge 3$. Notice that ${\gamma }_{tr}(K_2\odot H)=4$. The limit cases ${\gamma }_{tr}\left(G\right)=2$ and ${\gamma }_{tr}\left(G\right)=n$ will be discussed in Theorem 20.

Theorem 18 

([14]). Let G be a graph of order n. Then ${\gamma }_{st}\left(G\right)=n$ if and only if $V\left(G\right)\backslash \left(L\right(G)\cup S(G\left)\right)$ is an independent set.

Theorem 19 

([13]). If G is a connected graph, then the following statements are equivalent.

• ${\gamma }_{st}\left(G\right)={\gamma }_t\left(G\right)$.
• ${\gamma }_{st}\left(G\right)=2$.
• G has two universal vertices.

We now proceed to characterize all graphs achieving the limit cases of the trivial bounds $2\le {\gamma }_{tr}\left(G\right)\le n.$

Theorem 20.

Given a connected graph G of order n, the following statements hold.

(i)

The following statements are equivalent.

(a)

${\gamma }_{tr}\left(G\right)=2$.

(b)

${\gamma }_{tr}\left(G\right)={\gamma }_t\left(G\right)$.

(c)

${\gamma }_{st}\left(G\right)={\gamma }_t\left(G\right)$.

(d)

G has two universal vertices.

(ii)

${\gamma }_{tr}\left(G\right)=n$ if and only if G is $K_{1,(n-1)/2}^{*}$ or $H\odot N_1$ for some connected graph H.

Proof. 

We first proceed to prove (i). Notice that (a) directly implies (b), as $2\le {\gamma }_t\left(G\right)\le {\gamma }_{tr}\left(G\right)$. Now, suppose that (b) holds and let $f(V_0,V_1,V_2)$ be a ${\gamma }_{tr}\left(G\right)$-function. Since f is a TDF, ${\gamma }_t\left(G\right)\le |V_1\cup V_2|=|V_1|+|V_2|\le |V_1|+2|V_2|={\gamma }_{tr}\left(G\right)={\gamma }_t\left(G\right)$, so $V_2=\varnothing$ and, as a consequence, f is a STDF of weight ${\gamma }_t\left(G\right)$. Hence, (c) holds. On the other hand, by Theorem 19, (c) implies (d). Finally, it is straightforward that (d) implies (a).

We now proceed to prove (ii). If G is $K_{1,(n-1)/2}^{*}$ or $H\odot N_1$ for some connected graph H, then is straightforward that ${\gamma }_{tr}\left(G\right)=n$. From now on we assume that G is a connected graph such that ${\gamma }_{tr}\left(G\right)=n$. Since ${\gamma }_{tr}\left(G\right)\le {\gamma }_{st}\left(G\right)\le n$, we have that ${\gamma }_{st}\left(G\right)=n$ and so, by Theorem 18, $V\left(G\right)=L\left(G\right)\cup S\left(G\right)\cup I$, where I is an independent set. Moreover, notice that if $n=2$ then $G\cong P_2\cong N_1\odot N_1$, and if $\left|S\right(G\left)\right|=1$ then $G\cong P_3\cong K_{1,1}^{*}$. So, we assume that $n\ge 4$ and $\left|S\right(G\left)\right|\ge 2$.

Suppose that $v\in S_s\left(G\right)$ and let $h_1$ and $h_2$ be two leaves adjacent to v. We consider the function g defined by $g\left(h_1\right)=g\left(h_2\right)=0$, $g\left(v\right)=2$ and $g\left(x\right)=1$ if $x\in V\left(G\right)\backslash \{v,h_1,h_2\}$. Hence, g is a TWRDF on G and $\omega \left(g\right)=n-1$, which is a contradiction. Thus $S_s\left(G\right)=\varnothing$. We now differentiate two cases.

Case 1.

$I=\varnothing$. In this case, $V\left(G\right)=L\left(G\right)\cup S\left(G\right)$ and, since G is connected, the subgraph H induced by $S\left(G\right)$ is connected. Furthermore, since $S_s\left(G\right)=\varnothing$, we have that $G\cong H\odot N_1$.

Case 2.

$I\ne \varnothing$. Suppose that $S\left(G\right)$ is not an independent set. Notice that there exist two adjacent support vertices $v,w$ and a third vertex $s\in N\left(v\right)\cap I$. Let $h\in N\left(v\right)\cap L\left(G\right)$ and consider the function g defined by $g\left(v\right)=2$, $g\left(h\right)=g\left(s\right)=0$ and $g\left(x\right)=1$ if $x\in V\left(G\right)\backslash \{v,h,s\}$. Notice that g is a TWRDF on G and $\omega \left(g\right)=n-1$, which is a contradiction, so $S\left(G\right)$ is an independent set. Now, suppose that $\left|I\right|\ge 2$ and let $s_1,s_2\in I$ be two vertices at the shortest possible distance. Since $S\left(G\right)$ and I are independent sets, $s_1$ and $s_2$ are at distance two. Let $v\in S\left(G\right)\cap N\left(s_1\right)\cap N\left(s_2\right)$, let $h\in N\left(v\right)\cap L\left(G\right)$ and let $g^{\prime }$ be a function defined by $g^{\prime }\left(v\right)=2$, $g^{\prime }\left(s_1\right)=g^{\prime }\left(h\right)=0$, and $g^{\prime }\left(x\right)=1$ if $x\in V\left(G\right)\backslash \{v,s_1,h\}$. Observe that $g^{\prime }$ is a TWRDF on G and $\omega \left(g^{\prime }\right)=n-1$, which is a contradiction. Thus, $\left|I\right|=1$. Therefore, since $S_s\left(G\right)=\varnothing$, $S\left(G\right)$ is an independent set and $\left|I\right|=1$, we conclude that G is the subdivided star $K_{1,(n-1)/2}^{*}$ and this completes the proof. □

To conclude this section, we proceed to characterize all graphs with ${\gamma }_{tr}\left(G\right)=3$.

Theorem 21.

Let G be a graph and let $\mathcal{G}$ be the family of graphs H of order $n\ge 3$ such that the subgraph induced by three vertices of H contains a path $P_3$ and the remaining $n-3$ vertices have degree two and they form an independent set. Then ${\gamma }_{tr}\left(G\right)=3$ if and only if there exists $H\in \mathcal{G}\cup \left\{K_{1,n-1}\right\}$ which is a spanning subgraph of G and G has at most one universal vertex.

Proof. 

We first suppose that ${\gamma }_{tr}\left(G\right)=3$. Let $f(V_0,V_1,V_2)$ be a ${\gamma }_{tr}\left(G\right)$-function. By Theorem 20 (i), G has at most one universal vertex. If $|V_2|=1$, then $|V_1|=1$. In such a case, let $V_1=\left\{v\right\}$ and $V_2=\left\{u\right\}$. Notice that u and v are adjacent vertices. Since f is a TWRDF on G, any vertex must be adjacent to u, concluding that $K_{1,n-1}$ is a spanning subgraph of G. Now, if $|V_2|=0$, then $|V_1|=3$. With this assumption, let $V_1=\{u,v,w\}$ and notice that the subgraph of G induced by $V_1$ contains a path $P_3$, as $V_1$ is a total dominating set of G. We may suppose that v is adjacent to u and w. Since f is a TWRDF on G, we observe that $|N\left(z\right)\cap V_1|\ge 2$ for every $z\in V_0$. Hence, in this case, G contains a spanning subgraph belonging to $\mathcal{G}$.

Conversely, since G has at most one universal vertex, by Theorem 20 (i) we have that ${\gamma }_{tr}\left(G\right)\ge 3$. Moreover, it is readily seen that ${\gamma }_{tr}\left(K_{1,n-1}\right)=3$ and ${\gamma }_{tr}\left(H\right)\le 3$ for any $H\in \mathcal{G}$. Hence, if $H\in \mathcal{G}\cup \left\{K_{1,n-1}\right\}$ is a spanning subgraph of G, by Proposition 2 it follows that ${\gamma }_{tr}\left(G\right)\le 3$. Therefore, ${\gamma }_{tr}\left(G\right)=3$. □

5. Rooted Product Graphs and Computational Complexity

Let G and H be two graphs and let $v\in V\left(H\right)$. The rooted product graph $G{\circ }_{v}H$ is defined to be the graph obtained from G and H by taking one copy of G and $\left|V\right(G\left)\right|$ copies of H and identifying the ith-vertex of G with vertex v in the ith-copy of H for every $i\in \{1,\cdots ,|V\left(G\right)\left|\right\}$.

For every $x\in V\left(G\right)$, $H_x$ will denote the copy of H in $G{\circ }_{v}H$ containing x. The restriction of any ${\gamma }_{tr}\left(G{\circ }_{v}H\right)$-function f to $V\left(H_x\right)$ will be denoted by $f_x$, and the restriction to $V(H_x-\left\{x\right\})$ will be denoted by $f_x^{-}$. Notice that $V\left(G{\circ }_{v}H\right)={\cup }_{x\in V\left(G\right)}V\left(H_x\right)$ and so

$${\gamma }_{tr}\left(G{\circ }_{v}H\right)=\omega \left(f\right)=\sum _{x\in V\left(G\right)}\omega \left(f_x\right)=\sum _{x\in V\left(G\right)}\omega \left(f_x^{-}\right)+\sum _{x\in V\left(G\right)}f\left(x\right).$$

Lemma 1.

Let $f(V_0,V_1,V_2)$ be a ${\gamma }_{tr}\left(G{\circ }_{v}H\right)$-function. For any $x\in V\left(G\right)$, $\omega \left(f_x\right)\ge {\gamma }_{tr}\left(H\right)-2$. Furthermore, if $\omega \left(f_x\right)={\gamma }_{tr}\left(H\right)-2$, then $f\left(x\right)=0$ and $N\left(x\right)\cap V\left(H_x\right)\subseteq V_0$.

Proof. 

Let $x\in V\left(G\right)$. Notice that every vertex in $V_0\cap V\left(H_x\right)\backslash \left\{x\right\}$ is totally protected under $f_x$. Now, suppose that $\omega \left(f_x\right)\le {\gamma }_{tr}\left(H\right)-3$ and let $y\in N\left(x\right)\cap V\left(H_x\right)$. Observe that the function g, defined by $g\left(y\right)=2$ and $g\left(u\right)=f_x\left(u\right)$ whenever $u\in V\left(H_x\right)\backslash \left\{y\right\}$, is a TWRDF on $H_x$ of weight $\omega \left(g\right)\le {\gamma }_{tr}\left(H\right)-1$, which is a contradiction as $H_x\cong H$. Hence, $\omega \left(f_x\right)\ge {\gamma }_{tr}\left(H\right)-2$.

Now, suppose that $\omega \left(f_x\right)={\gamma }_{tr}\left(H\right)-2$. If $f\left(x\right)>0$ then given a vertex $y\in N\left(x\right)\cap V\left(H_x\right)$, the function h, defined by $h\left(y\right)=min\{f_x\left(y\right)+1,2\}$ and $h\left(u\right)=f_x\left(u\right)$ whenever $u\in V\left(H_x\right)\backslash \left\{y\right\}$, is a TWRDF on $H_x$ of weight $\omega \left(h\right)\le {\gamma }_{tr}\left(H\right)-1$, which is a contradiction. Hence, $f\left(x\right)=0$. Now, if there exists a vertex $y\in N\left(x\right)\cap V\left(H_x\right)\cap (V_1\cup V_2)$, then from $f_x$ we may define a TWRDF $f^{\prime }$ on $H_x$ with the only difference that $f^{\prime }\left(y\right)=2$, having weight at most ${\gamma }_{tr}\left(H\right)-1$, which is a contradiction again. Therefore, $N\left(x\right)\cap V\left(H_x\right)\subseteq V_0$. □

Lemma 2.

Let H be a graph with no isolated vertex. For any $v\in V\left(H\right)\backslash S\left(H\right)$,

$${\gamma }_{tr}(H-\left\{v\right\})\ge {\gamma }_{tr}\left(H\right)-2.$$

Furthermore, if ${\gamma }_{tr}(H-\left\{v\right\})={\gamma }_{tr}\left(H\right)-2,$ then the following statements hold.

(i)

$f\left(N\right(v\left)\right)=0$ for every ${\gamma }_{tr}(H-\left\{v\right\})$-function f.

(ii)

There exists a ${\gamma }_{tr}\left(H\right)$-function $h_0$ such that $h_0\left(v\right)=0$.

(iii)

There exists a ${\gamma }_{tr}\left(H\right)$-function $h_1$ such that $h_1\left(v\right)=1$.

Proof. 

Let f be a ${\gamma }_{tr}(H-\left\{v\right\})$-function and suppose that $\omega \left(f\right)\le {\gamma }_{tr}\left(H\right)-3$. Let $y\in N\left(v\right)$. Observe that the function g, defined by $g\left(y\right)=min\left\{f\right(y)+1,2\}$, $g\left(v\right)=1$ and $g\left(u\right)=f\left(u\right)$ whenever $u\in V\left(H\right)\backslash \{v,y\}$, is a TWRDF on H of weight $\omega \left(g\right)\le {\gamma }_{tr}\left(H\right)-1$, which is a contradiction. Hence, $\omega \left(f\right)\ge {\gamma }_{tr}\left(H\right)-2$.

Now, assume that $\omega \left(f\right)={\gamma }_{tr}\left(H\right)-2$. If there exists a vertex $y\in N\left(v\right)$ such that $f\left(y\right)>0$, then the function $f^{\prime }$, defined by $f^{\prime }\left(v\right)=0$, $f^{\prime }\left(y\right)=2$ and $f^{\prime }\left(u\right)=f\left(u\right)$ whenever $u\in V\left(H\right)\backslash \{v,y\}$, is a TWRDF on H of weight at most ${\gamma }_{tr}\left(H\right)-1$, which is a contradiction again. Therefore, $f\left(N\right(v\left)\right)=0$.

Furthermore, for any $y\in N\left(v\right)$, the function $h_0$, defined by $h_0\left(v\right)=0$, $h_0\left(y\right)=2$ and $h_0\left(u\right)=f\left(u\right)$ whenever $u\in V\left(H\right)\backslash \{v,y\}$, is a ${\gamma }_{tr}\left(H\right)$-function. Analogously, the function $h_1$, defined by $h_1\left(v\right)=1$, $h_1\left(y\right)=1$ and $h_1\left(u\right)=f\left(u\right)$ whenever $u\in V\left(H\right)\backslash \{v,y\}$, is a ${\gamma }_{tr}\left(H\right)$-function as well. Therefore, the result follows. □

Corollary 7.

Let H be a graph with no isolated vertex and $v\in V\left(H\right)\backslash S\left(H\right)$. Then the following statements hold.

• If $g\left(v\right)=0$ for every ${\gamma }_{tr}\left(H\right)$-function g, then ${\gamma }_{tr}(H-\left\{v\right\})\in \{{\gamma }_{tr}\left(H\right),{\gamma }_{tr}\left(H\right)-1\}$.
• If $h\left(v\right)>0$ for every ${\gamma }_{tr}\left(H\right)$-function h, then ${\gamma }_{tr}(H-\left\{v\right\})\ge {\gamma }_{tr}\left(H\right)-1$.

From Lemma 1 we deduce that any ${\gamma }_{tr}\left(G{\circ }_{v}H\right)$-function f induces a partition $\{{\mathcal{A}}_f,{\mathcal{B}}_f,{\mathcal{C}}_f\}$ of $V\left(G\right)$ as follows.

$${\mathcal{A}}_f=\{x\in V\left(G\right):\omega \left(f_x\right)\ge {\gamma }_{tr}\left(H\right)\},$$

$${\mathcal{B}}_f=\{x\in V\left(G\right):\omega \left(f_x\right)={\gamma }_{tr}\left(H\right)-1\},$$

$${\mathcal{C}}_f=\{x\in V\left(G\right):\omega \left(f_x\right)={\gamma }_{tr}\left(H\right)-2\}.$$

Proposition 3.

Let f be a ${\gamma }_{tr}\left(G{\circ }_{v}H\right)$-function. If ${\mathcal{C}}_f\ne \varnothing$, then ${\gamma }_{tr}(H-\left\{v\right\})={\gamma }_{tr}\left(H\right)-2.$

Proof. 

By Lemma 1, if $x\in {\mathcal{C}}_f$, then $f\left(x\right)=0$ and $f\left(y\right)=0$ for every $y\in N\left(x\right)\cap V\left(H_x\right)$, which implies that $f_x^{-}$ is a TWRDF on $H_x-\left\{x\right\}$ of weight $w\left(f_x^{-}\right)={\gamma }_{tr}\left(H\right)-2.$ Hence, ${\gamma }_{tr}(H-\left\{v\right\})={\gamma }_{tr}(H_x-\left\{x\right\})\le {\gamma }_{tr}\left(H\right)-2$, and by Lemma 2 we conclude the proof. □

We will show through Theorem 23 that if ${\gamma }_{tr}\left(G\right)<n$, then the converse of Proposition 3 holds. An example of graphs where it does not hold is the case of $G\cong K_2$ and $H\cong P_3\odot N_1$, where v is a leaf adjacent to a support vertex of degree two.

By Lemma 1 and Proposition 3 we deduce the following result.

Theorem 22.

Let G and H be two graphs with isolated vertex and let $v\in V\left(H\right)$. If ${\gamma }_{tr}(H-\left\{v\right\})\ge {\gamma }_{tr}\left(H\right)-1$, then ${\gamma }_{tr}\left(G{\circ }_{v}H\right)\ge n({\gamma }_{tr}\left(H\right)-1)$.

The inequality above is achieved, for instance, for any graph G with no isolated vertex and $H\cong C_5$.

It is readily seen that from any ${\gamma }_{tr}\left(G\right)$-function and any ${\gamma }_{tr}(H-\left\{v\right\})$-function we can construct a TWRDF on $G{\circ }_{v}H$ of weight ${\gamma }_{tr}\left(G\right)+n\left({\gamma }_{tr}(H-\left\{v\right\})\right)$. Therefore, we can state the following useful result.

Proposition 4.

Let G and H be two graphs with no isolated vertex. If G has order n and $v\in V\left(H\right)\backslash S\left(H\right)$, then

$${\gamma }_{tr}\left(G{\circ }_{v}H\right)\le {\gamma }_{tr}\left(G\right)+n{\gamma }_{tr}(H-\left\{v\right\}).$$

Theorem 23.

Let G and H be two graphs with no isolated vertex and let $v\in V\left(H\right)$. If ${\gamma }_{tr}\left(G\right)<n$, then the following statements are equivalent.

(a)

${\mathcal{C}}_f\ne \varnothing$ for any ${\gamma }_{tr}\left(G{\circ }_{v}H\right)$-function f.

(b)

${\gamma }_{tr}(H-\left\{v\right\})={\gamma }_{tr}\left(H\right)-2$.

Proof. 

Let f be a ${\gamma }_{tr}\left(G{\circ }_{v}H\right)$-function such that $x\in {\mathcal{C}}_f$. By Proposition 3, ${\gamma }_{tr}(H-\left\{v\right\})={\gamma }_{tr}\left(H\right)-2$.

Conversely, assume that ${\gamma }_{tr}(H-\left\{v\right\})={\gamma }_{tr}\left(H\right)-2$ and suppose that ${\mathcal{C}}_{f^{\prime }}=\varnothing$ for some ${\gamma }_{tr}\left(G{\circ }_{v}H\right)$-function $f^{\prime }$. By Lemma 1 and Proposition 4 we deduce that $n({\gamma }_{tr}\left(H\right)-1)\le {\gamma }_{tr}\left(G{\circ }_{v}H\right)\le {\gamma }_{tr}\left(G\right)+n({\gamma }_{tr}\left(H\right)-2)$, which is a contradiction whenever ${\gamma }_{tr}\left(G\right)<n$. Therefore, the result follows. □

The following result states the intervals in which the total weak Roman domination number of a rooted product graph can be found.

Theorem 24.

Let G and H be two graphs with no isolated vertex. If G has order n and $v\in V\left(H\right)$, then one of the following statements holds.

(i)

${\gamma }_{tr}\left(G{\circ }_{v}H\right)=n{\gamma }_{tr}\left(H\right)$.

(ii)

$n({\gamma }_{tr}\left(H\right)-1)\le {\gamma }_{tr}\left(G{\circ }_{v}H\right)\le {\gamma }_{tr}\left(G\right)+n({\gamma }_{tr}\left(H\right)-1)$.

(iii)

$2\gamma \left(G\right)+n({\gamma }_{tr}\left(H\right)-2)\le {\gamma }_{tr}\left(G{\circ }_{v}H\right)\le {\gamma }_{tr}\left(G\right)+n({\gamma }_{tr}\left(H\right)-2)$.

(iv)

${\gamma }_t\left(G\right)+n({\gamma }_{tr}\left(H\right)-2)\le {\gamma }_{tr}\left(G{\circ }_{v}H\right)\le {\gamma }_{tr}\left(G\right)+n({\gamma }_{tr}\left(H\right)-2)$.

Proof. 

Let $f(V_0,V_1,V_2)$ be a ${\gamma }_{tr}\left(G{\circ }_{v}H\right)$-function and consider the partition $\{{\mathcal{A}}_f,{\mathcal{B}}_f,{\mathcal{C}}_f\}$ of $V\left(G\right)$ defined above. We differentiate the following four cases.

Case 1.

${\mathcal{B}}_f\cup {\mathcal{C}}_f=\varnothing$. In this case, for any $x\in V\left(G\right)$ we have that $\omega \left(f_x\right)\ge {\gamma }_{tr}\left(H\right)$ and, as a consequence, ${\gamma }_{tr}\left(G{\circ }_{v}H\right)\ge n{\gamma }_{tr}\left(H\right)$. On the other hand, we can extend any ${\gamma }_{tr}\left(H\right)$-function to a TWRDF on $G{\circ }_{v}H$ of weight $n{\gamma }_{tr}\left(H\right)$. Therefore, (i) follows.

Case 2.

${\mathcal{B}}_f\ne \varnothing$ and ${\mathcal{C}}_f=\varnothing$. In this case, for any $x\in V\left(G\right)$ we have that $\omega \left(f_x\right)\ge {\gamma }_{tr}\left(H\right)-1$ and, as a result, ${\gamma }_{tr}\left(G{\circ }_{v}H\right)\ge n({\gamma }_{tr}\left(H\right)-1)$.

We now proceed to show that ${\gamma }_{tr}\left(G{\circ }_{v}H\right)\le {\gamma }_{tr}\left(G\right)+n({\gamma }_{tr}\left(H\right)-1)$. From f, some vertex $x^{\prime }\in {\mathcal{B}}_f$ and any ${\gamma }_{tr}\left(G\right)$-function h, we define a function g on $G{\circ }_{v}H$ as follows. For every $x\in V\left(G\right)$, the restriction of g to $V\left(H_x\right)\backslash \left\{x\right\}$ is induced by $f_{x^{\prime }}^{-}$ and we set $g\left(x\right)=min\left\{f\right(x)+h(x),2\}$. It is readily seen that g is a TWRDF on $G{\circ }_{v}H$ of weight at most ${\gamma }_{tr}\left(G\right)+n({\gamma }_{tr}\left(H\right)-1)$, concluding that ${\gamma }_{tr}\left(G{\circ }_{v}H\right)\le {\gamma }_{tr}\left(G\right)+n({\gamma }_{tr}\left(H\right)-1)$.

Case 3.

${\mathcal{B}}_f=\varnothing$ and ${\mathcal{C}}_f\ne \varnothing$. From Lemma 1 we deduce that ${\mathcal{A}}_f$ is a dominating set of G. Therefore, ${\gamma }_{tr}\left(G{\circ }_{v}H\right)\ge 2\left|{\mathcal{A}}_f\right|+n({\gamma }_{tr}\left(H\right)-2)\ge 2\gamma \left(G\right)+n({\gamma }_{tr}\left(H\right)-2)$.

On the other hand, by Proposition 3, ${\gamma }_{tr}(H-\left\{v\right\})={\gamma }_{tr}\left(H\right)-2$, and by Proposition 4 we conclude that ${\gamma }_{tr}\left(G{\circ }_{v}H\right)\le {\gamma }_{tr}\left(G\right)+n({\gamma }_{tr}\left(H\right)-2)$.

Case 4.

${\mathcal{C}}_f\ne \varnothing$. By Propositions 3 and 4 we conclude that ${\gamma }_{tr}\left(G{\circ }_{v}H\right)\le {\gamma }_{tr}\left(G\right)+n({\gamma }_{tr}\left(H\right)-2)$.

In order to conclude the proof of (iv), let us define a function g on G as follows. If $x\in {\mathcal{A}}_f$ then we set $g\left(x\right)=1$ and choose one vertex $u\in N\left(x\right)\cap V\left(G\right)$ and label it as $g\left(u\right)=1$. For the another vertices not previously labelled, if $x\in {\mathcal{B}}_f$ then we set $g\left(x\right)=1$, and if $x\in {\mathcal{C}}_f$ then we set $g\left(x\right)=0$. We will prove that g is a TDF on G. Notice that by construction of g, if $x\in {\mathcal{A}}_f$ then x is dominated by some vertex $y\in V\left(G\right)$ such that $g\left(y\right)=1$. Now, by Lemma 1, if $x\in C_f$ then x is totally protected under f by a vertex $w\in V\left(G\right)$. Furthermore, since $f\left(w\right)>0$, we have that $g\left(w\right)=1$, as required. If $x\in {\mathcal{B}}_f$, then it must be adjacent to some vertex $z\in V\left(G\right)$ such that $f\left(z\right)>0$, otherwise $f_x$ is a TWRDF on $H_x$ and $\omega \left(f_x\right)={\gamma }_{tr}\left(H\right)-1$, which is a contradiction. Hence, $g\left(z\right)=1$, as required. Therefore, g is a TDF on G and, as a consequence,

$$\begin{array}{cc}\hfill {\gamma }_{tr}\left(G{\circ }_{v}H\right)& =\sum _{x\in V\left(G\right)}\omega \left(f_x\right)\hfill \\ & =\sum _{x\in {\mathcal{A}}_f}\omega \left(f_x\right)+\sum _{x\in {\mathcal{B}}_f}\omega \left(f_x\right)+\sum _{x\in {\mathcal{C}}_f}\omega \left(f_x\right)\hfill \\ & \ge \sum _{x\in {\mathcal{A}}_f}({\gamma }_{tr}\left(H\right)-2+g\left(x\right))+\sum _{x\in {\mathcal{B}}_f}({\gamma }_{tr}\left(H\right)-2+g\left(x\right))+\sum _{x\in {\mathcal{C}}_f}({\gamma }_{tr}\left(H\right)-2+g\left(x\right))\hfill \\ & \ge \sum _{x\in V\left(G\right)}g\left(x\right)+\sum _{x\in V\left(G\right)}({\gamma }_{tr}\left(H\right)-2)\hfill \\ & =\omega \left(g\right)+n({\gamma }_{tr}\left(H\right)-2)\hfill \\ & \ge {\gamma }_t\left(G\right)+n({\gamma }_{tr}\left(H\right)-2).\hfill \end{array}$$

Therefore, (iv) follows. □

We now consider some particular cases in which we impose some additional restrictions on G and H. To begin with, we consider the case in which v is a support vertex of H.

Theorem 25.

Let G and H be two graphs with no isolated vertex. If G has order n and $v\in S\left(H\right)$, then

$${\gamma }_{tr}\left(G{\circ }_{v}H\right)\in \{n({\gamma }_{tr}\left(H\right)-1),n{\gamma }_{tr}\left(H\right)\}.$$

Furthermore, if $v\in S\left(H\right)\cap N\left(S\right(H\left)\right)$, then

$${\gamma }_{tr}\left(G{\circ }_{v}H\right)=n{\gamma }_{tr}\left(H\right).$$

Proof. 

Let f be a ${\gamma }_{tr}\left(G{\circ }_{v}H\right)$-function and $x\in V\left(G\right)$. Since $x\in S\left(G{\circ }_{v}H\right)$, we have that $f\left(x\right)>0$, so that Lemma 1 leads to ${\mathcal{C}}_f=\varnothing$, and, again by Lemma 1, $\omega \left(f_x\right)\ge {\gamma }_{tr}\left(H\right)-1$. Hence, ${\gamma }_{tr}\left(G{\circ }_{v}H\right)\ge n({\gamma }_{tr}\left(H\right)-1).$

If ${\mathcal{B}}_f=\varnothing$, then by Case 1 of the proof of Theorem 24, ${\gamma }_{tr}\left(G{\circ }_{v}H\right)=n{\gamma }_{tr}\left(H\right)$. Now, suppose that $x\in {\mathcal{B}}_f$. From f, we define a function h on $G{\circ }_{v}H$ as follows. For every $z\in V\left(G\right)$, the restriction of h to $V\left(H_z\right)$ is induced from $f_x$. It is readily seen that h is a TWRDF on $G{\circ }_{v}H$ of weight $n({\gamma }_{tr}\left(H\right)-1)$, which implies that ${\gamma }_{tr}\left(G{\circ }_{v}H\right)=n({\gamma }_{tr}\left(H\right)-1).$

From now on, suppose that $v\in S\left(H\right)\cap N\left(S\right(H\left)\right)$ and let $u\in N\left(x\right)\cap S\left(H_x\right)$ for some $x\in V\left(G\right)$. To conclude the proof we only need to show that ${\gamma }_{tr}\left(G{\circ }_{v}H\right)\ge n{\gamma }_{tr}\left(H\right)$. We can assume that $f(V_0,V_1,V_2)$ is a ${\gamma }_{tr}\left(G{\circ }_{v}H\right)$-function satisfying that $|V_2|$ is maximum. As x and u are adjacent, and hey are support vertices, $f\left(x\right)=f\left(u\right)=2$, so that $f_x$ is a TWRDF on $H_x$ and, as a consequence, $\omega \left(f_x\right)\ge {\gamma }_{tr}\left(H\right)$. Therefore, ${\gamma }_{tr}\left(G{\circ }_{v}H\right)\ge n{\gamma }_{tr}\left(H\right)$, as required. □

We now proceed to discuss some cases in which v is not a support vertex of H.

Theorem 26.

If ${\gamma }_{tr}(H-\left\{v\right\})={\gamma }_{tr}\left(H\right)-2$ and ${\gamma }_{tr}\left(G\right)={\gamma }_t\left(G\right)$, then

$${\gamma }_{tr}\left(G{\circ }_{v}H\right)=2+n({\gamma }_{tr}\left(H\right)-2).$$

Proof. 

By Theorem 24, we have that ${\gamma }_{tr}\left(G{\circ }_{v}H\right)\ge {\gamma }_t\left(G\right)+n({\gamma }_{tr}\left(H\right)-2)$. Now, if ${\gamma }_{tr}\left(G\right)={\gamma }_t\left(G\right)$, then Theorem 20 leads to ${\gamma }_{tr}\left(G\right)=2$, and so ${\gamma }_{tr}\left(G{\circ }_{v}H\right)\ge 2+n({\gamma }_{tr}\left(H\right)-2)$.

On the other hand, if ${\gamma }_{tr}(H-\left\{v\right\})={\gamma }_{tr}\left(H\right)-2$, then from Proposition 4 we conclude that ${\gamma }_{tr}\left(G{\circ }_{v}H\right)\le 2+n({\gamma }_{tr}\left(H\right)-2)$. □

Notice that in Theorem 26 we have the hypothesis ${\gamma }_{tr}(H-\left\{v\right\})={\gamma }_{tr}\left(H\right)-2$ and the conclusion ${\gamma }_{tr}\left(G{\circ }_{v}H\right)={\gamma }_{tr}\left(G\right)+n({\gamma }_{tr}\left(H\right)-2).$ On the other hand, we would emphasize that in all the examples in which we have observed that the left hand side inequalities of Theorem 24 (iii) or (iv) are achieved, we have that ${\gamma }_{tr}\left(G\right)=2\gamma \left(G\right)$ or ${\gamma }_{tr}\left(G\right)={\gamma }_t\left(G\right)$, respectively. Hence, in these cases, ${\gamma }_{tr}\left(G{\circ }_{v}H\right)={\gamma }_{tr}\left(G\right)+n({\gamma }_{tr}\left(H\right)-2).$ After numerous attempts, we have not been able to prove the following conjecture.

Conjecture. 

Let G and H be two graphs with no isolated vertex. For any $v\in V\left(H\right)$,

$${\gamma }_{tr}\left(G{\circ }_{v}H\right)\ge {\gamma }_{tr}\left(G\right)+n({\gamma }_{tr}\left(H\right)-2),$$

where n is the order of G. Furthermore, ${\gamma }_{tr}\left(G{\circ }_{v}H\right)={\gamma }_{tr}\left(G\right)+n({\gamma }_{tr}\left(H\right)-2)$ if and only if ${\gamma }_{tr}(H-\left\{v\right\})={\gamma }_{tr}\left(H\right)-2$.

In order to study the computational complexity of the problem of computing the total weak Roman domination number of a graph, we need to state the following result.

Theorem 27.

Let G and H be two graphs with no isolated vertex. Let n be the order of G and $v,u\in V\left(H\right)$ such that $u\in L\left(H\right)\backslash \left\{v\right\}$ and $N\left(v\right)\cap N\left(u\right)\ne \varnothing$. If ${\gamma }_{tr}(H-\left\{v\right\})={\gamma }_{tr}\left(H\right)-1$, then

$${\gamma }_{tr}\left(G{\circ }_{v}H\right)=\gamma \left(G\right)+n({\gamma }_{tr}\left(H\right)-1),$$

otherwise

$${\gamma }_{tr}\left(G{\circ }_{v}H\right)=n{\gamma }_{tr}\left(H\right).$$

Proof. 

If $v\in S\left(H\right)$, then Theorem 25 leads to ${\gamma }_{tr}\left(G{\circ }_{v}H\right)=n{\gamma }_{tr}\left(H\right).$ Hence, from now on we assume that $v\notin S\left(H\right)$. Let $y\in N\left(v\right)\cap N\left(u\right)$. Since u is a leaf in $H-\left\{v\right\}$ and y its support vertex, for any ${\gamma }_{tr}(H-\left\{v\right\})$-function g we have that $g\left(y\right)>0$. Hence, if ${\gamma }_{tr}(H-\left\{v\right\})={\gamma }_{tr}\left(H\right)-2$, then from any ${\gamma }_{tr}(H-\left\{v\right\})$-function we can construct a TWRDF on H of weight at most ${\gamma }_{tr}\left(H\right)-1$ by assigning weight 1 to v, which is a contradiction. Hence, ${\gamma }_{tr}(H-\left\{v\right\})\ge {\gamma }_{tr}\left(H\right)-1$.

Let $f(V_0,V_1,V_2)$ be a ${\gamma }_{tr}\left(G{\circ }_{v}H\right)$-function and consider the partition $\{{\mathcal{A}}_f,{\mathcal{B}}_f,{\mathcal{C}}_f\}$ of $V\left(G\right)$ defined previously. Notice that, for any $x\in V\left(G\right)$ there exist $u_x\in L\left(H_x\right)\backslash \left\{x\right\}$ and $y_x\in N\left(x\right)\cap N\left(u_x\right)$. With these tools in mind, we now proceed to study the structure of ${\mathcal{A}}_f,$ ${\mathcal{B}}_f$ and ${\mathcal{C}}_f$. Since $u_x$ is a leaf of $G{\circ }_{v}H$ and $y_x$ its support vertex, we have that $f\left(y_x\right)>0$, and since $y_x\in N\left(x\right)$, Lemma 1 leads to ${\mathcal{C}}_f=\varnothing$. We now differentiate two cases.

Case 1.

${\gamma }_{tr}(H-\left\{v\right\})={\gamma }_{tr}\left(H\right)-1$. Suppose that there exists $x\in {\mathcal{B}}_f$ with $f\left(x\right)>0$. Since $y_x$ is a support vertex, either $f\left(y_x\right)=2$ or $f\left(y_x\right)=1$ and no vertex in $V\left(H_x\right)$ is totally protected by $y_x$ under f. In any case, we can conclude that $f_x$ is a TWRDF on $H_x$ of weight $\omega \left(f_x\right)={\gamma }_{tr}\left(H\right)-1$, which is a contradiction. Hence, ${\mathcal{B}}_f\subseteq V_0$.

Now, since $(V_1\cup V_2)\cap V\left(G\right)\subseteq {\mathcal{A}}_f$, if there exists $x\in {\mathcal{B}}_f$ such that $N\left(x\right)\cap {\mathcal{A}}_f=\varnothing$, then $f_x$ must be a TWRDF on $H_x$, which is a contradiction, as $\omega \left(f_x\right)={\gamma }_{tr}\left(H\right)-1$. Thus, ${\mathcal{A}}_f$ is a dominating set and so,

$$\begin{array}{cc}\hfill {\gamma }_{tr}\left(G{\circ }_{v}H\right)=& \sum _{x\in {\mathcal{A}}_f\cup {\mathcal{B}}_f}\omega \left(f_x\right)\hfill \\ & \ge |{\mathcal{A}}_f|{\gamma }_{tr}\left(H\right)+\left|{\mathcal{B}}_f\right|({\gamma }_{tr}\left(H\right)-1)\hfill \\ & =|{\mathcal{A}}_f|+n({\gamma }_{tr}\left(H\right)-1)\hfill \\ & \ge \gamma \left(G\right)+n({\gamma }_{tr}\left(H\right)-1).\hfill \end{array}$$

On the other hand, since v is adjacent to a support vertex, from any ${\gamma }_{tr}(H-\left\{v\right\})$-function and any $\gamma \left(G\right)$-function we can construct a TWRDF on $G{\circ }_{v}H$ of weight $\gamma \left(G\right)+n({\gamma }_{tr}\left(H\right)-1)$. Therefore, ${\gamma }_{tr}\left(G{\circ }_{v}H\right)=\gamma \left(G\right)+n({\gamma }_{tr}\left(H\right)-1)$.

Case 2.

${\gamma }_{tr}(H-\left\{v\right\})\ge {\gamma }_{tr}\left(H\right)$. If there exists $x\in {\mathcal{B}}_f$ with $f\left(x\right)>0$, then $f_x$ is a TWRDF on $H_x$ of weight $\omega \left(f_x\right)={\gamma }_{tr}\left(H\right)-1$, which is a contradiction. Now, if $x\in {\mathcal{B}}_f$ and $f\left(x\right)=0$, then $f_x^{-}$ is a TWRDF on $H_x-\left\{x\right\}$ of weight $\omega \left(f_x^{-}\right)={\gamma }_{tr}\left(H\right)-1$, which is a contradiction again. Hence, $x\in {\mathcal{A}}_f$, and so ${\gamma }_{tr}\left(G{\circ }_{v}H\right)\ge n{\gamma }_{tr}\left(H\right).$ Therefore, by Theorem 24 we conclude that ${\gamma }_{tr}\left(G{\circ }_{v}H\right)=n{\gamma }_{tr}\left(H\right).$ □

Recent works have shown that graph operations are useful tools to study problems of computational complexity.

For instance, the authors of [18,19] have shown that results on the (local) metric dimension of corona product graphs enables us to deduce NP-hardness results for the (local) adjacency dimension; while the authors of [20] have shown that the study of lexicographic product graphs is useful to infer an NP-hardness result for the super domination number, based on a well-known result for the independence number. Our next result shows that we can use rooted product graphs to study the problem of finding the total weak Roman domination number of a graph. In this case, the key result is Theorem 27 which involves the domination number. It is well known that the dominating set problem is an NP-complete decision problem [21], i.e., given a positive integer k and a graph G, the problem of deciding if G has a dominating set D of cardinality $\left|D\right|\le k$ is NP-complete. Hence, the optimization problem of computing the domination number of a graph is NP-hard.

Corollary 8.

The problem of computing the total weak Roman domination number of a graph is NP-hard.

Proof. 

Let G be a graph with no isolated vertex and construct the graph $G{\circ }_v{P}_3$, where v is a leaf of $P_3$. By Theorem 27, it follows that ${\gamma }_{tr}\left(G{\circ }_v{P}_3\right)=\gamma \left(G\right)+2\left|V\left(G\right)\right|$. Therefore, the problem of computing the total weak Roman domination has the same computational complexity as the domination number problem. □

Theorem 28.

Let G and H be two graphs with no isolated vertex and $\left|V\right(G\left)\right|=n$. Then the following statements hold for every $v\in V\left(H\right)$ such that ${\gamma }_{tr}(H-\left\{v\right\})\ne {\gamma }_{tr}\left(H\right)-1$.

(i)

If $g\left(v\right)=0$ for every ${\gamma }_{tr}\left(H\right)$-function g, then ${\gamma }_{tr}\left(G{\circ }_{v}H\right)=n{\gamma }_{tr}\left(H\right)$.

(ii)

If $g\left(v\right)>0$ for every ${\gamma }_{tr}\left(H\right)$-function g, then ${\gamma }_{tr}\left(G{\circ }_{v}H\right)\in \{n{\gamma }_{tr}\left(H\right),n({\gamma }_{tr}\left(H\right)-1)\}$.

Proof. 

Let $f(V_0,V_1,V_2)$ be a ${\gamma }_{tr}\left(G{\circ }_{v}H\right)$-function and consider the partition $\{{\mathcal{A}}_f,{\mathcal{B}}_f,{\mathcal{C}}_f\}$ of $V\left(G\right)$ previously defined.

With the assumptions of (i) or (ii), Lemma 2 and Proposition 3 lead to ${\mathcal{C}}_f=\varnothing$. Moreover, if ${\mathcal{B}}_f=\varnothing$, then by analogy to Case 1 in the proof of Theorem 24 we deduce that ${\gamma }_{tr}\left(G{\circ }_{v}H\right)=n{\gamma }_{tr}\left(H\right)$. From now on suppose that $x\in {\mathcal{B}}_f$. If $f\left(x\right)=0$, then $f_x^{-}$ is a TWRDF on $H_x-\left\{x\right\}$, so that ${\gamma }_{tr}(H-\left\{v\right\})={\gamma }_{tr}(H_x-\left\{x\right\})\le \omega \left(f_x^{-}\right)=\omega \left(f_x\right)={\gamma }_{tr}\left(H\right)-1$. From the hypothesis of (i) and (ii) and Lemma 2 we deduce that ${\gamma }_{tr}(H-\left\{v\right\})={\gamma }_{tr}\left(H\right)-1$. Thus, if ${\gamma }_{tr}(H-\left\{v\right\})\ne {\gamma }_{tr}\left(H\right)-1$, then $f\left(x\right)>0$.

We now assume the hypothesis of (i) and take a vertex $u\in N\left(x\right)\cap V\left(H_x\right)$. If $f\left(u\right)=2$, then $f_x$ is a TWRDF on $H_x$ of weight $\omega \left(f_x\right)={\gamma }_{tr}\left(H\right)-1$, which is a contradiction. Hence, $f\left(u\right)\le 1$ and we can define a function g as $g\left(u\right)=f\left(u\right)+1$ and $g\left(w\right)=f\left(w\right)$ for every $w\in V\left(H_x\right)\backslash \left\{u\right\}$. Notice that g is a TWRDF on $H_x$ of weight ${\gamma }_{tr}\left(H\right)$, so g is a ${\gamma }_{tr}\left(H\right)$-function and satisfies that $g\left(v\right)>0$, which is a contradiction. Hence, ${\mathcal{B}}_f=\varnothing$ and we are done.

We now assume the hypothesis of (ii). By analogy to Case 2 in the proof of Theorem 24 we deduce that ${\gamma }_{tr}\left(G{\circ }_{v}H\right)\ge n({\gamma }_{tr}\left(H\right)-1)$. Now, we proceed to show that ${\gamma }_{tr}\left(G{\circ }_{v}H\right)\le n({\gamma }_{tr}\left(H\right)-1)$. From f, we define a function h on $G{\circ }_{v}H$ as follows. For every $z\in V\left(G\right)$, the restriction of h to $V\left(H_z\right)$ is induced from $f_x$. It is readily seen that h is a TWRDF on $G{\circ }_{v}H$ of weight $n({\gamma }_{tr}\left(H\right)-1)$, which completes the proof. □

As a particular case of Theorem 28 (i) we have the following result.

Corollary 9.

Let G and H be two graphs with no isolated vertex. Let n be the order of G, $v\in L\left(H\right)$ and $u,u^{\prime }\in S\left(H\right)$. If $u^{\prime },v\in N\left(u\right)$ and $\left|N\right(u)\cap L(H\left)\right|\ge 3$, then ${\gamma }_{tr}\left(G{\circ }_{v}H\right)=n{\gamma }_{tr}\left(H\right)$.

Theorem 29.

If G is a graph of order n with $\delta \left(G\right)\ge 1$, then for every graph H having a universal vertex $v\in V\left(H\right)$,

$${\gamma }_{tr}\left(G{\circ }_{v}H\right)=2n.$$

Proof. 

The upper bound ${\gamma }_{tr}\left(G{\circ }_{v}H\right)\le 2n$ is straightforward, as the function f, defined by $f\left(x\right)=2$ for every vertex $x\in V\left(G\right)$ and $f\left(x\right)=0$ for every $x\in V\left(G{\circ }_{v}H\right)\backslash V\left(G\right)$, is a TWRDF on $G{\circ }_{v}H$.

On the other hand, let f be a ${\gamma }_{tr}\left(G{\circ }_{v}H\right)$-function and suppose that there exists $x\in V\left(G\right)$ such that $\omega \left(f_x\right)\le 1$. In such a case, $f\left(N\right[y\left]\right)\le 1$ for every $y\in V\left(H_x\right)\backslash \left\{x\right\}$, which is a contradiction. Therefore ${\gamma }_{tr}\left(G{\circ }_{v}H\right)=\omega \left(f\right)\ge 2n$. □

Since any corona graph $G\odot G^{\prime }$ is a rooted product graph $G{\circ }_{v}H$ where $H\cong K_1+G^{\prime }$ and v is the vertex of $K_1$, the result above is equivalent to the following theorem.

Theorem 30.

If G is a graph of order n with no isolated vertex, then for every graph $G^{\prime }$,

$${\gamma }_{tr}(G\odot G^{\prime })=2n.$$

To conclude the analysis, we consider the extreme case in which ${\gamma }_{tr}\left(H\right)=2$.

Theorem 31.

If G is a graph of order n and H is a graph with ${\gamma }_{tr}\left(H\right)=2$, then for any $v\in V\left(H\right)$,

$${\gamma }_{tr}\left(G{\circ }_{v}H\right)=2n.$$

Proof. 

By Theorem 24, ${\gamma }_{tr}\left(G{\circ }_{v}H\right)\le 2n.$ Now, if ${\gamma }_{tr}\left(G{\circ }_{v}H\right)\le 2n-1$, then for any ${\gamma }_{tr}\left(G{\circ }_{v}H\right)$-function f, there exists $x\in V\left(G\right)$ such that $\omega \left(f_x\right)\le 1$. Hence, $f\left(N\right[y\left]\right)\le 1$ for every $y\in V\left(H_x\right)\backslash \left\{x\right\}$, which is a contradiction. □

6. Conclusions and Open Problems

This article is a contribution to the theory of total protection of graphs. In particular, we introduced the study of the total weak Roman domination number of a graph. We studied the properties of this novel parameter in order to obtain its exact value or general bounds. Among the main contributions we emphasize the following.

• The work proved several new theorems, thanks to which we have shown the close relationship that exists between the total weak Roman domination number and other domination parameters such as the (total) domination number, secure (total) domination number, weak Roman domination number, (total) Roman domination number and 2-packing number.
• We obtained general bounds and discussed some extreme cases.
• In a specific section of the paper, we focused on the case of rooted product graphs and we obtained closed formulas and tight bounds for the total weak Roman domination number of these graphs.
• Through the results obtained on rooted product graphs, we have shown that the problem of finding the total weak Roman domination number of a graph is NP-hard.

Among the open problems arising from the analysis, the following should be highlighted.

(a)

We have shown that if G is a $\{K_{1,3},K_{1,3}+e\}$-free graph with no isolated vertex, then ${\gamma }_{tr}\left(G\right)={\gamma }_{st}\left(G\right)$. We conjecture that these two parameters also coincide for lexicographic product graphs, and we propose the general problem of characterizing all graphs for which the equality holds.

(b)

We have shown that ${\gamma }_{tr}\left(G\right)=\gamma \left(G\right)+1$ if and only if ${\gamma }_{st}\left(G\right)=\gamma \left(G\right)+1$. Therefore, the problem of characterizing all graphs with ${\gamma }_{st}\left(G\right)=\gamma \left(G\right)+1$ is an open problem, which is a particular case of problem (a).

(c)

We have shown that ${\gamma }_{tr}\left(G\right)\le {\gamma }_t\left(G\right)+\gamma \left(G\right)$ and ${\gamma }_{tr}\left(G\right)\le {\gamma }_r\left(G\right)+\gamma \left(G\right).$ We propose the problem of characterizing all graphs for which these equalities hold; or providing necessary or sufficient conditions for achieving them.

(d)

Since the problem of finding ${\gamma }_{tr}\left(G\right)$ is NP-hard, we consider the following question. Is there a polynomial-time algorithm for finding ${\gamma }_{tr}\left(T\right)$ for any tree T of order n?