Structural Properties of Vicsek-like Deterministic Multifractals
Abstract
1. Introduction
2. Theoretical Background
2.1. Multifractals
2.2. Small-Angle Scattering
- if the particle’s length is scaled as ,
- if the particle is translated by the vector ,
- , if the particle can be decomposed as a union of two non-overlapping subsets I and .
3. Results and Discussions
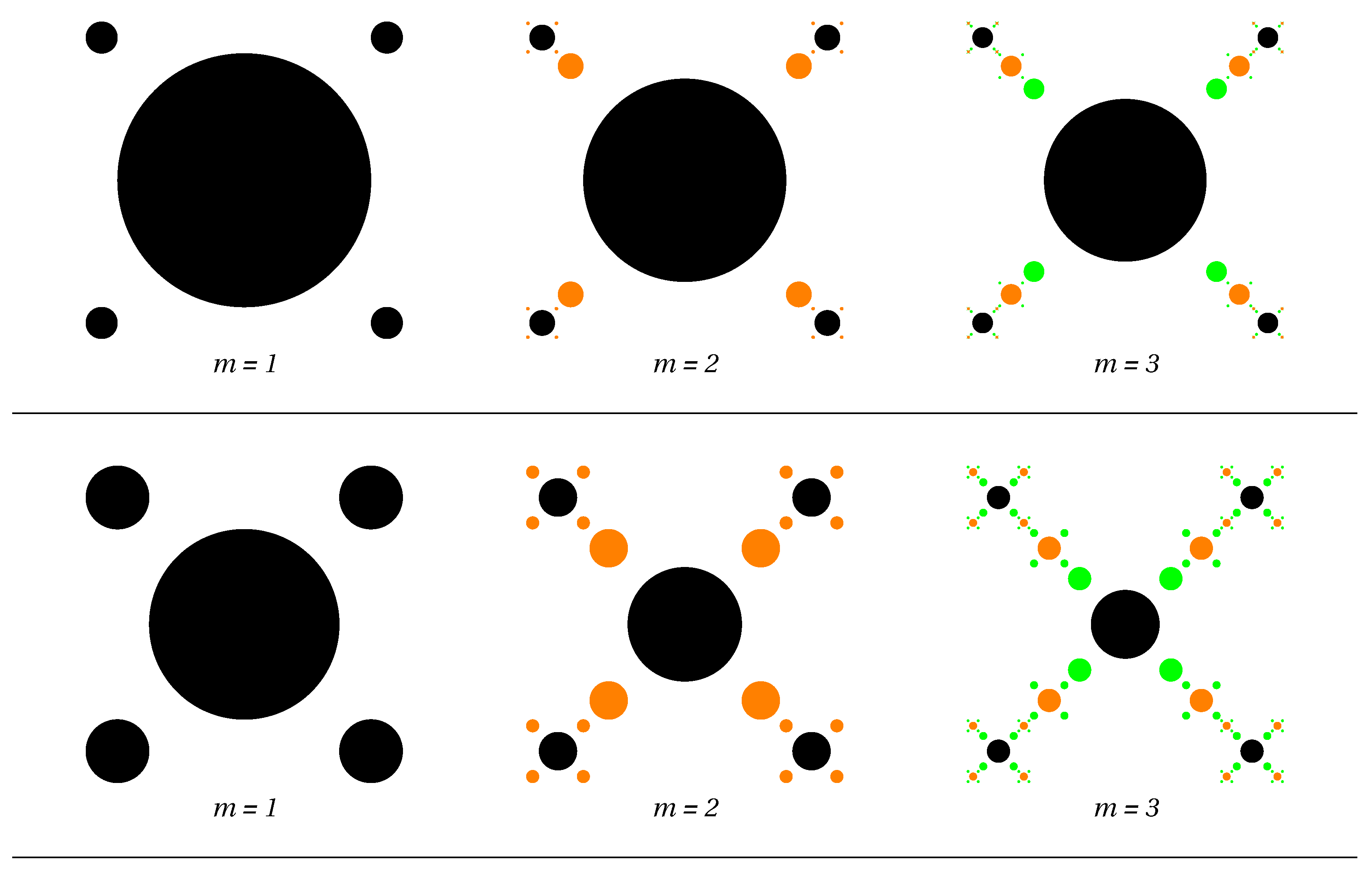
3.1. Construction of the Multifractal Model
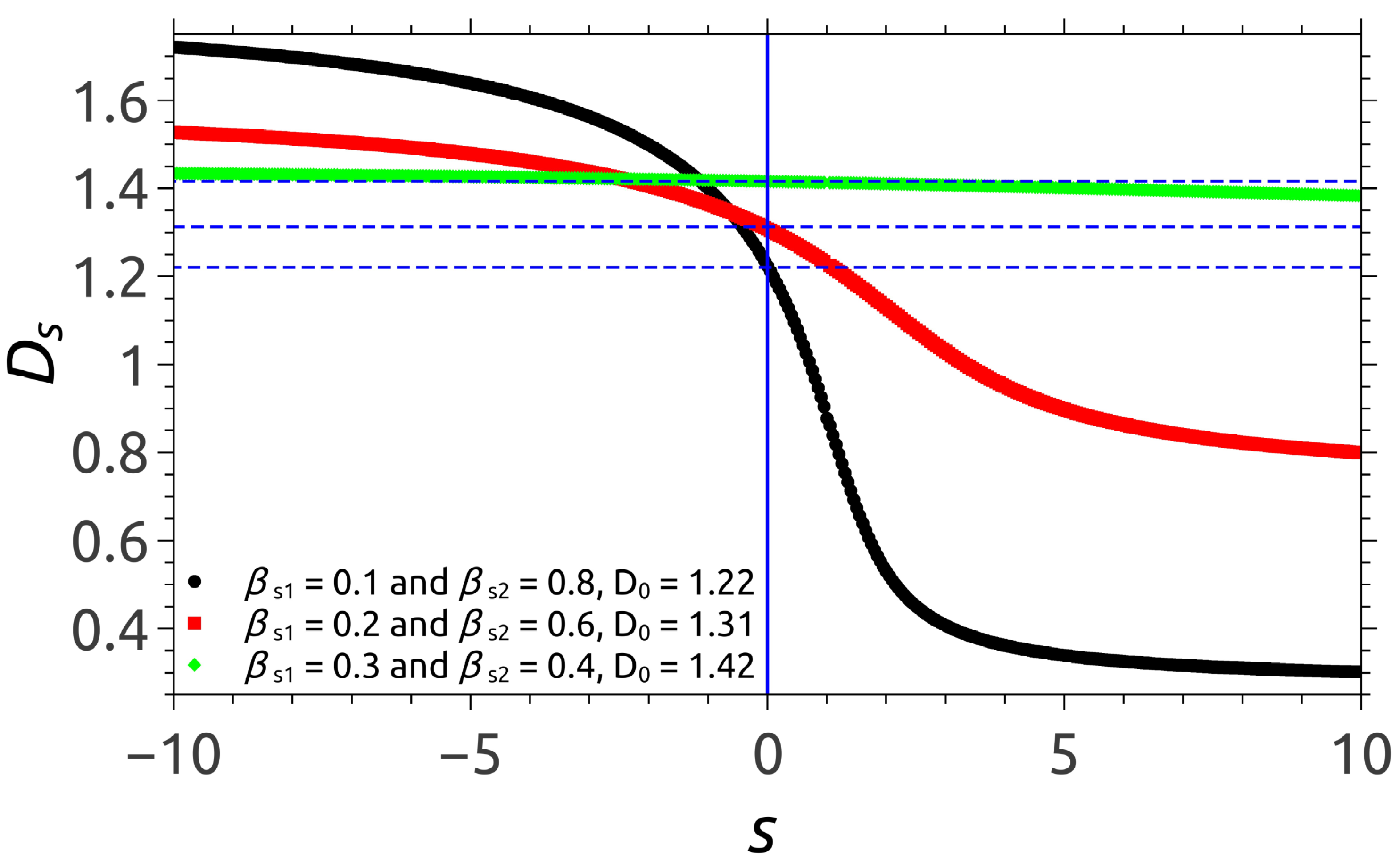
3.2. Dimension Spectra
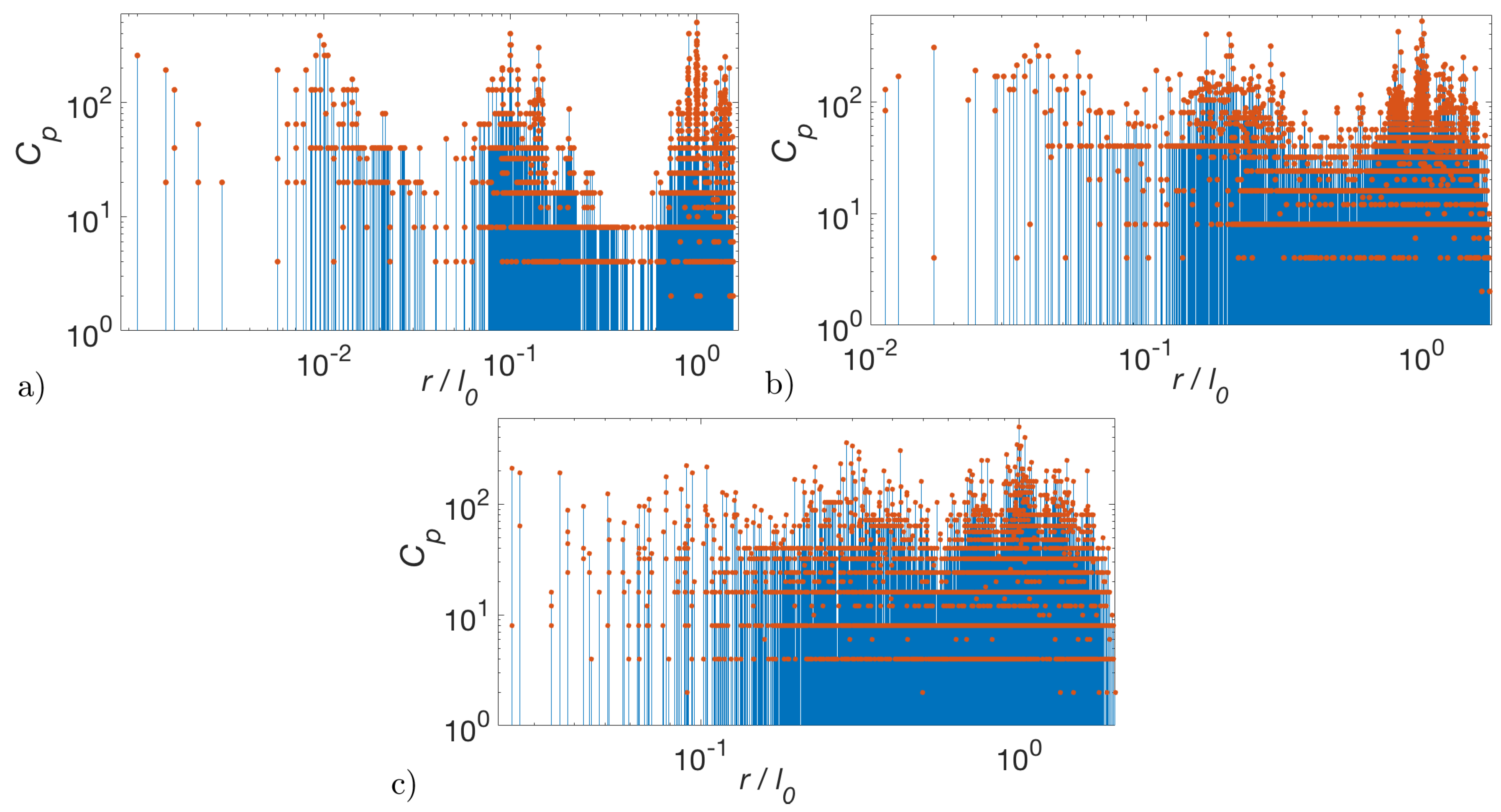
3.3. Pair Distance Distribution Function
3.4. Small-Angle Scattering Form Factor
4. Conclusions
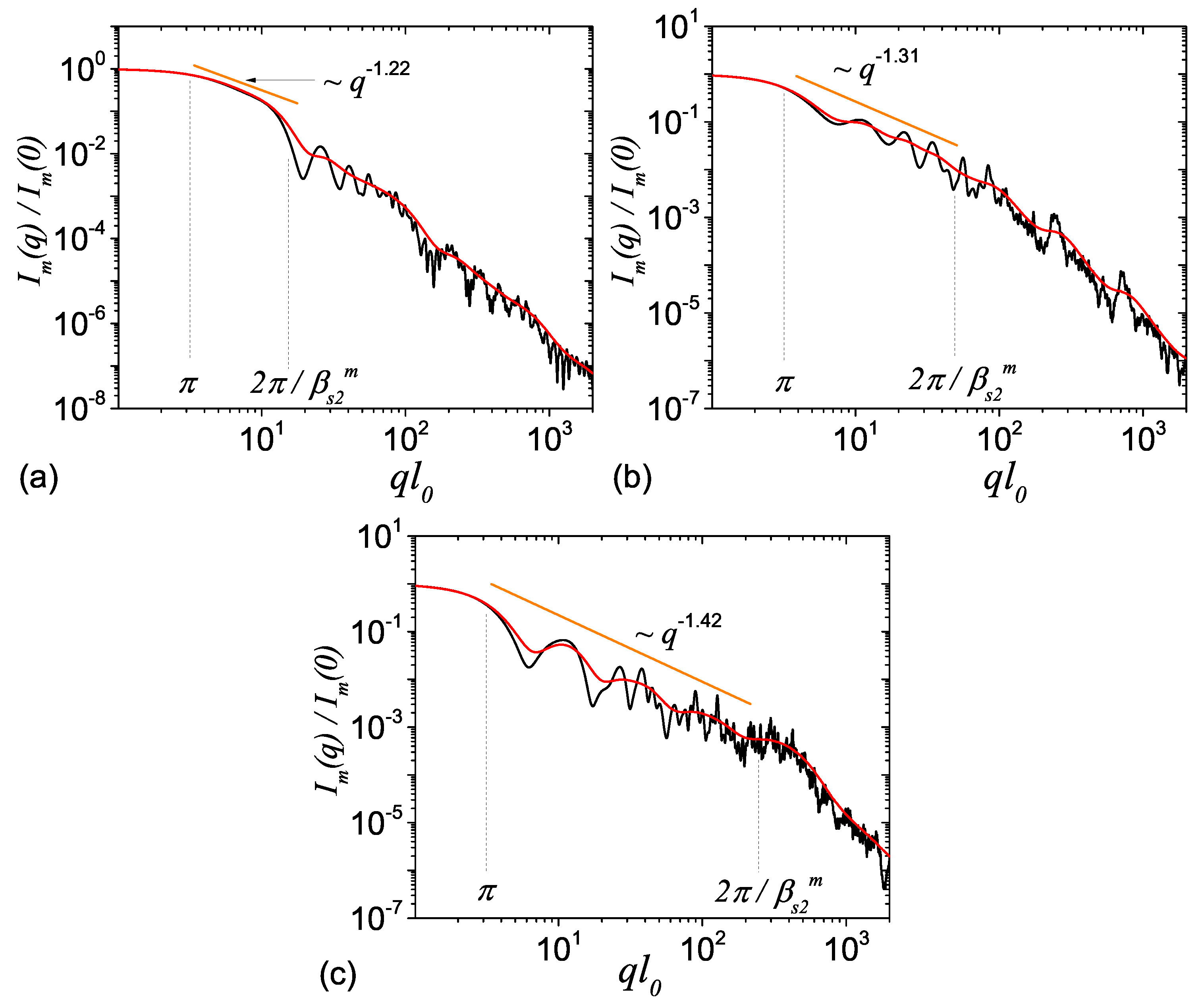
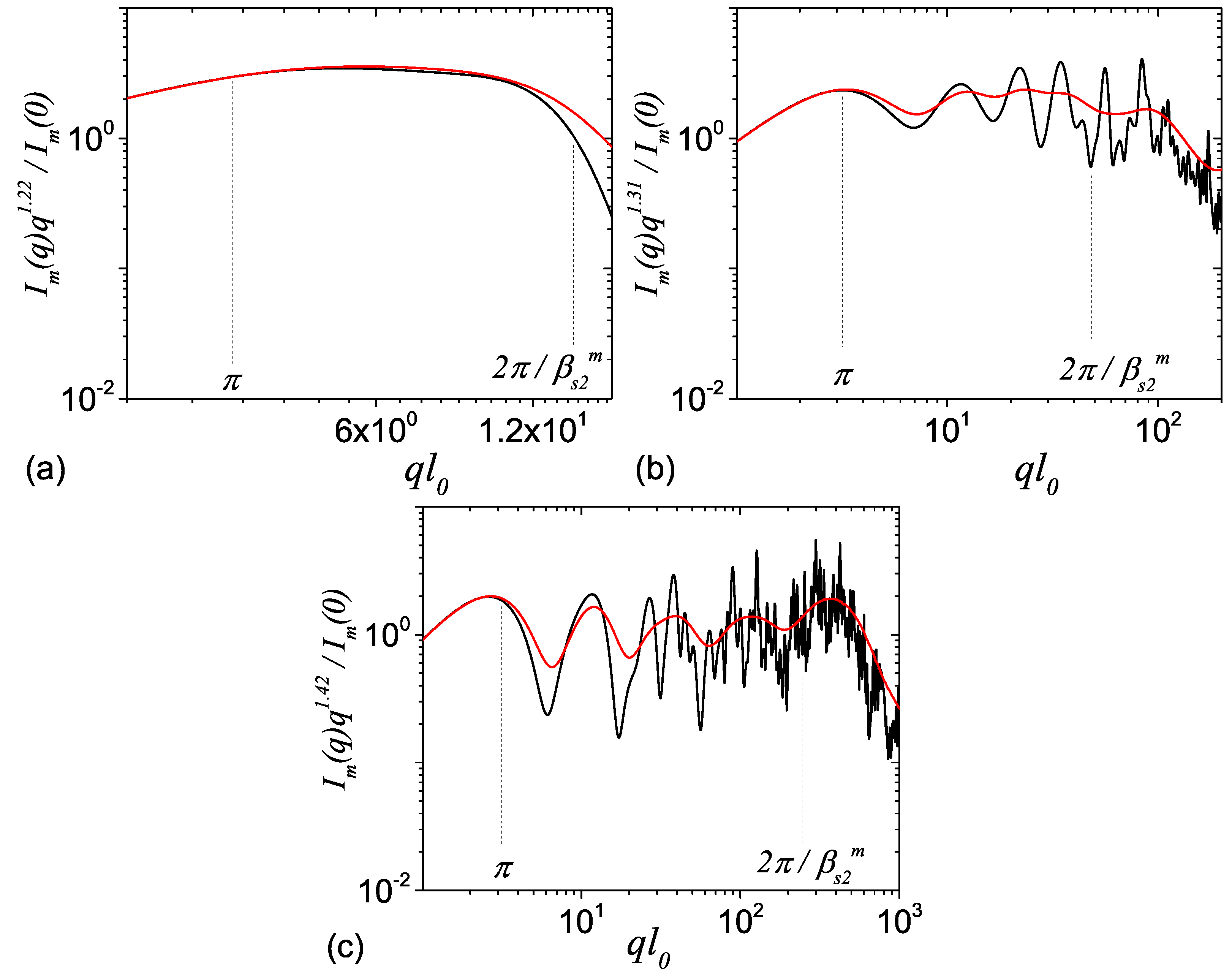
- If , the system is highly heterogeneous and structural parameters are more clearly visible in pddf (see Figure 3a), since the mass fractal region of the scattering intensity is very short Figure 4a). The scaling factor is extracted from the periodicity of large groups of distances, while can be extracted in a relatively good approximation, from the periodicity of smaller groups found inside larger ones. The number of fractal iterations coincide with the number of large distinct groups in pddf.
- If , separation of pddf in distinct groups of distance is not very clear since the values of distances arising from each of the scaling factors begin to mix with each other (see Figure 3b,c), and thus extracting exact values of the scaling factors can become a very difficult task. However, in the reciprocal space, the corresponding mass fractal region of scattering intensity is characterized by a succession of maxima and minima on a power-law decay (generalized power-law decay) and the value of the largest scaling factor can be clearly estimated from the periodicity of minima. In addition, the fractal dimension can be obtained from the scattering exponent of this power-law decay while the fractal iteration number can be obtained from the number of the minima.
- If , the system reduces to a single scale fractal. Structural properties of such systems have been studied elsewhere (see Reference [30]).
Author Contributions
Funding
Conflicts of Interest
References
- Acosta, K.L.; Wilkie, W.K.; Inman, D.J. Characterizing the pyroelectric coefficient for macro-fiber composites. Smart Mater. Struct. 2018, 27, 115001. [Google Scholar] [CrossRef]
- Bica, I.; Anitas, E.M.; Lu, Q.; Choi, H.J. Effect of magnetic field intensity and γ-Fe2O3 nanoparticle additive on electrical conductivity and viscosity of magnetorheological carbonyl iron suspension-based membranes. Smart Mater. Struct. 2018, 27, 095021. [Google Scholar] [CrossRef]
- Theerthagiri, J.; Durai, G.; Karuppasamy, K.; Arunachalam, P.; Elakkiya, V.; Kuppusami, P.; Maiyalagan, T.; Kim, H.S. Recent advances in 2-D nanostructured metal nitrides, carbides, and phosphides electrodes for electrochemical supercapacitors—A brief review. J. Ind. Eng. Chem. 2018, 67, 12–27. [Google Scholar] [CrossRef]
- Kim, K.W.; Ji, S.H.; Park, B.S.; Yun, J.S. High surface area flexible zeolite fibers based on a core-shell structure by a polymer surface wet etching process. Mater. Des. 2018, 158, 98–105. [Google Scholar] [CrossRef]
- Semitekolos, D.; Kainourgios, P.; Jones, C.; Rana, A.; Koumoulos, E.P.; Charitidis, C.A. Advanced carbon fibre composites via poly methacrylic acid surface treatment; surface analysis and mechanical properties investigation. Compos. Part B—Eng. 2018, 155, 237–243. [Google Scholar] [CrossRef]
- Anagnostou, D.; Chatzigeorgiou, G.; Chemisky, Y.; Meraghni, F. Hierarchical micromechanical modeling of the viscoelastic behavior coupled to damage in SMC and SMC-hybrid composites. Compos. Part B—Eng. 2018, 151, 8–24. [Google Scholar] [CrossRef]
- Bica, I.; Anitas, E.M. Magnetic flux density effect on electrical properties and visco-elastic state of magnetoactive tissues. Compos. Part B—Eng. 2019, 159, 13–19. [Google Scholar] [CrossRef]
- El Naschie, M.S. Nanotechnology for the developing world. Chaos Soliton Fract. 2006, 30, 769. [Google Scholar] [CrossRef]
- He, J.H.; Wan, Y.Q.; Xu, L. Nano-effects, quantum-like properties in electrospun nanofibers. Chaos Soliton Fract. 2007, 33, 26–37. [Google Scholar] [CrossRef]
- Zhang, Z.; Gao, C.; Wu, Z.; Han, W.; Wang, Y.; Fu, W.; Li, X.; Xie, E. Toward efficient photoelectrochemical water-splitting by using screw-like SnO2 nanostructures as photoanode after being decorated with CdS quantum dots. Nano Energy 2016, 19, 318–327. [Google Scholar] [CrossRef]
- Sichert, J.A.; Tong, Y.; Mutz, N.; Vollmer, M.; Fischer, S.; Milowska, K.Z.; García Cortadella, R.; Nickel, B.; Cardenas-Daw, C.; Stolarczyk, J.K.; et al. Quantum Size Effect in Organometal Halide Perovskite Nanoplatelets. Nano Lett. 2015, 15, 6521–6527. [Google Scholar] [CrossRef] [PubMed]
- Zhu, W.; Esteban, R.; Borisov, A.G.; Baumberg, J.J.; Nordlander, P.; Lezec, H.J.; Aizpurua, J.; Crozier, K.B. Quantum mechanical effects in plasmonic structures with subnanometre gaps. Nat. Commun. 2016, 7, 11495. [Google Scholar] [CrossRef] [PubMed]
- Newkome, G.R.; Wang, P.; Moorefield, C.N.; Cho, T.J.; Mohapatra, P.P.; Li, S.; Hwang, S.H.; Lukoyanova, O.; Echegoyen, L.; Palagallo, J.A.; et al. Nanoassembly of a fractal polymer: A molecular “Sierpinski hexagonal gasket”. Science 2006, 312, 1782–1785. [Google Scholar] [CrossRef] [PubMed]
- Cerofolini, G.F.; Narducci, D.; Amato, P.; Romano, E. Fractal Nanotechnology. Nanoscale Res. Lett. 2008, 3, 381–385. [Google Scholar] [CrossRef][Green Version]
- Berenschot, E.J.W.; Jansen, H.V.; Tas, N.R. Fabrication of 3D fractal structures using nanoscale anisotropic etching of single crystalline silicon. J. Micromech. Microeng. 2013, 23, 055024. [Google Scholar] [CrossRef]
- Li, C.; Zhang, X.; Li, N.; Wang, Y.; Yang, J.; Gu, G.; Zhang, Y.; Hou, S.; Peng, L.; Wu, K.; et al. Construction of Sierpiński Triangles up to the Fifth Order. J. Am. Chem. Soc. 2017, 139, 13749–13753. [Google Scholar] [CrossRef] [PubMed]
- Li, N.; Zhang, X.; Gu, G.C.; Wang, H.; Nieckarz, D.; Szabelski, P.; He, Y.; Wang, Y.; Lü, J.T.; Tang, H.; et al. Sierpiński-triangle fractal crystals with the C3v point group. Chin. Chem. Lett. 2015, 26, 1198–1202. [Google Scholar] [CrossRef]
- Zhang, X.; Li, R.; Li, N.; Gu, G.; Zhang, Y.; Hou, S.; Wang, Y. Sierpiński triangles formed by molecules with linear backbones on Au(111). Chin. Chem. Lett. 2018, 29, 967–969. [Google Scholar] [CrossRef]
- Fan, J.A.; Yeo, W.H.; Su, Y.; Hattori, Y.; Lee, W.; Jung, S.Y.; Zhang, Y.; Liu, Z.; Cheng, H.; Falgout, L.; et al. Fractal design concepts for stretchable electronics. Nat. Commun. 2014, 5, 3266. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. The Fractal Geometry of Nature; W.H. Freeman: New York, NY, USA, 1982; p. 460. [Google Scholar]
- Filoche, M.; Sapoval, B. Transfer Across Random versus Deterministic Fractal Interfaces. Phys. Rev. Lett. 2000, 84, 5776–5779. [Google Scholar] [CrossRef]
- Khoshhesab, M.M.; Li, Y. Mechanical behavior of 3D printed biomimetic Koch fractal contact and interlocking. Extrem. Mech. Lett. 2018, 24, 58–65. [Google Scholar] [CrossRef]
- Nikbakht, M. Radiative heat transfer in fractal structures. Phys. Rev. B 2017, 96, 125436. [Google Scholar] [CrossRef]
- Zhang, B.; Xiang, M.; Zhang, Q.; Zhang, Q. Preparation and characterization of bioinspired three-dimensional architecture of zirconia on ceramic surface. Compos. Part B—Eng. 2018, 155, 77–82. [Google Scholar] [CrossRef]
- Mayama, H.; Tsujii, K. Menger sponge-like fractal body created by a novel template method. J. Chem. Phys. 2006, 125, 124706. [Google Scholar] [CrossRef] [PubMed]
- Feigin, L.A.; Svergun, D.I. Structure Analysis by Small-Angle X-ray and Neutron Scattering; Springer: Boston, MA, USA, 1987; p. 335. [Google Scholar]
- Gille, W. Particle and Particle Systems Characterization: Small-Angle Scattering (SAS) Applications, 1st ed.; CRC Press: Boca Raton, FL, USA, 2013; p. 336. [Google Scholar]
- Teixeira, J. Small-angle scattering by fractal systems. J. Appl. Cryst. 1988, 21, 781–785. [Google Scholar] [CrossRef]
- Schmidt, P.W.; Dacai, X. Calculation of the small-angle x-ray and neutron scattering from nonrandom (regular) fractals. Phys. Rev. A 1986, 33, 560–566. [Google Scholar] [CrossRef]
- Cherny, A.Y.; Anitas, E.M.; Osipov, V.A.; Kuklin, A.I. Deterministic fractals: Extracting additional information from small-angle scattering data. Phys. Rev. E 2011, 84, 036203. [Google Scholar] [CrossRef] [PubMed]
- Anitas, E.M.; Slyamov, A.M. Small-angle scattering from deterministic mass and surface fractal systems. Proc. Rom. Acad. A 2018, 19, 353–360. [Google Scholar]
- Cherny, A.Y.; Anitas, E.M.; Osipov, V.A.; Kuklin, A.I. The structure of deterministic mass and surface fractals: Theory and methods of analyzing small-angle scattering data. Phys. Chem. Chem. Phys. 2019. [Google Scholar] [CrossRef]
- Anitas, E.M.; Slyamov, A.; Todoran, R.; Szakacs, Z. Small-Angle Scattering from Nanoscale Fat Fractals. Nanoscale Res. Lett. 2017, 12, 389. [Google Scholar] [CrossRef]
- Anitas, E.M.; Slyamov, A. Structural characterization of chaos game fractals using small-angle scattering analysis. PLoS ONE 2017, 12, e0181385. [Google Scholar] [CrossRef] [PubMed]
- Vicsek, T. Fractal Growth Phenomena, 2nd ed.; World Scientific: Singapore, 1992; p. 528. [Google Scholar]
- Gouyet, J.F. Physics and Fractal Structures; Elsevier: Masson, UK, 1996; p. 234. [Google Scholar]
- Arneodo, A.; Decoster, N.; Roux, S. A wavelet-based method for multifractal image analysis. I. Methodology and test applications on isotropic and anisotropic random rough surfaces. Eur. Phys. J. B 2000, 15, 567–600. [Google Scholar] [CrossRef]
- Decoster, N.; Roux, S.; Arnéodo, A. A wavelet-based method for multifractal image analysis. II. Applications to synthetic multifractal rough surfaces. Eur. Phys. J. B 2000, 15, 739–764. [Google Scholar] [CrossRef]
- Chhabra, A.; Jensen, R.V. Direct Determination of the f (alpha) Singularity Spectrum. Phys. Rev. Lett. 1989, 62, 1327. [Google Scholar] [CrossRef] [PubMed]
- Kantelhardt, J.W.; Zschiegner, S.A.; Koscielny-Bunde, E.; Havlin, S.; Bunde, A.; Stanley, H. Multifractal detrended fluctuation analysis of nonstationary time series. Phys. A 2002, 316, 87–114. [Google Scholar] [CrossRef]
- Muzy, J.F.; Bacry, E.; Arneodo, A. Multifractal formalism for fractal signals: The structure-function approach versus the wavelet-transform modulus-maxima method. Phys. Rev. E 1993, 47, 875–884. [Google Scholar] [CrossRef]
- Stuhrmann, H.B. Small-angle scattering and its interplay with crystallography, contrast variation in SAXS and SANS. Acta Cryst. 2008, 64, 181–191. [Google Scholar] [CrossRef]
- Izumi, A.; Shudo, Y.; Nakao, T.; Shibayama, M. Cross-link inhomogeneity in phenolic resins at the initial stage of curing studied by 1H-pulse NMR spectroscopy and complementary SAXS/WAXS and SANS/WANS with a solvent-swelling technique. Polymer 2016, 103, 152–162. [Google Scholar] [CrossRef]
- Dierolf, M.; Menzel, A.; Thibault, P.; Schneider, P.; Kewish, C.M.; Wepf, R.; Bunk, O.; Pfeiffer, F. Ptychographic X-ray computed tomography at the nanoscale. Nature 2010, 467, 436–439. [Google Scholar] [CrossRef]
- Martin, J.E.; Hurd, A.J. Scattering from fractals. J. Appl. Cryst. 1987, 20, 61–78. [Google Scholar] [CrossRef]
- Schmidt, P.W. Small-angle scattering studies of disordered, porous and fractal systems. J. Appl. Cryst. 1991, 24, 414–435. [Google Scholar] [CrossRef]
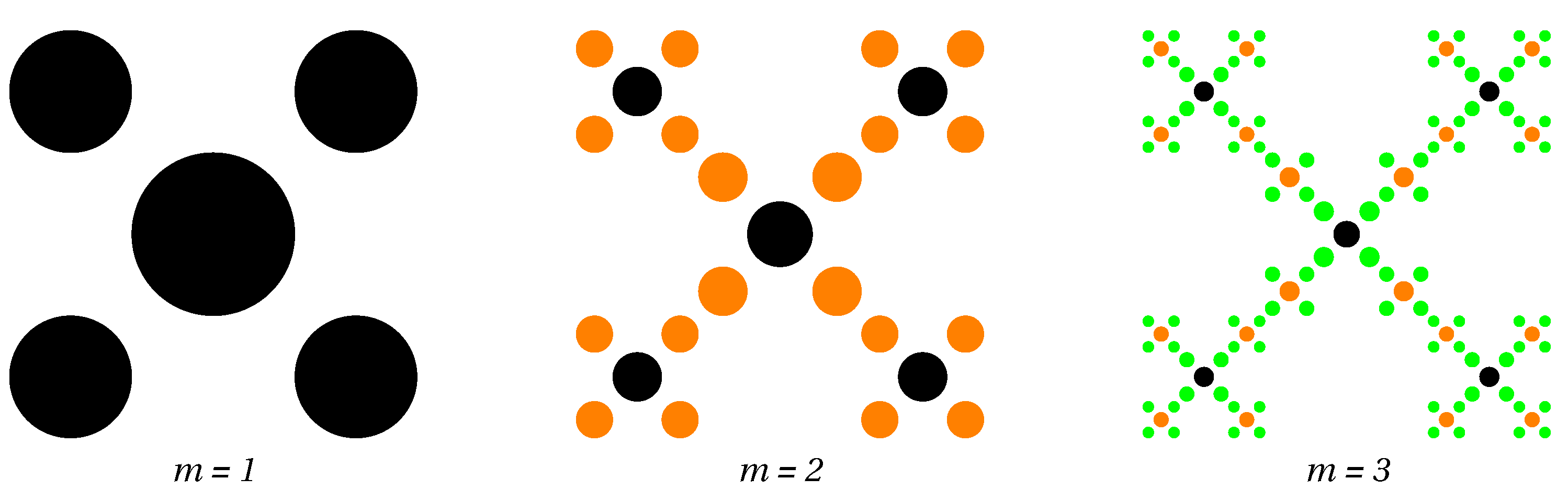
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anitas, E.M.; Marcelli, G.; Szakacs, Z.; Todoran, R.; Todoran, D. Structural Properties of Vicsek-like Deterministic Multifractals. Symmetry 2019, 11, 806. https://doi.org/10.3390/sym11060806
Anitas EM, Marcelli G, Szakacs Z, Todoran R, Todoran D. Structural Properties of Vicsek-like Deterministic Multifractals. Symmetry. 2019; 11(6):806. https://doi.org/10.3390/sym11060806
Chicago/Turabian StyleAnitas, Eugen Mircea, Giorgia Marcelli, Zsolt Szakacs, Radu Todoran, and Daniela Todoran. 2019. "Structural Properties of Vicsek-like Deterministic Multifractals" Symmetry 11, no. 6: 806. https://doi.org/10.3390/sym11060806
APA StyleAnitas, E. M., Marcelli, G., Szakacs, Z., Todoran, R., & Todoran, D. (2019). Structural Properties of Vicsek-like Deterministic Multifractals. Symmetry, 11(6), 806. https://doi.org/10.3390/sym11060806




